A一元二次方程的解法复习课件97

2x
-y
5y
请用四种方法解下列方程:
2 4(x＋1)
=
2 (2x－5)
先考虑开平方法, 再用因式分解法; 最后才用公式法和配方法;
1.关于y的一元二次方程2y(y-3)= 2 -4的一般形式是___________, 2y -6y+4=0 它 的二次项系数是_____, 2 一次项是 -6y 常数项是_____ _____, 4
a
b
这个方法也称为十字相乘法
5 十字相乘法
例1把下列式子分解因式
⑵ y2- 8y+15
=(y-3)( y-5)
y y
-3
-5
把下列式子分解因式 ⑴ x2 + 7x+12 =(x+3)(x+4)
x x
3
4
把下列式子分解因式
⑶x2 – 3x-4
=(x+1)(x-4)
x x
+1
-4
把下列各式分解因式 =(x+1)(x-8) (1) x2-7x-8 (2) m2-3m-10 =(m+2)(m-5) =(y+2)2 (3) y2+4y+4 2 (4) a -2a-8 =(a+2)(a-4)
(4)公式法
当b-4ac≥0时，x=
方程的左边是完全平方式,右边是非 负数;即形如x2=a(a≥0)
x1 a, x2 a
一 直接开平方法
依据：平方根的意义，即
如果 x2=a , 那么x = a.
这种方法称为直接开平方法。 解题步骤：
1，将一元二次方程常数项移到方程的一边。
2，利用平方根的意义，两边同时元二次方程一次项系数 为0时（ax2+c=0），应选用直接开平方 法；若常数项为0（ ax2+bx=0），应选 用因式分解法；若一次项系数和常数项 都不为0 (ax2+bx+c=0），先化为一般式， 看一边的整式是否容易因式分解，若容 易，宜选用因式分解法，不然选用公式 法；不过当二次项系数是1，且一次项系 数是偶数时，用配方法也较简单。
2
）
。
（D）0或2
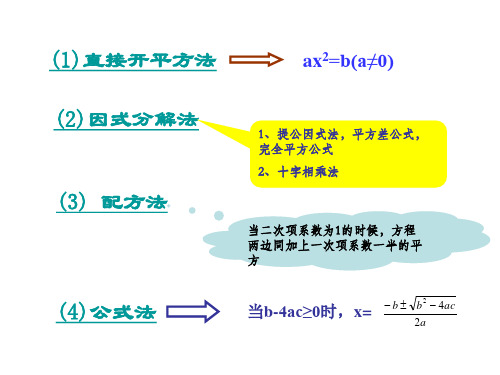
(1)直接开平方法
如果没有一次项，直接开方最理想
ax2=c(a≠0)
1、提公因式法，平方差公式，完 全平方公式
(2)因式分解法
如果缺少常数项，因式分解没商量 如：x 2 x 0
(3) 配方法
当二次项系数为1的时候，方程 两边同加上一次项系数一半的平 方
b b 2 4ac 2a
7.定解:写出原方程的解.
“配方法”解方程的基本步骤
1.化1:把二次项系数化为1; 2.移项:把常数项移到方程的右边; 3.配方:方程两边同加一次项系数 一半的平方;
3x( x 2) 5( x 2)
4.变形:化成
(x + m) = a
2
5.开平方，求解
★一化、二移、三配、四化、五解.
3x 2 0或x 6 0
2 x1 3

5 x1 3
x2 6
x2 2
用配方法解一元二次方程： 2x2-9x+8=0
1.化1:把二次项系数化为1; 2.移项:把常数项移到方程的右边; 3.配方:方程两边都加上一次项 系数绝对值一半的平方; 4.变形:方程左边分解因 式,右边合并同类; 5.开方:两边开平方; 6.求解:解一元一次方程;
1 3、x2+ ＝１ x
5、x３－２x２＝１
2 m 2 x m 2x 2 0 是关于x的一元二次 1、若
方程则m ≠－ 2
。
m2 2
2、若方程 (m 2) x
(m 1) x 2 0
是关于x的一元二次方程，则m的值为
3.若x=2是方程x2+ax-8=0的解，则a= 2 2、已知一元二次方程x2=2x 的解是（ （A）0 （B）2 （C）0或-2 ;
② 公式法虽然是万能的，对任何一元二 次方程都适用，但不一定是最简单的， 因此在解方程时我们首先考虑能否应用 “直接开平方法”、“因式分解法”等 简单方法，若不行，再考虑公式法（适 当也可考虑配方法）
用最好的方法求解下列方程 1)（3x-2）² -49=0 2)（3x-4）² =（4x-3）²
3 3) 4y=1－ y² 2
3，得到形如： x =
a.
的一元一次方程。 x2= ?
4，写出方程的解 x1= ?,
例题讲解
1、（3x -2）² -49=0 解：移项，得：（3x-2）²=49 两边开平方，得：3x -2=±7 2、（3x -4）² =（4x -3）² 解：两边开平方，得： 3x-4=±（4x-3） 3x -4=4x-3或3x-4= -4x+3
(5)
b2-2b-3 =(b+1)(b-3)
请你选择最恰当的方法解下列一元二次方程 1、3x² -1=0 3、x² -4x-2=0 2、x（2x +3）=5（2x +3） 4、2 x ² -5x+1=0
1、形如（x-k）² =h的方程可以用直接开平方法求解； 2、千万记住：方程的两边有相同的含有未知数的因式的时候不能两边都除以 这个因式，因为这样能把方程的一个跟丢失了。要利用因式分解法求解； 3、当方程的一次项系数是方程的二次项系数的两倍的时候可以用配方法求解； 4、当我们不能利用上边的方法求解的时候就就可以用公式法求解，公式法是 万能的。
一元二次方程的解法复习
时间：2012.12.4
知识要点说一说
方程两边都是整式 一元二次方程的定义 只含有一个未知数 ax²+bx+c=0（a0） 求知数的最高次数是2
直接开平方法
一 因 式 分解法 元 二 方 法 次 一元二次方程的解法 配 方 程
求 根 公式法
一元二次方程的应用
明辨是非
判断下列方程是不是一元二次方程，若不是一元二 次方程，请说明理由？ 1、(x－1)２＝４ √ × × ２、x2－2x=8 ４、x２＝y+１ 6、ax2 + bx + c＝１ √ × ×
4.代入:把有关数值代入公 式计算;
5.定解:写出原方程的根.
例题讲解
例2. 用公式法解方程 2x2+5x-3=0
解:
∵ a=2
b=5
c= -3
∴ b2-4ac=52-4×2×(-3)=49
∴x=
= 即 x1= - 3
=
x2=
用公式法解一元二次方程的一般步骤：
1、把方程化成一般形式。
并写出a，b，c的值。
三 配方法
我们通过配成完全平方式的方法,得到了一元二次方 程的根,这种解一元二次方程的方法称为配方法 用配方法解一元二次方程的方法的助手:
平方根的意义: 如果x2=a, 那么x=
a.
完全平方式:式子 a2±2ab+b2 叫完全平方式,且 a2±2ab+b2 =(a±b)2.
例题讲解
例1. 用配方法解下列方程
( x 1)2 0
3 2 x 4 11 5 x2 x1 4 4
x1 x2 1
1.用因式分解法的条件是:方程左边能够 分解,而右边等于零; 2.理论依据是:如果两个因式的积等于零 那么至少有一个因式等于零. 因式分解法解一元二次方程的一般步骤: 一移-----方程的右边=0; 二分-----方程的左边因式分解; 三化-----方程化为两个一元一次方程;
四解-----写出方程两个解;
二 因式分解法
1 提公因式法
3x( x 2) 5( x 2)
（2） x(3x 2) 6(3x
2) 0
解：提公因式得：
=0
(3x 2)( x 6) 0
提公因式得
(3x 5)( x 2) 0
3x 5 0或x 2 0
a1a2 x a1c2 a2c1 x c1c2
2
a1 x
c1
a2 x
所以原式可以分解为：a
c2
1 x c1 a2 x c2
例 因式分解：2x2-3x-2 解原式=(x-2)(2x+1)
x 2x
-2
+1
因式分解：
6 x 7 xy 5 y
2
2
2 x y 3x 5 y 3 x
A、若x2=4，则x=2
B、若3x2=6x，则x=2 C、若x2+x-k=0的一个根是1，则k=2
x D、若
2
3x 2
x 2
的值为零，则x 2
按要求解下列方程： 1.因式分解法： 3 x 2 x x 2
2
2.配方法： 2x 5 x 3 0 2 3.公式法：1 x x 1
1、
ax2+c=0
ax2+bx=0
====> 直接开平方法
====> 因式分解法 因式分解法 ax2+bx+c=0 ====> 公式法（配方法）
2、公式法虽然是万能的，对任何一元二次方程都适用， 但不一定 是最简单的，因此在解方程时我们首先考 虑能否应用“直接开平方法”、“因式分解法”等简单 方法，若不行，再考虑公式法（适当也可考虑配方法）
2、下列方程是一元二次方程的是 （ B）
A x 2 y 1 3 2 C x 8 x
B x 5 0 D 3x 8 6x 2
2
3.若x=2是方程x2+ax-8=0的解，则a=
2
4.下面是某同学在一次数学测验中解答 的填空题，其中答对的是（ C ）