线性规划模型的应用与灵敏度分析(DOC)
灵敏度分析
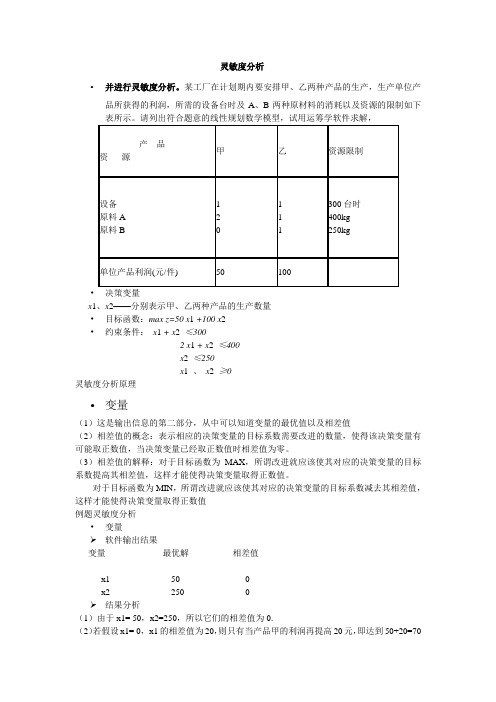
灵敏度分析•并进行灵敏度分析。
某工厂在计划期内要安排甲、乙两种产品的生产,生产单位产品所获得的利润,所需的设备台时及A、B两种原材料的消耗以及资源的限制如下表所示。
请列出符合题意的线性规划数学模型,试用运筹学软件求解,•决策变量x1、x2——分别表示甲、乙两种产品的生产数量•目标函数:max z=50 x1 +100 x2•约束条件:x1 + x2≤3002 x1 + x2≤400x2≤250x1、x2≥0灵敏度分析原理•变量(1)这是输出信息的第二部分,从中可以知道变量的最优值以及相差值(2)相差值的概念:表示相应的决策变量的目标系数需要改进的数量,使得该决策变量有可能取正数值,当决策变量已经取正数值时相差值为零。
(3)相差值的解释:对于目标函数为MAX,所谓改进就应该使其对应的决策变量的目标系数提高其相差值,这样才能使得决策变量取得正数值。
对于目标函数为MIN,所谓改进就应该使其对应的决策变量的目标系数减去其相差值,这样才能使得决策变量取得正数值例题灵敏度分析•变量软件输出结果变量最优解相差值------- -------- --------x1 50 0x2 250 0结果分析(1)由于x1= 50,x2=250,所以它们的相差值为0.(2)若假设x1= 0,x1的相差值为20,则只有当产品甲的利润再提高20元,即达到50+20=70(元),产品甲才可能生产,即x1才可能大于0.•约束(1)这是输出信息的第三部分,从中可以知道每个约束条件所添加的松弛/剩余变量的取值,以及该约束条件的对偶价格。
(2)对偶价格概念:在约束条件常数项中增加一个单位而使最优目标函数值得到改变的数量(可能变好或变坏,要取决于对偶价格的具体数值)称之为这个约束条件的对偶价格。
对偶价格可以大于零,等于零,也可以小于零。
(3)对偶价格解释:①若对偶价格大于零,则其最优目标函数值变好。
目标函数为MAX时,若约束条件常数项中增加一个单位时,最优目标函数值也相对应增加一个对偶价格目标函数为MIN时,若约束条件常数项中增加一个单位时,最优目标函数值也相对应减少一个对偶价格。
第2章 线性规划的对偶理论与灵敏度分析2.6

2.6.2汽油配料模型 汽油配料模型 例2.6.2 一种汽油的特性可用两个指标描述: 其点火性用 “辛烷数”描述,其挥发性用“蒸汽压力”描述。某炼油厂有四 种标准汽油, 其标号分别为1, 2, 3,4,其特性及库存量列于表 2.6.2中,将上述标准汽油适量混合,可得两种飞机汽油,某标 号为1,2,这两种飞机汽油的性能指标及产量需求列于表2.6.3 中。问应如何根据库存情况适量混合各种标准汽油,使既满足 飞机汽油的性能指标,而产量又最高。
解
设计划生产 A1 , A2 , A3的数量分别为 x1 , x2 , x3,则可建立线性规划 max S = 30 x1 + 20 x 2 + 50 x3 x1 + 2 x 2 + x3 ≤ 430 3 x + 2 x3 ≤ 460 1 x1 + 4 x 2 ≤ 420 s.t . x1 + x 2 + x3 ≤ 300 x ≥ 70 2 x3 ≤ 240 x1 , x 2 , x3 ≥ 0 用LINGO求解
数学模型:
max =30*x1+20*x2+50*x3; x1+2*x2+x3<=430; 3*x1+2*x3<=460; x1+4*x2<=420; x1+x2+x3<=300; x2>=70; x3<=240;
求解得最优解: x1 = 0, x2 = 70, x3 = 230, max = 12900。 (1)将目标函数中x3的系数由50增至60,约束条件x3 ≤ 240改为x3 ≤ 210。 40 230 , x2 = , x3 = 210, max = 14533 > 12900。可行! 3 3 即使要求是整数解(关于整数规划见第三章) 求解得最优解: x1 = 在上述LINGO求解的语句后增加x1 , x2 , x3取值为整数的语句: @gin(xl);gin(x2);@gin(x3); 得到结果: x1 = 13, x2 = 77, x3 = 210, max = 14530 > 12900也可行。
用excel进行线性规划的灵敏度分析

求解线性规划问题
01
点击“规划求解”对话框中的“求解”按钮,Excel将开始求 解线性规划问题。
02
Excel将显示求解结果,包括最优解、目标函数的值、可变单 元格的值等。
03
可以根据需要调整参数或约束条件,重新进行求解,以获得 更优的解或更全面的灵敏度分析。
03 灵敏度分析
灵敏度分析的定义
01
灵敏度分析是评估线性规划模型中参数变化对最优解
的影响程度的过程。
02
它有助于理解模型的最优解对各个参数的敏感程度,
从而更好地理解模型的行为。
03
通过灵敏度分析,可以确定哪些参数对模型的影响最
大,从而在实际情况中更好地调整这些参数。
灵敏度分析的步骤
2. 运行模型
案例二:运输问题优化
约束条件
车辆载重、运输时间、运输路线等。
目标函数
最小化运输成本,同时满足各分区的需求。
灵敏度分析
分析需求量、运输成本、运输时间等参数变 化对最优解的影响。
案例三:资源分配问题优化
01
目标函数
最大化资源利用效率,同时满足 生产需求。
约束条件
02
03
灵敏度分析
资源总量、生产能力、产品质量 等。
THANKS FOR WATCHING
感谢您的观看
分析资源价格、生产能力、产品 质量等参数变化对最优解的影响。
05 结论与展望
线性规划与灵敏度分析的意义
线性规划是一种数学优化技术,用于 在有限资源约束下实现特定目标。灵 敏度分析是线性规划的一个重要组成 部分,用于评估模型参数变化对最优 解的影响。
线性规划的灵敏度分析与最优解的解释

3.3 灵敏度分析:计算机求解
为了使用管理科学家软件,我们使用小数代替分数。Par 公司的问题用小数形式的系数表示如下:
现在,模型的最优解540个标准袋和252个高级袋。每个目 标函数系数都有一个最优范围,即目标函数系数在什么范围 内变化,模型的最优解保持不变。
3.2 图解法灵敏度分析
3.2.1 目标函数系数 认真观察图发现,只要
目标函数直线的斜率处于 直线A(和切割与印染约 束线重合)的斜率与直线 B(与成型约束线重合) 的斜率之间,极点3 (S=540,D=252)就是最 优解的点。
则直线A和直线B的斜率都已经计算出来了,我们来看 保持极点3仍然为最优解点,应满足条件:
-3/2≤目标函数的斜率≤-7/10
3.2 图解法灵敏度分析
现在让我们考虑目标直线斜率的一般形式。用CS表示标
准袋的利润,CD表示高级袋的利润,P表示目标函数值。 使用这些标识,目标函数直线可以写成:
P=CSS+CDD 把上面方程写成斜截式,得到
第三章 线性规划的灵敏度分析与最优解 的解释
引言
灵敏度分析是研究当一个线性规划问题中的系 数发生变化时,其对函数最优解的影响程度。运 用灵敏度分析,我们可以回答以下问题: 1.如果目标函数的系数发生了变化,对最优解会产 生什么影响? 2.如果改变约束条件的右端值,对最优解会产生什 么影响?
首先我们将介绍如何使用图解法进行双变量 线性规划问题的灵敏度分析,然后介绍如何使用 管理科学家软件得到灵敏度分析报告。
顺时针转动目标函数直线,使其斜率变成一个绝对值更 大的负数,从而斜率变小了。直到与B重合,我们又获得了 多重最优解——极点3和极点2之间都是最优点。因此B的斜 率是目标函数直线斜率的下限。
线性规划的对偶理论与灵敏度分析

第二章 线性规划的对偶理论与灵敏度分析主要内容 对偶问题、对偶基本性质、对偶单纯形方法、灵敏度分析、参数规划 讲授重点 对偶基本性质、对偶单纯形方法、灵敏度分析 讲授方式讲授式、启发式本章知识结构图第一节 线性规划的对偶问 题一、对偶问题的提出首先通过实际例子看对偶问题的经济意义。
例1 第一章例1中美佳公司利用该公司资源生产两种家电产品时,其线性规划问题为: (LP 1) max z =2x l +x 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,524261552121212x x x x x x x现从另一角度提出问题。
假定有另一公司想把美佳公司的资源收买过来,它至少应付出多大代价,才能使美佳公司愿意放弃生产活动,出让自己的资源.显然美佳公司愿出让自己资源的条件是,出让代价应不低于用同等数量资源由自己组织生产活动时获取的盈利.设分别用y 1、y 2、和y 3代表单位时间(h )设备A 、设备B 和调试工序的出让代价。
因美佳公司用6小时设备A 和1小时调试可生产一件家电I ,盈利2元;用5小时设备A,2小时设备B 及1小时调试可生产一件家电Ⅱ,盈利1元。
由此y1,y2,y3的取值应满足 6y 2+y 3≥25y 1+2y 2+y 3≥1 (2。
1) 又另一公司希望用最小代价把美佳公司的全部资源收买过来,故有min z =15y 1+24y 2+5y 3 (2。
2) 显然y i ≥0(i =l ,2,3),再综合(2。
1),(2。
2)式有。
(LP 2) min ω=15y 1+24y 2+5y 3⎪⎩⎪⎨⎧≥≥+≥+0,,125263212132y y y y y y y上述LP 1和LP 2是两个线性规划问题,通常称前者为原问题,后者是前者的对偶问题。
二、对称形式下对偶问题的一般形式定义:满足下列条件的线性规划问题称为具有对称形式:其变量均具有非负约束,其约束条件当目标函数求极大时均取“≤"号,当目标函数求极小时均取“≥”号’.对称形式下线性规划原问题的一般形式为:max z=c 1x 1+c 2x 2+…+c n x n ⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥≤+⋅⋅⋅++≤+⋅⋅⋅++≤+⋅⋅⋅++),,1(022112222212111212111n j x bx a x a x a b x a x a x a b x a x a x a j mn mn m m n n n n(2.3)用y i (i=1,…,m )代表第i 种资源的估价,则其对偶问题的一般形式为:min w=b 1y 1+b 2y 2+…+b m y m⎪⎪⎪⎩⎪⎪⎪⎨⎧⋅⋅⋅=≥≥+⋅⋅⋅++⋅⋅⋅⋅⋅⋅⋅⋅⋅≥+⋅⋅⋅++≥+⋅⋅⋅++),,1(022112222212111212111m i y cy a y a y a c y a y a y a c y a y a y a y i nm mn n n m m m m (2。
运筹学:第1章 线性规划 第3节 对偶问题与灵敏度分析

s.t.
4x1 3x1
5x2 200 10x2 300
x1, x2 0
9x1 4x2 360
s.t.
34xx11
5x2 10 x
200 2 300
3x1 10x2 300
x1, x2 0
则D为
min z 360y1 200y2 300y3 300y4
9 y1 4 y2 3y3 3y4 7 s.t.4 y1 5y2 10 y3 10 y4 12
amn xn bm ym xn 0
机会成本 a1 j y1 a2 j y2 aij yi amj ym
表示减少一件产品所节省的可以增加的利润
(3)对偶松弛变量的经济解释——产品的差额成本
机会成本
利润
min w b1 y1 b2 y2 bm ym
a11 y1
st
a12
y1
a1n y1
max z CX
(P)
AX b
s
.t
.
X
0
(D)
min w Yb
s.t.
YA C Y 0
• (2)然后按照(D)、(P)式写出其对偶
例:写出下面线性规划的对偶规划模型:
max z 2x1 3x2
min w 3 y1 5y2 1y3
x1 2x2 3 y1 0
s.t.
2xx11
例如,在前面的练习中已知
max z 2.5x1 x2 的终表为
3x1 5x2 15 s.t.5x1 2x2 10
x1, x2 0
0 x3 9 2.5 x1 2
0 19 1 - 3
5
5
1
2
0
1
5
EXCEL求解第一章线性规划和灵敏度分析
线性规划模型的描述
例1:某工厂生产两种新产品:门和窗。经测算,每 生产一扇门需要在车间1加工1小时、在车间3加工3小 时;每生产一扇窗需要在车间2和车间3各加工2小时。 而车间1每周可用于生产这两种新产品的时间为4小 时、车间2为12小时、车间3为18小时。已知每扇门 的利润为300元,每扇窗的利润为500元。根据市场 调查得到的这两种新产品的市场需求状况可以确定, 按当前的定价可确保所有的新产品均能销售出去。 问:该工厂如何安排这两种新产品的生产计划,才 能使总利润最大?
$D$12) 复制E7单元格到E8、E9
EXCEL求解线性规划模型
(3)总利润计算: 在G12单元格输入公式: =C4*C12+D4*D12 或: =SUMPRODUCT(C4:D4,C12:D12)
EXCEL求解线性规划模型
在电子表格中建立线性规划模型步骤总结
收集问题数据; 在电子表格中输入数据(数据单元格); 确定决策变量单元格(可变单元格); 输入约束条件左边的公式(输出单元格)使用
EXCEL求解线性规划模型
2、主要求解结果 ■两种新产品每周的产量; ■两种新产品每周各实际使用的工时 (不能超过计划工时); ■两种新产品的总利润
EXCEL求解线性规划模型
3、主要结果的计算方法
(1)两种新产品的每周产量:C12、D12,初始 值为0。
(2)实际使用工时计算(三种方法) 1)分别在E7、E8、E9中输入相应的计算公 式:
例:车间2:12——13,车间3:18——17 例:车间2:12——16,车间3:18——15
EXCEL求解线性规划模型
5、aij变化 例:由于车间2采用新的生产工艺,生产
用excel进行线性规划的灵敏度分析学习资料
用excel进行线性规划的灵敏度分析学习资料线性规划是一种数学优化方法,它提供了一种有效的方法来解决最优化问题。
灵敏度分析是线性规划中的一个非常重要的概念,它是用来研究一些关键参数的变化对于最优解的影响。
在Excel中进行线性规划和灵敏度分析非常方便,本文将介绍如何在Excel中进行线性规划的灵敏度分析。
首先,我们需要先了解Excel中进行线性规划的基本步骤。
以最简单的线性规划模型为例,我们可以用以下模型来说明:目标函数:Maximize f(x,y)=4x+3y约束条件:2x+y <= 8x,y >= 0要在Excel中求解这个问题,我们需要遵循以下步骤:1. 打开Excel,输入目标函数和约束条件。
公式应放在单元格中,约束条件应按行排列,用每行的最后一个单元格来设置限制。
还应设置变量的初始值,并将目标单元格格式设置为“最大值”或“最小值”。
2. 选择“数据”选项卡,在“分析”组内选择“规划问题”选项。
在弹出的窗口中,选择“线性规划”选项,并单击“确定”按钮。
3. 在线性规划窗口中,选择“目标单元格”和变量单元格,然后选择要优化的运算符(如“大于等于”或“小于等于”)。
选择“添加”按钮向模型添加约束条件,直到所有限制都添加完毕。
单击“求解”按钮,Excel将显示变量的最优解、目标函数的最优解以及约束条件的最佳值。
在完成线性规划模型的求解后,我们可以进行灵敏度分析来研究模型中不同参数的变化对最终解的影响。
在Excel中进行灵敏度分析有以下步骤:1. 求出每个决策变量的最优值和目标函数的最优值。
2. 使用Excel的数据表功能,建立一个数据表,将要变化的参数输入到数据表中。
可以一次性变化多个参数。
3. 将数据表的单元格链接到原始模型中的输入参数单元格。
4. 使用Excel的数据表的“展示数据表”功能,查看各参数的最优解或其他解所对应的目标函数的值。
5. 根据结果进行分析,确定哪些参数对最终结果有最大的影响。
第三章 线性规划的灵敏度分析和最优解的解释
3.1 灵敏度分析简介
灵敏度分析是研究线性规划的参数(非可控输入)发生 变化对最优解的影响程度
线性规划的参数包括:
• 目标函数系数 • 约束条件右侧值 • 约束条件系数矩阵
最优解中包含的信息:
• 目标函数值 • 决策变量值 • 递减成本(reduced cost) • 松弛/剩余变量
4
3.1 灵敏度分析简介
利用Lingo 软件做灵敏度分析
16
17
利用Excel做灵敏度分析
Microsoft Excel 16.0 敏感性报告 工作表: [数据模型与决策第3章例题.xlsx]第三章例题1 报告的建立: 2021/5/29 10:48:56
可变单元格
单元格 $B$15 $C$15
名称 决策变量值 x1 决策变量值 x2
作者
John Loucks
St. Edward’s University
1
第三章 线性规划的灵敏度分析和最优解的解释
3.1 灵敏度分析简介 3.2 目标函数系数变化的分析 3.3 约束条件右端值变化的分析 3.4 传统灵敏度分析的局限性
2
第三章 线性规划的灵敏度分析和最优解的解释
3.1 灵敏度分析简介 3.2 目标函数系数变化的分析 3.3 约束条件右端值变化的分析 3.4 传统灵敏度分析的局限性
6
x1 < 6
2x1 + 3x2 < 19 x1 + x2 < 8
x1, x2 > 0
固定x2的系数7,改变x1 的系数
5
最优解:
Max 14/3x1 + 7x2
4
x1 = 5, x2 = 3
3
Max 7x1 + 7x2
第二章 线性规划的对偶理论与灵敏度分析
解:原问题的对偶问题为 min W 2 y1 3 y2 5 y3
2 y1 3 y2 y3 2 3y y 4 y3 3 1 2 5 y1 7 y2 6 y3 4 y1 , y2 , y3 无约束
线性规划的对偶模型
例2.3 写出下列线性规划问题的对偶问题.
原问题 目标函数 约束条件
T
对偶问题 min ≥ 约束条件个数 变量数量
max ≤ 变量数量 约束条件个数
D : min W Y b A T Y CT Y0
线性规划的对偶模型
原问题(或对偶问题) 目标函数 约 束 max m个 ≤ ≥ 对偶问题(或原问题) 目标函数 m个 ≥0 ≤0 变 min
注意:以后不强调等 式右段项 b≥0,原因在对 偶单纯型表中只保证 j 0 而不保证 B 1b 0 ,故 b 可以是负数。
线性规划的对偶模型
对 偶 问 题 : minW 2 y1 3 y 2 5 y 3 2 y1 3 y 2 y 3 2 3 y1 y 2 4 y 3 3 5 y1 7 y 2 6 y 3 4 y1 , y 2 , y 3 0
条
件
量
=
n个
无约束
n个 约 束
变
≥0
≤0
≥
≤
量
条
件
无约束
b C 约束条件右端项 目标函数变量的系数
=
目标函数变量的系数 约束条件右端项
对称形式下的对偶关系(矩阵形式)
项目 A b 原问题 约束条件系数矩阵 约束条件右端项向量 对偶问题 约束条件系数矩阵转置 目标函数的系数向量
C
目标函数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
摘要线性规划是解决稀缺资源最优分配的有效方法,使付出的费用最少或获得的利益最大。
它的研究对象是有一定的人力、财力、资源条件下,如何合理安排使用,效益最高;某项任务确定后,如何安排人、财、物,使之最省。
它要解决的问题的目标可以用数值指标反映,对于要实现的目标有多种方案可以选择,有影响决策的若干约束条件。
本文主要介绍了线性规划模型在实际生活中的应用,其中包括解线性方程组的各种方法,如图解法、单纯形法、以及对偶单纯形法等等,以及简单介绍了有关灵敏度分析的方法。
由于许多问题仅仅利用线性规划的方法还不足以解决,因此用到了对偶理论,也因此引出了对偶单纯形法。
对偶规划是线性规划问题从另一个角度进行研究,是线性规划理论的进一步深化,也是线性规划理论整体的一个不可分割的组成部分。
灵敏度分析是对线性规划结果的再发掘,是对线性规划理论的充要应用,本文以实例验证灵敏度分析的实际应用。
关键词:线性规划;单纯形法;对偶单纯形法ABSTRCTLinear programming is an effective method to solve the optimal allocation of scarce resources, make the cost of pay or receive at least the interests of the largest. Its object of study is the human and financial resources, resource conditions, how to reasonably arrange to use, benefit is supreme; A task is determined, how to arrange people, goods, and make it the most provinces. It to the target can be used to solve the problem of the numerical indicators, to achieve a variety of solutions to choose from, have an impact on the decision of some constraint conditions. Through the subject design, can deepen the operations research, optimization method, linear programming, nonlinear programming, to improve the integrated use of knowledge, improve the ability of using the sensitivity analysis to solve various practical problems. This article mainly introduces the application of linear programming model in real life, including the various methods of solving linear equations, as shown in figure method, simplex method and dual simplex method, etc., and simply introduces the method of sensitivity analysis. Due to many problems just by using the method of linear programming is not enough to solve, so use the duality theory, thus raises the dual simplex method. The dual programming is linear programming problem from another Angle, is the further deepening of linear programming theory, linear planning theory as a whole is also an integral part of. Sensitivity analysis is to discover, the result of the linear programming is the charge to application of linear programming theory. Keywords: linear programming;Simplex method;The dual simplex method目录前言线性规划模型的应用与灵敏度分析 (1)第一章线性规划问题 (1)1. 线性规划及灵敏度分析简介 (1)2. 线性规划模型应用的发展 (1)3. 线性规划模型研究的问题 (2)4. 线性规划模型的应用 (2)4.1问题 (2)4.2线性规划方法的特点及局限性 (2)4.3线性规划模型的基本结构 (3)4.4线性规划模型的一般形式 (3)4.4线性规划的性质…………………………………………………………………………………5第二章求解线性规划的方法 (6)1. 图解法 (6)2. 单纯行法 (7)2.1 单纯行法的基本思路 (7)2.2 单纯形法的求解步骤 (11)2.3 单纯形法的求解过程小结 (12)2.3.1人造基、初始基本可行解 (12)2.3.2最优解判别定理: (14)2.3.3单纯行过程的两种方法 (14)3. 单纯行法 (14)3.1对偶问题的提出 (14)3.2线性规划的对偶理论 (15)3.3对偶单纯形法的步骤 (15)4. 单纯行表......................................................................................................错误!未定义书签。
第三章灵敏度分析 (17)1. 边际值(影子价)q (17)i2. 价值向量的灵敏度分析 (18)3. 灵敏度的应用 (18)第四章应用设计实例 (19)1. 目标函数系数灵敏度分析 (19)2. 右边值敏感性分析 (19)结论 (22)参考文献 (23)致谢 (24)前言线性规划是运筹学的一个重要分支。
1947年,当时正在美国空军担任数学顾问的Dantzig在《最优规划的科学计算》中提出“如何使规划过程机械化”问题,并着手建立数学模型。
他从改造投入产出模型入手,逐步研究,形成了“单纯形法”,并于1953年提出“改进单纯形法”,以解决计算机求解过程中的舍入误差问题。
之后,线性规划理论逐步趋于成熟,在实用中日益广泛和深入。
通过设计该课题,可以加深对运筹学、最优化、线性规划、非线性规划以及MATLAB 的认识,提高对这些知识的综合应用水平,提高利用灵敏度分析解决各种线性规划问题的能力。
本文章主要介绍了线性规划在实际生活中的应用,包括解线性方程组的各种方法,包括图解法,单纯形法,大M法,二阶段法以及对偶单纯形法,以及简要介绍了有关灵敏度分析的方法。
由于线性方程组是解决各种应用问题的主要工具,而有许多问题仅仅利用线性规划的解决方法还不足以解决问题,还用到了对偶理论,也因此引出了对偶单纯形法。
本课题当前的研究方向有:LP的内点算法,它通过非线性规划解决线性问题,其成功是对数学思想的革新;算法复杂度,评价算法好坏应从平均工作量出发;大型问题的分解算法、近似算法。
线性规划的应用正在不断扩大,企业成功确实通过提高生产和有效使用资源的竞争过程来达到。
线性规划模型的应用与灵敏度分析第一章线性规划问题1. 线性规划及灵敏度分析简介线性规划(Linear Programming)问题, 简称LP问题,是运筹学中最基本, 也是最重要的内容, 被广泛地应用于军事决策、企业管理、工程设计、交通运输等领域. 特别是经济领域应用更为广泛, 有资料称, 在对500家有相当效益的公司所作的评述中, 有85%的公司都曾应用了线性规划。
灵敏度分析对于决策者的重要性不言而喻,在真实世界里,周围的环境、条件是在不断变化的。
2. 线性规划模型应用的发展线性规划及其通用解法——单纯形法是由美国G.B.Dantzig在1947年研究空军军事规划提出来的。
法国数学家傅里叶和瓦莱-普森分别于1832和1911年独立地提出线性规划的想法,但未引起注意。
1939年苏联数学家康托罗维奇在《生产组织与计划中的数学方法》一书中提出线性规划问题,也未引起重视[1]。
1947年美国数学家丹齐克提出线性规划的一般数学模型和求解线性规划问题的通用方法──单纯形法,为这门学科奠定了基础。
1947年美国数学家诺伊曼提出对偶理论,开创了线性规划的许多新的研究领域,扩大了它的应用范围和解题能力[2]。
1951年美国经济学家库普曼斯把线性规划应用到经济领域,为此与康托罗维奇一起获1975年诺贝尔经济学奖。
50年代后对线性规划进行大量的理论研究,并涌现出一大批新的算法。
例如,1954年莱姆基提出对偶单纯形法,1954年加斯和萨迪等人解决了线性规划的灵敏度分析和参数规划问题,1956年塔克提出互补松弛定理,1960年丹齐克和沃尔夫提出分解算法等。
线性规划的研究成果还直接推动了其他数学规划问题包括整数规划、随机规划和非线性规划的算法研究[3]。
1984年美国贝尔电话实验室的印度数学家N.卡马卡提出解线性规划问题的新的多项式时间算法。
用这种方法求解线性规划问题在变量个数为5000时只要单纯形法所用时间的1/50。
现已形成线性规划多项式算法理论。
50年代后线性规划的应用范围不断扩大[4]。
3. 线性规划模型研究的问题建立线性规划模型线性规划研究的问题主要有两类:一类是当一项任务确定后,如何统筹安排,尽量做到以最少的人力、物力等资源去完成;另一类是在人力、物力等资源确定的情况下,如何安排使用这些资源,使创造的价值最多,其实质是解决稀缺资源在有竞争环境中如何进行最优分配的问题,即寻求整个问题的某个整体指标最优的问题[4]。
4.线性规划模型的应用4.1问题a.目标函数最优化——单一目标,多重目标问题如何处理?b.实现目标的多种方法,若实现目标只有一种方法不存在规划问题。
c.生产条件的约束——资源是有限的,资源无限不存在规划问题。
