江苏省金湖县外国语学校七年级数学下册《9.4 乘法公式(2)》课件 苏科版
合集下载
苏科初中数学七年级下册《9.4 乘法公式》PPT课件 (13).ppt

判断下面计算是否正确?如果有错误请改正
(1)(x+y)2 = x2+y2
()
(2)(x-y)2 = x2-2xy-y2
()
(3)(2x+y)2=4x2+2xy+y2 ( )
(4)(x2+y2)2=x2+2xy+y2 ( )
例2 用完全平方公式计算 (1)(-x+2y)2 (2) (-2a-5)2
课本P76 练一练1,2
文右字边语是言:两数:数 的的 乘平 积方 的和 两加 倍上(减去)这两 两个数和(差)的平方等于这两个
数的平方和,加上(减去)这两个数的 乘积的两倍.
例1 用完全平方公式计算 (1) (5+3p)2 (2) (2x-7y)2
变式: (1) (5+3p3)2 (2) (2ab-7c3)2
辨一辨:
思维扩展:
4.已知a+b=2,ab=1,求
求a2+b2、(a-b)2的值.
计算:(a+b+c)2
练习:(1)(x y 5)2 (2)(2m n 1)2
本节课你的收获是什么?
在解题过程中要准确确定a和b、对照公式原形
的两边, 做到不丢项、不弄错符号、2ab时不
少乘2;第一(二)数是乘积被平方时要注意添 括号, 是运用完全平方公式进行多项式乘法的 关键
(5) (2a-b)2=4a2+_____+b2
(6) (
)2=4a2+_____+b2
(7) (
)2=4a2-_____+b2
练习:P算一个二项整式的平方式时,得到
正确结果是4x2+ +25y2,但中间一项
(1)(x+y)2 = x2+y2
()
(2)(x-y)2 = x2-2xy-y2
()
(3)(2x+y)2=4x2+2xy+y2 ( )
(4)(x2+y2)2=x2+2xy+y2 ( )
例2 用完全平方公式计算 (1)(-x+2y)2 (2) (-2a-5)2
课本P76 练一练1,2
文右字边语是言:两数:数 的的 乘平 积方 的和 两加 倍上(减去)这两 两个数和(差)的平方等于这两个
数的平方和,加上(减去)这两个数的 乘积的两倍.
例1 用完全平方公式计算 (1) (5+3p)2 (2) (2x-7y)2
变式: (1) (5+3p3)2 (2) (2ab-7c3)2
辨一辨:
思维扩展:
4.已知a+b=2,ab=1,求
求a2+b2、(a-b)2的值.
计算:(a+b+c)2
练习:(1)(x y 5)2 (2)(2m n 1)2
本节课你的收获是什么?
在解题过程中要准确确定a和b、对照公式原形
的两边, 做到不丢项、不弄错符号、2ab时不
少乘2;第一(二)数是乘积被平方时要注意添 括号, 是运用完全平方公式进行多项式乘法的 关键
(5) (2a-b)2=4a2+_____+b2
(6) (
)2=4a2+_____+b2
(7) (
)2=4a2-_____+b2
练习:P算一个二项整式的平方式时,得到
正确结果是4x2+ +25y2,但中间一项
七年级数学下册 9.4乘法公式(第2课时)教案 苏科版

学生回答
由学生自己先做(或互相讨论)
板演
教师与同学共同订正
学生讨论
共同总结
作业
第83页3、5、6
板书设计
复习例1板演
………… ……
………………
……例2……
………………
………… ……
教学后记
教学方法
讲练结合、探索交流
课型
新授课
教具
投影仪
教师活动
学生活动
情景设置:
回忆上节课所学的乘法公式:
=
这节课我们利用乘法公式解决实际问题
新课讲解:
例1:用乘法公式计算
⑴ ;⑵ ;
⑶ ;⑷
例2:计算
⑴ ;⑵ ;
⑶ ;⑷[(a-b)2-(a+b)2]2
能够根据实际情况灵活运用乘法公式解题。
课堂练习:
P82练一练1、2、3、4
(2) (3x+2)2-(3x-5)2
(3) (x-2y+1)(x+2y-1)
(4) (2x+3y)2(2x-3y)2
(5) (2x+3)2-2(2x+3) (3x-2)+(3x-2)2
(6) (x2+x+1)(x2-ห้องสมุดไป่ตู้+1)
2.已知a+b=-2,ab=-15求a2+b2.
B组题:
1.若(x2+px+8)(x2-3x+q)的积中不含有x3和x 2项,求p,q的值
数学实验室:
制作若干张长方形和正方形硬纸片,通过图形计算(a+b+c)2的公式,并通过运算推导这个公式。
练习:已知3(a2+b2+c2)=(a+b+c)2,求证:a=b=c
由学生自己先做(或互相讨论)
板演
教师与同学共同订正
学生讨论
共同总结
作业
第83页3、5、6
板书设计
复习例1板演
………… ……
………………
……例2……
………………
………… ……
教学后记
教学方法
讲练结合、探索交流
课型
新授课
教具
投影仪
教师活动
学生活动
情景设置:
回忆上节课所学的乘法公式:
=
这节课我们利用乘法公式解决实际问题
新课讲解:
例1:用乘法公式计算
⑴ ;⑵ ;
⑶ ;⑷
例2:计算
⑴ ;⑵ ;
⑶ ;⑷[(a-b)2-(a+b)2]2
能够根据实际情况灵活运用乘法公式解题。
课堂练习:
P82练一练1、2、3、4
(2) (3x+2)2-(3x-5)2
(3) (x-2y+1)(x+2y-1)
(4) (2x+3y)2(2x-3y)2
(5) (2x+3)2-2(2x+3) (3x-2)+(3x-2)2
(6) (x2+x+1)(x2-ห้องสมุดไป่ตู้+1)
2.已知a+b=-2,ab=-15求a2+b2.
B组题:
1.若(x2+px+8)(x2-3x+q)的积中不含有x3和x 2项,求p,q的值
数学实验室:
制作若干张长方形和正方形硬纸片,通过图形计算(a+b+c)2的公式,并通过运算推导这个公式。
练习:已知3(a2+b2+c2)=(a+b+c)2,求证:a=b=c
苏科版七年级数学下册 9.4 乘法公式 3课时课件 (共3份打包)1

3.计算 (2 1)(2 1)(22 1)(24 1)(28 1)
原式=(22-1)(22+1)(24+1)(28+1) =(24-1)(24+1)(28+1) =(28-1)(28+1) =(28)2-12=216-1
(22)2=24 (24)2=28
变式: (2 1)(22 1)(24 1)(21024 1)
(4) 已知(x-ay)(x+ay)=x2-16y2, 那么a=_±__4_
拓展与延伸
1.若x2-y2=8, y-x=4,求x+y. 解:∵(x+y)(x-y)=x2-y2
又x2-y2=8, y-x=4 ∴(x+y) ×(-4)=8 ∴x+y=-2
2、计算(x+3)(x-3)(x2+9) 原式=(x2-32)(x2+9) =(x2-9)(x2+9) =(x2)2-92 =x4-81
2020
9.4 乘法公式(2)
苏科版七年级下册 数学
知识回顾
完全平方公式: (a+ = a2-2ab+b2
用乘法公式计算:
(1) (2a-3)2 =4a2-12a+9 (2) (-x+4y)2 =(4y-x)2 =16y2-8xy+x2 (3) (-3a-1) 2 =(3a+1)2 =9a2+6a+1
=(2x)2-y2-(4x2+4xy+y2) 原式=-2× (-2)2-4×(-1) ×(-2)
=4x2-y2-4x2-4xy-y2
=-8-8=-16
=-2y2-4xy
填空:
(1) (m+__6n__)(m-_6_n__)= m2-36n2 (2) (a+b)(__b_-a___)= b2-a2 (3) (_-_x_2_-1__)(1-x2)= x4-1
七年级数学下册 9.4 乘法公式教案(2) (新版)苏科版
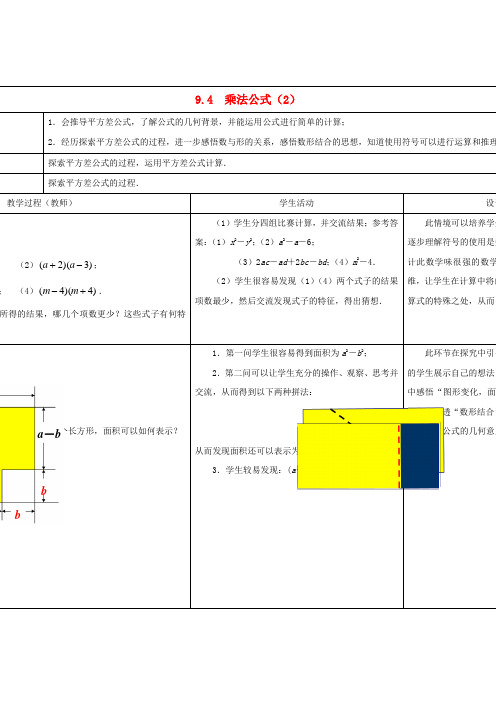
①(5x+y)(5x-y);②(a+2b)(2a-b);
③(2n+m)(-m+2n);④(c+d)(-c-d);
⑤(2a+b)(2a-c);⑥(3y-x)(-x-3y).
(1)学生借助多项式乘法法则计算说明结论的正确性,再归纳并相互完善得到“两个数的和与这两个数的差的积等于这两个数的平方差”.
(2)学生观察后判别,并讲述理由.
参考答案:①、③、⑥
让学生经历合情推理——演绎推理的过程,将情境引入中的猜想以及活动一得到的发现加以论证,从而感悟数学的严谨性.
通过判断引导学生认识平方差公式的本质特征为:两个二项式相乘,其中一项相同,另一项互为相反数.
三、例题讲解
例1用平方差公式计算:
(1)(5x+y)(5x-y);
(2)(2n+m)(-m+2n);
(3)9-4a2;(4)4y2- x2.
2.(1)错误,应该等于x2-4;
(2)错误,应该等于b2-a2.
3.(1)6,6;(2)5n,5n;
(3)b-a;(4)-x2-1.
补充练习:(1)396;(2) .
这些练习较系统全面地巩固了平方差公式.练习第三题的设置有利于培养学生逆向思维的习惯,并为后续因式分解的教学埋下伏笔.
9.4乘法公式(2)
教学目标
1.会推导平方差公式,了解公式的几何背景,并能运用公式进行简单的计算;
2.经历探索平方差公式的过程,进一步感悟数与形的关系,感悟数形结合的思想,知道使用符号可以进行运算和推理,得到的结论具有一般性.
教学重点
探索平方差公式的过程,运用平方差公式计算.
教学难点
探索平方差公式的过程.
在学生解答问题后,可根据学生完成情况,安排小组讨论学生集中出现的问题,找出对平方差公式理解的偏差,养成反思的好习惯,进一步加深对平方差公式的理解.
③(2n+m)(-m+2n);④(c+d)(-c-d);
⑤(2a+b)(2a-c);⑥(3y-x)(-x-3y).
(1)学生借助多项式乘法法则计算说明结论的正确性,再归纳并相互完善得到“两个数的和与这两个数的差的积等于这两个数的平方差”.
(2)学生观察后判别,并讲述理由.
参考答案:①、③、⑥
让学生经历合情推理——演绎推理的过程,将情境引入中的猜想以及活动一得到的发现加以论证,从而感悟数学的严谨性.
通过判断引导学生认识平方差公式的本质特征为:两个二项式相乘,其中一项相同,另一项互为相反数.
三、例题讲解
例1用平方差公式计算:
(1)(5x+y)(5x-y);
(2)(2n+m)(-m+2n);
(3)9-4a2;(4)4y2- x2.
2.(1)错误,应该等于x2-4;
(2)错误,应该等于b2-a2.
3.(1)6,6;(2)5n,5n;
(3)b-a;(4)-x2-1.
补充练习:(1)396;(2) .
这些练习较系统全面地巩固了平方差公式.练习第三题的设置有利于培养学生逆向思维的习惯,并为后续因式分解的教学埋下伏笔.
9.4乘法公式(2)
教学目标
1.会推导平方差公式,了解公式的几何背景,并能运用公式进行简单的计算;
2.经历探索平方差公式的过程,进一步感悟数与形的关系,感悟数形结合的思想,知道使用符号可以进行运算和推理,得到的结论具有一般性.
教学重点
探索平方差公式的过程,运用平方差公式计算.
教学难点
探索平方差公式的过程.
在学生解答问题后,可根据学生完成情况,安排小组讨论学生集中出现的问题,找出对平方差公式理解的偏差,养成反思的好习惯,进一步加深对平方差公式的理解.
苏科版七年级下册数学:9.4 乘法公式

【情境引入】
上节课我们一起学习了完全平方公式, 谁来说一说这个公式?本节课我们继续来 学习另外一个重要的乘法公式,它是什么 呢?
9.4 乘法公式(2)
【学习目标】
◆ 经历从不同角度探索平方差公式的形成 过程,让学生理解和掌握平方差公式。
◆会用平方差公式进行计算
【思考与探索】
活动一: 根据公式直接说出(a+b)2=
【火眼金星】
◆下列整式乘法中能不能用平方差公式计算? 如果能,请写出a、b的值。
(1)(1 x)(1 x) (2)(m 2n)(m n) (3)(2x y)(2x y) (4)(m 2n)(2n m) (5)(3y x)(x 3y)
【例3】
用平方差公式计算
(1)(5x y)(5x y)
【方法3】:阴影部分剪成两个梯形
上底: 下底: 高: S阴影=
【方法4】:
以上方法都是从“形Байду номын сангаас这个角度, 抓住面积不变进行计算的,你能从 “数”这个角度来思考如何计算 (a+b)(a-b)=?
【发现】: 由刚才的操作与计算,你能得
出(或者验证)一个什么结论?
(a+b)(a-b)=a2-b2
平方差 公式
【思考与探索】
活动二: (a+b)(a-b)=?你有哪些方法?
【探究1】
(1)操作与思考: 在边长为a的正方形纸片上剪去一个边长为b(b﹤a) 的小正方形,怎样计算图中的阴影部分的面积?
方法1:用整体减去部分求得阴影部分面积 S阴影=a2-b2
方法2:将阴影部分剪拼成一个长方形计算它的面积 S阴影=(a+b)(a-b)
【练一练】
3、(m+5n)(m-5n)=
上节课我们一起学习了完全平方公式, 谁来说一说这个公式?本节课我们继续来 学习另外一个重要的乘法公式,它是什么 呢?
9.4 乘法公式(2)
【学习目标】
◆ 经历从不同角度探索平方差公式的形成 过程,让学生理解和掌握平方差公式。
◆会用平方差公式进行计算
【思考与探索】
活动一: 根据公式直接说出(a+b)2=
【火眼金星】
◆下列整式乘法中能不能用平方差公式计算? 如果能,请写出a、b的值。
(1)(1 x)(1 x) (2)(m 2n)(m n) (3)(2x y)(2x y) (4)(m 2n)(2n m) (5)(3y x)(x 3y)
【例3】
用平方差公式计算
(1)(5x y)(5x y)
【方法3】:阴影部分剪成两个梯形
上底: 下底: 高: S阴影=
【方法4】:
以上方法都是从“形Байду номын сангаас这个角度, 抓住面积不变进行计算的,你能从 “数”这个角度来思考如何计算 (a+b)(a-b)=?
【发现】: 由刚才的操作与计算,你能得
出(或者验证)一个什么结论?
(a+b)(a-b)=a2-b2
平方差 公式
【思考与探索】
活动二: (a+b)(a-b)=?你有哪些方法?
【探究1】
(1)操作与思考: 在边长为a的正方形纸片上剪去一个边长为b(b﹤a) 的小正方形,怎样计算图中的阴影部分的面积?
方法1:用整体减去部分求得阴影部分面积 S阴影=a2-b2
方法2:将阴影部分剪拼成一个长方形计算它的面积 S阴影=(a+b)(a-b)
【练一练】
3、(m+5n)(m-5n)=
乘法公式-苏科版七年级数学下册课件
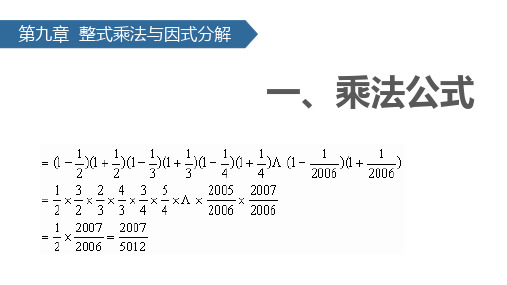
C. (a-b)2 = a2-b2
D. (a+b)(a-b)=a2+b2
2. (2014•临沂)请你计算:(1﹣x)(1+x),(1﹣x)
(1+x+x2),…,猜想(1﹣x)(1+x+x2+…+xn)的结果是
()
A.1﹣xn+1 B. 1+xn+1
C. 1﹣xn
D. 1+xn
知识梳理
3.(2014•包头)计算:( x+1)2-(x+2)(x-2)= . 4. (2014•厦门)设a=192×918,b=8882-302,c= 10532-7472,则数a,b,c 按从小到大的顺序排列,结果是
x
x2
D (a 2b)2 a 2 2ab 4b 2
知识梳理
2. 有若干张面积分别为纸片,阳阳从中抽取了1张面积为a2的
正方形纸片,4张面积为ab的长方形纸片,若他想拼成一个大
正方形,则还需要抽取面积为b2的正方形纸片( B )
A.2张
B.4张
C.6张
D.8张
3. 计算:(1)(-2a+1b)2; (2)(-4b-2)2
C.(ab)2=a2b2
D.(a+b)2=a2+b2
2. 图9.4-2的图①是一个边长为(m+n)的正方形,小颖将图 ①中的阴影部分拼成图②的形状,由图①和图②能验证的式子 是( B )
A.(m+n)2﹣(m﹣n)2=4mn B.(m+n)2﹣(m2+n2)=2mn
C.(m﹣n)2+2mn=m2+n2
D.(m+n)(m﹣n)=m2﹣n2
课堂练习
2020-2021学年七年级数学苏科版下册-9.4 乘法公式-课件
例2 计算: (1)(a-2)(a2 + 4) (a+2).
2
4
(2)(2+1)(2 +1)(2 +1).
(1) (2+1)(22+1)(24+1)(28+1)(216+1);
(2) (1+½)(1+¼)(1+1/8)(1+1/16).
例3 计算: (a+b+c)(a-b-c) 计算: (1) (a-b+c)(a-b-c) (2) (a-b+c)(a+b+c)
(4) (4x2+3)(4x2−3).
为了准备大合唱比赛,某班级去商 店购买单价是51元/件的衬衫49件,售货 员刚拿起扫描枪,A同学就立刻说出应付 2499元,结果与售货员扫描出的结果完 全一样.售货员惊讶地说:“你简直是个 小神童,怎么算得这么快?”
51×49 ×2501
填空:
(1) (x+—(±—-6—6)—)(x-—±—(6—-66—))=x2-36; (2) (m+—(±-—555n—n)—)(m-—(±—5-5—n5n—n))=m2-25n2; (3) (a+b)(—b—-—a—)=b2-a2; (4) (—-—x2—-1—)(1-x2)=x4-1.
乘法公式
为了准备大合唱比赛,某班级去商 店购买单价是51元/件的衬衫49件,售货 员刚拿起扫描枪,A同学就立刻说出应付 2499元,结果与售货员扫描出的结果完 全一样.售货员惊讶地说:“你简直是个 小神童,怎么算得这么快?”
你能说出A同学神速 计算的秘诀吗?
操作:1、请在长方形纸片上裁剪出一个正方形, 使该正方形的面积最大;
B.(-x+2y)(-x-2y)
C.(-2y-x)(x+2y)
苏科初中数学七年级下册《9.4 乘法公式》PPT课件 (14).ppt
——平方差公式
计算: (1) (-x-3y)2= (2) (2x-5)(2x-5)= (3) (a+1)(a-1)= (4) (mn+a) (mn-a)= (5) (a+b)(a-b) =
1.在边长为a的正方形纸片上剪去边长为b(b<a)的小 正方形,如图(1),怎样计算图中阴影部分的面积? 2.沿图(1)中的虚线将阴影部分剪开拼成图(2),它的 面积是多少?由此,你发现了什么? 3.你还有其他方法计算图(1)中阴影部分的面积吗?
通过这节课的学习活动你有 哪些收获?
①熟记公式,弄清公式的特征
②关键是如何判断a、b
(2) (m n)(n m) (4) (2a b)(2a c)
例1 用平方差公式计算
(5x y)(5x y)
变式:
(5x2 y3 )(5x2 y3 ) (5ax2 by)(5ax2 by)
快速计算
(1)(5x y)(5x y)
(2)(5x y)(5x y) (3)(5x y)(5x y)
下列计算是否正确?如有错误,请改 正
(1) (x+2y)(x-2y)=x2-2y2
(2) (-a+b)(3;y)(x2-y)=x2-y2
(4) (-2x+3)(2x-3)=4x2-9
例3 用平方差公式计算
(1)102 98 (2)19972 19991995
……
(4)(5x y)(5x y)
怎样形式的多项式相乘可以
运用平方差公式呢?
运用平方差公式的条件: 相乘的两多项式的两项分别是
“一同一反”
例2 计算
(1)(3y x)(x 3y) (2)(m 2n)(2n m) (3)(2a b)(2a b)
计算: (1) (-x-3y)2= (2) (2x-5)(2x-5)= (3) (a+1)(a-1)= (4) (mn+a) (mn-a)= (5) (a+b)(a-b) =
1.在边长为a的正方形纸片上剪去边长为b(b<a)的小 正方形,如图(1),怎样计算图中阴影部分的面积? 2.沿图(1)中的虚线将阴影部分剪开拼成图(2),它的 面积是多少?由此,你发现了什么? 3.你还有其他方法计算图(1)中阴影部分的面积吗?
通过这节课的学习活动你有 哪些收获?
①熟记公式,弄清公式的特征
②关键是如何判断a、b
(2) (m n)(n m) (4) (2a b)(2a c)
例1 用平方差公式计算
(5x y)(5x y)
变式:
(5x2 y3 )(5x2 y3 ) (5ax2 by)(5ax2 by)
快速计算
(1)(5x y)(5x y)
(2)(5x y)(5x y) (3)(5x y)(5x y)
下列计算是否正确?如有错误,请改 正
(1) (x+2y)(x-2y)=x2-2y2
(2) (-a+b)(3;y)(x2-y)=x2-y2
(4) (-2x+3)(2x-3)=4x2-9
例3 用平方差公式计算
(1)102 98 (2)19972 19991995
……
(4)(5x y)(5x y)
怎样形式的多项式相乘可以
运用平方差公式呢?
运用平方差公式的条件: 相乘的两多项式的两项分别是
“一同一反”
例2 计算
(1)(3y x)(x 3y) (2)(m 2n)(2n m) (3)(2a b)(2a b)
【最新苏科版精选】苏科初中数学七下《9.4 乘法公式》PPT课件 (7).ppt
= a 2 + 2 a (-b) + (-b) 2 =a2- 2ab+ b2.
(a-b)2=a2-2ab+b2
也称为完全平方公式.
9.4 乘法公式(1)——完全平方公式
完全平方公式:
(a+b)2=a2 + 2ab + b2 (a-b)2=a2- 2ab + b2
语言表述:两项和(或差)的平方,等于它 们的平方和加上(或减去)它们乘积的两倍.
这个公式称为完全平方公式.
用语言叙述为:两项和的平方,等于这两个项的 平方和加上它们的积的2倍.
小试牛刀
1、 (m+n)2
2、 (2x+y)2 3、 (a+5b)2 4、 (3x+2y )2
9.4 乘法公式(1)——完全平方公式
合作探究
【例1】计算: (a-b)2.
解:(a-b)2 = [a+(-b)]2
完全平方公式的灵活运用,应掌握公式的简单变形.
9.4 乘法公式(1)——完全平方公式
【有效测试】
公式的结构特征:
首平方,尾平方,首尾二倍在中央,符号看前方.
9.4 乘法公式(1)——完全平方公式
【例2】用完全平方公式计算:
(1)(5+3p)2;
(2) (x-7y)2; (3) (4a-3)2;
请你来诊断: 下面的做法对吗?若不对,你怎么想?
(1)(x+y)2=x2+y2;
(2)(x-y)2 = x2-y2;
9.4 乘法公式(1)——完全平方公式
【拓展】
1.用简便方法计算 -- 9.82.
2. 计算 (a+b+c)2.
9.4 乘法公式(1)——完全平方公式
完全平方公式:(a+b)2=a2+2ab+b2 ; (a−b)2=a2 −2ab+b2.
(a-b)2=a2-2ab+b2
也称为完全平方公式.
9.4 乘法公式(1)——完全平方公式
完全平方公式:
(a+b)2=a2 + 2ab + b2 (a-b)2=a2- 2ab + b2
语言表述:两项和(或差)的平方,等于它 们的平方和加上(或减去)它们乘积的两倍.
这个公式称为完全平方公式.
用语言叙述为:两项和的平方,等于这两个项的 平方和加上它们的积的2倍.
小试牛刀
1、 (m+n)2
2、 (2x+y)2 3、 (a+5b)2 4、 (3x+2y )2
9.4 乘法公式(1)——完全平方公式
合作探究
【例1】计算: (a-b)2.
解:(a-b)2 = [a+(-b)]2
完全平方公式的灵活运用,应掌握公式的简单变形.
9.4 乘法公式(1)——完全平方公式
【有效测试】
公式的结构特征:
首平方,尾平方,首尾二倍在中央,符号看前方.
9.4 乘法公式(1)——完全平方公式
【例2】用完全平方公式计算:
(1)(5+3p)2;
(2) (x-7y)2; (3) (4a-3)2;
请你来诊断: 下面的做法对吗?若不对,你怎么想?
(1)(x+y)2=x2+y2;
(2)(x-y)2 = x2-y2;
9.4 乘法公式(1)——完全平方公式
【拓展】
1.用简便方法计算 -- 9.82.
2. 计算 (a+b+c)2.
9.4 乘法公式(1)——完全平方公式
完全平方公式:(a+b)2=a2+2ab+b2 ; (a−b)2=a2 −2ab+b2.
2015年春季新版苏科版七年级数学下学期9.4、乘法公式课件15
初中数学 七年级(下册)
9.4
乘法公式(2)
教学目标:
• 1.会推导平方差公式
• 2.能运用平方差公式计算.
自学指导:
• 看书77页“数学实验室”部分内容思考下 面内容: • 1、阴影面积怎么算?你有几ห้องสมุดไป่ตู้方法? • 2、观察求阴影面积几个表达式?你有什么 发现? • 3、你能利用多项式乘以多项式推导平方差 公式吗?平方差公式如何理解如何记忆?
① (5x+y)(5x-y); ② (a+2b)(2a-b); ③ (2n+m)(-m+2n);④ (c+d )(-c-d ); ⑤ (2a+b)(2a-c); ⑥ (3 y-x)(-x-3 y);
9.4 乘法公式(2)
例1 用平方差公式计算: (1)(5 x+y )(5 x-y );
(2)(2n+m)(-m+2n);
9.4 乘法公式(2)
你能用多项式乘法法则说明 (a +b)(a -b)=a2-b2 的正确性吗? 解:(a+b)(a-b)=a2-ab+ba-b2
=a2-b2.
这个公式称为平方差公式. 用语言叙述为:
两个数的和与这两个数的差的积等于
这两个数的平方差.
9.4 乘法公式(2)
1、判断下列各式可以利用平方差公式吗?为什 么?
(3)(3 y-x)(-x-3 y);
练一练:1
9.4 乘法公式(2)
例2 用简便方法计算: (1)101×99;
1 2 (2)20 ×19 . 3 3
9.4 乘法公式(2)
补充练习 用简便方法计算:
(1)22×18;
1 3 (2)10 × 9 . 4 4
练一练:1
作业
1.课本P80第 3、4 题.
9.4
乘法公式(2)
教学目标:
• 1.会推导平方差公式
• 2.能运用平方差公式计算.
自学指导:
• 看书77页“数学实验室”部分内容思考下 面内容: • 1、阴影面积怎么算?你有几ห้องสมุดไป่ตู้方法? • 2、观察求阴影面积几个表达式?你有什么 发现? • 3、你能利用多项式乘以多项式推导平方差 公式吗?平方差公式如何理解如何记忆?
① (5x+y)(5x-y); ② (a+2b)(2a-b); ③ (2n+m)(-m+2n);④ (c+d )(-c-d ); ⑤ (2a+b)(2a-c); ⑥ (3 y-x)(-x-3 y);
9.4 乘法公式(2)
例1 用平方差公式计算: (1)(5 x+y )(5 x-y );
(2)(2n+m)(-m+2n);
9.4 乘法公式(2)
你能用多项式乘法法则说明 (a +b)(a -b)=a2-b2 的正确性吗? 解:(a+b)(a-b)=a2-ab+ba-b2
=a2-b2.
这个公式称为平方差公式. 用语言叙述为:
两个数的和与这两个数的差的积等于
这两个数的平方差.
9.4 乘法公式(2)
1、判断下列各式可以利用平方差公式吗?为什 么?
(3)(3 y-x)(-x-3 y);
练一练:1
9.4 乘法公式(2)
例2 用简便方法计算: (1)101×99;
1 2 (2)20 ×19 . 3 3
9.4 乘法公式(2)
补充练习 用简便方法计算:
(1)22×18;
1 3 (2)10 × 9 . 4 4
练一练:1
作业
1.课本P80第 3、4 题.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课堂练习二:
已知 x y z 2, xy yz xz 5 , 求 x 2 y 2 z 2 的值。
例5、条件求值:
⑴已知a+b=-2,ab=-15求a2+b2.
⑵已知:a b2 4, a b2 6 ,
求:① ab ,② a2 b2 的值.
⑶已知 x y 7, xy 9,求(x y)2的值.
课堂练习三:
已知a+b=5, ab=3,求下列各式的值: ⑴(a-b)2 ;
⑵a2+b2 ;
⑶a4+b4.
例6、解方程: ⑴ 3(x 1)(x 1) 3(x 1)2 10 2
⑵ 2x 12 1 3x2 51 xx 1
课堂练习四:
解方程:
⑴ (x 3) 2 (5 x) 2 2x 2 6
) ( )( ) ( )(
) ( ) ) ( )
③(a bc)(a bc) ( ) ( )( ) ( )
例1、计算:
(1)(2x+3)2(2x-3)2
[(2x 3)(2x 3)]2
(4x2 9)2
16x4 72x2 81
(2(x) 3)( x 3)( x2 9)
(x2 9)(x2 9)
1 [a2 2ab b2 a2 2ac c2 b2 2bc c2 ] 2
1 [(a b)2 (a c)2 (b c)2 ] 2
1 [(2008x 2004 2008x - 2005)2 2
(2008x 2004 2008x 2006)2 (2008x 2005 2008x 2006)2 ] 1 [1 4 1] 3
⑴
⑵
⑵(x 5)(x 5) 2(x 1)2 3x 2 x 2
通过这节课的学习活动你有哪 些收获?
①熟记公式和公式的拓展 ②灵活运用公式进行计算
解:(1)若所填项是首项或是尾项。
则: ( )2+2(2x2)(1)+(1)2 根据完全平方式的形式,所以括号内应填±2x2 即:此单项式为4x4
(2)若所填项是中间项。 则: (2x)2±2(2x)(1)+(1)2
所以中间项是±4x
即:此单项式为±4x
数学实验室:
制作若干张长方形和正方形硬纸 片,通过图形计算(a+b+c)2的公式, 并通过运算推导这个公式.
例3、计算: ⑴ (a b c)2
⑵ (2x 3y 1)2
例4、已知 a=2008x+2004,b=2008x+2005,c=2008x+2006,求 a2+b2+c2-ab-ac-bc的值。
解:a 2 b2 c2 ab ac bc
1 (2a2 2b2 2c2 2ab 2ac 2bc) 2
x4 81
(3)(x y 4)(x y 4)
(x y) 4(x y) 4
(x y)2 42
x2 2xy y2 16
(4)2 1 22 1 24 1 264 1 1 (2 1)(2 1)(22 1)(24 1)(264 1) 1 (22 1)(22 1)(24 1)(264 1) 1 (24 1)(24 1)(264 1) 1
9.4 乘法公式(3)
乘法公式
完全平方公式:
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
平方差公式:
(a+b)(a-b)=a2-b2
公式运用
1.填空:
① a 2 b2 a b2
② a 2 b2 a b2
③ a b2 a b2
④ a b2 a b2
(264 1)(264 1) 1 2128 11 2128
课堂练习一:
计算:
①m nm2 n2 m n
②(xy 1)2 (xy 1)2
③(a b 3)(a b 3)
④ a b ca b
⑤ x 2 y 3 x 2 y 3
2
2
例2、多项式4x2+1加上一个单项式后,使它能 成为一个整式的完全平方,那么加上的单项式可 以是___________(请尽可能多的填 写正确答案).
⑤a b2 a b2
⑥a b2 a b2
公式运用 2.用乘法公式计算:
⑴ (5 3 p)2
⑵(2 7 y)2
⑶ (2a 5)2 ⑷ (5a b)(5a b)
公式运用
3.填空:
① (a b c)(a b c) (
②(a b c)(a b c) (
