人教版高中数学B版1.1.3循环结构公开课教学课件共17张(共17张)
合集下载
高中数学 1.1.3 逻辑结构 第2课时 循环结构课件 新人教A版必修3

t
程序框图:
开始 n=2015 a=200 t=0.05a a=a+t
n=n+1
a>300? 是 输出n 结束 否
开始
1、右边的程序框图,
i=1 S=0 S=S+i2
14 ? 输出S=———
i=i+1
i>3?
是 输出S 结束
否
2、画出计算 1 1 1
2 3
1 10
值的一个算法程序框图.
解答:
开始 i=1 s=0
i=i+1
s=s+1/i i≤10 否 输出s 结束 是
3、设计计算13+33+53+„+993的算法程序, 并画出相应的流程图。 解答: 算法如下:
开始
p=0 i=1 p= p+i3 i=i+2 否
S1 S2
S3 S4
p=0; i=1;
p=p+i3; i=i+2;
S5 若i>99,则输出p,否则转S3.
算法分析:
第一步,输入2015年的年生产总值. 第二步,计算下一年的年生产总值. 第三步,判断所得的结果是否大于300.若是,则 输出该年的年份;否则,返回第二步.
循环结构:
(1)循环体:设a为某年的年生产总值, 为年生产总值的年增长量,n为年份,则 t=0.05a,a=a+t,n=n+1.
(2)初始值:n=2015,a=200. (3)控制条件:当“a>300”时终止循环.
循环体 循环体 否 是 满足条件? 否
满足条件? 是
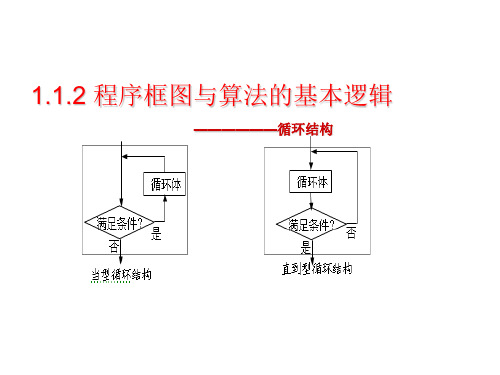
2、循环结构分为两种------当型和直到型.
(1)直到型循环在执行了一次 循环体之后,对条件进行判断,如 果条件不满足就执行循环体,直 到条件满足时终止循环.(反复执 行循环体,直到条件满足)
《循环结构》示范公开课教学PPT课件【高中数学必修3(北师大版)】

随堂练习
例1 阅读如图所示的流程图,解答下列问题:
开始
y=2000
①
4整除y 否 输出“y不是闰年”
是
100整除y
是
否 输出“y是闰年”
否 400整除y 是
输出“y 不是闰年”
输出“y 是闰年”
y:=y+1
②
否 y>2500
③
是结束
(1)变量 y 在这个算法中的
作用是什么? (2)这个算法的循环体是哪一 部分,功能是什么? (3)这个算法的处理功能是什 么?
开始
是 a=(a+b)/2
否
a=0,b=1
f((a+b)/2)=0 否
f(a)f((a+b)/2)>0
是 否 b=(a+b)/2
b-a<10-5
是 输出(a+b)/2
结束
随堂练习
3、画出计算1+2+3+……+100的值的程序框图。
解:
开始 Sum=0,i=1
Sum=Sum+i
i=i+1
否 i>100 是 输出Sum
解: 引入变量a 表示待输出的数,则 a=15n (n=1,2,3,…,66)n从 1变到66,反复输出a,就输出1000以内的所有能被3和5整除的正整数。
开始
n=1
a=15n
输出a
n=n+1 否
n>66 是
结束
新课学习
一般地,循环结构中都有 一个计数变量和累加变量。 计数变量用于记录循环次数, 同时它的取值还用于判断循 环是否终止,累加变量用于输 出结果。累加变量和计数变 量一般是同步执行的,累加一 次,记数一次。
人教版高中数学必修三课件:1.1.2-4第4课时 循环结构

学号,G1 代表第 1 个学生的成绩,Gi 代表第 i 个学生的成绩,那 么如图所示,它表示一个什么样的算法?
【思路】 本题的算法流程图是条件结构和循环结构的综合 应用,要弄清变量的含义,按流程图的流向,执行即可. 【解析】 算法如下: 第一步,i=1. 第二步,若 Gi≥90,则打印 Ni,Gi 后转到第三步,否则,直 接转到第三步.
探究 1 (1)每次循环都要注意记数变量和累加变量的变化. (2)每次循环都要验证是否满足判断条件. (3)高考中对程序框图的考查类型之一就是读图, 解决此类问 题的关键是根据程序框图理解算法的功能.考查的重点是程序框 图的输出功能、程序框图的补充,以及算法思想和基本的运算能 力、逻辑思维能力,试题难度不大,大多可以按照程序框图的流 程逐步运算而得到.
思考题 1 (1)某程序框图如图①所示,该程序运行后输出 的 k 的值是( A.4 C.6 ) B.5 D.7
(2)如图②是一个算法的程序框图,该算法所输出的结果是 ( ) 1 A. 2 3 C.4 2 B.3 4 D.5
【解析】 (1)当k=0时,S=0S=1k=1, 当S=1时,S=1+21=3k=2, 当S=3时,S=3+23=11<100k=3, 当S=11时,S=11+211>100,k=4,故k=4.
相应程序框图如图所示.
探究 2 (1)本题在设计算法时, 要注意前后两个加数相差 2, 此时计数变量表达式可以相应变成 i=i+2,又如果计算 1+4+7 +10+„+31,此时表达式可变为 i=i+3.一般地累加变量的初 始值取 0,累乘变量的初始值取 1.
(2)直到型与当型循环的本质区别:直到型循环先执行 i=i+ 2, 再判断“i>99?”, 若不满足则进入循环, 直到满足才输出 S; 而当型循环先判断“i≤99?”,若满足,则使 i =i+2,直到条 件 i≤99 不成立才结束循环,输出 S,即直到型循环先循环,再 判断,直到满足条件结束循环;而当型循环是先判断是否满足条 件,若满足,则循环,直到不满足条件才终止循环.
人教A版 高中数学 必修3 第一章 1.1.2 循环结构的程序框图课件(共16张PPT)
巩固提高
1、设计一算法,求 积:1×2×3×…×100, 画出流程图
思考:该流程图与前面 的例1中求和的流程图有 何不同?
开始 i=0,S=1
i=i+1 S=S*i 否 i>=100?
是 输出S 结束
巩固提高
2、设计一算法输出1~1000以内能被3整除的整数
开始
算法:
i=0
S1:确定i的初始值为0;
开始 i=0,S=0
否 i<100? 是 i=i+1 S=S+ i
输出S 结束
思考:将步骤A和步骤B交换位 置,结果会怎样?能达到预期结果 吗?为什么?要达到预期结果,还 需要做怎样的修改?
步骤A
步骤B 答:达不到预期结果;
当i = 100时,退出循环,i 的值未能加入到S中;修 改的方法是将判断条件改 为i<101
1.1.2 程序框图与算法的基本逻辑
——————循环结构
复习回顾
1、程序框图(流程图)的概念: 2、算法的三种逻辑结构: 3、顺序结构的概念及其程序框图: 4、条件结构的概念及其程序框图:
复习回顾
i) 顺序结构
ii) 条件结构
Yp N A
A
B
B
循环结构
循环结构:在一些算法中,也经常会出现从某处开始,
小结:
4.画循环结构流程图前: ①确定循环变量和初始条件; ②确定算法中反复执行的部分,即循环体; ③确定循环的转向位置; ④确定循环的终止条件.
循环结构的三要素:
循环变量,循环体、循环的终止条件。
其中顺序结构是最简单的结构,也是最基 本的结构,循环结构必然包含条件结构,所以 这三种基本逻辑结构是相互支撑的,无论怎样 复杂的逻辑结构,都可以通过这三种结构来表 达。
高中数学必修三1.1.2.3循环结构课件人教A版

第3课时 循环结构
-1-
第3课时 循环结构
目标导航
Z 知识梳理 Z重难聚焦
HISHISHULI
HONGNANJUJIAO
D典例透析
IANLITOUXI
1.了解两种循环结构的概念以及各自的运行过程,明确循环终止 的条件. 2.能用循环结构设计程序框图解决有关问题.
-2-
第3课时 循环结构
目标导航
Z 知识梳理 Z重难聚焦
HISHISHULI
HONGNANJUJIAO
D典例透析
IANLITOUXI
循环结构 (1)概念:在一些算法中,经常会出现从某处开始,按照一定的条件 反复执行某些步骤的情况,这就是循环结构.反复执行的步骤称为 循环体.
-3-
第3课时 循环结构
目标导航
Z 知识梳理 Z重难聚焦
HISHISHULI
HONGNANJUJIAO
-8-
第3课时 循环结构
题型一 题型二 题型三 题型四
目标导航
Z 知识梳理 Z重难聚焦 D典例透析
HISHISHULI
HONGNANJUJIAO
IANLITOUXI
含循环结构程序框图的运行 【例1】 如图,程序框图的输出结果是( )
A. B.
6
1
25 24
C. D.
4
3
11 12
-9-
第3课时 循环结构
HISHISHULI
HONGNANJUJIAO
D典例透析
IANLITOUXI
2.对循环结构的理解 剖析:(1)循环结构中包含顺序结构、条件结构. (2)循环结构内不存在无终止的循环. (3)循环结构实质上是判断和处理的结合,可以先判断,再处理,此 时是当型循环结构;也可以先处理再判断,此时是直到型循环结构. (4)循环结构中常用的几个变量: 计数变量:即计数器,用来记录执行循环体的次数,如i=i+1,n=n+1. 累加变量:即累加器,用来计算数据之和,如S=S+i. 累乘变量:即累乘器,用来计算数据之积,如P=P×i. (5)在程序框图中,一般要根据实际情况先给这些变量赋初始值. 一般情况下,计数变量的初始值为1,累加变量的初始值为0,累乘变 量的初始值为1.
-1-
第3课时 循环结构
目标导航
Z 知识梳理 Z重难聚焦
HISHISHULI
HONGNANJUJIAO
D典例透析
IANLITOUXI
1.了解两种循环结构的概念以及各自的运行过程,明确循环终止 的条件. 2.能用循环结构设计程序框图解决有关问题.
-2-
第3课时 循环结构
目标导航
Z 知识梳理 Z重难聚焦
HISHISHULI
HONGNANJUJIAO
D典例透析
IANLITOUXI
循环结构 (1)概念:在一些算法中,经常会出现从某处开始,按照一定的条件 反复执行某些步骤的情况,这就是循环结构.反复执行的步骤称为 循环体.
-3-
第3课时 循环结构
目标导航
Z 知识梳理 Z重难聚焦
HISHISHULI
HONGNANJUJIAO
-8-
第3课时 循环结构
题型一 题型二 题型三 题型四
目标导航
Z 知识梳理 Z重难聚焦 D典例透析
HISHISHULI
HONGNANJUJIAO
IANLITOUXI
含循环结构程序框图的运行 【例1】 如图,程序框图的输出结果是( )
A. B.
6
1
25 24
C. D.
4
3
11 12
-9-
第3课时 循环结构
HISHISHULI
HONGNANJUJIAO
D典例透析
IANLITOUXI
2.对循环结构的理解 剖析:(1)循环结构中包含顺序结构、条件结构. (2)循环结构内不存在无终止的循环. (3)循环结构实质上是判断和处理的结合,可以先判断,再处理,此 时是当型循环结构;也可以先处理再判断,此时是直到型循环结构. (4)循环结构中常用的几个变量: 计数变量:即计数器,用来记录执行循环体的次数,如i=i+1,n=n+1. 累加变量:即累加器,用来计算数据之和,如S=S+i. 累乘变量:即累乘器,用来计算数据之积,如P=P×i. (5)在程序框图中,一般要根据实际情况先给这些变量赋初始值. 一般情况下,计数变量的初始值为1,累加变量的初始值为0,累乘变 量的初始值为1.
人教A版高中数学必修三课件1.1.2第3课时循环结构、程序框图的画法(共32张PPT)

是 S=S+i*i
i=i+1
输出S
结束
设计一个算法的程序框图的基本思路: 第一步,用自然语言表述算法步骤. 第二步,确定每个算法步骤所包含的逻辑结构,并用相应 的程序框图表示. 第三步,将所有步骤的程序框图用流程线连接起来,并加 上两个终端框.
修凿可以使道路平直,但只有崎岖的未经 修凿的道路才是天才的道路.
上述算法的程序框图表示为: 开始
当型循环结构.
i=1
S=0
i=i+1
i≤100? 否
输出S
S=S+i 是
结束
如果用直到型循环结构,上述算法的 程序框图如何表示? 第一步,令i=1,S=0. 第二步,计算S+i,仍用S表示. 第三步,计算i+1,仍用i表示. 第四步,判断i>100是否成立.若是, 则输出S,结束算法;否则,返回第 二步.
在一些算法中,经常会出 现从某些地方开始,按照 一定条件,反复执行某一 步骤的情况,这就是循环 结构.
算法的循环结构 在一些算法中,经常会出现从某处开始,按照一定
的条件反复执行某些步骤的情况,这就是循环结构,反 复执行的步骤称为循环体.
一些循环结构用程序框图可以表示为:
循环体
否
满足条件?
是
特征:在执行了一次循环体 后,对条件进行判断,如果 条件不满足,就继续执行循 环体,直到条件满足时终止 循环.
程序框图如下: 开始 输入误差d i=1 将 2 的到小数点后第i位的不足近似值记为a
将 2 的到小数点后第i位的过剩近似值记为b
i=i+1
m=5b-5a
否 m<d?
是
输出5a
结束
4.设计一个算法求12+22+32+...+992+1002的值,并画
i=i+1
输出S
结束
设计一个算法的程序框图的基本思路: 第一步,用自然语言表述算法步骤. 第二步,确定每个算法步骤所包含的逻辑结构,并用相应 的程序框图表示. 第三步,将所有步骤的程序框图用流程线连接起来,并加 上两个终端框.
修凿可以使道路平直,但只有崎岖的未经 修凿的道路才是天才的道路.
上述算法的程序框图表示为: 开始
当型循环结构.
i=1
S=0
i=i+1
i≤100? 否
输出S
S=S+i 是
结束
如果用直到型循环结构,上述算法的 程序框图如何表示? 第一步,令i=1,S=0. 第二步,计算S+i,仍用S表示. 第三步,计算i+1,仍用i表示. 第四步,判断i>100是否成立.若是, 则输出S,结束算法;否则,返回第 二步.
在一些算法中,经常会出 现从某些地方开始,按照 一定条件,反复执行某一 步骤的情况,这就是循环 结构.
算法的循环结构 在一些算法中,经常会出现从某处开始,按照一定
的条件反复执行某些步骤的情况,这就是循环结构,反 复执行的步骤称为循环体.
一些循环结构用程序框图可以表示为:
循环体
否
满足条件?
是
特征:在执行了一次循环体 后,对条件进行判断,如果 条件不满足,就继续执行循 环体,直到条件满足时终止 循环.
程序框图如下: 开始 输入误差d i=1 将 2 的到小数点后第i位的不足近似值记为a
将 2 的到小数点后第i位的过剩近似值记为b
i=i+1
m=5b-5a
否 m<d?
是
输出5a
结束
4.设计一个算法求12+22+32+...+992+1002的值,并画
