静压以及动静压轴承流场计算基本方程以及计算方法
静压与动压及全压的计算关系

静压与动压及全压的计算关系在空气流动的世界里,静压、动压和全压就像是空气的三兄弟,各自有各自的特长,简直就像在一家餐馆里,静压是端菜的服务员,动压是那个飞奔的跑腿,而全压呢,嗯,就像是老板,统筹全局,保证一切顺利。
咱们先说说静压,这家伙可稳重了,负责的是流体对物体表面的压力。
想象一下,你在海边,风轻轻吹拂,水面平静。
这个时候,水的压力不会变化,你就能感觉到那种温柔的包围感,没错,这就是静压的魅力。
再看看动压,嘿,这家伙就有点活泼了!动压可是和流动的速度挂钩的,越快,动压就越大。
想想你在风筝放飞时的感觉,越放越高,风越猛,脸上的风劲儿那叫一个爽,动压就像那种能量,瞬间把你推向前方。
动压就像是车子在高速路上飞驰,那个加速的瞬间,真的是让人心跳加速,仿佛所有的烦恼都抛在了脑后,迎面而来的风让你感觉自己是个飞行员,酷炫无比。
全压嘛,就是这两者的结合,算得上是老大哥了。
全压是静压和动压的总和,通俗一点说,就是空气给你提供的“全方位服务”。
你在高空飞翔,既能感受到静压的安稳,又能体验到动压的刺激,那感觉简直无与伦比。
就像是你在游乐园坐过山车,静止的时候是安全的,快速的时候又能感受到心跳加速的快乐,全压就是那种混合的感受,真让人陶醉。
这三者之间的关系又是如何的呢?简单说,咱们可以用一个公式来表达它们之间的关系,静压加动压就等于全压。
这就像是一个小小的数学公式,简单得令人惊讶,但背后的意义却深得让人瞠目结舌。
你可以把它想象成一场派对,静压是稳重的守门员,动压是活跃的DJ,而全压就是热闹非凡的派对气氛,三者缺一不可,缺了哪一个,整个派对都不成其为派对。
在实际应用中,这三者的关系可不仅仅是理论上的空中楼阁。
比如在航空领域,飞行员得好好了解这些概念,才能确保飞机的安全飞行。
想象一下,如果飞行员只关心动压而忽视了静压,那可就麻烦大了。
就像一个不顾安全的骑车小子,非要追风,最后不小心摔了个四脚朝天,那可是笑话都笑不完。
又比如在风洞实验中,科学家们为了测试飞机的性能,静压和动压的变化直接影响了实验结果。
轴承的计算公式.
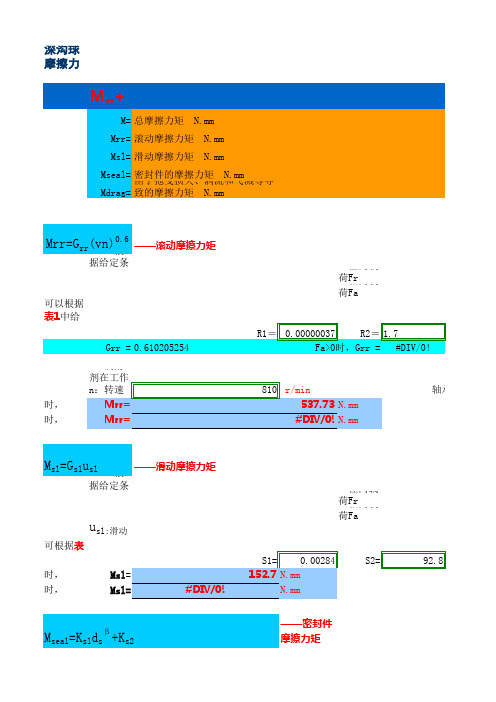
M=Mrr+Msl+Mseal+Mdrag
M= 总摩擦力矩 N.mm Mrr= 滚动摩擦力矩 N.mm Msl= 滑动摩擦力矩 N.mm Mseal= 密封件的摩擦力矩 N.mm Mdrag= 由于拖曳损失、涡流和飞溅等导致的摩擦力矩 N.mm
轴向载荷Fa
usl:滑动摩擦系数,当润滑条件良好,可取以下值:0.05(矿物油);0.04(合成油);0.1(以传动液润滑)
Gsl的值可根据表1中给出的公式计算,几何常数S则可从表2中找到
当Fa=0时, Msl=
S1= 0.00284
S2=
152.7 N.mm
92.8
当Fa>0时, Msl=
#DIV/0!
N.mm
Mseal=Ksldsβ +Ks2
——密封件摩擦力矩
Ksl:根据轴承类型而定的常数,查表3
ds:轴承肩部直径,
需轴承厂商提供:
β :根据轴承和密封圈类型而定的指数,表3可查:
Ks2:根据轴承和密封圈类型而定的常数,表3可查:
Mseal=
853.93 N.mm
0.028 98.3
Mdrag=Vm Kball dm5 n2
v:润滑剂在工作温度的运动粘度,对于脂润滑,则为基础油的粘度
n:转速
810 r/min
当Fa=0时, Mrr=
537.73 N.mm
当Fa>0时, Mrr=
#DIV/0! N.mm
轴承额定动载荷
Msl=Gslusl
——滑动摩擦力矩
Байду номын сангаас
Gsl:根据给定条件计算该变量:轴承平均直径 dm=0.5(D+d)
流体静力学基本方程

流体静力学基本方程一、静止液体中的压强分布规律重力作用下静止流体质量力:X=Y=0,Z=-g代入 Zdz)Ydy (Xdx dp ++=ρ (压强p 的全微分方程)得:dp =ρ(-g )dz =-γdz积分得: p=-γz +c即: 常数=+γpz 流体静力学基本方程对1、2两点: γγ2211p z p z +=+结论: 1)仅在重力作用下,静止流体中某一点的静水压强随深度按线性规律增加。
2)自由表面下深度h 相等的各点压强均相等——只有重力作用下的同一连续连通的静止流体的等压面是水平面。
3)推广:已知某点的压强和两点间的深度差,即可求另外一点的压强值。
p 2=p 1+γΔh4)仅在重力作用下,静止流体中某一点的静水压强等于表面压强加上流体的容重与该点淹没深度的乘积。
观看录像: 水静力学 观看动画: 静水力学基本方程演示 >>二、静止液体中的压强计算自由液面处某点坐标为z 0,压强为p 0;液体中任意点的坐标为z ,压强为p ,则:γγ00p z pz +=+∴坐标为z 的任意点的压强 :p =p 0+γ(z 0-z ) 或 p =p 0+γh三、静止液体中的等压面静止液体中质量力――重力,等压面垂直于质量力,∴静止液体中的等压面必为水平面算一算:1. 如图所示的密闭容器中,液面压强p 0=9.8kPa ,A 点压强为49kPa ,则B 点压强为39.2kPa ,在液面下的深度为3m 。
四、绝对压强、相对压强和真空度的概念1.绝对压强(absolute pressure ):是以绝对真空状态下的压强(绝对零压强)为起点基准计量的压强。
一般 p =p a +γh2. 相对压强(relative pressure ):又称“表压强”,是以当时当地大气压强为起点而计算的压强。
可“+”可“– ”,也可为“0”。
p '=p-p a3.真空度(Vacuum ):指某点绝对压强小于一个大气压p a 时,其小于大气压强p a 的数值。
第二节 流体静力学基本方程式

p P A
上式中, p — 流体的静压强,单位Pa P — 垂直作用在流体表面上的压力,单位N A — 作用面的面积,单位m2
第二节 流体静力学基本方程式
流体静力学是研究流体在外力作用下的平衡规律。 无论是在日常生活中、工业生产中,各行各业,都大量 的用到了流体的平衡规律;如流体在设备或管道内压强 的变化与测量、液体贮罐内液位的测量、设备的液封等 都以这一规律为依据。
在这一章中我们只讨论流体在重力作用下的平衡 规律。
一、压力和压强:
真
大 气
空 度
测定压强
压
绝
强
对 压
强
测定压强<大气压强
给出一压强的数值时,均应注明是表压强还是真空度;若未 注明则视为绝对压强。在记录一压强数值时,还应注明当时当地 的大气压,若未注明时,即认为当时当地的大气压为一个标准大 气压。
二、流体静力学基本方程式:
当流体相对静止而没有流动时,仍然受到重力和流体内压 力的作用;这时的重力可以认为是恒定的,而压力则是变化的。 反映静止流体内部压力(压强)变化规律的数学表达式称为流 体静力学基本方程式,它可以通过分析流体内部的静力平衡所 获得。
Z1 p2
Z2
液柱的上、下底的 面积为A
若将液柱的上底面取在液面上,设液面上方的压强为 ,
液柱下p0底面压强为 ,液柱的高p度为 ,
,则
上式改h 写为 h Z1 Z2
p p0 gh
此式即为流体静力学基本方程式。
由对上式的分析可见: (1)当液面上方的压强一定时,静止流体内任意一点压力 的大小只与液体密度及该点距液面的深度有关。因此在静止且 连续的同一种液体内,处在同一水平面上的各点压强相等;该 压力相等的水平面称为等压面。
静压力的计算

静压力的计算在物理学中,静压力是指由于流体对物体的压强而产生的力。
静压力是很多工程和科学领域中的重要概念,它的计算涉及多个因素,包括流体的密度、速度和表面积等。
本文将从理论和应用两个方面来探讨静压力的计算方法。
理论计算方法静压力的计算基于流体力学的基本原理,主要包括质量守恒和动量守恒定律。
根据质量守恒,流体通过某一截面的质量流量应保持恒定;而根据动量守恒,流体在某一截面上受到的压力和摩擦力之和等于零。
在理论计算中,我们可以利用流体的密度、速度和截面积等参数,以及流体静压力的定义来计算静压力。
静压力的定义是指一个物体受到的垂直于其表面的压力。
根据牛顿第二定律,物体所受的压力等于单位面积上施加的力。
因此,静压力可以通过将施加在物体表面上的压力乘以其表面积来计算。
静压力的计算公式为 P = F/A,其中 P 代表静压力,F 代表施加在物体上的力,A 代表物体的表面积。
如果流体是静止的,那么施加在物体上的力就是由于流体自身的压强所产生的。
根据流体静压力的公式,我们可以将静压力表达为P = ρgh,其中ρ 代表流体的密度,g 代表重力加速度,h 代表流体的垂直高度。
应用与实例静压力的计算不仅在理论研究中有重要应用,也在实际工程和科学实验中起到关键作用。
下面将通过一些实际例子来说明静压力计算的应用。
在航空航天工程中,静压力的计算对于设计和测试飞机和航天器的气动性能非常重要。
静压力传感器被安装在飞机的机身上,用于测量飞机周围流体的静压力。
通过测量静压力分布,可以评估飞机在不同速度和高度下的气动性能,进而优化设计和改进飞行控制系统。
在液压系统中,静压力的计算用于确定系统中液体的压力分布。
液压系统是一种广泛应用于机械和工程领域的控制系统,它利用液体的力学性质来传递力和能量。
静压力的计算对于设计和分析液压系统的效率和可靠性非常重要。
除此之外,静压力的计算还在地下水和地质工程中有所应用。
地下水的静压力对于地下水位和水文循环的研究至关重要。
完整的轴承选型计算方法PPT课件

Fr
为了与 C 在相同的条件下进行比较,引入 当量动载荷的概念。
19
推力轴承: 45°<α ≤90° ,主要承受轴向载荷; 推力角接触轴承—— 45°<α< 90°的推力轴承 轴向接触轴承——α=90°的推力轴承
20
2、按滚动体的种类可分为:球轴承和滚子轴承
Gzxz.avi
21
22
23
24
25
26
27
28
29
滚动轴承代号: 前置代号
基本代号
•装拆需要 •摩擦状态
整体轴承(特殊类型:自动调心式轴承)
剖分轴承 液体摩擦(长期运转,精度要求高)
动压轴承 静压轴承
非液体摩擦
5
1.径向滑动轴承 (1)整体式滑动轴承
轴承座
螺纹孔
油杯孔
整体轴套(轴瓦)
特点:结构简单,成本低廉。 因磨损而造成的间隙无法调整。 只能从沿轴向装入或拆出。
应用:低速、轻载或间歇性工作的机器中。
(二)、寿命计算
目的 — 根据工作条件和设计要求,选择合适的轴承尺寸。
载荷与额定寿命的关系曲线:
P
轴承的疲劳曲线
PL10 常数
C P1
式中:P 为当量动载荷;
P2
L10为P 作用下的额定寿命。
ε为寿命指数,球轴承ε =3,滚 子轴承ε =10/3 。
1 L1 L2
L10 106r
37
当载荷为额定动载荷C 时:PL10C106
Fa
Fa
Fa
Fa
8
轴瓦的材料
•减摩性:材料副具有较低的摩擦系数。 •耐磨性:材料的抗磨性能,通常以磨损率表示。 •抗咬粘性(胶合):材料的耐热性与抗粘附性。 •摩擦顺应性:材料通过表层弹塑性变形来补偿轴承滑动表面初始配合 不良的能力。
流体静力学基本方程式
第一节 流体静力学基本方程式流体静力学是研究流体在外力作用下达到平衡的规律。
在工程实际中,流体的平衡规律应用很广,如流体在设备或管道内压强的变化与测量、液体在贮罐内液位的测量、设备的液封等均以这一规律为依据。
1-1-1流体的密度一、密度单位体积流体所具有的质量,称为流体的密度,其表达式为:Vm =ρ (1-1) 式中 ρ——流体的密度,kg/m 3;m ——流体的质量,kg ;V ——流体的体积,m 3。
不同的流体密度不同。
对于一定的流体,密度是压力P 和温度T 的函数。
液体的密度随压力和温度变化很小,在研究流体的流动时,若压力和温度变化不大,可以认为液体的密度为常数。
密度为常数的流体称为不可压缩流体。
流体的密度一般可在物理化学手册或有关资料中查得,本教材附录中也列出某些常见气体和液体的密度值,可供查用。
二、气体的密度气体是可压缩的流体,其密度随压强和温度而变化。
因此气体的密度必须标明其状态,从手册中查得的气体密度往往是某一指定条件下的数值,这就涉及到如何将查得的密度换算为操作条件下的密度。
但是在压强和温度变化很小的情况下,也可以将气体当作不可压缩流体来处理。
对于一定质量的理想气体,其体积、压强和温度之间的变化关系为将密度的定义式代入并整理得'''Tp p T ρρ= (1-2) 式中 p ——气体的密度压强,Pa ;V ——气体的体积,m 3;T ——气体的绝对温度,K ;上标“'”表示手册中指定的条件。
一般当压强不太高,温度不太低时,可近似按下式来计算密度。
RTpM =ρ (1-3a ) 或 000004.22Tp p T Tp p T M ρρ== (1-3b ) 式中 p ——气体的绝对压强,kPa 或kN/m 2;M ——气体的摩尔质量,kg/kmol ;T ——气体的绝对温度,K ;R ——气体常数,8.314kJ/(kmol ·K )下标“0”表示标准状态(T 0=273K ,p 0=101.3kPa )。
滑动轴承计算
层流流动、不计重力、 大气压影响、油不可压缩
平衡方程:
∂p ∂τ ∂τ pdzdy − p + dx dzdy + τ + dydz − τ+ dy dzdx = 0 ∂x ∂y ∂y
整理可得: ∂p = − ∂τ ∂x ∂y
∂v τ = -η ∂y
∂p ∂ 2v ⇒ =η 2 ∂x ∂y
流体的压力变化与速度的变化情况成正比
1.油层的速度分布
1 ∂p = 2 η ∂x ∂y ∂ 2v
v(h - y ) y (h − y ) ∂p 积分得:u = − h 2η ∂x
直线 抛物线
2.润滑油流量
vh h ∂p Q = udy ⇒ − 0 2 12η ∂x
两相对运动物体的摩擦表面借助相对速度产生的油膜把两表面完全隔开由油膜产生的压力来平衡外载荷楔效应承载机理平行板相对运动流速直线分布油无内压力不平行板相对运动流速变化油有内压力假设
§12—7 液体动力润滑径向滑动轴承设计计算 一.流体摩擦
流体中任意点处切应力均与该处流体的速度梯度成正比
比例系数η—粘度—流体的
c —比热容 见附录 ρ—密度 αs—传热系数 f—摩擦系数
q ψvBd —耗油量系数
3 校核进口油温ti
两种情况:
∆t ti = t m − 2
tm——给定的平均温度 tm =50~75℃
ti >35~40℃ 容易达到热平衡,可降低tm ,增大粗造度 ti <35~40℃ 不易达到热平衡,可加大间隙,降低粗造度
减少 增大
流体动力润滑的必要条件:
⑴ 流体必须有粘度,供应充分 ⑵ 两表面必须有相对速度,油从大口进,小口出 ⑶ 相对滑动两表面必须现成收敛的楔形油隙
高速动静压气体轴承动态流场模拟与失稳分析
高速动静压气体轴承动态流场模拟与失稳分析高速动静压气体轴承动态流场模拟与失稳分析引言:高速动静压气体轴承是一种重要的工业设备,广泛应用于航空航天、汽车、机械制造等行业。
其作用是通过动态气膜压力来支撑轴承的转动部件,减小接触面的摩擦和磨损,提高设备的运行效率和寿命。
然而,在轴承运行过程中,由于复杂的流场变化,会产生不稳定现象,甚至导致轴承失效。
因此,通过动态流场模拟和失稳分析研究高速动静压气体轴承的运行机理和优化设计具有重要意义。
一、高速动静压气体轴承的运行原理高速动静压气体轴承由固定套、转动套、导向螺旋槽和气体供应系统等组成。
在轴承运转时,通过润滑气体的高速旋转和压力控制,形成动态气膜,使转动套浮起于固定套之上,实现轴向和径向的支撑和导向作用。
动静压气体轴承的运行机理主要包括气体压力、气膜形成和维持、轴心位移等关键参数。
二、动态流场模拟方法1. 基于Navier-Stokes方程的数值模拟方法:基于连续介质假设,通过求解Navier-Stokes方程组,考虑非定常性、可压缩性和湍流效应,描述高速动静压气体轴承的动态流场变化。
采用数值方法可以较为准确地模拟轴承工作过程中气膜厚度、气膜压力分布等重要参数的变化规律。
2. 流体-结构耦合方法:考虑到高速动静压气体轴承在工作过程中受到的外部加载和转动套的变形,采用流体-结构耦合方法对轴承进行模拟。
该方法将轴承系统划分为流体域和结构域,通过求解流体域和结构域的相互作用,可以更加真实和准确地描述轴承的动态特性和失稳机理。
三、失稳分析方法1. 线性稳定性分析:通过对动静压气体轴承系统进行线性稳定性分析,得到关键频率和振型。
通过求解特征值问题,可以判断系统的稳定性和失稳特性,并对参数进行优化。
2. 非线性动力学分析:考虑到高速动静压气体轴承系统存在非线性特性,如气体的可压缩性、流体力学的非粘性等,采用非线性动力学分析方法来研究系统的运行稳定性和失稳机理。
通过数值求解非线性动力学方程,可以得到系统的运动状态、相位图和吸引子等信息,进而对轴承的设计和改进提供指导。
流体动力润滑的基本方程(参考模板)
流体动力润滑的基本方程流体动力润滑理论的基本方程是流体膜压力分布的微分方程。
它是从粘性流体动力学的基本方程出发,作了一些假设条件后得出的,这些假设条件是:流体为牛顿流体;流体膜中流体的流动是层流;忽略压力对流体粘度的影响;略去惯性力及重力的影响;认为流体不可压缩;流体膜中的压力沿膜厚方向不变。
下图中,两平板被润滑油隔开,设板A沿x轴方向以速度v移动;另一板B为静止。
再假定油在两平板间沿z轴方向没有流动(可视此运动副在z轴方向的尺寸为无限大)。
现从层流运动的油膜中取一微单元体进行分析。
由图可见,作用在此微单元体右面和左面的压力分别为p 及,作用在单元体上,下两面的切应力分别为τ及。
根据x方向的平衡条件,得整理后得根据牛顿流体摩擦定律,得,代入上式得该式表示了压力沿x 轴方向的变化与速度沿y轴方向的变化关系。
下面进一步介绍流体动力润滑理论的基本方程。
1、油层的速度分布将上式改写成(a)对y 积分后得(b)(c)根据边界条件决定积分常数C1及C2:当y=0时,v= V; y=h(h 为相应于所取单元体处的油膜厚度)时,v=0,则得代入(c)式后,即得(d)由上可见,v由两部分组成:式中前一项表示速度呈线性分布,这是直接由剪切流引起的;后一项表示速度呈抛物线分布,这是由油流沿x方向的变化所产生的压力流所引起的。
2、润滑油流量当无侧漏时,润滑油在单位时间内流经任意截面上单位宽度面积的流量为(e)将式(d)代入式(e)并积分后,得(f)设在p=pmax处的油膜厚度为h0(即时,h=h0),在该截面处的流量为(g)当润滑油连续流动时,各截面的流量相等,由此得整理后得该式为一维雷诺方程。
它是计算流体动力润滑滑动轴承(简称流体动压轴承)的基本方程。
可以看出,油膜压力的变化与润滑油的粘度、表面滑动速度和油膜厚度及其变化有关。
经积分后可求出油膜的承载能力。
由雷诺方程及图示的压力分布也可以看出,在h>h0段,速度分布曲线呈凹形,,即压力沿x方向逐渐增大;而在h<h0段,速度分布曲线呈凸形,,压力沿x方向逐渐降低。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
流场基本方程在静压和动静压轴承设计当中,为了计算油膜的承载能力,就需要计算油膜的压力分布。
而计算流体的流量,就需要计算油膜内的速度分布。
另外,需要计算轴承的摩擦阻力,那就要计算轴承面上的剪应力分布。
特别的,在轴高速转动时,进油温度和出油温度之间有温度差。
考虑到粘度和温度之间的耦合关系,若要准确计算油膜的压力分布,还需要计算轴承面上的温度分布。
轴承间隙中的润滑液体为黏性流体,根据动量、质量和能量守恒定律以及微元的力平衡条件,可以推导出纳维-斯托克斯方程(流体的动量方程)、连续方程、剪应力方程、能量方程和热传导方程。
再加上润滑液体的状态方程(粘温方程、粘压方程)、油膜的几何方程以及轴颈和轴承的变形方程,通过这些方程之间的联立,就可以求解流固耦合、粘温耦合下的油膜压力分布。
纳维-斯托克斯方程(Navier-Stokes)和雷诺方程(Reynolds)黏性流体运动方程是研究润滑流体的基本方程。
对于不可压缩的牛顿流体,其运动方程,即纳维-斯托克斯方程可以表示为公式1{ρdudt=ρX−ðpðx+μ∇2uρdvdt=ρY−ðpðy+μ∇2vρdwdt =ρZ−ðpðz+μ∇2w式中,u、v、w分别为流速沿x、y、z坐标轴方向的分量;X、Y、Z为单位质量的体力沿着x、y、z坐标轴方向的分量;p为油膜压力;ρ为液压油的密度;μ为液压油的粘度;对时间的全微分可以表示为ddt =ððt+uððx+vððy+wððz;定义拉普拉斯算子∇2=ð2ðx2+ð2ðx2+ð2ðz2。
等式的左侧项为微元体的惯性力,而等式的右侧项表示的是微元体的体力、压力和黏性剪切力。
将x-y-z坐标系下的纳维-斯托克斯方程展开后可以表示为:{ρdudt=ρX−ðpðx+μ(ð2uðx2+ð2uðy2+ð2uðz2)ρdvdt=ρY−ðpðy+μ(ð2vðx2+ð2vðy2+ð2vðz2)ρdwdt=ρZ−ðpðz+μ(ð2wðx2+ð2wðy2+ð2wðz2)对于有些流场(比如环形的止推轴承面或是展开后为部分圆环的圆锥轴承面),圆柱坐标下进行计算会变得更加容易些。
在这里也给出了圆柱坐标下的纳维-斯托克斯方程。
公式 2{ðV rðt+(V∙∇)V r−Vθ2r=X−1ρðpðr+υ(∇2V r−2r2ðVθðθ−V rr2)ðVθðt+(V∙∇)Vθ+V r Vθr=θ−1ρrðpðθ+υ(∇2Vθ+2r2ðV rðθ−Vθr2)ðV zðt+(V∙∇)V z=Z−1ρðpðz+υ∇2V z式中,υ为液压油的运动粘度。
上式中,(V∙∇)()=V rð()ðr +Vθrð()ðθ+V zð()ðz。
拉普拉斯算子在圆柱坐标下的表达式是∇2()=1rððr[rð()ðr]+1r2ð()ðθ2+ð2()ðz2纳维-斯托克斯方程共三个方程但是含有了四个未知量,分别为u、v、w和p,为了是方程有解,必须补充流体连续方程。
在x-y-z坐标系统下的流体连续方程表示如下:公式 3 dpdt +ð(pu)ðx+ð(pv)ðy+ð(pw)ðz=0如果研究轴承稳定转动时的情况,液压油的状态与时间无关(即视为定常流动),dpdt=0,则上式可以写为公式 4 ð(pu)ðx +ð(pv)ðy+ð(pw)ðz=0圆柱坐标系下的流体连续方程为,公式 5 ðpðt +1rð(rρV r)ðr+1rð(ρVθ)ðθ+ð(ρV z)ðz=0对于定常流动和不可压缩流体,上式可以写为公式 6 1r ð(rρV r)ðr+1rð(ρVθ)ðθ+ð(ρV z)ðz=0公式7 1r ð(rV r)ðr+1rð(Vθ)ðθ+ð(V z)ðz=0联立纳维-斯托克斯方程和流体连续方程,理论上式可以求解流场的压力分布问题的。
然而直接求解这四个方程联立的解是相对比较困难的。
由于油膜厚度相较于油膜的长度和宽度,其尺度要小的多,我们往往做出如下的假设(该假设主要是针对x-y-z坐标系下纳维-斯托克斯方程的简化进行叙述的。
但大同小异,略加修改就可以用在圆柱坐标下的纳维-斯托克斯方程上):图 1 流体在间隙中流动示意图(1)由于油膜的厚度h(x)与它的宽度x和长度z比较起来非常小,所以可以忽略油膜的弯曲,并且用平动代替其他运动(在径向轴承,液压油的流动存在转动)。
(2)流体的流动为层流,即流体分层地沿着X轴和Z轴方向运动,即ðpðy=0实际上,流态是通过雷诺数计算后决定的。
当雷诺数达到一定值时,流体就从层流转变为紊流。
滑动轴承中的雷诺数的表达式为:公式8 R e=U∗ℎaλ式中,U是轴的圆周速度,ℎa为平均油膜厚度(即半径间隙),λ为运动粘度。
对于移动引起的剪切流,实验求得的临界雷诺数R ec=1900;对于压力引起的压力流,一般临界雷诺数R ec=2000。
在轴承当中,同时存在表面移动和由压力差引起的流动,在这种情况下的流动更不稳定,R ec<2000。
一般轴承设计当中取R ec=1000。
——《基于FLUENT的机床主轴动压轴承静特性研究》黄首峰(3)作用于油膜的体力为0,即X=Y=Z=0(4)与黏性剪应力相比,油膜的惯性力可以忽略不计,即du dt =dvdt=dwdt=0对于圆柱坐标下的纳维斯托克斯方程来说,方程左侧的部分惯性力项也可以直接忽略掉。
(5)流体在固体表面无滑动,即所谓的无滑移边界条件。
也就是说,与轴表面相接触的一层流体是与轴颈表面一起运动的。
(6)与速度梯度ðuðy 、ðwðy相比,其他的速度梯度都可以忽略不计。
做出这个假设的原因是u、w都要比v大得多,然而y方向油膜厚度的尺度却要比轴承展开后x、z方向的尺度要小得多,因此可以得到:∇2u=ð2u ðy2∇2v=0∇2w=ð2w ðy2(7)如图1所示,U1、U2为油膜上下固体表面沿X方向的运动速度,且为常数。
(8)如果暂时不考虑轴承温度场的温度分布,认为液压油的粘度μ和密度ρ为常数。
直角坐标系下的雷诺方程推导在这一系列假设条件之下,纳维-斯托克斯方程就可以简化为欧拉方程的形式,即:公式9 {ð2uðy2=1μðpðxð2w ðy2=1μðpðz上式,只含有了三个未知量分别为u、w、p。
将上两式在边界油膜上下边界方向积分。
y=0,u=U1;y=h,u=U2y=0,w=0;y=h,w=0可以得到x方向流速u和z方向流速w分布的表达式:公式 10 {u =12μðp ðx[y (y −ℎ)]+ℎ−y ℎU 1+yℎU 2w =12μðp ðz[y(y −ℎ)]对上式作如下的说明:x 方向的流速u 为压力梯度引起的压力流动和由表面滑动引起的剪切流动的流速分布之总和。
z 方向的流速w 只由压力梯度引起的压力流动一项。
将上式带入流量连续方程当中,并对油膜的厚度方向进行积分:公式 11 ∫ðv ðydy ℎ0=−12(∫ððx [ðpμðxy(y −ℎ)]dy ℎ0+∫ððz ℎ0[ðpμðzy(y −ℎ)]dy)−∫ððx[ℎ−y ℎU 1+ℎ0y ℎU 2]dy方程左边,因为轴承是固定不动的,∫ðvðydy =u y |0ℎℎ=−U y U y 为轴沿y 方向的运动速度。
右侧积分上下限h 为x 、z 的函数h(x,z)。
利用如下关系进行积分: ∫ðða ℎ(a )f (y,a )dy =ðða ∫f(y,a)dy ℎ(a)0−f(ℎ,a)ðℎða则公式 11的右端可以表示为:ð12μðx (ℎ3ðp ðx )+ð12μðz (ℎ3ðp ðz )−(U 1−U 22)ðℎðx 则雷诺方程可以写为公式 12 −U y =ð12μðx(ℎ3ðp ðx)+ð12μðz(ℎ3ðp ðz)−(U 1−U 22)ðℎðx也可以写成:公式 13ð12μðx(ℎ3ðp ðx)+ð12μðz(ℎ3ðp ðz)=(U 1−U 22)ðℎðx+ðℎðt在径向轴承当中,如果载荷稳定,则ðℎðt=0。
而轴承又是不动的,即U 2=0。
则上式可以进一步写为:公式 14ððx(ℎ3ðp ðx)+ððz(ℎ3ðp ðz)=6μUðℎðx式中,U 为轴转动的线速度大小,但并不包括方向。
由于数学上的困难,它并未有解析解。
关于该二阶偏微分方程的数值解法有有限差分法、有限元法。
在后面的章节会对有限元法进行详细的叙述。
当设计静压支撑(包括直线轴承)时,雷诺方程表示为最简形式:公式 15ððx(ℎ3ðp ðx)+ððz(ℎ3ðp ðz)=0圆柱坐标下的雷诺方程推导类似的,圆柱坐标系下的纳维-斯托克斯方程可以简化为公式 16 {−V θ2r=−1ρðp ðr +υ(ð2V r ðz 2−V rr2)V r V θr =−1ρr ðpðθ+υ(ð2V θðz 2−V θr 2)当转速不太高的时候,还可以将这些项略去,V θ2r(离心加速度项),V r V θr(科式加速度项),Vrr2,V θr 2。
