小学三年级奥数_____一笔画问题
小学奥数习题版三年级几何一笔画学生版

知识要点一笔画一笔画【例1】 判断下列各图能否一笔画出,并说明理由。
【例2】 判断下列各图能否一笔画出,并说明理由。
(6)(4)(3)(2)(1)多笔画【例3】 下面各图至少需要几笔才能画成?(3)(2)(1)【例4】判断图中的三个图形各需要几笔才能画出?请把能一笔画的图形的画法用字母和箭头表示出来。
【例5】观察下面的图形,判断其需要几笔才能画出?多笔画改一笔画【例6】下图中的两个图形均不能一笔画出,你能将原图形中的某一线段取消使之能够一笔画成吗?【例7】下图能一笔画成吗?如果不能,请你添上或减去一根线段使它能一笔画出来。
【例8】 判断下列图形能否一笔画.若能,请给出一种画法,若不能,请说明需要几笔才能画出,并请加一条线或去一条线,将其改成可一笔画的图形.FI H EBA G图aD C 图 bJ I H GDCLKF E BA 图 c【例9】 将下图改为一笔画.生活中的一笔画【例10】 (第十二届“华罗庚金杯”少年数学邀请赛初赛试题(小学组))同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻的旗帜色彩不同,则贝贝至少需要___种颜色的旗子。
如果贝贝从某营地出发,不走重复的路就______(填“能”或“不能”)完成这项任务。
【例11】 下图是一个公园的道路平面图,要使游客走遍每条路且不重复,问出、入口应设在哪里?HI FED CBA【例12】下图中每个小正方形的边长都是100米。
小明沿线段从A点到B点,不许走重复路,他最多能走多少米?【例13】小明假日去看画展,展览分四个展区,展览馆内外一共有六扇门,平面图如下,请问小明能否不重复地穿过每一扇门?如果不能,请说明理由。
如果能,应从哪开始走?【例14】下图是某博物馆的平面图,共有五个主题展馆,相邻两馆之间有门相通,并且设有入口.博物馆的入口以及展馆门口挂了颜色各异的彩旗,请问你能否从入口进入一次不重复地穿过所有的门采集到所有颜色的彩旗吗?如果可以,请指明穿行路线,如果不能,应关闭哪个门就可以办到?【例15】在一条河的中间有两个小岛,周围有六座桥与两岸相通.问能否找到一条路线,从一岸出发,不重复走遍所有的桥,然后到达对岸?【例16】如下图所示,两条河流的交汇处有两个岛,有七座桥连接这两个岛及河岸.问:一个散步者能否一次不重复地走遍这七座桥?两条支流在城市中心汇合,汇合处有一座小岛A和一座半岛D,人们在这里建了一座公园,公园中有七座桥把河两岸和两个岛连接起来(如下图所示).如果游人要一次走过这七座桥,而且对每座桥只许走一次,问如何走才能成功?这个有趣的问题引起了著名数学家欧拉的注意,他证明了七桥问题中提到的走法根本不存在.下面,我们考虑如下两个问题:⑴若再架一座桥,游人能否走遍所有这八座桥?若能,这座桥应架在何处?若不能,请说明理由.⑵架设几座桥可以使游人走遍所有的桥回到出发地?【例18】下图是某博物馆的平面图,相邻两个展厅之间有一扇门相通,每一个展厅都有一门通往馆外.问参观者能否不重复地一次穿过每一扇门?若能,请找出一条可行路径,若不能,请说明理由.如果允许关闭某一扇门,问参观者能否不重复地穿过每一扇开着的门?【例19】(2008年中国台湾小学数学竞赛选拔赛复赛)有一个城市的街道图是由一些矩形所构成,如下图。
小学三年级奥数-一笔画问题

1727年在欧拉20岁的时候,被俄国请去在圣彼得堡(原列宁格勒)的科学院做研究。他的德国朋友告诉了他这个曾经令许多人困惑的问题。 欧拉并没有跑到哥尼斯堡去走走。他把这个难题化成了这样的问题来看:把二岸和小岛缩成一点,桥化为边,于是“七桥问题”就等价于下图中所画图形的一笔画问题了, 这个图如果能够一笔画成的话,对应的“七桥问题”也就解决了。
画一画,找一找
下面的图形,哪些能一笔画出?哪些不能一笔画出
根据今天学习知识,先判断下列图形能不能一笔画成?再想一想该从哪里开始画?最后再动手画画看。
练习
一辆洒水车要给某城市的街道洒水,街道地图如下:你能否设计一条洒水车洒水的路线,使洒水车不重复地走过所有的街道,再回到出发点?
菜市场
小广场
园林工人张大伯为花园浇花,怎样走才能不重复地走遍图中的每条小路?
演讲完毕,感谢观看
邮递员叔叔向10个地点送信一次走完,不走重 复路,应该怎样走合适?(看下图)
文具店
超市
电器城
服装城
甲乙两个邮递员去送信,两人以同样的速度走遍所有的街道,甲从A点出发,乙从B点出发,最后都回到邮局(C)。如果要选择最短的线路,谁先回到邮局?
甲
邮局
乙
下面的图能不能一笔画成?如果能,应怎样画? 2、3、4、5、6六个点都是两条线的交点,是偶点,7是四条线的交点,,也是偶点,没有奇点,能一笔画成。
两条相交的线处都有一个交点。
数一数下列图形各有几个交点?
( )个
( )个
( )个
( )个
我们刚才画的图形都有几个交点?几个双数点?几个单数点?
判断下列图形能否一笔画
不连通的图形不能一笔画
连通的图形有可能一笔画
一笔画问题-三年级-奥数

例1
计算
(1010)2+(1100)2
一位数加法口诀; 0+0=0, 1+0=1, 0+1=1, 1+1=10. 即“满二进一”。
例2
• 计算
• (1101)2-(110)2
从以上例题中可以看出,二进制数的加 减法比十进制的加减法更简单,数位对 齐以后要记住其特点是“满二进一”、 “借一当二”即可
公元3012年,火星上有了人类。还有一片人类从 未发现的原始森林,森林里树木杂草丛生,有各种各 样的怪兽和外星人出没。突然有一天有个人类在森林 里发现了一条奇怪的路线,这是外星人设计的挑选精 英伙伴的谜题。题是这样要求的:选择一个图形,并 且不重复的走过每条路。选错图形或走错了路都要被 送回被污染的地球。 下面哪条路线可以呢?
练习
• 计算
• (1).(1010)2+(1001)2
• (2).(1111)2+(1001)2
• (3).(1101101)2-(101101)2 • (4).(1011)2-(101)2
哈哈,本故事纯属虚构, 如有雷同不胜荣幸!
通过观察我们发现:
图1,经过几次尝试后我们发现不能一笔画。
图2,无论从哪一点起都能一笔画成。
事实上,一笔画是有规律的:能一笔画 的图,要么只有偶点(从这个点出发的线段 有偶数条),没有奇点。要么只有两个奇点。
图1
图2
例2.判断下列图形能否一笔画成。
A
C
小窗口播放
二进制数的加减法
什么叫二进制呢?
18世纪德国数理哲学大师莱布尼兹从他的传教士 朋友鲍威特寄给他的拉丁文译本《易经》中,读到 了八卦的组成结构,惊奇地发现其基本素数(0) (1),即《易经》的阴爻- -和__阳爻,其进位制就 是二进制,并认为这是世界上数学进制中最先进的。 二进制数据是用0和1两个数码来表示的数。它 的基数为2,进位规则是“逢二进一”,借位规则是 “借一当二”。 二进制是一种非常古老的进位制,由于在现代 被用于电子计算机中,而旧貌换新颜变得身价倍增 起来。
三年级上册数学课件奥数一笔画全国通用版共7张PPT

❖ 3、如何改成一笔画
❖ 关键是想办法减少奇点得个数
2
提示:要想走完每 一条路,又能尽快 出来,那么最短的 路线就是第一步:先看是不是连通图 ❖ 第二步:标奇偶点,看奇点个数(两个以 上的不可以)
❖ 2、如何一笔画出
❖ 第一种:都是偶点的,从任意点开始,还是到这一点结束 ❖ 第二种:只有两个奇点的,必须以其中一个奇点位起点,
6
3
3
4
3
4
3
3
2
(2)
方法:
2
2
2
(3)
1、标奇偶点;2、看奇点个数:都是偶点 得一定可以,并且从任意点开始,还是到 这一点结束;只有两个奇点,其余都是偶 点得可以一笔画出,但必须以其中那个一 个奇点位起点,另一几点位终点;奇点个 数超过两个就一定不能一笔画出。
例3
23
判断下面图形是否能一笔画出,如果不能请改
学习目标
❖ 1、判断是不是一笔画图形; ❖ 2、怎么画; ❖ 3、怎么改成一笔画。
例1 判断一下图形是否能一笔画出
(1)
(2)
(3)
特点:(1) (2)是不连通图 (3)(4)是连通图
(4)
例2 下面的连通图那些可以一笔画出,那些不能?
22
3
2
2
3
2
2
44 2
2
44
2
22 (1)
3
3
3 (4)
3
成可以一笔画得图形
4 32
3
4
4
4
4
4
4
4
3
4
3
2 33
2
4
4
(1)
三年级奥数有趣的一笔画
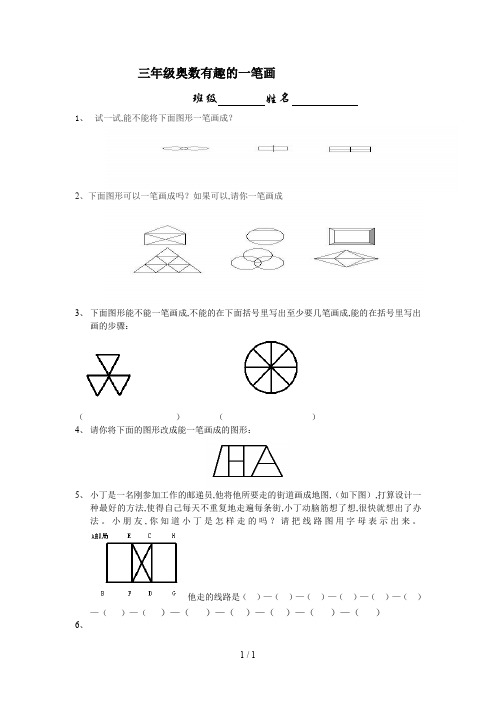
1 / 1 三年级奥数有趣的一笔画
班级 姓名
1、 试一试,
能不能将下面图形一笔画成?
2、下面图形可以一笔画成吗?如果可以,
请你一笔画成
3、 下面图形能不能一笔画成,不能的在下面括号里写出至少要几笔画成,能的在括号里写出
画的步骤:
( ) ( )
4、 请你将下面的图形改成能一笔画成的图形:
5、 小丁是一名刚参加工作的邮递员,他将他所要走的街道画成地图,(如下图),打算设计一
种最好的方法,使得自己每天不重复地走遍每条街,小丁动脑筋想了想,很快就想出了办法。
小朋友,你知道小丁是怎样走的吗?请把线路图用字母表示出来。
他走的线路是( )—( )—( )—( )—( )—( )
—( )—( )—( )—( )—( )—( )—( )
6、。
小学奥数 奇妙的一笔画 精选例题练习习题(含知识点拨)

所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 一笔画问题:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点; (4)奇点个数超过两个的图形,一定不能一笔画. 多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?J O I H G FED CBA【例 2】 同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻营地的旗帜色彩不同,则贝贝最少需要 种颜色的旗子,如果贝贝从某营地出发,不走重复路线就 (填“能”或“不能”)完成任务.【例 3】 判断下列图a 、图b 、图c 能否一笔画.图aNML KF DECBA 图bODCBA图cGFEDCBA例题精讲知识点拨4-1-5.奇妙的一笔画【例 4】 下面图形能不能一笔画成?若果能,应该怎样画?(1)(2)(3)【例 5】 下面的图形,哪些能一笔画出?哪些不能一笔画出?【例 6】 右图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?【巩固】右图是某展览馆的平面图,一个参观者能否不重复地穿过每一扇门?如果不能,请说明理由.如果能,应从哪开始走?E CDB A【例 7】 下图中的线段表示小路,请你仔细观察,认真思考,能够不重复的爬遍小路的是甲蚂蚁还是乙蚂蚁?该怎样爬?乙甲【例 8】 能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形?【例 9】 下图是儿童乐园的道路平面图,要使游客走遍每条路并且不重复,那么出、入口应设在哪里?IHGFEDC BA【例 10】 邮递员叔叔向11个地点送信一次信,不走重复路,怎样走最合适?【例 11】 观察下面的图,看各至少用几笔画成?(1)A ED HCF G B (2)(3)【例 12】 在3×3的方阵中每个小正方形的边长都是100 米.小明沿线段从A 点到B 点,不许走重复路,他最多能走多少米?【例 13】 有16个点排成的44 方阵。
三年级上册数学试题-奥数.几何.一笔画与多笔画(C级)沪教版(含答案)
一、一笔画的认识所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从上图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.所谓一笔画,就是从图形上的某点出发,笔不离开纸,而且每条线都只画一次不准重复.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 二、 一笔画问题(1) 能一笔画出的图形必须是连通的图形;(2) 凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3) 凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点.以另一个奇点作为终点;(4) 奇点个数超过两个的图形,一定不能一笔画.三、多笔画问题我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.(1) 知道什么样的的是奇点?什么样的点是偶点.重难点知识框架一笔画与多笔画C(2)知道什么样的图形可以一笔画出.(3)不能一笔画出的图形叫做多笔画图形,多笔画图形的笔画数与什么有关呢?例题精讲【例 1】下图是某地区所有街道的平面图.甲、乙二人同时分别从A、B出发,以相同的速度走遍所有的街道,最后到达C.如果允许两人在遵守规则的条件下可以选择最短路径的话,问两人谁能最先到达C?【解析】本题要求二人都必须走遍所有的街道最后到达C,而且两人的速度相同.因此,谁走的路程少,谁便可以先到达C.容易知道,在题目的要求下,每个人所走路程都至少是所有街道路程的总和.仔细观察上图,可以发现图中有两个奇点:A和C.这就是说,此图可以以A、C两点分别作为起点和终点而一笔画成.也就是说,甲可以从A出发,不重复地走遍所有的街道,最后到达C;而从B出发的乙则不行.因此,甲所走的路程正好等于所有街道路程的总和,而乙所走的路程则必定大于这个总和,这样甲先到达C.【答案】甲先到达C.【例 2】右图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?【考点】一笔画问题【难度】2星【题型】解答【解析】将图形中的6个区域看成6个点,每个门看成连结他们的线段,显然6个点都是偶点,所以有人能一次不重复的走过所有的门.【答案】能【巩固】 右图是某展览馆的平面图,一个参观者能否不重复地穿过每一扇门?如果不能,请说明理由.如果能,应从哪开始走?【考点】一笔画问题 【难度】2星【题型】解答【解析】 不能【例 3】 下图中的每条线都表示一条街道,线上的数字表示这条街道的里数.邮递员从邮局出发,要走遍各条街道,最后回到邮局.问:邮递员怎样走,路线最合理?【解析】 邮递员走的路程最短时,路线最合理.利用一笔画的知识分析可得:因为邮递员从邮局作为起点和终点,所以没有奇点是最理想的,但实际上图中却有8个奇点,邮递员必须重复走某些路线.根据多笔画改为一笔画的方法得知:重复走的路线的两个端点应为奇点.重复的总路程应该尽可能短.我们把需重复走的路线,用虚线添在图中,通过分析与计算可知;当邮递员所走的路线如右图时,重复的路程最短,全程共走了56+4=60(里).其中56为所有街道的总长,4为所重复走的路程.小结:本题属于最短邮递路线问题.解决这样的题目时,有两点值得注意:①在所给图中,每条边都有具体的长度,这与前面其他问题中不考虑长度是不同的;②邮递路线中,邮递员必须以邮局作为起点和终点,即在最后能一笔画出的图中,所有的点都必须是偶点.这也与前面游人可以选择进出口的问题不同.E CDBA【例 4】右图是某地区街道的平面图,图上的数字表示那条街道的长度.清晨,洒水车从A出发,要洒遍所有的街道,最后再回到A.问:如何设计洒水路线最合理?【解析】这又是一个最短路线的问题.通过分析可以知道:在洒水路线中,K是中间点,因此必须成为偶点,这样洒水车必须重复走KC这条边(如下左图).至此,奇点的个数并未减少,仍是6个,但问题却转化为例6的类型.类似于例6,容易得出,洒水车必须重复走的路线有:GF、IJ、BC.即洒水路线如下右图.全程45+3+6=54(里).【例 5】在3×3的方阵中每个小正方形的边长都是100 米.小明沿线段从A点到B 点,不许走重复路,他最多能走多少米?【考点】一笔画问题【难度】3星【题型】解答【解析】这道题大多数同学都采用试画的方法,实际上可以用一笔画原理求解.首先,图中有8 个奇点,在8 个奇点之间至少要去掉4 条线段,才能使这8 个奇点变成偶点;其次,从A点出发到B 点,A,B 两点必须是奇点,现在A,B 都是偶点,必须在与A,B 连接的线段中各去掉1 条线段,使A,B 成为奇点.所以至少要去掉6 条线段,也就是最多能走1800 米,走法如图【答案】【例 6】如图是某餐厅的平面图,共有五个小厅,相邻两厅之间有门相通,并且设有入口.请问你能否从入口进入一次不重复地穿过所有的门.如果可以,请指明穿行路线,如果不能,应关闭哪个门就可以办到?【考点】一笔画问题【难度】4星【题型】解答【解析】可以将图中的五个小厅以及厅外的部分都抽象成点,为方便解题,给它们分别编号.这时,连通厅与厅之间的门就相当于各点之间的连线.于是题目中餐厅平面图就抽象成为一个连通的图形,如下:求穿形路线的问题就转化成一笔画的问题.在抽象出的图形中,我们可以找到四个奇点,即②、③、④和厅外,所以图形不能一笔画出也就是说,从入口进入不可能一次不重复的穿过所有的门.但根据一笔画问题的知识,只要关闭门,把③、④变为偶点,就可以办到,关闭B门,可行路线如上图.【答案】关闭B门.【例 7】(2009“数学解题能力展示"读者评选活动五年级初赛6题)某城市的交通系统由若干个路口(右图中线段的交点)和街道(右图中的线段)组成,每条街道都连接着两个路口.所有街道都是双向通行的,且每条街道都有一个长度值(标在图中相应的线段处).一名邮递员传送报纸和信件,要从邮局出发经过他所管辖的每一条街道最后返回邮局(每条街道可以经过不止一次).他合理安排路线,可以使得自己走过最短的总长度是.【考点】一笔画问题 【难度】4星 【题型】填空【解析】 根据一笔画的有关概念,道路图中有6个奇点,邮递员不可能不重复地走遍所有街道并返回邮局.但可以对道路图作一些处理,相当于邮递员通过走重复的道路,完成一笔画,如下图:总路程为3102846⨯+⨯=.【答案】46【例 8】 18世纪的哥尼斯堡城是一座美丽的城市,在这座城市中有一条布勒格尔河横贯城区,这条河有两条支流在城市中心汇合,汇合处有一座小岛A 和一座半岛D ,人们在这里建了一座公园,公园中有七座桥把河两岸和两个小岛连接起来(如图a ).如果游人要一次走过这七座桥,而且对每座桥只许走一次,问如何走才能成功?【考点】一笔画问题 【难度】4星 【题型】解答【解析】 欧拉解决这个问题的方法非常巧妙.他认为:人们关心的只是一次不重复地走遍这七座桥,而并不关心桥的长短和岛的大小,因此,岛和岸都可以看作一个点,而桥则可以看成是连接这些点的一条线.这样,一个实际问题就转化为一个几何图形(如下图)能否一笔画出的问题了.而图B 中有4个奇点显然不能一笔画出.【答案】不能【巩固】 如下图所示,两条河流的交汇处有两个岛,有七座桥连接这两个岛及河岸.问:一个散步者能否一次不重复地走遍这七座桥?【考点】一笔画问题 【难度】4星 【题型】解答 【答案】能.【例 9】 一个邮递员投递信件要走的街道如右图所示,图中的数字表示各条街道的千米数,他从邮局出发,要走遍各街道,最后回到邮局.怎样走才能使所走的行程最短?全程多少千米?【考点】一笔画问题 【难度】5星 【题型】解答【解析】 图中共有8 个奇点,必须在8 个奇点间添加4 条线,才能消除所有奇点,成为能从邮局出发最后返回邮局的一笔画.在距离最近的两个奇点间添加一条连线,如左下图中虚线所示,共添加4 条连线,这4 条连线表示要重复走的路,显然,这样重复走的路程最短,全程30千米.走法参考右下图(走法不唯一).【答案】30千米【随练1】 一辆清洁车清扫街道,每段街道长1公里,清洁车由A 出发,走遍所有的街道再回到A.怎样走路程最短,全程多少公里?例题精讲【考点】一笔画问题【难度】2星【题型】解答【解析】【答案】如图,27;【随练2】 右图是某展览馆的平面图,一个参观者能否不重复地穿过每一扇门?如果不能,请说明理由.如果能,应从哪开始走?【解析】 我们将每个展室看成一个点,室外看成点E ,将每扇门看成一条线段,两个展室间有门相通表示两个点间有线段相连,于是得到右图.能否不重复地穿过每扇门的问题,变为右图是否一笔画问题.上图中只有A ,D 两个奇点,是一笔画,所以答案是肯定的,应该从A 或D 展室开始走.【答案】能,应该从A 或D 展室开始走.EDCBA【作业1】 下列图形分别是几笔画?怎样画?【答案】(1)1笔 (2)2笔 (3)1笔【作业2】 从A 点出发,走遍右上图中所有的线段,再回到A 点,怎样走才能使重复走的路程最短?【答案】【作业3】 邮递员要从邮局出发,走遍左下图(单位:千米)中所有街道,最后回到邮局,怎样走路程最短?全程多少千米?A例题精讲【答案】【作业4】 有一个邮局,负责21个村庄的投递工作,下图中的点表示村庄,线段表示道路.邮递员从邮局出发,怎样才能不重复地经过每一个村庄,最后回到邮局?【答案】邮局213332邮局33322111 / 11【作业5】 一只木箱的长、宽、高分别为5,4,3厘米(见右图),有一只甲虫从A 点出发,沿棱爬行,每条棱不允许重复,则甲虫回到A 点时,最多能爬行多少厘米?【答案】34厘米.【作业6】 在六面体的顶点B 和E 处各有一只蚂蚁(见右图),它们比赛看谁能爬过所有的棱线,最终到达终点D.已知它们的爬速相同,哪只蚂蚁能获胜?【解析】 许多同学看不出这是一笔画问题,但利用一笔画的知识,能非常巧妙地解答这道题.这道题只要求爬过所有的棱,没要求不能重复.可是两只蚂蚁爬速相同,如果一只不重复地爬遍所有的棱,而另一只必须重复爬某些棱,那么前一只蚂蚁爬的路程短,自然先到达D 点,因而获胜.问题变为从B 到D 与从E 到D 哪个是一笔画问题.图中只有E ,D 两个奇点,所以从E 到D 可以一笔画出,而从B 到D 却不能,因此E 点的蚂蚁获胜.【答案】E 点的蚂蚁获胜.【作业7】 下图是一个街区街道的平面图.邮递员从邮局出发,跑遍所有街道投送信件.请你为他安排一条最短的路线,并按图中标出的千米数算出这条路线的长度(单位:千米).△ 邮局3。
奥数-03一笔画+答案
【例 8】 如图 A 所示,两条河流的交汇处有两个岛,有七座桥连接这两个岛及河 岸。问:一个散步者能否一次不重复地走遍这七座桥?
解析:通过画图,把一个实际问题转化为一个几何图形(如图 B),成为一笔画 的问题了,而图 B 中有 2 个奇点,所以能一笔画出。 练习四 1、右边各图至少要用几笔画完?
1
【例 1】 右图中,哪些点是偶点?哪些点是奇点? 解析:我们把一个图形上与偶数条线相连的点叫
做偶点,与奇数条线相连的点叫做奇点。奇点有 J、D、 H,偶点有 A、B、C、E、F、G、I。
【例 2】 下面图形能不能一笔画成?如果能,应该怎样画?
解析:图 1 能一笔画,因为图中只有两个奇点。图 2 也能一笔画,因为图中全 是偶点,图 3 不能一笔画,因为有 4 个奇点。
条线,将其改成成可一笔画的图形。
G
H
A
I
J
F
B
K
L
E
C
图b
D
【例 2】 右图是某展览厅的平面图,它由五个展室组 成,任两展室之间都有门相通,整个展览厅还有一个进 口和一个出口,问游人能否从入口进,从出口出,并且 一次不重复地穿过所有的门?
解析:将图形中的 6 个区域看成 6 个点,每个门看 成连结他们的线段,显然 6 个点都是偶点,所以游人能 一次不重复的走过所有的门。
2
【例 4】 右图中的线段表示小路,请你仔细观 察,认真思考,能够不重复地爬遍小路的是甲蚂 蚁还是乙蚂蚁?该怎样爬?
解析:要想不重复爬遍小路,需要图形能 一笔画出,由于图中有两个奇点,所以应该从 奇点出发才能一笔画出图形,所以甲蚂蚁能够。
三年级奥数一笔画
作业
1.如图每个小正方形边长为1,从A点出发,走遍右上图中所有的线段,再回到A点,怎样走才能使重复走的路程最短?最短是多少?(在图上添上需要重复走的线段)
2.图中是一辆越野车爬过两个山峰的路一线图,试这辆车该从那个点上山,经过全部路段,且不重复.最后终点落在哪个结点上?
笑笑去公园游玩,下图为公园简易地图,菱形四角为公园四个出入口,笑笑要从一个门进公园,从另一个门出来,要走遍各条小路,怎样走才能使所走的行程最短?
例5:一个邮递员投递信件要走的街道如下页左上图所示,图中的数字表示各条街道的千米数,他从邮局出发,要走遍各街道,最后回到邮局。怎样走才能使所走的行程最短?全程多少千米?
练一练:图中是一个社区公园的平面图,要使社区群众走遍公园每一条路,且不重复,出人口应设在哪个交点上?请你在这个位置标上字母A和B.
例2:六面体的顶点B和E处各有一只蚂蚁(见右图),它们比赛看谁能爬过所有的棱线,最终到达终点D。已知它们的爬速相同,哪只蚂蚁能获胜?
再回头看看七桥问题,能否转换成一笔画问题呢
你学会了吗
1.下列图形分别是几笔画?怎样画?
2.能否用剪刀从左下图中一次连续剪下三个正方形和两个三角形?为什么?
3.如下图所示,两条河流的交汇处有两个岛,有七座桥连接这两个岛及河岸。问:一个散步者能否一次不重复地走遍这七座桥?
4.邮递员要从邮局出发பைடு நூலகம்走遍左下图(单位:千米)中所有街道,最后回到邮局,怎样走路程最短?全程多少千米?
例3:有三个小岛,分别有七座桥相通请回答,能不能一次不重复走完这七座桥呢?
三年级奥数几何一笔画与多笔画
一笔画与多笔画知识框架一、一笔画的认识所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从上图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法。
什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.所谓一笔画,就是从图形上的某点出发,笔不离开纸,而且每条线都只画一次不准重复.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 二、一笔画问题(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点;(3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点.以另一个奇点作为终点;(4)奇点个数超过两个的图形,一定不能一笔画.三、多笔画问题我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n个奇点(n为自然数),那么这个图一定可以用n笔画成.重难点(1)知道什么样的的是奇点?什么样的点是偶点。
(2)知道什么样的图形可以一笔画出。
(3)不能一笔画出的图形叫做多笔画图形,多笔画图形的笔画数与什么有关呢?例题精讲【例 1】我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?【巩固】 下图中,哪些点是奇点,哪些点是偶点?【例 2】 观察下面的图形,说明哪些图可以一笔画完,哪些不能,为什么?对于可以一笔画的图形,指明画法.【巩固】 下面的图形,哪些能一笔画出?哪些不能一笔画出?J O I H G FED CBA GF E D CBA【例 3】 同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻营地的旗帜色彩不同,则贝贝最少需要种颜色的旗子,如果贝贝从某营地出发,不走重复路线就(填“能”或“不能”)完成任务.【例 4】 右图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?【巩固】 右图是某展览馆的平面图,一个参观者能否不重复地穿过每一扇门?如果不能,请说明理由.如果能,应从哪开始走?【例 5】 下图中的线段表示小路,请你仔细观察,认真思考,能够不重复的爬遍小路的是甲蚂蚁还是乙蚂蚁?该怎样爬?E CDB A 乙甲【例 6】 邮递员叔叔向11个地点送信一次信,不走重复路,怎样走最合适?【例 7】 (2010年第8届走美杯3年级初赛第6题)有16个点排成的44 方阵。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
“一笔画”是指笔不 离开纸,而且每条线 都只画一次不准重复 而画成的图形。
“一笔画”是一种有趣 的数学游戏,那么什么 样的图形可以一笔画成 呢?试一试,画一画, 发挥你的想象力,发现 一笔画的规律。
你能用一笔画出下列图形吗?
问题分析
问题的答案如何呢?让我们先来了解三个新概念。
①有奇数条边相连的点叫奇点。如:
●
●
●
②有偶数条边相连的点叫偶点。如:
●
●
●
③一笔画指:1、下笔后笔尖不能离开纸。 2、每条线都只能画一次而不能重复。
奇点 偶点
从一点出发的线的数 目是单数条的叫单数 点。
从一点出发的线的数 目是双数条的叫双数 点。
交点分为两种
(1)从这点出发的线的数目 是双数的,叫双数点(偶点)。 (2)从这点出发的线的数目 是单数的,叫单数点(奇点)。
一笔画
趣味小故事
250年前,有一个问题曾吸引了许多人,连大数学 家欧拉也对这个问题产生了兴趣。问题是这样的:
德国有一个城市叫哥尼斯岛。城中有一条河,河 中有一个岛,岛上架有七座桥,这些桥把陆地、小岛 连接起来,(见下图)人们经常在这里游玩,他们在 游玩的时候提出了这样一个问题:一个人要连续地走 完这七座桥,每座桥只许通过一次,该怎么走?
1727年在欧拉20岁的时候,被俄国请去在圣彼得堡 (原列宁格勒)的科学院做研究。他的德国朋友告 诉了他这个曾经令许多人困惑的问题。
欧拉并没有跑到哥尼斯堡去走走。他把这个难题化成了这样 的问题来看:把二岸和小岛缩成一点,桥化为边,于是“七 桥问题”就等价于下图中所画图形的一笔画问题了, 这个 图如果能够一笔画成的话,对应的“七桥问题”也就解决了。
画一画,找一找
下面的图形,哪些能一笔画出?哪些不能一笔画出
根据今天学习知识,先判断下列图 形能不能一笔画成?再想一想该从 哪里开始画?最后再动手画画看。
练习
一辆洒水车要给某城市的街道洒水,街道地 图如下:你能否设计一条洒水车洒水的路线 ,使洒水车不重复地走过所有的街道,再回 到出发点?
小广场
点,,也是偶点,Βιβλιοθήκη 有奇点,能一笔画成。园林工人张大伯为花园浇花,怎样走才 能不重复地走遍图中的每条小路?
邮递员叔叔向10个地点送信一次走 完,不走重 复路,应该怎样走合适?(看下图)
知识回顾 Knowledge Review
超市 菜市场
文具店 电器城
服装城
甲乙两个邮递员去送信,两人以同样的速度
走遍所有的街道,甲从A点出发,乙从B点出发, 最后都回到邮局(C)。如果要选择最短的线路, 谁先回到邮局?
邮
乙
甲
局
下面的图能不能一笔画成?如果能, 应怎样画?
1
2
7
3
4
5
6
1、2、3、4、5、6六个点都是两条线
的交点,是偶点,7是四条线的交
②只有2个奇点的连通图,画时必须以 一个奇点为起点,另一个奇点为终点。
③其余情况的图都不能一笔画。
下面的图形可不可以一笔画成?如果 能,怎么画
下面的图能否一笔画成?如果能, 应该怎么画?
观察以后发现,没有奇点,都是偶点,所以, 可以一笔画成。从一点出发,再从这点结束。
填空
一笔画图形(判断,说明理由并画出)
两条相交的线处都有一个交点。
数一数下列图形各有几个交点?
( 4 )个
( 2 )个
( 9 )个
( 5 )个
我们刚才画的图形都有几个交点? 几个双数点?几个单数点?
判断下列图形能否一笔画
不连通的图形不能一笔画
图1
图2
图3
连通的图形有可能一笔画
图4
图5
①只有偶点的连通图画时可以任一偶 点为起点,最后以这个点为终点画完全图。
