第八节 多元函数的极值及其求法
10.8多元函数的极值及其求法 (2)

多元函数的极值
观察二元函数 z
xy e x2 y2
的图形
一、二元函数的极值及最大值最小值
1、二元函数极值的定义
设 函 数 z f ( x, y) 在 点( x0 , y0 ) 的 某邻域 内 有 定 义 , 对 于 该 邻 域 内 异 于 ( x0 , y0 ) 的 点 (x, y):
例2 求内接于半径为 a 的球且有最大体积的长方体。
求函数z f ( x, y)极值的一般步骤:
第一步 解方程组 fx ( x, y) 0, f y ( x, y) 0
求出实数解,得驻点. 第二步 对于每一个驻点 ( x0 , y0 ),
求出二阶偏导数的值 A、B、C 定出 AC B2的符号,再判定是否是极值.
例1 求函数 解:第一步 求驻点。
为极小值;
在点(1,2) 处
AC B2 12 (6) 0,
不是极值;
在点(3,0) 处
AC B2 12 6 0,
在点(3,2) 处
不是极值;
AC B2 12 (6) 0, A 0,
为极大值。
f xx (x, y) 6x 6, f xy (x, y) 0, f yy (x, y) 6 y 6
若满足不等式 f ( x, y) f ( x0 , y0 ),则称函 数在( x0 , y0 )有极大值;
若满足不等式 f ( x, y) f ( x0 , y0 ),则称函 数在( x0 , y0 )有极小值;
极大值、极小值统称为极值。 使函数取得极值的点称为极值点。
例 1 函数 z 3x2 4 y2
分析:
此问题是在 x2 y2 z2 1 的条件下, 求解 f(x, y, z) xy z 的最大值,
多元函数的极值及最大值

例5 求表面积为 a 而体积为最大的长方体 的体积 .
2
三、最小二乘法
作业:P70 1 5 8
要找函数z f ( x, y)在附加条件 ( x, y) 0 下的可能极值点,可以 先构成辅助函数 F ( x, y) f ( x, y) ( x, y) f x ( x, y ) x ( x, y ) 0 由: f y ( x, y ) y ( x, y ) 0 ( x, y ) 0
例3:某厂要用铁板做成一 个体积为2m 的有盖 长方形水箱 .问长、宽、高各取怎样 的尺 寸时,才能使用料最省 ?
例4:有一宽为 24cm的长方形铁板,把它两 边 折起来做成一个断面为 等腰梯形的水槽 . 问怎样折法才能使断面 的面积最大?
3
二、条件极值 拉格郎日乘数法
无条件极值 条件极值 拉格郎日乘数法
(1) AC B 2 0时具有极值,且当 A 0时有极大 值,当A 0时有极小值;
(2) AC B2 0时没有极值;
(3) AC B 2 0时可能有极值,也可能 没有极值, 还需另作讨论 . 3 3 2 2 例2:求函数f ( x, y) x y 3x 3 y 9x的极值 .
驻点:能使 f x ( x, y) 0, f y ( x, y) 0同时成立的点 .
可导:极值点 驻点. 驻点 ?极值点.
定理2(充分条件):设函数z f ( x, y )在点( x0 , y0 )的 某邻域内连续且有一阶 及二阶连续偏导数,又 f x ( x0 , y0 ) 0, f y ( x0 , y0 ) 0.令 f xx ( x0 , y0 ) A, f xy ( x0 , y0 ) B, f yy ( x0 , y0 ) C , 则f ( x, y )在( x0 , y0 )处是否取得极值的条件 如下:
8.8_多元函数的极值及其求法

考研数学二, 选择题, 4分
设函数 z f ( x , y ) 的全微分 d z x d x y d y ,
则点 ( 0 , 0 ) (D )
(A) 不是f (x, y)的连续点. (B) 不是f (x, y)的极值点.
(C) 是f (x, y)的极大值点. (D) 是f (x, y)的极小值点.
定义 设函数z = f (x, y) 在点P0 (x0, y0)的某
邻域内有定义, 若在此邻域内对异于P0的点, 恒有
f ( x , y ) f ( x , y ) ( 或 f ( x , y ) f ( x , y ) ) , 0 0 0 0
则称点P0 (x0, y0)为函数的极大 (或极小) 值点,
8
8.8 多元函数的极值与最值
仿照一元函数, 凡能使一阶偏导数同时为零的点, 均称为函数的 驻点 (稳定点). 从几何上看, 此时如曲面z = f (x, y)在点(x0, y0, z0)
处有切平面, 则
z z f ( x , y )( x x ) f ( x , y )( y y ) 0 x 0 0 0 y 0 0 0
2 2 2 求由方程 x y z 2 x 2 y 4 z 10 0 例2
确定的函数 z f ( x ,y ) 的极值 .
解 将方程两边分别对x, y求偏导数,
2 x 2 z z 2 4 z 0 0 0 x x y 2 z z 2 4 z 0 2 0 0 y y z x 0 驻点为 P ( 1 , 1 ), 令 z y 0
2
2 2 2 x y z 2 x 2 y 4 z 10 0
1 故 AC ) 0 (z 2 B 1 2 (2z) Az xx|P 2z 函数在 P 有极值. 将 驻点 P ( 1 , 1 ) B | z 0
极值

x
fx
fy
y
14
f x x 0
极值点必满足
f y y 0 ( x, y) 0
引入辅助函数 F f ( x , y ) ( x , y )
则极值点满足:
辅助函数F 称为拉格朗日( Lagrange )函数. 利用拉格 朗日函数求极值的方法称为拉格朗日乘数法.
思考: 1) 当水箱封闭时, 长、宽、高的尺寸如何? x 提示: 利用对称性可知, x y z 3 V0 2) 当开口水箱底部的造价为侧面的二倍时, 欲使造价
y
最省, 应如何设拉格朗日函数? 长、宽、高尺寸如何?
提示: F 2( x z y z ) 2 x y ( x y z V0 )
2
则: 1) 当AC B 0 时, 具有极值
A<0 时取极大值;
A>0 时取极小值.
AC B 2 0 时, 没有极值. 2) 当
3) 当 AC B 2 0 时, 不能确定, 需另行讨论.
证明见第九节(同济P65,合肥工大P349) .
4
例1. 求函数 解: 第一步 求驻点. 解方程组 得驻点: (1, 0) , (1, 2) , (–3, 0) , (–3, 2) . 第二步 判别. 求二阶偏导数
解方程组
可得到条件极值的可疑点 .
16
例5.
要设计一个容量为 V0 的长方体开口水箱, 试问
水箱长、宽、高等于多少时所用材料最省? 解: 设 x , y , z 分别表示长、宽、高,则问题为求x , y , z 使在条件 x y z V0 下水箱表面积 S 2( x z y z ) x y 最小. 令 F 2( x z y z ) x y ( x y z V0 )
多元函数的极值

x yz xy z x y z定理1 (必要条件)函数偏导数,证:据一元函数极值的必要条件可知定理结论成立.0),(,0),(0000=′=′y x f y x f yx 取得极值,取得极值取得极值且在该点取得极值,则有),(),(00y x y x f z 在点=存在),(),(00y x y x f z 在点因=在),(0y x f z =0x x =故在),(0y x f z =0y y =zox y对于三元函数,若M 0是f (x , y , z )的驻点,f (x , y , z )在M 0处所有的二阶偏导数连续,则当矩阵在M 0处为正定阵时( ),M 0为极小值点,为负定阵时( ),M 0为极大值点.类似的,可以将以上结论推广到三元以上的函数.H=xx xy xz xyyy yz xz yz zz f f f f f f f f f ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦112233H 0,H 0,H 0>>>112233H 0,H 0,H 0<><αcos 24x αcos 22x −)sin (cos 222−+ααx =x A αsin 24αsin 4x −0cos sin 2=+ααx =αA 解得:由题意知,最大值在定义域D 内达到,而在域D 内只有一个驻点,故此点即为所求.,0sin ≠α0≠x ααααsin cos sin 2sin 2422x x x A +−=)0,120:(2πα<<<<x D 0cos 212=+−αx x 0)sin (cos cos 2cos 2422=−+−ααααx x (cm)8,603===x D πα作业P121 4, 6, 7, 13。
7.8 多元函数的极值及其求法

目录 上页 下页 返回
例3 有一宽为 24cm 的长方形铁板 , 把它折起来做成 一个断面为等腰梯形的水槽, 问怎样折法才能使断面面 积最大. (课本 例6) 解: 设折起来的边长为 x cm, 倾角为α , 则断面面积 1 为 A = ( 24 − 2 x + 2 x cos α + 24 − 2 x ) ⋅ x sin α 2 = 24 x sin α − 2 x 2 sin α + x 2 cos α sin α
z z z
y y
z = x y 在点 (0,0) 无极值.
2009年7月6日星期一 2
目录
x
上页
x
下页
y
返回
定理1 (必要条件) 函数 z = f ( x, y ) 在点 ( x0 , y0 ) 存在 偏导数, 且在该点取得极值 , 则有
′ f x′ ( x0 , y0 ) = 0 , f y ( x0 , y0 ) = 0
由题意可知合理的设计是存在的, 因此 , 当高为 3 长、宽为高的 2 倍时,所用材料最省. 思考: 1) 当水箱封闭时, 长、宽、高的尺寸如何? x 提示: 利用对称性可知, x = y = z = 3 V0
V0 , 4
z
y
(课本 例7)
2) 当开口水箱底部的造价为侧面的二倍时, 欲使造价 最省, 应如何设拉格朗日函数? 长、宽、高尺寸如何? 提示: F = 2( x z + y z ) + 2 x y + λ ( x y z − V0 ) 长、宽、高尺寸相等 .
2009年7月6日星期一 16
目录 上页 下页 返回
例 5 抛物面 z = x 2 + y 2 被平面 x + y + z = 1 截成一椭圆, 求原点到这椭圆的最长与最短距离.
第八节 多元函数的极值及其求法

第八节 多元函数的极值及其求法
一、选择题
1. 点(0, 0)是函数f (x , y ) = x 2 - y 2的
( ) A . 驻点但不是极值点; B . 极小值点; C . 极大值点; D . 非驻点. 2. 函数1),(22+-+++=y x y xy x y x f 的驻点为
( ) A . (1,-1) B . (-1,-1) C . (-1,1) D . (1,1) 3. 设函数f (x , y ) =22y x +, 则点(0, 0)是f (x , y )的
( ) A . 驻点; B . 极小值点; C . 极大值点; D . 非极值点.
4. 设f 'x (x 0, y 0) = 0, f ’y (x 0, y 0) = 0, 则在点(x 0, y 0)处函数f (x , y ) ( )
A . 连续;
B . 一定取得极值;
C . 可能取得极值;
D . 的全微分为零.
二、解答题
1. 求1)(444+--+=y x y x z 的极值.
2. 求函数z = xy 在适合附加条件x + y = 1下的最大值.
3. 在xOy 上求一点, 使它到x = 0, y = 0及x + 2y - 16 = 0三直线的距离平方之和为最小.
4. 欲造一无盖的长方形容器, 已知底部造价为每平方米3元, 侧面造价为每平方米1元, 现想用36元造一容积为最大的容器, 求它的尺寸.
5. 某厂要用铁板做成一个体积为43m 的无盖长方体水箱, 问当长、宽、高各取怎样的尺寸时, 才能使用料最省.。
§8.8 多元函数极值及其求法
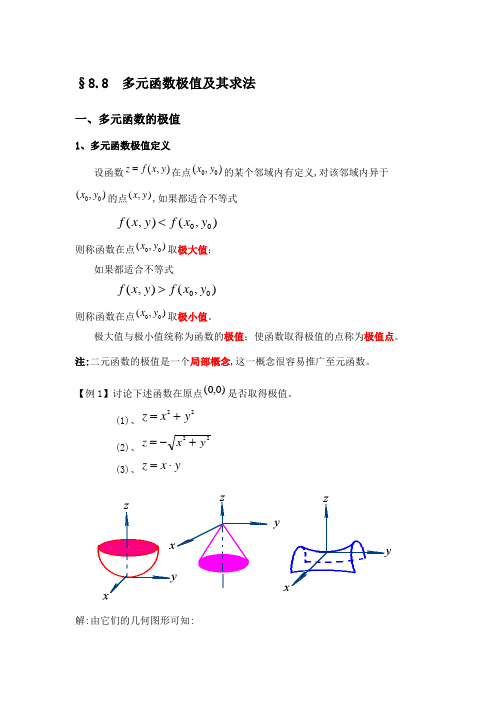
§8.8 多元函数极值及其求法一、多元函数的极值1、多元函数极值定义设函数z f x y =(,)在点(,)x y 00的某个邻域内有定义,对该邻域内异于(,)x y 00的点(,)x y ,如果都适合不等式f x y f x y (,)(,)<00则称函数在点(,)x y 00取极大值;如果都适合不等式f x y f x y (,)(,)>00则称函数在点(,)x y 00取极小值。
极大值与极小值统称为函数的极值;使函数取得极值的点称为极值点。
注:二元函数的极值是一个局部概念,这一概念很容易推广至元函数。
【例1】讨论下述函数在原点(,)00是否取得极值。
(1)、z x y =+22(2)、z x y =-+22 (3)、z x y =⋅解:由它们的几何图形可知:z x y =+22是开口向上的旋转抛物面,在(,)00取得极小值;z x y =-+22是开口向下的锥面,在(,)00取得极大值; z x y =⋅是马鞍面, 在(,)00不取得极值。
2、函数取得极值的必要条件 【定理一】设函数zf x y =(,)在点(,)x y 00具有偏导数且取得极值,则它在该点的偏导数必为零,即f x y f x y x y (,)(,)00000==【证明】不妨设zf x y =(,)在点(,)x y 00处有极大值。
依极值定义,点(,)x y 00的某一邻域内的一切点(,)x y 适合不等式f x y f x y (,)(,)<00特殊地,在该邻域内取y y =0,而x x ≠0的点,也应有不等式f x y f x y (,)(,)000<这表明:一元函数z f x y =(,)0在 x x =0处取得极大值,因而必有f x y x (,)000=同理可证f x y y (,)000=【注一】当f x y f x y x y (,)(,)00000==(,)x y 00时, 曲面在点处有切平面z z f x y x x f x y y y x y -=-+-=00000000(,)()(,)()此切平面平行于水平面xoy 面。
