最新苏教版高中数学必修三《选择结构》课时同步练习及解析.docx
高中数学 第一章 §1.2.2选择结构配套课件 苏教版必修3

研一研·问题(wèntí)探究、课堂更高
效 跟踪训练 2
1 已知函数 y=xx12
x>0 x<0
,试设计一个算法
的流程图,使输入自变量 x 的值时,输出 y 的值.
解 流程图:
第十二页,共16页。
练一练·当堂检测、目标(mùbiāo)达成落实 处
1.下面三个问题中必须用选择结构才能实现的是_(_2_)(_3_)___.
50 kg,然后再选用相应的公式进行计算.
第四页,共16页。
研一研·问题探究(tànjiū)、课堂更高 效
问题 2 该算法的流程图还能不能只用顺序结构表示?为什么? 答 不能只用顺序结构表示.因为对于不同的行李重量其托运 费用需要用不同的公式来计算,所以流程图不能由若干个依次 执行的步骤组成,因此不能只用顺序结构表示.
为 c=05.05×3×0.w53,+w-50×0.85,
w≤50, w>50,
其中 w(单位:
kg)为行李的重量.试给出计算费用 c(单位:元)的一个算法, 并画出流程图.
问题 1 在设计算法时,要计算某一行李的重量对应的托运费用 应该首先做什么?
答 为了计算行李的托运费用,应先判断行李的重量是否大于
例 1 设计求解一元二次方程 ax2+bx+c=0(a≠0)的一个算法,
并画出流程图.
解 算法如下: S1 输入 a,b,c; S2 Δ←b2-4ac;
S3 如果 Δ<0,则输出“方程无实
数根”,否则
x1←
-b+ 2a
Δ,
x2←-b2-a Δ,并输出 x1,x2.
流程图如图:
第七页,共16页。
研一研·问题探究(tànjiū)、课堂更高效
苏教版高中数学必修三同步课堂精练-1.2.3循环结构.docx
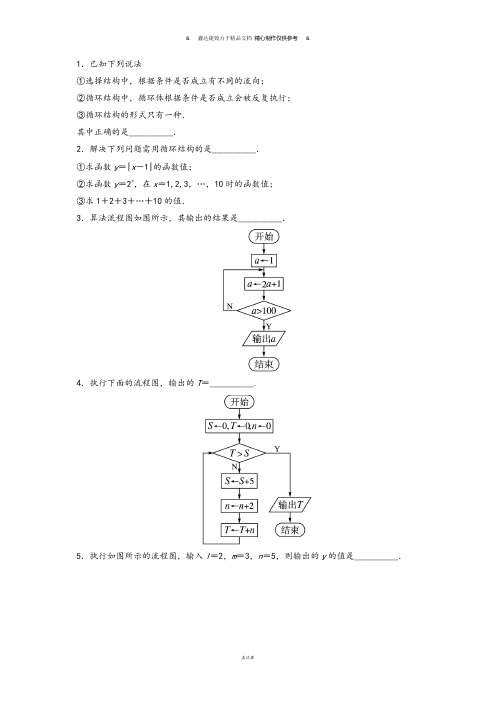
1.已知下列说法①选择结构中,根据条件是否成立有不同的流向;②循环结构中,循环体根据条件是否成立会被反复执行;③循环结构的形式只有一种.其中正确的是__________.2.解决下列问题需用循环结构的是__________.①求函数y=|x-1|的函数值;②求函数y=2x,在x=1,2,3,…,10时的函数值;③求1+2+3+…+10的值.3.算法流程图如图所示,其输出的结果是__________.4.执行下面的流程图,输出的T=__________.5.执行如图所示的流程图,输入l=2,m=3,n=5,则输出的y的值是__________.6.下面算法流程图的功能是__________.7.执行下面的流程图,如果输入的n是4,则输出的p是________.8.以下是某次考试中某班15名同学的数学成绩:72,91,58,63,84,88,90,55,61,73,64,77,82,94,60.要求将80分以上的同学的平均分求出来,画出流程图.参考答案1答案:①②解析:循环结构有“当型”和“直到型”两种,故③不正确;由选择结构和循环结构的条件知①②正确.2答案:②③解析:①应用选择结构;②③都涉及到多次重复计算,需用循环结构.3答案:127解析:a的值依次为3,7,15,31,63,127,∵127>100,∴输出的结果是127.4答案:30解析:执行流程图,依次得5,2,2,SnT=⎧⎪=⎨⎪=⎩10,4,6,SnT=⎧⎪=⎨⎪=⎩15,6,12,SnT=⎧⎪=⎨⎪=⎩20,8,20,SnT=⎧⎪=⎨⎪=⎩25,10,30,SnT=⎧⎪=⎨⎪=⎩故此时应输出T=30.5答案:68解析:由流程图可知,y的变化情况为y=70×2+21×3+15×5=278,进入循环,显然278>105,因此y=278-105=173;此时173>105,故y=173-105=68.经判断68>105不成立,输出此时y的值68.6答案:计算S=1×2×3×…×10的值解析:由流程图知,初值S=1,i=1,循环体为S=S×i,且终止循环的条件是i>10,故算法功能是计算从1到10的正整数之积.7答案:3解析:初始值p=1,s=0,t=1,k=1,循环开始,第一次,p=1,s=1,t=1,k=2;第二次,p=2,s=1,t=2,k=3;第三次,p=3,s=2,t=3,k=4.此时,k<n不成立,跳出循环,输出p=3.8解:用选择结构来判断成绩是否高于80分,用循环结构控制输入的次数,同时引进两个累加变量,分别计算高于80分的成绩的总和与人数.流程图如图所示.。
苏教版高中数学必修三教案:1.2.2 选择结构

1.2.2 选择构造江苏省姜堰中学 陈文国教学目的:1.理解流程图的选择构造这种根本逻辑构造.2.能识别和理解简单的框图的功能.3. 能运用三种根本逻辑构造设计流程图以解决简单的问题. 教学重点:1. 选择构造及画法.2. 用流程图表示算法.教学难点:1. 选择构造.2. 用流程图表示算法.教学方法:1. 通过模拟、操作、探究,经历设计流程图表达求解问题的过程,加深对流程图的感知.2. 在详细问题的解决过程中,掌握根本的流程图的画法和流程图的三种根本逻辑构造.教学过程:一、问题情境1.情境: 某铁路客运部门规定甲、乙两地之间旅客托运行李的费用为 0.53,50,500.53(50)0.85,50,c ωωωω⨯≤⎧=⎨⨯+-⨯>⎩其中ω〔单位:kg 〕为行李的重量. 试给出计算费用c 〔单位:元〕的一个算法,并画出流程图.二、学生活动学生讨论,老师引导学生进展表达.解 算法为:1S 输入行李的重量ω;2S 假如50ω≤,那么0.53c ω←⨯,否那么500.53(50)0.85c ω←⨯+-⨯;3S 输出行李的重量ω和运费c . 上述算法可以用流程图表示为:老师边讲解边画出第10页图1-2-6.在上述计费过程中,第二步进展了判断.三、建构数学1.选择构造的概念: 先根据条件作出判断,再决定执行哪一种操作的构造称为选择构造.如图:虚线框内是一个选择构造,它包含一个判断框,当条件p 成立〔或称条件p 为“真〞〕时执行A ,否那么执行B .2.说明:〔1〕有些问题需要按给定的条件进展分析、比拟和判断,并按判 断的不同情况进展不同的操作,这类问题的实现就要用到选择构造的设计;〔2〕选择构造也称为分支构造或选取构造,它要先根据指定的条件进展判断,再由判断的结果断定执行两条分支途径中的某一条;〔3〕在上图的选择构造中,只能执行A 和B 之一,不可能既执行A ,又执行B ,但A 或B 两个框中可以有一个是空的,即不执行任何操作;〔4〕流程图图框的形状要标准,判断框必须画成菱形,它有一个进入点和 两个退出点.3.考虑:教材第7页图121--所示的算法中,哪一步进展了判断?四、数学运用1.选择构造举例.例1 〔教材第10页例3〕设计求解一元二次方程20(0)ax bx c a ++=≠的一个算法,并画出流程图.分析 由于一元二次方程未必总有实数根,因此,求解时,要先计算判别式△24b ac =-,然后比拟△与0的大小,再决定能否用求根公式求解.所以,在算法中应含有选择构造.考虑:假如要输出根的详细信息〔区分是两个相等的实数根还是不等的实数根〕,如何修改上述算法和流程图?例2 设计一个求任意数的绝解 1S 输入任意实数x ;2S 假设0≥x ,那么y x ←;否那么y x ←-; 3S 输出y . 算法流程图如右.2.练习:课本第11页练习第1,2,3题.五、要点归纳与方法小结本节课学习了以下内容:1.选择构造的概念:先根据条件作出判断,再决定执行哪一种操作的构造称为选择构造.2.理解选择构造的逻辑以及框图的标准画法,选择构造主要用在判断、分类或分情况的问题解决中.N 0x ≥ y x ←输入x 输出y Yy x ←-。
数学第1章1.2.2选择结构课件(苏教版必修3)

变式训练
1.设计一个求任意数的绝对值的算法,并画 出流程图.
解:根据绝对值定义:
|a|=a-,a,
a≥0 a<0
,
算法如下:
S1 输入任意实数 x; S2 若 x≥0,则 y←x;否则 y←-x; S3 输出 y.
流程图如下图.
题型二 选择结构的嵌套
例2
1,
x>0,
已知函数 y=0, x=0,
写出
-1, x<0,
求该函数值的算法,并画出流程图.
【解】 算法如下: S1 输入x; S2 如果x>0,那么y←1;否则, 如果x=0,那么y←0;否则y←-1; S3 输出y. 流程图如图所示.
【规律方法】 本题中的分段函数称为“符 号函数”.一般分段函数的流程图需要用选 择结构,如果是分两段的函数,直接使用一 个判断框;如果是分三段的函数,那么就需 要引入两个判断框,即将另一个选择结构放 至前一个选择结构的一支中,形成结构的嵌 套.类似地,可以写出其他分段函数值的求 法.
解:(1)若输入四个数5,9,4,6,则最终输出的结果
为4.
(2)该流程图所对应的问题是求a,b,c,d四个数
中的最小的数.算法如下:
S1
输入a,b,c,d.
S2 如果a<b,a<c,a<d,则输出a,否则,执
行S3.
S3 如果b<c,b<d,则<d,则输出c,否则,执行S5.
变式训练
1-x,x<-1, 2.画出求函数 y=x2,-1≤x≤1,
1+x,x>1,
值的算法
流程图.
解:流程图如图所示.
题型三 选择结构的应用 (本题例满3 分16分)对一批货物征收税金,
价格在10000元以上的货物征税5%;在5000元 以上,10000元以下(含10000元)的货物征税3%; 在1000元以上,5000元以下(含5000元)的货物 征税2%;在1000元以下(含1000元)的货物免 税.请设计一个算法,根据货物价格输出税 金,画出流程图.
高中数学 1.2.2 选择结构课件 苏教版必修3

解析: 设路程为 x km 时,收费额为 y 元,则由题意
得:当 x≤3 时,y=7;当 x>3 时,y=7+2.4(x-3).
栏
于是,收费额关于路程的函数解析式为
目 链
接
y=77,+02<.4(x≤x-3,3),x>3,
即 y=72,.4x0-<0x.2≤,3,x>3.
第十九页,共20页。
流程图如下(rúxià)图所示:
第十页,共20页。
解析: 算法过程如下:
S1 输入 x;
S2 若 x≤3,则 y←5;否则(x>3),y←5+1.2(x-3);
S3 输出 y.
流程图如下图所示:
栏
目
链
接
第十一页,共20页。
规律总结(1):解决求分段函数的函数值问题时,一般
要采用选择结构来设计(shèjì)算法.
栏
目
(2)分清“是”与“否”所对应的处理框中的内容
的.
第十七页,共20页。
典例 剖析
变式训 练
(xù2n.lià某n)市出租车收费标准如下:在3 km以内(含3
km)路程按起步价7元收费,超过3 km以外的路程按2.4
元/km收费.试写出收费额关于路程的函数解析式并画
栏 目
出计算(jìsuàn)收费额的一个算法的流程图.
链 接
第十八页,共20页。
链 接
是解决此类问题的关键.
第十二页,共20页。
典例
剖析
变式训
练
(xùnliàn) log2x,x≥2, 1.已知函数 y=2-x,x<2. 下图是求函数值的程序框
图,则①处应填写___x_<_2___,②处应填写__y_←__lo_g_2_x.
高中数学苏教版必修三能力提升习题:(二)顺序结构选择结构含答案
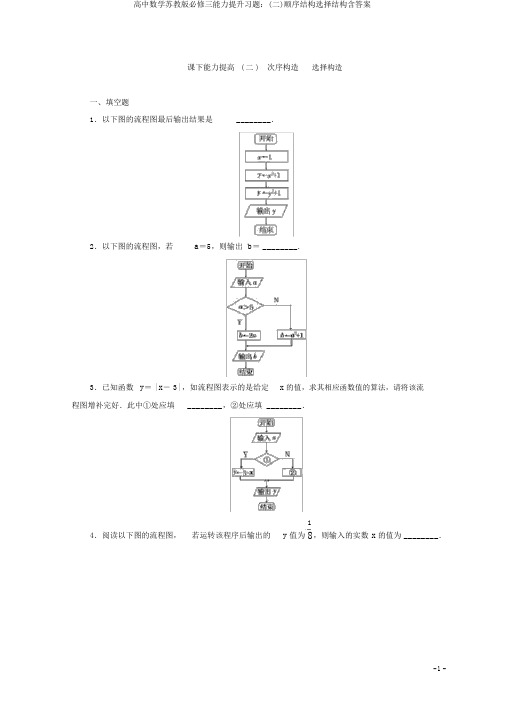
课下能力提高( 二 )次序构造选择构造一、填空题1.以下图的流程图最后输出结果是________.2.以下图的流程图,若a=5,则输出 b=________.3.已知函数y=| x-3|,如流程图表示的是给定x 的值,求其相应函数值的算法,请将该流程图增补完好.此中①处应填________,②处应填 ________.14.阅读以下图的流程图,若运转该程序后输出的y 值为8,则输入的实数x 的值为________.5.如图是一个算法的流程图,当输入的值为 3 时,输出的结果是________.二、解答题6.某学生五门功课成绩为80,95,78,87,65.写出均匀成绩的算法,画出流程图.7. 某电信部门规定:拨打市内电话时,假如通话时间不超出 3 分钟,则收取通话费0.2 元;假如通话时间超出 3 分钟,则超出部分以0.1 元/ 分收取通话费( 时间以分钟计,不足 1 分钟按 1分钟计算 ) ,画出计算话费的流程图.8.求方程ax2+( a+1) x+1=0根的算法流程图以下图,依据流程图,回答以下问题:(1)此题中所给的流程图正确吗?它表示的是哪一个问题的算法流程图?(2)写出一个正确的算法,并画出流程图.答案1.分析:第二步中y= 2,第三步中y=22+1= 5.答案: 5a2+1,a≤5,b=52 2.分析:这是一个分段函数b=的求值问题.依据条件易知,2a,a>5,+ 1= 26.答案: 26x-3, x≥3,3.分析:由y=| x-3|=3-x,x< 3.∴①处应填“ x<3”,②处应填“y← x-3”.答案: x<3y← x-32134.分析:由流程图知:令2x- 1=8( x>0) ,则x=4,1 x13令( 2)=8( x≤0) ,无解,∴输入的实数x=4.3答案:45.分析:流程图反应的是分段函数y=x2-1x<5,的求值问题,2x2+ 2x≥5∴当 x=3时, y=32-1=8.答案: 86.解:算法以下:流程图S1S←80S2S← S+95S3S← S+78S4S← S+87S5S← S+65S6A← S/5S7输出A7.解:依据题意:话费S(元)与时间 t (分钟)有以下函数关系:0.2, t ≤3, t >3且 t ∈N*= 0.2+ 0.1t -3S0.2+ 0.1[ t ] -2, t >3且t ?N*流程图以以下图所示.8.解:此题中给出的流程图不正确.由于它没有表现出对a的取值的判断,它只解决了算法中的一部分,即a≠0时的情况,这样是达不到求解的目的的.(2) 算法以下:S1输入a;S2假如a=0,则x←-1,输出x,1不然 x1←-1, x2←-a,输出 x1, x2.流程图如右图所示.。
2020-2021学年苏教版高中数学必修三《条件语句》课时同步练习及解析
(新课标)2018-2019学年苏教版高中数学必修三1.3.3 条件语句课时目标1.理解条件语句.2.能够用条件语句编写选择结构的程序.1.条件语句表达算法的__________结构.2.条件语句的一般形式为:If A ThenBElseCEnd If其中____表示判断的条件,____表示满足条件时执行的操作内容,____表示不满足条件的操作内容,__________表示条件语句结束.3.数学中的分类讨论在算法中一般用________语句.一、填空题1.条件语句实现算法中________结构.2.执行下面的伪代码,若输入的x的值为-2,则输出的y的值为________.If x ≥0 Then y ←x Else y ←-x End If Print y3.给出以下四个问题,其中需要用条件语句来描述其算法的有________. ①输入一个数x ,输出它的绝对值;②求函数f(x)=⎩⎨⎧x 2-1, x ≥0,x +2, x<0的函数值;③求面积为6的正方形的周长;④求三个数a ,b ,c 中的最大数. 4.阅读下列伪代码 x ←4If x>3 Theny ←x 2Else y ←2x End If Print y则该伪代码执行后,变量y 的值为________.5.当a =3时,所给出的伪代码输出的结果是________. Read aIf a<10 Then y ←2a Else y ←a 2End If Print y6.伪代码: Read a ,b ,c m ←aIf b>m Then m ←b End If If c>m Then m ←c End If Print m若执行伪代码时输入10,12,8,则输出的结果为________. 7.下面给出的是条件语句编写的伪代码,该伪代码的功能是求函数________的函数值.If x ≤3 Then y ←2x Else y ←x 2-1End If Print y8.如下图所给出的是一个算法的伪代码.如果输出的y 的值是20,则输入的x 的值是________. Read xIf x ≤5 Then y ←10x Else y ←2.5x +5End If Print y9.为了在执行下面的伪代码之后得到输出y =25,输入的x 应该是________. Read x If x<0 Theny ←(x +1)2Else y ←(x -1)2End If Print y二、解答题10.已知函数y =⎩⎨⎧x 2+1 (x ≤2.5),x 2-1 (x>2.5),根据输入x 的值,计算y 的值,写出伪代码.11.某工厂有一批计时工,8小时内每小时工资6元,8小时外加班每小时10元,会计当天就要向工人付清工钱.请编写一个根据小时数计算当天工资的算法,并用伪代码表示这个算法.能力提升12.发动机的推力F(kg)与温度t(℃)的关系是F =⎩⎨⎧1 860, t ≤10;2 080, 10<t ≤20;2 867, 20<t ≤30;3 250, 30<t ≤40.用伪代码编写程序,根据温度计算发动机的推力.13.儿童乘坐火车时,若身高不超过1.1 m ,则无须购票;若身高超过1.1 m 但不超过1.4 m ,可买半票;若超过1.4 m ,应买全票.试写出一个购票算法伪代码.使用条件语句时应注意的问题(1)条件语句是一个语句,If,Then,Else,End If都是语句的一部分.(2)条件语句必须是以If开始,以End If结束,一个If必须与一个End If相对应.(3)如果程序中只需对条件为真的情况作出处理,不用处理条件为假的情况时,Else分支可以省略,此时条件语句就由双支变为单支.(4)为了程序的可读性,一般If、Else与End If顶格书写,其他的语句体前面则空两格.答案知识梳理1.选择 2.A B C EndIf 3.条件 作业设计 1.选择解析 条件语句是处理选择结构的算法语句. 2.23.①②④ 4.16解析 因x =4满足“x>3”的条件,所以执行的是Then 后面的y =42=16. 5.6解析 因为3<10,所以y =2×3=6. 6.12解析 本伪代码的功能是筛选出a 、b 、c 中的最大值,故输出的m 的值为12.7.y =⎩⎨⎧2x , x ≤3x 2-1, x>3解析 该伪代码的主要功能是对分段函数y 求值.当x ≤3时,y =2x ;当x>3时,y =x 2-1.所以y =⎩⎨⎧2x , x ≤3x 2-1, x>3.8.2或6解析 当x ≤5时,10x =20,即x =2; 当x>5时,2.5x +5=20,解出x =6. 9.-6或6解析 伪代码对应的函数是y =⎩⎨⎧(x +1)2, x<0,(x -1)2, x ≥0. 由⎩⎨⎧ x<0,(x +1)2=25或⎩⎨⎧x ≥0(x -1)2=25, 得x =-6,或x =6. 10.解 算法分析: 第一步,输入x 的值.第二步,判断x 的范围,若x>2.5,则y ←x 2-1.若x ≤2.5,则y ←x 2+1. 第三步,输出y 的值. 伪代码如下:If x>2.5 Theny ←x 2-1Else y ←x 2+1EndIf Print y11.解 设某工人一天工作x 小时,则当天工资y 可表示为y =⎩⎨⎧6x , 0<x ≤8,6×8+10(x -8), x>8.用伪代码可表示为: Read xIf x ≤8 Then y ←6x Else y ←6×8+10(x -8)EndIf Print y 12.解 Read tIf t ≤10 Then F ←1 860ElseIf t ≤20 Then F ←2 080ElseIf t ≤30 Then F ←2 867 ElseF ←3 250 EndIf EndIf EndIf Print F13.解 伪代码如下:If h≤1.1 Then Print 免费乘车ElseIf h≤1.4 Then Print 半票乘车ElsePrint 全票乘车End IfEnd If。
苏教版必修3高中数学1.2.2《选择结构》ppt课件
输出x1 , x2
结束
编后语
老师上课都有一定的思路,抓住老师的思路就能取得良好的学习效果。在上一小节中已经提及听课中要跟随老师的思路,这里再进பைடு நூலகம்步论述听课时如何 抓住老师的思路。
① 根据课堂提问抓住老师的思路。老师在讲课过程中往往会提出一些问题,有的要求回答,有的则是自问自答。一般来说,老师在课堂上提出的问 题都是学习中的关键,若能抓住老师提出的问题深入思考,就可以抓住老师的思路。
S2 b2 4ac ;
S3 如果 0为真,则输出"方程无实数根",否则
x1
b 2a
,
x2
b 2a
.
根据上述步骤 , 我们可以画出如下的算法 流程图.
开始
输入a,b, c
b2 4ac
Y
0
N
输出 "方和无实数根"
x1
b 2a
,
x2
b 2a
2
使 n 的
值
增
加
1
2004
表示执行步骤的路
流 程 线 径,可用箭头表示
输出n 结束
表示算法的开始或结
起 止 框 束,常用圆角矩形表示
例3 设计求解一元二次方程ax2 bx c 0 a 0
的 一 个 算 法, 并 用 流 程 图 表 示.
分析 由于一元二次方程未必总有实数根,因此求解时, 要先计算判别式 b2 4ac ,然后比较判别式与0的大 小 , 再决定能否用求根公式进行求解 .因此, 在算法中应 含有选择结构. 解 算法如下: S1 输入 a,b, c ;
2017_2018学年高中数学课时跟踪检测三选择结构苏教版必修320180125182
课时跟踪检测(三)选择结构[层级一学业水平达标]1.下列函数求值算法中需要用到选择结构的是________.①f(x)=x2-1;②f(x)=2x+1;③f(x)=Error!④f(x)=2x.答案:③2.指出流程图的运行结果,若输入-4,则输出结果为________.答案:是负数3.如图是求某函数值的流程图,则满足该流程图的函数是______________.答案:y=Error!4.如图所示的流程图,若a=5,则输出b=________.解析:这是一个分段函数b=Error!的求值问题.根据条件易知,b=52+1=26.答案:265.设计一个判断正整数p是否是正整数q的约数的算法,并画出其流程图.1解:算法如下:S1输入p,q;S2判断p除q的余数r是否为零,如果r=0,则输出“p是q的约数”;否则,输出“p不是q的约数”.流程图:[层级二应试能力达标]1.如图所示的流程图的功能是________.解析:根据条件结构的定义,当a≥b时,输出a-b;当a<b时,输出b-a.故输出|a-b|.答案:计算|a-b|12.阅读如图所示的流程图,若运行该程序后输出的y值为,则输入的实数x的值为8________.21 3解析:由流程图知:令2x2-1=(x>0),则x=,8 41 1 3令(2 )x=(x≤0),无解,∴输入的实数x=.8 43答案:43.已知函数y=|x-3|,如流程图表示的是给定x的值,求其相应函数值的算法,请将该流程图补充完整.其中①处应填________,②处应填________.解析:由y=|x-3|=Error!∴①处应填“x<3”,②处应填“y←x-3”.答案:x<3y←x-34.阅读如图所示的流程图,若输入值x=3,则输出的结果是________.答案:1.55.对任意非零实数a,b,若a⊗b的运算原理如流程图所示,则3⊗2=________.解析:由于a=3,b=2,3则a≤b不成立,a+1 3+1则输出==2.b 2答案:26.如图,x1,x2,x3为某次考试三个评阅人对同一道题的独立评分,p为该题的最终得分,当x1=6,x2=9,p=8.5时,x3等于________.解析:x1=6,x2=9,|x1-x2|=3≤2不成立,即为“N”,所以再输入x3;由绝对值的意义(数轴上一个点到另一个点的距离)和不等式|x3-x1|<|x3-x2|知,点x3到点x1的距离小于点x3到x2的距离,所以当x3<7.5时,|x3-x1|<|x3-x2|成立,即为“Y”,此时x2=x3,x1+x3 6+x3所以p=,即=8.5,2 2解得x3=11>7.5,不合题意;当x3≥7.5时,|x3-x1|<|x3-x2|不成立,即为“N”,此时x1=x3,x3+x2 x3+9所以p=,即=8.5,2 2解得x3=8>7.5,符合题意.答案:87.下图的流程图,如果输入三个实数a,b,c,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入__________________.4答案:c >x8.给定下面的流程图,要使输出的结果在区间[-1,0]上,则输入的 x 的取值范围是 __________.5 解析:此流程图对应函数为 y =Error!若 y ∈[-1,0],则Error!或Error!解得 2≤x ≤ .2 5答案:[2,2 ]9.求方程 ax 2+(a +1)x +1=0根的算法流程图如图所示,根据流程图,回答下列问题:(1)本题中所给的流程图正确吗?它表示的是哪一个问题的算法流程图?(2)写出一个正确的算法,并画出流程图.解:(1)本题中给出的流程图不正确.因为它没有体现出对 a 的取值的判断,它只解决了 算法中的一部分,即 a ≠0 时的情形,这样是达不到求解的目的.(2)算法如下:S1 输入 a ;S2 如果 a =0,则 x ←-1,输出 x ,1否则 x 1←-1,x 2←- ,输出 x 1,x 2. a流程图如图所示.510.已知下列算法:S1输入x;S2若x>0,执行S3,否则执行S4;S3y←2x+1,转S7;S4若x=0,执行S5,否则执行S6;1S5y←,转S7;2S6y←-x,转S7;S7输出y;S8结束.(1)指出其功能(用算式表示);(2)画出该算法的流程图.解:(1)求函数y=Error!的函数值.(2)流程图如下:6。
推荐-高中数学苏教版必修3课件1.2.2 选择结构
自主预习 合作探究
问题导学 即时检测 一 二 三
解:算法步骤如下: S1 输入a,b; S2 若a≠0,则x← ������������,输出x,并执行S4,否则,执行S3; S3 如果b≠0,则输出“方程无实数根”,否则,输出“方程的根为全 体实数”; S4 结束. 流程图如图.
问题导学 即时检测 一 二 三
问题导学 即时检测 一 二 三
自主预习 合作探究
大部分流程图的流程是按自上而下的顺序进行.但当遇到根据条 件作出判断,然后再决定执行哪一个步骤的问题时,必须使用选择 结构.选择结构一般有一个入口、两个出口,算法的流程根据条件 是否成立有不同的流向,故选择结构看似有两个出口,而实际执行 时,程序只能执行其中一支的步骤.
析式为
.
解析:当满足x<0时,f(x)=2x-3;当不满足x<0,即x≥0时,f(x)=5-4x,所
以满足该程序的函数解析式为f(x)=25���-���4-3������,,������������
< ≥
0, 0.
答案:f(x)=
2������-3,������ 5-4������,������
< ≥
自主预习 合作探究
利用选择结构解决数学问题的方法 (1)分析题目,确定分类的原则和方法; (2)明确每个分类中执行的步骤; (3)写出合理的自然语言算法; (4)画出流程图.
问题导学 即时检测 一 二 三
自主预习 合作探究
三、选择结构的实际应用 活动与探究3 某居民区的物业部门每月向居民收取卫生费,计费方法如下:3人 和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2 元.设计一个算法,根据输入的人数,计算应收取的卫生费,并画出流 程图. 思路分析:本题为实际应用题,重点是要建立卫生费与人数的函 数关系,画流程图时要注意选择结构的应用.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(新课标)2018-2019学年苏教版高中数学必修三
1.2.2 选择结构
课时目标 1.进一步熟悉流程图的画法.2.掌握选择结构的流程图的画法.3.能用选择结
构框图描述实际问题.
1.选择结构
先根据条件______________,再决定执行哪一种操作的结构称为选择结构(或称为“分支
结构”).
2.选择结构的结构形式
当条件p成立时执行______,否则执行______.
一、填空题
1.下列算法中,含有选择结构的是________.(填序号)
①求两个数的积;
②求点到直线的距离;
③解一元二次方程;
④已知梯形两底和高求面积.
2.流程图中,具有赋值、计算功能的是________框.
3.下列关于选择结构的描述,不正确的是________.
①选择结构的出口有两个,但在执行时,只有一个出口是有效的;
②选择结构的判断条件要写在判断框内;
③双选择结构有两个出口,单选择结构只有一个出口;
④选择结构根据条件是否成立,选择不同的分支执行.
4.中山市的士收费办法如下:不超过2公里收7元(即起步价7元),超过2公里的里
程每公里收2.6元,另每车次超过2公里收燃油附加费1元(不考虑其他因素).相应收
费系统的流程图如图所示,则①处应填________.
5.输入-5,按图中所示流程图运行后,输出的结果是________.
6.给出一个流程图,如图所示,其作用是输入x的值,输出相应的y的值.若要使输
入的x的值与输出的y的值相等,则输入的这样的x的值有________个.
7.如图是求实数x的绝对值的流程图,则判断框①中可填________.
8.函数y= x2+1 x>00 x=0x+6 x<0的流程图如图所示,则①②③处分别填________、
________、________.
9.已知函数y= log2x, x≥2,2-x, x<2.下图表示的是给定x的值,求其对应的函数值
y
的流程图.
①处应填写________;②处应填写________.
二、解答题
10.画出计算函数y=|2x-3|的函数值的流程图.
11.已知函数y= 1x x>00 x=01x2 x<0,试设计一个算法的流程图,计算输入自变量
x
的值时,输出y的值.
能力提升
12.画出解一元一次不等式ax>b的流程图.
13.到银行办理个人异地汇款(不超过100万)时,银行要收取一定的手续费.汇款额不 当x>5时,x=1x不成立,所以满足题意的x的值有1,0,3.
超过100元,收取1元手续费;超过100元但不超过5 000元,按汇款额的1%收取;
超过5 000元,一律收取50元手续费,其他情况不予办理.试设计一个算法描述汇款
额为x元时,银行收取手续费为y元的过程,并画出流程图.
1.对需要按给定的条件进行分析、比较和判断,并按判断的不同情况进行不同的操作
的问题,设计算法时就要用到选择结构.
2.选择结构要先根据指定的条件进行判断,再由判断的结果决定选取执行两条分支路
径中的某一条.
答案
知识梳理
1.作出判断 2.A B
作业设计
1.③
解析 解一元二次方程时,当判别式Δ<0时,方程无解,当Δ≥0时,方程有解,
由于分情况,故用到选择结构.
2.处理
3.③
4.y←8+2.6(x-2)
解析 当x>2时,2公里内的收费为7元,
2公里外的收费为(x-2)×2.6,
另外燃油附加费为1元,
∴y=7+2.6(x-2)+1=8+2.6(x-2).
5.1
解析 因x=-5,不满足x>0,所以在第一个判断框中执行“N”,在第2个判断框中,
由于-5<0,执行“Y”,所以得y=1.
6.3
解析 当x≤2时,x=1或x=0则x=y;
当2
7.x≥0(或x>0)
8.y←x2+1 x=0 y←0
解析 由分段函数的表达式知,x>0时,y=x2+1,故①处填y←x2+1;由②的否执行
y=x+6知②处填x=0;当x=0时,y=0知③处填y←0.
9.x<2 y←log2x
解析 ∵满足判断框中的条件执行y=2-x,
∴①处应填x<2.
不满足x<2即x≥2时,y=log2x,故②处应填y←log2x.
10.解
11.解
12.解
13.解 由题意知本题是一个分段函数问题,分段函数解析式为
y= 1 0
第一步,输入汇款额x;
第二步,判断x≤100是否成立;若成立,则y←1,转执行第五步,若不成立,则执行
第三步;
第三步,判断x≤5 000是否成立;若成立,则y←0.01x,转执行第五步,若不成立,则
执行第四步;
第四步,判断x≤1 000 000是否成立;若成立,则y←50,转执行第五步,若不成立,
则输出“不予办理”;
第五步,输出y.
流程图如图
