第七章耦合电感与理想变压器
电路第7章含有耦合电感的电与变压器精品文档
i 1 2 2 c o s ( 2 0 0 0 t 5 3 . 1 ) A u 2 8 2 c o s ( 2 0 0 0 t 3 6 . 9 ) V
开关S闭合时:
U 1 (R 1 jL 1 )I 1 jM I 2 (R 2jL 2)I2jM I1 ＝ 0
dt
M
di1 dt
线圈1的自感电压 线圈2的互感电压
u11
e1
L1
d i1 dt
u 21 e2 M
d i1 dt
e 1 称为自感电动势 e 2 称为互感电动势
返回
电路分析基础
第7章 含有耦合电感的电路与变压器
同理：对于b)图有
e1
d12
dt
M
di2 dt
e2
返回
电路分析基础
第7章 含有耦合电感的电路与变压器
（2）反接 （同名端相连）
u
u1
u2
L1
di dt
M
di dt
L2
di dt
M
di dt
di (L1 L2 2M) dt
Ldi dt
相量式为 U U 1 U 2 j(L 1 L 2 2 M )I
返回
电路分析基础
返回
电路分析基础
第7章 含有耦合电感的电路与变压器
【例7.3】如图电路中，输入电压 u1102co2s0t0V 0，
R1 3，L 1 2 m ,L 2 3 H m ， M H 2 m ， R 2 H 8 。
i 试求开关S打开与闭合时的 1 和u 2 。
耦合电感的功率 、变压器原理、理想变压器
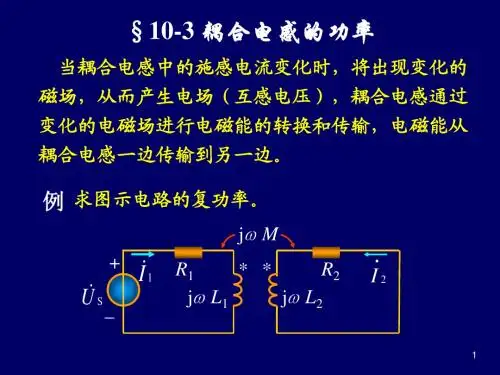
k 1 M L1 L2
变比（匝数比）
L1 L2 N1 N 2 n
在一些实际工程概算中，在误差允许的范围内，把 实际变压器当理想变压器对待，可使计算过程简化。
12
2.理想变压器的主要性能
1
i
N2
1）电压变换关系 1' 1 2 11 22 k 1 N1 d 1 d d 2 d u1 N1 u2 N2 dt dt dt dt n:1
R2
jL2
U S
+ –
I1
I 2
RL
L1=3.6H , L2=0.06H , M=0.465H , R1=20 , R2=0.08 , RL=42 1150o V 314rad/s, U S , I . 求: I
1 2
I 1
Z11
解
(M ) 2 Z 22
应用原边等效电路
3
§10-4 变压器原理
变压器是利用互感来实现从一个电路向另一个电 路传输能量或信号的器件。当变压器线圈的芯子为 非铁磁性物质时，称为空心变压器。
1.空心变压器的电路
I1
R1 j L1
j M
* *
R2
US
一次 回路
+ –
I2
j L2 ZL=RL+jXL
二次 回路
4
2.分析方法
1）列方程分析 回路电流方程：
2
2'
u1 N1 n u2 N 2
n:1 + u1 _ * + u2 _
+ u1 _
*
*
+ u2 _
范世贵-电路基础2版-答案(第7章)
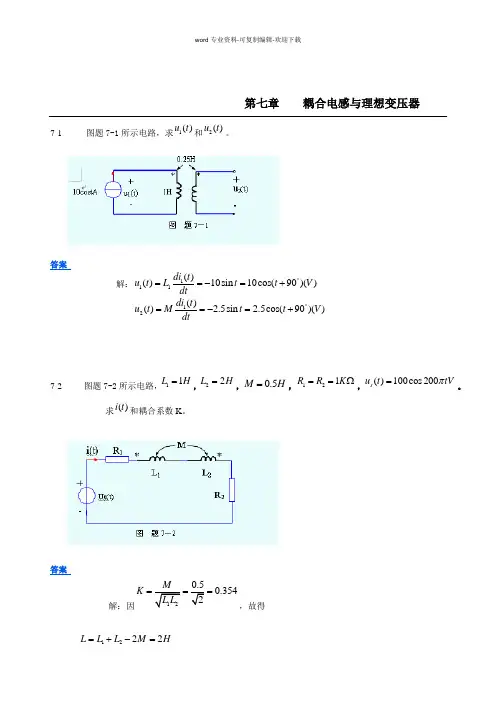
第七章 耦合电感与理想变压器7-1 图题7-1所示电路，求和。
答案解：7-2 图题7-2所示电路，，，，，。
求和耦合系数K 。
答案解：因，故得1()u t 2()ut 111()()10sin 10cos(90)()di t u t L t t V dt ︒==-=+12()() 2.5sin 2.5cos(90)()di t u t M t t V dt︒==-=+11L H=22L H=0.5M H =121R R K ==Ω()100cos 200s u t tVπ=()it 0.354K ===1222L L L M H=+-=7-3 耦合电感，，。
求它们作串联、并联时的各等效电感。
答案解：两电感串联时：a)顺接：b)反接：两电感并联时：a)同名端同侧：b)同名端异侧：7-4 图题7-4所示为变压器电路，已知V 。
今测得。
求两种不同连接法时伏特计的读数。
121002000400m m U I R R j L j ωπ••==+++42.332.14()mA ︒=∠-()42.3cos(20032.14)i t t mA π︒∴=-16L H=24L H=3M H =12216()L L L M H =++=1224()L L L M H =+-=2121215/4()2L L M L H L L M -==+-2121215/16()2L L M L H L L M -==++12220u =345612u u V==图 题 7-4 答案解：得所以电压表的读数为0V 。
,，由图（b ）所示所以电压表的读数为。
7-5 图题7-5所示示电路，。
（1），求、；（2），再求、；答案解：(1)12)2200a U V•︒=∠设3412U V•=5612U V•=-34560U U U V•••=+=34)12b U V •=-5612U V•=-345624U U U V•••=+=-24V 10/rad s ω=0.5K =1I •2I •1K =1I •2I•0.5K=0.5M H∴==12120.51000.5(10)0j I j I j I j I ωωωω••••⎧-=⎪⎨⎪-++=⎩解得（2）列方程组:解得7-6 图示电路,,。
耦合电感和理想变压器
本章重点
• 耦合电感中的磁耦合现象 • 互感和耦合电感的同名端 • 互感线圈中电压与电流的关系 • 互感电路的分析与计算 • 空心变压器、理想变压器的初步概念
8.1 耦合电感
8.1.1 基本概念
1
2
11
21
自感 磁通
i1
N1
N2
互 感
磁
当两个线圈相距较近时，各自线圈上的电流变化会通
2013.3农业部的调查
家庭农场初具规模
——截至2012年底，全国30个省、区、市(不含西藏)共有符 合本次统计调查条件的家庭农场87.7万个，经营耕地面积 达到1.76亿亩，占全国承包耕地面积的13.4%。平均每个 家庭农场有劳动力6.01人，其中家庭成员4.33人，长期雇 工1.68人。
家庭农场以种养业为主
家庭农场注册
——已被有关部门认定或注册的共有3.32万个，其中农业部 门认定1.79万个，工商部门注册1.53万个。
家庭工业概念和地位
概念
——主要指以家庭为基本生产单位，以家庭住宅或承租场 地为生产场所，以家庭成员为主要劳动力，生产资料归 家庭所有，劳动成果归家庭共同所有，并以家庭财产对 债务承担相应责任的一种工业生产组织形式。
农户与农村常住户
农户 ——农业户口、农村常住户 ——基本经营单位、农村经济社会发展基本细胞 农村常住户 ——长期(一年以上)居住在乡镇(不包括城关镇)行
政管理区域内的住户，以及长期居住在城关镇所 辖行政村范围内的农村住户。
种粮大户肖建军
思考题：肖建军在生产经营中面临的主要困难及解 决方案？
1.耕种面积1020亩，遍布双江口镇3个村，仅日常管理工 作雇工6人。
07电路基础
ψ 12 = N1ϕ12
ψ 12 = M 12i2
(7.1-5)
对于线性耦合电感，自感和互感磁通链都正比于电流i2， (7.1-6)
式中L2为线圈2的自感系数，M12是互感系数，单位是亨利。
第七章 耦合电感与理想变压器 式(7.1-3)和(7.1-6)中的互感系数可写为
M 21 = M 12 =
第七章 耦合电感与理想变压器 同理，当线圈2通以电流i2、线圈1开路时：在线圈2中产 生自感磁通Ф22，其中有一部分也穿过线圈1，记为Ф12，称 为互感磁通。同样有，
ϕ12 ≤ ϕ22
链和互感磁通链分别为
(7.1-4)
电流i2(称为施感电流)在线圈2、线圈1中产生的自感磁通
ψ 22 = N 2ϕ22
图7.1-7 例7.1-1用图
第七章 耦合电感与理想变压器 解 由于第2个线圈开路，其电流为零，所以R2上电压为 零，L2上自感电压为零，L2上仅有电流i1在其上产生的互感电 压。这一电压也就是d , e开路时的电压。根据i1的参考方向及 同名端位置，可知
di1 (t ) ude (t ) = M dt di1 (t ) ubc (t ) = L1 dt
从感应电压角度定义
第七章 耦合电感与理想变压器
di1 di2 u1 = L1 +M dt dt di2 di1 u2 = L2 +M dt dt
di1 di2 u1 = L1 −M dt dt di2 di1 u2 = L2 −M dt dt
图7.1-3 互感线圈的同名端：a.磁通相助情况 b.磁通相消情况
在t≥2s时,
i1 (t ) = 0
uab = 0, ubc = 0, uac = 0, ude = 0
耦合电感与变压器(3)
•
I 1 Z11
+
•
US –
( M )2 Zref1 Z22
初级等效电路
•
•
即： I1
US
Z11 Zref1
•
次级：
•
I2
j M I 1
Z 22
27
关于反映阻抗：
1. 次级在初级中的反映阻抗： 2. 与同名端无关。
( M )2
Zref1
Z22
3. 当Z22为容性 →Zref1为感性。 当Z22为感性 →Zref1为容性 。 当Z22为电阻 →Zref1为电阻 。
•
I 1 R1
j M
R2
•
+
**
I2
•
US
–
j L1
j L2
ZL
空芯变压器： （非铁磁性骨架材料） 主圈（原边、初级线圈）： 副圈（副边、次级线圈）：
24
一、回路分析法
•
I 1 R1
j M
R2
•
+
**
I2
•
US
–
I1 j L1
j L2 I2
ZL
•
•
•
(R1 jL1 )I1 j M I 2 U S
(R1 j L1)I1 (R1 j L1 j M )I2 U -(R1 j L1 j M )I1 (R1 R2 j L1 j L2 2 j M )I2 0
可见，此法麻烦！
19
四、互感去耦法
1. 同名端相连
i1
M
1
**
L1
i2
2
L2
i1
1
(L1–M)
i2
2
电路分析第七章-含有耦合电感的电路
* --
(a)
+
i1 +
M **
u1u12L1
i2
+
L2u21
-
u2
--
-+
(b)
解:图(a)中
u1
=
L1
di1 dt
+
u12
u12
=
−M
di2 dt
∴u1
=
L1
di1 dt
−M
di2 dt
u2
=
L2
di2 dt
+ u21
u21
=
−M
di1 dt
∴u2
=
L2
di2 dt
−M
di1 dt
图(b)中
u1
若u21
=
−M
di1 dt
线圈1 线圈2
i1 ∆1’
*1
2*’
u21+2∆
1端与2’端互为同名端 1’端与2端互为同名端
N1
Φ1
N2
Φ2
i1
i2
1‘ - u1+ 1 2‘- u2+ 2
图(a)
N1
Φ1
N2
Φ2
i1
i2
1‘ - u1+ 1 2‘+ u2 - 2
图(b)
M
*
*
L1
L2
1‘
1 2‘
2
图(a)的电路符号
图(b)
u1
=
L1
di1 dt
+
M
di2 dt
u2
=
L2
di2 dt
+
M
电路分析基础耦合电感和理想变压器
电路分析基础耦合电感和理想变压器耦合电感（mutual inductance）是指两个或多个电感器件之间由于相互作用而产生的互感现象，其中一个电感器件的磁通变化会在另一个电感器件中感应出电动势。
理想变压器（ideal transformer）是一种特殊的耦合电感，其工作原理是利用磁感应定律，将输入电压和输出电压之间按一定的变比比例转换。
在电路分析中，耦合电感和理想变压器经常被用来探讨和解决一些特定的问题。
下面将分别介绍其基本原理和应用。
1.耦合电感：耦合电感的基本原理是根据电磁感应定律，当一个电感器件中通过的电流变化时，会在另一个电感器件中感应出电动势。
考虑两个简单的线圈，分别为主线圈和副线圈。
当主线圈中的电流变化时，根据电磁感应定律，在副线圈中也会感应出一个与主线圈中电流变化相关的电动势。
这种相互作用可以由一个耦合系数k表示，取值范围为0-1，表示两个线圈之间磁通的共享程度。
耦合电感可以用于共振电路、振荡电路等。
在共振电路中，当主线圈与副线圈之间有耦合时，可以通过调整耦合系数k来改变电路的共振频率，实现频率调谐的效果。
在振荡电路中，耦合电感可以提供正反馈，增强电路的振荡效果。
2.理想变压器：理想变压器是电路分析中常用的电气元件之一，其特点是无能量损耗、无电阻、无磁滞，能够以一定的变比将输入电压转换为输出电压。
理想变压器的基本结构由两个线圈绕制在共同的磁芯上组成。
理想变压器的工作原理是利用电磁感应定律和电压平衡原理。
当输入线圈（初级线圈）中通过的电流变化时，根据电磁感应定律，在输出线圈（次级线圈）中也会感应出一个与输入电流变化相关的电动势。
由于磁通守恒，输入线圈的磁通变化与输出线圈的磁通变化成一定的比例，从而实现输入电压和输出电压之间的变比转换。
理想变压器可以用于电压调整、功率传递等电路。
在电压调整电路中，通过改变输入线圈和输出线圈的匝数比例，可以实现对输入电压和输出电压之间的调整。
在功率传递电路中，根据变压器的功率平衡原理，输入功率和输出功率之间的关系可以用变压器变比关系表示。