西安石油大学计算方法实验1--非线性方程的迭代数值解法
《计算方法》
实验报告
二级学院： 计算机学院
专 业： 计算机科学与技术
指导教师： 爨莹
班级学号： 201107010122
姓 名： 张文江
实验一 非线性方程的迭代数值解法
实验目的：
① 通过编程和插值与拟合中的某种具体算法解决具体问题，更深一步
的体会计算方法这门课的重要性，同时加深对插值与拟合公式某种具体算法
的理解。
② 熟悉编程环境。
2、实验要求:
实现插值与拟合中的某种具体算法编写并执行
3、实验内容：
1)用牛顿法求解01553x的根，取初始值为10。
2) 用弦截法求解数学方程，()^310fxxx在[1,1.5]内的根。
4、题目：
1)用牛顿法求解01553x的根，取初始值为10。
2) 用弦截法求解数学方程，()^310fxxx在[1,1.5]内的根
5、原理：
编程实现牛顿法、弦截法求非线性方程的根。
(1)牛顿法
x1=(x0-f/f1)；
（2）单点弦截法
x2=x0-f0*(xn-x0)/(fn-f0);
6、设计思想：
(1)牛顿法
首先找到初始值，将初始值带入到方程中，计算一次求导和二次求导的值，确
定x0和x1的值，然后利用循环x1=(x0-f/f1)，条件为（x0-x1）>1e-6,循环一
次的x1的值给x0；直到找到符合的x1为止。
（2）单点弦截法
首先找到初始值，将初始值带入到方程中，计算一次求导和二次求导的值，确
定x0和x1的值，然后利用循环x2=x0-f0*(x1-x0)/(f1-f0);，条件为
（x0-x1）>1e-6, 循环一次的x2的值给x1；直到找到符合的x2为止。
7、对应程序：
（1）牛顿法：
#include
#include
float f(float a,float b,float c,float d,float x)
{
float f;
f=a*x*x*x+b*x*x+c*x+d;
return f;
}
float f1(float a,float b,float c,float x)
{
float f1;
f1=(x*3*a+2*b)*x+c;
return f1;
}
float root(float a,float b,float c,float d)
{
float x0,x1=6;
do
{
x0=x1;
x1=x0-f(a,b,c,d,x0)/f1(a,b,c,x0);
}while(fabs(x1-x0)>=1e-6);
return x0;
}
void main()
{
float a,b,c,d,x;
printf("input four float numbers:\n");
scanf("%f%f%f%f",&a,&b,&c,&d);
x=root(a,b,c,d);
printf("%.1fX^3+%.1fX^2+%.1fX+%.1f=0 its root near x=1.5
is :%.3f\n",a,b,c,d,x);
}
（2）迭代法：
#include
#include
void main()
{
float f(float x);
float root(float x1, float x2);
float xpoint(float x1,float x2);
float x1,x2,f1,f2,x;
do
{
printf("input x1,x2:\n");
scanf("%f,%f",&x1,&x2);
f1=f(x1);
f2=f(x2);
}while(f1*f2>=0);
x=root(x1,x2);
printf("A root of equation is %.3f\n",x);
}
float root(float x1, float x2)
{
float xpoint(float x1,float x2);
float f(float x);
float x,y,y1;
y1=f(x1);
do
{
x=xpoint(x1,x2);
y=f(x);
if(y*y1>0)
{
y1=y;
x1=x;
}else
x2=x;
}while(fabs(y)>=0.0001);
return (x);
}
float f(float x)
{
float y;
y=x*x*x-x-1;
return (y);
}
float xpoint(float x1,float x2)
{
float y;
y=(x1*f(x2)-x2*f(x1)) / (f(x2) - f(x1));
return (y) ;
}
8、实验结果：
（1）牛顿法结果：
X=5.372
（2）迭代法结果
X=1.325
9、图形
（1）
（2）
10、
实验体会：
通过编程，切身感到计算方法这门课绝不仅仅是数学，是图形的
观察和实际计算方法的应用，从而解决一些复杂的数值问题。
求解非线性方程的三种新的迭代法
求解非线性方程的三种新的迭代法
迭代法是一种通过迭代逼近的方式来求解方程的方法。
它的基本思想是通过不断逼近
方程的解，使得逼近值与真实解的差距越来越小，最终得到方程的解。
下面介绍三种新的迭代法：牛顿迭代法，弦截法和切线法。
一、牛顿迭代法
牛顿迭代法是一种通过利用函数导数的信息来逼近方程解的方法。
它的迭代公式为：
x_(n+1) = x_n - f(x_n)/f'(x_n)
x_n表示第n次迭代得到的逼近解，f(x_n)表示在x_n处的函数值，f'(x_n)表示在x_n 处的导数值。
牛顿迭代法的优点是收敛速度快，通常是二阶收敛，但其缺点是需要计算函数的导数，如果导数计算困难或者导数为零的情况下，该方法可能不适用。
二、弦截法
三、切线法
切线法的优点和牛顿迭代法类似，但其缺点是需要计算函数的导数，且对于初始逼近
解的选择比较敏感。
牛顿迭代法、弦截法和切线法都是三种常用的非线性方程迭代法。
它们各自有着优点
和缺点，适用的领域和条件也不尽相同。
在实际问题中，需要根据具体情况选择合适的方
法来求解非线性方程。
求解非线性方程的三种新的迭代法
求解非线性方程的三种新的迭代法迭代法是一种通过反复递推计算得到逼近解的方法，对于非线性方程求解而言，迭代法通过不断更新变量的值，使得方程逐渐趋近于真实解。
下面将介绍三种新的迭代法：逐次缩小区间法、割线法和弦截法。
第一种迭代法是逐次缩小区间法。
逐次缩小区间法是一种通过不断递推缩小变量的取值范围来求解非线性方程的方法。
算法步骤如下：1. 选取一个初始区间[a, b]，使得f(a)和f(b)异号，即f(a)*f(b)<0。
2. 将区间[a, b]均分，得到区间的中点c=(a+b)/2。
3. 比较f(a)*f(c)和f(b)*f(c)，如果f(a)*f(c)<0，则说明解在区间[a, c]内；如果f(b)*f(c)<0，则说明解在区间[c, b]内。
4. 重复步骤2和步骤3，直到得到精度要求的解。
逐次缩小区间法的优点是简单易懂，计算量较小；但缺点是需要事先给出一个初始区间，初始区间的选择对结果有影响，并且对于复杂的方程可能需要很多次均分才能逼近解。
第二种迭代法是割线法。
割线法是一种通过利用连续两个点的斜率来逼近解的方法。
算法步骤如下：1. 选取两个初始点x0和x1，计算出对应斜率f(x0)和f(x1)。
2. 利用斜率和已知点构造直线方程，得到直线和x轴的交点x2，并将x1更新为新的x0，x2更新为新的x1。
3. 重复步骤2，直到满足精度要求。
割线法的优点是不需要计算导数，因此适用于不易求导的情况；但缺点是可能出现迭代过程不收敛的情况，需要事先给出两个初始点，并且计算量相对较大。
弦截法与割线法相似，也是通过利用连续两个点的连线来逼近解的方法，但不同之处在于弦截法的直线是通过前两个点的连线来构造的。
弦截法的优缺点与割线法类似，不需要计算导数，但迭代过程可能不收敛。
三种新的迭代法均有各自的特点和适用范围，适合于不同类型的非线性方程。
在实际应用中，需要根据具体的方程和精度要求选择合适的迭代方法。
第7章.非线性方程迭代法
f
的重根
=
的单根。
➢ 正割法 / Secant Method / ：
Newton’s Method 一步要计算 f 和 f ’，相当于2个函数值， 比较费时。现用 f 的值近似 f ’，可少算一个函数值。
割线
/ secant line /
收敛比Newton’s Method 慢， 且对初值要求同样高。
牛顿迭代法的改进与推广
➢ 重根 / multiple root / 加速收敛法：
Q1: 若 f (x*) ，0 Newton’s Method 是否仍收敛？ 设 x* 是 f 的 n 重根，则：f ( x) ( x x*)n q( x) 且 q( x*) 0。
因为 Newton’s Method 事实上是一种特殊的不动点迭代，
④
|
x
*
xk
|
1
1
L
|
xk 1
xk
|
?
✓ | xk1 xk | | x * xk | | x * xk1 | | x * xk | L | x * xk |
⑤
|
x*
xk
|
Lk 1 L
|
x1
x0
|
?
可用 | xk1 xk |来 控制收敛精度
| xk1 xk | | g( xk ) g( xk1 ) | | g(ξk )(xk xk1 ) |
3
| g( x) | | x2 | 1
现令 ( x) (1 K )x Kg( x) (1 K )x K ( x3 1)
3
希望 | ( x) | | 1 K Kx2 | 1，即
2 K 0 x2 1
在 (1, 2) 上可取任意 2 K，例0如K = 0.5，则对应
计算方法 6 非线性方程迭代法资料
推论 设 C[a, b]满足上面的条件1),且对x [a, b],存在常数L (0,1)，使
| ( x) | L 1， 则 ( x)在[a, b]上存在唯一的不动点.
充分性条件
迭代法的全局收敛性
定理2.2. 设 C[a, b]满足定理2.1中的条件,则对x0 [a, b],由格式
产生的序列{xk }收敛到的不动点x* ,且有误差估计 收敛速度？误差估计？
1)如果对x [a, b],有a ( x) b,则 ( x)在[a, b]上一定存在不动点.
2)在条件1)的基础上，且存在常数L (0,1)，使对x, y [a, b]都有
| ( x) - ( y) | L | x - y |， 称为全局Lipschitz条件
则不动点唯一.
证明. 令g( x) x- ( x), 注意到，
是：a2 : a1; b2 : x1.
否：a2 : x1; b2 : b1. 可知,[a2,b2 ] [a1,b1]. 上述过程继续下去
长度为b - a . 22
可得出一系列有根区间 [ak ,bk ] [a2,b2] [a1,b1] [a,b]. 区间[ak ,bk ]的长度为b2-ka .
事前误差估计
| xk
-
x*
|
L 1 L
|
xk
xk 1
|,
k
1, 2,
| xk
事后误差估计
-
x*
|
Lk 1 L
|
x1
x0
|,
k
1, 2,
称序列是适定的，它表明 迭代法算出的每个点是有 意义的！
证明. 设x*是在[a, b]上的唯一不动点.由格式产生的序列{xk }[a, b],
非线性方程组的牛顿迭代法-最速下降法
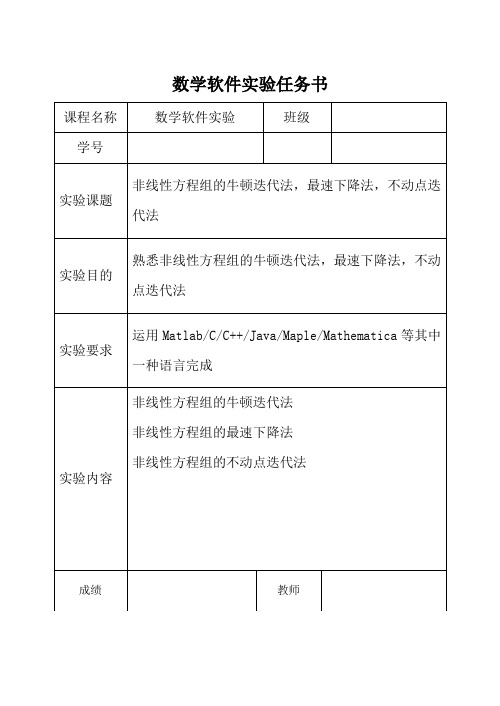
数学软件实验任务书实验一 非线性方程组的牛顿迭代法 1 实验原理对于非线性方程11221212(,,,)(,,,)(,,,)n n n n f x x x f x x x f f x x x ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭ 在x (k )处按照多元函数的泰勒展开，并取线性项得到 ()()()()(1)()1111()()()()(1)()()122()()()()(1)()1(,,,)(,,,)()0(,,,)k k k k k k n n k k k k k k k n n n k k k k k k n n n nn f x x x x x f x x x x x f x f x x x x x +++⎛⎫⎛⎫- ⎪ ⎪- ⎪ ⎪'+= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭ 其中1111()n n n n f f x x f x f f x x ∂∂⎛⎫ ⎪∂∂ ⎪' ⎪= ⎪∂∂ ⎪ ⎪∂∂⎝⎭(1)()()()()()1111(1)()()()()()()1221(1)()()()()()1(,,,)(,,,)[()](,,,)k k k k k k n n k k k k k k k n n n k k k k k k n n n n n x x f x x x x x f x x x f x x x f x x x ++-+⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪'=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 2 数据来源计算非线性方程组22220.50440x x y x y ⎧--+=⎨+-=⎩ 初值取11x y ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦3 实验步骤步骤一：编写牛顿迭代法的基本程序。
打开Editor 编辑器，输入以下语句：function [x,n,data]=new_ton(x0,tol)if nargin==1tol=1e-10;endx1=x0-f1(x0)/df1(x0);MATLAB 241 数值分析与应用n=1;%迭代过程while (norm(x1-x0)>tol)x0=x1;x1=x0-f1(x0)/df1(x0);n=n+1;%data 用来存放中间数据data(:,n)=x1;endx=x1;以文件名new_ton.m保存。
非线性方程数值解法详解课件
例如，对于求解非线性方程$f(x)=0$的 应用实例中需要注意选择合适的初始近
根，可以先选择一个初始近似解$x_0$， 似解和设置合适的精度要求，以确保算
然后按照弦截法的迭代过程逐步逼近方
法能够快速收敛到真实解。
程的真实解。
05 共轭梯度法
共轭梯度法的原理
它利用共轭方向的概念，通过迭代过程中不断更新搜 索方向，使得函数值逐渐减小，最终找到方程的解。
牛顿法的实现步骤
确定初始点x0，计算f(x0)和f'(x0)，如果f(x0)不等于0，则按照牛顿法的迭代公式 进行迭代，直到满足精度要求。
1. 选取初始点x0；2. 计算函数值f(x0)和导数值f'(x0)；3. 如果f(x0)不等于0，则 按照牛顿法的迭代公式x1=x0-f(x0)/f'(x0)进行迭代；4. 重复步骤2和3，直到满 足精度要求。
以求解非线性方程为例，通过选择合 适的迭代法和初值，可以有效地求解 非线性方程的近似解。
03 牛顿法
牛顿法的原理
01
基于函数f(x)的泰勒级数的前两项， 通过迭代的方式逼近方程f(x)=0 的解。
02
牛顿法的基本思想是通过泰勒级 数的近似，将非线性方程f(x)=0 转化为线性方程，然后利用线性 方程的解来逼近非线性方程的解。
当达到预设的迭代次数或满足一定的收敛 条件时，停止迭代，输出结果。
共轭梯度法的收敛性分析
共轭梯度法具有全局收敛性和局部收敛性，即只要初始点 选择得当，算法能够找到方程的解，且在局部范围内具有 快速收敛的特点。
收敛性分析主要涉及算法的迭代矩阵和函数的性质，如连 续性和可微性等。
共轭梯度法的应用实例
牛顿法的收敛性分析
在一定的条件下，牛顿法是收敛的， 且具有二阶收敛速度。
第7章-非线性方程迭代解法yjs讲解
lnim(bn
an )
lim
n
1 2 n 1
(b
a)
0
lim
n
an
lim
n
bn
x
•
取
x
cn
1 2 (an
bn )为
x*
的近似解
7
科大研究生学位课程 数值分析
求方程f(x)=0的根的二分法算法
(1) 输入 : 有根区间[a,b]的a,b值及精度控制量; (2)置x:=(a+b)/2, (3)若f(x)=0，输出x，停算；否则，转步(4); (4)若f(a)f(b)<0，则置b:=x ；否则，置a:=x ;
xk
|
?
✓ | xk1 xk | | x * xk | | x * xk1 | | x * xk | L | x * xk |
⑤
|
x*
xk
|
Lk 1 L
|
x1
x0
|
?
可用 | xk1 xk |来 控制收敛精度
| xk1 xk | | (xk ) (xk1 ) | | (ξk )(xk xk1 ) |
定理 若x*为上式定义的函数g(x)的不动点，则x* 为(x)
的不动点.反之，若x*是(x)的不动点，设’’(x)存
在, ’(x* ) ≠0，则x*是(x)的不动点且斯蒂芬森迭代法 是二阶收敛的.(证明略）
例：求 f ( x) x3 3x 1 0 在 (1, 2) 的实根。
如果用 x 1 (x3 1)进行(迭x) 代，则在(1, 2)中有
3
| (x) | | x2 | 1
现令 g(x) (1 K)x K(x) (1 K)x K (x3 1)
数值分析非线性方程求根实验
实验报告一、实验目的1．迭代函数对收敛性的影响。
2．初值的选择对收敛性的影响。
二、实验题目1．用简单迭代法求方程01)(3=--=x x x f 的根。
分别化方程为如下等价方程： 31+=x x ；13-=x x ；x x 11+=；213-+=x x x 取初值5.10=x ，精度为410-，最大迭代次数为500，观察其计算结果并加以分析。
2．①用牛顿法求方程01)(3=-+=x x x f 在0.5附近的根，分别取初值1000,100,2,1,5.0,5.0,1,2,100,10000-----=x观察并比较计算结果，并加以分析。
②用牛顿法求方程0)(3=-=x x x f 所有根。
三、实验原理简单迭代法程序，牛顿迭代法程序。
四、实验内容及结果fun=inline('x^3-x-1');dfun=inline('3*x^2-1');-1000,x1=manewton(fun,dfun,-1000,1e-4) -100,x2=manewton(fun,dfun,-100,1e-4)-2,x3=manewton(fun,dfun,-2,1e-4)-1,x4=manewton(fun,dfun,-1,1e-4)-0.5,x5=manewton(fun,dfun,-0.5,1e-4) 0.5,x6=manewton(fun,dfun,0.5,1e-4)1,x7=manewton(fun,dfun,1,1e-4)2,x8=manewton(fun,dfun,2,1e-4)100,x9=manewton(fun,dfun,100,1e-4) 1000,x10=manewton(fun,dfun,1000,1e-4)3）在MA TLAB的主程序窗口输出以下结果：ans =-1000k=21x1 =0.682327804075895ans =-100k=16x2 =0.682327803903413ans =-2k=6x3 =0.682327803828020ans =-1k=5x4 =0.682327803828020ans =-0.500000000000000k=4x5 =0.682327803903932ans =0.500000000000000k=3x6 =0.682327803828347五、实验结果分析(1)实验1中用简单迭代法求方程01)(3=--=x x x f 的根：取初始值5.10=x 的时候，等价方程2和4是不收敛的。
数值分析 数值分析 Newton迭代法求解非线性方程实验
}//计算出u[i][j]并输出.
第二部分 for(i=k+1;i<n;i++)
{s=0.0;
for(r=0;r<k-1;r++)
{s=s+l[k][r]*u[r][k];}
l[i][k]=(a[i][k]-s)/u[k][k];
printf("%Lf\n",l[i][k]);
{s=0.0;
for(r=0;r<k-1;r++)
{s=s+l[k][r]*u[r][k];}
l[i][k]=(a[i][k]-s)/u[k][k];
printf("l[%d][%d]%Lf\n",i,k,l[i][k]);}
}
}
六、实验结果
七、上机实验体会
在这个试验中同样叶出现了很多问题，对L，U的求解输出中，输出的位置的不同，结果也就会出差错.经过多次调整，结果总算输出了.
通过此次试验，我理解了多重循环的运用，并了解了古人的聪明智慧，]讲将复杂问题简单化，现在的大学生们，应该学习他们的创新及钻研精神。
for(k=0;k<n;k++)
{for(j=k;j<n;j++)
{s=0.0;
for (r=0;r<k-1;r++)
{s=s+l[k][r]*u[r][j];}
u[k][j]=a[k][j]-s;
printf("u[%d][%d]=%Lf\n",k,j,u[k][j]); }
for(i=k+1;i<n;i++)
求解非线性方程的三种新的迭代法
求解非线性方程的三种新的迭代法1. 引言1.1 介绍迭代法迭代法是一种重要的数值计算方法，广泛应用于非线性方程的求解、函数极值点的求解等问题中。
迭代法的基本思想是通过逐步逼近的方式，找到函数的根或者极值点。
这种方法在面对复杂的数学问题时具有很大的优势，可以通过简单的计算步骤逐渐接近最终解。
与解析解相比，迭代法更适用于无法通过代数运算求解的问题，或者求解过程较为繁琐的问题。
迭代法的实现通常需要选择一个初始值，并通过反复迭代计算来逼近真实解。
在每一步迭代中，都会根据当前的估计值计算新的估计值，直到满足一定的精度要求为止。
迭代法虽然不能保证每次都能得到精确解，但在实际应用中往往能够取得较好的结果。
迭代法是一种简单而有效的数值计算方法，尤其适用于非线性方程求解等复杂问题。
通过逐步逼近的方式，迭代法可以帮助我们解决那些传统方法难以处理的问题，为现代科学技术的发展提供重要支持。
1.2 非线性方程的求解意义非线性方程在数学和工程领域中广泛存在，其求解具有重要的理论和实际意义。
非线性方程的求解能够帮助解释和预测许多自然现象，包括流体动力学、电路分析、材料力学等领域中的问题。
非线性方程的求解也是许多科学研究和工程设计中必不可少的一环，例如在经济学、生物学、物理学等多个学科中都有非线性方程存在。
传统的解析方法难以解决非线性方程，因此迭代法成为求解非线性方程的重要工具。
迭代法是一种通过不断逼近解的方法，逐步逼近方程的解。
通过迭代法，可以在复杂的非线性方程中找到数值解，从而解决实际问题。
非线性方程的求解意义在于帮助我们更好地理解和掌握复杂系统的性质和行为。
通过求解非线性方程，我们可以揭示系统中隐藏的规律和关系，为科学研究和工程设计提供重要的参考和支持。
发展高效的迭代法求解非线性方程具有重要意义，可以推动科学技术的进步，促进社会的发展和进步。
2. 正文2.1 牛顿迭代法牛顿迭代法是一种非常经典的求解非线性方程的方法，其基本思想是通过不断逼近函数的零点来求解方程。