基于公钥密码体制的数据加密
公钥密码体制公钥密码体制

首次公开提出了“公开密钥密码编码学”的概念。
这是一个与对称密码编码截然不同的方案。
提出公开密钥的理论时,其实用性并没有又得到证明:
❖ 当时还未发现满足公开密钥编码理论的算法; ❖ 直到 1978 年,RSA 算法的提出。
2.基本特征
❖ 加密和解密使用两个不同的密钥 公钥PK:公开,用于加密,私钥SK:保密,用作解密 密钥
3.优点
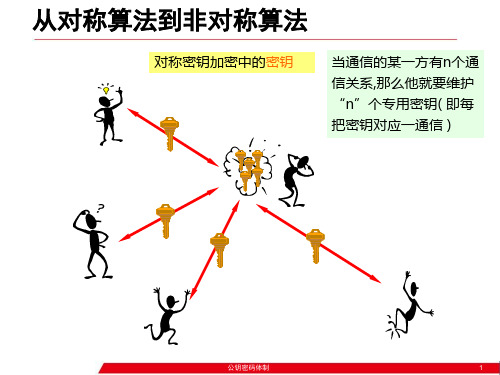
❖ 密钥管理
加密密钥是公开的; 解密密钥需要妥善保存; 在当今具有用户量大、消息发送方与接收方具有明显的信息不对称
特点的应用环境中表现出了令人乐观的前景。 新用户的增加只需要产生一对公共/私有密钥。
❖ 数字签名和认证
只有解密密钥能解密,只有正确的接收者才拥有解密密钥。
缺点:公共密钥系统的主要弱点是加密和解密速度慢。
加密与解密由不同的密钥完成; 知道加密算法,从加密密钥得到解密密钥在计算上是不可行的; 两个密钥中任何一个都可以作为加密而另一个用作解密。
6.公钥密码算法
除RSA算法以外,建立在不同计算问题上的其他公钥密码算法 有:
基于因子分解问题的Rabin算法; 椭圆曲线公钥算法; 基于有限域中离散对数难题的ElGamal公钥密码算法 基于代数编码系统的McEliece公钥密码算法; 基于“子集和”难题的Merkle-Hellman Knapsack(背包)公钥密码算 法; 目前被认为安全的Knapsack型公钥密码算法Chor-Rivest。
实际应用中的加密方式
❖ 混合加密技术 对称密码体制:密钥分发困难 公钥体制:加解密效率低 将对称加密算法的数据处理速度和公钥算法对密钥的保 密功能相结合 利用对称加密算法加密传输数据 利用非对称加密算法交换会话密钥
实际应用中的加密方式
第13次课 公钥密码

研究公钥密码算法就是找出合适的单向限门函数。
对公钥密码体制的攻击
穷搜索攻击。
寻找从公开钥计算秘密钥的方法。
可能字攻击。
对称密码
一般要求: 1、加密解密用相同的密钥 2、收发双方必须共享密钥 一般要求:
公钥密码
1、加密解密算法相同,但使用不同 的密钥 2、发送方拥有加密或解密密钥,而 接收方拥有另一个密钥
Alice发送“Hi”给Bob。
“Hi” 01001000 01101001 72 105
加密:72139 (mod253) = 2 解密:219 (mod253) = 72
Bob查ASCII表得 “Hi”
105139 (mod253) = 101 10119 (mod253) = 105
Bob收到消息(2 101) ,用自己的私钥解密。
安全性要求: 1、密钥必须保密 2、没有密钥,解密不可行 3、知道算法和若干密文不足以确定 密钥
安全性要求: 1、两个密钥之一必须保密
2、无解密密钥,解密不可行
3、知道算法和其中一个密钥以及若 干密文不能确定另一个密钥
关于公钥密码的几种误解
公钥密码比传统密码安全?
公钥密码是通用方法,所以传统密码已经过时?
RSA算法的安全性基于数论中大整数分解的困难性。
Euler 函数
φ(n): 设n是一个正整数,小于n且与n互素的正整数的个 数称为n的欧拉函数。
当n是素数时,小于n的所有整数均与n互素,因此 φ(n)=n-1 . 对n=pq, p和q 是素数, φ(n)=φ(p)φ(q)=(p-1)(q-1)
多个用户加密的消息 只能由一个用户解读。
公钥密码体制认证 框图
不具有保密性!
只能由一个用户加密消息而使多个 用户可以解读。
信息安全概论 ppt 公钥密码体制PPT
公钥密码体制
7
4.1 公钥密码体制的基本原理
如何设计一个公钥算法
公钥和私钥必须相关,而且从公钥到私钥不可推断
必须要找到一个难题,从一个方向走是容易的,从另一个方向 走是困难的
如何把这个难题跟加、解密结合起来
一个实用的公开密钥方案的发展依赖于找到一个陷门单向函数。
陷门单向函数
单向陷门函数是满足下列条件的函数f:
公钥密码体制 4
Bob:
Plain Text E
Cipher Text Network
Cipher Text D
Plain Text
Alice
Secret Key
Bob
公钥密码体制 5
公钥体制的主要特点:
加密和解密能力分开
多个用户加密的消息只能由一个用户解读,(用于公共网络中实现 保密通信)
这一体制的出现为解决计算机信息网中的安全提供了新的理论和 技术基础,被公认为现代公钥密码学诞生的标志。 1978 年, MIT 三位数学家 R.L.Rivest , A.Shamir 和 L.Adleman
发明了一种用数论构造双钥体制的方法,称作MIT体制,后来 被广泛称之为RSA体制。
公钥密码体制
3
4.1 公钥密码体制的基本原理
公钥密码学与其他密码学完全不同:
公钥算法基于数学函数而不是基于替换和置换 使用两个独立的密钥 公钥密码学的提出是为了解决两个问题:
密钥的分配 数字签名
基本思想和要求
用户拥有自己的密钥对(KU,KR),即(公开密钥,私有密钥)
公钥KU公开,私钥KR保密 AB:Y=EKUb(X) B:DKRb(Y)= DKRb(EKUb(X))=X
基于公钥密码体制的动态无线传感器网络安全数据聚合研究

基于公钥密码体制的动态无线传感器网络 安全数据聚合研究
卢 伟 龙
( 广 州大学数 学与信 息科 学学院 ,广 东广州 5 1 0 0 0 6)
摘 要: 无线 传 感 器 网络 通 常 由 大量 有 限存储 、计 算 和通 信 资 源 的传 感 设备 组 成 ,在 军事 和 民 用 中
Re s e a r c h o n Pub l i c - Ke y ba s e d Cr y p t o s ys t e ms f o r Se c ur e Da t a A ̄ Ag ¥ g r e g a t i o n i n ’ Dyn ’ 、 a mi ‘ c W Wl i r e l e s s Se e n s o r Ne e t wo O r k K
n e wo t r k s . T h e a p p e a r a n c e o f t h e n e w s e c u r i y t r e q u i r e me n t s a n d a p p l i c a t i o n e n v i r o n me n t s ma k e s p u b l i c - k e y b a s e d
s t o r a g e ,c o mp u t i n g a n d c o mm u n i c a t i o n r e s o ur c e s .Du e t o i t s wi d e l y u s e i n mi l i t a r y a nd c i vi l i a n, i t s s e c ur i t y i s s u e s h a v e b e e n of c on c e r n . No wa da y s s y mm e t r i c ke y b a s e d c r y p t os ys t e ms f o r d a t a a g g r e g a t i o n h a s be e n f r u i t f ul i n s t a t i c
两类密码体制

三重 DES
使用两个 56 位的密钥。 把一个 64 位明文用一个密钥加密,再用另一个密钥解密,然后再使用第一个
密钥加密,即
Y = DESK1(DES-1K2(DESK1(X)))
(7-3)
K1
明文 E
K2
D
加密
K1
密文 E
K1
密文 D
K2
E
解密
K1
明文 D
2 公钥密码体制
公钥密码体制(又称为公开密钥密码体制)使用不同的加密密钥与解 密密钥,是一种“由已知加密密钥推导出解密密钥在计算上是不可行 的”密码体制。
若 A 要抵赖曾发送报文给 B,B 可将明文和对应的密文出示给第三者
。第三者很容易用 A 的公钥去证实 A 确实发送 X 给 B。 反之,若 B 将 X 伪造成 X',则 B 不能在第三者前出示对应的密文。
这样就证明了 B 伪造了报文。
具有保密性的数字签名
同时实现秘密通信和数字签名
A 的私钥 SKA B 的公钥 PKB
公钥密码体制产生的主要原因: 1. 常规密钥密码体制的密钥分配问题。 2. 对数字签名的需求。
加密密钥与解密密钥
在公钥密码体制中,加密密钥 PK(public key,即公钥)是向公众 公开的,而解密密钥 SK(secret key,即私钥或秘钥)则是需要保
密的。
加密算法 E 和解密算法 D 也都是公开的。 虽然私钥 SK 是由公钥 PK 决定的,但却不能根据 PK 计算出 SK。
基于公钥的数字签名的实现
A 的私钥 SKA
A 的公钥 PKA
A
明文 X
签名
D 运算 密文 Y
加密算法
互联网
公钥密码体制的研究与发展的基本理解

公钥密码体制的研究与发展的基本理解Abstract:⽂中对于公钥密码体制的研究与发展进⾏了介绍,其中着重介绍了⼏个⽐较常⽤的公钥密码体制RSA,EIGamal Keywords: 公钥密码体制,RSA,离散对数问题1. 引⾔公钥密码体制⼜称公开密钥密码体系,公钥密码体制是现代密码学的最重要的发明和进展,在1976年,Whitfield Diffie和Martin Hellman发表了“New directions in cryptography”这篇划时代的⽂章奠定了公钥密码系统的基础。
在公钥密码体制之中,加密密匙和解密密匙是不⼀样的,⽆法通过加密密匙的反推得到解密密匙,所以加密密匙是可以公开的,并且不会危及密码体制的安全性。
因为对称密钥密码体制有⼀个缺点是必须要在Alice和Bob之间⾸先在传输密⽂之前使⽤⼀个安全信道交换密钥。
实际上,这是很难达到的,⽽公钥密码体制改善了这⼀点,Alice可以利⽤公钥加密规则发出⼀条加密的消息给Bob,Bob是唯⼀能够运⽤解密规则对其解密的⼈,例如保险箱的传递,只有接收的⼈知道密码并且能够打开。
【1】要在⾃从公钥密码的概念被提出以来,相继提出了许多公钥密码⽅案,如RSA、ElGamal、基于离散对数问题的公钥密码体制等[2]。
2. 预备知识公钥密码的理论基础,在公钥密码中,加密密钥和解密密钥是不⼀样的,加密密钥为公钥,解密密钥为私钥。
⼀个问题是难解的,直观上讲,就是不存在⼀个计算该问题的有效算法,也可称之为按照⽬前的计算能⼒,⽆法在⼀个相对的短时间内完成,即解决这个问题所付出的成本远远超过了解决之后得到的结果,计算应⼀个难解的问题所需要的时间⼀般是以输⼊数据长度的指数函数形式递增,所以随着输⼊数据的增多,复杂度会急剧的增⼤,对于⼀个问题,如果存在⼀个求其解的有效算法,则称其为有效问题,否则为⽆效问题。
在公钥密码机制之中,进⾏破译已经加密后的密码应该是⼀个难解问题。
大连理工大学网络安全与密码学 chap5-公钥密码

基于背包问题的公钥密码系统 ——MH公钥算法
• 加密 – 将明文分为长度为n的块X=(x1,…,xn) – 然后用公钥A ' = (a1 ', …, an '),将明文变为密文 S = E(X) = ∑ai ' xi
• 解密 – 先计算S ' = w-1S mod m – 再求解简单背包问题 S ' = ∑aixi
Eaxmple-从私钥计算公钥
• 私钥{2,3,6,13,27,52} • N=31, m=105 2*31 mod 105= 62 3*31 mod 105=93 6*31 mod 105=81 13*31 mod 105= 88 27*31 mod 105=102 52*31 mod 105= 37 • 公钥{62,93,81,88,102,37}
• 涉及到各方:发送方、接收方、攻击者 • 涉及到数据:公钥、私钥、明文、密文 • 公钥算法的条件: – 产生一对密钥是计算可行的 – 已知公钥和明文,产生密文是计算可行的 – 接收方利用私钥来解密密文是计算可行的 – 对于攻击者,利用公钥来推断私钥是计算不可行的 – 已知公钥和密文,恢复明文是计算不可行的 – (可选)加密和解密的顺序可交换
公钥密码
一般要求: 1、加密解密算法相同,但使用不同 的密钥 2、发送方拥有加密或解密密钥,而 接收方拥有另一个密钥 安全性要求: 1、两个密钥之一必须保密 2、无解密密钥,解密不可行 3、知道算法和其中一个密钥以及若 干密文不能确定另一个密钥
对公钥密码算法的误解
• 公开密钥算法比对称密钥密码算法更安全? – 任何一种算法都依赖于密钥长度、破译密码的工 作量,从抗分析角度,没有一方更优越 • 公开密钥算法使对称密钥成为过时了的技术? – 公开密钥很慢,只能用在密钥管理和数字签名, 对称密钥密码算法将长期存在 • 使用公开密钥加密,密钥分配变得非常简单? – 事实上的密钥分配既不简单,也不有效
信息安全概论第四章公钥密码体制

14
Diffie-Hellman密钥交换算法 密钥交换算法
Diffie和Hellman在其里程碑意义的文章中, 虽然给出了密码的思想,但是没有给出真正意 义上的公钥密码实例,也既没能找出一个真正 带陷门的单向函数 然而,他们给出单向函数的实例,并且基于此 提出Diffie-Hellman密钥交换算法
13
常用的公开密钥算法
公钥算法的种类很多,具有代表性的三种密码: 公钥算法的种类很多,具有代表性的三种密码: 基于整数分解难题(IFP)的算法体制 基于整数分解难题(IFP)的算法体制(RSA) 基于离散对数难题(DLP)算法体制 基于离散对数难题(DLP)算法体制(ElGamal) 基于椭圆曲线离散对数难题( ECDLP ) 的算法体制 基于椭圆曲线离散对数难题 ( ECDLP) (ECC)
3
4.1 公钥密码体制的基本原理
对称算法的不足
(1)密钥管理量的困难 传统密钥管理:两两分别用一个密钥时, 传统密钥管理:两两分别用一个密钥时,则n个用户需 C(n,2)=n(n-1)/2个密钥 当用户量增大时, 个密钥, 要C(n,2)=n(n-1)/2个密钥,当用户量增大时,密钥空 间急剧增大。 间急剧增大。如: n=100 时, C(100,2)=4,995 n=5000时 n=5000时, C(5000,2)=12,497,500 (2)密钥必须通过某一信道协商,对这个信道的安全 密钥必须通过某一信道协商, 性的要求比正常的传送消息的信道的安全性要高
7
公开密钥密码的重要特性
加密与解密由不同的密钥完成 Y: X: Y = EKU(X) X = DKR(Y) = DKR(EKU(X))
加密: X 解密: Y
知道加密算法,从加密密钥得到解密密钥在计算上 , 是不可行的 两个密钥中任何一个都可以用作加密而另一个用 作解密(不是必须的) X = DKR(EKU(X))
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于公钥密码体制的数据加密 摘要:公开密钥算法的原理是加密密钥和解密密钥分离,可将加密密钥公之于众,谁都可以使用;而解密密钥只有解密人自己知道。任何人利用这个加密密钥和算法向该用户发送的加密信息,该用户均可以将之还原。公钥加密算法中使用最广的是RSA。RSA使用两个密钥,一个公共密钥,一个专用密钥。如用其中一个加密,则可用另一个解密。本文综述了公钥体系及其应用RSA算法,也讨论了相关的攻击手段。 关键字:公钥密码 加密技术 RSA
Abstrat:Public-key algorithm encryption and decryption key principle is key separation, but will encryption key in the
open, who can use; And decryption decryption key only themselves know. Any person to use the encryption key and to the user to send the algorithm of the encrypted information, the user can be will restore. Public key encryption algorithm used in the most extensive is RSA. RSA use two keys, a public key, a special key. If use one of the encryption, usable another decryption. This paper reviewed the application of RSA public key system and its algorithm, and also discussed the related attack means.
Key:Public key password Encryption technology RSA
1 公钥密码体系背景 通常信息安全的目标可以概括为解决信息的以下问题:保密性(Confidentiality)保证信息不泄露给未经授权的任何人;完整性(Integrity)防止信息被未经授权的人篡改;可用性(Availability)保证信息和信息系统确实为授权者所用;可控性(Controllability)对信息和信息系统实施安全监控,防止非法利用信息和信息系统。 密码是实现一种变换,利用密码变换保护信息秘密是密码的最原始的能力,然而,随着信息和信息技术发展起来的现代密码学,不仅被用于解决信息的保密性,而且也用于解决信息的完整性、可用性和可控性。可以说,密码是解决信息安全的最有效手段,密码技术是解决信息安全的核心技术。 公开密钥算法是在1976年由当时在美国斯坦福大学的迪菲(Diffie)和赫尔曼(Hellman)两人首先发明的(论文"New Direction in Cryptography"),思想不同于传统的对称密钥密码体制,它要求密钥成对出现,一个为加密密钥(e),另一个为解密密钥(d),且不可能从其中一个推导出另一个,其原理是加密密钥和解密密钥分离。在公钥体制中,加密密钥不同于解密密钥。人们将加密密钥公之于众,谁都可以使用;而解密密钥只有解密人自己知道。这样,一个具体用户就可以将自己设计的加密密钥和算法公诸于众,而只保密解密密钥。任何人利用这个加密密钥和算法向该用户发送的加密信息,该用户均可以将之还原。 自1976年以来,已经提出了多种公开密钥密码算法,其中许多是不安全的, 一些认为是安全的算法又有许多是不实用的,它们要么是密钥太大,要么密文扩展十分严重。多数密码算法的安全基础是基于一些数学难题, 这些难题专家们认为在短期内不可能得到解决。因为一些问题(如因子分解问题)至今已有数千年的历史了。 一般理解密码学(Cryptography)就是保护信息传递的机密性,而对信息发送与接收人的真实身份的验证、对所发出/接收信息在事后的不可抵赖以及保障数据的完整性是现代密码学主题的另一方面。公开密钥密码体制对这两方面的问题都给出了出色的解答,并正在继续产生许多新的思想和方案。 公用密钥的优点就在于,也许你并不认识某一实体,但只要你的服务器认为该实体的CA是可靠的,就可以进行安全通信,而这正是Web商务这样的业务所要求的。例如信用卡购物。服务方对自己的资源可根据客户CA的发行机构的可靠程度来授权。目前国内外尚没有可以被广泛信赖的CA。美国Natescape公司的产品支持公用密钥,但把Natescape公司作为CA。由外国公司充当CA在我国是一件不可想象的事情。 公共密钥方案较保密密钥方案处理速度慢,因此,通常把公共密钥与专用密钥技术结合起来实现最佳性能。即用公共密钥技术在通信双方之间传送专用密钥,而用专用密钥来对实际传输的数据加密解密。另外,公钥加密也用来对专用密钥进行加密。 在这些安全实用的算法中,有些适用于密钥分配,有些可作为加密算法,还有些仅用于数字签名。多数算法需要大数运算,所以实现速度很慢,不能用于快的数据加密。 早在1973年,英国国家通信总局的数学家Clifford Cocks就发现了类似的算法。但是他的发现被列为绝密,直到1998年才公诸于世。1978年提出公共密钥密码的具体实施方案,由MIT教授Ronald L.Rivest,Adi Shamir和Leonard M.Adleman共同开发的,分别取自三名数学家的名字的第一个字母来构成的,即RSA方案。迄今为止的所有公钥密码体系中,RSA系统是最著名、使用最广泛的一种。
2 公钥体系结构中的概念 在基于公钥体系的安全系统中,密钥是成对生成的,每对密钥由一个公钥和一个私钥组成。在实际应用中,私钥由拥有者自己保存,而公钥则需要公布于众。为了使基于公钥体系的业务(如电子商务等)能够广泛应用,一个基础性关键的问题就是公钥的分发与管理。 公钥本身并没有什么标记,仅从公钥本身不能判别公钥的主人是谁。 2.1 证书 互联网络的用户群决不是几个人互相信任的小集体,在这个用户群中,从法律角度讲用户彼此之间都不能轻易信任。所以公钥加密体系采取了另一个办法,将公钥和公钥的主人名字联系在一起,再请一个大家都信得过有信誉的公正、权威机构确认,并加上这个权威机构的签名。这就形成了证书。 由于证书上有权威机构的签字,所以大家都认为证书上的内容是可信任的;又由于证书上有主人的名字等身份信息,别人就很容易地知道公钥的主人是谁。
2.2 电子签证机关CA(Certificate Authority) 前面提及的权威机构就是电子签证机关(即CA)。CA也拥有一个证书(内含公钥),当然,它也有自己的私钥,所以它有签字的能力。网上的公众用户通过验证CA的签字从而信任CA,任何人都应该可以得到CA的证书(含公钥),用以验证它所签发的证书。 如果用户想得到一份属于自己的证书,他应先向CA提出申请。在CA判明申请者的身份后,便为他分配一个公钥,并且CA将该公钥与申请者的身份信息绑在一起,并为之签字后,便形成证书发给那个用户(申请者)。 如果一个用户想鉴别另一个证书的真伪,他就用CA的公钥对那个证书上的签字进行验证(如前所述,CA签字实际上是经过CA私钥加密的信息,签字验证的过程还伴随使用CA公钥解密的过程),一旦验证通过,该证书就被认为是有效的。 CA除了签发证书之外,它的另一个重要作用是证书和密钥的管理。 由此可见,证书就是用户在网上的电子个人身份证,同日常生活中使用的个人身份证作用一样。CA相当于网上公安局,专门发放、验证身份证。
3 RSA公开密钥算法 公钥加密算法中使用最广的是RSA。RSA使用两个密钥,一个公共密钥,一个专用密钥。如用其中一个加密,则可用另一个解密,密钥长度从40到2048bit可变,加密时也把明文分成块,块的大小可变,但不能超过密钥的长度,RSA算法把每一块明文转化为与密钥长度相同的密文块。密钥越长,加密效果越好,但加密解密的开销也大,所以要在安全与性能之间折衷考虑,一般64位是较合适的。RSA的一个比较知名的应用是SSL,在美国和加拿大SSL用128位RSA算法,由于出口限制,在其它地区(包括中国)通用的则是40位版本。 RSA算法研制的最初理念与目标是努力使互联网安全可靠,旨在解决DES算法秘密密钥的利用公开信道传输分发的难题。而实际结果不但很好地解决了这个难题;还可利用RSA来完成对电文的数字签名以抗对电文的否认与抵赖;同时还可以利用数字签名较容易地发现攻击者对电文的非法篡改,以保护数据信息的完整性。目前为止,很多种加密技术采用了RSA算法,比如PGP(PrettyGoodPrivacy)加密系统,它是一个工具软件,向认证中心注册后就可以用它对文件进行加解密或数字签名,PGP所采用的就是RSA算法。由此可以看出RSA有很好的应用。
3.1 RSA数学基础 对极大整数做因数分解的难度决定了RSA算法的可靠性。换言之,对一极大整数做因数分解愈困难,RSA算法愈可靠。尽管如此,只有一些RSA算法的变种被证明为其安全性依赖于因数分解。假如有人找到一种快速因数分解的算法的话,那么用RSA加密的信息的可靠性就肯定会极度下降。但找到这样的算法的可能性是非常小的。今天只有短的RSA钥匙才可能被强力方式解破。到2008年为止,世界上还没有任何可靠的攻击RSA算法的方式。只要其钥匙的长度足够长,用RSA加密的信息实际上是不能被解破的。但在分布式计算和量子计算机理论日趋成熟的今天,RSA加密安全性受到了挑战。 RSA算法是一种非对称密码算法,所谓非对称,就是指该算法需要一对密钥,使用其中一个加密,则需要用另一个才能解密。 RSA的算法涉及三个参数,n、e1、e2。 其中,n是两个大质数p、q的积,n的二进制表示时所占用的位数,就是所谓的密钥长度。 e1和e2是一对相关的值,e1可以任意取,但要求e1与(p-1)*(q-1)互质;再选择e2,要求(e2*e1)mod((p-1)*(q-1))=1。 (n及e1),(n及e2)就是密钥对。 RSA加解密的算法完全相同,设A为明文,B为密文,则:A=B^e1 mod n;B=A^e2 mod n; e1和e2可以互换使用,即: A=B^e2 mod n;B=A^e1 mod n
3.2 RSA密钥生成 密钥生成首先要使用概率算法来验证随机产生的大的整数是否质数,这样的算法比较快而且可以消除掉大多数非质数。假如有一个数通过了这个测试的话,那么要使用一个精确的测试来保证它的确是一个质数。 除此之外这样找到的p和q还要满足一定的要求,首先它们不能太靠近,此外p-1或q-1的因子不能太小,否则的话N也可以被很快地分解。 此外寻找质数的算法不能给攻击者任何信息,这些质数是怎样找到的,尤其产生随机数的软件必须非常好。要求是随机和不可预测。这两个要求并不相同。一个随机过程可能可以产生一个不相关的数的系列,但假如有人能够预测出(或部分地预测出)这个系列的话,那么它就已经不可靠了。比如有一些非常好的随机数算法,但它们都已经被发表,因此它们不能被使用,因为假如一个攻击者可以猜出p和q一半的位的话,那么他们就已经可以轻而易举地推算出另一半。 此外密钥d必须足够大,1990年有人证明假如p大于q而小于2q(这是一个很经常的情况)而d < N1/4/3,那么从N和e可以很有效地推算出d。此外e = 2永远不应该被使用。 速度比起DES和其它对称算法来说,RSA要慢得多。实际上Bob一般使用一种对称算法来加密他的信息,然后用RSA来加密他的比较短的对称密码,然后将用RSA加密的对称密码和用对称
