山西省运城市2020届高三6月考前适应性测试文综答案A
山西省临汾市2020届高三高考考前适应性训练考试(二)文科综合试题 含答案

临汾市二模政治试题答案38.意义:有利于优化农村产业结构,深化农村供给侧改革,解决农村发展不平衡不充分问题,提高农业发展质量和效益;②有利于落实发展新理念和乡村振兴战略,增强农业可持续发展;③有利于推动农民创业、增加农民就业,提高农民生活水平;④有利于更好满足人民群众的消费需求,促进消费升级;⑤有利于全面打赢脱贫攻坚战、全面建成小康社会,体现社会主义优越性。
(每点2 分,总分不得超过8 分)建议:①积极稳妥的推进市场化改革,充分发挥市场对资源配置的决定作用;②坚持开放发展新理念,实行科学的宏观调控,用政策引导市场用,规划明确投资方向,用法治规范行为;③坚持科技兴国战略和人才强国战略,培养一批本地区农村产业发展的带头人,通过“双创”活动带动农村发展。
(每点2 分,总分不得超过6 分)39.①中国共产党的领导是中国特色社会主义最本质的特征,是中国特色社会主义制度的最大优势;提升国家治理体现和治理能力现代化,必须坚持党的领导;②坚持全面依法治国,建设社会主义发展国家,切实保障社会公平正义和人民权利是我国国家制度和国家治理体系显著优势之一;在党的领导下,坚持了依法治国、依法执政、依法行政共同推进。
③坚持党的领导、人民当家作主、依法治国有机统一是社会主义政治发展的必然要求。
依法治国是党领导人民治理国家的基本方式,坚持党的领导是全面推进依法治国总目标的最根本保证。
④党领导立法,坚持科学立法,加强社会主义法制体系建设,完善国家治理体系,实现党的领导与社会主义法治的统一,提高了治国理政水平;⑤党在推进全面依法治国进程中,加快法规制度体系建设,完善中国特色社会主义法治体系,推进了国家治理体系和治理能力现代化。
(每点3 分,总分不得超过12 分)40.(1)①伟大的创造精神、伟大的奋斗精神、伟大的团结精神、伟大的梦想精神是中华民族精神的基本内涵,爱国主义是民族精神的核心。
抗疫精神是中华民族精神的具体体现,为战胜新冠肺炎提供了强大的精神动力。
山西省运城市高中联合体2020届高三第三次模拟测试文科综合地理试题 含答案

山西省运城市高中联合体2020高三模拟测试(三)文科综合一、选择题:本题共35小题,每小题4分,共140分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
我国古人把十二个月中的太阳升落方向用一首歌诀来概括,这首歌诀就是《定太阳出没歌》。
其中一句是:“五月出良归乾上,仲冬出EE3没坤方。
”歌诀中的月份为阴历月。
下图为后天八卦图。
据此完成1一2题。
1.表示正南的宫位是A.离B.震C.坎D.兑2.当太阳从震宫方向升起、兑宫方向落下时,我国A.各地昼夜等长B.云贵高原冰天雪地C.江淮地区阴雨绵绵D.三江平原春耕大忙一排排共享电动车入驻河北省邯郸馆陶县。
共享电动车,代替了共享自行车,让馆陶县更智能化、现代化。
据此完成3一5题。
3.影响馆陶县由共享自行车到共享电动车转变的主要因素是A.历史因素B.经济因素C.社会因素D.政治因素4.共享电动车的出现,不会A.影响市区电动车的销售B.缓解城市环境压力C.提高出行效率D.扩大城市中心范围5.国庆节,上午(9 ; 00-11 ; 00 )电动车最可能集中于A.学校附近B.商场附近C.居民区附近D.医院附近下图示意2017年我国部分省(区、市)发展潜力。
其中圆圈大小表示近一年常住人口增量,圆圈越大,增量越大,空心圆圈表示人口减少。
灰色圆圈表示人口规模较大居全国前列,但老龄化现象却较突出,城镇化率并不高(低于全国平均城镇化率水平)的省份。
据此完成6 -8题。
6.由示意图可以推断A.上海城镇化率增长最快B.北京人口迁入量大于迁出量C.安徽劳动力需求量增加D.广东省人口自然增长率最高7.广东省常住人口增加明显的主要原因是A.经济发展水平较高B.户籍管理政策严格C.全面二胎政策见效D.生活消费水平较低8.灰色圆圈表示的省份应对老龄化问题的合理措施是A.优化产业结构B.限制人口外迁C.鼓励晚婚晚育D.提前退休年龄青海三江源地区是中国生态系统最为敏感和脆弱的地区,其降水的波动是影响本区及江河中下游水资源安全、生态系统可持续发展的关键因素。
山西运城市高中联合体2020年高三模拟测试(一)文综地理试题Word版
运城市高中联合体2020高三模拟测试文科综合一、选择题:本题共35小题,每小题4分,共140分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
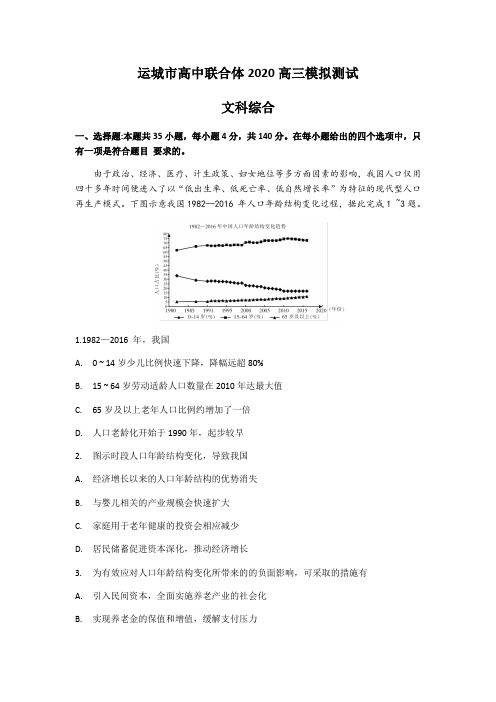
由于政治、经济、医疗、计生政策、妇女地位等多方面因素的影响,我国人口仅用四十多年时间便进入了以“低出生率、低死亡率、低自然增长率”为特征的现代型人口再生产模式。
下图示意我国1982—2016 年人口年龄结构变化过程,据此完成1 ~3题。
1.1982—2016 年,我国A. 0 ~ 14岁少儿比例快速下降,降幅远超80%B. 15 ~ 64岁劳动适龄人口数量在2010年达最大值C. 65岁及以上老年人口比例约增加了一倍D. 人口老龄化开始于1990年,起步较早2. 图示时段人口年龄结构变化,导致我国A. 经济增长以来的人口年龄结构的优势消失B. 与婴儿相关的产业规模会快速扩大C. 家庭用于老年健康的投资会相应减少D. 居民储蓄促进资本深化,推动经济增长3. 为有效应对人口年龄结构变化所带来的的负面影响,可采取的措施有A. 引入民间资本,全面实施养老产业的社会化B. 实现养老金的保值和增值,缓解支付压力C.发展高等教育,保证产业转型对普通劳动力需求D.推动就业结构转型,重点支持大型企业的创新和发展九州岛曾是日本重工业基地,后来转型为日本集成电路工业生产基地,九州岛上建有6个科技新城,这里的电子工业以生产与组装为主,而日本电子工业的研制、开发设计多集中于本州岛的东京和阪神地区。
九州岛电子工业布局,多以一个地方中心城市为依托,在机场附近形成几个团状的工业集群。
据统计,全球半导体材料对日本的依赖程度超过50%。
据此完成4 ~ 6题。
4.促使科技新城在九州岛集中选址的主导因素是A.人才集中,科技力量强B.经济实力强,市场广阔C.资源丰富,原料供应充足D.开发历史悠久,劳动力丰富5. 电子工业依托地方中心城市布局,并在机场附近形成工业集群的主要目的是A.缩短运距,降低物流运输成本B.减少中转环节,压缩运送周期C.获取市场信息,加强交流协作D.优化产业布局,减轻环境压力6. 2011年日本大地震后,该电子产品生产企业向中国大陆地区转移,说明A.电子产品生产对环境要求高B.老龄化导致劳动力短缺C.中国市场的吸引力增强D.落后产能遭到了淘汰下图为我国西北内陆某山间盆地的地质剖面图。
山西省运城市2022届高三5月考前适应性测试数学(文)试题(A卷)(含答案解析)

山西省运城市2022届高三5月考前适应性测试数学(文)试题(A 卷)学校:___________姓名:___________班级:___________考号:___________ 一、单选题1.已知全集R U =,集合{}|12A x x =-≤<,{}|21B x x =-≤<,则()U A B ⋃=( )A .{}|22x x x 或<-≥B .{}|21x x x 或≤-≥C .{}|12x x x 或≤->D .{}|11x x x 或<-≥2.设复数2105i(2i)z -=-(i 为虚数单位),则z 的虚部为( ) A .2B .2iC .1D .i3.已知0.42a =,5log 2b =,0.43c =,则( ) A .a c b << B .b a c <<C .c a b <<D .b c a <<4.已知双曲线2222:1(0,0)x y C a b a b -=>>的左、右焦点分别为1F ,2F ,点A 为虚轴上的端点,若12AF F △是顶角为120︒的等腰三角形,则C 的渐近线方程为( )A .2y x =±B .y =C .2y x =±D .y =±5.函数()sin f x x x =的部分图象大致为( )A .B .C .D .6.2021年,我国各地落实粮食生产责任和耕地保护制度,加大粮食生产扶持力度,支持复垦撂荒地,2021年全国粮食总产量13657亿斤,比上年增长约2.0%,全年粮食产量再创新高,且连续7年保持在1.3万亿斤以上,我国2020—2021年粮食产量种类分布及占比统计图如图所示,则下列说法不正确的是( )A .我国2020年的粮食总产量为13390亿斤B .我国2021年豆类产量比2020年减产明显,下降了约14.2%C .我国2021年的各类粮食产量中,增长量最大的是玉米D .我国2021年的各类粮食产量中,增长速度最快的是薯类7.已知等差数列{}n a 的公差0d ≠,其前n 项和为n S ,411a =,且1a ,3a ,11a 成等比数列,若40m S =,则m =( ) A .5B .6C .7D .88.如图,何尊是我国西周早期的青铜礼器,造型浑厚,工艺精美,其形状可视为圆台和圆柱的组合体,口径为28.8cm ,经测量计算可知圆台和圆柱的高度之比约为57,体积之比约为2521,则圆柱的底面直径约为( )A .4cmB .14cmC .18cmD .22cm9.已知三棱锥的三视图如图所示,则该三棱锥的表面积为( )A .B .6C .D .810.若函数32()52f x x x x =+--在区间(,5)m m +内有最小值,则实数m 的取值范围是( ) A .(4,1)-B .(4,0)-C .[3,1)-D .(3,1)-11.已知函数π()cos (0)3f x x ωω⎛⎫=+> ⎪⎝⎭的图象在区间[0,]π上有且仅有两条对称轴,则()f x 在以下区间上一定单调的是( ) A .π2π,23⎛⎫⎪⎝⎭B .ππ,62⎛⎫ ⎪⎝⎭C .π,03⎛⎫- ⎪⎝⎭D .ππ,23⎛⎫-- ⎪⎝⎭12.已知数列{}n a 中,14a =,()11333n n n a a a +=-+,数列1n a 的前n 项和为n S ,则( ) A .202201S << B .2022312S <<C .2022322S <<D .202223S <<二、填空题13.已知2sin 53πα⎛⎫+= ⎪⎝⎭,则2cos 25πα⎛⎫+= ⎪⎝⎭___________. 14.若非零向量a →,b →满足||2||b a →→=,225a b b →→→⋅=,则a →与b →夹角的余弦值为___________.15.已知椭圆2222:1(0)x y C a b a b+=>>的右焦点为F (5,0),点A ,B 为C 上关于原点对称的两点,且AF BF ⊥,||4||3AF BF =,则C 的离心率为___________.16.已知正三棱锥P ABC -的所有棱长都为P A 为直径的球的球面被侧面PBC 所截得曲线的长为___________. 三、解答题17.在ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,cos sin cos sin )a C A A c A =-.(1)求A ;(2)a =ABC 的外接圆圆心为点P ,求PBC 的周长.18.随着北京冬奥会的成功举办,冰雪运动成为时尚.“三亿人参与冰雪运动”与建设“健康中国”紧密相连,对我国经济发展有极大的促进作用,我国冰雪经济市场消费潜力巨大.为了更好地普及冰雪运动知识,某市十几所大学联合举办了大学生冰雪运动知识系列讲座,培训结束前对参加讲座的学生进行冰雪知识测试,现从参加测试的大学生中随机抽取了100名大学生的测试成绩(满分100分),将数据分为5组:[50,60),[60,70),[70,80),[80,90),[90,100],得到如下频数分布表(同一组中的数据用该组区间的中点值作代表):(1)若成绩不低于60分为合格,不低于80分为优秀,根据样本估计总体,估计参加讲座的学生的冰雪知识的合格率和优秀率;(2)若x 为样本成绩的平均数,样本成绩的标准差为s ,计算得12.1s ≈,若255x s -,则不及格学生需要参加第二次讲座,否则,不需要参加第二次讲座,试问不及格学生是否需要参加第二次讲座?19.如图,四棱柱1111ABCD A B C D -中,底面ABCD 为平行四边形,侧面11ADD A 为矩形,22AB AD ==,160D DB ∠=︒,1BD AA =(1)证明:平面ABCD ⊥平面11BDD B ; (2)求三棱锥11D BCB -的体积.20.已知抛物线2:2(0)E y px p =>,点(3,3)M 在E 上. (1)求E 的方程;(2)设动直线l 交E 于A ,B 两点,点P ,Q 在E 上,且90APB ∠=︒,若直线l 始终平分弦PQ ,求点P 的坐标.21.已知函数2()(1)e 4x f x a x x x a =--+--. (1)当4a =时,求()f x 的单调区间;(2)若不等式2()(2)f x x ≤-对任意,()0x ∈+∞恒成立,求实数a 的最大整数值.22.在直角坐标系xOy 中,直线l 的参数方程为12,x t y t =-+⎧⎨=⎩(t 为参数),以原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为2cos sin ρθθ=+. (1)求直线l 的极坐标方程与曲线C 的直角坐标方程; (2)直线l 与曲线C 交于A ,B 两点,求22||||OA OB +的值. 23.已知函数()|2|2|5|f x x x =---. (1)画出()y f x =的图象;(2)若()|2|f x x t +,求实数t 的取值范围.参考答案:1.A 【解析】 【分析】先求出A B ,再求()UA B 即可求解.【详解】根据题意得:{}|22A B x x ⋃=-≤<,所以{}()|22UA B x x x 或⋃=<-≥.故选:A. 2.C 【解析】 【分析】根据复数的乘法和除法运算,即可求出复数z ,进而求出z 的虚部. 【详解】 由题得,2105i 105i (105i)(34i)2i (2i)34i (34i)(34i)z ---+====+---+,所以z 的虚部为1.故选:C. 3.B 【解析】 【分析】根据对数函数的性质可知(0,1)b ∈,根据幂函数的性质可知0.40.4321>>,由此即可得到结果. 【详解】因为555log 1log 2log 5<<,所以5log 2(0,1)b =∈,又函数0.4y x =在()0,+∞上单调递增,所以0.40.403221>>=,所以c a b >>. 故选:B. 4.A 【解析】 【分析】由题得=c ,求出b a =即得解.【详解】解:设原点为O ,由12AF F △是顶角为120︒的等腰三角形,可1||tan 30OA b OF c ==︒=c ∴,a,b a ∴ 故C的渐近线方程为y =. 故选:A. 5.D 【解析】 【分析】利用函数的奇偶性可排除A ,利用(0)f 的值排除B ,利用当π()0,x ∈时, ()0f x >可排除C ,进而得出结论. 【详解】由题可知,函数()f x 的定义域为(,)-∞+∞, 又()()sin()sin ()f x x x x x f x -=--==,所以 ()f x 为定义域上的偶函数,图象关于y 对称,可排除A ; 又(0)0sin 00f ==,可排除B ;当π()0,x ∈时,sin 0x >,则()sin 0f x x x =>,可排除C. 故选:D. 6.D 【解析】 【分析】计算出我国2020年的粮食总产量,即可判断A ;计算出我国2021年豆类产量比2020年豆类产量下降比例,即可判断B ;分别计算出我国2021年各类粮食产量的增减情况,即可判断C ,D. 【详解】由题得,我国2020年的粮食总产量为42372685521359745820013390+++++=(亿斤),故A 正确;我国2021年豆类产量比2020年豆类产量下降了458393100%14.2%458-⨯≈.故B 正确;我国2021年各类粮食产量中,只有豆类产量下降,而稻谷增长了4257423720-=(亿斤),小麦增长了2739268554-=(亿斤),玉米增长了54515213238-=(亿斤),薯类增长了60959712-=(亿斤),其他增长了2082008-=(亿斤),由此可得增长量最大的是玉米,增长速度最快的也是玉米.故C 正确,D 错误. 故选:D. 7.A 【解析】 【分析】由题知23111a a a =,411a =,进而转化为1a ,d 的方程求解得12a =,3d =,再根据前n 项和公式求解即可. 【详解】解:由题得23111a a a =,则2111(2)(10)a d a a d +=+,得123d a =,又411a =.则1311a d +=,解得12a =,3d =, 所以31n a n =-,所以2(312)322n n n n nS -++==, 故23402m m mS +==,又*m ∈N ,所以5m =. 故选:A. 8.C 【解析】 【分析】设圆台的底面半径为r cm.圆台,圆柱的高分别为5h cm ,7h cm ,根据圆台和圆柱的体积公式即可得结果. 【详解】设圆台的底面半径为r cm.圆台,圆柱的高分别为5h cm ,7h cm ,则()2222128.828.85514.414.43223V r r h r r h ππππ⎡⎛⎫⎤=⨯+⨯+⨯⨯⨯=++⨯⎢ ⎪⎥⎝⎭⎦⎢⎣圆台, 又2277V r h r h ππ=⨯⨯=圆柱,所以2225(14.414.4)253=721r r h V V r h ππ++=圆台圆柱, 即2 3.614.4 3.60r r --⨯=,解得9r ≈,所以218r ≈.故选:C. 9.B 【解析】 【分析】将几何体置于长方体中,根据三视图还原几何体可得该三棱锥的四个面是全等的等腰三角形,从而即可求解. 【详解】解:将几何体置于长方体中,如图所示,=所以表面积为1462⨯.故选:B. 10.C 【解析】 【分析】先利用导数求出函数的单调区间,得到15m m <<+,令()5f x =-得到3x =-或1,即得解. 【详解】解:由题得,2()325(35)(1)f x x x x x '=+-=+-.令()0f x '>,解得53x <-或1x >;令()0f x '<,解得531x <-<,所以()f x 在区间5,3⎛⎫-∞- ⎪⎝⎭内单调递增,在区间5,13⎛⎫- ⎪⎝⎭内单调递减,在区间(1,)+∞内单调递增,所以函数的极小值(1)5f ==-.若()f x 在区间(,5)m m +内有最小值,则极小值即最小值, 所以15m m <<+,解得41m -<<,令()5f x =-,可得32530x x x +-+=,可得2(1)(3)0x x -+=,解得3x =-或1,由题得3m -,综上31m -<. 故选:C. 11.D 【解析】 【分析】根据余弦函数的对称轴方程求得ππ3x k ω+=,解得(31)π3k x ω-=,结合在区间[0,]π上有且仅有两条对称轴,求得πππ835ω<≤,由此依次取1,0,1,2k =- 求得函数图象相应的对称轴的范围,比较和四个选项中区间的关系,即可判断答案. 【详解】令()1f x =±,即πcos 13x ω⎛⎫+=± ⎪⎝⎭,所以ππ3x k ω+=,Z k ∈,所以(31)π3k x ω-=,Z k ∈;分别取1,2,3k =,得2π5π8π,,333x ωωω=,所以5π8ππ33ωω≤<,得πππ835ω<≤; 当1k =-时,得对称轴方程为43πx ω=-,且44,35π2ππω⎡⎫-∈--⎪⎢⎣⎭; 当0k =时,得对称轴方程为π3x ω=-,且ππ,358πω⎡⎫-∈--⎪⎢⎣⎭,,,0583πππ⎡⎫--⊂-⎪⎛⎫ ⎪⎝⎣⎭⎭⎢, 故π,03⎛⎫- ⎪⎝⎭不是函数的单调区间,C 错误; 当1k =时,得对称轴方程为23x πω=,且2ππ2π,345ω⎛⎤∈ ⎥⎝⎦,π2πππ,45,62⎛⎤⊂⎛⎫ ⎪⎝ ⎥⎝⎭⎦, 故ππ,62⎛⎫⎪⎝⎭不是函数的单调区间,B 错误; 当2k =时,得对称轴方程为5π3x ω=,且5π5π,π38ω⎛⎤∈ ⎥⎝⎦,π2π2π,25π5π,π,8338⎛⎫⎛⎫=≠∅ ⎪ ⎪⎝⎭⎝⎤ ⎥⎦⎭⎛⎝,故A 错误,由以上分析可以看到,ππ,23⎛⎫-- ⎪⎝⎭介于1k =- 和0k = 时的相邻的对称轴之间,故()f x 在区间ππ,23⎛⎫-- ⎪⎝⎭上一定单调,故选:D 12.A 【解析】【分析】根据数列单调性的定义及裂项相消法求出n S ,进而即可求解.【详解】 由题得,2111(3)3(3)033n n n n n n a a a a a a +-=-+-=-,又143a =>, 所以210a a ->.所以213a a >>,可得1n n a a +>.所以数列{}n a 是递增数列. 又113113(3)3n n n n na a a a a +==----,所以111133n n n a a a +=---,所以 1212231111111111333333n n n n S a a a a a a a a a +⎛⎫⎛⎫⎛⎫=+++=-+-++-= ⎪ ⎪ ⎪------⎝⎭⎝⎭⎝⎭1111111333n n a a a ++-=----,所以20222023113S a =--,又20234a >,所以202331a ->,所以20231013a <<-,所以202201S <<.故选:A.13.19【解析】【分析】根据余弦的二倍角公式,即可求出结果.【详解】 由题得,22221cos 2cos 212sin 1255539πππααα⎛⎫⎛⎫⎛⎫⎛⎫+=+=-+=-⨯= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 故答案为:19. 14.45##0.8 【解析】【分析】直接利用平面向量的夹角公式求解.【详解】解:由题得,22245cos ,15||||||2b a b a b a b b →→→→→→→→⋅〈〉===⋅.故答案为:4515.57【解析】【分析】 根据题意可得10AB =,结合||4||3AF BF =,AF BF ⊥求得||8AF =,||6BF =,继而可求出a ,求得答案.【详解】因为点A ,B 为C 上关于原点对称的两点,故连接AB ,则AB 过原点O ,又因为AF BF ⊥,||5OF = ,故10AB =, 又||4||3AF BF =,所以||8AF =,||6BF =, 取C 的左焦点为F ' ,连接AF ' ,则||6AF BF '==, 所以||142AF AF a '+==,所以7a =,所以C 的离心率为57c a =, 故答案为:57 16.2π3##2π3【解析】【分析】 作出辅助线,找到球面被侧面PBC 所截得曲线是一段圆弧,求出弧长.【详解】如图,分别取P A ,BC 的中点为O ,D ,连接AD ,PD .则BC AD ⊥,BC PD ⊥,AD PD D =,所以BC ⊥平面P AD .又BC ⊂平面PBC ,所以平面PAD ⊥平面PBC ,交线为PD ,过A 作AE PD ⊥,垂足为E ,则AE ⊥平面PCD .过O 作OM PD ⊥.垂足为M ,所以OM ⊥平面PCD ,由于平面截球所得的为圆面,且球心与这个圆的圆心所在直线与该平面垂直,所以以P A 为直径的球的球面被侧面PBC 所截得曲线是以点M 为圆心的一段圆弧.易知E 是PBC 的中心,M 是PE 的中点,所以M ,E 分别是线段PD 的两个三等分点, 即MP ME =,所以所求曲线对应劣弧上的圆周角为π3BPC ∠=, 所以对应的圆心角为2π3,易知11133PM PD ===, 所以所截得曲线长度22π1π33l =⨯=. 故答案为:2π317.(1)π3(2)4+【解析】【分析】(1)结合正弦定理及已知条件,即可化简求得A 的值;(2)利用正弦定理解得ABC 外接圆的半径,即可求得PBC 的周长.(1)由已知及正弦定理,得sin cos sin cos sin sin cos A C A B A C A A =-,所以sin (sin cos cos sin )cos A A C A C B A +=,即sin sin cos A B B A =,又()0,πB ∈,所以sin 0B >.所以tan A =又()0,πA ∈,所以π3A =. (2)设ABC 的外接圆半径为r.则由正弦定理2sin a r A =.又==a BC π3A =, 所以2r =.即2PB PC ==,所以4PB PC BC ++=+即PBC 的周长为4+18.(1)合格率为92%,优秀率为52%(2)不需要对不及格学生进行第二次培训【解析】【分析】(1)根据表格即可算出格率和优秀率(2)先计算出均值,再根据2x s -的值,即可求解.(1)根据表格可知成绩不低于60分的频率为10080.92100-=, 所以估计参加培训讲座的学生的冰雪知识的合格率为92%;根据表格可知成绩不低于80分的频率为30220.52100+=, 所以估计参加培训讲座的学生的冰雪知识的优秀率为52%.(2) 由题得,815253022556575859579.3100100100100100x =⨯+⨯+⨯+⨯+⨯=, 所以279.312.1255.155x s -=-⨯=>,故不需要对不及格学生进行第二次培训.19.(1)证明见解析【解析】【分析】(1)根据勾股定理可证AD BD ⊥,易证1AD DD ⊥,再根据面面垂直的判定定理即可证明结果;(2)因为AD BC ∥,由(1)可知BC ⊥平面11BDD B ,由此可知BC 是三棱锥11C BB D -的高,再根据1111D BCB C BB D V V --=,由此即可求出结果.(1)证明:ABD △中,因为2AB =,1AD =,BD =所以222AB AD BD =+.所以AD BD ⊥,又侧面11ADD A 为矩形,所以1AD DD ⊥,又1BD DD D =,BD ,1DD ⊂平面11BDD B .所以AD ⊥平面11BDD B ,又AD ⊂平面ABCD ,所以平面ABCD ⊥平面11BDD B .(2)解:因为AD BC ∥,AD ⊥平面11BDD B ,所以BC ⊥平面11BDD B ,易得1BC =,11B D 1B B ,1160D B B ∠=︒,所以11BB D △的面积1112BB D S ==△.三棱锥11D BCB -的体积11111111133D BCB C BB D BB D V V S BC --==⋅==△. 20.(1)23y x =(2)33,42⎛⎫± ⎪⎝⎭【解析】【分析】(1)根据已知抛物线过点(3,3)M 可求得抛物线方程;(2)利用点差法可求得AB k ,表示出l 的方程,再根据90APB ∠=︒,以及直线l 始终平分弦PQ ,可得到关于P 点横纵坐标的方程组,即可求得点P 的坐标.(1)因为(3,3)M 在抛物线上,所以236p =,解得32p =, 所以E 的方程为23y x =.(2)设00(,)P x y ,211(,)3y A y ,222(,)3y B y , 则21222121333AB y y k y y y y -==+-, 则直线l 的方程为11123()-=-+y y x x y y , 化简为2121211()33=+++-y y y x y y y x ,又∵2113y x =∵1212()3y y y x y y +=+.∵ 由10202222001213333AP BP y y y y k k y y y y --=⋅=---,得0202331⋅=-++y y y y 整理得2012120()9y y y y y y +++=-,∵由∵+∵得,1200(()3())3y y y y x x ++=--,故直线l 恒过点00(3,)H x y +-,由题意知H 为弦PQ 的中点,所以点00(6,3)Q x y +-.又因为P 、Q 在E 上,所以2002003,(3)3(6),y x y x ⎧=⎨-=+⎩解得034x =,032y =±, 即点P 的坐标为33,42⎛⎫± ⎪⎝⎭. 【点睛】圆锥曲线的中点弦问题是高考常见的题型。
2020年山西运城高三下学期高考模拟理科数学试卷(6月适应性测试)-学生用卷

2020年山西运城高三下学期高考模拟理科数学试卷(6月适应性测试)-学生用卷一、选择题(本大题共12小题,每小题5分,共60分)1、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第1题5分⩽0},B={x|lnx>1},则A∩B=().已知集合A={x|x−3x−1A. {x|e<x<3}B. {x|e<x⩽3}C. {x|1<x<e}D. {x|1⩽x<e}2、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第2题5分若复数z=(a2−4)+ai2021(a∈R),i为虚数单位,则“z为纯虚数”是“a=2”的().A. 必要不充分条件B. 充分不必要条件C. 充要条件D. 既不充分也不必要条件3、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第3题5分已知a=log42.5,b=log21.5,c=0.4−1.5,则().A. a<b<cB. a<c<bC. b<a<cD. c<a<b4、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第4题5分函数f(x)=xtanx(−1⩽x⩽1)的图象可能是().A.B.C.D.5、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第5题5分在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0),若ξ在(0,2)内取值的概率为0.6,则ξ在(2,+∞)内取值的概率为().A. 0.8B. 0.4C. 0.3D. 0.26、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第6题5分执行如图所示的程序框图,则输出的T=().A. 85B. 43C. 32D. 17、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第7题5分已知向量a →,b →满足|a →|=1,|b →|=√3,且a →与b →的夹角为π6,则|2a →−b →|=( ). A. 12 B. √13 C. 13 D. 18、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第8题5分已知S n 为等差数列{a n }的前n 项和,若S 13=135,则a 7=( ). A. 15 B. 25 C. −15 D. −259、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第9题5分根据散点图,对两个具有非线性关系的相关变量x ,y 进行回归分析,设u =lny ,v =(x −4)2,利用最小二乘法,得到线性回归方程为u ^=−0.5v +2,则变量y 的最大值的估计值是( ).A. eB. ln2C. e 2D. 2ln210、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第10题5分已知函数f (x )=Asin(ωx +φ)(A >0,ω>0,0<φ<π)的部分图象如图所示,则下列结论不正确的是( ).A. f (x )的最小正周期为π2B. f (x )的最大值为4C. (−7π24,0)是f (x )的一个对称中心 D. 函数f (x )在区间(−π,−512π)上单调递增11、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第11题5分 已知直线y =34x 与双曲线C :x 2a 2−y 2b 2=1(a >0,b >0)相交于不同的两点A 和B ,F 为双曲线C的左焦点,且满足AF ⊥BF ,则双曲线C 的离心率为( ).A. √10+12B. √104C. √102D. √10−112、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第12题5分已知函数f(x)=ln(x +√x 2+1)满足对于任意x 1∈[12,2],存在x 2∈[12,2],使得f (x 12+2x 1+a )⩽f (ln x 2x 2)成立,则实数a 的取值范围为( ).A. (−∞,ln22−8]B. [ln22−8,−54−2ln2]C. [ln22−8,+∞)D. (−∞,−54−2ln2]二、填空题(本大题共4小题,每小题5分,共20分)13、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第13题5分我校高一、高二、高三共有学生2400名,为了了解同学们对“智慧课堂”的意见,计划采用分层抽样的方法,从这2400名学生中抽取一个容量为48的样本.若从高一、高二、高三抽取的人数恰好是从小到大排列的连续偶数,则我校高二年级的学生人数为.14、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第14题5分已知函数f(x)={x2−2ax+12,x⩽1x+4x+a,x>1,若f(x)的最小值为f(1),则实数a的取值范围是.15、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第15题5分已知衡量病毒传播能力的最重要指标叫做传播指数RO.它指的是,在自然情况下(没有外力介人,同时所有人都没有免疫力),一个感染到某种传染病的人,会把疾病传染给多少人的平均数.它的简单计算公式是RO=1+确诊病例增长率×系列间隔,其中系列间隔是指在一个传播链中,两例连续病例的间隔时间(单位:天).根据统计,确诊病例的平均增长率为40%,两例连续病例的间隔时间的平均数5天,根据以上RO计算,若甲得这种传染病,则4轮传播后由甲引起的得病的总人数约为.16、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第16题5分农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,古称角黍,是端午节大家都会品尝的食品.如图,平行四边形形状的纸片是由六个边长为2的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为;若该六面体内有一球,当该球体积最大时,球的表面积是.三、解答题(本大题共5小题,每小题12分,共60分)17、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第17题12分(sinB−sinC).△ABC的角A,B,C的对边分别为a,b,c,已知sinA−sinC=ba+c(1) 求角A.(2) 从三个条件:①a=3;②b=3;③△ABC的面积为3√3中任选一个作为已知条件,求△ABC周长的取值范围.18、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第18题12分如图,由直三棱柱ABC−A1B1C1和四棱锥D−BB1C1C构成的几何体中,∠BAC=90°,AB= 2,BC=CC1=4,C1D=CD=2√5,平面CC1D⊥平面ACC1A1.(1) 求证:A1C1⊥DC.(2) 在线段BC上(含端点)是否存在点P,使直线DP与平面DBB1所成的角的正弦值为√3?若存在,3的值,若不存在,说明理由.求BPBC19、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第19题12分,(a∈R).已知函数f(x)=e x+ax−12(1) 判断函数f(x)的单调性.(2) 设g(x)=12−lnx,F(x)=f(x)−g(x),求证:当a∈(−2,0)时,函数F(x)只有一个零点.20、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第20题12分已知椭圆E:x 2a2+y2=1(a>1)的离心率为√32,右顶点P(a,0)是抛物线C:y2=2px的焦点.(1) 求抛物线C:y2=2px的标准方程.(2) 若C上存在两动点A,B(A,B在x轴异侧)满足OA→⋅OB→=20,且△PAB的周长为2|AB|+4,求|AB|的值.21、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第21题12分某工厂为提高生产效率,需引进一条新的生产线投入生产,现有两条生产线可供选择,生产线①:有A,B两道独立运行的生产工序,且两道工序出现故障的概率依次是0.01,0.05.若两道工序都没有出现故障,则生产成本为16万元;若A工序出现故障,则生产成本增加2万元;若B工序出现故障,则生产成本增加3万元;若A,B两道工序都出现故障,则生产成本增加5万元.生产线②:有a,b两道独立运行的生产工序,且两道工序出现故障的概率依次是0.04,0.02.若两道工序都没有出现故障,则生产成本为15万元;若a工序出现故障,则生产成本增加8万元;若b工序出现故障,则生产成本增加5万元;若a,b两道工序都出现故障,则生产成本增加13万元.(1) 若选择生产线②,求生产成本恰好为20万元的概率.(2) 为最大限度节约生产成本,你会给工厂建议选择哪条生产线?请说明理由.四、选做题(本大题共2小题,共10分,选做1题)选修4-4:坐标系与参数方程22、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第22题10分在平面直角坐标系xOy中,直线l的参数方程是:{x=m+√22ty=√22t(t是参数).以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程是ρ=6sinθ.(1) 若直线l与曲线C相交于A、B两点,且|AB|=2,试求实数m值.(2) 设M(x,y)为曲线C上任意一点,求y−x的取值范围.选修4-5:不等式选讲23、【来源】 2020年山西运城高三下学期高考模拟理科(6月适应性测试)第23题10分已知函数f(x)=|2x−a|+|x−1|,a∈R.(1) 若不等式f(x)⩽2−|x−1|无解,求实数a的取值范围.(2) 当a<2时,函数f(x)的最小值为2,求实数a的值.1 、【答案】 B;2 、【答案】 A;3 、【答案】 C;4 、【答案】 B;5 、【答案】 D;6 、【答案】 B;7 、【答案】 D;8 、【答案】 A;9 、【答案】 C;10 、【答案】 D;11 、【答案】 C;12 、【答案】 A;13 、【答案】800;14 、【答案】[3,+∞);15 、【答案】120;;16 、【答案】4√2;2717 、【答案】 (1) π.3;(2) ①(6,9];②(6,+∞);③[6√3,+∞).;18 、【答案】 (1) 证明见解析.;(2) 存在,BPBC =√29−25.;19 、【答案】 (1) 当a⩾0时,f(x)在R上单调递增;当a<0时,f(x)在(ln(−a),+∞)上单调递增,在(−∞,ln(−a))上单调递减.;(2) 证明见解析.;20 、【答案】 (1) y2=8x.;(2) 30.;21 、【答案】 (1) 0.0192.;(2) 应选生产线②;证明见解析.;22 、【答案】 (1) m=1或m=−7.;(2) [3−3√2,3+3√2].;23 、【答案】 (1) (−∞,0)∪(4,+∞).;(2) a=−2.;。
山西省临汾市2020届高三考前适应性训练考试(三)文科综合地理试题word版有答案(精校版)

山西省临汾市高三考前适应性训练考试(三)文科综合地理试题注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、考生号填写在答题卡上。
2. 回答第Ⅰ卷时,选出每小题的答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在试卷上无效。
3. 回答第Ⅱ卷时,将答案填写在答题卡上,写在试卷上无效。
4. 考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷本卷共35小题。
每小题4分,共140分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
2019年4月1日,中央设立河北省雄县、客城、安新3县及其周边部分区域为雄安新区(如图),将其定位为疏解北京非首都功能集中承载地,并努力打造为创新发展示范区:绿色生态宜居新城区、创新驱动发展引领区、协调发展示范区、开放发展先行区。
此举必将对京津冀乃至全国经济发展格局产生重要影响。
据此完成1~2题。
1.雄安新区设立的优势条件有①地处北京、天津、保定腹地,地理位置优越②土地资源丰富,资源环境承载能力较强③生态环境优良④水陆交通便捷⑤现有开发程度较高⑥国家政策支持A. ①②③⑥B. ①②④⑥C. ①③⑤⑥D. ②③⑤⑥2.雄安新区的设立将会A.加快北京城市规模扩大,促进首都核心功能的发挥B.引导高端服务业和劳动密集型企业向新区集聚C.优化京津冀城市布局和空间结构D.扩大雄安新区全方位对外开放和趋同化发展20世纪90年代之前,粤西山区的云浮石材加工业大多靠山食山,有“中国石都”之称,如今每年都要从欧美、中东等地紧扣石材建筑,经加工销往国内外市场。
改革开放后,福建水头镇的石材产业依托厦门港强势崛起,目前该地以发展成为我国最大的石材产销基地。
据此完成3~4题。
3.云浮石材加工业兴起的主导因素是A.政策B.市场C.原料D.劳动力4.与云浮相比,福建省水头镇石材产业迅速发展的优势是A. 市场广阔B.交通便利C.技术领先D.基础雄厚“保护性耕作法”是指对耕地实行免耕或浅耕措施,并在粮食收割时及时将作物秸秆粉归还农田,或者将庄稼茬子留在田地果冻。
山西省2020届高三高考考前适应性测试(5月)理科数学·A卷试题(含答案)
积是
A. 4 15
B. 5 15 4
C. 3 3 2
D. 5 3 3
12. 设函数 f (x)是定义在 (0, +∞)上的可导函数,满足① f (x) > 0,② 2xf ′(x) + f (x) < 0,其中
f ′(x)为 f (x)的导函数 . 对于任意 a > b > 0,必有
A. a2 f (a) > b2 f (b)
题计分,作答时请用 2B 铅笔在答题卡上将所选题号后的方框涂黑。
22.[选修 4-4:坐标系与参数方程](10 分) 过点 P(2,0)的直线 l 与抛物线 C:y2 = 2x 相交于 A,B 两点 .
(1)求 AB 中点轨迹的直角坐标方程;
(2)若 P 满足| | PA | - | PB | |=2 2 时,求 l 的方程 .
OCPD(O 为坐标原点)面积的最小值是
A. 3
B. 2
C. 1
D. 2
8. 某病毒引起的肺炎的潜伏期平均为 7 天左右,短的约 2~3 天,长的约 10~14 天,甚至有 20
余天 . 某医疗机构对 400 名确诊患者的潜伏期进行统计,整理得到以下频率分布直方图 .
根据该直方图估计:要使 90% 的患者显现出明显病状,需隔离观察的天数至少是
2020 年山西省高考考前适应性测试(二)
理科数学参考答案详解及评分说明
评分说明: 1. 考生如按其他方法或步骤解答,正确的,同样给分;有错的,根据错误的性质,参照评分说明中相应的规定
评分 . 2. 计算题只有最后答案而无演算过程的,不给分;只写出一般公式但未能与试题所给的具体条件联系的,不
给分 .
C. 若 a⫽α,b ⊂ α,则 a⫽b
2020届山西省运城市高三6月考前适应性测试 英语试题
2020届山西省运城市高三6月考前适应性测试英语试题第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话,每段对话后有一个小题。
从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A.£19.15.B.£9.18.C.£9.15.答案是C。
1. How far is the woman from the railway station?A. About 100 metres.B. About 200 metres.C. About 300 metres.2. What will the woman do for the man?A. Keep the new book for him.B. Call him if the book comes back.C. Recommend another book to him.3. What is the woman doing?A. Cooking.B. Watching TV.C. writing a recipe.4. Who is Rachel?A. Tom's sister.B. John's friend.C. John and Tom's classmate.5. Where does this conversation take place?A. In Kate's classroom.B. In the teacher' s office.C. On the competition site.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
