新浙教版数学,特殊的平行四边形知识点
《特殊平行四边形》知识讲解
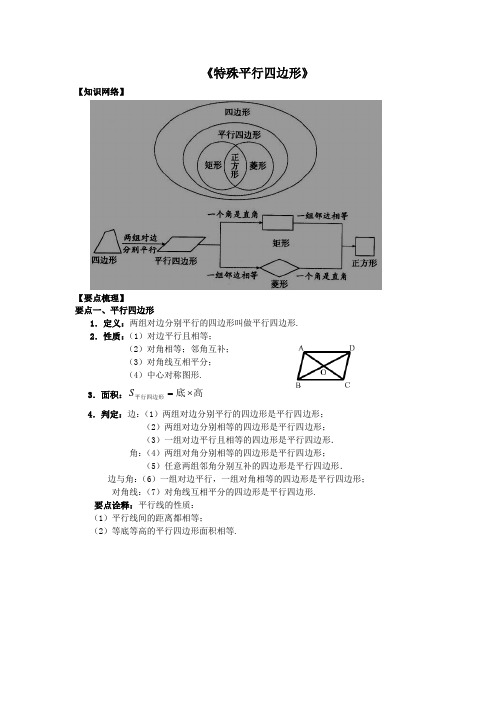
《特殊平行四边形》【知识网络】【要点梳理】要点一、平行四边形1.定义:两组对边分别平行的四边形叫做平行四边形.2.性质:(1)对边平行且相等;(2)对角相等;邻角互补;(3)对角线互相平分;(4)中心对称图形.3.面积:高底平行四边形⨯=S4.判定:边:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形. 角:(4)两组对角分别相等的四边形是平行四边形;(5)任意两组邻角分别互补的四边形是平行四边形. 边与角:(6)一组对边平行,一组对角相等的四边形是平行四边形; 对角线:(7)对角线互相平分的四边形是平行四边形.要点诠释:平行线的性质:(1)平行线间的距离都相等;(2)等底等高的平行四边形面积相等.要点二、菱形1. 定义:有一组邻边相等的平行四边形叫做菱形.2.性质:(1)具有平行四边形的一切性质;(2)四条边相等;(3)两条对角线互相平分且垂直,并且每一条对角线平分一组对角;(4)中心对称图形,轴对称图形.3.面积:2对角线对角线高==底菱形⨯⨯S 4.判定:(1)一组邻边相等的平行四边形是菱形;(2)对角线互相垂直的平行四边形是菱形;(3)四边相等的四边形是菱形.要点三、矩形1.定义:有一个角是直角的平行四边形叫做矩形.2.性质:(1)具有平行四边形的所有性质;(2)四个角都是直角;(3)对角线互相平分且相等;(4)中心对称图形,轴对称图形.3.面积:宽=长矩形⨯S4.判定:(1) 有一个角是直角的平行四边形是矩形.(2)对角线相等的平行四边形是矩形.(3)有三个角是直角的四边形是矩形.要点诠释:由矩形得直角三角形的性质:(1)直角三角形斜边上的中线等于斜边的一半;(2)直角三角形中,30度角所对应的直角边等于斜边的一半.要点四、正方形1. 定义:四条边都相等,四个角都是直角的四边形叫做正方形.2.性质:(1)对边平行;(2)四个角都是直角;(3)四条边都相等;(4)对角线互相垂直平分且相等,对角线平分对角;(5) 两条对角线把正方形分成四个全等的等腰直角三角形;(6)中心对称图形,轴对称图形.3.面积:=S 正方形边长×边长=12×对角线×对角线 4.判定:(1)有一个角是直角的菱形是正方形;(2)一组邻边相等的矩形是正方形;(3)对角线相等的菱形是正方形;(4)对角线互相垂直的矩形是正方形;(5)对角线互相垂直平分且相等的四边形是正方形;(6)四条边都相等,四个角都是直角的四边形是正方形.。
特殊平行四边形主要知识点
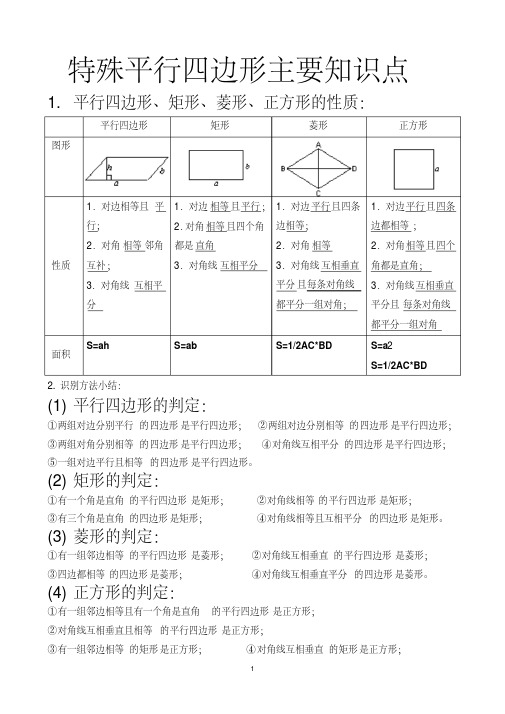
特殊平行四边形主要知识点1. 平行四边形、矩形、菱形、正方形的性质:
平行四边形矩形菱形正方形图形
性质1.对边相等且平
行;
2.对角相等邻角
互补;
3.对角线互相平
分
1.对边相等且平行;
2.对角相等且四个角
都是直角
3.对角线互相平分
1.对边平行且四条
边相等;
2.对角相等
3.对角线互相垂直
平分且每条对角线
都平分一组对角;
1.对边平行且四条
边都相等;
2.对角相等且四个
角都是直角;
3.对角线互相垂直
平分且每条对角线
都平分一组对角
面积S=ah S=ab S=1/2AC*BD S=a2
S=1/2AC*BD
2. 识别方法小结:
(1)平行四边形的判定:
①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;
③两组对角分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;
⑤一组对边平行且相等的四边形是平行四边形。
(2)矩形的判定:
①有一个角是直角的平行四边形是矩形;②对角线相等的平行四边形是矩形;
③有三个角是直角的四边形是矩形;④对角线相等且互相平分的四边形是矩形。
(3)菱形的判定:
①有一组邻边相等的平行四边形是菱形;②对角线互相垂直的平行四边形是菱形;
③四边都相等的四边形是菱形;④对角线互相垂直平分的四边形是菱形。
(4)正方形的判定:
①有一组邻边相等且有一个角是直角的平行四边形是正方形;
②对角线互相垂直且相等的平行四边形是正方形;
③有一组邻边相等的矩形是正方形;④对角线互相垂直的矩形是正方形;
1。
特殊的平行四边形知识点归纳

特殊的平行四边形平行四边形的性质平行四边形的两组对边分别相等平行四边形的两组对角分别相等平行四边形的两组对角分别相等平行四边形的邻角互补平行线间的高距离处处相等平行四边形的对角线互相平分过平行四边形对角线交点的直线,将平行四边形分成全等的两部分图形平行四边形不是轴对称图形,但平行四边形是中心对称图形。
矩形和菱形是轴对称图形平行四边形的判定方法(共7种)1.两组对边分别平行的四边形是平行四边形(定义判定法);2.一组对边平行且相等的四边形是平行四边形;3.对角线互相平分的四边形是平行四边形;4.两组对边分别相等的四边形是平行四边形。
5.两组对角分别相等的四边形是平行四边形;6 一组对边平行,一组对角相等7 一组对边平行,一组对角线平分菱形的性质:(1)边:菱形的对边平行,且四条边都相等(2)角:菱形的对角相等,邻角互补。
(3)对角线:菱形的对角线互相垂直平分,并且每一条对角线平分一组对角。
(4)对称性:中心对称图形,轴对称图形(5)菱形的面积=底×高=对角线乘积的一半菱形的判定:(1)一组邻边相等的平行四边形是菱形。
(2)对角线互相垂直的平行四边形是菱形。
(3)对角线平分一组内角的平行四边形是菱形。
(4)四边相等的四边形是菱形。
(5)对角线互相垂直平分的四边形是菱形。
矩形的性质:(1)边:矩形的对边平行且相等。
(2)角:矩形的四个角都是直角。
(3)对角线:矩形的对角线相等且互相平分。
(4)对称性:中心对称图形,轴对称图形矩形的判定:(1)有一个角是直角的平行四边形是矩形。
(2)对角线相等的平行四边形是矩形。
(3)对角线相等且互相平分的四边形是矩形(4)三个角都是直角的四边形是矩形。
(5)四个角都相等角的四边形是矩形。
正方形的性质:(1)四边都相等,对边平行(2)四个角都是直角(2)对角线相等且互相垂直平分,每一条对角线平分一组对角。
(3)中心对称图形,轴对称图形(4条对称轴)正方形的判定:(1)一组邻边相等的矩形是正方形(2)对角线互相垂直的矩形是正方形(3)一个角是直角的菱形是正方形(4)对角线相等的菱形是正方形。
八年级数学下册 4.2 平行四边形及其性质课件1 (新版)浙教版

• 例2:已知,如图所示,E,F分别(fēnbié)是 ABCD的边AD,BC上的点,
• 且AF∥CE. • 求证:DE=BF, ∠BAF=∠DCE
第六页,共11页。
悟学提高(tí gāo)
• 学校(xuéxiào)买了四棵树,准备栽在花园里, 已经栽了三棵(如图),现在学校(xuéxiào) 希望这四棵树能组成一个平行四边形,你觉 得第四棵树应该栽在哪里?
第七页,共11页。
课后练习
• 1.ABCD中,AB∥ ,AD∥ . • 2.Aห้องสมุดไป่ตู้CD中,∠A+∠D= ,∠A+∠B
= ,∠B+∠C= ,∠C+∠D= . • 3.已知ABCD中,∠A=55°,则∠B=
°,∠C= °,∠D= °.
第八页,共11页。
• 4.在平行四边形ABCD中,∠BAC=26°, ∠ACB=34°,则∠DAC= °,∠ACD= °,∠D= °
4.2平行四边形及其性质 (xìngzhì)
第一页,共11页。
• 自学 • 认真阅读教材P80~5完成以下(yǐxià)问题(时间:6
分钟) • 1.平行四边形的概念: • _______________________叫做平行四边形. • 平行四边形用符号”____________”表示,平行
四边形ABCD可记作“______________”. • 2、平行四边形的性质定理: • 1)______________________________ • 2)_____________________________
第九页,共11页。
• 5.学校门口的伸缩门应用了四边形的 ____________性.
• 6.已知平行四边形相邻(xiānɡ lín)两个角的 度数之比为3∶2,求平行四边形各个内角的 度数.
特殊的平行四边形知识梳理

【学习目标】1. 掌握平行四边形、矩形、菱形、正方形的概念, 了解它们之间的关系.2. 探索并掌握平行四边形、矩形、菱形、正方形的有关性质和常用判别方法, 并能运用这些知识进行有关的证明和计算.3. 掌握三角形中位线定理. 【要点梳理】 要点一、平行四边形1.定义:两组对边分别平行的四边形叫做平行四边形. 2.性质:(1)对边平行且相等; (2)对角相等;邻角互补; (3)对角线互相平分; (4)中心对称图形. 3.面积:4.判定:边:(1)两组对边分别平行的四边形是平行四边形; (2)两组对边分别相等的四边形是平行四边形; (3)一组对边平行且相等的四边形是平行四边形. 角:(4)两组对角分别相等的四边形是平行四边形; (5)任意两组邻角分别互补的四边形是平行四边形. 边与角:(6)一组对边平行,一组对角相等的四边形是平行四边形;对角线:(7)对角线互相平分的四边形是平行四边形. 要点诠释:平行线的性质:高底平行四边形⨯=S(1)平行线间的距离都相等; (2)等底等高的平行四边形面积相等.要点二、矩形1.定义:有一个角是直角的平行四边形叫做矩形. 2.性质:(1)具有平行四边形的所有性质;(2)四个角都是直角; (3)对角线互相平分且相等;(4)中心对称图形,轴对称图形. 3.面积:4.判定:(1) 有一个角是直角的平行四边形是矩形.(2)对角线相等的平行四边形是矩形.(3)有三个角是直角的四边形是矩形. 要点诠释:由矩形得直角三角形的性质: (1)直角三角形斜边上的中线等于斜边的一半;(2)直角三角形中,30度角所对应的直角边等于斜边的一半. 要点三、菱形1. 定义:有一组邻边相等的平行四边形叫做菱形. 2.性质:(1)具有平行四边形的一切性质; (2)四条边相等;(3)两条对角线互相平分且垂直,并且每一条对角线宽=长矩形 S平分一组对角;(4)中心对称图形,轴对称图形.3.面积:4.判定:(1)一组邻边相等的平行四边形是菱形;(2)对角线互相垂直的平行四边形是菱形; (3)四边相等的四边形是菱形.要点四、正方形1. 定义:四条边都相等,四个角都是直角的四边形叫做正方形.2.性质:(1)对边平行; (2)四个角都是直角;(3)四条边都相等;(4)对角线互相垂直平分且相等,对角线平分对角; (5) 两条对角线把正方形分成四个全等的等腰直角三角形;(6)中心对称图形,轴对称图形.3.面积:边长×边长=×对角线×对角线 4.判定:(1)有一个角是直角的菱形是正方形;(2)一组邻边相等的矩形是正方形; (3)对角线相等的菱形是正方形;2对角线对角线高==底菱形⨯⨯S =S 正方形12(4)对角线互相垂直的矩形是正方形;(5)对角线互相垂直平分且相等的四边形是正方形;(6)四条边都相等,四个角都是直角的四边形是正方形.【知识网络】例1、菱形具有而一般平行四边形不具有的性质是()A.对边相等 B.对角相等C.对角线互相平分D.对角线互相垂直例2、如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于()A.B.C.5 D.4例3、如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为()A.2 B.3C.D.2例4、如图,菱形ABCD的对角线AC、BD相交于点O,AC=8,BD=6,过点O作OH ⊥AB,垂足为H,则点O到边AB的距离OH等于()A.2 B.C.D.例5、如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个锐角为60°的菱形,剪口与折痕所成的角a的度数应为.例1、如图,在矩形ABCD中,点O为对角线AC、BD的交点,点E为BC上一点,连接EO,并延长交AD于点F,则图中全等三角形共有()A.3对B.4对C.5对D.6对例2、如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2,DE=2,则四边形OCED的面积()A.2 B.4C.4D.8例3、如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE =S△COE,其中正确结论有()A.1个 B.2个C.3个D.4个例4、如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点,则DC和EF的大小关系是()A.DC>EF B.DC<EFC.DC=EF D.无法比较例5、如图,在Rt△ABC中,∠ACB=90°,将边BC沿斜边上的中线CD折叠到CB′,若∠B=50°,则∠ACB′=.例1、下列说法正确的是()A.对角线相等且互相垂直的四边形是菱形B.对角线互相垂直平分的四边形是正方形C.对角线互相垂直的四边形是平行四边形D.对角线相等且互相平分的四边形是矩形例2、已知:如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,面积记作S1;再作第二个正方形A2B2C2A3,面积记作S2;继续作第三个正方形A3B3C3A4,面积记作S3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第6个正方形的面积S6是()A.256 B.900 C.1024 D.4096例3、如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=2,则正方形的边长为()A.4 B.3 C.2+ D.例4、如图,正方形AEFG的顶点E,G在正方形ABCD的边AB,AD上,连接BF,DF.则BE:CF的值为.例5、如图,正方形ABCD中,以对角线BD为边作菱形BDFE,使B,C,E三点在同一直线上,连接BF,交CD与点G.(1)求证:CG=CE;(2)若正方形边长为4,求菱形BDFE的面积.。
特殊的平行四边形初中数学知识点总结

特别的平行四边形初中数学知识点总结一、特别的平行四边形1.矩形:(1)定义:有一个角是直角的平行四边形。
(2)性质:矩形的四个角都是直角;矩形的对角线均分且相等。
(3)判断定理:①有一个角是直角的平行四边形叫做矩形。
②对角线相等的平行四边形是矩形。
③有三个角是直角的四边形是矩形。
直角三角形的性质:直角三角形中所对的直角边等于斜边的一半。
2.菱形:(1)定义:邻边相等的平行四边形。
(2)性质:菱形的四条边都相等;菱形的两条对角线相互垂直,而且每一条对角线均分一组对角。
(3)判断定理:①一组邻边相等的平行四边形是菱形。
②对角线相互垂直的平行四边形是菱形。
③四条边相等的四边形是菱形。
(4)面积:3.正方形:(1)定义:一个角是直角的菱形或邻边相等的矩形。
(2)性质:四条边都相等,四个角都是直角,对角线相互垂直均分。
正方形既是矩形,又是菱形。
(3)正方形判断定理:①对角线相互垂直均分且相等的四边形是正方形;②一组邻边相等,一个角为直角的平行四边形是正方形;③对角线相互垂直的矩形是正方形;④邻边相等的矩形是正方形⑤有一个角是直角的菱形是正方形;⑥对角线相等的菱形是正方形。
二、矩形、菱形、正方形与平行四边形、四边形之间的联系:1.矩形、菱形和正方形都是特别的平行四边形,其性质都是在平行四边形的基础上扩大来的。
矩形是由平行四边形增添“一个角为90°”的条件获得的,它在角和对角线方面拥有比平行四边形更多的特征;菱形是由平行四边形增添“一组邻边相等”的条件获得的,它在边和对角线方面拥有比平行四边形更多的特征;正方形是由平行四边形增添“一组邻边相等”和“一个角为90°”两个条件获得的,它在边、角和对角线方面都拥有比平行四边形更多的特征。
2.矩形、菱形的判断能够依据出发点不一样而分红两类:一类是以四边形为出发点进行判断,另一类是以平行四边形为出发点进行判断。
而正方形除了上述两个出发点外,还能够从矩形和菱形出发进行判断。
特殊平行四边形知识点
第六章特殊平行四边形补充说明:1、在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心。
旋转前后图形上能够重合的点叫做对称点。
例如:矩形,菱形,正方形,平行四边形2、如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴。
例如:长方形,正方形,菱形一、平行四边形1、平行四边形的定义:两组对边分别平行的四边形2、平行四边形的性质:①对边平行②对边相等③对角相等④对角线互相平分3、平行四边形的判定:①两组对边分别平行的四边形②两组对边分别相等的四边形③一组对边平行且相等的四边形④两组对角分别相等的四边形⑤对角线互相平分的四边形二、菱形1、菱形的定义:一组邻边相等的平行四边形叫菱形2、菱形的性质:①具备平行四边形的所有性质.②菱形的四条边都相等.③菱形的对角线互相垂直,且每条对角线平分一组对角.④菱形既是中心对称图形,又是轴对称图形,它有2条对称轴3、菱形的判定:①一组邻边相等的平行四边形是菱形.②对角线互相垂直的平行四边形是菱形.③四条边都相等的四边形菱形.4、菱形的面积与两对角线的关系:菱形的面积等于两对角线乘积的一半,也等于底*高注意:对角线互相垂直的四边形的面积等于两对角线乘积的一半三、矩形1、矩形的定义:有一个角是直角的平行四边形叫矩形.2、矩形的性质:①具备平行四边形的所有性质②矩形的四个角都是直角.③矩形的对角线相等.④矩形既是中心对称图形,又是轴对称图形,它有2条对称轴3、矩形的判定:①有一个角是直角的平行四边形是矩形.②对角线相等的平行四边形是矩形③有三个角是直角的四边形是矩形.4、直角三角形斜边上的中线等于斜边的一半.5、勾股定理:在直角三角形中,两直角边的平方和等于斜边的平方.6、在直角三角形中,30度角所对的直角边是斜边的一半7、矩形的面积:长*宽;矩形的周长:2*(长+宽)四、正方形1、正方形的定义:有一组邻边相等的矩形叫正方形2、正方形的性质:①正方形的四个角都是直角②正方形的四条边都相等③正方形的对角线相等且互相垂直平分④正方形是中心对称图形,又是轴对称图形,它有四条对称轴3、正方形的判定:①对角线相等的菱形是正方形②有一个角是直角的菱形是正方形③对角线互相垂直的矩形是正方形④有一组邻边相等的矩形是正方形4、正方形的面积与两对角线的关系:正方形的面积等于两对角线乘积的一半正方形面积:边长*边长;正方形周长:4*边长。
专题06特殊平行四边形重点知识讲义解析版
专题06 特殊平行四边形重点知识讲义性质判定矩形①边——两组对边分别平行且相等;②角——每个角都是90°;③对角线——两条对角线相等且互相平分.①有一个角是90°的平行四边形是矩形;②对角线相等的平行四边形是矩形;③有三个角90°的四边形是矩形.菱形①边——两组对边分别平行且相等,邻边相等;②角——两组对角分别相等;③对角线——两条对角线垂直且互相平分,每条对角线平分一组对角.①一组邻边相等的平行四边形是菱形;②对角线垂直的平行四边形是菱形;③四条边相等的四边形是菱形.正方形四条边都相等;四个角都是90°;对角线相等且互相垂直平分;每条对角线平分一组对角;正方形的中点四边形是正方形;矩形四个角平分线所成的四边形是正方形.四边相等,有三个角是直角的四边形是正方形;一组邻边相等的矩形是正方形;一组邻边相等且有一个角是直角的平行四边形是正方形;有一个角是直角的菱形是正方形;对角线相等的菱形是正方形;对角线互相垂直的矩形是正方形;对角线互相垂直平分且相等的平行四边形是正方形.几个结论1. 平行四边形对角线与边关系AC 2+BD 2=2(AB 2+BC 2)思考:在证明含有线段平分的关系时,考虑勾股定理,而勾股定理离不开直角三角形,故而需要作垂线构造直角三角形.理由:过A ,D 分别作AE ⊥BC 于E ,DF ⊥BC 于F ,则AC 2+BD 2=AE 2+CE 2+BF 2+DF 2= AE 2+(BC -BE )2+(BC +CF )2+DF 2=AE 2+BC 2-2BC ·BE +BE 2+BC 2+2BC ·CF +CF 2+DF 2= AE 2+BC 2+BE 2+BC 2+CF 2+DF 2=2(AB 2+BC 2)2. 对角线互相垂直四边形四边形ABCD 对角线,AC ⊥BD ,结论:S =12AC ·BD AB 2+CD 2=BC 2+AD 23. 中点四边形任意四边形中点四边形均为平行四边形对角线垂直的四边形的中点四边形为矩形对角线相等的四边形的中点四边形为菱形对角线垂直且相等的四边形的中点四边形为正方形4. 三角形一边的中线等于这边的一半,则该三角形为直角三角形.由图,知∠ACB=x+y=90°.5. 正方形中的“蝴蝶”四边形ABCD为正方形,BN⊥AM,则BN=AM.典例解析1.【特殊四边形判定】【例1】(2021·重庆渝中区月考)下列命题中,是真命题的是( )A.对角线相等的平行四边形是菱形B.一组邻边相等的四边形是菱形C.对角线互相垂直的平行四边形是菱形D.四个角相等的四边形是菱形【答案】C.【解析】解:A、对角线相等的平行四边形是矩形,A错误;B、一组邻边相等的平行四边形是菱形,B错误;C、对角线互相垂直的平行四边形是菱形,C正确;D、四个角相等的四边形是矩形,D错误;故答案为:C.【变式1-1】下列命题中,正确的是()A.两邻边相等的四边形是菱形B.一条对角线平分一个内角的平行四边形是菱形C.对角线垂直且一组邻边相等的四边形是菱形D.对角线垂直的四边形是菱形【答案】B.【解析】解:两邻边相等的平行四边形是菱形,故A错误;一条对角线平分一个内角的平行四边形是菱形,故B正确;对角线垂直且一组邻边相等的四边形不一定是菱形,比如筝形,故C错误;对角线垂直的平行四边形是菱形,故D错误;故答案为:B.【例2】(2020·银翔实验中学月考)下列四个命题中,假命题是()A.对角线互相平分的四边形是平行四边形B.对角线互相垂直平分的四边形是矩形C.对角线互相垂直的平行四边形是菱形D.对角线互相垂直且相等的平行四边形是正方形【答案】B.【解析】A、对角线互相平分的四边形是平行四边形,是真命题;B、对角线相等且平分的四边形是矩形,原命题是假命题;C、对角线互相垂直的平行四边形是菱形,是真命题;D、对角线互相垂直且相等的平行四边形是正方形,是真命题;故答案为:B.【变式2-1】(2020·河南开封期末)下列命题中,真命题是()A.一组对边平行且另一组对边相等的四边形是平行四边形B.有一个角是直角的四边形是矩形C.一组邻边相等且对角线互相垂直的四边形是菱形D.有一个角是直角且对角线互相垂直平分的四边形是正方形【答案】D.【解析】A.一组对边平行且另一组对边相等的四边形是平行四边形或等腰梯形,错误;B.有一个角是直角的平行四边形是矩形,错误;C.一组邻边相等且对角线互相垂直的四边形不一定是菱形,错误;D.有一个角是直角且对角线互相垂直平分的四边形是正方形,正确.故答案为:D.【变式2-2】(2020·河南驻马店期末)下列说法正确的个数是()①对角线互相垂直或有一组邻边相等的矩形是正方形;②对角线相等或有一个角是直角的菱形是正方形;③对角线互相垂直且相等的平行四边形是正方形;④对角线互相垂直平分且相等的四边形是正方形.A.1个B.2个C.3个D.4个【答案】D.【解析】解:①对角线互相垂直或有一组邻边相等的矩形是正方形,正确;②对角线相等或有一个角是直角的菱形是正方形,正确;③对角线互相垂直且相等的平行四边形是正方形,正确;④对角线互相垂直平分且相等的四边形是正方形,正确;故答案为:D.【例3】(2020·石家庄市期中)如图,在△ABC中,点D是边BC上的点(与B、C两点不重合),过点D作DE//AC,DF//AB,分别交AB、AC于E、F两点,下列说法错误的是()A.四边形AEDF是平行四边形B.若AD平分∠BAC,则四边形AEDF是菱形C.若AB⊥AC,则四边形AEDF是矩形D.若BD=CD,则四边形AEDF是正方形【答案】D.【解析】解:∵DE//AC,DF//AB,∴四边形AEDF是平行四边形,故A正确;若AD平分∠BAC,则∠EAD=∠FAD,又∵∠EAD=∠FDA,∴∠FAD=∠FDA∴FA=FD,∴平行四边形AEDF是菱形,故B正确;∵AB⊥AC,∴平行四边形AEDF是矩形,故C正确;若BD=CD,则四边形AEDF不一定是正方形;选项D错误.故答案为:D.【变式3-1】(2021·上海月考)已知四边形ABCD是平行四边形,下列结论中不正确的是()=时,四边形ABCD是菱形A.当AB BC^时,四边形ABCD是菱形B.当AC BDÐ=o时,四边形ABCD是矩形C.当90ABC=时,四边形ABCD是正方形D.当AC BD【答案】D.【解析】解:根据邻边相等的平行四边形是菱形,A叙述正确;根据对角线互相垂直的平行四边形是菱形,B叙述正确;根据有一个角是直角的平行四边形是矩形,C叙述正确;根据对角线相等的平行四边形是矩形,D叙述错误,符合题意;故答案为:D.>,【变式3-2】(2021·辽宁铁岭市期末)如图,点O为矩形ABCD的对称中心,AD AB 点E从点B出发(不含点B)沿BC向点C运动,移动到点C停止,延长EO交AD于点F,则四边形BEDF形状的变化依次为()A.平行四边形→菱形→正方形→矩形B.平行四边形→正方形→菱形→矩形C.平行四边形→菱形→平行四边形→矩形D.平行四边形→正方形→平行四边形→矩形【答案】C.【解析】解:连接BD∵点O为矩形ABCD的对称中心,∴BD经过点O,OD=OB,∵AD∥BC,∴∠FDO=∠EBO,∴△DFO≌△BEO,∴DF=BE,∵DF∥BE,∴四边形BEDF是平行四边形,观察图形可知,四边形AECF形状的变化依次为平行四边形→菱形→平行四边形→矩形.故答案为:C.【例4】(2021·广东模拟)如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC.(1)求证:四边形DBEC是菱形;(2)若AD=5,DF=2,求四边形DBEC面积.【答案】(1)见解析;(2)【解析】(1)证明:∵CE∥DB,BE∥DC,∴四边形DBEC为平行四边形.∵Rt△ABC中,∠ABC=90°,点D是AC的中点,∴CD=BD=12 AC,∴平行四边形DBEC是菱形;(2)∵点D,F分别是AC,AB的中点,AD=5,DF=2,∴DF是△ABC的中位线,AC=2AD=10,S△BCD =12S△ABC∴BC=2DF=4.∵∠ABC=90°,∴AB==,∵平行四边形DBEC是菱形,∴S 四边形DBEC =2S △BCD =S △ABC =12AB •BC =142´=.【变式4-1】(2021·山东济宁市)在Rt △ABC 中,∠BAC =90°,D 是BC 的中点,E 是AD 的中点,过点A 作AF ∥BC 交BE 的延长线于点F .(1)求证:△AEF ≌△DEB ;(2)证明四边形ADCF 是菱形.【答案】见解析.【解析】解:(1)∵AF ∥BC ,∴∠AFE =∠DBE ,∵E 是AD 的中点,∴AE =DE ,∵∠AEF =∠DEB ∴△AEF ≌△DEB ;(2)由(1)可知,AF =BD ,∵D 是BC 的中点,∴BD =CD ,∴AF =CD ,∵AF ∥CD ,∴四边形ADCF 是平行四边形,∵△ABC 为直角三角形,∴AD =CD ,∴四边形ADCF 是菱形.【例5】(2021·湖南娄底市)如图,已知平行四边形ABCD ,若M ,N 是BD 上两点,且BM =DN ,AC =2OM ,(1)求证:四边形 AMCN 是矩形;(2)△ABC 满足什么条件,四边形AMCN 是正方形,请说明理由.【答案】见解析.【解析】(1)证明:四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵BM=DN,∴OB-BM=OD-DN,即OM=ON,∴四边形AMCN是平行四边形,∴MN=2OM,∵AC=2OM,∴MN=AC,∴四边形AMCN是矩形;(2)当AB=BC时,四边形AMCN是正方形;∵AB=BC,四边形ABCD是平行四边形,∴四边形ABCD是菱形,∴AC⊥BD,∴AC⊥MN,由(1)可知四边形ABCD是矩形,∴四边形ABCD是正方形;【变式5-1】(2020·赣州市期中)如图,在Rt△ABC中,∠ACB=90°,过点C的直线m//AB,D为AB边上一点,过点D作DE⊥BC,交直线m于点E,垂足为点F,连接CD、BE.(1)求证:CE=AD;(2)当点D是AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)若点D是AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?【答案】见解析.【解析】(1)证明:∵直线m//AB,∴EC//AD.∵∠ACB=90°,∴BC⊥AC.又∵DE⊥BC,∴DE//AC.∵EC//AD,DE//AC,∴四边形ADEC是平行四边形,∴CE=AD.(2)当点D是AB中点时,四边形BECD是菱形.证明:∵D是AB中点,∴DB=DA,又∵直线m//AB,CE=AD,∴DB=CE,DB//CE,∴四边形BDCE是平行四边形,又∵DE⊥BC,∴四边形BECD是菱形,(3)当∠A的大小是45°时,四边形BECD是正方形.证明:∵D是AB中点,∴DB=DA,又∵直线m//AB,CE=AD,∴DB=CE,DB//CE,∴四边形BDCE是平行四边形,∵DE⊥BC,∴四边形BECD是菱形,∴BC 平分∠EBD ,∵∠A =45°,∴∠CBA =45°,∴∠EBD =90°,∴菱形BECD 是正方形.【变式5-2】(2020·四川广安市期末)如图,在ABC V 中,点O 是AC 边上的一个动点,过点O 作直线//BC MN ,设MN 交BCA Ð的角平分线于点E ,交BCA Ð的外角ACG Ð的平分线于点F ,连接AF .(1)求证:EO FO =;(2)当点O 运动到何处时,四边形AECF 是矩形?并证明你的结论.(3)在(2)的条件下,ABC V 满足什么条件时,四边形AECF 是正方形?并说明理由.【答案】见解析.【解析】(1)证明:∵MN ∥BC∴∠3=∠2.又∵CF 平分∠ACG ,∴∠1=∠2,∴∠1=∠3,∴OC =OF ,同理,OC =OE ,∴OE =OF .(2)解:当点O运动到AC的中点时,四边形AECF是矩形,证明如下:当点O运动到AC的中点时,OA=OC.又∵OE=OF,∴四边形AECF是平行四边形,由(1)可知,OC=OF,∴AC=EF,∴四边形AECF是矩形.(3)在(2)的条件下,∠ACB=90°时,四边形AECF是正方形.理由:由(2)知,当点O运动到AC的中点时,四边形AECF是矩形.∵MN∥BC,∴∠AOE=∠ACB,当∠ACB=90°时,∠AOE=90°,即AC⊥EF,∴四边形AECF是正方形.2.【特殊四边形性质应用】【例6】(2020·吉水县期末)如图,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长是_____.【解析】解:连接CH,∵四边形ABCD,四边形EFCG都是正方形,∴∠F=∠D=90°,∴△CFH与△CDH都是直角三角形,在Rt△CFH与Rt△CDH中,∵CF CD CH CH=ìí=î,∴△CFH≌△CDH(HL).∴∠DCH=12∠DCF=12(90°﹣30°)=30°.在Rt△CDH中,CD=3,∴DH..【变式6-1】(2021·重庆南开中学月考)如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF,8BD=,则菱形ABCD的周长为( )A.B.16C.D.32【答案】C.【解析】解:∵E,F分别是AB,BC边上的中点,EF=∴AC=2EF=∵四边形ABCD是菱形,BD=8,∴AC ⊥BD ,OA =12AC=,OB =12BD =4,∴AB,∴菱形ABCD的周长为:4=.故答案为:C .【变式6-2】(2021·四川成都市期中)如图,在等腰Rt △ABC 中,∠ACB =90°,AC =3,以斜边AB 为边向外作正方形ABDE ,连接CE ,则CE 的长为( )A .5BC .D【答案】C .【解析】解:过E 作EF ⊥AC ,交CA 的延长线于F ,∵四边形ABDE 为正方形,∴∠BAE =90°,AE =AB ,∵∠EAF +∠AEF =90°,∠EAF +∠BAC =90°,∴∠AEF =∠BAC ,在△AEF 和△BAC 中,F ACBAEF BAC AE ABÐ=ÐìïÐ=Ðíï=î,∴△AEF ≌△BAC (AAS ),∴EF =AC =AF =BC =3,在Rt △ECF 中,EF =3,FC =FA +AC =3+3=6,根据勾股定理得:CE =.故答案为:C .【例7】(2020·渠县期末)如图,在ABC V 中,90ABC Ð=°,BD 为AC 的中线,过点C 作CE BD ^于点E ,过点A 作BD 的平行线,交CE 的延长线于点F ,在AF 的延长线上截取FG BD =,连接BG ,DF .若13AG =,6CF =,则四边形BDFG 的周长为______.【答案】20.【解析】解:∵AG ∥BD ,BD =FG ,∴四边形BGFD 是平行四边形,∵CF ⊥BD ,∴CF ⊥AG ,又∵点D 是AC 中点,∴BD =DF =12AC ,∴四边形BGFD 是菱形,设GF =x ,则AF =13-x ,AC =2x ,在Rt △AFC 中,由勾股定理可得:36+(13-x )2=(2x )2,解得:x =5,即GF =5∴四边形BDFG 的周长=4GF =20.故答案为:20.【例8】(2021·沭阳县月考)如图,在四边形ABCD 中,AC =BD =6,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点,则EG 2+FH 2的值为( )A .9B .18C .36D .48【答案】C .【解析】解:连接EF 、FG 、GH 、EH ,设EG 和FH 交于点O ,∵E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点,∴EF ∥AC ,HG ∥AC ,EF =12AC ,FG =12BD ,∴EF ∥HG ,同理:EH ∥FG ,∴四边形EFGH 为平行四边形,∵AC =BD ,∴EF =FG ,∴平行四边形EFGH 为菱形,∴EG ⊥FH ,EG =2OG ,FH =2OH ,∴EG 2+FH 2=(2OE )2+(2OH )2=4(OE 2+OH 2)=4EH 2=4×(12BD )2=62=36;故答案为:C .【例9】(2020·四川广安市期末)如图,O 是菱形ABCD 的对角线,AC BD 的交点,E ,F 分别是,OA OC 的中点给出下列结论:①ADE EOD S S V V =;②四边形BFDE 也是菱形;③四边形ABCD 的面积大小等于EF BD ×;④ADE EDO Ð=Ð;⑤是轴对称图形.其中正确的结论有( )A .2个B .3个C .4个D .5个【答案】C .【解析】解:∵E 、F 分别是OA 、OC 的中点.∴AE =OE .∵S △ADE 12=´AE ×OD 12=´OE ×OD =S △EOD ∴S △ADE =S △EOD ①正确.∵四边形ABCD 是菱形,E ,F 分别是OA ,OC 的中点.∴EF ⊥OD ,OE =OF .∵OD =OB .∴四边形BFDE 是菱形.②正确∵菱形ABCD 的面积12=AC ×BD .∵E 、F 分别是OA 、OC 的中点.∴EF 12=AC .∴菱形ABCD 的面积=EF ×BD .③正确由已知可求得∠FDO =∠EDO ,而无法求得∠ADE =∠EDO .④不正确∵EF ⊥OD ,OE =OF ,OD =OD .∴△DEO ≌△DFO .∴△DEF 是轴对称图形.⑤正确∴正确的结论有四个,分别是①②③⑤,故答案为:C .【例10】(2020·浙江杭州月考)如图,菱形ABCD 的边长为4cm ,且60ABC °Ð=,E 是BC 中点,P 点在BD 上,则PE PC +的最小值为_______.【答案】【解析】解:在菱形ABCD 中,点A 、C 关于BD 对称,AB =BC ,连接AE ,与BD 的交点即为所求作的点P ,∵∠ABC = 60°,AB =BC ,∴△ABC 是等边三角形,∵AB =BC =4,点E 是BC 的中点,∴BE =2,∴AE ⊥BC ,∴AE =即PE +PC 的最小值为故答案为:【例11】(2020·广东惠州市期末)如图,在矩形ABCD 中,点O 为对角线AC 的中点,过点O 作EF AC ^交BC 于点E ,交AD 于点F ,连接AE ,CF .(1)求证:四边形AECF 是菱形;(2)连接OB ,若4AB =,5AF =,求OB 的长.【答案】见解析.【解析】证明:(1)∵O 是AC 的中点,且EF ⊥AC ,∴AF =CF ,AE =CE ,OA =OC ,∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠AFO =∠CEO ,在△AOF 和△COE 中,AFO CEO AOF COE OA OC Ð=ÐìïÐ=Ðíï=î,∴△AOF ≌△COE (AAS ),∴AF =CE ,∴AF =CF =CE =AE ,∴四边形AECF 是菱形;(2)如图,连接BO ,∵AB =4,AF =AE =EC =5,∴BE3==,∴BC =8,∴AC==,∵AO =CO ,∠ABC =90°,∴BO =12AC =【变式11-1】(2021·山东潍坊市期末)如图,在四边形ABCD 中,,E F 分别是,AD BC 的中点,,G H 分别是对角线,BD AC 的中点,依次连接,,,E G F H 连接,EF GH.(1)求证:四边形EGFH 是平行四边形;(2)当AB CD =时,EF 与GH 有怎样的位置关系?请说明理由;(3)若,20,70AB CD ABD BDC =Ð=°Ð=°,则GEF Ð= °.【答案】(1)(2)见解析;(3)25.【解析】证明:(1)∵E 、G 分别是AD 、BD 的中点,∴EG ∥AB ,AB =2EG同理可证:FH ∥AB ,AB =2HF∴EG ∥HF ,EG =HF∴四边形EGFH 是平行四边形;(2)GH ⊥EF ,理由:∵G 、F 分别是BD 、BC 的中点,∴FG =12CD ,由(1)知GE =12AB ,又∵AB =CD ,∴GE =GF又四边形EGFH 是平行四边形,∴四边形EGFH 是菱形,∴GH ⊥EF ;(3)由题意,EG ∥AB ,HF ∥AB ,GE =12AB ∴EG ∥HF ,同理,EH ∥FG ,GF =12CD ∴四边形EGFH 是平行四边形,∵AB =CD ,∴GE =GF ,∴四边形EGFH 是菱形,∵∠ABD =20°,∠BDC =70°,EG ∥AB ,GF ∥CD ,∴∠EGD =∠ABD =20°,∠BGF =∠BDC =70°,∴∠DGF =180°-∠BGF =110°,∴∠EGF =∠EGD +∠DGF =20°+110°=130°,∴∠GEH =180°-∠EGF =50º,∵FE 平分∠GEH ,∴∠GEF =12∠GEH =25°.故答案为:25.【例12】(2020·河南郑州月考)如图,在平行四边形ABCD 中,AE 是BC 边上的高,将ABE △沿BC 方向平移,使点E 与点C 重合,得GFC V .(1)求证:BE DG =;(2)若60B Ð=°,当BC =______AB 时,四边形ABFG 是菱形;(3)若60B Ð=°,当BC =______AB 时,四边形AECG 是正方形.【答案】(1)见解析;(2)32;(3.【解析】(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,AB =CD .∵AE ⊥BC ,∴CG ⊥AD ,AE =CG ,∴∠AEB =∠CGD =90°.在Rt △ABE 与Rt △CDG 中,AE CG AB CD =ìí=î,∴Rt △ABE ≌Rt △CDG (HL ),∴BE =DG .(2)当BC =32AB 时,四边形ABFG 是菱形.证明:∵AB ∥GF ,AG ∥BF ,∴四边形ABFG 是平行四边形.∵Rt△ABE中,∠B=60°,∴∠BAE=30°,∴BE=12 AB,∵BE=CF,BC=32 AB,∴EF=12 AB.∴AB=BF.∴四边形ABFG是菱形.故答案是:32;(3)BC AB时,四边形AECG是正方形.∵AE⊥BC,GC⊥CB,∴AE∥GC,∠AEC=90°,∵AG∥CE,∴四边形AECG是矩形,当AE=EC时,矩形AECG是正方形,∵∠B=60°,∴EC=AE,BE=12 AB,∴BC AB..【变式12-1】(2020·渠县月考)如图所示,O为ABCV的边AC上一动点,过点O的直//MN BC,设MN分别交ACBÐ的平分线及其外角平分线于点,E F.=(1)求证:OE OF(2)当点O在何处时,四边形AECF是矩形?V中添加条件,使四边形AECF变为正方形,并说明你(3)在(2)的条件下,请在ABC的理由.【答案】见解析.【解析】(1)证明:∵MN∥BC,∴∠OEC=∠BCE,∵CE平分∠ACB,∴∠BCE=∠OCE,∴∠OEC=∠OCE,∴EO=CO,同理:FO=CO,∴EO=FO;(2)解:当点O运动到AC的中点时,四边形CEAF是矩形;理由如下:由(1)得:EO=FO,又∵O是AC的中点,∴AO=CO,∴四边形CEAF是平行四边形,∵EO=FO=CO,∴EO=FO=AO=CO,∴EF=AC,∴四边形CEAF是矩形;(3)解:当点O运动到AC的中点时,且∠ACB为直角时,四边形AECF是正方形.理由如下:∵当点O运动到AC的中点时,四边形AECF是矩形,∵MN∥BC∠ACB=90°,∴∠AOE=∠ACB=90°,∴AC⊥EF,∴四边形AECF是正方形.【例13】(2021·广东深圳期末)如图,在直角坐标系中,四边形OABC是矩形,OA=8,OC=6,点D是对角线AC的中点,过点D的直线分别交OA、BC边于点E、F.(1)求证:四边形EAFC是平行四边形;(2)当CE=CF时,求EF的长;(3)在条件(2)的情况下,P为x轴上一点,当以E,F,P为顶点的三角形为等腰三角形时,请求出点P的坐标.【答案】(1)见解析;(2)152;(3)点P的坐标为(8,0)或(374,0)或(﹣234,0)或(434,0).【解析】(1)证明:∵四边形OABC是矩形,∴BC∥OA,∴∠FCD=∠DAE,∠CFD=∠AED,∵D是AC的中点,∴CD=AD,∴△CDF≌△ADE,∴DF=DE,∴四边形EAFC是平行四边形;(2)解:∵四边形EAFC是平行四边形,CE=CF,∴四边形EAFC是菱形,∴CE=EA,AC⊥EF,设CE=AE=x,∵OC2+OE2=CE2,∴62+(8﹣x)2=x2,∴x=25 4,∴CE=25 4,∵OA=8,OC=6,∴AC=10,∴CD=12AC=5,∴ED=15 4,∴EF=2ED=15 2;(3)由(2)可知,AE=CE=254,OE=74,①若PE=PF,点P与点A重合,∴P(8,0),②若EF=EP=15 2,当点P在x轴的正半轴上,OP=OE+PE=71542+=374,∴P(374,0),当点P在x轴的负半轴上,OP=PE﹣OE=15724-=234,∴P(﹣234,0),③若EF=FP,过点F作FG⊥AE于点G,则EG=CF﹣OE=254﹣74=92,∴EP=9,∴OP=OE+EP=74+9=434,∴P(434,0).综上可得,点P 的坐标为(8,0)或(374,0)或(﹣234,0)或(434,0).【变式13-1】(2021·广东佛山期末)如图,在Rt ABC △中,90C Ð=°,10AC =,60A Ð=°.点P 从点B 出发沿BA 方向以每秒2个单位长度的速度向点A 匀速运动,同时点Q 从点A 出发沿AC 方向以每秒1个单位长度的速度向点C 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点P 、Q 运动的时间是t 秒.过点P 作PM BC ^于点M ,连接PQ 、QM .(1)请用含有t 的式子填空:AQ =______,AP =______,PM =______;(2)是否存在某一时刻使四边形AQMP 为菱形?如果存在,求出相应的t 值;如果不存在,说明理由;(3)当t 为何值时,PQM V 为直角三角形?请说明理由.(备用图)【答案】见解析.【解析】解:(1)由题意知,AQ =t ,∵∠C =90°,AC =10,∠A =60°,∴∠B =30°,∴AB =2AC =20,∴AP =AB -BP =20-2t ,∵PM⊥BC,∴∠PMB=90°,∴PM=12PB=t.故答案为:AQ=t,AP=20-2t,PM=t.(2)存在,理由如下:由(1)知,AQ=PM ∵AC⊥BC,PM⊥CB∴AQ∥PM∴四边形AQMP是平行四边形.当AP=AQ时,四边形AQMP是菱形即20-2t=t,解得:t=20 3.故当t=203时四边形AQMP为菱形.(3)①当∠MPQ=90°时,此时四边形CMPQ为矩形在Rt△APQ中,∠A=60°,∠APQ=30°∴AP=2AQ,即20-2t=2t,解得:t=5②当∠MQP=90°时,同理,AQ=2AP,即t=2(20-2t),解得:t=8③当∠PMQ=90°时,此种情况不存在.综上所述,t=5或t=8时,△PQM为直角三角形.【变式13-2】(2020·江苏泰州市月考)对于平面直角坐标系xOy中的线段MN及点Q,给出如下定义:若点Q满足QM=QN,则称点Q为线段MN的“中垂点”;当QM=QN=MN 时,称点Q为线段MN的“完美中垂点”.(1)如图1,A(4,0),在Q1(0,4)、Q2(2,-4)、Q3(1)中,可以是线段OA的中垂点是;(2)如图2,点A为x轴上一点,若点Q(2,为线段OA的“完美中垂点”,请求出线段OQ的“完美中垂点”的坐标;(3)若点A为x轴正半轴上一点,点Q为线段OA的“完美中垂点”,点P(0,m)在y轴上,在线段PA上方画出线段AP的“完美中垂点”M,请问∠MQA的度数是否是一个定值?若是,请求出这个定值;若不是,请说明理由.【答案】(1)(2,-4);(2)(4,0)或(-2,);(3)∠MQA =90°,见解析.【解析】解:(1)根据“中垂点”的定义得:QM=QN,∴点Q在线段OA的垂直平分线上,∵O(0,0),A(4,0),∴线段OA的垂直平分线是:x=2,在Q1(0,4)、Q2(2,-4)、Q3(1)中,只有Q2(2,-4)符合题意,∴可以是线段OA的中垂点是Q2(2,-4),故答案为:Q2(2,-4);(2) ∵Q(2,),∴OQ=4,∵点Q(2,为线段OA的“完美中垂点”,∴OA=QA=OQ=4,即A(4,0)为线段OQ的“完美中垂点”,设线段OQ的另外一个“完美中垂点”为D,如图所示:则OD=QD=OA=QA=OQ=4,∴四边形AODQ为菱形,∴DQ∥OA,∴D (-2,),∴线段 OQ 的“完美中垂点”的坐标为(4,0)或(-2,);(3) ∠MQA 的度数是一个定值,∠MQA =90°,理由如下:如图所示,点M 为线段 AP 的“完美中垂点”,∵点Q 为线段 OA 的“完美中垂点”,∴PA =PM =AM ,OA =QA =OQ ,∴△OAQ 和△PAM 为等边三角形,∴∠OAQ =∠PAM =60°,∴∠OAP =∠QAM ,在△OAP 和△QAM 中,OA QA OAP QAM PA AM =ìïÐ=Ðíï=î,∴△OAP ≌△QAM (SAS ),∴∠MQA =∠POA =90°.【变式13-3】(2020·株洲市期中)如图所示,在四边形ABCD 中,AD ∥BC ,∠B =90°,AD =24cm ,BC =26cm 动点P 从点A 出发沿AD 方向向点D 以1cm /s 的速度运动,动点Q 从点C 出发沿着CB 方向向点B 以3cm /s 的速度运动.点P ,Q 分别从点A 和点C 同时出发,当其中一点到达端点时,另一点随之停止运动.。
浙教版第4章 平行四边形复习
B
C、18cm
D、24cm B
E C
D
例1、如图,在平行四边形ABCD中,已知两条对 角线相交于点O,E,F,G,H分别是AO,BO,CO,DO 的中点,以图中的点为顶点,尽可能多地画出平 行四边形。
A F. B
E .
O G.
.H
C
D
例2、如图,O为平行四边形ABCD对角线AC中 点,EF经过点O交AD于点E,交BC于点F,连结 BF,DF (1)△ABC与△DCF能全等吗?请说明理由。 (2)四边形BEDF是平行四边形吗?你能说出几 种不同的理由来?
• 四边形的内角和等于 3600 , 外角和等于 。 3600 0 (n-2) × 180 • n多边形的内角和为 , 0 360 外角和为 。
四边形的定义&平行四边形的定义
四边形的定义:在平面内,由不在同一条直线上 的四条线段首尾顺次相接而成的图形叫四边形
平行四边形:两组对边分别平行的四边形
1. 2. 3. 4. 5. 6. 7. 8. 9.
(7)如图,□ABCD中,EF//BC,GH//AB,EF, GH的交点P在BD上,图中面积相等的四边形 A G D 有_________对
E
B
P
H C
(8)如图,□ABCD中,AE⊥BC,AF⊥CD, E,F为垂足,已知AB=5cm,BE=3cm,AE=4cm, AF=8cm,则□ABCD周长为____cm,面积为 A _____cm D
边的角度
角的角度 对角线的角度
A
o
3、平行四边形的特征:
B C
D
(1)∵四边形ABCD是平行四边形 ∴ AD// BC,AB// DC
边的角度
角的角度 (2)∵四边形ABCD是平行四边形 ∴∠ BAD=∠DCB,∠ABC=∠ADC (3)∵四边形ABCD是平行四边形 ∴OA=OC,OB=OD 对角线的角度
八年级数学下册 第五章 特殊平行四边形 5.2 菱形(第1课时)课件 (新版)浙教版.ppt
边 对边平行且相等
对边平行 四条边都相等
对角线 对角线互相平分
对角线互相垂直平分,并且每 条对角线平分一组对角.
2、菱形是特殊的平行四边形,那么它和平行四 边 有形改相变比?特殊在哪里?A哪些性质改变了,哪些性质没
B
OD
1、四个角是直角; 2、对角线相等。
1、四条边相等; 2、对角线互相垂直, 并且每条对角线平分 一组对角。
观察以下由火柴棒摆成的图形:
议一议:(1)三个图形都是平行四边形吗? (2)与图1相比,图2与图3有什么共同特点?
理解 定义 有一一组组邻邻边边相相等等的的平平行行四四边边形形叫做菱形.
一组邻边相等的平行四边形叫做菱形.
1、平行四边形有哪些性质? 元素 平行四边形的性质
菱形的性质
内角 对角相等,邻角互补 对角相等,邻角互补
思考:菱形ABCD,对角线AC、BD相交于点O,图中
①有哪些特殊的三角形?
D
多少个直角三角形,多少个等腰
三角形?
A
4个直角三角形, 4个等腰三角形
O B
请你添加一个条件,使得△ADB是等边三角形.
AB=BD ∠DAB=60°
②有多少对全等三角形?
∠ADC=120°……
△ADC≌△ABC, △ABD≌△CBD, △ABO≌△CBO ≌△CDO ≌△ADO
8对
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
特殊性质
1、四个角都是直角; 2、矩形的对角线相等; 3、既是中心对称图形,又是轴 对称图形。
1、 四个角都是直角,四条边相 1、 四条边都相等; 等; 2、 对角线互相垂直, 并且 2、 对角线相等,并且互相垂直 每条对角线平分一组对角。 平分,每条对角线平分一组对 3、 既是中心对称图形, 又 角。 是轴对称图形。 3、 既是中心对称图形,又是轴 对称图形。
学业有所建树的学生,都是在努力做好一个题,背好一个知识点的过程中,逐渐累积和锻炼的结果
平பைடு நூலகம்四边形及特殊的平行四边形知识点
类 类 别 型
平行四边形
矩形
菱形
正方形
一般性质
1、边:对边平行,对边相等。 2、角: (1)对角相等,邻角互补; (2)内角和均为 360°,外角和均为 360°。 3、对角线:对角线互相平分。 4、对称性:都是中心对称图形,对称中心为对角线的交点。
1、 一组邻边相等,一个角为直 角的平行四边形; 2、 有一组邻边相等的矩形; 3、 有一个角为直角的菱形。
学业有所建树的学生,都是在努力做好一个题,背好一个知识点的过程中,逐渐累积和锻炼的结果
平行四边形和特殊平行四边形的关系图
图形判定
1、 两组对边分别平行的四 边形; 2、 一组对边平行且相等的 四边形; 3、 对角线互相平分的四边 形。
1、 有一个角是直角的平行四边 形; 2、 有三个角是直角的四边形; 3、 对角线相等的平行四边形。
1、 一组邻边相等的平行 四边形; 2、 四条边相等的四边形; 3、 对角线互相垂直的平 行四边形。
