实验 三 用凯泽窗设计线性相位带通FIR滤波器(中国地质大学北京)
编程实现任意确定信号的频谱分析算法

广西科技大学学生姓名:指导教师:目录摘要 (3)一、设计内容 (3)4779212133353636摘要:随着计算机和信息科学的飞速发展,信号处理逐渐发展成为一门独立的学科,成为信息科学的重要组成部分,在语音处理、雷达、图像处理、通信、生物医学工程等众多领域中得到广泛应应用。
Matlab语言是一种广泛应用于工程计算及数值分析领域的新型高级语言,Matlab功能强大、简单易学、编程效率高,深受广大科技设(1)对给定的CEG和弦音音频文件取合适长度的采样记录点,然后进行频谱分析(信号的时域及幅频特性曲线要画出)。
(2)分析CEG和弦音频谱特点,对该信号频谱能量相对较为集中的频带(分低、中、高频)实现滤波(分别使用低通,带通及高通),显示滤波后信号的时域和频域曲线,并对滤波后的信号与原信号的音频进行声音回放比较。
(3)在低、中、高三个频带中,各滤出三个能量最集中的频簇,显示滤波后信号的时域和频域曲线。
(4)任意选择几个滤出的频带(或频簇)进行时域信号重建(合成),与原信号的音频进行声音回放比较。
.线性相位FIR滤波器通常采用窗函数法设计。
窗函数法设计FIR 滤波器的基本思想是:根据给定的滤波器技术指标,选择滤波器长度N和窗函数ω(n),使其具有最窄宽度的主瓣和最小的旁瓣。
其核心是从给定的频率特性,通过加窗确定有限长单位脉冲响应序列h(n)。
工程中常用的窗函数共有6种,即矩形窗、巴特利特(Bartlett)窗、汉宁(Hanning)窗、汉明(Hamming)窗、布莱克曼(Blackman)窗和凯塞(Kaiser)。
FIR数字滤波器的设计原理:采用窗口法线性相位实系数FIR滤波器按其N值奇偶和h(n)的奇偶对称性分为四种:1、h(n)为偶对称,N为奇数H(ejω)的幅值关于ω=0,π,2π成偶对称。
2、h(n)为偶对称,N为偶数H(ejω)的幅值关于ω=π成奇对称,不适合作高通。
3、h(n)为奇对称,N为奇数H(ejω)的幅值关于ω=0,π,2π成奇对称,不适合作高通和低通。
标准摘要样本

摘要此文根据FIR滤波器的原理。
运用MATLAB进行窗函数设计。
FIR滤波器是一种被广泛用于基本的数字信号处理部件,针对常用的软件、硬件方法设计实现FIR滤波器存在的问题,提出采用MATLAB的窗函数方法设计并在FPGA上高速并行实现严格的线性相位FIR滤波器方案,它可以方便地调熬滤波器的阶数和系数,适用于不同的场合。
本文主要讨论FIR滤波器的功能,并且利用MATLAB软件实现窗函数的多级FIR滤波器设计,设计出滤波器的相关参数。
其中,滤波器设计是信号处理的核心问题,MATLAB软件在多个研究领域有着广泛的应用。
本文介绍了基于MATLAB环境下,用窗函数设计法实现FIR滤波器的设计,以及其与以前常用的设计方法的区别,并给出了设计实例。
关键词:窗函数;FIR滤波器;MATLAB;AbstractIn this paper, based on the principle of FIR filter. The use of MATLAB for the design of window function. FIR filter is a widely used basic digital signal processing part, aiming at the design ofcommonly used software, and hardware implementation method of FIR filter problems, proposed to use the window function design method of MATLAB and FPGA on the high-speed parallel implementation of strict linear phase FIR filter scheme, order and coefficient which can be conveniently adjustable boil filter, suitable for different occasions. This paper mainly discusses the FIR filter function, and the design and implementation of multilevel FIR filter window functionby using MATLAB software, design related parameter filter. Among them, the filter design is the core problem in signal processing, MATLAB software is widely used in many research fields. This paper introduces the MATLAB based environment, the design and implementation of FIR filterwith window function design method, and the difference with the previous common design method,and gives a design example.Key Words:Window function; FIR filter; MATLAB;引言随着信息和数字技术的发展,数字信号已经成为当今极其重要的学科和技术领域之一。
MATLAB窗函数

4.3 实验原理 数字滤波器的设计是数字信号处理中的一个重要内容。
数字滤波器设计包括FIR(有限单位脉冲响应)滤波器与IIR(无限单位脉冲响应)滤波器两种。
与IIR滤波器相比,FIR滤波器在保证幅度特性满足技术要求的同时,很容易做到严格的线性相位特性。
设FIR滤波器单位脉冲响应h(n)长度为N,其系统函数H(z)为: H(z)是z-1的N-1次多项式,它在z平面上有N-1个零点,原点z=0是N-1阶重极点,因此H(z)是永远稳定的。
稳定和线性相位特性是FIR滤波器突出的优点。
FIR滤波器的设计任务是选择有限长度的h(n)。
使传输函数H( )满足技术要求。
FIR滤波器的设计方法有多种,如窗函数法、频率采样法及其它各种优化设计方法,本实验介绍窗函数法的FIR滤波器设计。
窗函数法是使用矩形窗、三角窗、巴特利特窗、汉明窗、汉宁窗和布莱克曼窗等设计出标准响应的高通、低通、带通和带阻FIR滤波器。
一、firl函数的使用 在MA TLAB 下设计标准响应FIR滤波器可使用firl函数。
firl函数以经典方法实现加窗线性相位FIR滤波器设计,它可以设计出标准的低通、带通、高通和带阻滤波器。
firl函数的用法为: b=firl(n,Wn,/ftype/,Window) 各个参数的含义如下: b—滤波器系数。
对于一个n阶的FIR滤波器,其n+1个滤波器系数可表示为:b(z)=b(1)+b(2)z-1+…+b(n+1)z-n。
n—滤波器阶数。
Wn—截止频率,0≤Wn≤1,Wn=1对应于采样频率的一半。
当设计带通和带阻滤波器时,Wn=[W1 W2],W1≤ω≤W2。
ftype—当指定ftype时,可设计高通和带阻滤波器。
Ftype=high时,设计高通FIR滤波器;ftype=stop时设计带阻FIR滤波器。
低通和带通FIR滤波器无需输入ftype参数。
Window—窗函数。
窗函数的长度应等于FIR滤波器系数个数,即阶数n+1。
数字信号处理课后习题答案
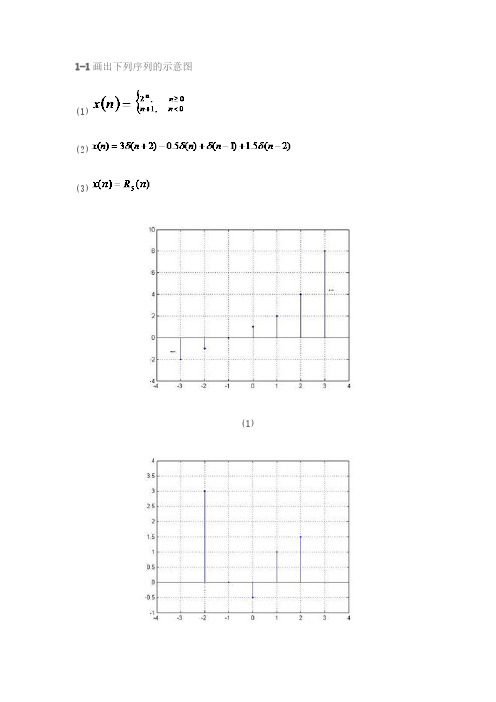
(修正:此题有错,
(3)系统的单位脉冲响应 而改变,是两个复序列信号之和)
(4)
(修正: 随上小题答案
(修正:此图错误,乘系数应该为 0.5,输出端 y(n)应该在两个延迟器 D 之间)
1-25 线性移不变离散时间系统的差分方程为
(1)求系统函数 ; (2)画出系统的一种模拟框图; (3)求使系统稳定的 A 的取值范围。 解:(1)
(2)
(3)
解:(1)
(2)
(3)
1-7 若采样信号 m(t)的采样频率 fs=1500Hz,下列信号经 m(t)采样后哪些信号不 失真? (1) (2) (3) 解:
(1)
采样不失真
(2)
采样不失真
(3)
,
采样失真
1-8 已知
,采样信号 的采样周期为 。
(1) 的截止模拟角频率 是多少?
(2)将 进行 A/D 采样后, 如何?
(3)最小阻带衰减 5-4
由分式(5.39)根据 A 计算 ,如下: 由表 5.1 根据过度带宽度 计算窗口:
单位脉冲响应如下:
单位脉冲响应如下:
其中 为凯泽窗。 5-5 答:减小窗口的长度 N,则滤波器的过度带增加,但最小阻带衰减保持不变。 5-6:图 5.30 中的滤波器包括了三类理想滤波器,包括了低通,带通和高通,其响应的单位
(1)
,
(2)
1-18 若当 时
;时
(1)
,其中
(2) 证明:
,收敛域
,其中 N 为整数。试证明: ,
(1) 令 其中
,则 ,
(2)
,
1-19 一系统的系统方程及初时条件分别如下: ,
(1)试求零输入响应 ,零状态响应 ,全响应 ; (2)画出系统的模拟框图 解: (1)零输入响应
第4章5-7 数字滤波器的原理和设计方法

为了减小波纹幅度,一方面可以加大窗的长度N,但效果并不 显著;另一方面可采用不同的窗函数来改善不均匀收敛性。图 4.50所示的是几种常用的窗函数:
它们的定义式和频谱函数分述如下: 1、矩形窗
2、Bartlett窗(三角形窗)
3、汉宁(Hanning)窗(升余弦窗)
或
ห้องสมุดไป่ตู้
利用傅里叶变换的调制特性,即利用 和
图4.53所示的是用这5种窗函数设计的低通FIR数字滤波器的频 率响应特性。窗函数的长度N=51,理想低通滤波器的截止频 ωc=π/2。 从图中可看出,用矩形窗设计的滤波器的过渡带最窄,但阻带 衰减指标最差,仅有-21dB左右。而用布莱克曼窗设计的阻带衰 减指标最好,可达-74dB,但过渡带最宽,约为矩形窗的3倍。
对比等式两边,有
如果把变量代换的有理函数F(z-1)看成是一个系统函数,那么该系 统的幅频特性曲线在任何ω处恒为1,这样的函数就是全通函数。 任何全通函数都可表示为
其中αk是F(z-1)的极点。为了满足稳定性的要求,必须有|αk|<1。这 样,通过选择适当的N值和αk值,可以得出各种各样的映射。
1)低通→低通的z平面变换
这里用v-1是因为系统函数的标准形 式,一般写成z-1的形式,换到v平面 即是v-1。
频率变换中的变量代换公式必须满足下列条件: (1)F(z-1)必须是z-1的有理函数; (2)v平面的单位圆内部映射到z平面的单位圆内部。
从这些条件出发,我们可推导出频率变换的实用公式。 设v平面单位圆是v=ejθ,z平面单位圆是z=ejω,则
其中 矩形窗ωR(n)的频谱的图形如下 图所示。
ω从-2π/N到-2π/N之间的WR(ω)称 为窗函数的主瓣,主瓣两侧呈衰 减振荡的部分称为旁瓣。
数字信号处理期末考题

(c)对Y[m]做8点IDFT得y[k]。
3.X=fft(x,8);
H=fft(y,8);
y=real(ifft(X.*H));
四、
(1) ,
(2)Tmax=1/8秒。
(3)
五、
1. 。
2.加窗,分段求平均。
六、周期序列:无误差。
非周期序列:泄漏误差,加非矩形窗;栅栏效应,补零;谱分辨率,增加所取序列长度。
2.平滑周期图和平均周期图改善了周期图的方差性能,但却降低了谱分辨率和增大了偏差。
3.可能使短序列的功率谱估计出现错误的结果。
现代功率谱估计的基本思想:根据所研究信号的先验知识,对观测数据以外的数据作出某种比较合理的假设,以达到提高谱估计质量的目的。
六、
(1)类型:Ⅰ型或Ⅱ型
(2)采用Ⅰ型时,M=8
(3)用MATLAB函数fftshift对DFT的结果X[m]进行重新排序,试确定重新排序后的序列中,m=300点和m=1200点所对应的连续信号频谱X(j)中的频率点。
八、已知某因果稳定离散LTI系统的系统函数为
(1)试画出系统 的零极点分布图,确定系统的收敛域;
(2)试判断该系统是IIR系统还是FIR系统,求出系统的单位脉冲响应h[k];
(4)画出(3)中数字滤波器的直接型结构图。
六、利用矩形窗函数法设计一个线性相位FIR数字低通滤波器,使其逼近截频为C=rad的理想低通数字滤波器。
(1)确定可选用的线性相位FIR系统的类型(I,II,III,IV);
(2)若FIR数字滤波器的阶数M=8,试求h[k]的表达式;
(3)画出该滤波器的线性相位直接型结构图,不带h[k]的具体值。
2.简述x(t), ,x[k]和 四类信号频谱的特点,及它们之间的对应关系。
FIR
基于MATLAB的FIR数字低通滤波器的实现1 MATLAB编程基础MATLAB是一种科学计算软件,主要使用与矩阵运算及控制和信息处理领域的分析设计。
它使用方便,输入简捷,运算高效,内容丰富,并且很容易由用户自行扩展。
因此,当前已成为美国和其它发达国家中大学教学和科学研究中最常用而必不可少的工具。
MATLAB是由美国Mathwork公司于1986年推出的,到1992年已推出了4.x版本,目前已升级到7.1版本。
随着版本的升级,内容不断扩展,人机界面更加生动易学,并且有使用于各种工作站和微机的版本出现。
另一方面,版本的升级对使用环境也提出了更高的要求。
MATLAB是Matrix Laboratory的缩写,它是一种进行科学和工程计算的交互式程序语言,与其它计算机语言相比,其特点是灵活性和智能化,适应科技专业人员的思维方式,使得编程效率大大提高。
例如,它的基本数据单元是矩阵,而进行赋值和运算时却无需指定矩阵的维数,程序会自动对维数进行判别和分配;又如在进行时域和频域仿真和结果显示时,一般也无需给出时间和频率取样点及纵横坐标,MATLAB会自动选择工程人员最关心的曲线区间。
以适当的比例尺充分显示出它的形状,这使得人们用MATLAB进行仿真和设计的效率可高过手工方式百倍,比用一般算法语言编程高出数倍。
随着 MATLAB的不断完善,尤其是MATLAB的信号处理工具箱的推出,如今MATLAB已经成为数字信号处理(digital signal processing)应用中分析和仿真设计的主要工具。
MATLAB提供了丰富的函数,其中firl函数实现了加窗线性相位FIR滤波器设计的经典方法,firl主要用于常用的标准通带滤波器设计,包括低通、带通、高通和带阻数字滤波器。
除此之外,MATLAB还提供了多带 FIR滤波器的设计函数 fir2、Hilbe变换器及其它具有奇对称系数的滤波器设计函数firl和remez等[36]。
数字信号处理实验报告_2_
实验四
实验目的
FIR 数字滤波器的设计
1. 掌握 FIR 数字滤波器的设计方法与步骤; 2. 理解系统频率响应的概念,学习编写计算系统频率响应的方法。
实验原理
1. FIR 数字滤波器设计的详细内容见教材第 4 章。 窗口法:窗口法设计 FIR 数字滤波器的步骤: A 给出希望的滤波器频率响应函数 H d (e j ) ; B 根据允许的过渡带宽度及阻带衰减确定所采用的窗函数和 N 值; C 做 H d (e
0.6 0.4 0.2 0 -0.2
|H(ejw )| h(n)
) 曲线。
0.6 0.4 0.2 0 -0.2
|H(ejw )| h(n)
1.5
1
0.5
0
5 n
10
15
0
0
0.2
0.4 f
0.6
0.8
1.5
1
0.5
0
5 n
10
15
0
0
0.2
0.4 f
0.6
0.8
grid; f=0:0.5/M:0.5-0.5/M; M1=M/4; for k=1:M1 hd(k)=1; hd(k+M1)=0; hd(k+2*M1)=0; hd(k+3*M1)=0; end subplot(222) plot(f,abs(h1),'b-',f,hd,'-'); xlabel('f');ylabel('|H(e^{jw})|'); grid; 2 给定一理想低通 FIR 滤波器的频率特性
e j , 0 c H d (e j ) c 0,
要求其最小阻带衰减为-45dB,过渡带宽为 8 / 51 , (1) 已知 c 0.5 ,求出 h(n) 并画出 20 lg H (e
FIR数字滤波器设计及MATLAB实现
l 2 9
FR 字 滤 波 器 设 计 及 MA L 实现 I数 T AB
冯 冠超 ( 哈尔滨工业大学 ( 威海 ) 山东威海
24 0) 6 2 9
摘 要 :主要 研 究在 MA IBt境 T FR ̄ 字滤 波 器的 典 型设计 方 法 ,应 用MA L B 号 处理 工 具箱及 其 扩展 函数 ,使 得如 TA  ̄ . IA c TA信 何在 数 字信 号 处理过 程 中较 复杂 的数 字 滤波 器设计 问题 得 以解 决 。
gr i d
1 引 言 .
数字 信 号 处理 是在 2 世 纪6 年 代 ,用 数字 的数 值 计 算 方法 0 O 对 信号 进 行 处 理 ,以达 到 提 取 有 用信 息 便 于应 用 的 目的 , 目前 数 字信号 处理 技术 已广 泛 应用 于 多个领 域 数 字 滤 波器 根 据 其 单 位 冲激 响应 函数 的 时域 特 性 可 分 为两 类 :无 限冲激 响 应 l 滤波 器和 有 限 冲激 响 应 FR 波器 。 F R l R I滤 I 滤 波器 最 重要 的 优点 就是 由于 不存 在 系统 极点 ,FR 波器 是绝 对 I滤 稳 定 的系 统 。MA L B为数 字 滤 波 的研 究 提供 了一 个直 观 、高 TA 效 、便 捷 的 利器 。 它 以矩 阵 运算 为基 础 ,把 计 算 、 可视 化 、程 序 设计融 合到 一 个交互 式 的工 作环 境 中。
参 考文 献 [13 14 晓晨, 李涛, 刘路 . MATL B3 箱应 用指 南[ .电子工业 出 A - M】
版 社 .0 0 20 .
3 窗函数 设 计的基 本 思想 .
窗 函数 法 设 计 的基 本 思 想 是 把给 定 的频 率 响应 通 过 离 散傅 里 叶逆 变换 ,求 得 脉 冲 响应 ,然 后利 用 加 窗 函 数对 它进 行 截 断 和 平 滑 ,以 实现 一 个物理 可 实 现且 具 有线 性相 位 的 FR I 滤波 器 的 设 计 目的。 其 核 心 是从 给 定 的 频 率特 性 ,通 过 加窗 确 定 有 限 长 单 位脉 冲 Ⅱ 应序  ̄ h n ,过 程 如下 : 向 J ()
FIR设计
第1章 FIR 滤波器的原理与技术FIR 滤波器是数字滤波器的一种。
数字滤波器是用于修正或改变时域或频域中信号的属性。
常见的是数字滤波器是线性时间不变(LineTime-Invariant,LTI)滤波器。
2.1 FIR 滤波器的特点FIR 滤波器有有限个采样值组成,将卷积的数量降低到每个采样时刻为有限个。
FIR 滤波器相对于IIR 滤波器的优点与不足如下:优点:(1) 有严格的相位又具有任意的幅度;(2) IIR 滤波器的单位抽样响应是有限长的,因而滤波器性能稳定;(3) FIR 滤波器由于单位冲击响应是有限长的,因而可用快速傅立叶变换(FFT )算法来实现过滤信号,可大大提高运算效率。
不足:(1) FIR 系统的系数长度比较大,即设计一个符合要求的滤波器,FIR 系统需要较多的乘法器。
(2)此系统的输出延迟时间长。
2.2线性相位FIR 数字滤波器的条件和特点本节中主要介绍FIR 滤波器具有的线性相位的条件及滤波其器的特点以及其网络结构和特性。
2.2.1 线性相位条件对于长度为N 的h(n),传输函数为1()()N j j n n H e h n e ωω--==∑ 式(2-1)()()()j j g H e H e ωθωω-= 式(2-2)式中,H g (ω)称为幅度特性,θ(ω)称为相位特性。
注意,这里H g (ω)不同于 |H(e j ω)|,H g (ω)为ω的实函数,可能取负值,而|H(e j ω)|总是正值。
H(e j ω)线性相位是指θ(ω)是ω的线性函数,即θ(ω)=τω, τ为常数 如果θ(ω)满足下式:θ(ω)=θ0-τω, θ0是起始相位严格地说,此时θ(ω)不具有线性相位,但以上两种情况都满足群时延是一个常数,即式(2-3)也称这种情况为线性相位。
2.2.2 线性相位型 FIR 滤波器的特点按结构划分,FIR 滤波器有四种类型:直接型、级联型、线性相位型和频率采样型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验 三 用凯泽窗设计线性相位带通FIR 滤波器
实验目的:
基于MATLAB 环境,熟悉利用窗函数法设计线性相位FIR 滤波器的原理和方法。
实验环境:
硬件环境:计算机,软件环境:MATLAB 平台。
实验原理:
凯泽窗是对于给定的阻带衰减,使主瓣具有最大能量意义下的最佳窗函数,因此具有最陡的过渡带。
窗函数的形式为
10 )
(] )121(1 [)(02
0-≤≤--
-=
N n I N n I n w k ,ββ 其中β为形状参数,I 0[x ]是第一类修正零阶贝塞尔函数,其幂函数展开式为
∑∞
=+=120])2
(!1[1][k k x
k x I
若给定滤波器的过渡带宽度∆ω (rad)和阻带衰减A s (dB),则滤波器的长度和形状参数β 可由下列经验公式给出:
ω
Δ286.295
.7-≈
s A N
⎪⎩
⎪
⎨⎧≤≤≤-+-≥-=dB 210dB 5021)21(07886.0)21(5842.0dB 50)7.8(1102.04.0s s s s s s A A A A A A β,,,
设计流程图
实验内容要求:
1. 编写计算凯泽窗函数w k (n )的M 函数文件kaiser_WF.m ,各变量定义如下: function wk= kaiser_WF(N, beta)
% N ---凯泽窗序列的长度 % beta---凯泽窗参数 % wk ---凯泽窗序列
计算贝塞尔函数的参考程序bessel_IM.m 如下:
function s=bessel_IM (x) eps= 10^(-12); k=1; s=1; D= 1; while D>(eps*s) T= x/(2*k); D= D *T^2; s= s+D;
k= k+l;
end
所用的公式为 ∑∞
=+
=1
20])2(!1[1][k k x k x I
2. 编写计算理想低通滤波器单位抽样响应h d (n )的M 函数文件ideal_LP_FIR .m ,各变量定义如下:
function [hd]=ideal_LP_FIR (wc,N)
% 理想低通滤波器单位冲激响应的计算
%------------------------------------------ %hd ---理想低通滤波器单位冲激响应(0<=n<=(n-1)) %wc ---截至频率(单位弧度/秒) %N ---理想低通滤波器的长度 %
3. 编写dbpfilter.m 程序文件,通过调用kaiser_WF.m 文件,设计下列带通FIR 滤波器: 通带截止频率ωp 1=0.3π,ωp 2=0.5π
阻带衰减大于60 dB ,ωs 1=0.15π,ωs 2=0.65π 主程序文件 dbpfilter_FIR
% d_omega ---输入数字频率数组(向量); % d_omega(1)---阻带下边缘截止频率 % d_omega(2)---通带下边缘截止频率 % d_omega(3)---通带上边缘截止频率 % d_omega(4)---阻带上边缘截止频率 % N ---数字带通滤波器的长度
% hd ---理想数字带通滤波器单位冲激响应
% h ---实际数字带通滤波器单位冲激响应(所设计的) %wk ---凯泽窗序列 % beta ---凯泽窗参数
思考题:
1.窗函数有哪些指标要求?
2. 用窗函数法设计FIR滤波器时,滤波器的过渡带宽度和阻带衰减各与哪些因素有关?
3. 凯泽窗函数的β参数一般选取范围是多少? β的大小对窗函数形状以及频谱有何影响?
报告要求:
1. 列出本实验编写的所有文件及各项结果(包括数据、曲线),并加注必要的说明。
2. 写出计算理想带通滤波器单位抽样响应h d(n)的方法。
3. 对给定指标要求的带通滤波器,理论计算用凯泽窗设计所需的滤波器长度N和形状参数β
4. 分析实验结果,写出实验体会及实验中存在的问题。
注:实验报告的写作格式见《中国地质大学(北京)小学期实习报告撰写规范》。
评分标准:满分100分。
