丰台区2011年高三年级第二学期统一练习(二)
北京市昌平区2011-2012学年度第二学期高三年级第二次统一练习理(昌平二模理)-含答案

昌平区2011-2012学年度第二学期高三年级第二次统一练习数 学 试 卷(理科) 2012. 4考生注意事项:1.本试卷共6页,分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分,满分150分,考试时间 120分钟.2.答题前,考生务必将学校、班级、姓名、考试编号填写清楚.答题卡上第一部分(选择题)必须用2B 铅笔作答,第二部分(非选择题)必须用黑色字迹的签字笔作答,作图时必须使用2B 铅笔.3.修改时,选择题用塑料橡皮擦干净,不得使用涂改液.请保持卡面整洁,不要折叠、折皱、破损.不得在答题卡上作任何标记.4.请按照题号顺序在各题目的答题区域内作答,未在对应的答题区域作答或超出答题区域的作答均不得分.第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知全集U = R ,集合}{42≤-=x x |x A ,}2{<=x |x B ,则B A =A. {0≥x |x } B . {20<≤x |x } C. {42≤<x |x } D. {40≤≤x |x } 2. 在复平面内,与复数i+11对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限3. “1=a ” 是“002=-=+y a x y x 和直线直线垂直”的A. 充分而不必要条件 B 必要而不充分条件 C. 充要条件 D.既不充分也不必要条件4. 已知直线l :为参数)t t y tx (1⎩⎨⎧+==,圆C :2cos ρθ=,则圆心C 到直线l 的距离是 A. 2 B.3 C.2 D. 15.已知空间几何体的三视图如图所示,则该几何体的各侧面图形中,是直角三角形的有 A. 0个 B. 1个C. 2个D. 3 个左视图6. 某电视台曾在某时间段连续播放5个不同的商业广告,现在要在该时间段新增播一个商业广告与两个不同的公益宣传广告,且要求两个公益宣传广告既不能连续播放也不能在首尾播放,则在不改变原有5个不同的商业广告的相对播放顺序的前提下,不同的播放顺序共有 A. 60种 B. 120种 C. 144种 D. 300种7.如图,在棱长为a 的正方体1111D C B A ABCD -中,P 为11D A 的中点,Q 为11B A 上 任意一点,F E 、为CD 上任意两点,且EF 的长为定值,则下面的四个值中不为定值的是 A. 点P 到平面QEF 的距离B . 直线PQ 与平面PEF 所成的角 C. 三棱锥QEF P -的体积 D.二面角Q EF P --的大小8. 设等差数列{}n a 的前n 项和为n S ,已知()37712012(1)1a a -+-=,()32006200612012(1)1a a -+-=-,则下列结论正确的是A .20122012S =,20127a a <B .20122012S =,20127a a >C .20122012S =-,20127a a <D .20122012S =-,20127a a >第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分. 9.在∆ABC 中,4,2,2π===A b a 那么角C =_________.10.已知双曲线的方程为1422=-y x ,则其渐近线的方程为____________,若抛物线px y 22=的焦点与双曲线的右焦点重合,则_______p =.C 1A 1C11. 如图给出了一个程序框图,其作用是输入x 的值,输出相应的y 值,若要使输入的x 值与输出的y 值相等,则这样的x 值有 ___________个.12. 如图,AB 是⊙O 的直径,CD 切⊙O 于点D ,CA 切⊙O 于点A ,CD 交AB 的延长线于点E .若3AC =,2ED =,则BE =________;AO =________.13. 若变量 x , y 满足约束条件⎪⎩⎪⎨⎧≤-≥≤400x y y x 表示平面区域M ,则当-42≤≤a 时,动直线a y x =+所经过的平面区域M 的面积为_____________.14. 若对于定义在R 上的函数f (x ) ,其图象是连续不断的,且存在常数λ(∈λR )使得 f (x +λ) +λf (x ) = 0对任意实数x 都成立,则称f (x ) 是一个“λ—伴随函数”. 有下列关于“λ—伴随函数”的结论:①f (x ) =0 是常数函数中唯一个“λ—伴随函数”;②f (x ) = x 不是“λ—伴随函数”;③f (x ) = x 2是一个“λ—伴随函数”; ④“21—伴随函数”至少有一个零点. 其中不正确...的序号是________________(填上所有不.正确..的结论序号).三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(本小题满分13分)已知向量a (cos ,sin ),θθ= b = (13-,), 22π≤θ≤π-. (Ⅰ)当b a ⊥时,求θ的值; (Ⅱ)求||b a +的取值范围.EA某游乐场将要举行狙击移动靶比赛. 比赛规则是:每位选手可以选择在A 区射击3 次或选择在B 区射击2次,在A 区每射中一次得3分,射不中得0分; 在B 区每射中一次得2分,射不中得0分. 已知参赛选手甲在A 区和B 区每次射中移动靶的概率分别是41和)10(<<p p .(Ⅰ) 若选手甲在A 区射击,求选手甲至少得3分的概率;(Ⅱ) 我们把在A 、B 两区射击得分的数学期望高者作为选择射击区的标准,如果选手甲最终选择了在B 区射击,求p 的取值范围.17.(本小题满分14分)在正四棱柱1111ABCD A B C D -中, 122AA AB ==,E 为AD 中点,F 为1CC 中点.(Ⅰ)求证:1AD D F ⊥; (Ⅱ)求证://CE 平面1AD F ;(Ⅲ) 求平面1AD F 与底面ABCD 所成二面角的余弦值.18.(本小题满分13分) 已知函数∈+--=a x a xax x f ,ln )1()(R . (Ⅰ)当1>a 时,求)(x f 的单调区间;(Ⅱ)若)(x f 在]1[e ,上的最小值为2-,求a 的值.如图,已知椭圆M :)0(12222>>=+b a by a x ,离心率36=e ,椭圆与x 正半轴交于点A ,直线l 过椭圆中心O ,且与椭圆交于B 、C 两点,B (1,1).(Ⅰ) 求椭圆M 的方程;(Ⅱ)如果椭圆上有两点Q P 、,使PBQ ∠的角平分线垂直于AO ,问是否存在实数)0(≠λλ使得AC PQ λ=成立?20. (本小题满分13分)实数列 3210a ,a ,a ,a ,由下述等式定义123,0,1,2,3,.n n n a a n +=-=(Ⅰ)若0a 为常数,求123,,a a a 的值; (Ⅱ)求依赖于0a 和n 的n a 表达式;(Ⅲ)求0a 的值,使得对任何正整数n 总有1n n a a +>成立.昌平区2011-2012学年度第二学期高三年级第二次统一练习数学( 理科)试卷参考答案及评分标准 2012.4一、选择题(本大题共8小题,每小题5分,共40分.)二、填空题(本大题共6小题,每小题5分,共30分.)9.127π 10. x y 21±= , 52 11. 3 12. 1 , 2313. 714. ① ③ 注:10,12题第一空2分三、解答题(本大题共6小题,共80分) 15.(本小题满分13分) 解:(Ⅰ) a ⊥b ∴b a ⋅0sin cos 3=-=θθ ……… 2分得3tan =θ 又∵22π≤θ≤π-……… 4分 即:θ=3π………6分 (Ⅱ)||b a +=4)sin cos 3(21||2||22+-+=+⋅+θθb b a a )3sin(45π--=θ ……… 9分22π≤≤π-θ 6365π≤π-≤π-∴θ ……… 11分 21)3s i n (1≤π-≤-∴θ 4)3sin(42≤π--≤-∴θ∴33≤+≤||b a ……… 13分16.(本小题满分13分)解:(Ⅰ)设“选手甲在A 区射击得0分”为事件M ,“选手甲在A 区射击至少得3分”为事件N ,则事件M 与事件N 为对立事件, 6427)411(41)(3003=-⋅⋅=)(C M P ………2分6437642711=-=-=)M (P )N (P ………4分 (Ⅱ) 设选手甲在A 区射击的得分为ξ,则ξ的可能取值为0,3,6,9.6427)41-(10)(3===ξP ;6427)411(41C 3)(213=-⋅⋅==ξP ; 649)411()41(6)(223=-==ξC P ; 641)41(9)(3===ξP 所以ξ的分布列为49641964966427364270=⨯+⨯+⨯+⨯=ξ∴E 设选手甲在B 区射击的得分为η,则η的可能取值为0,2,4.2)-(10)(p P ==η;)1(2)1(C 2)(12p p p p P -=-⋅⋅==η;24)(p P ==η所以η的分布列为p p )p (p )p (E 441221022=⋅+-⋅+-⨯=η∴根据题意, 有 ξηE E > ∴1169494<<∴>p ,p ……… 13分 17.(本小题满分14分)(Ⅰ)证明:在正四棱柱1111ABCD A B C D -中四边形ABCD 是正方形, AD CD ∴⊥1DD ABCD AD ABCD ⊥⊂平面,平面1AD DD ∴⊥ 1DD CD D = 11AD CDD C ∴⊥平面111D F CDD C ⊂平面 1A D D F∴⊥ ……… 4分 (Ⅱ)证明:在正四棱柱1111ABCD A B C D -中,连结1A D ,交1AD 于点M ,连结,ME MF .M ∴为1AD 中点.E 为AD 中点,F 为1CC 中点. 111//2ME DD ME DD ∴=且……… 6分 又1121DD CF DD //CF =且 ∴四边形CEMF 是平行四边形. MF //CE ∴ ……… 8分CE ⊄平面1AD F ,MF ⊂平面1AD F .//CE ∴平面1AD F . ………9分(Ⅲ)解:以D 为坐标原点,分别以1,,DA DC DD 为,,x y z 轴建立空间直角坐标系如图. 则1(0,0,0),(1,0,0),(1,1,0),(0,1,0),(0,0,2),(0,1,1)D A B C D F……… 10分∴平面ABCD 的法向量为1(0,0,2)DD =………11分设平面1AD F 的法向量为(,,)x y z =n .1(1,1,1),(1,0,2)AF AD =-=-,分则有10,0.AF AD ⎧⋅=⎪⎨⋅=⎪⎩n n所以 0,20.x y z x z -++=⎧⎨-+=⎩取1z =,得(2,1,1)=n .1116cos ,DD DD DD ⋅〈〉==n n n . ………13分平面F AD 1与平面所成二面角为锐角.所以平面1AD F 与底面ABCD ……… 14分 18.(本小题满分13分)解:(Ⅰ)f (x )的定义域为{x |0>x }……………1分.2222))(1()1(11)(xa x x x x a a x x a x a x f --=+-+=+-+='…………3分 1>a 令0)(>'x f ,即a x x x a x x ><>--或得1,0))(1(2,∴)(x f 的增区间为(0,1),),(+∞a ……………4分 令0)(<'x f ,即a x xa x x <<<--1,0))(1(2得, ∴)(x f 的减区间为),1(a ………………5分(Ⅱ)①当1≤a 时, 0)(≥'x f 在]1[e ,上恒成立,∴)(x f 在]1[e ,恒为增函数. ……… 6分21)1()]([min -=-==∴a f x f ,得.(3舍去)=a ……… 7分②当e a <<1 时,令0)(='x f ,得1或a x =. 当a x <<1时,0)(<'x f ∴)(x f 在),1(a 上为减函数; 当e x a <<时,0)(>'x f ∴)(x f 在),(e a 上为增函数;2)ln()1(1)()]([min -=+--==∴a a a a f x f ,得(舍)……… 10分③当e a >时,0)(≤'x f 在],1[e 上恒成立,此时)(x f 在],1[e 恒为减函数.2)1()()]([min -=+--==∴a eae ef x f ,得 .e a = ………12分 综上可知 .e a = ……… 13分19.(本小题满分14分) 解:(Ⅰ)由题意可知2)(136abe -==,得 223b a = ……… 2分 )11(,B 点 在椭圆上11122=+ba 解得:34422==b ,a ……… 4分 故椭圆M 的方程为:143422=+y x ……… 4分 (Ⅱ)由于PBQ ∠的平分线垂直于OA 即垂直于x 轴,故直线PB 的斜率存在设为k ,则QB 斜率为 - k ,因此PB 、QB 的直线方程分别为y = k (x -1)+1, y = -k (x -1) +1 ……… 6分由⎪⎩⎪⎨⎧=++-=14341)1(22y x x k y 得01631631222=--+--+k k x )k (k x )k (①由0>∆ ,得31-≠k ……… 8分 点B 在椭圆上,x =1是方程①的一个根,设),(),,(Q Q p p y x Q y x P13163122+--=⋅∴k k k x P 即1316322+--=∴k k k x P ,同理1316322+-+=k k k x Q ………10分∴=PQk 311312213)13(22)(222=+--+-⋅=--+=--k k k k k k x x k x x k x x y y Q P Q P Q P Q P)1,1(),0,2(--C A 31=∴AC k 即:AC PQ k k =∴向量//,则总存在实数λ使λ=成立. ………13分20.(本小题满分13分)解:(Ⅰ)0131a a -=,0291a a +-=,03277a a -= ……… 2分(Ⅱ)由123,nn n a a +=-得1112(3)(3)(3)nn n n n n a a +++-=--- ……… 3分 令(3)n n na b =-,所以112(3)nn n n b b ++-=-所以121321()()()n n n b b b b b b b b -=+-+-++-23112342222(3)(3)(3)(3)n nb -=+++++---- 2111222()[()()()]3333n b -=+--+-++-1122()(1())133()231()3n b ----=+--- 1122(1()),153n b -=+-- ……… 6分所以1122(1())(3)3153n n n a a -=+---- ……… 7分 所以1112(3)[(3)32]15n n n n a a --=⋅-+-+⋅ 1102(13)(3)[(3)32]15n n n a --=--+-+⋅101[2(1)3](1)35n n n n n a -=+-⋅+-⋅⋅ ……… 8分(Ⅲ)1111101[2(1)3](1)35n n n n n n n a a a +++++-=+-⋅+-⋅⋅101[2(1)3](1)35n n n n n a --+-⋅--⋅⋅ 0112(1)43()55n n n a =⋅+-⋅⋅- 所以101121()()(1)4()3535n n n n n a a a +-=+-⋅⋅- ……… 10分 如果0105a ->,利用n 无限增大时,2()3n 的值接近于零,对于非常大的奇数n ,有10n n a a +-<;如果0105a -<,对于非常大的偶数n ,10n n a a +-<,不满足题目要求.当015a =时,112,5n n n a a +-=⋅于是对于任何正整数n ,1n n a a +>,因此015a =即为所求. ……… 13分【 以上答案仅供参考,若有其它解法,请酌情给分】。
丰台区2018年高三年级第二学期统一练习

丰台区2018年高三年级第二学期统一练习(二)数 学(理科)参考答案一、选择题:本大题共8小题,每小题5分,共40分。
二、填空题:本大题共6小题,每小题5分,共30分。
(9)1i - (10)121(11)1± (12)18000018y v v =+(0120)v <≤;100 (13)4;π3- (14)①②注:第12,13题第一个空填对得3分,第二个空填对得2分;第14题只写对一个得2分,有一个错误不得分.三、解答题: (15)(本小题共13分)解:(Ⅰ)在△ACD 中,因为 π()DAC ADC C ∠=-∠+∠,π3ADC ∠=, 所以 πsin sin()3DAC C ∠=+∠1cos sin 22C C =∠+∠. …………………2分因为 cos C ∠=, 0πC <∠<,所以 sin C ∠==…………………4分所以 1sin 272714DAC ∠=⨯⨯. …………………5分 (Ⅱ)在△ABD 中,由余弦定理可得2222cos AB BD AD BD AD ADB =+-⋅⋅∠, …………………7分所以 222214626cos3AD AD π=+-⨯⨯⨯, 所以 261600AD AD +-=, 即 (16)(10)0AD AD +-=.所以 10AD =或16AD =-(舍).所以 10AD =. …………………8分 在△ACD 中,由正弦定理得sin sin CD ADDAC C=∠∠,即= …………………10分 所以 15CD =. …………………11分 所以11sin sin 222ABC S AD BD ADB AD DC ADC ∆=⨯⨯⨯∠+⨯⨯⨯∠=.即ABC S ∆=…………………13分(16)(本小题共13分) 解:(Ⅰ)m n <. …………………3分 (Ⅱ)设“从抽取的20位客户中任意抽取2位,至少有一位是A 组的客户”为事件M ,则11210101022029()38C C C P M C +==. …………………6分 所以从抽取的20位客户中任意抽取2位至少有一位是A 组的客户的概率是2938. (III )依题意ξ的可能取值为0,1,2.则119811101018(0)25C C P C C ξ===; 1111189211101013(1)50C C C C P C C ξ+===; 11121110101(2)50C C P C C ξ===. …………………10分 所以随机变量ξ的分布列为:所以随机变量ξ的数学期望01225505010E ξ=⨯+⨯+⨯=. …………………12分 即103=ξE . …………………13分(17)(本小题共14分)(Ⅰ)证明:在三棱柱 111ABC A B C -中,侧面 11A ABB 为平行四边形, 所以 11B B A A ∥.又因为 1B B ⊄平面11A ACC ,1A A ⊂平面11A ACC,所以 1B B ∥平面11A ACC . …………………2分 因为 1B B ⊂平面1BB D ,且平面1BB D 平面11A ACC DE =,所以 1B B DE ∥. …………………4分(Ⅱ)证明:在△ABC 中,因为 =AB BC ,D 是AC 的中点,所以BD AC ⊥.因为1A D ⊥平面ABC ,如图建立空间直角坐标系D xyz -. …………………5分 设=BD a ,=AD b ,在△1AA D 中 1=2AA AD ,190A DA ∠=︒, 所以 1AD ,所以 (0,0,0)D ,(0,,0)A b -1)A ,(,0,0)B a .所以 1(0,)AA b = ,(,0,0)DB a = .…………………7分所以 10000AA DB a b ⋅=⨯+⨯⨯= ,所以 1AA BD ⊥. …………………9分(Ⅲ)解:因为 (0,)E b , 所以 1(,)DB DE DB a b =+=,即1(,)B a b .因为 (0,,0)C b ,所以 1()CB a =. …………………10分 设平面11ABB A 的法向量为 =(,,)n x y z,因为 100n AA n AB ⎧⋅=⎪⎨⋅=⎪⎩ ,即00by ax by ⎧+=⎪⎨+=⎪⎩, 令 =z a ,则y =,x =,EDA 1C 1B 1CABA1所以,,)n a =. …………………12分因为111|||cos ,|||||n CB n CB n CB ⋅<>==所以422441390a a b b -+=, 所以 =a b 或23a b =,即=2AC BD 或4=3AC BD . …………………14分(18)(本小题共13分)(Ⅰ)解:依题意 ()cos sin f x x x x a '=--. …………………2分令 ()cos sin g x x x x a =--,π[0,]2x ∈, 则 ()2sin cos 0g x x x x '=--≤.所以()g x 在区间π[0,]2上单调递减.因为 (0)10g a =-≤,所以 ()0g x ≤,即 ()0f x '≤, …………………4分 所以()f x 的单调递减区间是π[0,]2,没有单调递增区间. …………………5分 (Ⅱ)证明:由(Ⅰ)知,()g x 在区间π[0,]2上单调递减,且(0)1g a =-,ππ()22g a =--. 当 1a ≥时,()f x 在π[0,]2上单调递减. 因为 (0)0f a =>,ππ()(1)022f a =-<,所以()f x 有且仅有一个零点. …………………7分当 π02a --≥,即π2a ≤-时,()0g x ≥,即 ()0f x '≥,()f x 在π[0,]2上单调递增.因为 (0)0f a =<,ππ()(1)022f a =->,所以()f x 有且仅有一个零点. …………………9分当 π12a -<<时,(0)10g a =->,ππ()022g a =--<, 所以存在0π(0,)2x ∈,使得0()0g x =. …………………10分x ,()f x ',()f x 的变化情况如下表:所以 ()f x 在0(0,)x 上单调递增,在0(,)2x 上单调递减. …………………11分 因为 (0)f a =,ππ()(1)22f a =-,且0a ≠, 所以 2ππ(0)()(1)022f f a =-<,所以()f x 有且仅有一个零点.…………………12分 综上所述,()f x 有且仅有一个零点. …………………13分(19)(本小题共14分) 解:(Ⅰ)依题意得 24a =,所以 2a =. …………………1分因为 12c e a ==,所以 1c =. …………………2分所以 23b =. …………………3分所以椭圆C 的方程为 22143x y +=. …………………4分(Ⅱ)椭圆的右焦点 (1,0)F . …………………5分设直线 l :(1)(0)y k x k =-≠,设 11(,)M x y ,22(,)N x y . …………………6分联立方程组 ⎪⎩⎪⎨⎧-==+)1(13422x k y y x , 消y 得 2222(34)84(3)0k x k x k +-+-=,0∆>成立. …………………8分所以 2122834k x x k +=+,21224(3)34k x x k-=+. …………………9分 因为 1212120y y k k m x m x --+=+=--, …………………10分所以122112()()0()()y m x y m x m x m x ----=--,即 1221()()0y m x y m x -+-=,…………11分所以 2112()(1)()(1)0k m x x k m x x --+--=恒成立. …………………12分因为 0k ≠,所以 1212(1)()220m x x x x m ++--=,即 222284(3)(1)2203434k k m m k k-+⋅-⋅-=++, …………………13分 化简为 2228(1)8(3)2(34)0k m k m k +---+=,所以 4m =. …………………14分(20)(本小题共13分) 解:(Ⅰ)因为1=0a ,2=5a , 所以 12a a <,所以 3214a a =-=. …………………1分因为 23a a >,所以 1234341a a a a ++==-. …………………2分因为 34a a >,所以 54+14a a ==. …………………4分 所以 34a =,43a =,54a =.(Ⅱ)当 0m =时,30a =,40a =, …………………5分当 0m >时,因为 12a a <,所以 32211a a m a =-=-<,所以 12342133a a a m a ++-==.因为 34a a =,所以 2113m m --=,所以 2m =. …………………7分当 0m <时,因为 12a a >,所以 32211a a m a =+=+>,所以 12342133a a a m a +++==.因为 34a a =,所以 2113m m ++=,所以 2m =-. …………………9分所以 3n ≥时,1n n a a +=为常数的必要条件是 {2,0,2}m ∈-. 当2m =时,341a a ==,因为当 3(3)n k k ≤≤>时,1n a =,都有 102111n n S a n n+++++=== , 所以当 2m =符合题意,同理 2m =-和0m =也都符合题意. …………………10分 所以m 的取值范围是 {2,0,2}-.(Ⅲ){|2m m ≤-或02}m ≤≤. …………………13分(若用其他方法解题,请酌情给分)。
丰台区2011年初三统一练习(二)

奉港初中初三模拟测试数学试卷2010.4一、选择题(每题3分,共36分) 1. 计算(-3)3的结果是( )A .9B .-9C .27D .-272. 下列运算正确的是 ( ) A.()()22a b a b a b +--=-B.()2239a a +=+C.()22424aa -= D.2242a a a +=3. 下列事件是不确定事件的是( )A .宁波今年国庆节当天的最高气温是35℃B .在一个装着白球和黑球的袋中摸球,摸出红球C .抛掷一石头,石头终将落地D .有一名运动员奔跑的速度是20米/秒4. 如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面,与“我”相对的面上的汉字是( ) A .祝B .福C .博D .会5. 四个直立在地面上的字母广告牌在不同情况下,在地面上的投影(阴影部分)效果如图。
则在字母“L ”、“K ”、“C ”的投影中,与字母“N ”属同一种投影的有( )A.“L ”、“K ” B.“C ” C.“K ” D.“L ”、“K ”、“C ”6. 如图,已知□ABCD 的对角线交于平面直角坐标系的原点,点A 为(2-,3),则点C 的坐标为( ) A (3-,2) B (2,3-) C .(3,2-) D .(2-,3-)7. 已知相交两圆的圆心距为4,其中一个圆的半径为3,则另一个圆的半径可能是( )A .1B .5C .7D .108. 已知圆锥的高为4,底面半径为3,则圆锥的表面积...为( ) A .π12 B .π21 C .π24 D .39π9. 有一个人患了流感,经过两轮传染后共有100人患了流感,设每轮传染中平均一个人传染的人数是x 人,则下列方程正确的是( )A.10012=+x B.1002=xC .100)1()1(=+++x x xD .100)1()1(2=+++x x第4题x(第6题)第11题10. 如图,直线24y x =-+与x 轴,y 轴分别相交于A B ,两点,C 为OB 上一点,且12∠=∠,则ABC S =△ ( )A .1B .2C .3D .411. 已知函数2y ax bx c =++的图象如图所示,那么关于x 的方程220ax bx c +++=的根的情况是( )A .无实数根B .有两个相等实数根C .有两个异号实数根D .有两个同号不等实数根12. 如图,在直线m 上摆放着三个正三角形:△ABC 、△HFG 、△DCE , 已知BC =12CE ,F 、G 分别是BC 、CE 的中点,FM ∥AC ,GN ∥DC .设图中三个平行四边形的面积依次是S 1,S 2,S 3,若S 1+S 3=20,则S 2等于( ) A .7B .8C . 9D . 10二、填空题(每题3分,共18分)13. 函数x y 21-=的自变量x 的取值笵围是___ ____。
三角函数2011高三二模分类
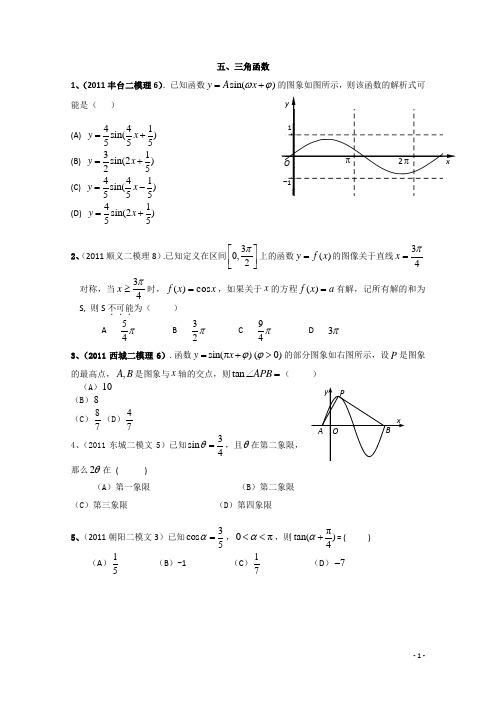
xyO π2π1-1五、三角函数1、(2011丰台二模理6).已知函数sin()y A x ωϕ=+的图象如图所示,则该函数的解析式可能是( ) (A) 441sin()555y x =+(B) 31sin(2)25y x =+(C) 441sin()555y x =-(D) 41sin(2)55y x =+2、(2011顺义二模理8).已知定义在区间⎥⎦⎤⎢⎣⎡23,0π上的函数)(x f y =的图像关于直线43π=x 对称,当43π≥x 时,x x f cos )(=,如果关于x 的方程a x f =)(有解,记所有解的和为S, 则S 不可能...为( ) Aπ45 B π23 C π49D π3 3、(2011西城二模理6).函数sin()(0)y x ϕϕ=π+>的部分图象如右图所示,设P 是图象的最高点,,A B 是图象与x 轴的交点,则tan APB ∠=( ) (A )10(B )8 (C )87(D )474、(2011东城二模文5)已知3sin 4θ=,且θ在第二象限,那么2θ在 ( )(A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限5、(2011朝阳二模文3)已知3cos 5α=,0πα<<,则πtan()4α+= ( ) (A )15 (B )-1 (C )17(D )7-xyO π2π1-16、(2011丰台二模文6)已知函数sin()y A x ωϕ=+的图象如图所示,则该函数的解析式可能是( )(A) 441sin()555y x =+ (B) 31sin(2)25y x =+(C) 441sin()555y x =-(D) 41sin(2)55y x =+7、(2011海淀二模文4)若函数sin()3y x π=+的图象上所有点的横坐标扩大到原来的2倍,纵坐标不变,则得到的图象所对应的函数解析式为( ) A .1sin()26y x π=+B. 1sin()23y x π=+ C. 2sin(2)3y x π=+D. s i n (2)3y x π=+8、1(2011东城二模理11)在△ABC中,若π,4B b ∠==,则C ∠= . 2、(2011丰台二模理11).函数2cos sin y x x x =-的最小正周期为π ,最大值为 . 3、(2011西城二模理9).在ABC ∆中,若2B A =,:a b =A =_____. 4、(2011东城二模文11)在△ABC中,若45,B b ∠=︒,则C ∠=5、(2011朝阳二模文11)如图,一艘船上午8:00在A 处测得灯塔S 在它的北偏东30°处,之后它继续沿正北方向匀速航行,上午8:30到达B 处,此时又测得灯塔S 在它的北偏东75°处,且与它相距mile ,则此船的航行速度是 n mile/h.6、(2011海淀二模文12)已知ABC ∆的面积3=S ,3A π∠=,则=⋅AC AB .7、(2011顺义二模文11)在△ABC 中,若b=1,c=3,6π=∠A ,则a= ,=B sin __ __.8、(2011西城二模文6)函数sin ()y x x =π∈R 的部分图象如图所示,设O 为坐标原点,P 是图象的最高点,B 是图象与x 轴的交点,则tan OPB ∠=( )(A )10 (B )8(C )87 (D )479、(2011西城二模文11)在ABC ∆中,若2B A =,:a b =A =_____1、(2011朝阳二模理15)(本小题满分13分)已知函数2()2sin sin()2sin 12f x x x x π=⋅+-+ ()x ∈R .[来源:] (Ⅰ)求函数()f x 的最小正周期及函数()f x 的单调递增区间;(Ⅱ)若0()23x f =,0ππ(, )44x ∈-,求0cos 2x 的值.2、(2011昌平二模理15). (本小题满分13分)已知函数)0(cos 22sin 3)(2>+=ωωωx x x f 的最小正周期为.π(I ) 求的值ω;(II )求函数)(x f 在区间]2,0[π的取值范围.3、(2011东城二模理15)(本小题共13分)已知πsin()410A +=ππ(,)42A ∈. (Ⅰ)求cos A 的值; (Ⅱ)求函数5()cos 2sin sin 2f x x A x =+的值域.已知函数2()cos cos f x x x x ωωω= (0)ω>的最小正周期为π.(Ⅰ)求2()3f π的值;(Ⅱ)求函数()f x 的单调区间及其图象的对称轴方程.已知函数x x x f 2sin 262sin 2)(-⎪⎭⎫⎝⎛+-=π,R x ∈ (1) 求函数)(x f 的最小正周期;(2)记A B C ∆的内角A,B,C 的对边长分别为c b a ,,,若3,1,1)2(===c b B f ,求a 的值。
2011北京市丰台初三语文二模

丰台区2011年初三统一练习(二)语文试卷 2011.61.下列词语中加点字的读音完全正确的一项是A.颈.椎(jìnɡ)赈.灾(zhèn) 鲜.为人知(xiǎn)B.逮.捕(dài)狭隘.(ài)言简意赅.(ɡāi)C.庇.护(bì)滑稽.(jì)厚此薄.彼(bó)D.憎.恶(zènɡ)笨拙.(zhuō) 毛遂.自荐(suì)2.下列词语中加点字字义相同的一项是A.搬弄是.非——唯利是.图B.锐不可当.——当.之无愧C.饮水思源.——源.远流长D.谈笑风生.——栩栩如生.3.下面句子中,没有语病的一项是A.我这次考试成绩不理想的原因是因为我没有按老师的要求仔细审题。
B.能否构建和谐社会,是我党开创中国特色社会主义事业新局面的一项重大任务。
C.那篇小说的作者以他高度的艺术手法塑造了丰满鲜活的人物和欢快热闹的场面。
D.为了预防大灾之后出现大的疫情,卫生防疫部门采取了许多行之有效的措施。
〖ZK)〗4.依次填写关联词语恰当的一项是一个人总是按照别人的意见生活,没有自己的独立思考,总是为外在的事务忙碌,没有自己的内心生活,,说他不是他自己一点儿也没冤枉他。
确确实实,从他的头脑到他的心灵,你在其中已经找不到丝毫真正属于他自己的东西了,他只是别人的一个影子或事务的一架机器罢了。
A.因为所以因此B.尽管所以因而C.如果那么因为D.尽管但是因为5.下列句子的标点符号使用错误的一项是A.绿色是多么宝贵啊!它是生命,它是希望,它是慰安,它是快乐。
B.无私,敬业,诚信,友善,谦和,宽容——是中国人民提倡和追求的道德境界。
C.几个“慈祥”的老板到小菜场去收集一些菜叶,用盐一浸,这就是包身工们难得的佳肴了。
D.据《西域水道记》记载,20世纪20年代前,塔里木河下游河水丰盈,碧波荡漾;岸边胡杨丛生,林木茁壮。
6.对下列句子运用的修辞方法理解有误的一项是A.小麻雀垂头丧气地站在那里,只有那么一点活气,像是等着猫再去扑它,它没力量反抗或逃避。
2011年北京市朝阳区高三下统一练习(二)

2011年北京市朝阳区高三下统一练习(二)一、选择题(共8小题;共40分)1. 已知全集,集合,,则 ______A. B.C. D.2. 设,,那么" "是" "的______A. 必要不充分条件B. 充分不必要条件C. 充分必要条件D. 既不充分又不必要条件3. 三棱柱的侧棱与底面垂直,且底面是边长为的等边三角形,其正视图(如图所示)的面积为,则侧视图的面积为______A. B. C. D.4. 已知随机变量服从正态分布,且,则实数的值为______A. B. C. D.5. 若一个三位数的十位数字比个位数字和百位数字都大,则称这个数为"伞数".现从这六个数字中任取个数,组成无重复数字的三位数,其中"伞数"有______A. 个B. 个C. 个D. 个6. 点是抛物线上一动点,则点到点的距离与到直线的距离和的最小值是______A. B. C. D.7. 已知棱长为的正方体中,点,分别是棱,上的动点,且.设与所成的角为,与所成的角为,则的最小值______A. 不存在B. 等于C. 等于D. 等于8. 已知点是的中位线上任意一点,且,实数,满足.设,,,的面积分别为,,,,记,,.则当取最大值时,的值为______A. B. C. D.二、填空题(共6小题;共30分)9. 已知复数满足,则 ______.10. 曲线(为参数)的普通方程为______.11. 曲线与轴所围成的图形面积为______.12. 已知数列满足,且,则 ______;并归纳出数列的通项公式 ______.13. 如图,与圆相切于点,为圆的割线,并且不过圆心,已知,,,则 ______;圆的半径等于______.14. 已知函数,且,则对于任意的,函数总有两个不同的零点的概率是______.三、解答题(共6小题;共78分)15. 已知函数.(1)求函数的最小正周期和函数的单调递增区间;(2)若,,求的值.16. 为了防止受到核污染的产品影响我国民众的身体健康,要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为,第二轮检测不合格的概率为,两轮检测是否合格相互没有影响.(1)求该产品不能销售的概率;(2)如果产品可以销售,则每件产品可获利元;如果产品不能销售,则每件产品亏损元(即获利元).已知一箱中有产品件,记一箱产品获利元,求的分布列,并求出均值.17. 在长方形中,,,分别是,的中点(如图1).将此长方形沿对折,使二面角为直二面角,,分别是,的中点(如图2).(1)求证: 平面;(2)求证:平面平面;(3)求直线与平面所成角的正弦值.18. 设函数()(),.(1)若,求函数在上的最小值;(2)若函数在上存在单调递增区间,试求实数的取值范围;(3)求函数的极值点.19. 已知椭圆:经过点,离心率为.过点的直线与椭圆交于不同的两点,.(1)求椭圆的方程;(2)求的取值范围;(3)设直线和直线的斜率分别为和,求证:为定值.20. 对于正整数、,存在唯一一对整数和,使得,其中.特别地,当时,称能整除,记作.已知.(1)存在,使得,试求,的值;(2)求证:不存在这样的函数,使得对任意的整数,,若,则;(3)若,(指集合中的元素的个数),且存在,,,,则称为"和谐集".求最大的,使含的集合的有个元素的任意子集为"和谐集",并说明理由.答案第一部分1. D2. B3. C4. A5. C6. D7. C8. A第二部分9.10.11.12. ;13. ;14.第三部分15. (1)=,所以函数的最小正周期.令,得,即.所以函数的单调递增区间为.(2)解法一:由已知得,两边平方,得,所以.因为,所以.所以.解法二:因为,所以.又因为得.所以.所以16. (1)记"该产品不能销售"为事件,则.所以,该产品不能销售的概率为.(2)由已知,可知的取值为,,,,.所以的分布列为所以均值为.17. (1)取的中点,连接,.,分别是,的中点,所以是的中位线.所以,且.又因为是的中点,所以.所以,且.所以四边形是平行四边形.所以.又平面,平面,所以 平面.(2)因为,且,所以平面.因为,所以平面.因为平面,所以.又,且是的中点,所以.因为,所以平面.由⑴知.所以平面.又因为平面,所以平面平面.(3)因为,,又因为二面角为直二面角,所以,为原点,以为轴,以为轴,以为轴,建立空间直角坐标系,所以,,,.所以,,.设平面的法向量为,则,即,取得平面的法向量为.设直线与平面所成角为,则所以直线与平面所成角的正弦值为.18. (1)的定义域为.因为,所以在上是增函数.当时,取得最小值.所以在上的最小值为.(2)解法一:.设,依题意,在区间上存在子区间使得不等式成立.注意到抛物线开口向上,所以只要,或即可.由,即,得;由,即,得.所以,所以实数的取值范围是.解法二:,依题意得,在区间上存在子区间使不等式成立.又因为,所以.设,所以小于函数在区间上的最大值.又因为,由解得;由解得.所以函数在区间上递增,在区间上递减.所以函数在,或处取得最大值.又,,所以,.所以实数的取值范围是.(3)因为,令.①显然,当时,在上恒成立,,此时,函数没有极值点;②当时,(ⅰ)当,即时,在上恒成立,这时,函数没有极值点;(ⅱ)当,即时,易知,当时,,这时;当或时,,这时;所以,当时,是函数的极大值点;是函数的极小值点.综上,当时,函数没有极值点;当时,是函数的极大值点;是函数的极小值点.19. (1)由题意得解得,.故椭圆的方程为.(2)由题意显然直线的斜率存在,设直线的方程为,由得.因为直线与椭圆交于不同的两点,,所以解得.设的坐标分别为,,则所以因为,所以.故的取值范围为.(3)由(2)得所以为定值.20. (1)因为,所以,.(2)假设存在这样的函数,使得对任意的整数,,若,则.设,,,,由已知.由于,,所以,.不妨令,,这里,且.同理,且.因为只有三个元素,所以.即,但是,与已知矛盾.因此假设不成立,即不存在这样的函数,使得对任意的整数,,若,则.(3)当时,记,,记,则,显然对任意的,不存在,使得成立,故是非"和谐集",此时.同理,当时,存在含的集合的有个元素的子集为非"和谐集".因此.下面证明:含的任意集合的有个元素的子集为"和谐集".设.若中之一为集合的元素,显然为"和谐集".现考虑都不属于集合,构造集合,,,,,.以上每个集合中的元素都是倍数关系.考虑的情况,也即中个元素全都是的元素,中剩下个元素必须从这个集合中选取,那么至少有一个集合有两个元素被选,即集合中至少有两个元素存在倍数关系.综上所述,含的任意集合的有个元素的子集为"和谐集",即的最大值为。
北京丰台区2012高三年级第二学期第二次统一练习理科数学试题试题及答案
北京市丰台区2012年高三二模 2012.5数学(理科)第一部分 (选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.复数1i2i-+的虚部是 (A) i -(B) 3i 5-(C) –1(D) 35-2.一个正四棱锥的所有棱长均为2,其俯视图如右图所示,则该正四棱锥的正 视图的面积为(A)2 (B)3 (C) 2 (D) 43.由曲线1y x =与y =x ,x =4以及x 轴所围成的封闭图形的面积是 (A) 3132 (B) 2316(C) 1ln 42+ (D) ln 41+4.执行如图所示的程序框图,若输出的结果为63,则判断框中应填(A) 7n ≤ (B) 7n > (C) 6n ≤ (D) 6n >5.盒子中装有形状、大小完全相同的3个红球和2个白球,从中随机 取出一个记下颜色后放回,当红球取到2次时停止取球.那么取球次 数恰为3次的概率是(A) 18125 (B)36125 (C) 44125(D) 811256.在△ABC 中,∠BAC =90º,D 是BC 中点,AB =4,AC =3,则AD BC ⋅=(A) 7- (B) 72-(C)72(D) 77.已知函数sin (0)y ax b a =+>的图象如图所示,则函数log ()a y x b =+的图象可能是开始结束0S =,1n =,3a =S S a =+2a a =+1n n =+输出S 是 否俯视图(A)(B)(C)(D)8.已知平面上四个点1(0,0)A ,2(23,2)A ,3(234,2)A +,4(4,0)A .设D 是四边形1234A A A A 及其内部的点构成的点的集合,点0P 是四边形对角线的交点,若集合0{|||||,1,2,3,4}i S P D PP PA i =∈≤=,则集合S 所表示的平面区域的面积为 (A) 2(B) 4(C) 8(D) 16第二部分 (非选择题 共110分)二、填空题共6小题,每小题5分,共30分.9.在极坐标系中,圆2sin ρθ=的圆心的极坐标是____.10.已知椭圆22221(7)7x y m m m +=>-上一点M 到两个焦点的距离分别是5和3,则该椭圆的离心率为______.11.如图所示,AB 是圆的直径,点C 在圆上,过点B ,C 的切线交于点P ,AP 交圆于D ,若AB =2,AC =1,则PC =______,PD =______.12.某地区恩格尔系数(%)y 与年份x 的统计数据如下表:年份x 2004 2005 2006 2007 恩格尔系数y (%)4745.543.541PDC BA从散点图可以看出y 与x 线性相关,且可得回归方程为ˆˆ4055.25ybx =+,据此模型可预测2012年该地区的恩格尔系数(%)为______.13.从5名学生中任选4名分别参加数学、物理、化学、生物四科竞赛,且每科竞赛只有1人参加,若甲不参加生物竞赛,则不同的选择方案共有 种. 14. 在平面直角坐标系中,若点A ,B 同时满足:①点A ,B 都在函数()y f x =图象上;②点A ,B 关于原点对称,则称点对(A ,B )是函数()y f x =的一个“姐妹点对”(规定点对(A ,B )与点对(B ,A )是同一个“姐妹点对”).那么函数24,0,()2,0,x x f x x x x -≥⎧=⎨-<⎩的“姐妹点对”的个数为_______;当函数()x g x a x a =--有“姐妹点对”时,a 的取值范围是______.三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(本小题共13分)已知函数()cos (3cos sin )3f x x x x =--. (Ⅰ)求()3f π的值;(Ⅱ)求函数()y f x =在区间[0,]2π上的最小值,并求使()y f x =取得最小值时的x 的值.16.(本小题共13分)某商场举办促销抽奖活动,奖券上印有数字100,80,60,0.凡顾客当天在该商场消费每.超过1000元,即可随机从抽奖箱里摸取奖券一张,商场即赠送与奖券上所标数字等额的现金(单位:元).设奖券上的数字为ξ,ξ的分布列如下表所示,且ξ的数学期望E ξ=22.ξ 100 80 60 0P0.05ab0.7(Ⅰ)求a ,b 的值;(Ⅱ)若某顾客当天在商场消费2500元,求该顾客获得奖金数不少于160元的概率.17.(本小题共14分)在如图所示的几何体中,四边形ABCD 为矩形,平面ABEF ⊥平面ABCD , EF // AB ,∠BAF =90º,AD = 2,AB =AF =2EF =1,点P 在棱DF 上.(Ⅰ)若P 是DF 的中点,(ⅰ) 求证:BF // 平面ACP ;(ⅱ) 求异面直线BE 与CP 所成角的余弦值;(Ⅱ)若二面角D -AP -C 的余弦值为63,求PF 的长度. PFEDCAB18.(本小题共13分)已知数列{a n }满足14a =,131n n n a a p +=+⋅+(n *∈N ,p 为常数),1a ,26a +,3a 成等差数列.(Ⅰ)求p 的值及数列{a n }的通项公式;(Ⅱ)设数列{b n }满足2n n n b a n=-,证明:49n b ≤.19.(本小题共14分)在平面直角坐标系xOy 中,抛物线C 的焦点在y 轴上,且抛物线上的点P (x 0,4)到焦点F 的距离为5.斜率为2的直线l 与抛物线C 交于A ,B 两点.(Ⅰ)求抛物线C 的标准方程,及抛物线在P 点处的切线方程;(Ⅱ)若AB 的垂直平分线分别交y 轴和抛物线于M ,N 两点(M ,N 位于直线l 两侧),当四边形AMBN 为菱形时,求直线l 的方程.20.(本小题共13分)设函数()ln ()ln()f x x x a x a x =+--(0)a >. (Ⅰ)当1a =时,求函数()f x 的最小值;(Ⅱ)证明:对∀x 1,x 2∈R +,都有[]11221212ln ln ()ln()ln2x x x x x x x x +≥++-; (Ⅲ)若211nii x==∑,证明:21ln ln 2nn i i i x x =≥-∑ *(,)i n ∈N . (考生务必将答案答在答题卡上,在试卷上作答无效)北京市丰台区2012年高三二模数 学(理科)参考答案一、选择题:本大题共8小题,每小题5分,共40分.题号 1 2 3 4 5 6 7 8 答案DACDBBCB二、填空题:本大题共6小题,每小题5分,共30分.9.(1,)2π10.7411.3,37712.31.25 13. 96 14.1,1a >注:第11题第一个空答对得2分,第二个空答对得3分;第14题第一个空答对得3分,第二个空答对得2分.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.解:因为()cos (3cos sin )3f x x x x =--=23cos sin cos 3x x x --=1cos 213()sin 2322x x +-- =313cos 2sin 2222x x --=3cos(2)62x π+-. (Ⅰ)3()cos(2)3362f πππ=⨯+-=33322--=-. ……………………7分(Ⅱ)因为 [0,]2x π∈,所以2666x ππ7π≤+≤. 当 26x π+=π,即512x π=时,函数()y f x =有最小值是312--. 当512x π=时,函数()y f x =有最小值是312--. ……………………13分16.解:(Ⅰ)依题意,1000.05806000.722E a b ξ=⨯+++⨯=,所以 806017a b +=.因为 0.050.71a b +++=,所以0.25a b +=. 由806017,0.25,a b a b +=⎧⎨+=⎩ 可得00.15.a b =⎧⎨=⎩ ……………………7分(Ⅱ)依题意,该顾客在商场消费2500元,可以可以抽奖2次.奖金数不少于160元的抽法只能是100元和100元; 100元和80元; 100元和60元;80元和80元四种情况. 设“该顾客获得奖金数不少于160元”为事件A ,则()0.050.0520.050.120.050.150.10.10.0375P A =⨯+⨯⨯+⨯⨯+⨯=.答:该顾客获得奖金数不少于160元的概率为0.0375. ……………………13分17.(Ⅰ)(ⅰ)证明:连接BD ,交AC 于点O ,连接OP .OBA CDEFP z yx PFEDCAB 因为P 是DF 中点,O 为矩形ABCD 对角线的交点, 所以OP 为三角形BDF 中位线,所以BF // OP ,因为BF ⊄平面ACP ,OP ⊂平面ACP ,所以BF // 平面ACP . ……………………4分 (ⅱ)因为∠BAF =90º, 所以AF ⊥AB ,因为 平面ABEF ⊥平面ABCD , 且平面ABEF ∩平面ABCD = AB ,所以AF ⊥平面ABCD , 因为四边形ABCD 为矩形,所以以A 为坐标原点,AB ,AD ,AF 分别为x ,y ,z 轴,建立如图所示空间直角坐标系O xyz -.所以 (1,0,0)B ,1(,0,1)2E ,1(0,1,)2P ,(1,2,0)C .所以 1(,0,1)2BE =- ,1(1,1,)2CP =-- ,所以45cos ,15||||BE CP BE CP BE CP ⋅<>==⋅,即异面直线BE 与CP 所成角的余弦值为4515. ……………………9分(Ⅱ)解:因为AB ⊥平面ADF ,所以平面APF 的法向量为1(1,0,0)n =.设P 点坐标为(0,22,)t t -,在平面APC 中,(0,22,)AP t t =- ,(1,2,0)AC =,所以 平面APC 的法向量为222(2,1,)t n t-=- , 所以 12122212||26cos ,3||||22(2)1()n n n n n n t t⋅<>===⋅--++, 解得23t =,或2t =(舍). 此时5||3PF =. ……………………14分18.解:(Ⅰ)因为14a =,131n n n a a p +=+⋅+,所以1213135a a p p =+⋅+=+;23231126a a p p =+⋅+=+. 因为1a ,26a +,3a 成等差数列,所以2(26a +)=1a +3a , 即610124126p p ++=++, 所以 2p =. 依题意,1231n n n a a +=+⋅+, 所以当n ≥2时,121231a a -=⋅+,232231a a -=⋅+,……212231n n n a a ----=⋅+, 11231n n n a a ---=⋅+.相加得12212(3333)1n n n a a n ---=+++++- ,所以 113(13)2(1)13n n a a n ---=+--, 所以 3n n a n =+.当n =1时,11314a =+=成立, 所以3n n a n =+. ……………………8分(Ⅱ)证明:因为 3n n a n =+,所以 22(3)3n n n n n b n n ==+-.因为 2221+11(1)22+1=333n n n n n n n n n b b +++-+-=-,*()n ∈N . 若 22+210n n -+<,则132n +>,即 2n ≥时 1n n b b +<.又因为 113b =,249b =, 所以49n b ≤. ……………………13分19.解:(Ⅰ)依题意设抛物线C :22(0)x py p =>,因为点P 到焦点F 的距离为5,所以点P 到准线2py =-的距离为5. 因为P (x 0,4),所以由抛物线准线方程可得 12p=,2p =. 所以抛物线的标准方程为24x y =. ……………………4分即 214y x =,所以 1'2y x =,点P (±4,4), 所以 41'|(4)22x y =-=⨯-=-,41'|422x y ==⨯=.所以 点P (-4,4)处抛物线切线方程为42(4)y x -=-+,即240x y ++=; 点P (4,4)处抛物线切线方程为42(4)y x -=-,即240x y --=.P点处抛物线切线方程为240x y ++=,或24x y --=. ……………………7分(Ⅱ)设直线l 的方程为2y x m =+,11(,)A x y ,22(,)B x y ,联立 242x y y x m⎧=⎨=+⎩,消y 得 2840x x m --=,64160m ∆=+>.所以 128x x +=,124x x m =-, 所以1242x x +=,1282y y m +=+, 即AB 的中点为(4,8)Q m +.所以 AB 的垂直平分线方程为1(8)(4)2y m x -+=--. 因为 四边形AMBN 为菱形,所以 (0,10)M m +,M ,N 关于(4,8)Q m +对称,所以 N 点坐标为(8,6)N m +,且N 在抛物线上, 所以 644(6)m =⨯+,即10m =, 所以直线l的方程为210y x =+. ……………………14分20.解:(Ⅰ)1a =时,()ln (1)ln(1)f x x x x x =+--,(01x <<),则()ln ln(1)ln 1xf x x x x'=--=-. 令()0f x '=,得12x =. 当102x <<时,()0f x '<,()f x 在1(0,)2是减函数,当112x <<时,()0f x '>,()f x 在1(,1)2是增函数, 所以 ()f x 在12x =时取得最小值,即11()ln 22f =. ……………………4分 (Ⅱ)因为 ()ln ()ln()f x x x a x a x =+--,所以 ()ln ln()ln xf x x a x a x'=--=-. 所以当2ax =时,函数()f x 有最小值. ∀x 1,x 2∈R +,不妨设12x x a +=,则121211221111ln ln ln ()ln()2ln()22x x x xx x x x x x a x a x +++=+--≥⋅[]1212()ln()ln 2x x x x =++-. ……………………8分(Ⅲ)(证法一)数学归纳法ⅰ)当1n =时,由(Ⅱ)知命题成立. ⅱ)假设当n k =( k ∈N *)时命题成立,即若1221k x x x +++= ,则112222ln ln ln ln2k k kx x x x x x +++≥- . 当1n k =+时,1x ,2x ,…,121k x +-,12k x +满足 11122121k k x x x x ++-++++= .设11111122212122()ln ln ln ln k k k k F x x x x x x x x x ++++--=++++ ,- 11 -由(Ⅱ)得111212212()()l nk k k F x x x x+++--≥++-++++- =111111212122122122()ln()()ln()(...)ln 2k k k k k x x x x x x x x x x x +++++--++++++-+++=11111212212212()ln()()ln()ln 2k k k k x x x x x x x x ++++--++++++- .由假设可得 1()ln 2ln 2ln 2k k F x +≥--=-,命题成立. 所以当 1n k =+时命题成立.由ⅰ),ⅱ)可知,对一切正整数n ∈N *,命题都成立, 所以若211nii x==∑,则21ln ln 2nniii x x =≥-∑*(,)i n ∈N . ……………………13分 (证法二)若1221n x x x +++= , 那么由(Ⅱ)可得112222ln ln ln n n x x x x x x +++1212212212()ln[()ln 2]()ln[()ln 2]n n n n x x x x x x x x --≥++-++++- 1212122122122()ln()()ln()(...)ln 2n n n n n x x x x x x x x x x x --=++++++-+++ 1212212212()ln()()ln()ln 2n n n n x x x x x x x x --=++++++-12341234212212()ln()()ln()2ln 2n n n n x x x x x x x x x x x x --≥+++++++++- 121222(...)ln[()ln 2](1)ln 2n n x x x x x x n ≥≥++++++--- ln 2n =-.……………………13分(若用其他方法解题,请酌情给分)。
高三数学下学期统一练习(丰台二模)试题 理试题
心尺引州丑巴孔市中潭学校丰台区2021年高三年级第二学期统一练习〔二〕数学〔理科〕第一局部〔选择题 共40分〕一、选择题:本大题共8小题,每题5分,共40分。
在每题列出的四个选项中,选出符合题目要求的一项。
〔1〕假设复数(1)(2)m m -+-i 〔m ∈R 〕是纯虚数,那么实数m 等于 〔A 〕0 〔B 〕1 〔C 〕2 〔D 〕1或2 (2) 数列{}n a 是等差数列,且394a a +=,那么数列{}n a 的前11项和等于〔A 〕22 〔B 〕24 〔C 〕44 〔D 〕48〔3〕直线1:0l x y +-=与直线2,2:(2x l t y ⎧=⎪⎪⎨⎪=⎪⎩为参数〕的交点到原点O 的距离是 〔A 〕1 〔B〔C 〕2 〔D 〕〔4〕将函数2()log (2)f x x =的图象向左平移1个单位长度,那么所得图象的函数解析式为〔A 〕2log (21)y x =+ 〔B 〕2log (21)y x =- 〔C 〕2log (1)1y x =++ 〔D 〕2log (1)1y x =-+〔5〕sin()cos 2y x x π=+-,那么y 的最小值和最大值分别为〔A 〕9,28-〔B 〕-2,98 〔C 〕3,24- 〔D 〕-2,34〔6〕设m ,n 是两条不同的直线,α,β是两个不同的平面. 〔A 〕m ⊥α,n ⊂β,m ⊥n ⇒α⊥β 〔B 〕α⊥β,α∩β=m ,n ⊥m ⇒n ⊥β〔C 〕α⊥β,m ⊥α,n ∥β⇒m ⊥n 〔D 〕α∥β,m ⊥α,n ∥β⇒m ⊥n 〔7〕抛物线C :)0(22>=p px y的焦点为F ,过点F 倾斜角为60°的直线l 与抛物线C 在第一、四象限分别交于A 、B 两点,那么||||BF AF 的值等于 〔A 〕2 〔B 〕3 〔C 〕4 〔D 〕5〔8〕定义在R 上的函数()f x 和()g x 的导函数分别为'()f x ,'()g x ,那么下面结论正确的选项是①假设'()'()f x g x >,那么函数()f x 的图象在函数()g x 的图象上方;②假设函数'()f x 与'()g x 的图象关于直线x a =对称,那么函数()f x 与()g x 的图象关于点〔a ,0〕对称; ③函数()()f x f a x =-,那么'()'()f x f a x =--;④假设'()f x 是增函数,那么1212()()()22x x f x f x f ++≤. 〔A 〕①② 〔B 〕①②③ 〔C 〕③④ 〔D 〕②③④第二局部〔非选择题 共110分〕二、填空题:本大题共6小题,每题5分,共30分。
北京市丰台区2011高三一模数学文科.doc
北京市丰台区2011年高三年级第二学期统一练习(一)数 学 试 题(文)2011.3一、本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,选出符合题目要求的一项。
1.已知集合2,{|560},U U R A x x x C A ==-+≥那么=( )A .(|23)x x x <>或B .{|23}x x <<C .{|23}x x x ≤≥或D .{|23}x x ≤≤ 2.“a=2”是“直线2010ax y x y +=++=与直线平行”的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.已知平面向量,a b 的夹角为60,||4,||3,||a b a b ︒==+则= ( )A .37BC .13D4.记集合22{(,)|4}{(,)|20,0}A x y x y B x y x y y =+≤=+-≤≥和集合表示的平面区域分别为12,ΩΩ,若在区域1Ω内任取一点(,)M x y ,则点M 落在区域2Ω内的概率为( )A .12πB .1πC .14D .24ππ- 5.如图所示,O 是正方体ABCD —A 1B 1C 1D 1对角线A 1C 与AC 1的交点,E 为棱BB 1的中点,则空间四边形OEC 1D 1在正方体各面上的正投影不可能...是 ( )C BAC16.程序框图如图所示,若输入a 的值是虚数单位i ,则输出的结果是 A .-1 B .i-1 C .0 D .-i7.设m ,n 是两条不同的直线,α,β,γ有下列四个命题: ①若,,;m m βαβα⊂⊥⊥是②若//,,//m m αβαβ⊂则;③若,,,n n m m αβαβ⊥⊥⊥⊥则;④若,,,m m αγβγαβ⊥⊥⊥⊥则。
其中正确命题的序号是 ( ) A .①③B .①②C .③④D .②③8.若函数()f x 满足条件:当121212,[1,1]x x ∈-≤时,有|f(x )-f(x )|3|x -x |成立,则称()f x ∈Ω。
【恒心】【好卷速递】北京市丰台区2012年高三年级第二学期统一练习(二)(word版)理综
丰台区2012年高三年级第二学期统一练习(二)理科综合2012.5 本试卷分为选择题和非选择题两部分。
满分300分。
考试时间150分钟。
注意事项:1. 答题前,考生务必先将答题卡上的学校、班级、姓名、准考证号用黑色字迹签字笔填写清楚,并认真核对条形码上的准考证号、姓名,在答题卡的“条形码粘贴区”贴好条形码。
2. 本次考试所有答题均在答题卡上完成。
选择题必须使用2B铅笔以正确填涂方式将各小题对应选项涂黑,如需改动,用橡皮擦除干净后洱选涂其它选项。
非选择题必须使用标准黑色字迹签字笔书写,要求卞体工整、字迹清楚。
作图题用2B铅笔作图,要求线条、图形清晰。
3. 请严格按照答题卡题号在相应答题区内作答,超出答题区域书写的答案无效,在试题、草稿纸上答题无效。
4. 请保持答题卡卡面清洁,不要装订、不要折叠字、不要破损。
第I卷(选择题共120分)可能用到的相对原子质量:H-1 O-16 Ca-40 Fe-56 Cu-641 有关下图所示四种不同生物的叙述正确的是A. 甲、乙两种细胞的细胞壁都可用纤维素酶完令分解B. 乙为低等植物细胞,细胞中的核糖体和叶绿体均含RNAC. 丙的遗传物质是单链RNA,其突变率远高于DNA病毒D 丁细胞的有氧呼吸被抑制会影响脂溶性小分子物质的运输2. 下图表示某种生物的部分染色体发生了两种变异的示意图,图中①和②,③和④互为同源染色体,则图a,图b所示的变异A. 均为染色体结构变异B. 基因的数目和排列顺序均发生改变C. 均使生物的性状发生改变D. 均可发生在减数分裂过程中3.下图为人体某一反射弧的示意图,a、b为微型电流计F的两极,下列叙述错误的是A. 神经元静息吋,细胞膜对Na+的通透性增加以维持电位差B. 从a处切断神经纤维,刺激b处,效应器能产生反应C. 刺激皮肤细胞A,电流汁指针将发牛两次方向相反的偏转D.兴奋从细胞B传到细胞D,存D 在化学信号与电信号的转换4. 下列调节过程不属于负反馈调节作用的是A. 人体血糖浓度上升引起胰岛素分泌增加,血糖浓度降低B. 在酶促反应中,反应终产物过量致使酶的活性下降C. 大量猎杀草原食肉动物,导致食草动物的数量先升后降D. T细胞产生的淋巴因子可促进B细胞增殖、分化,产生抗体5.下列有关生物工程的叙述正确的是A. 应用基因诊断技术,可检测受体细胞中的目的基因是否表达B. 筛选产生抗体的杂交瘤细胞需要使用特定的选择培养基C. 茎尖细胞具有很强的分裂能力,离体培养吋不耑要脱分化即可培养成完整植株D. 将牛的体细胞核移植到去核卵细胞中,获得克隆牛是一种培育新品种的方式6.化学与科学、技术、社会、环境密切相关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
丰台区2011年高三年级第二学期统一练习(二)数 学(文科) 2011.5 一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.若2∈{1,a,a2-a},则a=
(A) -1(B) 0(C) 2(D) 2或-12.下列四个命题中,假命题为(A) ,(B) ,(C) ,(D) ,.已知a>0且a≠1,函数,在同一坐标系中的图象可能是
(A)(B)(C)(D)4.已知数列中,,,则(A)(B)(C)(D)
5.如图所示,已知,,,,则下列等式中成立的是ABCO(A)(B)(C)(D) 6.已知函数的图象如图所示,则该函数的解析式可能是xyO21-1
(A)
(B)(C)(D)
7.已知x,y的取值如下表:x0134y2.24.34.86.7从散点图可以看出y与x线性相关,且回归方程为,则(A) 3.25(B) 2.6(C) 2.2(D) 0
8.用表示a,b两个数中的最大数,设,若函数有2个零点,则k的取值范围是(A)(B)(C)(D)
二、填空题:本大题共6小题,每小题5分,共30分.9.在复平面内,复数对应的点位于第 象限.10.圆C:的圆心到直线3x+4y+14=0的距离是 .11.若,则函数的单调递增区间是 .12.已知签字笔2元一只,练习本1元一本.某学生欲购买的签字笔不少于3只,练习本不少于5本,但买签字笔和练习本的总数量不超过10,则支出的钱数最多是___元.13.一个几何体的三视图如图所示,则该几何体的体积是 .
11正视图侧视图2
0.62.4俯视图0.6ABCADP1
P2
P3
P4
P5
14.如图所示,已知正方形ABCD的边长为1,以A为圆心,AD长为半径
画弧,交BA的延长线于P1,然后以B为圆心,BP1长为半径画弧,交CB的延长线于P2,再以C为圆心,CP2长为半径画弧,交DC的延长线于P3,再以D为圆心,DP3长为半径画弧,交AD的延长线于P4,再以A为圆心,AP4长为半径画弧,…,如此继续下去,画出的第8道弧的半径是___,画出第n道弧时,这n道弧的弧长之和为___.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(本小题共13分)已知函数.(Ⅰ)求的值;(Ⅱ)若,求函数的最小值及取得最小值时的x值.16.(本小题共13分)已知梯形ABCD中,,,,G,E,F分别是AD,BC,CD的中点,且,沿CG将△CDG翻折到△.(Ⅰ)求证:EF//平面;(Ⅱ)求证:平面⊥平面.
ABCEDFGFGEABC17.(本小题共13分)
某校从高一年级学生中随机抽取60名学生,将其期中考试的数学成绩(均为整数)分成六段:,,…,后得到如下频率分布直方图.(Ⅰ)求分数在内的频率;(Ⅱ)根据频率分布直方图,估计该校高一年级学生期中考试数学成绩的平均分;(Ⅲ)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任意选取2人,求其中恰有1人的分数不低于90分的概率.18.(本小题共14分)已知函数.(Ⅰ)当时函数取得极小值,求a的值;(Ⅱ)求函数的单调区间.19.(本小题共14分) 已知椭圆C的长轴长为,一个焦点的坐标为(1,0).(Ⅰ)求椭圆C的标准方程;(Ⅱ)设直线l:y=kx与椭圆C交于A,B两点,点P为椭圆的右顶点.(ⅰ)若直线l斜率k=1,求△ABP的面积;(ⅱ)若直线AP,BP的斜率分别为,,求证:为定值.20.(本小题共13分)已知数列的前项和为,且.数列为等比数列,且,.(Ⅰ)求数列,的通项公式;(Ⅱ)若数列满足,求数列的前项和;(Ⅲ)在(Ⅱ)的条件下,数列中是否存在三项,使得这三项成等差数列?若存在,求出此三项;若不存在,说明理由.丰台区2011年高三年级第二学期统一练习(二)数 学(文科)参考答案2011.5
一、选择题:本大题共8小题,每小题5分,共40分.题号12345678答案ABDCAABC
二、填空题:本大题共6小题,每小题5分,共30分.9.Ⅲ 10.3 11.写成闭区间也给满分12.15 13.12 14. 8,注:两个空的填空题第一个空填对得2分,第二个空填对得3分.
三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(本小题共13分)已知函数.(Ⅰ)求的值;(Ⅱ)求函数的最小值,及取得最小值时的x的值.解:(Ⅰ)∵, ………………5分∴ . ………………7分(Ⅱ)∵ ∴.∴. ………………9分∴, 即. ………………11分∴ 此时 ∴. ………………12分∴当时,. ………………13分
16.(本小题共13分)已知梯形ABCD中,,,,G,E,F分别是AD,BC,CD的中点,且,沿直线CG将△CDG翻折成△.(Ⅰ)求证:EF//平面;(Ⅱ)求证:平面⊥平面.
ABCEDFGFGEABC证明:(Ⅰ)∵E,F分别是BC,CD的中点,即E,F分别是BC,C的中点, ∴EF为△的中位线. ∴EF//. ………………2分又∵平面,平面, ………………4分∴EF // 平面. ………………6分 (Ⅱ)∵G是AD的中点,,即, ∴. 又∵,,∴在中, ∴. ………………9分∴,.∵∩=,∴平面. ………………12分又∵平面,∴平面⊥平面. ………………13分
17.(本小题共13分)某校从高一年级学生中随机抽取60名学生,将其期中考试的数学成绩(均为整数)分成六段,,…,后得到如下频率分布直方图.(Ⅰ)求分数在内的频率;(Ⅱ)根据频率分布直方图,估计该校高一年级学生期中考试数学成绩的平均分;(Ⅲ)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任意选取2人,求其中恰有1人的分数不低于90分的概率.解:(Ⅰ)分数在内的频率为:. ………………3分(Ⅱ)平均分为:. ………………6分(Ⅲ)由题意,分数段的人数为:人; ………………7分分数段的人数为:人; ………………8分∵用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,∴分数段抽取5人,分别记为A,B,C,D,E;分数段抽取1人,记为M. ………………9分因为从样本中任取2人,其中恰有1人的分数不低于90分,则另一人的分数一定是在分数段,所以只需在分数段抽取的5人中确定1人.设“从样本中任取2人,其中恰有1人的分数不低于90分为”事件, ………………10分则基本事件空间包含的基本事件有:(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),(C,D),(C,E),(D,E),(A,M),(B,M),(C,M),(D,M),(E,M)共15种.事件包含的基本事件有(A,M),(B,M),(C,M),(D,M),(E,M)5种.………………12分∴恰有1人的分数不低于90分的概率为. ………………13分
18.(本小题共14分)已知函数.(Ⅰ)当时函数取得极小值,求a的值;(Ⅱ)求函数的单调区间.解:(Ⅰ)函数的定义域为∪, ………………1分. ………………3分∵时函数取得极小值,∴. ………………4分∴. ………………5分当时,在内,在内, ………………6分∴是函数的极小值点.∴有意义. ………………7分(Ⅱ)的定义域为∪,. 令,得. ………………9分(ⅰ)当时,
0极小值
11分(ⅱ)当时,
0极小值综上所述: ………………13分当时,函数的单调递减区间为,单调递增区间为,;当时,函数的单调递减区间为,,单调递增区间为.
14分19.(本小题共14分) 已知椭圆C的长轴长为,一个焦点的坐标为(1,0).(Ⅰ)求椭圆C的标准方程;(Ⅱ)设直线l:y=kx与椭圆C交于A,B两点,点P为椭圆的右顶点.(ⅰ)若直线l斜率k=1,求△ABP的面积;(ⅱ)若直线AP,BP的斜率分别为,,求证:为定值.(实际上,P是不同于A,B的任一点,结论都成立.)解:(Ⅰ)依题意椭圆的焦点在x轴上,且,, ………………1分∴, . ………………2分∴椭圆C的标准方程为. ………………4分(Ⅱ)(ⅰ) ………………5分∴ 或 , ………………7分即,, .所以. ………………9分(ⅱ)证明:设,.椭圆的右顶点为 , 消y整理得 ,不妨设x1>0>x2,∴ ,;,.……………12分 ………………13分
∴ 为定值. ………………14分20.(本小题共13分)已知数列的前项和为,且.数列为等比数列,且首项,.(Ⅰ)求数列,的通项公式;(Ⅱ)若数列满足,求数列的前项和为;(Ⅲ)在(Ⅱ)的条件下,问数列中是否存在三项,使得这三项成等差数列.若存在,求出此三项,若不存在,说明理由.解:(Ⅰ)∵ 数列的前项和为,且,∴ 当时,.当时,亦满足上式,故,. ………………3分 又 数列为等比数列,设公比为,∵ ,, ∴.
