九年级数学竞赛讲座 24第二十四讲 几何的定值与最值
第24章 与圆有关的最值

《专题复习四几何图形中的最值探究》教学设计马寨中心学校刘洪贺教学目标:1、通过几何图形中的最值探究题的专题复习,培养学生观察、分析的探究能力,进而提高学生的综合解题能力。
2、通过解法归类总结,增强学生解答数学几何图形中的最值探究题的兴趣。
教学重点:几何图形中的最值探究题型的分析解答。
教学难点:几何图形中的最值探究题的解法归类总结。
教学流程:一、安徽中考热点命题预测几何图形中的最值探究题是近两年安徽中考中常见的题型之一,一般涉及“轴对称型”最值探究、“圆型”最值探究、“勾股定理型”最值探究等。
2015年的第20题是“勾股定理型”最值探究的问题,2016年的第10题是“圆型”最值探究,题型以解答题和选择题为主,分值为4~10分。
预计2017年中考中仍会以几何图形中的最值探究作为考查对象。
二、专题题型及解法特点·最值问题:可以分为最大值和最小值·求最值:借助于“两点之间线段最短”或“三角形三边之间的关系(两边之和大于第三边或勾股定理)”。
·类型:与圆(定弦定角)有关、与轴对称有关、与直角三角形有关三、解题方法指导·一般解法:最值线段——(转化构造三角形)——使最值线段与定长线段构成三角形——三角形三边关系定理三点共线时取得最值(或勾股定理三边关系)解法归类一“轴对称型”:与对称点有关·解法:作对称点,利用两点之间线段最短【典型例题1】如图,菱形ABCD中,对角线AC=6,BD=8,M,N分别是BC,CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是. .解析:根据轴对称性,作出点N关于直线BD对称的点H,连接MH,求MH的长即可。
【针对练习】如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上的一个动点,则PB+PE的最小值是. .解法归类二“圆型”:与定弦定角的圆有关·解法:最值线段与定线段构成三角形,三点共线时取得最值【典型例题2】(2016安徽第10题)如图,Rt△ABC中AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC.则线段CP长的最小值为()解析:本题是与定弦定角有关的圆有关。
中考数学复习专题讲座(九)几何最值问题的解法浅探

中考数学复习专题讲座(九)---几何最值问题解法探讨在平面几何的动态问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的周长或面积、角的度数以及它们的和与差)的最大值或最小值问题,称为最值问题。
解决平面几何最值问题的常用的方法有:(1)应用两点间线段最短的公理(含应用三角形的三边关系)求最值;(2)应用垂直线段最短的性质求最值;(3)应用轴对称的性质求最值;(4)应用二次函数求最值;(5)应用其它知识求最值。
一用两点之间线段最短的公理(含应用三角形的三边关系)求最值:典型例题:例1.如图,∠MON =90°,矩形ABCD 的顶点A 、B 分别在边OM ,ON 上,当B 在边ON 上运动时,A 随之在边OM 上运动,矩形ABCD 的形状保持不变,其中AB =2,BC =1,运动过程中,点D 到点O 的最大距离为【 】A .21+B .5C .14555 D .52 【答案】A 。
【考点】矩形的性质,直角三角形斜边上的中线性质,三角形三边关系,勾股定理。
【分析】如图,取AB 的中点E ,连接OE 、DE 、OD ,∵OD ≤OE +DE ,∴当O 、D 、E 三点共线时,点D 到点O 的距离最大,此时,∵AB =2,BC =1,∴OE =AE =12AB =1。
DE =2222AD AE 112=+=+=,∴OD 的最大值为:21+。
故选A 。
例2.在锐角三角形ABC 中,BC =24,∠ABC =45°,BD 平分∠ABC ,M 、N 分别是BD 、BC 上的动点,则CM +MN 的最小值是 ▲ 。
【答案】4。
【考点】最短路线问题,全等三角形的判定和性质,三角形三边关系,垂直线段的性质,锐角三角函数定义,特殊角的三角函数值。
【分析】如图,在BA 上截取BE =BN ,连接EM 。
∵∠ABC 的平分线交AC 于点D ,∴∠EBM =∠NBM 。
在△AME 与△AMN 中,∵BE =BN ,∠EBM =∠NBM ,BM =BM ,∴△BME ≌△BMN (SAS )。
中考数学复习《几何最值---瓜豆原理》考点例题PPT讲义

如图,△APQ 是直角三角形,∠PAQ=90°且 AP=2AQ,当 P 在圆 O 运动时,Q 点轨迹是? 【分析】考虑 AP⊥AQ,可得 Q 点轨迹圆圆心 M 满足 AM⊥AO;
考虑 AP:AQ=2:1,可得 Q 点轨迹圆圆心 M 满足 AO:AM=2:1. 即可确定圆 M 位置,任意时刻均有△APO∽△AQM,且相似比为 2.
【模型总结】 为了便于区分动点 P、Q,可称点 P 为“主动点”,点 Q 为“从动点”. 此类问题的必要条件:两个定量 主动点、从动点与定点连线的夹角是定量(∠PAQ 是定值); 主动点、从动点到定点的距离之比是定量(AP:AQ 是定值).
【结论】(1)主、从动点与定点连线的夹角等于两圆心与定点连线的夹角: ∠PAQ=∠OAM; (2)主、从动点与定点的距离之比等于两圆心到定点的距离之比: AP:AQ=AO:AM,也等于两圆半径之比. 按以上两点即可确定从动点轨迹圆,Q 与 P 的关系相当于旋转+伸缩. 古人云:种瓜得瓜,种豆得豆.“种”圆得圆,“种”线得线,谓之“瓜豆原理”.
中考数学复习《几何最值---瓜豆原理》 考点例题PPT讲义
动点的轨迹为定圆时,可利用:“一定点与圆上的动点距离最大值为定点到圆心的距离与半 径之和,最小值为定点到圆心的距离与半径之差”的性质求解。 确定动点轨迹为圆或者圆弧型的方法: (1)动点到定点的距离不变,则点的轨迹是圆或者圆弧。 (2)当某条边与该边所对的角是定值时,该角的顶点的轨迹是圆,具体运用如下; ①见直角,找斜边,想直径,定外心,现圆形 ②见定角,找对边,想周角,转心角,现圆形
【小结】确定 Q 点轨迹圆即确定其圆心与半径, 由 A、Q、P 始终共线可得:A、M、O 三点共线, 由 Q 为 AP 中点可得:AM=1/2AO. Q 点轨迹相当于是 P 点轨迹成比例缩放. 根据动点之间的相对位置关系分析圆心的相对位置关系; 根据动点之间的数量关系分析轨迹圆半径数量关系. 如图,P 是圆 O 上一个动点,A 为定点,连接 AP,作 AQ⊥AP 且 AQ=AP. 考虑:当点 P 在圆 O 上运动时,Q 点轨迹是?
2020年九年级数学中考经典几何题讲义系列:几何最值问题

3 / 18
(4) 两点两线的最值问题: (两个动点+两个定点)
问题特征:两动点分别在两条直线上独立运动,一动点分别到一定点和另一动点的距离和最小。 核心思路:利用轴对称变换,使一动点在另一动点的对称点与定点的线段上(两点之间线段最 短),且这条线段垂直于另一动点的对称点所在直线(连接直线外一点与直线上各点的所有线 段中,垂线段最短)时,两线段和最小,最小值等于这条垂线段的长。 变异类型:演变为多边形周长、折线段等最值问题。 1. 如图,点 A 是∠MON 内的一点,在射线 ON 上作点 P,使 PA 与点 P 到射线 OM 的距离之 和最小。
A.
B.
C.
D.1
考点: 轴对称-最短路线问题;正方形的性质. 菁优网版权所有
分析: 根据题意得出作 EF∥AC 且 EF= ,连结 DF 交 AC 于 M,在 AC 上截取 MN=
,此时四边形 BMNE
解答: 的周长最小,进而利用相似三角形的判定与性质得出答案. 解:作 EF∥AC 且 EF= ,连结 DF 交 AC 于 M,在 AC 上截取 MN= ,延长 DF 交 BC 于 P,作
2.连结对称点与另一个定点,则直线段长度就是我们所求。 变异类型:实际考题中,经常利用本身就具有对称性质的图形,比如等腰三角形,等边三角形、 正方形、圆、二次函数、直角梯形等图形,即其中一个定点的对称点就在这个图形上。 1.如图,直线 l 和 l 的同侧两点 A、B,在直线 l 上求作一点 P,使 PA+PB 最小。
∵LN=AS=
=40.
人教版九年级上册 第24章: 圆的最值专题
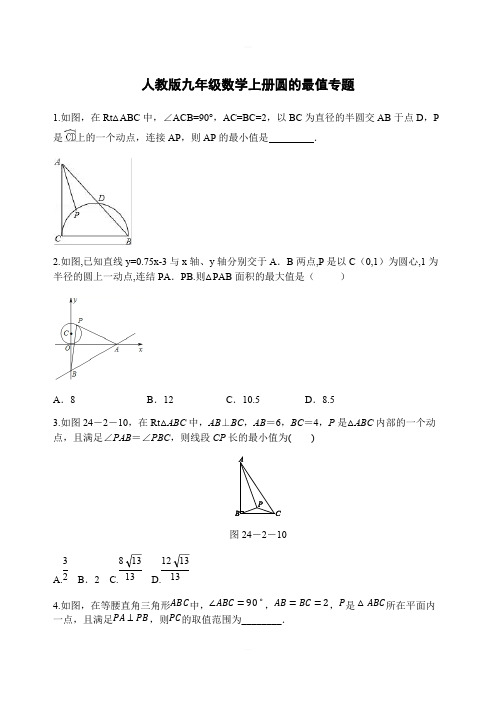
是上的一个动点,连接如图,已知直线y=0.75x-3与x轴、y轴分别交于A.B两点,P是以C(0,1)为圆心,1半径的圆上一动点,连结PA.PB.则△PAB面积的最大值是()8B.12C.10.5D.8.5如图24-2-10,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )CH⊥BD过点C作于H,连接AH,则AH的最小值为______如图,等边三角形ABC中,D是边BC上一点,过点C作AD垂线段,垂足为点E 连接BE,若AB=2,则BE的最小值是____________如图,等边△ABC的边长为6,D为BC边上的中点,P为直线BC上方的一个动点,且满足∠PAD=∠PDB,则线段CP长的最大值为 .在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是以点A为圆心4为半径的圆上一点,连接BD,点M为BD中点,线段CM长度的最大值为 .12.如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ的最小值()A.5B.4C.4.75D.4.813.如图,在边长为6的正方形ABCD中,点E、F、G分别在边AB、AD、CD上,EG与BF交于点I,AE=2,BF=EG,DG>AE,则DI的最小值等于( )A. +3B.2﹣2C.2﹣D.2+314.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点.若PB切⊙O于点B,则PB的最小值是( )A. B.PQ,Q为切点,则切线长PQ的最小值为( )A. B. 3 C. 3 D.如图,已知菱形ABCD的边长为8,∠B=60°,点O为对角线AC的中点,⊙O半径,点P为CD边上一动点,PE与⊙O相切于点E,则PE的最小值是 .如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是(A-2-3132B.1C.D.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=,D是线段BC上的一个动点,以22为直径画⊙O分别交AB.AC于点E,F,连接EF,则线段EF长度的最小值为()A. 1 B. C. D. 223且始终满足∠BPC=90°,则t的最小值是.。
九年级数学上册 第二十四章 圆 专题42 圆中的最值问题

6.如图,⊙O的半径为1,弦AB=1,点P为优弧AB上一动点,AC⊥AP交直线PB于点C,求△ABC的最大 面积.
3.如图,在平面直角坐标系中,等边△OAB的边OB在x轴正半轴上,点A(3,m),m>0,点D,E分别从 B,O以相同的速度向O,A运动,连接AD,BE,交点为F,M是y轴上一点,则FM的最小6-值2 是3 __
4.如图,在平面直角坐标系中,分别以点A(2,3),点B(3,4)为圆心,1,3为半径作⊙A,⊙B,M, N分别是⊙A,⊙B上的动点,P为x轴上的动点,求PM+PN的最小值.
第二十四章 圆
1.如图,在平面直角坐标系中,点A的坐标是(4,3),动⊙M经过A,O两点,分别与两轴的正半轴交 5 于点B,C,则BC的最小值为____.
2.如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx-3k+4与⊙O交于 B,C两24点,则弦BC的长的最小值为____.
九年级数学中考典型及竞赛训练专题25平面几何的最值问题2(附答案解析)
九年级数学中考典型及竞赛训练专题25 平面几何的最值问题阅读与思考几何中的最值问题是指在一定的条件下,求平面几何图形中某个确定的量(如线段长度、角度大小、图形面积)等的最大值或最小值.求几何最值问题的基本方法有:1.特殊位置与极端位置法:先考虑特殊位置或极端位置,确定最值的具体数据,再进行一般情形下的推证.2.几何定理(公理)法:应用几何中的不等量性质、定理.3.数形结合法等:揭示问题中变动元素的代数关系,构造一元二次方程、二次函数等.例题与求解【例1】在RtA ABC中,CB=3, C4=4, M为斜边AB ±一动点.过点M作MD丄AC于点D,过M 作ME丄CB于点E,则线段DE的最小值为__________________ .(四川省竞赛试题)解题思路:四边形CDMF为矩形,连结CM,则DE= CM,将问题转化为求CM的最小值.【例2】如图,在矩形ABCD中,4B=20cm, BC=10cm.若在AC, AB上各取一点M, N,使BM+M/V 的值最小,求这个最小值.(北京市竞赛试题)解题思路:作点8关于&C的对称点连结B'M, B'A,贝'J BM= B'M,从而BM+MN= B'M+MN.要使BM+MN的值最小,只需使FM十M/V的值最小,当B', M, N三点共线且B7V丄AB时,B'M+MN的值最小.【例3】如图,己知DABCD, AB=a, BC=b(a>b), P为边上的一动点,直线DP交CB的延长线于Q.求AP+BQ的最小值. (永州市竞赛试题)解题思路:设AP=x,把AP, BQ分别用x的代数式表示,运用不等式以a2+b2>2ab或a+b》2范 (当且仅当a=b时取等号)来求最小值.【例4]阅读下列材料:问题如图1, 一圆柱的底面半径为5dm,高为5dm, BC是底面直径,求一只蚂蚁从A点出发沿圆柱表面爬行到C点的最短路线.小明设计了两条路线:沿AB剪开路线1:侧面展开图中的线段AC.如图2所示.设路线I的长度为/i,则/i2=AC2=AB2 +BC2 =25+(571)2=25+25n2.路线2:高线AB十底面直径BC.如图1所示.设路线 / 的长度为b,则 F = (BCMB)2=(5+10)2 =225.••/I2-/22 = 25+257T2-225=257r2-200=25(7T2-8), /. 42 >/22 , /. h>l2 .所以,应选择路线2.(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1分米,高AB为5分米"继续按前面的路线进行计算.请你帮小明完成下面的计算:路线1:h2=AC2= ____________ :路线2: /22= (AB+BC) 2= __________ .•••/『______ 於,・・・h___ /2(填“〉"或“<"),所以应选择路线__________ (填“1"或"2")较短.(2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为门高为h时,应如何选择上面的两条路线才能使蚂蚁从点&出发沿圆柱表面爬行到C点的路线最短. (衢州市中考试题)解题思路:本题考查平面展开一最短路径问题•比较两个数的大小,有时比较两个数的平方比较简便.比较两个数的平方,通常让这两个数的平方相减.【例5】如图,己知边长为4的正方形钢板,有一个角锈蚀,其中AF=2, BF=1.为了合理利用这块钢板,将在五边形EABCD内截取一个矩形块MD/VP,使点P在AB上,且要求面积最大,求钢板的最大利用率. (中学生数学智能通讯赛试题)解题思路:设DN* PN=y,则S=xy.建立矩形MD/VP的面积S与x的函数关系式,利用二次函数性质求S的最大值,进而求钢板的最大利用率.【例6】如图,在四边形ABCD 中,AD=DC=1, Z DAB=A DCB=90°, BC, AD 的延长线交于P,求AB& PAB 的最小值.(中学生数学智能通讯赛试题)AR PA解题思路:设PD=x (x>l ),根据勾股定理求出PC,证RtA PCD- RtA PAB,得到 ——=——,求出 P AB,根据三角形的面积公式求出y=AB^P AB .整理后得到y$4,即可求出答案.能力训练A 级1. 如图,将两张长为8、宽为2的矩形纸条交叉,使重叠部分是一个菱形.容易知道当两张纸条 垂直时,菱形的周长有最小值,那么菱形周长的最大值是 ________________ .(烟台市中考试题)2. D 是半径为5cm 的O0内一点,且OD=3cm,则过点0的所有弦中,最短的弦 _______________ cm.(广州市中考试题)3. 如图,有一个长方体,它的长BC=4,宽AB=3,高BBi=5. —*只小虫由A 处出发,沿长方体表面 爬行到G ,这时小虫爬行的最短路径的长度是 ___________ .("希望杯"邀请赛试题)4.如图,Uh ABC 中,AB=1Q, BC=6,经过点C 且与边AB 相切的动圆与CB, CA 分别相交于点E, F,则线段EF 长度的最小值是()(兰州市中考试题)5. 如图,圆锥的母线长04=6,底面圆的半径为2. —小虫在圆锥底面的点&处绕圆锥侧面一周又第1题图A. 4A /2B. 4.75C. 5D. 4.8第4題图回到点则小虫所走的最短距离为()(河北省竞赛试题)A. 12B. 4TIC. 6 VID. 6 羽6. 如图,已知Z MON= 40°, P 是Z MO N 内的一定点,点A, B 分别在射线OM, OA/上移动,当△网3 周长最小时,ZAPB 的值为()(武汉市竞赛试题)A. 80°B. 100°C. 120°D. 140°7. 如图,血是以等边三角形ABC-边AB 为半径的四分之一圆周,P 为AD 上任意一点.若4C=5, 则四边形ACBP 周长的最大值是()(福州市中考试题)A. 15B. 20C. 15+5V2D. 15+5 石交AB 于M,交DC 与N.⑴设AE=x,四边形ADNM 的面积为S,写出S 关于x 的函数关系式. (2)当AE 为何值时,四边形ADNM 的面积最大?最大值是多少?(山东省中考试题)9. 如图,六边形ABCDEF 内接于半径为/•的O0,其中AD 为直径,且AB=CD=DE=FA.(1)当Z BAD=75°时,求处的长; (2)求证:BCII 40II FE :⑶设AB=X t 求六边形ABCDEF 的周长/关于x 的函数关系式,并指出x 为何值时,/取得最大值.10. 如图,已知矩形ABCD 的边长AB=2, BC=3,点P 是AD 边上的一动点(P 异于A 、D ). Q 是BC第6题图&如图,在正方形ABCD 中,AB=2,第8題图E 是AD 边上一点(点E 与点A, D 不重合),BE 的垂直平分线第7題图边上任意一点.连结AQ ,DQ,过P 作PEII DQ 交于AQ 于F,作PF//AQ 交DQ 于F.(1) 求证:△&PE-厶 ADQ ;(2) 设&P 的长为X,试求APEF 的面积关于x 的函数关系式,并求当P 在何处时,取得 最大值?最大值为多少?(3)当Q 在何处时,AADQ 的周长最小?(须给出确定Q 在何处的过程或方法,不必证明)(无锡市中考试题)11. 在等腰AABC 中,AB=AC=5, BC=6.动点M, N 分别在两腰AB, AC 上(M 不与B 重合,N 不与A, C 重合),且M/VII BC.将NAMN 沿M/V 所在的直线折叠,使点A 的对应点为P.(1) 当MN 为何值时,点P 恰好落在BC 上?(2)设MN=x, △ MNP 与等腰NABC 重叠部分的面积为y,试写出y 与x 的函数关系式,当x 为何值时,y 的值最大,最大值是多少?(宁夏省中考试题)B 级1. 己知凸四边形ABCD 中,AB+AC+CD= 16,且S 馳彤MCO =32,那么当AC= _____________________ , BD= 时,四边形4BCD 面积最大,最大值是 _________ .(“华杯赛"试题)2. 如图,已知ZkABC 的内切圆半径为门Z4=60°, BC=2y[3 ,则/■的取值范围是 ___________ •(江苏 省竞赛试题)3. 如图O0的半径为2, O0内的一点P 到圆心的距离为1,过点P 的弦与劣弧金组成一个弓形,则此弓形面积的最小值为 __________4. 如图,A4BC 的面积为 1,点 D, G, E 和 F 分别在边 AB, AC, BC 上,BD<DA, DGII BC, DEWAC,A B第2题图 第3题图第4题图GFIIAB,则梯形DEFG面积的最大可能值为.(上海市竞赛试题)5.已知边长为a的正三角形ABC,两顶点A, B分别在平面直角坐标系的x轴,y轴的正半轴上滑动,点C在第一象限,连结0C,则0C的最大值是____________ •(潍坊市中考试题)6.已知直角梯形ABCD中,ADW BC,丄BC, AD=2, BC=DC=5,点P在BC上移动,则当必+ PD取最小值时,"PD中边AP上的高为()(鄂州市中考试题)D. 3第6題图第7题图第8题图7.如图,正方形&BCD的边长为4cm,点P是BC边上不与点B, C重合的任意一点,连结AP,过点P 作PQ丄&P交DC于点Q.设BP的长为xcm, CQ的长为ycm.(1)求点P在BC上运动的过程中y的最大值;(2)当尸丄cm时,求x的值. (河南省中考试题)4&如图,y轴正半轴上有两点A(0, a), 8(0, b),其中a>b>0.在x轴上取一点C,使乙ACB最大, 求C点坐标. (河北省竞赛试题)9.如图,正方形&BCD的边长为1,点M, /V分别在BC, CD上,使得△ CMN的周长为2.求:(1)Z MAN的大小;(2)△MAN的面积的最小值. (“宇振杯"上海市竞赛试题)10,如图,四边形ABCD中,AD= CD, Z DAB=A ACB=90°,过点D作DE丄AC于F, DE与相交于GFIIAB,则梯形DEFG 面积的最大可能值为 .(上海市竞赛试题)点E.(1) 求证:AB AF=CB ・CD ;(2) 已知AB=15cm, 8C=9cm, P 是射线DE 上的动点,设DP=xcm(x>0),四边形BCDP 的面积为ycm 2. ① 求y 关于x 的函数关系式;② 当x 为何值时,NPBC 的周长最小?求出此时y 的值.(南通市中考试题)11. 如图,己知直线/: y = Rx+2 — 4R 伙为实数).(1) 求证:不论k 为任何实数,直线/都过定点M,并求点M 的坐标;(2) 若直线/与x 轴、y 轴的正半轴交于A, B 两点,求AAOB 面积的最小值.(太原市竞赛试题)12. 如图,在RtA ABC 中,Z C=90°, BC=2, AC=x,点F 在边AB ±,点G, H 在边BC 上,四边形 EFGH 是一个边长为y 的正方形,且AE=AC.(1) 求y 关于x 的函数解析式;(2) 当x 为何值时,y 取得最大值?求出y 的最人值.(上海市竞赛试题)第6题图第9题图专题25 平面几何的最值问题12~5提示:当CM丄AB时,CM值最小,CM =警詈例2如图.蜩+ M/V的最小值为点厅到离B'F, BE= ABBC = 4^5 cm, BB' = 8>/5 cm , AE = ACJ AB'_ BE'= 8>/5cm.在△ABF中,由丄BB,2AB的距•处=丄AB'B'F,得B'F=16cm.故BM + MN的最小值为216旳例3由5DS△呻得話喘’即话畔:.AP+BQ=x+--b. \'x+ — >2jx— = 2y/ab,・••当且仅当x x V x= 俪时,上式等号成立.故当AP=y^b时.AP+BQ最小,其最小值为2他(例5题图)-b.例4⑴£=25 + *, /; =49, /i</2,故要选择路线/较短.(2)/;=//+(〃)',f =(方+ 2r)‘,一g=r[(沪一4”一4/?].当r=斗时,/f = 1},当r> 严厶时,I; > I;,当r<-^—时,/; < 7;. 例 5 设DN=x, PN=y,贝!)S=xy.由厶APQc^^ABF,得=丄_兀__4 _2-(4-x) 2即x=10—2y,代入S=xy 得S=xy=y(10—2y),即S=-2(y-# 25 5+ —.因3<y<4,而)/=空不在自变量y的取值范围内,所以y=仝不是极值点.当y=3时.S(3)=12.当y=4时,S(4)=&故Smax=12.此2时,钢板的最大利用率——j ---------- =80%. 例6设PD=x(x〉l),则PC= ,由RtAPCDcoA42— x2xl2咙得妇警.眉,令FS.则尸敎5如=斜’求y的最小值有时’y有最小值4.②运用基本不等式"弓+占S23222 r-1 2口+心•••当〒=口即当口时宀有最小值丄③借用判别式.去分母’得塔+2 (1—y) x+l+2y=0,由A=4 (1—y) 2—4 (l+2y) =4y (y —4) >0,得y>4, .'.y 的最小值为 4. A 级1. 17提示:当两张纸条的对角重合时,菱形周长最大.2.83. >/744.D5.D6. B7. C 提示:当点P 与点D 重合时.四边形ACBP 的周长最大.& ⑴连结 ME,过N 作 NF 丄ABTF.可证明 R^EBA^Rt^MNF,得 MF=AE=x.\'ME 2=AE 2+AM 2, 故 .即(2-AM) —X+AM, AM=1 一丄x 2,.・.S=人“十xAD=人“十力尸 x2422=AM+AM+MF=2AM+AE=2 (1 一丄F) +/= — 丄x 2+x+2.42(2) S=~- (x 2-2x+l) +-= 一丄(x-1)计?.故当胚=x=l 时,四边形ADNM 的面积最大,2 2 2 2 此时最大值为-.29. (1) BC 长为迥.(2)提示:连结BD (3)过点B 作BM 丄AD T M ・由 ⑵ 知四边形ABCD3AB , x 2,W为等腰梯形.从而 BC=AD-2 AM=2r-2AM.由厶BAM^^DAB,得 AM=・・・BC=2/•—一.AD 2rr最大值6 r.10. (1) Z.APE= Z.ADQ, Z.AEP=Z.AQD.・'.^APE^^ADQ. (2)由厶APE^>^ADQ, 'PDFs'1 1 13 3 3ADQ, S\PEF = — SmPfQf,得 S APEF = — — x~~^~x =—— (x — — ),+—.故当 x=—时,即 P 是 AD 的中点2 3 3 2 4 2 时,Sw 取得最大值.(3)作A 关干直线BC 的对称点A f.连结D 川交BC 干Q,则这个Q 点就是使 △AD0周长最小的点,此时0是BC 的中点.11. (1)点P 恰好在BC 上时,由对称性知MN 是厶4肚 的中位线・・••当MN=^BC=3时,点P 在r"r"x同理.EF=2r- — .l=4x+2 (2 r-—)=--r r r(x-r) 2+6r (0<v<V2 r)..当 x=r^, l 取得(第8題图)5. 卑丄4提示:当04=03时.0C 的长最大.6.CBC 上.( 2)由已知得"BC 底边上的高力=J5L32 =4.①当0<疋3时.如图1,连结AP 并延长交BC 干点D, AD 与MN 交干点0.2 12 1 1由MAWC,得A 。
2024年中考数学专题复习定值与最值问题
定值与最值问题1、平面几何最值问题:在平面几何问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的面积、角的度数)的最大值或最小值问题,称为最值问题。
线段最值问题的解决通常方法:应用几何性质.①三角形的三边关系:两边之和大于第三边,两边之差小于第三边;②两点间线段最短;③连结直线外一点和直线上各点的所有线段中,垂线段最短;④定圆中的所有弦中,直径最长.基本类型有:将军饮马、选址造桥、线段之差的最大值,隐圆最值,瓜豆原理,胡不归最值,阿氏圆等。
2、立体几何最值问题:展开平面图形,根据平面几何最值问题方法去做!3、代数最值问题:无非就是根据完全平方公式或者二次函数的知识去求解!例1.如图,A、B两个机离线l的距离分别是3米,5米,CD=6米,若由l上一点分别向A,B连线,最短为()A.11米B.10米C.9米D.8米1.如图Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED、EB,则△BDE周长的最小值为()A.2 5 B.2 3 C.25+2 D.23+22.如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB 的中点,P是直径AB上的一动点.若MN=1,则△PMN周长的最小值为__ .3.直线l1、l2交于点O,A、B是两直线间的两点,从点A出发,先到l1上一点P,再从点P到l2上一点Q,再回到点B,求作P、Q两点,使四边形APQB周长最小.4.A、B是位于河流两旁的两个村庄,要在这条宽度为d的河上建一条垂直的桥,使得从A村到B村的距离之和最短.试着画出桥应该建在何处?例2.如图,AC⊥BC于C,连接AB,点D是AB上的动点,AC=6,BC=8,AB=10,则点C到点D的最短距离是()A.6 B.8 C.403D.2451.如图,点A 的坐标为(1,0),点B 在直线y x =上运动,当线段AB 最短时,点B 的坐标为( )A .(0,0)B .(21-,21-)C .(22,22-)D .(22-,22-) 2.如图,在平面直角坐标系xOy 中,直线AB 经过点A (﹣4,0)、B (0,4),⊙O 的半径为1,点P 在直线AB 上,过点P 作⊙O 的一条切线PQ ,Q 为切点,则切线长PQ 的最小值为_________.例3.如图,在菱形ABCD 中,AB =4,∠A =135°,点P 、M 、N 分别为对角线BD 及边BC ,CD 上的动点,则PM +PN 的最小值为__ .1.如图,∠ABC =45°,BC =42,BD 平分∠ABC 交AC 于点D ,M 、N 分别是BD 和BC 上的动点(M 与B ,D 两点不重合,N 与B ,C 两点不重合),则CM +MN 的最小值为__ .2.如图,∠AOB =45°,P 是∠AOB 内一定点,PO =10,Q 、R 分别是OA ,OB 上的动点,则△PQR 周长的最小值为__ .例4.如图,两点A 、B 在直线MN 外的同侧,A 到MN 的距离AC =8,B 到MN 的距离BD =5,CD =4,P 在直线MN 上运动,则PB PA -的最大值等于 .1.如图所示,已知11(,)2A y ,2(2,)B y 为反比例函数1y x =图象上的两点,动点(,0)P x 在x 正半轴上运动,当线段AP 与线段BP 之差达到最大时,点P 的坐标是( )A .1(,0)2B .(1,0)C .3(,0)2D .5(,0)22.点A 、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P 是x 轴上使得PA PB -的值最大的点,Q 是y 轴上使得QA +QB 的值最小的点,则OP *OQ = .例5.在坐标系中,点A 的坐标为(3,0),点B 为y 轴正半轴上的一点,点C 是第一象限内一点,且AC =2.设tan ∠BOC =m ,则m 的取值范围是_________.1.如图, △ABC 中,∠ABC =90°,AB =6,BC =8,O 为AC 的中点,过O 作OE ⊥OF ,OE 、OF 分别交射线AB 、BC 于E 、F ,则EF 的最小值为 .2.如图,已知Rt △ABC 中,∠ACB =90°,AC =3,BC =4,点D 是AB 的中点,E 、F 分别是直线AC 、BC 上的动点,∠EDF =90°,则EF 的最小值是_____________.例6.如图,圆柱的轴截面ABCD 是边长为4的正方形,动点P 从A 点出发,沿看圆柱的侧面移动到BC 的中点S 的最短距离是( )A .212π+B .2412π+C .214π+D .242π+1.如图,长方体的底面边长分别为2cm 和4cm ,高为5cm .若一只蚂蚁从P 点开始经过4个侧面爬行一圈到达Q 点,则蚂蚁爬行的最短路径长为( )A .13cmB .12cmC .10cmD .8cm2.如图,圆柱底面半径为2cm ,高为9cm π,点A 、B 分别是圆柱两底面圆周上的点,且A 、B 在同一母线上,用一棉线从A 顺着圆柱侧面绕3圈到B ,求棉线最短为 cm .第1题 第2题例7.求二次三项式2x 2x +3的最小值.1.求代数式﹣2x 2+3x +5的最大值.例9.如果P 是边长为2的正方形ABCD 的边CD 上任意一点且PE ⊥DB ,PF ⊥CA ,垂足分别为E ,F ,则PE +PF =__ __.1.如图、已知矩形ABCD ,R ,P 户分别是DC 、BC 上的点,E ,F 分别是AP 、RP 的中点,当P 在BC 上从B 向C 移动而R 不动时,那么下列结论成立的是( )A .线段EF 的长逐渐增大B .线段EF 的长逐渐减小C .线段EF 的长不改变D .线段EF 的长不能确定2.如图,在平面直角坐标系x O y 中,矩形AOCD 的顶点A 的坐标是(0,4),现有两动点P 、Q ,点P 从点O 出发沿线段OC (不包括端点O ,C )以每秒2个单位长度的速度,匀速向点C 运动,点Q 从点C 出发沿线段CD (不包括端点C ,D )以每秒1个单位长度的速度匀速向点D 运动.点P ,Q 同时出发,同时停止,设运动时间为t 秒,当t =2秒时PQ =52.(1)求点D 的坐标,并直接写出t 的取值范围;(2)连接AQ 并延长交x 轴于点E ,把AE 沿AD 翻折交CD 延长线于点F ,连接EF ,则△A EF 的面积S 是否随t 的变化而变化?若变化,求出S 与t 的函数关系式;若不变化,求出S 的值.1.如图,在正方形ABCD 中,G 是正方形内一点,AD =4,P 是BC 的中点,且BG =BP ,则DG +12GC 的最小值是__________.(提示:考虑用相似转化,系数需要化成相同)。
成武县二中九年级数学上册第二十四章圆专题课堂(十二)圆中的最值问题课件新版新人教版35
A
F O
D C
G
说说以上作法的道理.
• 在上面的作图过程中 , 因 为直线 DE 和 FG 只有一个交点
E
O , 并且点 O 到 A , B , C 三个点
的距离相等 , 所以经过 A , B , C B 三个点可以作一个圆 , 并且只
能作一个圆.
A
F O
D C
G
• 不在同一直线上的三个点确定一个圆.
分别作AB、BC垂直平分线l1、l2.
l1
l2
显然l1∥l2 ,
l1与l2无交点 , 故产生矛盾. 所以假设不成立.
A
B
C
即过同一直线上的三点不能作圆.
• 三角形的三个顶点确定一 个圆 , 这个圆叫做三角形的外 接圆 , 外接圆的圆心是三角形 三边垂直平分线的交点 , 叫做 B 这个三角形的外心.
●O
B
C
锐角三角形的外心位于三角形内. 直角三角形的外心位于直角三角形斜边中点. 钝角三角形的外心位于三角形外.
• 现在你知道了怎样要将一个如下图的破
损的圆盘复原了吗?
A
• 方法:
• 1、在圆弧上任取三点A、
B、C。
• 2、作线段AB、BC的垂直
第二十四章 圆
24.4 弧长和扇形面积
专题课堂(十二) 圆中的最值问题
1.(2018·宜宾)在△ABC 中,若 O 为 BC 边的中点, 则必有:AB2+AC2=2AO2+2BO2 成立. 依据以上结论,解决如下问题:如图,在矩形 DEFG 中,已知 DE=4, EF=3,点 P 在以 DE 为直径的半圆上运动,则 PF2+PG2 的最小值为 D A. 10 B.129 C.34 D.10
A •●
九年级数学平面几何中的定值问题例题讲解
九年级数学平面几何中的定值问题例题讲解知识点,重点,难点所谓定值问题,是指按照一定条件构成的几何图形,当某些几何元素按一定的规律在确定的范围内变化时,与它有关的某种几何量却始终保持不变(或几何元素间的某种几何性质或位置关系不变)。
平面几何定值一般可分为两类:一类是定量问题(如定长度、定角、定比、平方和或倒数和为定值等);一类是定形问题(如定点、定线、定圆或弧、定方向等),它们有共同的基本特点,即给定条件中一般由固定条件和变动条件两部分组成。
一般来说,求解定值问题的方法有:图形分析法。
画出符合条件的图形后,分析图中几何元素的数量关系及位置关系,直接寻求出定值并证明。
特殊位置法。
不论图形如何变动,定值这一共性始终不变,因此可选择图形的特殊位置(如极限位置、临界位置)加以探求。
参数计算法。
图形运动中,选取其中的变量(如线段长、角度、面积等)作为参数,将要求的定值用参数表出,然后消去参数即得定值。
例题精讲例1:如图,已知⊙O 及弦AB ,P 为⊙O 上任一点,PA 、PB 分别交AB 中垂线于E 、F ,求证:OE ·OF 为定值。
分析 若在⊙O 上的点P 运动到特殊位置点Q ,则点E ,点F 都和Q 点重合,于是得到OE ·OF =OQ 2,由此可推想,该定值可能为⊙O 半径的平方。
证明 因为OE 是弦AB 的中垂线,所以 AQ BQ=,所以∠AOE=∠BOE , 所以 1.2mAOE AB ∠=又因为 1,2m PAB BP ∠= 1,2m PBA AP ∠=∠EPB =∠PAB +∠ABP ,所以∠AOE = ∠EPB ,所以A 、O 、F 、P 四点共圆,所以∠OFB =∠OAE .又因为∠FOB =∠AOE ,所以△FOB ∽△OAE ,所以,OF OB OA OE =即OE ·OF =OA ·OB .因为OA =OB ,所以OE ·OF =OA 2(定值)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【例题就解】
【例1】 如图,已知AB=10,P是线段AB上任意一点,在AB的同侧分别以AP和PB为
边作等边△APC和等边△BPD,则CD长度的最小值为 .
思路点拨 如图,作CC′⊥AB于C,DD′⊥AB于D′,DQ⊥CC′,CD2=DQ2+CQ2,DQ=21AB
一常数,当CQ越小,CD越小,本例也可设AP=x,则PB=x10,从代数角度探求CD的
最小值.
注:从特殊位置与极端位置的研究中易得到启示,常能找到解题突破口,特殊位置与极端位
置是指:
(1)中点处、垂直位置关系等;
(2)端点处、临界位置等.
【例2】 如图,圆的半径等于正三角形ABC的高,此圆在沿底边AB滚动,切点为T,圆
交AC、BC于M、N,则对于所有可能的圆的位置而言, MTN为的度数( )
A.从30°到60°变动 B.从60°到90°变动
C.保持30°不变 D.保持60°不变
(湖北赛区选拔赛试题);
思路点拨 先考虑当圆心在正三角形的顶点C时,其弧的度数,
再证明一般情形,从而作出判断.
注:几何定值与最值问题,一般都是置于动态背景下,动与静是相对的,我们可以研究问题
中的变量,考虑当变化的元素运动到特定的位置,使图形变化为特殊图形时,研究的量取得
定值与最值.
⌒
【例3】 如图,已知平行四边形ABCD,AB=a,BC=b(a>b),P为AB边上的一动点,
直线DP交CB的延长线于Q,求AP+BQ的最小值.
(永州市竞赛题)
思路点拨 设AP=x,把AP、BQ分别用x的代数式表示,运
用不等式abba222 (当且仅当ba时取等号)来求最小值.
【例4】 如图,已知等边△ABC内接于圆,在劣弧AB上取异于A、B的点M,设直线AC
与BM相交于K,直线CB与AM相交于点N,证明:线段AK和BN的乘积与M点的选
择无关.
思路点拨 即要证AK·BN是一个定值,在图形中△ABC的边
长是一个定值,说明AK·BN与AB有关,从图知AB为△ABM
与△ANB的公共边,作一个大胆的猜想,AK·BN=AB2,从而
我们的证明目标更加明确.
注:只要探求出定值,那么解题目标明确,定值问题就转化为一般的几何证明问题.
【例5】 已知△XYZ是直角边长为1的等腰直角三角形(∠Z=90°),它的三个顶点分别在
等腰Rt△ABC(∠C=90°)的三边上,求△ABC直角边长的最大可能值.
( “宇振杯”上海市初中数学竞赛题)
思路点拨 顶点Z在斜边上或直角边CA(或CB)上,当顶点Z在斜边AB上时,取xy的中点,
通过几何不等关系求出直角边的最大值,当顶点Z在(AC或CB)上时,设CX=x,CZ=y,
建立x,y的关系式,运用代数的方法求直角边的最大值.
注:数形结合法解几何最值问题,即适当地选取变量,建立几何元素间的函数、方程、不等
式等关系,再运用相应的代数知识方法求解.常见的解题途径是:
(1)利用一元二次方程必定有解的代数模型,运用判别式求几何最值;
(2)构造二次函数求几何最值.
⌒
学力训练
1.如图,正方形ABCD的边长为1,点P为边BC上任意一点(可与B点或C点重合),
分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′
的最大值为 ,最小值为 .
(江苏省竞赛题)
2.如图,∠AOB=45°,角内有一点P,PO=10,在角的两边上有两点Q,R(均不同于点
O),则△PQR的周长的最小值为 .
(湖北省黄冈市竞赛题)
3.如图,两点A、B在直线MN外的同侧,A到MN的距离AC=8,B到MN的距离BD=5,
CD=4,P在直线MN上运动,则PBPA的最大值等于 .
( “希望杯”邀请赛试题)
4.如图,A点是半圆上一个三等分点,B点是弧AN的中点,P点是直径MN上一动点,
⊙O的半径为1,则AP+BP的最小值为( )
A.1 B.22 C.2 D.13
(湖北省荆州市中考题)
5.如图,圆柱的轴截面ABCD是边长为4的正方形,动点P从A点出发,沿看圆柱的侧面
移动到BC的中点S的最短距离是( )
A.212 B.2412 C.214 D.242
(贵阳市中考题)
6.如图、已知矩形ABCD,R,P户分别是DC、BC上的点,E,F分别是AP、RP的中点,
当P在BC上从B向C移动而R不动时,那么下列结论成立的是( )
A.线段EF的长逐渐增大 B.线段EF的长逐渐减小
C.线段EF的长不改变 D.线段EF的长不能确定
(桂林市中考题)
7.如图,点C是线段AB上的任意一点(C点不与A、B点重合),分别以AC、BC为边在
直线AB的同侧作等边三角形ACD和等边三角形BCE,AE与CD相交于点M,BD与CE
相交于点N.
(1)求证:MN∥AB;
(2)若AB的长为l0cm,当点C在线段AB上移动时,是否存在这样的一点C,使线段MN
的长度最长?若存在,请确定C点的位置并求出MN的长;若不存在,请说明理由.
(2002年云南省中考题)
8.如图,定长的弦ST在一个以AB为直径的半圆上滑动,M是ST的中点,P是S对AB
作垂线的垂足,求证:不管ST滑到什么位置,∠SPM是一定角.
(加拿大数学奥林匹克试题)
9.已知△ABC是⊙O的内接三角形,BT为⊙O的切线,B为切点,P为直线AB上一点,
过点P作BC的平行线交直线BT于点E,交直线AC于点F.
(1)当点P在线段AB上时(如图),求证:PA·PB=PE·PF;
(2)当点P为线段BA延长线上一点时,第(1)题的结论还成立吗?如果成立,请证明,如果
不成立,请说明理由.
10.如图,已知;边长为4的正方形截去一角成为五边形ABCDE,其中AF=2,BF=l,在
AB上的一点P,使矩形PNDM有最大面积,则矩形PNDM的面积最大值是( )
A.8 B.12 C.225 D.14
11.如图,AB是半圆的直径,线段CA上AB于点A,线段DB上AB于点B,AB=2;AC=1,
BD=3,P是半圆上的一个动点,则封闭图形ACPDB的最大面积是( )
A.22 B.21 C.23 D.23
12.如图,在△ABC中,BC=5,AC=12,AB=13,在边AB、AC上分别取点D、E,使线
段DE将△ABC分成面积相等的两部分,试求这样线段的最小长度.
(全国初中数学联赛试题)
13.如图,ABCD是一个边长为1的正方形,U、V分别是AB、CD上的点,AV与DU相
交于点P,BV与CU相交于点Q.求四边形PUQV面积的最大值.
( “弘晟杯”上海市竞赛题)
14.利用两个相同的喷水器,修建一个矩形花坛,使花坛全部都能喷到水.已知每个喷水器
的喷水区域是半径为l0米的圆,问如何设计(求出两喷水器之间的距离和矩形的长、宽),才
能使矩形花坛的面积最大?
(河南省竞赛题)
15.某住宅小区,为美化环境,提高居民生活质量,要建一个八边形居民广场(平面图如图
所示).其中,正方形MNPQ与四个相同矩形(图中阴影部分)的面积的和为800平方米.
(1)设矩形的边AB=x(米),AM=y(米),用含x的代数式表示y为 .
(2)现计划在正方形区域上建雕塑和花坛,平均每平方米造价为2100元;在四个相同的矩形
区域上铺设花岗岩地坪,平均每平方米造价为105元;在四个三角形区域上铺设草坪,平均
每平方米造价为40元.
①设该工程的总造价为S(元),求S关于工的函数关系式.
②若该工程的银行贷款为235000元,仅靠银行贷款能否完成该工程的建设任务?若能,
请列出设计方案;若不能,请说明理由.
③若该工程在银行贷款的基础上,又增加资金73000元,问能否完成该工程的建设任务?
若能,请列出所有可能的设计方案;若不能,请说明理由.
(镇江市中考题)
16.某房地产公司拥有一块“缺角矩形”荒地ABCDE,边长和方向如图,欲在这块地上建
一座地基为长方形东西走向的公寓,请划出这块地基,并求地基的最大面积(精确到1m2).
(北京市数学知识应用竞赛试题)
参考答案
