高中物理相遇和追及问题
追及相遇问题----高中物理模块典型题归纳(含详细答案)

追及相遇问题----高中物理模块典型题归纳(含详细答案)一、单选题1.甲、乙两车从同一地点沿相同方向由静止开始做直线运动,它们运动的加速度随时间变化图象如图所示。
关于两车的运动情况,下列说法正确的是()A.在0~4 s内两车的合力不变B.在t=2 s时两车相遇C.在t=4 s时两车相距最远D.在t=4 s时甲车恰好追上乙车2.某人驾驶一辆质量为m=5×103kg汽车甲正在平直的公路以某一速度匀速运动,突然发现前方50m处停着一辆乙车,立即刹车,刹车后做匀减速直线运动.已知该车刹车后第I个2s 内的位移是24m,第4个2s内的位移是1m.则下列说法正确的是()A.汽车甲刹车后做匀减速直线运动的加速度为B.汽车甲刹车后做匀减速直线运动的加速度为2m/s2C.汽车甲刹车后停止前,可能撞上乙车D.汽车甲刹车前的速度为14m/s3.甲、乙两物体从同一地点同时开始沿同一方向运动,甲物体运动的vt图象为两段直线,乙物体运动的v-t图象为两段半径相同的圆弧曲线,如图所示,图中t4=2t2,则在0~t4时间内,以下说法正确的是()A.甲物体的加速度不变B.乙物体做曲线运动C.甲物体的平均速度等于乙物体的平均速度D.两物体t1时刻相距最远,t4时刻相遇4.甲乙两辆汽车在平直的公路上沿同一方向作直线运动,t=0时刻同时经过公路旁的同一个路标。
在描述两车运动的v-t图中(如图),直线a、b分别描述了甲乙两车在0~20秒的运动情况。
关于两车之间的位置关系,下列说法正确的是()A.在0~10秒内两车逐渐靠近B.在10~20秒内两车逐渐远离C.在5~15秒内两车的位移相等D.在t=10秒时两车在公路上相遇5.甲、乙两质点沿同一方向做直线运动,某时刻经过同一地点.若以该时刻作为计时起点,得到两质点的x﹣t图像如图所示.图像中的OC与AB平行,CB与OA平行.则下列说法中正确的是()A.t1~t2时间内甲和乙的距离越来越远B.0~t2时间内甲的速度和乙的速度始终不相等C.0~t3时间内甲和乙的位移相等.0~t3时间内甲的平均速度大于乙的平均速度6.甲、乙两车同时同地同向出发,在同一水平公路上做直线运动,甲的初速度v甲=16m/s,加速度大小a甲=2m/s2,做匀减速直线运动,乙以初速度v乙=4m/s,加速度大小a乙=1m/s2,做匀加速直线运动,下列叙述正确的是()A.两车再次相遇前二者间的最大距离为20mB.两车再次相遇所需的时间为4sC.两车再次相遇前二者间达到最大距离用时8sD.两车再次相遇在64m处二、多选题7.a、b两车在平直公路上沿同一方向行驶,运动的v﹣t图像如图所示,在t=0时刻,b车在a车前方s0处,在t=t1时间内,a车的位移为s,则()A.若a、b在t1时刻相遇,则B.若a、b在时刻相遇,则下次相遇时刻为2t1C.若a、b在时刻相遇,则D.若a、b在t1时刻相遇,则下次相遇时刻为2t18.物体A以10m/s的速度做匀速直线运动。
高中物理必修一 2.6追及相遇问题详解

高中物理必修一| 2.6追及相遇问题详解追及和相遇问题的处理方法两个物体在同一直线上运动,往往涉及追及,相遇或避免碰撞等问题,解答此类问题的关键条件是:两物体能否同时达到空间某位置。
基本思路是:①分别对两物体进行研究;②画出运动过程示意图;③列出位移方程④找出时间关系,速度关系⑤解出结果,必要时进行讨论。
方法是:(1)临界条件法:当二者速度相等时,二者相距最远(最近)。
(2)图象法:画出x-t图象或v-t图象,然后利用图象进行分析求解。
(3)数学判别式法:设相遇时间为t,根据条件列方程,得到关于t的一元二次方程,用判别式进行讨论,若Δ>0,即有两个解,说明可以相遇两次;若Δ=0,说明刚好追上或相遇;若Δ<0,说明追不上或不能相遇。
追及同向运动的两个物体,追和被追的两个物体的速度相等(同向运动)时能否追上和两者距离有极值的临界条件。
1第一类:速度大者减速(如匀减速直线运动)追速度小者(如匀减速直线运动)①当两者速度相等时,追者位移追者位移仍小于被追者位移,则永远追不上,此时两者之间有最小距离。
②若两者位移相等,且两者速度相等时,则恰能追上,也是两者避免碰撞的临界条件。
③若两者位移相等时,追着速度仍大于被追者的速度,则被追者还有一次追上追者的机会,当速度相等时两者之间距离有一个最大值。
在具体求解时,可以利用速度相等这一条件求解,也可以利用二次函数的知识求解,还可以利用图像等求解。
2第二类速度小者加速(如初速度为零的匀加速直线运动)追速度大者(匀速直线运动)。
①当两者速度相等时有最大距离。
②当两者位移相等时,则追上。
具体的求解方法与第一类相似,即利用速度相等进行分析还可利用二次函数图像和图像法。
相遇①同向运动的两物体追及即相遇。
②相向运动的物体,当各自发生的位移大小之和等于开始时两物体间的距离时相遇分析追及相遇问题分析追击,一个条件,两个关系。
一个条件是:两物体速度相等时满足的临界条件,如两物体的距离是最大还是最小及是否恰好追上等。
高中物理——相遇和追及问题教案
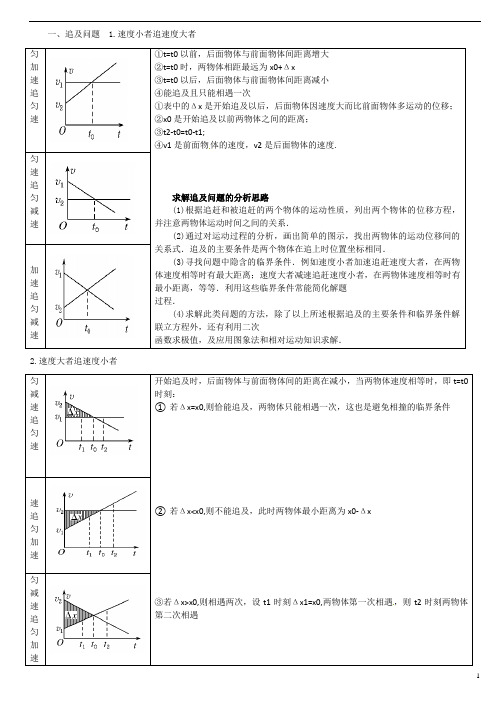
一、追及问题 1.速度小者追速度大者匀加速追匀速①t=t0以前,后面物体与前面物体间距离增大②t=t0时,两物体相距最远为x0+Δx③t=t0以后,后面物体与前面物体间距离减小④能追及且只能相遇一次①表中的Δx是开始追及以后,后面物体因速度大而比前面物体多运动的位移;②x0是开始追及以前两物体之间的距离;③t2-t0=t0-t1;④v1是前面物体的速度,v2是后面物体的速度.求解追及问题的分析思路(1)根据追赶和被追赶的两个物体的运动性质,列出两个物体的位移方程,并注意两物体运动时间之间的关系.(2)通过对运动过程的分析,画出简单的图示,找出两物体的运动位移间的关系式.追及的主要条件是两个物体在追上时位置坐标相同.(3)寻找问题中隐含的临界条件.例如速度小者加速追赶速度大者,在两物体速度相等时有最大距离;速度大者减速追赶速度小者,在两物体速度相等时有最小距离,等等.利用这些临界条件常能简化解题过程.(4)求解此类问题的方法,除了以上所述根据追及的主要条件和临界条件解联立方程外,还有利用二次函数求极值,及应用图象法和相对运动知识求解.匀速追匀减速匀加速追匀减速2.速度大者追速度小者匀减速追匀速开始追及时,后面物体与前面物体间的距离在减小,当两物体速度相等时,即t=t0时刻:①若Δx=x0,则恰能追及,两物体只能相遇一次,这也是避免相撞的临界条件②若Δx<x0,则不能追及,此时两物体最小距离为x0-Δx③若Δx>x0,则相遇两次,设t1时刻Δx1=x0,两物体第一次相遇,则t2时刻两物体第二次相遇匀速追匀加速匀减速追匀加速。
高中物理追及相遇问题笔记

高中物理追及相遇问题笔记追及相遇问题是高中物理中一个常见的问题类型,在研究运动与速度之间的关系时十分重要。
这种问题的解决方法基于物理原理,通过分析速度以及相对距离等因素来求解。
追及相遇问题例题一:小明和小红在一个300米的跑道上相向而行,小明的速度是 4 m/s,小红的速度是6 m/s。
求小明和小红相遇需要多长时间。
解答:设小明从与小红相遇点开始计时,时间为t秒。
则小明在t秒内行驶的距离为4t米,小红在t秒内行驶的距离为6t米。
由于他们相向而行,所以他们的相对速度是10 m/s(即6 m/s - 4 m/s)。
根据速度等于路程除以时间的公式,我们可以得到以下等式:10 m/s = (4t + 6t) / t解方程可得 t = 10/10 = 1因此,小明和小红需要1秒的时间才能相遇。
追及相遇问题例题二:一个小车以30 m/s的速度向东行驶,另一个小车以20 m/s的速度向西行驶,两车之间的距离为1000米。
求两车相遇需要的时间。
解答:设两车相遇的时间为t秒。
由于两车相向而行,所以他们的相对速度是50 m/s(即30 m/s + 20 m/s)。
同样地,我们可以通过以下公式求解:50 m/s = (30t + 20t) / t解方程可得 t = 1000/50 = 20因此,两车需要20秒的时间才能相遇。
追及相遇问题例题三:小明骑自行车以10 km/h的速度向北行驶,小红以8 km/h的速度向东行驶。
两者的初始距离为5 km,求小明和小红相遇需要的时间。
解答:设两者相遇的时间为t小时。
小明在t小时内行驶的距离为10t km,小红在t小时内行驶的距离为8t km。
由于小明和小红垂直相向而行,所以他们相对速度的大小为\sqrt{10^2 + 8^2} km/h ≈ 13 km/h。
同样地,我们可以通过以下公式求解:13 km/h = (10t + 8t) / t解方程可得 t = 5/13因此,小明和小红需要约0.38小时(约23分钟)的时间才能相遇。
高中物理高考复习课件:竖直上抛运动、追及和相遇问题

目标要求 1. 知道什么是竖直上抛运动,理解竖直上抛运动是匀变速直线运 动. 2.会分析竖直上抛运动的运动规律.会利用分段法或全程法求解竖 直上抛运动的有关问题. 3.知道竖直上抛运动的对称性. 4.会分析追及相遇问题,理解两者速度相等为临界条件. 5.会根据位移关系、时间关系列方程求解.
(1)求公交车刹车过程中加速度a2的大小; (2)当小明达到最大速度时,与车站相距多远? (3)从相遇时开始计时,公交车至少需在车站停留多长时间小明才能赶上? (4)分析小明在追赶公交车过程中与公交车相距最远的距离是多少?(不计车长)
例 4 两玩具车在两条平行的车道上行驶,t=0时两车都在同一计时 线处,它们在四次比赛中的v-t图像如图所示.在0~3 s内哪幅图对应 的比赛中两车可能再次相遇( )
答案:C
例 5 [2023·山东济南高一上检测]某天,小明在上学途中沿人行道以v1=1 m/s的 速度向一公交车站走去,发现一辆公交车正以v2=15 m/s的速度从身旁的平直公 路同向驶过,此时他距车站的距离s=25 m.为了乘上该公交车,他匀加速向前 跑去,加速度大小a1=2.5 m/s2,达到最大速度vm=6 m/s后匀速前进.假设公交车 从相遇处开始匀减速刹车,刚好到车站停下.
变速直线运动(通常规定初速度v0的 方向为正方向,g为重力加速度的大小). 3.竖直上抛运动的v-t图像
6.竖直上抛运动的处理方法
分段分 上升阶段是初速度为v0、a=-g的匀减速直线运动; 析法 下落阶段是自由落体运动 全过程看作初速度为v0、a=-g的匀变速直线运动
拓展1 竖直上抛运动 【归纳】 1.竖直上抛运动 如图1所示,将一个物体以某一初速度v0竖直向上抛出,抛出的物体 只在重力作用下运动,这种运动就是竖直上抛运动.
高中物理精讲---相遇和追及问题稿

两车恰不相撞的条件是两车速度相同时相遇。
由A、B 速度关系: v1 at v2
由A、B位移关系:v1t
1 2
at 2
v2t
x0
(包含时 间关系)
a (v1 v2 )2 (20 10)2 m / s2 0.5m / s2
2 x0
2 100
a 0.5m / s2
解2:(图像法)
20
A
10
B
a tan 20 10 0.5 o
t0
t/s
20
a 0.5m / s2
物体的v-t图像的斜率表示加 速度,面积表示位移。
解3:(二次函数极值法)
若两车不相撞,其位移关系应为
v1t
1 2
at 2
v2t
x0
代入数据得 1 at 2 10t 100 0
2
其图像(抛物线)的顶点纵坐标必为正值,故有
第二章 直线运动
1. 相遇和追及问题的实质 研究的两物体能否在相同的时刻到达相同的空
间位置的问题。 2. 画出物体运动的情景图,理清三大关系
(1)时间关系 tA tB t0
(2)位移关系 sA sB s0
(3)速度关系
两者速度相等。它往往是物体间能否追上或 (两者)距离最大、最小的临界条件,也是分析判断 的切入点。
3. 两种典型追及问题
(1)速度大者(匀减速)追速度小者(匀速)
a
v1> v2
A
v1
B
v2
①当v1=v2时,A未追上B,则A、B永不相遇,此时 两者间有最小距离;
②当v1=v2时,A恰好追上B,则A、B相遇一次, 也是避免相撞刚好追上的临界条件;
2024届高中物理一轮复习:第七讲:追及与相遇问题

第七讲:追及与相遇问题一、单选题1.甲、乙两汽车同时同地出发,甲车做匀速运动,乙车做初速度为零的匀加速直线运动,两车的位移与时间的关系如图所示。
下列说法正确的是( )A .t =10s 时,甲车追上乙车B .t =10s 时,两车相距最远C .t =5s 时,两车速度相同D .t =10s 时,两车速度相同2.在一条平直道路上,汽车甲从静止开始启动做加速度为25m/s 的匀加速直线运动,在汽车甲刚开始启动时,汽车乙恰好从汽车甲旁以10m/s 的速度做匀速直线运动,甲乙两车同向运动,则甲车追上乙车所经过的时间为( )A .2sB .4sC .5sD .10s 3.汽车在晴天干燥沥青路面上以108km/h 的速度匀速行驶时,刹车距离为50m ;货车在晴天干燥沥青路面上以72km/h 的速度行驶时,刹车距离为40m 。
若雨天时在沥青路面上汽车与货车所受阻力均为晴天时的0.8倍,则其他条件不变的情况下,雨天时汽车与前方货车在沥青路面上同时刹车的最小安全距离约为( )A .12mB .16mC .20mD .24m 4.甲、乙两物体从同一位置出发沿同一直线运动,它们的v t 图象如图所示,下列说法正确的是( )A .乙物体先向负方向运动,后向正方向运动B .2t 时刻,二者共速并再次处于同一位置C .20~t 时间内,两者距离先增大后减小,1t 时刻相距最远D .20~t 时间内,乙的速度和加速度都是先减小后增大5.甲、乙两车从同一地点沿同一平直公路运动它们的v -t 图象如图所示,则下列说法中正确的是()A.甲车做匀减速运动,乙车做匀加速运动B.甲、乙两车在t=3s时相遇C.甲、乙两车在t=6s前必定相遇D.甲、乙两车相遇前二者之间的最大距离为15m 6.甲、乙两小车在同一地点同时开始往相同方向做直线运动的v-t图像如图所示(甲小车速度减为0后不再运动),根据图像提供的信息可知()A.甲车在0-4s内的加速度大小为2m/s2B.甲车0-4s内与4-6s内的速度方向相反C.在乙追上甲之前,4s末两小车相距最远D.8s末甲、乙两小车相遇,且离出发点距离为32m7.甲、乙两车在一平直公路上从同一地点沿同一方向做直线运动,它们的v t-图像如图所示。
高中物理追击和相遇问题专题(含详解)之欧阳语创编

直线运动中的追及和相遇问题一、相遇和追及问题的实质研究的两物体能否在相同的时刻到达相同的空间位置的问题。
二、 解相遇和追及问题的关键1.画出物体运动的情景图2.理清三大关系(1)时间关系 :0t t t B A ±=(2)位移关系:0A B x x x =±(3)速度关系:vA=vB两者速度相等往往是物体间能否追上或(两者)距离最大、最小的临界条件,也是分析判断的切入点。
三、追及、相遇问题的分析方法:A. 画出两个物体运动示意图,根据两个物体的运动性质,选择同一参照物,列出两个物体的位移方程;B. 找出两个物体在运动时间上的关系C. 找出两个物体在运动位移上的数量关系D. 联立方程求解.说明:追及问题中常用的临界条件:⑴速度小者加速追速度大者,速度在接近,但距离在变大。
追上前两个物体速度相等时,有最大距离;⑵速度大者减速追赶速度小者,速度在接近,但距离在变小。
追上前在两个物体速度相等时,有最小距离.即必须在此之前追上,否则就不能追上.四、典型例题分析:(一).匀加速运动追匀速运动的情况(开始时v1< v2):1.当v1< v2时,两者距离变大;2.当v1= v2时,两者距离最大;3.v1>v2时,两者距离变小,相遇时满足x1=x2+Δx,全程只相遇(即追上)一次。
【例1】一小汽车从静止开始以3m/s2的加速度行驶,恰有一自行车以6m/s的速度从车边匀速驶过.求:(1)小汽车从开动到追上自行车之前经过多长时间两者相距最远?此时距离是多少?(2)小汽车什么时候追上自行车,此时小汽车的速度是多少?(二).匀速运动追匀加速运动的情况(开始时v1> v2):1.当v1> v2时,两者距离变小;2.当v1= v2时,①若满足x1< x2+Δx,则永远追不上,此时两者距离最近;②若满足x1=x2+Δx,则恰能追上,全程只相遇一次;③若满足x1> x2+Δx,则后者撞上前者(或超越前者),此条件下理论上全程要相遇两次。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中物理相遇和追及问题(总17页)
-CAL-FENGHAI.-(YICAI)-Company One1 -CAL-本页仅作为文档封面,使用请直接删除 相遇追及问题 一、考点、热点回顾 一、追及问题 1.速度小者追速度大者
类型 图象 说明 匀加速追匀速 ①t=t0以前,后面物体与前面物体间距离增大
②t=t0时,两物体相距最远为x0+Δx
③t=t0以后,后面物体与前面物体间距离减小
④能追及且只能相遇一次
匀速追匀减速
匀加速追匀减速 2.速度大者追速度小者 度大者追速度小者
匀减速追匀速 开始追及时,后面物体与前面物体间的距离在减小,当两物体速度相等时,即t=t0时刻:
①若Δx=x0,则恰能追及,两物体只能相遇一次,匀速追匀加速 这也是避免相撞的临界条件 ②若Δx及,此时两物体最小距离为x0-Δx
③若Δx>x0,则相遇两次,设t1时刻Δx1=x0,两物体第一次相遇,则t2时刻两物体第二次相遇
匀减速追匀加速
①表中的Δx是开始追及以后,后面物体因速度大而比前面物体多运动的位移; ②x0是开始追及以前两物体之间的距离; ③t2-t0=t0-t1; ④v1是前面物体的速度,v2是后面物体的速度. 二、相遇问题 这一类:同向运动的两物体的相遇问题,即追及问题. 第二类:相向运动的物体,当各自移动的位移大小之和等于开始时两物体的距离时相遇. 解此类问题首先应注意先画示意图,标明数值及物理量;然后注意当被追赶的物体做匀减速运动时,还要注意该物体是否停止运动了.
求解追及问题的分析思路 (1)根据追赶和被追赶的两个物体的运动性质,列出两个物体的位移方程,并注意两物体运动时间之间的关系. (2)通过对运动过程的分析,画出简单的图示,找出两物体的运动位移间的关系式.追及的主要条件是两个物体在追上时位置坐标相同. (3)寻找问题中隐含的临界条件.例如速度小者加速追赶速度大者,在两物体速度相等时有最大距离;速度大者减速追赶速度小者,在两物体速度相等时有最小距离,等等.利用这些临界条件常能简化解题 过程. (4)求解此类问题的方法,除了以上所述根据追及的主要条件和临界条件解联立方程外,还有利用二次 函数求极值,及应用图象法和相对运动知识求解. 相遇问题 相遇问题的分析思路: 相遇问题分为追及相遇和相向运动相遇两种情形,其主要条件是两物体在相遇处的位置坐标相同. (1)列出两物体运动的位移方程、注意两个物体运动时间之间的关系. (2)利用两物体相遇时必处在同一位置,寻找两物体位移间的关系. (3)寻找问题中隐含的临界条件. (4)与追及中的解题方法相同.
二、典型例题 【例1】物体A、B同时从同一地点,沿同一方向运动,A以10m/s的速度匀速前进,B以2m/s2的加速度从静止开始做匀加速直线运动,求A、B再次相遇前两物体间的最大距离. 【解析一】 物理分析法 A做 υA=10 m/s的匀速直线运动,B做初速度为零、加速度a=2 m/s2的匀
加速直线运动.根据题意,开始一小段时间内,A的速度大于B的速度,它们间的距离逐渐变大,当B的速度加速到大于A的速度后,它们间的距离又逐渐变小;A、B间距离有最大值的临界条件是υA=
υB. ① 5
设两物体经历时间t相距最远,则υA=at ②
把已知数据代入①②两式联立得t=5 s 在时间t内,A、B两物体前进的距离分别为 sA=υAt=10×5 m=50 m
sB=12at2=12×2×52 m=25 m A、B再次相遇前两物体间的最大距离为 Δsm=sA-sB=50 m-25 m=25 m 【解析二】 相对运动法 因为本题求解的是A、B间的最大距离,所以可利用相对运动求解.选B为参考系,则A相对B的初速度、末速度、加速度分别是υ0=10 m/s、υt=υA-
υB=0、a=-2 m/s
2
.
根据υt2-υ0=2as.有0-102=2×(-2)×sAB
解得A、B间的最大距离为sAB=25 m.
【解析三】 极值法
物体A、B的位移随时间变化规律分别是sA=10t,sB=12at2=12×2×t2 =t5.
则A、B间的距离Δs=10t-t2,可见,Δs有最大值,且最大值为Δsm=4×(-1)×0-1024×(-1) m=25 m 【解析四】 图象法 根据题意作出A、B两物体的υ-t图象,如图1-5-1所示.由图可知,A、B再次相遇前它们之间距离有最大值的临界条件是υA=υB,得t1=5 s. 6
A、B间距离的最大值数值上等于ΔOυAP的面积,即Δsm=12×5×10 m=25 m. 【答案】25 m 【点拨】相遇问题的常用方法 (1)物理分析法:抓好“两物体能否同时到达空间某位置”这一关键,按(解法一)中的思路分析. (2)相对运动法:巧妙地选取参考系,然后找两物体的运动关系. (3)极值法:设相遇时间为t,根据条件列方程,得到关于t的一元二次方程,用判别式进行讨论,若△>0,即有两个解,说明可以相遇两次;若△=0,说明刚好追上或相碰;若△<0,说明追不上或不能相碰. (4)图象法:将两者的速度时间图象在同一个坐标系中画出,然后利用图象求解. 拓展 如图1-5-2所示是甲、乙两物体从同一地点,沿同一方向做直线运动的υ-t图象,由图象可以看出 ( 〕 A.这两个物体两次相遇的时刻分别是1s末和4s末 B.这两个物体两次相遇的时刻分别是2s末和6s末 C.两物体相距最远的时刻是2s末 D.4s末以后甲在乙的前面 【解析】从图象可知两图线相交点1s末和4s末是两物速度相等时刻,从0→2s,乙追赶甲到2s末追上,从2s开始是甲去追乙,在4s末两物相距最远,到6s末追上乙.故选B. 【答案】B 【实战演练1】(2011·新课标全国卷)甲乙两辆汽车都从静止出发做加速直线运动,加速度方向一直不变。在第一段时间间隔内,两辆汽车的加速度大小不变,汽车乙的加速度大小是甲的两倍;在接下来的相同时间间隔内,汽车甲的加速度大小增加为原来的两倍,汽车乙的加速度大小减小为原来的一半。求甲乙两车各自在这两段时间间隔内走过的总路程之比。 【思路点拨】解答本题时可由运动学公式分别写出两汽车的速度和位移方程,再根据两车加速度的关系,求出两车路程之比。 【精讲精析】设汽车甲在第一段时间间隔末(时刻t0)的速度为v,第一段时
间间隔内行驶的路程为s1,加速度为a,在第二段时间间隔内行驶的路程为
s2,由运动学公式有, v=a t0 ①
s1=12 a t02 ②
s2=v t0+12 2a t02 ③ 设汽车乙在时刻t0的速度为v′,在第一、二段时间间隔内行驶的路程分别为
s1′、s2′,同理有, v′=2a t0 ④
s1′=12 2a t02 ⑤ s2′=v′ t0+12 a t02 ⑥ 设甲、乙两车行驶的总路程分别为s、s′,则有 s= s1+s2 ⑦ s′= s1′+s2′ ⑧ 联立以上各式解得,甲、乙两车各自行驶路程之比为 ss′ =57
答案:57
【实战演练2】(2011·安徽省级示范高中名校联考)甲、乙两辆汽车,同时在一条平直的公路上自西向东运动,开始时刻两车平齐,相对于地面的v-t图象如图所示,关于它们的运动,下列说法正确的是( )
A.甲车中的乘客说,乙车先以速度v0向西做匀减速运动,后向东做匀加速运动 B.乙车中的乘客说,甲车先以速度v0向西做匀减速运动,后做匀加速运动 C.根据v-t图象可知,开始乙车在前,甲车在后,两车距离先减小后增大,当乙车速度增大到v0时,两车恰好平齐 D.根据v-t图象可知,开始甲车在前,乙车在后,两车距离先增大后减小,当乙车速度增大到v0时,两车恰好平齐 【答案】A 【详解】甲车中的乘客以甲车为参考系,相当于甲车静止不动,乙车以初速度v0向西做减速运动,速度减为零之后,再向东做加速运动,所以A正确;乙车中的乘客以乙车为参考系,相当于乙车静止不动,甲车以初速度v0向东做减速运动,速度减为零之后,再向西做加速运动,所以B错误;以地面为参考系,当两车速度相等时,距离最远,所以C、D错误.
考点2 相遇问题 相遇问题的分析思路: 相遇问题分为追及相遇和相向运动相遇两种情形,其主要条件是两物体在相遇处的位置坐标相同. (1)列出两物体运动的位移方程、注意两个物体运动时间之间的关系. (2)利用两物体相遇时必处在同一位置,寻找两物体位移间的关系. (3)寻找问题中隐含的临界条件. (4)与追及中的解题方法相同. 【例2】甲、乙两物体相距s,同时同向沿同一直线运动,甲在前面做初速度为零、加速度为a1的匀加速直线运动,乙在后做初速度为υ0,加速度为a2的匀
加速直线运动,则 ( ) A.若a1=a2,则两物体可能相遇一次 B.若a1>a2,则两物体可能相遇二次 C.若a1<a2,则两物体可能相遇二次 D.若a1>a2,则两物体也可相遇一次或不相遇
【解析】 设乙追上甲的时间为t,追上时它们的位移有υ0t+12a2t2-12a2t2=s 上式化简得:(a1-a2)t2-2υ0t+2s=0
解得:t=2υ0±4υ02-8s(a1-a2)2(a1-a2)
(1)当a1>a2时,差别式“△”的值由υ0、a1、a2、s共同决定,且△<2υ0,而△的值可能小于零、等于零、大于零,则两物体可能不相遇,相遇一次,相遇两次,所以选项B、D正确.
(2)当a1<a2时,t的表达式可表示为t=-2υ0±4υ02-8s(a2-a1)2(a2-a1)
显然,△一定大于零.且△>2υ0,所以t有两解.但t不能为负值,只有一
解有物理意义,只能相遇一次,故C选项错误. (3)当a1=a2时,解一元一次方程得t=s/υ0,一定相遇一次,故A选项正确.
