The near-IR shape of the big blue bump emission from quasars under the hot dust emission
引力波观测原文PhysRevLett.116.061102

Observation of Gravitational Waves from a Binary Black Hole MergerB.P.Abbott et al.*(LIGO Scientific Collaboration and Virgo Collaboration)(Received21January2016;published11February2016)On September14,2015at09:50:45UTC the two detectors of the Laser Interferometer Gravitational-Wave Observatory simultaneously observed a transient gravitational-wave signal.The signal sweeps upwards in frequency from35to250Hz with a peak gravitational-wave strain of1.0×10−21.It matches the waveform predicted by general relativity for the inspiral and merger of a pair of black holes and the ringdown of the resulting single black hole.The signal was observed with a matched-filter signal-to-noise ratio of24and a false alarm rate estimated to be less than1event per203000years,equivalent to a significance greaterthan5.1σ.The source lies at a luminosity distance of410þ160−180Mpc corresponding to a redshift z¼0.09þ0.03−0.04.In the source frame,the initial black hole masses are36þ5−4M⊙and29þ4−4M⊙,and the final black hole mass is62þ4−4M⊙,with3.0þ0.5−0.5M⊙c2radiated in gravitational waves.All uncertainties define90%credible intervals.These observations demonstrate the existence of binary stellar-mass black hole systems.This is the first direct detection of gravitational waves and the first observation of a binary black hole merger.DOI:10.1103/PhysRevLett.116.061102I.INTRODUCTIONIn1916,the year after the final formulation of the field equations of general relativity,Albert Einstein predicted the existence of gravitational waves.He found that the linearized weak-field equations had wave solutions: transverse waves of spatial strain that travel at the speed of light,generated by time variations of the mass quadrupole moment of the source[1,2].Einstein understood that gravitational-wave amplitudes would be remarkably small;moreover,until the Chapel Hill conference in 1957there was significant debate about the physical reality of gravitational waves[3].Also in1916,Schwarzschild published a solution for the field equations[4]that was later understood to describe a black hole[5,6],and in1963Kerr generalized the solution to rotating black holes[7].Starting in the1970s theoretical work led to the understanding of black hole quasinormal modes[8–10],and in the1990s higher-order post-Newtonian calculations[11]preceded extensive analytical studies of relativistic two-body dynamics[12,13].These advances,together with numerical relativity breakthroughs in the past decade[14–16],have enabled modeling of binary black hole mergers and accurate predictions of their gravitational waveforms.While numerous black hole candidates have now been identified through electromag-netic observations[17–19],black hole mergers have not previously been observed.The discovery of the binary pulsar system PSR B1913þ16 by Hulse and Taylor[20]and subsequent observations of its energy loss by Taylor and Weisberg[21]demonstrated the existence of gravitational waves.This discovery, along with emerging astrophysical understanding[22], led to the recognition that direct observations of the amplitude and phase of gravitational waves would enable studies of additional relativistic systems and provide new tests of general relativity,especially in the dynamic strong-field regime.Experiments to detect gravitational waves began with Weber and his resonant mass detectors in the1960s[23], followed by an international network of cryogenic reso-nant detectors[24].Interferometric detectors were first suggested in the early1960s[25]and the1970s[26].A study of the noise and performance of such detectors[27], and further concepts to improve them[28],led to proposals for long-baseline broadband laser interferome-ters with the potential for significantly increased sensi-tivity[29–32].By the early2000s,a set of initial detectors was completed,including TAMA300in Japan,GEO600 in Germany,the Laser Interferometer Gravitational-Wave Observatory(LIGO)in the United States,and Virgo in binations of these detectors made joint obser-vations from2002through2011,setting upper limits on a variety of gravitational-wave sources while evolving into a global network.In2015,Advanced LIGO became the first of a significantly more sensitive network of advanced detectors to begin observations[33–36].A century after the fundamental predictions of Einstein and Schwarzschild,we report the first direct detection of gravitational waves and the first direct observation of a binary black hole system merging to form a single black hole.Our observations provide unique access to the*Full author list given at the end of the article.Published by the American Physical Society under the terms of the Creative Commons Attribution3.0License.Further distri-bution of this work must maintain attribution to the author(s)and the published article’s title,journal citation,and DOI.properties of space-time in the strong-field,high-velocity regime and confirm predictions of general relativity for the nonlinear dynamics of highly disturbed black holes.II.OBSERVATIONOn September14,2015at09:50:45UTC,the LIGO Hanford,W A,and Livingston,LA,observatories detected the coincident signal GW150914shown in Fig.1.The initial detection was made by low-latency searches for generic gravitational-wave transients[41]and was reported within three minutes of data acquisition[43].Subsequently, matched-filter analyses that use relativistic models of com-pact binary waveforms[44]recovered GW150914as the most significant event from each detector for the observa-tions reported here.Occurring within the10-msintersite FIG.1.The gravitational-wave event GW150914observed by the LIGO Hanford(H1,left column panels)and Livingston(L1,rightcolumn panels)detectors.Times are shown relative to September14,2015at09:50:45UTC.For visualization,all time series are filtered with a35–350Hz bandpass filter to suppress large fluctuations outside the detectors’most sensitive frequency band,and band-reject filters to remove the strong instrumental spectral lines seen in the Fig.3spectra.Top row,left:H1strain.Top row,right:L1strain.GW150914arrived first at L1and6.9þ0.5−0.4ms later at H1;for a visual comparison,the H1data are also shown,shifted in time by this amount and inverted(to account for the detectors’relative orientations).Second row:Gravitational-wave strain projected onto each detector in the35–350Hz band.Solid lines show a numerical relativity waveform for a system with parameters consistent with those recovered from GW150914[37,38]confirmed to99.9%by an independent calculation based on[15].Shaded areas show90%credible regions for two independent waveform reconstructions.One(dark gray)models the signal using binary black hole template waveforms [39].The other(light gray)does not use an astrophysical model,but instead calculates the strain signal as a linear combination of sine-Gaussian wavelets[40,41].These reconstructions have a94%overlap,as shown in[39].Third row:Residuals after subtracting the filtered numerical relativity waveform from the filtered detector time series.Bottom row:A time-frequency representation[42]of the strain data,showing the signal frequency increasing over time.propagation time,the events have a combined signal-to-noise ratio(SNR)of24[45].Only the LIGO detectors were observing at the time of GW150914.The Virgo detector was being upgraded, and GEO600,though not sufficiently sensitive to detect this event,was operating but not in observational mode.With only two detectors the source position is primarily determined by the relative arrival time and localized to an area of approximately600deg2(90% credible region)[39,46].The basic features of GW150914point to it being produced by the coalescence of two black holes—i.e., their orbital inspiral and merger,and subsequent final black hole ringdown.Over0.2s,the signal increases in frequency and amplitude in about8cycles from35to150Hz,where the amplitude reaches a maximum.The most plausible explanation for this evolution is the inspiral of two orbiting masses,m1and m2,due to gravitational-wave emission.At the lower frequencies,such evolution is characterized by the chirp mass[11]M¼ðm1m2Þ3=5121=5¼c3G596π−8=3f−11=3_f3=5;where f and_f are the observed frequency and its time derivative and G and c are the gravitational constant and speed of light.Estimating f and_f from the data in Fig.1, we obtain a chirp mass of M≃30M⊙,implying that the total mass M¼m1þm2is≳70M⊙in the detector frame. This bounds the sum of the Schwarzschild radii of thebinary components to2GM=c2≳210km.To reach an orbital frequency of75Hz(half the gravitational-wave frequency)the objects must have been very close and very compact;equal Newtonian point masses orbiting at this frequency would be only≃350km apart.A pair of neutron stars,while compact,would not have the required mass,while a black hole neutron star binary with the deduced chirp mass would have a very large total mass, and would thus merge at much lower frequency.This leaves black holes as the only known objects compact enough to reach an orbital frequency of75Hz without contact.Furthermore,the decay of the waveform after it peaks is consistent with the damped oscillations of a black hole relaxing to a final stationary Kerr configuration. Below,we present a general-relativistic analysis of GW150914;Fig.2shows the calculated waveform using the resulting source parameters.III.DETECTORSGravitational-wave astronomy exploits multiple,widely separated detectors to distinguish gravitational waves from local instrumental and environmental noise,to provide source sky localization,and to measure wave polarizations. The LIGO sites each operate a single Advanced LIGO detector[33],a modified Michelson interferometer(see Fig.3)that measures gravitational-wave strain as a differ-ence in length of its orthogonal arms.Each arm is formed by two mirrors,acting as test masses,separated by L x¼L y¼L¼4km.A passing gravitational wave effec-tively alters the arm lengths such that the measured difference isΔLðtÞ¼δL x−δL y¼hðtÞL,where h is the gravitational-wave strain amplitude projected onto the detector.This differential length variation alters the phase difference between the two light fields returning to the beam splitter,transmitting an optical signal proportional to the gravitational-wave strain to the output photodetector. To achieve sufficient sensitivity to measure gravitational waves,the detectors include several enhancements to the basic Michelson interferometer.First,each arm contains a resonant optical cavity,formed by its two test mass mirrors, that multiplies the effect of a gravitational wave on the light phase by a factor of300[48].Second,a partially trans-missive power-recycling mirror at the input provides addi-tional resonant buildup of the laser light in the interferometer as a whole[49,50]:20W of laser input is increased to700W incident on the beam splitter,which is further increased to 100kW circulating in each arm cavity.Third,a partially transmissive signal-recycling mirror at the outputoptimizes FIG. 2.Top:Estimated gravitational-wave strain amplitude from GW150914projected onto H1.This shows the full bandwidth of the waveforms,without the filtering used for Fig.1. The inset images show numerical relativity models of the black hole horizons as the black holes coalesce.Bottom:The Keplerian effective black hole separation in units of Schwarzschild radii (R S¼2GM=c2)and the effective relative velocity given by the post-Newtonian parameter v=c¼ðGMπf=c3Þ1=3,where f is the gravitational-wave frequency calculated with numerical relativity and M is the total mass(value from Table I).the gravitational-wave signal extraction by broadening the bandwidth of the arm cavities [51,52].The interferometer is illuminated with a 1064-nm wavelength Nd:Y AG laser,stabilized in amplitude,frequency,and beam geometry [53,54].The gravitational-wave signal is extracted at the output port using a homodyne readout [55].These interferometry techniques are designed to maxi-mize the conversion of strain to optical signal,thereby minimizing the impact of photon shot noise (the principal noise at high frequencies).High strain sensitivity also requires that the test masses have low displacement noise,which is achieved by isolating them from seismic noise (low frequencies)and designing them to have low thermal noise (intermediate frequencies).Each test mass is suspended as the final stage of a quadruple-pendulum system [56],supported by an active seismic isolation platform [57].These systems collectively provide more than 10orders of magnitude of isolation from ground motion for frequen-cies above 10Hz.Thermal noise is minimized by using low-mechanical-loss materials in the test masses and their suspensions:the test masses are 40-kg fused silica substrates with low-loss dielectric optical coatings [58,59],and are suspended with fused silica fibers from the stage above [60].To minimize additional noise sources,all components other than the laser source are mounted on vibration isolation stages in ultrahigh vacuum.To reduce optical phase fluctuations caused by Rayleigh scattering,the pressure in the 1.2-m diameter tubes containing the arm-cavity beams is maintained below 1μPa.Servo controls are used to hold the arm cavities on resonance [61]and maintain proper alignment of the optical components [62].The detector output is calibrated in strain by measuring its response to test mass motion induced by photon pressure from a modulated calibration laser beam [63].The calibration is established to an uncertainty (1σ)of less than 10%in amplitude and 10degrees in phase,and is continuously monitored with calibration laser excitations at selected frequencies.Two alternative methods are used to validate the absolute calibration,one referenced to the main laser wavelength and the other to a radio-frequencyoscillator(a)FIG.3.Simplified diagram of an Advanced LIGO detector (not to scale).A gravitational wave propagating orthogonally to the detector plane and linearly polarized parallel to the 4-km optical cavities will have the effect of lengthening one 4-km arm and shortening the other during one half-cycle of the wave;these length changes are reversed during the other half-cycle.The output photodetector records these differential cavity length variations.While a detector ’s directional response is maximal for this case,it is still significant for most other angles of incidence or polarizations (gravitational waves propagate freely through the Earth).Inset (a):Location and orientation of the LIGO detectors at Hanford,WA (H1)and Livingston,LA (L1).Inset (b):The instrument noise for each detector near the time of the signal detection;this is an amplitude spectral density,expressed in terms of equivalent gravitational-wave strain amplitude.The sensitivity is limited by photon shot noise at frequencies above 150Hz,and by a superposition of other noise sources at lower frequencies [47].Narrow-band features include calibration lines (33–38,330,and 1080Hz),vibrational modes of suspension fibers (500Hz and harmonics),and 60Hz electric power grid harmonics.[64].Additionally,the detector response to gravitational waves is tested by injecting simulated waveforms with the calibration laser.To monitor environmental disturbances and their influ-ence on the detectors,each observatory site is equipped with an array of sensors:seismometers,accelerometers, microphones,magnetometers,radio receivers,weather sensors,ac-power line monitors,and a cosmic-ray detector [65].Another∼105channels record the interferometer’s operating point and the state of the control systems.Data collection is synchronized to Global Positioning System (GPS)time to better than10μs[66].Timing accuracy is verified with an atomic clock and a secondary GPS receiver at each observatory site.In their most sensitive band,100–300Hz,the current LIGO detectors are3to5times more sensitive to strain than initial LIGO[67];at lower frequencies,the improvement is even greater,with more than ten times better sensitivity below60Hz.Because the detectors respond proportionally to gravitational-wave amplitude,at low redshift the volume of space to which they are sensitive increases as the cube of strain sensitivity.For binary black holes with masses similar to GW150914,the space-time volume surveyed by the observations reported here surpasses previous obser-vations by an order of magnitude[68].IV.DETECTOR VALIDATIONBoth detectors were in steady state operation for several hours around GW150914.All performance measures,in particular their average sensitivity and transient noise behavior,were typical of the full analysis period[69,70]. Exhaustive investigations of instrumental and environ-mental disturbances were performed,giving no evidence to suggest that GW150914could be an instrumental artifact [69].The detectors’susceptibility to environmental disturb-ances was quantified by measuring their response to spe-cially generated magnetic,radio-frequency,acoustic,and vibration excitations.These tests indicated that any external disturbance large enough to have caused the observed signal would have been clearly recorded by the array of environ-mental sensors.None of the environmental sensors recorded any disturbances that evolved in time and frequency like GW150914,and all environmental fluctuations during the second that contained GW150914were too small to account for more than6%of its strain amplitude.Special care was taken to search for long-range correlated disturbances that might produce nearly simultaneous signals at the two sites. No significant disturbances were found.The detector strain data exhibit non-Gaussian noise transients that arise from a variety of instrumental mecha-nisms.Many have distinct signatures,visible in auxiliary data channels that are not sensitive to gravitational waves; such instrumental transients are removed from our analyses [69].Any instrumental transients that remain in the data are accounted for in the estimated detector backgrounds described below.There is no evidence for instrumental transients that are temporally correlated between the two detectors.V.SEARCHESWe present the analysis of16days of coincident observations between the two LIGO detectors from September12to October20,2015.This is a subset of the data from Advanced LIGO’s first observational period that ended on January12,2016.GW150914is confidently detected by two different types of searches.One aims to recover signals from the coalescence of compact objects,using optimal matched filtering with waveforms predicted by general relativity. The other search targets a broad range of generic transient signals,with minimal assumptions about waveforms.These searches use independent methods,and their response to detector noise consists of different,uncorrelated,events. However,strong signals from binary black hole mergers are expected to be detected by both searches.Each search identifies candidate events that are detected at both observatories consistent with the intersite propa-gation time.Events are assigned a detection-statistic value that ranks their likelihood of being a gravitational-wave signal.The significance of a candidate event is determined by the search background—the rate at which detector noise produces events with a detection-statistic value equal to or higher than the candidate event.Estimating this back-ground is challenging for two reasons:the detector noise is nonstationary and non-Gaussian,so its properties must be empirically determined;and it is not possible to shield the detector from gravitational waves to directly measure a signal-free background.The specific procedure used to estimate the background is slightly different for the two searches,but both use a time-shift technique:the time stamps of one detector’s data are artificially shifted by an offset that is large compared to the intersite propagation time,and a new set of events is produced based on this time-shifted data set.For instrumental noise that is uncor-related between detectors this is an effective way to estimate the background.In this process a gravitational-wave signal in one detector may coincide with time-shifted noise transients in the other detector,thereby contributing to the background estimate.This leads to an overestimate of the noise background and therefore to a more conservative assessment of the significance of candidate events.The characteristics of non-Gaussian noise vary between different time-frequency regions.This means that the search backgrounds are not uniform across the space of signals being searched.To maximize sensitivity and provide a better estimate of event significance,the searches sort both their background estimates and their event candidates into differ-ent classes according to their time-frequency morphology. The significance of a candidate event is measured against the background of its class.To account for having searchedmultiple classes,this significance is decreased by a trials factor equal to the number of classes [71].A.Generic transient searchDesigned to operate without a specific waveform model,this search identifies coincident excess power in time-frequency representations of the detector strain data [43,72],for signal frequencies up to 1kHz and durations up to a few seconds.The search reconstructs signal waveforms consistent with a common gravitational-wave signal in both detectors using a multidetector maximum likelihood method.Each event is ranked according to the detection statistic ηc ¼ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi2E c =ð1þE n =E c Þp ,where E c is the dimensionless coherent signal energy obtained by cross-correlating the two reconstructed waveforms,and E n is the dimensionless residual noise energy after the reconstructed signal is subtracted from the data.The statistic ηc thus quantifies the SNR of the event and the consistency of the data between the two detectors.Based on their time-frequency morphology,the events are divided into three mutually exclusive search classes,as described in [41]:events with time-frequency morphology of known populations of noise transients (class C1),events with frequency that increases with time (class C3),and all remaining events (class C2).Detected with ηc ¼20.0,GW150914is the strongest event of the entire search.Consistent with its coalescence signal signature,it is found in the search class C3of events with increasing time-frequency evolution.Measured on a background equivalent to over 67400years of data and including a trials factor of 3to account for the search classes,its false alarm rate is lower than 1in 22500years.This corresponds to a probability <2×10−6of observing one or more noise events as strong as GW150914during the analysis time,equivalent to 4.6σ.The left panel of Fig.4shows the C3class results and background.The selection criteria that define the search class C3reduce the background by introducing a constraint on the signal morphology.In order to illustrate the significance of GW150914against a background of events with arbitrary shapes,we also show the results of a search that uses the same set of events as the one described above but without this constraint.Specifically,we use only two search classes:the C1class and the union of C2and C3classes (C 2þC 3).In this two-class search the GW150914event is found in the C 2þC 3class.The left panel of Fig.4shows the C 2þC 3class results and background.In the background of this class there are four events with ηc ≥32.1,yielding a false alarm rate for GW150914of 1in 8400years.This corresponds to a false alarm probability of 5×10−6equivalent to 4.4σ.FIG.4.Search results from the generic transient search (left)and the binary coalescence search (right).These histograms show the number of candidate events (orange markers)and the mean number of background events (black lines)in the search class where GW150914was found as a function of the search detection statistic and with a bin width of 0.2.The scales on the top give the significance of an event in Gaussian standard deviations based on the corresponding noise background.The significance of GW150914is greater than 5.1σand 4.6σfor the binary coalescence and the generic transient searches,respectively.Left:Along with the primary search (C3)we also show the results (blue markers)and background (green curve)for an alternative search that treats events independently of their frequency evolution (C 2þC 3).The classes C2and C3are defined in the text.Right:The tail in the black-line background of the binary coalescence search is due to random coincidences of GW150914in one detector with noise in the other detector.(This type of event is practically absent in the generic transient search background because they do not pass the time-frequency consistency requirements used in that search.)The purple curve is the background excluding those coincidences,which is used to assess the significance of the second strongest event.For robustness and validation,we also use other generic transient search algorithms[41].A different search[73]and a parameter estimation follow-up[74]detected GW150914 with consistent significance and signal parameters.B.Binary coalescence searchThis search targets gravitational-wave emission from binary systems with individual masses from1to99M⊙, total mass less than100M⊙,and dimensionless spins up to 0.99[44].To model systems with total mass larger than 4M⊙,we use the effective-one-body formalism[75],whichcombines results from the post-Newtonian approach [11,76]with results from black hole perturbation theory and numerical relativity.The waveform model[77,78] assumes that the spins of the merging objects are alignedwith the orbital angular momentum,but the resultingtemplates can,nonetheless,effectively recover systemswith misaligned spins in the parameter region ofGW150914[44].Approximately250000template wave-forms are used to cover this parameter space.The search calculates the matched-filter signal-to-noiseratioρðtÞfor each template in each detector and identifiesmaxima ofρðtÞwith respect to the time of arrival of the signal[79–81].For each maximum we calculate a chi-squared statisticχ2r to test whether the data in several differentfrequency bands are consistent with the matching template [82].Values ofχ2r near unity indicate that the signal is consistent with a coalescence.Ifχ2r is greater than unity,ρðtÞis reweighted asˆρ¼ρ=f½1þðχ2rÞ3 =2g1=6[83,84].The final step enforces coincidence between detectors by selectingevent pairs that occur within a15-ms window and come fromthe same template.The15-ms window is determined by the10-ms intersite propagation time plus5ms for uncertainty inarrival time of weak signals.We rank coincident events basedon the quadrature sumˆρc of theˆρfrom both detectors[45]. To produce background data for this search the SNR maxima of one detector are time shifted and a new set of coincident events is computed.Repeating this procedure ∼107times produces a noise background analysis time equivalent to608000years.To account for the search background noise varying acrossthe target signal space,candidate and background events aredivided into three search classes based on template length.The right panel of Fig.4shows the background for thesearch class of GW150914.The GW150914detection-statistic value ofˆρc¼23.6is larger than any background event,so only an upper bound can be placed on its false alarm rate.Across the three search classes this bound is1in 203000years.This translates to a false alarm probability <2×10−7,corresponding to5.1σ.A second,independent matched-filter analysis that uses adifferent method for estimating the significance of itsevents[85,86],also detected GW150914with identicalsignal parameters and consistent significance.When an event is confidently identified as a real gravitational-wave signal,as for GW150914,the back-ground used to determine the significance of other events is reestimated without the contribution of this event.This is the background distribution shown as a purple line in the right panel of Fig.4.Based on this,the second most significant event has a false alarm rate of1per2.3years and corresponding Poissonian false alarm probability of0.02. Waveform analysis of this event indicates that if it is astrophysical in origin it is also a binary black hole merger[44].VI.SOURCE DISCUSSIONThe matched-filter search is optimized for detecting signals,but it provides only approximate estimates of the source parameters.To refine them we use general relativity-based models[77,78,87,88],some of which include spin precession,and for each model perform a coherent Bayesian analysis to derive posterior distributions of the source parameters[89].The initial and final masses, final spin,distance,and redshift of the source are shown in Table I.The spin of the primary black hole is constrained to be<0.7(90%credible interval)indicating it is not maximally spinning,while the spin of the secondary is only weakly constrained.These source parameters are discussed in detail in[39].The parameter uncertainties include statistical errors and systematic errors from averaging the results of different waveform models.Using the fits to numerical simulations of binary black hole mergers in[92,93],we provide estimates of the mass and spin of the final black hole,the total energy radiated in gravitational waves,and the peak gravitational-wave luminosity[39].The estimated total energy radiated in gravitational waves is3.0þ0.5−0.5M⊙c2.The system reached apeak gravitational-wave luminosity of3.6þ0.5−0.4×1056erg=s,equivalent to200þ30−20M⊙c2=s.Several analyses have been performed to determine whether or not GW150914is consistent with a binary TABLE I.Source parameters for GW150914.We report median values with90%credible intervals that include statistical errors,and systematic errors from averaging the results of different waveform models.Masses are given in the source frame;to convert to the detector frame multiply by(1þz) [90].The source redshift assumes standard cosmology[91]. Primary black hole mass36þ5−4M⊙Secondary black hole mass29þ4−4M⊙Final black hole mass62þ4−4M⊙Final black hole spin0.67þ0.05−0.07 Luminosity distance410þ160−180MpcSource redshift z0.09þ0.03−0.04。
蓝移名词解释

什么是“蓝移”?
蓝移也称蓝位移,与红移相对。
在光化学中,蓝移也非正式地指浅色效应。
是由于结构或实验条件的变化,使吸收峰向短波长方向移动的现象,亦称紫移或短移。
蓝移是一个移动的发射源在向观测者接近时,所发射的电磁波(例如光波)频率会向电磁频谱的蓝色端移动(也就是波长缩短)的现象。
这种波长改变的现象在相互间有移动现象的参考座标系中就是一般所说的多普勒位移或是多普勒效应。
蓝移(或紫移,hypsochromic shift or blue shift)是吸收峰向短波长移动。
例如-COOR基团,能产生紫外-可见吸收的官能团,如一个或几个不饱和基团,或不饱和杂原子基团,C=C, C=O, N=N。
2019年“逐星·开信杯”广东省中小学生天文知识竞赛试题(低年组)

2019年“逐星·开信杯”广东省中小学生天文知识竞赛试题(低年组)注意事项:1、本卷为闭卷考试,请答卷人按照自己的真实水平独立完成。
在监考老师宣布考试结束时应停止答卷。
交卷时只须将答题卡交回。
2、选择题全部为单项选择,选择一个最接近正确的答案,答错不扣分。
用2B铅笔将答题卡上相应的答案选框涂黑涂满,并用钢笔或签字笔在答题卡上写上姓名、学校、考号等信息。
切勿用钢笔、圆珠笔或自动铅笔涂答题卡,以免影响成绩。
答题卡采用机器阅卷,由答卷人填涂答题卡失误或不规范造成的失分由其本人承担。
3、总分100分,每题2分,考试时间90分钟。
4、本场考试允许使用不具编程功能的计算器。
5、比赛结果将在广东天文学会网站和广东天文学会微信公众号公布。
Part 1. 天文热点1. 2019年2月,天文学家公布发现了人类已知最远的太阳系内天体,这颗天体昵称叫?BA. Farout (遥远)B. FarFarout (遥遥远)C. Ultima Thule (天涯海角)D. Oumuamua (奥陌陌)本题考查了新视野号飞跃冥王号后对编号2014 MU69(临时名:Ultima Thule/天涯海角,正式名:Arrokoth/阿罗科斯)进行探测的时事新闻,2019年1月1日的时候“新视野号”在3500km处近掠过“天涯海角”,使得这个天体成为人类在太阳系中探测过最遥远的天体,但是太阳系中最遥远的天体是2019年2月宣布发现的在140AU外的“Farfarout”。
2. 今年__________,NASA正式宣布机遇号火星车在失联8个月后,唤醒无效,结束任务。
AA. 2月14日B. 3月14日C. 4月14日D. 5月14日在2018年6月,火星大冲前地面观测到火星表面全球性的沙尘暴,在尘暴期间失去了和机遇号的联系,随后执行了六周的无线电唤醒无果后,NASA在2019年2月14日正式结束了持续15年的机遇号火星车的探测任务。
九年级英语天文知识单选题50题

九年级英语天文知识单选题50题1. The first planet discovered by using a telescope was Uranus. Which of the following statements about Uranus is correct?A. It is the closest planet to the SunB. It has the most visible rings in the solar systemC. It rotates on its sideD. It is the hottest planet答案:C。
解析:A选项,离太阳最近的行星是水星,不是天王星。
B选项,太阳系中拥有最明显光环的是土星,而非天王星。
C选项,天王星的自转轴几乎平行于黄道面,也就是它是躺着自转的,这一特征是天王星比较独特的地方,所以该选项正确。
D选项,太阳系中最热的行星是金星,不是天王星。
2. The Milky Way is a huge ______ that contains our solar system.A. planetB. starC. galaxyD. comet答案:C。
解析:A选项,planet( 行星)是围绕恒星运行的天体,而银河系不是行星。
B选项,star( 恒星)是单个的天体,银河系包含众多恒星等天体,不是单纯的一颗恒星。
C选项,galaxy(星系),银河系是一个巨大的星系,我们的太阳系就在银河系当中,该选项正确。
D选项,comet( 彗星)是一种特殊的小天体,和银河系的概念不同。
3. Galileo Galilei made many important astronomical observations. He discovered four of Jupiter's moons. Which of the following is NOT one of them?A. IoB. EarthC. EuropaD. Ganymede答案:B。
类星体Quasar和耀变体Blazar
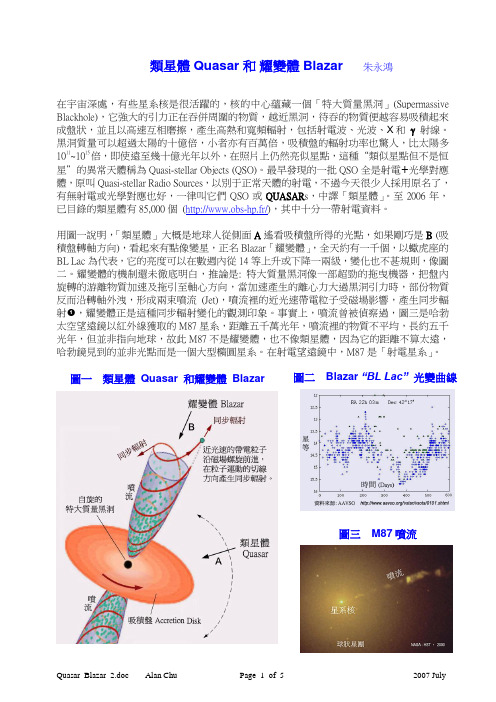
類星體Quasar 和 耀變體 Blazar 朱永鴻在宇宙深處,有些星系核是很活躍的,核的中心蘊藏一個「特大質量黑洞」(Supermassive Blackhole),它強大的引力正在吞併周圍的物質,越近黑洞,待吞的物質便越容易吸積起來成盤狀,並且以高速互相磨擦,產生高熱和寬頻輻射,包括射電波、光波、X 和 射線。
黑洞質量可以超過太陽的十億倍,小者亦有百萬倍,吸積盤的輻射功率也驚人,比太陽多1011~1015倍,即使遠至幾十億光年以外,在照片上仍然亮似星點,這種“類似星點但不是恒星”的異常天體稱為Quasi-stellar Objects (QSO)。
最早發現的一批QSO 全是射電+光學對應體,原叫Quasi-stellar Radio Sources ,以別于正常天體的射電,不過今天很少人採用原名了,有無射電或光學對應也好,一律叫它們QSO 或QUASAR s ,中譯「類星體」。
至2006年,已目錄的類星體有85,000個 (http://www.obs-hp.fr/),其中十分一帶射電資料。
用圖一說明,「類星體」大概是地球人從側面A 遙看吸積盤所得的光點,如果剛巧是B (吸積盤轉軸方向),看起來有點像變星,正名Blazar 「耀變體」,全天約有一千個,以蠍虎座的BL Lac 為代表,它的亮度可以在數週內從14等上升或下降一兩級,變化也不甚規則,像圖二。
耀變體的機制還未徹底明白,推論是: 特大質量黑洞像一部超勁的拖曳機器,把盤內旋轉的游離物質加速及拖引至軸心方向,當加速產生的離心力大過黑洞引力時,部份物質反而沿轉軸外洩,形成兩束噴流 (Jet),噴流裡的近光速帶電粒子受磁場影響,產生同步輻射 ,耀變體正是這種同步輻射變化的觀測印象。
事實上,噴流曾被偵察過,圖三是哈勃太空望遠鏡以紅外線獲取的M87星系,距離五千萬光年,噴流裡的物質不平均,長約五千光年,但並非指向地球,故此M87不是耀變體,也不像類星體,因為它的距離不算太遠,哈勃鏡見到的並非光點而是一個大型橢圓星系。
Er3+,Yb3+BaWO4晶体的光谱特性及上转换发光

2.1 晶体生长
晶体采用提拉法在大气气氛中进行生长,生长设备为DJ-400 型单晶炉。原料为光谱纯 的为BaCO3,WO3, Yb2O3,Er2O3。BaCO3,WO3按 1:1 的摩尔比配料,Er2O3和Yb2O3的掺杂浓度 1mol%。固相反应的方程式为:
*中国科学院物理研究所光物理重点实验室资助。
− 0.02476λ2
(5)Βιβλιοθήκη ne2=3.28033 +
0.03538 λ2 − 0.02810
− 0.01077λ2
(6)
对同一波长BaWO4晶体的no和ne差别不大,计算过程中n值取no和ne的平均值。由吸收光谱求出 Г值,进而求出SedJJ’,代入(3)式中,采用最小二乘法可拟合出Ωt。本实验选取了6个只涉 及到电偶极跃迁的吸收峰对Ωt进行拟合,计算得到的Г及SedJJ’ 值在表2中列出。最终拟合 的结果为:Ω2=0.3926×10-20cm2,Ω4=0.0721×10-20cm2,Ω6=0.0028×10-20cm2。
at room temperature
2S+1LJ
Energy levels/cm-1
∆E/cm-1
α(cm-1)
σabs(×10-21cm2)
4I15/2
0,69,126,159,182,227,243,293
293
---
---
4I13/2
6476,6517*,6564,6609,6641
38.3
表 1. 室温下Er3+,Yb3+:BaWO4晶体中Er3+的能级分裂、吸收系数和吸收截面 Table 1. Value of energy slips, absorption coefficient, absorption cross section of Er3+ in Er3+:Yb3+:BaWO4 crystal
蓝移
说明
蓝移(blue shift)蓝位移也称蓝移,与红移相对。在光化学中,蓝移也非正式地指浅色效应。蓝移指一个 正向观察者移动的物体所散射的电磁波(比如光)的频率在光谱线上向蓝端的方向移动(意味着频率升高)。在 互相移动的参考系之间频率的移动又叫做多普勒移动或者多普勒效应。
1993年,美国贝尔实验室在硒化镉中发现随着粒子尺寸的减小光颜色从红变成绿进而蓝,有人把这种发光带 颜色从红变成绿进而蓝或吸收由低频移向高频的现象称为“蓝移”。
例如-COOR基团,能产生紫外-可见吸收的官能团,如一个或几个不饱和基团,或不饱和杂原子基团,C=C, C=O, N=N, N=O等称为生色团(chromophore);
助色团(auxochrome):本身在200nm以上不产生吸收,但其存在能增强生色团的生色能力(改变分子的吸 收位置和增加吸收强度)的一类基团。
当一般将星光的红移被视为是宇宙膨胀的证据时,天文学中同样有很多蓝移现象,例如:同在本星系群的仙 女座星系正在向银河系移动;所以从地球的角度看,仙女座星系发出的光有蓝移现象。观察螺旋星系时,旋臂朝 向地球接近的一端会呈现蓝移(参考塔利-费舍尔关系)。临近太阳系的巴纳德星就是恒星观察的典型例子。还有, 蝎虎座BL类星体被推挤出的相对喷流中朝向地球的一支,辐射出的同步加速辐射和韧致辐射都会呈现蓝移。
产生情况
很多星体的红移是宇宙膨胀的证据,但天文学中同样有很多蓝移现象,例如:同在本星系群的仙女座星系正 在向银河系移动;所以从地球的角度看,仙女座星系发出的光有蓝移现象。螺旋星系中正在向地球旋转的一边会 有细微的蓝移现象。
的成因
ቤተ መጻሕፍቲ ባይዱ
这些是在天文学上已知可以造成蓝移的原因:
光学原理
蓝移(或紫移,hypsochromic shift or blue shift)是吸收峰向高频移动。
(宇宙)高中英语阅读短文《发现黑洞》及答案
(宇宙)高中英语阅读短文《发现黑洞》及答案北京时间2019年4月10日21时,天文学家召开全球新闻发布会,宣布首次直接拍摄到黑洞的照片。
阅读题目,回答问题文本选自:The Guardian(卫报)Recently,scientists produced the first real image of a black hole,shining a light onone of the universe’s great mysteries,in a galaxy called Messier87.The image is not a photograph but an image created by the Event Horizon Telescope(EHT)ing a network of eight ground-based telescopes across the world,the EHT collected data to produce the image.The black hole itself is unseeable,as it’s impossible for light to escape from it;what we can see is its even thorizon.The EHT was also observing a black hole located at the centre of the Milky Way, but was unable to produce an image.While Messier87is furtheraway,it was easier to observe,due to its larger size.The golden ring is the event horizon,the moment an object approaching a black hole reaches a point of no return,unable to escape its gravitational pull.Objects that pass into the event horizon are thought to go through spaghettification(意大利面条化),a process,first described by Stephen Hawking,in which they will be stretchedout like a piece of pasta by gravitational forces.Heino Falcke,professor of radio astronomy and astroparticle physics at Radboud University in Nijmegen,and chair of the EHT science council, says the image shows asilhouette(剪影)of the hole against the surrounding glow of the event horizon,all of the matter being pulled into the hole.At the centre of the black hole is a gravitational singularity, where all matter is crushed into an infinitely small space.The black hole lies55m light years away from us.It is around100bn km wide,larger than the entire solar system and6.5bn times the mass of our sun.Through creating an image of a black hole,something previously thought to be impossible,the EHT project has made a break through in the understanding ofblack holes,whose existence has long been difficult to prove.The image will help physicists to better understand how black holes work and images of the event horizon are particularly important for testing the theory of general relativity.1.What’s the text mainly about?A.The image of a black hole.B.The photo created by the EHT.C.The event horizon of the black hole.D.The introduction of the EHT project.2.How does EHT collect data?A.By producing the image of a black hole.0B.By studying the golden ring in the photo.C.By observing the center of the Milky Way.D.By using a network of eight ground-based telescopes.3.What do we know about the black hole fromthe text?A.Its image shows a silhouette of the event horizon.B.There is a possibility that light can escape from it.C.All matter is crushed into small space at its centre.D.Objects will be stretched out outside the event horizon.4.What does the last paragraph mainly present?A.Creating an image of a black hole is thought to be impossible.B.It’sstill hard for physicists to prove the existence of the black hole.C.The image will help physicists to test the theory of general relativity.D.The image of a black hole created by EHT project is highly significant.参考答案:ADCD生词及长难句1.Galaxy n.星系the galaxy银河系2.event horizon视界德国天文学家卡尔·史瓦西计算出一个巨大天体可扭曲周围空间,以至于连光都无法逃脱,这个特定的半径就是我们所致的史瓦西半径,也可以称之为“视界”。
chip-sized_spectrometers
Solid Phase Spectroscopy
• Tunable SLED spectrometers work well for gases, liquids and solutions • However, diffuse reflectance spectroscopy of solids is a very ‘lossy’ application, especially if large areas are illuminated • So let’s look at the implications of diffuse reflectance for sources, especially for miniature spectrometers
~1 mm
Assembly
Lid
Optical components on LIGA structures Optical bench Thermoelectric cooler 14-pin butterfly package
Optical fiber
Complete Spectrometer
MEMS Filter Assembly
Fabry-Perot Filter Assembly
Flat Mirror with Integrated Spacer High Reflectivity Coating
SOI MEMS Structure [SOI= silicon on insulator]
Etendue (1)
• For all spectrometers using these sources, the power emitted per unit area of the source will be the same, so as the area drops, so does the emitted power. • The useful power emitted by the source is proportional to A•Ω
热红外高光谱成像仪(ATHIS)对矿物和气体的实验室光谱测量
第 39 卷第 6 期2020 年 12 月Vol. 39 No. 6December 2020红外与毫米波学报J. Infrared Millim. Waves文章编号:1001-9014(2020)06-0767-11DOI :10. 11972/j. issn. 1001-9014. 2020. 06.015热红外高光谱成像仪(ATHIS)对矿物和气体的实验室光谱测量李春来匸刘成玉],金健],徐睿],谢佳楠],吕刚-袁立银-柳潇3,徐宏根3**,王建宇心收稿日期:2020- 05- 06 ,修回日期:2020- 10- 14 Received date :2020- 05- 06 , Revised date :2020- 10- 14基金项目:中国科学院青年创新促进会项目(2016218),“十三五”民用航天预研项目(D040104)”Foundation items : Supported by Youth Innovation Promotion Association CAS (2016218), and the National Defense Pre -Research Foundation of China during the 13th Five -Year Plan Period (D040104)作者简介(Biography ):李春来(1982-),男,汉族,湖北当阳人,博士 ,研究员,主要研究方向为高分辨率红外高光谱成像技术、新型计算光谱成 像技术等.E -mail :lichunlai@mail. sitp. ac. cn* 通讯作者(Corresponding author ) : E -mail : honggen_xu@163. com , jywang@mail. sitp. ac. cn(1.中国科学院空间主动光电技术重点实验室,上海200083;2.中国科学院大学杭州高等研究院,浙江杭州310024;3.中国地质调查局武汉地质调查中心,湖北武汉430205)摘要:首先介绍了热红外高光谱成像应用的独特优势,然后论述了机载热红外高光谱成像仪(Airborne Thermal Infrared Hyperspectral Imaging System ,ATHIS )灵敏度优化设计方法,结合仪器特点介绍了实验室矿物发射光谱和 气体吸收光谱测量的辐射模型,分析了样本红外光谱与温度分离的数据处理流程。
