江苏小升初数学目标班图形专题
苏教版六年级数学小升初专题复习五几何初步知识
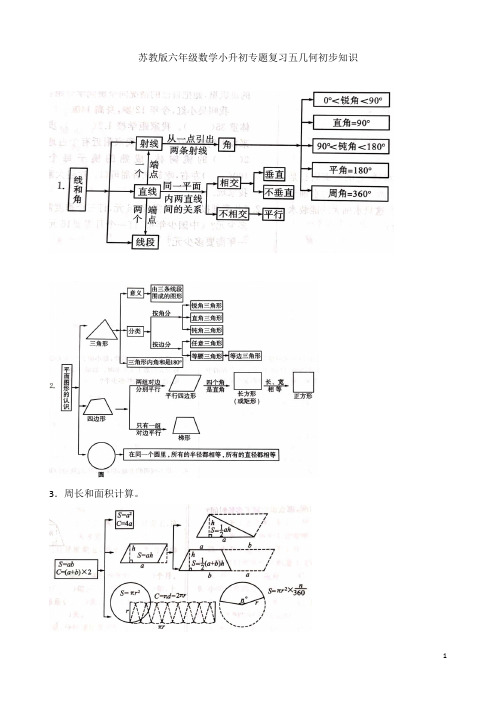
苏教版六年级数学小升初专题复习五几何初步知识3.周长和面积计算。
4.立体图形一、定义1.线段:用直尺把两点连接起来,就得到一条线段,线段长就是这两点间的距离。
两点间所有连线中线段最短。
2.射线:把线段的一端无限延长,可以得到条射线。
手电筒发出的光、太阳射出的光线都可看成是射线。
3.直线:把线段的两端无限延长,可以得到一条直线。
二、直线、线段、射线的比较名称三、同一平面上线与线的关系同一平面上的两条直线或平行或相交。
1.垂线:两条直线相交成直角时,这两条直线叫作互相垂直,其中一条直线叫作另一条直线的垂线,这两条直线的交点叫作垂足。
2.平行线:在同一平面内不相交的两条直线叫作平行线。
(1)平行线之间的距离处处相等;(2)平行线间垂线段最短,并且有无数条;(3)垂直于同一条直线的两条直线互相平行。
3.点到直线的连线中,垂线段最短4.线段AB的垂直平分线上的任意一点到线段两端的连线相等。
一、角的分类角:从一点起画两条射线,所组成的图形叫作角。
角两边叉开得越大,角越大;角的大小与角两边的长短无关。
二、角的测量利用量角器可以画角或量出角的度数。
首先将量角器的中心与角的顶点重合,然后再将量角器的零刻度线与角的一边重合,另一条边所对准的刻度就是这个角的度数。
注意要分清是内刻度线还是外刻度线。
三、画角画角的方法有很多,我们应该学会用量角器画指定大小的角。
画角时,首先要确定角的顶点,并画出角的一条边,然后将量角器的中心和零刻度线与角的顶点和画好的一条边都分别重合,数出量角器上所画角的度数,做好标记,然后连接顶点和标记,这样就画好了一个指定度数的角。
要注意美观。
形一、平行四边形和梯形(四边形)圆定义:两组对边分别平行的四边形叫作平行四边形。
只有一组对边平行的四边形叫作梯形。
二、三角形(由三条线段围成的图形)1.按角分2.按边分3.等腰三角形的特征和性质两腰相等,两底角相等,底边上的高是底边的垂直平分线。
4.等边三角形的特征和性质,5.三角形的一些特征和性质 (1)三角形具有稳定性; (2)三角形内角和是180º(3)三角形中任意两边之和大于第三边(4)在三角形中大角所对的边也大;在直角三角形中,斜边最长 (5)在等腰直角三角形中,斜边上的高等于斜边的一半三、圆(封闭的曲线图形) 1.圆的各部分名称在同一个圆内,有无数条直径和半径,所有的直径都相等,所有的半径都相等。
小升初一对一《平面图形》专项复习

小考体验题:
1、 左边阴影部分图形的周长是()厘米。
2、下图中阴影部分的面积是50平方厘米,求环形的面积。
课题
小升初专项复习:空间与图形(一)——平面图形
教学目标
1、利用计算公式解题
2、利用倍比关系解题
3、比较图形的形状、面积及周长,灵活运用割补、平移、旋转、代换等方法解题
4、利用包含于排除关系解题
5、图形的计数及拆拼
重点难点考点
1、利用计算公式解题
2、利用倍比关系解题
3、比较图形的形状、面积及周长,灵活运用割补、平移、旋转、代换等方法解题
练习6右图中,共有个三角形,其中直角三角形有个。
例7把下图中的图形分成五个大小相等的图形。
练习7把下图中的等腰梯形分成形状大小相同的四块。
课后练习
1、求下面图形中阴影部分的面积。(单位:厘米)
2、把一个长方形的长和宽各增加8厘米,这个长Байду номын сангаас形的面积就增加208平方厘米,求原长方形的周长。
3、如下图,长方形ABCD中,E、F、G分别是BC、CD、DA边上的重点,已知长方形ABCD的面积是30平方厘米,求阴影部分的面积。
4、利用包含于排除关系解题
5、图形的计数及拆拼
教案
题型一灵活运用计算公式解题
例1如右图,已知梯形的上底是25厘米,下底是40厘米,其中阴影部分的面积是400平方厘米,这个梯形面积是多少?
练习1把一个正方形的一边的长度减少20%,相邻的一边的长度增加2厘米,得到一个长方形,它与原来正方形的面积相等,求原正方形的面积。
练习3如图,△AOD的面积为18平方厘米,线段AO:OC=3:2,那么梯形ABCD的面积是多少平方厘米?
(小升初押题卷)江苏省苏州市2024年六年级下学期小升初择校分班考数学试卷 解析版参考答案

参考答案:1.C【分析】长方体有12条棱,相对的四条棱长度相等,按长度可分为三组,每一组有4条棱。
长方体有8个顶点,每个顶点连接三条棱,三条棱分别叫做长方体的长、宽、高。
因此只要确定了长方体的长、宽、高,即可确定这个长方体的形状和大小。
【详解】A.,只能确定2条棱,无法确定这个长方体的形状和大小;B.,只能确定2条棱,无法确定这个长方体的形状和大小;C.,相交于同一个顶点的三条棱,即长方体的长、宽、高,能确定这个长方体的形状和大小。
故答案为:C2.B【详解】试题分析:等底等高的圆锥和圆柱,圆锥的体积是圆柱体积的,把一个圆柱形木料加工成一个和它等底等高的圆锥,体积比原来减少了(1);由此解答.解:根据分析,把一个圆柱形木料加工成一个和它等底等高的圆锥,体积比原来减少了:1=;答:体积比原来减少了.故选B.点评:此题主要考查等底等高的圆锥和圆柱体积之间的关系,等底等高的圆锥和圆柱,圆锥的体积是圆柱体积的,由此解决问题.3.C【分析】把长方体木材平均截成3段,表面积增加了4个横截面面积。
已知表面积增加了240平方分米,即1个横截面面积=240÷4=60(平方分米)。
长方体的体积=横截面面积×长,据此解答。
【详解】240÷4=60(平方分米)2米=20分米60×20=1200(立方分米)故答案为:C【点睛】考查长方体的体积和立体图形的切拼。
明确表面积增加的240平方分米是4个长方体横截面的面积是解题的关键。
4.①5.C【分析】把一个图形放大或缩小后所得到的图形与原图形相比,形状相同,大小不同,周长扩大的倍数等于边长扩大的倍数,面积扩大的倍数等于边长扩大的倍数的平方。
【详解】比例尺4∶1是把一个图形按4倍放大,则其各边的长度分别扩大4倍,则周长扩大到原来的4倍,其面积扩大4×4=16倍。
故答案为:C。
【点睛】图形的放大和缩小是生活中常见的现象,把一个图形放大或缩小后所得到的图形与原图形相比,形状相同,大小不同,周长扩大的倍数等于边长扩大的倍数,面积扩大的倍数等于边长扩大的倍数的平方。
小升初数学图形专题

第二部分空间与图形量一长度(一) 什么是长度:长度是一维空间的度量。
(二) 长度常用单位* 千米(km) * 米(m) * 分米(dm) * 厘米(cm) * 毫米(mm) (三) 单位之间的换算1米=10 分米1分米=10 厘米1厘米=10 毫米1米=100厘米1千米=1000 米二面积(一)什么是面积面积,就是物体所占平面的大小。
对立体物体的表面的多少的测量一般称表面积。
(二)常用的面积单位* 平方千米*公顷*平方米* 平方分米* 平方厘米(三)面积单位的换算* 1平方分米=100平方厘米* 1平方米=100 平方分米* 1公顷=10000 平方米* 1平方千米=100 公顷三体积和容积(一)什么是体积、容积体积,就是物体所占空间的大小。
容积,箱子、油桶、仓库等所能容纳物体的体积,通常叫做它们的容积。
(二)常用单位体积单位:* 立方米* 立方分米* 立方厘米容积单位:* 升* 毫升(三)单位换算体积单位:* 1立方米=1000立方分米* 1立方分米=1000立方厘米* 1立方米=1000000立方厘米容积单位:* 1升=1000毫升* 1升=1立方分米* 1毫升=1立方厘米四质量(一)什么是质量:质量,就是表示表示物体有多重。
(二)常用单位* 吨t * 千克kg * 克g(三)常用换算* 1吨=1000千克* 1千克=1000克* 1吨=1000000克五时间(一)什么是时间:是指有起点和终点的一段时间(二)常用单位世纪、年、月、日、时、分、秒(三)单位换算* 1世纪=100年* 1年=365天(平年)* 1年=366天(闰年)*1年=4个季度*1个季度=3个月* 一、三、五、七、八、十、十二是大月大月有31 天* 四、六、九、十一是小月小月小月有30天* 平年2月有28天闰年2月有29天* 1天= 24小时* 1小时=60分* 1分=60秒六货币(一)什么是货币货币是充当一切商品的等价物的特殊商品。
人教版 小升初数学专题:空间与图形-平面图形的认识 测试卷优质期末总复习教学课件PPT 苏教版

5.钟面上如果分针旋转半周,那么时针旋转的角是
( A )度。
A.15
B.30
C.180
九、AB 是一条街道,要从点 P 修一条小路通向街道 AB,
怎么修最省料?(在图上画出表示这条小路的线段)如 果这幅图的比例尺是 1∶20000,这条小路实际是多少 米?(测量时取整厘米)(9 分)
小升初数学专题知识点总复习
第七章 空间与图形
3.下面图形中,四边形有( 10 )个,其中长方 形有( ②③⑫ ),正方形有( ⑥⑨ ),平行四边 形有( ⑤⑧⑬ ),梯形有( ①⑦ )。
4.只有一组对边平行的四边形是( 梯形 ),它 有( 无数 )条高。
5.两条直线相交成四个角,其中一个角是 50°, 其 余 三 个 角 分 别 是 ( 50° ) , ( 130° ) , ( 130° )。
6.用圆规画一个直径 6 厘米的圆,圆规两脚间的 距离是( 3 )厘米。
3
1
7.平角的4是( 135 )度,直角的6是( 15 )
度。
8.在 3 时整,时针和分针组成的角的度数是 ( 90° );在 6 时整,时针和分针组成的角的度数 是( 180° )。
二 、 判 断 题 。 ( 正 确 的 打 “√” , 错 误 的 打
“×”相交。
(×)
2.大圆的圆周率比小圆的圆周率大一些。
(×)
3.两个完全一样的直角三角形只能拼成一个长方
形。
(×)
4.圆有无数条对称轴。
(√)
5.钝角三角形中的两个锐角之和一定小于 90°。
(√)
6.两条平行线间有无数条垂线,这些垂线互相平
行。
(√)
4.一条( C )长是 1.5 米。 A.直线 B.射线 C.线段
小升初图形专题——五大模型
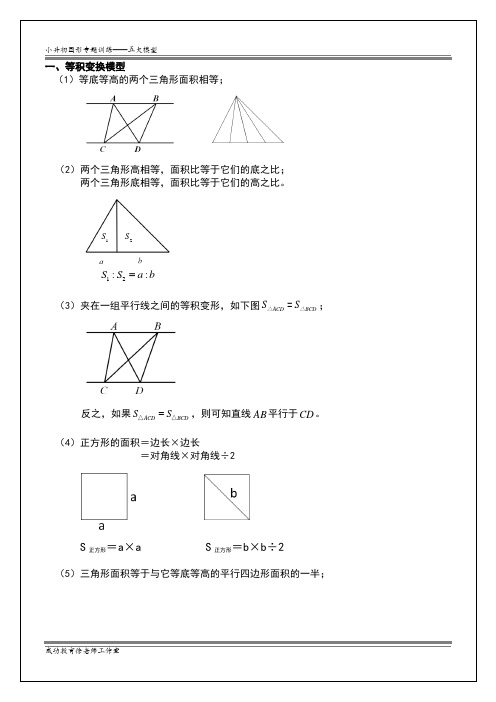
一、等积变换模型(1)等底等高的两个三角形面积相等;(2)两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
12::S S a b =(3)夹在一组平行线之间的等积变形,如下图ACD BCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD 。
(4)正方形的面积=边长×边长=对角线×对角线÷2S 正方形=a ×a S 正方形=b×b÷2(5)三角形面积等于与它等底等高的平行四边形面积的一半;1S 2S二、鸟头定理(共角定理)模型【共角三角形】定义:两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
规律:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△图1 图2三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
通过构造模型:一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
梯形中比例关系(“梯形蝴蝶定理”)①2213::S S a b =②221324::::::S S S S a b ab ab =;③梯形S 的对应份数为()2a b +。
四、相似模型相似三角形性质:金字塔模型沙漏模型①AD AE DE AFAB AC BC AG===;②22::ADE ABCS S AF AG=△△。
所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:(1)相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;(2)相似三角形的面积比等于它们相似比的平方。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目标班专题图形题
1、如图所示,正方形ABCD 的边长为4,求阴影部分的周长和面积。
2、如图,三角形1S 的面积比三角形2S 的面积大多少平方厘米?(单位:厘米)
3、一个长方形分成4个不同的三角形,绿色三角形面积是长方形面积的0.15倍,黄色三角形的面积是21平方厘米。
问:长方形的面积是多少平方厘米?
4、图中阴影部分的面积是57平方厘米,求这个正方形的面积。
5、在三角形ABC 中,点E 是BC 边上的中点,点F 是中线AE 上的点,其中AE=3AF ,并且延长BF 与AC 相交于D ,如下图所示。
若三角形ABC 的面积为48,请问三角形AFD 的面积为多少?
6、左图是一个直径是3厘米的半圆,AB 是直径,让A 点不动,把整个半圆逆时针转60°,此时B 点移动到C 点,如右图所示。
那么图中阴影部分的面积是多少平方厘米?( 取3.14)
7、如图,有8个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。
求花瓣图形的面积是多少平方厘米?
8、如图所示,已知ABC S △=1,AE=ED ,BD=3
2BC 求阴影的面积。
9、如图所示,把△ABC 的BA 边延长1倍到D 点,AC 边延长3倍到F 点,CB 边延长2倍到E 点,连接DE 、EF 、FD ,得到△DEF 。
已知三角形DEF 的面积为54平方厘米,求△ABC 的面积。
10、下图中的三角形被分成了甲(阴影部分)、乙两部分,AE=1,CE=2,BD=3,CD=1,求两部分的面积之比。
11、如下图,在△ABC 中,BD=DC,AD AA 311=,B A B A 1113
1=,C C C B 111=,111C B A △的面积为1平方厘米,则ABC △的面积为多少平方厘米?
12、如图,AB=6,BC=4,求阴影部分面积。
(单位:厘米)(π取3.14)
13、如图,长方形ABCD 中,AB=12厘米,BC=8厘米,平行四边形BCEF 的一边BF 交CD 于G ,若梯形CEFG 的面积为64平方厘米,求DG 的长。
14、小明家的院内有一间地基是边长600厘米的正方形杂物间。
小明用一条14米的绳子将狗拴在杂物间的一角。
现将狗从A 地出发,将绳子拉紧按顺时针方向跑,可以跑多少米?(π取3)
15、如右图所示,长方形ABCD 中,△ABP 的面积为20平方厘米,△CDQ 的面积为35平方厘米,求阴影四边形的面积。
16、图中是两个正方形,大正方形边长为8,小正方形边长为4,求图中阴影部分面积。
(单位:厘米,π取3.14)
17、在桌面上,有一个半径为1cm的圆盘沿着一个半径为4cm的圆盘外侧滚动(如图),当小圆盘的中心绕大圆盘的中心转动90°后,小圆盘运动过程中扫出的面积是多少?(π取3)
18、如图,两个四分之一圆弧的半径分别是2和4.求两个阴影部分的面积差。
19、用四个边长为10厘米的正方形拼成右图的形状,现有一个半径为2厘米的小圆仅靠此图形内侧滚动一圈后回到出发点,求圆心经过的路线的长度是多少厘米?(π=3.14)
20、三角形ABC中,C角是直角,已知AC=2,CD=2,CB=3,AE=BE,那么三角形AEN(阴影部分)的面积为多少?
21、在下图中,三角形ABC的面积为180平方厘米,BD=DC,AE=3ED,EF=2FB,求三角形AEF的面积。
22、如图,AF=3FB,FD=3EF,直角三角形ABC的面积是48平方厘米。
求平行四边形EBCD和三角形AFD的面积。
23、如图,BD、CF将长方形分成4块,△DEF的面积是4平方厘米,△CED的面积是6平方厘米,求四边形ABEF的面积。
24、如图,是大小两个正方形组成的图形,大正方形边长是8厘米,小正方形边长为6厘米,求阴影部分的面积。
25、求图中阴影部分的面积。
(图中三角形是等腰直角三角形,π=3.14)
26、如图,在梯形ABCD 内有两个三角形的面积分别是10与12,已知梯形的上底AB 的长是下底DC 长的3
2,那么余下的阴影部分的面积是多少?
27、如图,梯形ABCD 的面积为12平方厘米,上、下底之比AD :BC=1:2,DE=3厘米,求AH 的长。
28、图中阴影部分的面积是多少平方厘米?
29、如图,E 、D 分别在AC 、BC 上,且AE :EC=2:3,BD :DC=1:2,AD 与BE 交于点F ,四边形DFEC 的面积等于22平方厘米,求三角形ABC 的面积。
30、如图,Q 、E 、P 、M 分别为直角梯形ABCD 两边AB 、CD 上的点,且DQ 、CP 、ME 彼此平行,已知AD=5、BC=7、AE=5、EB=3,求阴影部分三角形PQM 的面积。
