选修2-1第一章椭圆的定义及方程课时作业
选修2-1 2.2.1椭圆及其标准方程

选修2-1 2.2.1椭圆及其标准方程一、选择题1、设F 1、F 2是椭圆x 216+y 212=1的两个焦点,P 是椭圆上一点,且P 到两个焦点的距离之差为2,则△PF 1F 2是( )A .钝角三角形B .锐角三角形C .斜三角形D .直角三角形2、若椭圆的两焦点为(-2,0),(2,0),且该椭圆过点⎝⎛⎭⎫52,-32,则该椭圆的方程是( ) A .y 28+x 24=1 B .y 210+x 26=1 C .y 24+x 28=1 D .y 26+x 210=13、方程x 2|a|-1+y 2a +3=1表示焦点在x 轴上的椭圆,则实数a 的取值范围是( )A .(-3,-1)B .(-3,-2)C .(1,+∞)D .(-3,1)4、椭圆2x 2+3y 2=1的焦点坐标是( )A .⎝⎛⎭⎫0,±66 B .(0,±1)C .(±1,0)D .⎝⎛⎭⎫±66,05、椭圆x 216+y 27=1的左右焦点为F 1,F 2,一直线过F 1交椭圆于A 、B 两点,则△ABF 2的周长为( ) A .32 B .16 C .8 D .46、设F 1,F 2为定点,|F 1F 2|=6,动点M 满足|MF 1|+|MF 2|=6,则动点M 的轨迹是( )A .椭圆B .直线C .圆D .线段二、填空题7、“神舟六号”载人航天飞船的运行轨道是以地球中心为一个焦点的椭圆,设其近地点距地面n 千米,远地点距地面m 千米,地球半径为R ,那么这个椭圆的焦距为________千米.8、P 是椭圆x 24+y 23=1上的点,F 1和F 2是该椭圆的焦点,则k =|PF 1|·|PF 2|的最大值是______,最小值是______.9、椭圆x 29+y 22=1的焦点为F 1、F 2,点P 在椭圆上.若|PF 1|=4,则|PF 2|=________,∠F 1PF 2的大小为________.三、解答题10、如图△ABC 中底边BC =12,其它两边AB 和AC 上中线的和为30,求此三角形重心G 的轨迹方程,并求顶点A 的轨迹方程.11、已知点A(0,3)和圆O 1:x 2+(y +3)2=16,点M 在圆O 1上运动,点P 在半径O 1M 上,且|PM|=|PA|,求动点P 的轨迹方程.12、根据下列条件,求椭圆的标准方程.(1)两个焦点的坐标分别是(-4,0),(4,0),椭圆上任意一点P 到两焦点的距离之和等于10;(2)两个焦点的坐标分别是(0,-2),(0,2),并且椭圆经过点⎝⎛⎭⎫-32,52.以下是答案 一、选择题1、D [由椭圆的定义,知|PF 1|+|PF 2|=2a =8.由题可得||PF 1|-|PF 2||=2,则|PF 1|=5或3,|PF 2|=3或5. 又|F 1F 2|=2c =4,∴△PF 1F 2为直角三角形.]2、D [椭圆的焦点在x 轴上,排除A 、B ,又过点⎝⎛⎭⎫52,-32验证即可.]3、B [|a |-1>a +3>0.]4、D5、B [由椭圆方程知2a =8,由椭圆的定义知|AF 1|+|AF 2|=2a =8, |BF 1|+|BF 2|=2a =8,所以△ABF 2的周长为16.]6、D [∵|MF 1|+|MF 2|=6=|F 1F 2|,∴动点M 的轨迹是线段.]二、填空题7、m -n解析 设a ,c 分别是椭圆的长半轴长和半焦距,则⎩⎪⎨⎪⎧a +c =m +R a -c =n +R ,则2c =m -n .8、4 3解析 设|PF 1|=x ,则k =x (2a -x ),因a-c≤|PF1|≤a+c,即1≤x≤3.∴k=-x2+2ax=-x2+4x=-(x-2)2+4,∴k max=4,k min=3.9、2120°解析∵|PF1|+|PF2|=2a=6,∴|PF2|=6-|PF1|=2.在△F1PF2中,cos∠F1PF2=|PF1|2+|PF2|2-|F1F2|22|PF1|·|PF2|=16+4-282×4×2=-12,∴∠F1PF2=120°.三、解答题10、解以BC边所在直线为x轴,BC边中点为原点,建立如图所示坐标系,则B(6,0),C(-6,0),CE、BD为AB、AC边上的中线,则|BD|+|CE|=30.由重心性质可知|GB |+|GC |=23(|BD |+|CE |)=20.∵B 、C 是两个定点,G 点到B 、C 距离和等于定值20,且20>12, ∴G 点的轨迹是椭圆,B 、C 是椭圆焦点. ∴2c =|BC |=12,c =6,2a =20,a =10, b 2=a 2-c 2=102-62=64,故G 点的轨迹方程为x 2100+y 264=1,去掉(10,0)、(-10,0)两点.又设G (x ′,y ′),A (x ,y ),则有x ′2100+y ′264=1.由重心坐标公式知⎩⎨⎧x ′=x 3,y ′=y 3.故A 点轨迹方程为(x 3)2100+(y 3)264=1.即x 2900+y2576=1,去掉(-30,0)、(30,0)两点.11、解 ∵|PM |=|P A |,|PM |+|PO 1|=4,∴|PO 1|+|P A |=4,又∵|O 1A |=23<4, ∴点P 的轨迹是以A 、O 1为焦点的椭圆, ∴c =3,a =2,b =1, ∴动点P 的轨迹方程为x 2+y 24=1.12、解 (1)∵椭圆的焦点在x 轴上,∴设椭圆的标准方程为x 2a 2+y 2b 2=1 (a >b >0).∵2a =10,∴a =5,又∵c =4.梦想不会辜负每一个努力的人∴b 2=a 2-c 2=52-42=9.故所求椭圆的标准方程为x 225+y 29=1.(2)∵椭圆的焦点在y 轴上,∴设椭圆的标准方程为y 2a 2+x 2b2=1 (a >b >0).由椭圆的定义知,2a = ⎝⎛⎭⎫-322+⎝⎛⎭⎫52+22+ ⎝⎛⎭⎫-322+⎝⎛⎭⎫52-22=3102+102=210, ∴a =10.又∵c =2,∴b 2=a 2-c 2=10-4=6.故所求椭圆的标准方程为y 210+x 26=1.。
人教版数学高二数学人教A版选修2-1学案第一课时椭圆的简单几何性质
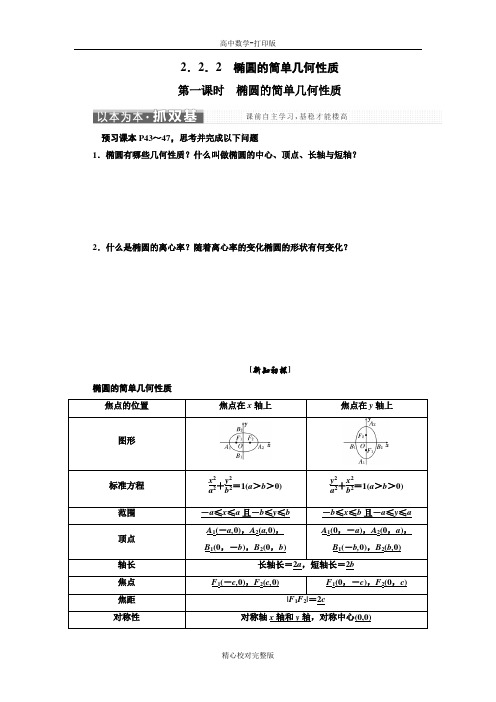
2.2.2椭圆的简单几何性质第一课时椭圆的简单几何性质预习课本P43~47,思考并完成以下问题1.椭圆有哪些几何性质?什么叫做椭圆的中心、顶点、长轴与短轴?2.什么是椭圆的离心率?随着离心率的变化椭圆的形状有何变化?[新知初探]椭圆的简单几何性质焦点的位置焦点在x轴上焦点在y轴上图形标准方程x2a2+y2b2=1(a>b>0)y2a2+x2b2=1(a>b>0) 范围-a≤x≤a且-b≤y≤b -b≤x≤b且-a≤y≤a 顶点A1(-a,0),A2(a,0),B1(0,-b),B2(0,b)A1(0,-a),A2(0,a),B1(-b,0),B2(b,0) 轴长长轴长=2a,短轴长=2b焦点F1(-c,0),F2(c,0)F1(0,-c),F2(0,c) 焦距|F1F2|=2c对称性对称轴x轴和y轴,对称中心(0,0)离心率e =ca(0<e <1) [小试身手]1.判断下列命题是否正确.(正确的打“√”,错误的打“×”) (1)椭圆x 2a 2+y 2b 2=1(a >b >0)的长轴长等于a ( )(2)椭圆上的点到焦点的距离的最小值为a -c ( ) (3)椭圆的离心率e 越小,椭圆越圆( ) 答案:(1)× (2)√ (3)√2.椭圆25x 2+9y 2=225的长轴长、短轴长、离心率依次是( ) A .5,3,45B .10,6,45C .5,3,35D .10,6,35答案:B3.若椭圆x 2a 2+y 2=1的焦点在x 轴上,长轴长是短轴长的两倍,则椭圆的离心率为( )A .32B .12C .22D .52 答案:A4.若焦点在y 轴上的椭圆x 2m +y 22=1的离心率为12,则m 的值为________.答案:32由标准方程研究几何性质[典例] [解] 椭圆方程变形为x 29+y 24=1,∴a =3,b =2,∴c =a 2-b 2=9-4=5.∴椭圆的长轴长和焦距分别为2a =6,2c =25, 焦点坐标为F 1(-5,0),F 2(5,0),顶点坐标为A 1(-3,0),A 2(3,0),B 1(0,-2),B 2(0,2), 离心率e =c a =53.求椭圆的性质时,应把椭圆化为标准方程,注意分清楚焦点的位置,这样便于直观地写出a ,b 的数值,进而求出c ,求出椭圆的长轴和短轴的长、离心率、焦点和顶点的坐标等几何性质.[活学活用]已知椭圆C 1:x 2100+y 264=1,设椭圆C 2与椭圆C 1的长轴长、短轴长分别相等,且椭圆C 2的焦点在y 轴上.(1)求椭圆C 1的长半轴长、短半轴长、焦点坐标及离心率; (2)写出椭圆C 2的方程,并研究其性质.解:(1)由椭圆C 1:x 2100+y 264=1可得其长半轴长为10,短半轴长为8,焦点坐标(6,0),(-6,0),离心率e =35;(2)椭圆C 2:y 2100+x 264=1,性质:①范围:-8≤x ≤8,-10≤y ≤10; ②对称性:关于x 轴、y 轴、原点对称;③顶点:长轴端点(0,10),(0,-10),短轴端点(-8,0),(8,0); ④焦点:(0,6),(0,-6); ⑤离心率:e =35.利用几何性质求标准方程[典例] (1)长轴长是10,离心率是45;(2)在x 轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6. [解] (1)设椭圆的方程为x 2a 2+y 2b 2=1(a >b >0)或y 2a 2+x 2b 2=1(a >b >0). 由已知得2a =10,a =5. 又∵e =c a =45,∴c =4.∴b 2=a 2-c 2=25-16=9.∴椭圆方程为x 225+y 29=1或y 225+x 29=1.(2)依题意可设椭圆方程为x 2a 2+y 2b2=1(a >b >0).如图所示,△A 1FA 2为一等腰直角三角形,OF 为斜边A 1A 2的中线(高),且|OF |=c ,|A 1A 2|=2b ,则c =b =3, a 2=b 2+c 2=18,故所求椭圆的方程为x 218+y 29=1.(1)利用椭圆的几何性质求标准方程通常采用待定系数法.(2)根据已知条件求椭圆的标准方程的思路是“选标准,定参数”,即先明确焦点的位置或分类讨论.一般步骤是:①求出a 2,b 2的值;②确定焦点所在的坐标轴;③写出标准方程.[活学活用]求适合下列条件的椭圆的标准方程. (1)长轴长是短轴长的5倍,且过点A (5,0). (2)离心率e =35,焦距为12.解:(1)若椭圆焦点在x 轴上,设其标准方程为x 2a 2+y 2b 2=1(a >b >0),由题意得⎩⎪⎨⎪⎧ 2a =5×2b ,25a 2+0b 2=1,解得⎩⎪⎨⎪⎧a =5,b =1.故所求椭圆的标准方程为x 225+y 2=1;若焦点在y 轴上,设其标准方程为y 2a 2+x 2b 2=1(a >b >0),由题意,得⎩⎪⎨⎪⎧2a =5×2b ,0a 2+25b 2=1,解得⎩⎪⎨⎪⎧a =25,b =5.故所求椭圆的标准方程为y 2625+x 225=1.综上所述,所求椭圆的标准方程为x 225+y 2=1或y 2625+x 225=1.(2)由e =c a =35,2c =12,得a =10,c =6,则b 2=a 2-c 2=64.当焦点在x 轴上时,所求椭圆的标准方程为x 2100+y 264=1;当焦点在y 轴上时,所求椭圆的标准方程为y 2100+x 264=1.综上所述,所求椭圆的标准方程为 x 2100+y 264=1或y 2100+x 264=1.求椭圆的离心率[典例] 设椭圆C :x a 2+y b 2=1(a >b >0)的左、右焦点分别为F 1,F 2,P 是C 上的点,PF 2⊥F 1F 2,∠PF 1F 2=30°,则C 的离心率为( )A .36B .13C .12D .33[解析] 法一:由题意可设|PF 2|=m ,结合条件可知|PF 1|=2m ,|F 1F 2|=3m ,故离心率e =c a =2c 2a =|F 1F 2||PF 1|+|PF 2|=3m 2m +m =33.法二:由PF 2⊥F 1F 2可知P 点的横坐标为c ,将x =c 代入椭圆方程可解得y =±b 2a ,所以|PF 2|=b 2a .又由∠PF 1F 2=30°可得|F 1F 2|=3|PF 2|,故2c =3·b 2a ,变形可得3(a 2-c 2)=2ac ,等式两边同除以a 2,得3(1-e 2)=2e ,解得e =33或e =-3(舍去). [答案] D[一题多变]1.[变条件]若将本例中“PF 2⊥F 1F 2,∠PF 1F 2=30°”改为“∠PF 2F 1=75°,∠PF 1F 2=45°”,求C 的离心率.解:在△PF 1F 2中,∵∠PF 1F 2=45°,∠PF 2F 1=75°, ∴∠F 1PF 2=60°,设|PF 1|=m ,|PF 2|=n ,|F 1F 2|=2c ,椭圆的长轴长为2a ,则在△PF 1F 2中, 有m sin 75°=n sin 45°=2csin 60°, ∴m +n sin 75°+sin 45°=2csin 60°,∴e =c a =2c 2a =sin 60°sin 75°+sin 45°=6-22. 2.[变条件,变设问]若将本例中“PF 2⊥F 1F 2,∠PF 1F 2=30°”改为“C 上存在点P ,使∠F 1PF 2为钝角”,求C 的离心率的取值范围.解:由题意,知c >b ,∴c 2>b 2. 又b 2=a 2-c 2,∴c 2>a 2-c 2, 即2c 2>a 2. ∴e 2=c 2a 2>12,∴e >22. 故C 的离心率的取值范围为⎝⎛⎭⎫22,1.求椭圆离心率及范围的两种方法(1)直接法:若已知a ,c 可直接利用e =ca 求解.若已知a ,b 或b ,c 可借助于a 2=b 2+c 2求出c 或a ,再代入公式e =ca 求解.(2)方程法:若a ,c 的值不可求,则可根据条件建立a ,b ,c 的关系式,借助于a 2=b 2+c 2,转化为关于a ,c 的齐次方程或不等式,再将方程或不等式两边同除以a 的最高次幂,得到关于e 的方程或不等式,即可求得e 的值或范围.层级一 学业水平达标1.椭圆以两条坐标轴为对称轴,一个顶点是(0,13),另一个顶点是(-10,0),则焦点坐标为( )A .(±13,0)B .(0,±10)C .(0,±13)D .(0,±69)解析:选D 由题意知椭圆焦点在y 轴上,且a =13,b =10,则c =a 2-b 2=69,故焦点坐标为(0,±69).2.若椭圆的两个焦点与短轴的一个端点构成一个正三角形,则该椭圆的离心率为( ) A .12B .32 C .34D .64解析:选A 依题意,△BF 1F 2是正三角形,∵在Rt △OBF 2中,|OF 2|=c ,|BF 2|=a ,∠OF 2B =60°, ∴cos 60°=c a =12,即椭圆的离心率e =12,故选A .3.已知椭圆x 2a 2+y 2b 2=1与椭圆x 225+y 216=1有相同的长轴,椭圆x 2a 2+y 2b 2=1的短轴长与椭圆y 221+x 29=1的短轴长相等,则( ) A .a 2=25,b 2=16 B .a 2=9,b 2=25C .a 2=25,b 2=9或a 2=9,b 2=25D .a 2=25,b 2=9解析:选D 因为椭圆x 225+y 216=1的长轴长为10,焦点在x 轴上,椭圆y 221+x 29=1的短轴长为6,所以a 2=25,b 2=9.4.已知椭圆x 2a 2+y 2b 2=1(a >b >0)的左焦点为F ,右顶点为A ,点B 在椭圆上,且BF ⊥x轴,直线AB 交y 轴于点P .若AP =2PB ,则椭圆的离心率是( )A .32B .22C .13D .12解析:选D ∵AP =2PB ,∴|AP |=2|PB |. 又∵PO ∥BF ,∴|PA ||AB |=|AO ||AF |=23,即a a +c =23,∴e =c a =12.5.椭圆mx 2+ny 2+mn =0(m <n <0)的焦点坐标是( ) A .(0,±m -n ) B .(±m -n ,0) C .(0,±n -m )D .(±n -m ,0)解析:选C 化为标准方程是x 2-n +y 2-m =1,∵m <n <0,∴0<-n <-m .∴焦点在y 轴上,且c =-m -(-n )=n -m . 6.椭圆x 24+y 2m =1的离心率为12,则m =________.解析:当焦点在x 轴上时,4-m 2=12⇒m =3; 当焦点在y 轴上时,m -4m=12⇒m =163. 综上,m =3或m =163. 答案:3或1637.已知椭圆的中心在原点,焦点在x 轴上,离心率为55, 且过P (-5,4),则椭圆的方程为________________.解析:∵e =c a =55,∴c 2a 2=a 2-b 2a 2=15, ∴5a 2-5b 2=a 2即4a 2=5b 2.设椭圆的标准方程为x 2a 2+5y 24a 2=1(a >0),∵椭圆过点P (-5,4),∴25a 2+5×164a 2=1. 解得a 2=45.∴椭圆方程为x 245+y 236=1. 答案:x 245+y 236=18.设F 1,F 2分别为椭圆x 23+y 2=1的左,右焦点,点A ,B 在椭圆上,若1F A =5F B 2,则点A 的坐标是________.解析:设A (m ,n ).由1F A =5F B 2,得B ⎝ ⎛⎭⎪⎫m +625,n 5.又A ,B 均在椭圆上,所以有⎩⎪⎨⎪⎧m 23+n 2=1,⎝ ⎛⎭⎪⎫m +62523+⎝⎛⎭⎫n 52=1,解得⎩⎪⎨⎪⎧ m =0,n =1或⎩⎪⎨⎪⎧m =0,n =-1,所以点A 的坐标为(0,1)或(0,-1). 答案:(0,1)或(0,-1)9.在平面直角坐标系xOy 中,椭圆C 的中心为原点,焦点F 1,F 2在x 轴上,离心率为22,过点F 1的直线l 交椭圆C 于A ,B 两点,且△ABF 2的周长为16,求椭圆C 的标准方程.解:设椭圆C 的标准方程为x 2a 2+y 2b2=1(a >b >0).由e =22知c a =22,故c 2a 2=12,从而a 2-b 2a 2=12,b 2a 2=12.由△ABF 2的周长为|AB |+|BF 2|+|AF 2|=|AF 1|+|AF 2|+|BF 1|+|BF 2|=4a =16,得a =4,∴b 2=8.故椭圆C 的标准方程为x 216+y 28=1.10.椭圆x 2a 2+y 2b 2=1(a >b >0)的右顶点是A (a,0),其上存在一点P ,使∠APO =90°,求椭圆离心率的取值范围.解:设P (x ,y ),由∠APO =90°知,点P 在以OA 为直径的圆上,圆的方程是⎝⎛⎭⎫x -a 22+y 2=⎝⎛⎭⎫a 22.∴y 2=ax -x 2.①又P 点在椭圆上,故x 2a 2+y 2b2=1.②把①代入②化简,得(a 2-b 2)x 2-a 3x +a 2b 2=0,即 (x -a )[(a 2-b 2)x -ab 2]=0,∵x ≠a ,x ≠0, ∴x =ab 2a 2-b 2,又0<x <a ,∴0<ab 2a 2-b 2<a ,即2b 2<a 2. 由b 2=a 2-c 2,得a 2<2c 2,∴e >22. 又∵0<e <1,∴22<e <1. 层级二 应试能力达标1.椭圆x 225+y 29=1与x 29-k +y 225-k =1(0<k <9)的关系为( )A .有相等的长轴长、短轴长B .有相等的焦距C .有相同的焦点D .有相同的顶点 解析:选B c 21=25-9=16,c 22=(25-k )-(9-k )=25-9=16,所以两椭圆有相等的焦距.故选B .2.过椭圆x 24+y 23=1的焦点的最长弦和最短弦的长分别为( )A .8,6B .4,3C .2, 3D .4,2 3解析:选B 过椭圆焦点的最长弦为长轴,其长度为2a =4;最短弦为垂直于长轴的弦,因为c =1,将x =1代入x 24+y 23=1,得124+y 23=1,解得y 2=94,即y =±32,所以最短弦的长为2×32=3.故选B .3.与椭圆9x 2+4y 2=36有相同焦点,且短轴长为2的椭圆的标准方程为( ) A .x 22+y 24=1B .x 2+y 26=1 C .x 26+y 2=1D .x 28+y 25=1解析:选B 椭圆9x 2+4y 2=36可化为x 24+y 29=1,可知焦点在y 轴上,焦点坐标为(0,±5),故可设所求椭圆方程为y 2a 2+x 2b 2=1(a >b >0),则c =5.又2b =2,即b =1,所以a 2=b 2+c 2=6, 则所求椭圆的标准方程为x 2+y 26=1. 4.(全国丙卷)已知O 为坐标原点,F 是椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左焦点,A ,B 分别为C 的左、右顶点.P 为C 上一点,且PF ⊥x 轴.过点A 的直线l 与线段PF 交于点M ,与y 轴交于点E .若直线BM 经过OE 的中点,则C 的离心率为( )A .13B .12C .23D .34解析:选A 如图所示,由题意得A (-a,0),B (a,0),F (-c,0). 设E (0,m ), 由PF ∥OE ,得|MF ||OE |=|AF ||AO |, 则|MF |=m (a -c )a .①又由OE ∥MF ,得12|OE ||MF |=|BO ||BF |,则|MF |=m (a +c )2a.② 由①②得a -c =12(a +c ),即a =3c , ∴e =c a =13.故选A . 5.已知椭圆x 2a 2+y 2b 2=1(a >b >0),A ,B 分别为椭圆的左顶点和上顶点,F 为右焦点,且AB ⊥BF ,则椭圆的离心率为________.解析:在Rt △ABF 中,|AB |=a 2+b 2,|BF |=a ,|AF |=a +c ,由|AB |2+|BF |2=|AF |2,得a 2+b 2+a 2=(a +c )2.将b 2=a 2-c 2代入,得a 2-ac -c 2=0,即e 2+e -1=0,解得e =-1±52. 因为e >0,所以e =5-12. 答案:5-12 6.已知椭圆的长轴长为20,短轴长为16,则椭圆上的点到椭圆中心的距离的取值范围是________.解析:由题意,知a =10,b =8,不妨设椭圆方程为x 2100+y 264=1,其上的点M (x 0,y 0),则|x 0|≤a =10,|y 0|≤b =8,点M 到椭圆中心的距离d =x 20+y 20.因为x 20100+y 2064=1,所以y 20=64⎝⎛⎭⎫1-x 20100=64-1625x 20,则d =x 20+64-1625x 20= 925x 20+64,因为0≤x 20≤100,所以64≤925x 20+64≤100,即8≤d ≤10. 答案:[8,10]7.已知椭圆x 2+(m +3)y 2=m (m >0)的离心率e =32,求实数m 的值及椭圆的长轴长和短轴长,并写出焦点坐标和顶点坐标.解:椭圆方程可化为x 2m +y 2m m +3=1,由m -m m +3=m (m +2)m +3>0,可知m >m m +3,所以a 2=m ,b 2=m m +3,c =a 2-b 2= m (m +2)m +3, 由e =32,得 m +2m +3=32,解得m =1. 于是椭圆的标准方程为x 2+y 214=1, 则a =1,b =12,c =32. 所以椭圆的长轴长为2,短轴长为1;两焦点坐标分别为⎝⎛⎭⎫-32,0,⎝⎛⎭⎫32,0;四个顶点坐标分别为(-1,0),(1,0),⎝⎛⎭⎫0,-12,⎝⎛⎭⎫0,12.8.设F 1,F 2分别是椭圆E :x 2a 2+y 2b2=1(a >b >0) 的左、右焦点,过点 F 1的直线交椭圆 E 于 A ,B 两点,|AF 1|=3|F 1B |.(1)若|AB |=4,△ABF 2 的周长为16,求|AF 2|;(2)若cos ∠AF 2B =35,求椭圆E 的离心率. 解:(1)由|AF 1|=3|F 1B |,|AB |=4,得|AF 1|=3,|F 1B |=1.因为△ABF 2的周长为16,所以由椭圆定义可得4a =16,|AF 1|+|AF 2|=2a =8. 故|AF 2|=8-3=5.(2)设|F 1B |=k ,则k >0且|AF 1|=3k ,|AB |=4k . 由椭圆定义可得,|AF 2|=2a -3k ,|BF 2|=2a -k . 在△ABF 2中,由余弦定理可得,|AB |2=|AF 2|2+|BF 2|2-2|AF 2|·|BF 2|·cos ∠AF 2B ,即(4k )2=(2a -3k )2+(2a -k )2-65(2a -3k )·(2a -k ). 化简可得(a +k )(a -3k )=0,而a +k >0,故a =3k . 于是有|AF 2|=3k =|AF 1|,|BF 2|=5k .因此|BF 2|2=|F 2A |2+|AB |2,可得F 1A ⊥F 2A ,故△AF 1F 2为等腰直角三角形.从而c =22a ,所以椭圆E 的离心率e =c a =22.。
【红对勾】高中数学 2-2-2-2 椭圆几何性质的应用课时作业 新人教A版选修2-1(1)

课时作业12 椭圆几何性质的应用时刻:45分钟 分值:100分一、选择题(每题6分,共36分)1.线段|AB|=4,N 为AB 的中点,动点P 知足条件|PA|+|PB|=6,当P 点在同一平面内运动时,|PN|的最大值M ,最小值m 别离是( )A .M =4,m = 3B .M =3,m =5C .M =5,m = 5D .M =3,m =3解析:由|PA|+|PB|=6>|AB|=4,∴P 的轨迹是以A 、B 为核心,N 为中心的椭圆.那么M =|PN|max =a =3,m =|PN|min =b =a 2-c 2=9-4= 5.答案:B2.已知点(m ,n)在椭圆8x 2+3y 2=24上,那么2m +4的取值范围是( ) A .[4-23,4+23] B .[4-3,4+3]C .[4-22,4+22]D .[4-2,4+2]解析:由8x 2+3y 2=24,得x 23+y 28=1.∴-3≤m≤3.∴4-23≤2m+4≤4+2 3.答案:A3.已知椭圆x 24+y 2=1的核心为F 1、F 2,点M 在该椭圆上,且MF 1→·MF 2→=0,那么点M 到y 轴的距离为( ) A .233 B .263C .33D .3 解析:由题意知,F 1(-3,0),F 2(3,0).设M(x 0,y 0),由MF 1→·MF 2→=0,可得x 0=±263.应选B . 答案:B4.假设AB 为过椭圆x 225+y 216=1中心的线段,F 1为椭圆的核心,那么△F 1AB 面积的最大值为( ) A .6 B .12C .24D .48图1解析:如图1,S△ABF 1=S△AOF 1+S△BOF 1=2S△AOF 1.又∵OF 1=c =3为定值,∴点A 与(0,4)重合时,OF 1边上的高最大,现在S△AOF 1的面积最大为12×4×3=6. ∴S△ABF 1的最大值为12.答案:B5.椭圆x 216+y 24=1上的点到直线x +2y -2=0的最大距离是( )A .3B .11C .2 2D .10图2解析:设与直线x +2y -2=0平行的直线为x +2y +m =0与椭圆联立得,(-2y -m)2+4y 2-16=0,即4y 2+4my +4y 2-16+m 2=0得2y 2+my -4+m 24=0. Δ=m 2-8(m 24-4)=0,即-m 2+32=0,∴m=±4 2.∴两直线间距离最大是当m =42时,d max =|2+42|5=10.答案:D 6.过点M(-2,0)的直线m 与椭圆x 22+y 2=1交于P 1,P 2,线段P 1P 2的中点为P ,设直线m 的斜率为k 1(k 1≠0),直线OP 的斜率为k 2,那么k 1k 2的值为( )A .2B .-2C .12D .-12图3解析:设P 1(x 1,y 1),P 2(x 2,y 2),P(x 0,y 0)则x 212+y 21=1 ① x 222+y 22=1 ② ①-②得x 1+x 2x 1-x 22=-(y 1+y 2)(y 1-y 2)∴y 1-y 2x 1-x 2=-x 1+x 22y 1+y 2=-x 02y 0. ∵k 1=y 1-y 2x 1-x 2,k 2=y 0x 0, ∴k 1=-12k 2.∴k 1·k 2=-12. 答案:D二、填空题(每题8分,共24分)7.过椭圆x 25+y 24=1的右核心作一条斜率为2的直线与椭圆交于A ,B 两点,O 为坐标原点,那么△OAB 的面积为________.解析:由已知可得直线方程为y =2x -2,联立方程得方程组⎩⎪⎨⎪⎧ x 25+y 24=1,y =2x -2,解得A(0,-2),B(53,43). ∴S △AOB =12|OF||y A -y B |=53. 答案:538.假设F 1,F 2是椭圆C :x 28+y 24=1的核心,那么在C 上知足PF 1⊥PF 2的点P 的个数为________. 解析:∵椭圆C :x 28+y 24=1,∴c =2. ∴F 1(-2,0),F 2(2,0),其短轴的端点为B(0,2),A(0,-2),∴∠F 1BF 2=∠F 1AF 2=90°.又短轴端点与F 1,F 2连线所成的角是椭圆上动点P 与F 1,F 2连线所成角中的最大角,∴在C 上知足PF 1⊥PF 2的点有2个.答案:29.假设直线mx +ny =4与圆x 2+y 2=4没有交点,那么过点P(m ,n)的直线与椭圆x 29+y 24=1的交点个数为________.解析:∵直线mx +ny =4与圆x 2+y 2=4没有交点 ∴|-4|m 2+n 2>2∴m 2+n 2<4即点P(m ,n)在以原点为圆心,以2为半径的圆内,故直线mx +ny =4与椭圆x 29+y 24=1也有两个交点. 答案:2三、解答题(共40分)10.(10分)已知椭圆4x 2+y 2=1及直线y =x +m ,(1)当直线和椭圆有公共点,求实数m 的取值范围.(2)求被椭圆截得的最长线段所在的直线方程.解:(1)联立方程组⎩⎪⎨⎪⎧ 4x 2+y 2=1,y =x +m ,消去y ,整理得5x 2+2mx +m 2-1=0(*).假设直线和椭圆有公共点,那么Δ=(2m)2-20(m 2-1)≥0,即m 2≤54,解得-52≤m≤52. (2)设直线y =x +m 与椭圆4x 2+y 2=1交于A(x 1,y 1),B(x 2,y 2)两点,对方程(*),由根与系数的关系,得⎩⎪⎨⎪⎧ x 1+x 2=-2m 5,x 1x 2=m 2-15.|AB|=1+k 2[x 1+x 22-4x 1x 2] =2[-2m 52-4m 2-15]=2510-8m 2. 当m =0时,线段|AB|取最大值2105,现在直线方程为y =x.11.(15分)已知中心在原点的椭圆C 的两个核心和椭圆C 1:4x 2+9y 2=36的两个核心是一个正方形的四个极点,且椭圆C 通过点A(2,-3).(1)求椭圆C 的方程;(2)假设PQ 是椭圆C 的所截线段,O 是坐标原点,OP ⊥OQ 且P 点的坐标为(2,23),求点Q 的坐标. 解:(1)由已知C 1:x 29+y 24=1得核心F 1′(-5,0),F 2′(5,0). 又椭圆C 与C 1的核心F 1,F 2,F 1′,F 2′是一个正方形的四个极点,椭圆的中心在原点, ∴F 1,F 2关于原点对称.∴F 1(0,-5),F 2(0,5).故设C :x 2b 2+y 2a2=1(a>b>0), ∵椭圆C 过点A(2,-3),∴4b 2+9a 2=1且a 2-b 2=5. 解出a 2=15,b 2=10.∴椭圆C 的方程为x 210+y 215=1. (2)设Q(x 0,y 0),那么由OP ⊥OQ 得k OP ·k OQ =232·y 0x 0=-1, 即y 0=-16x 0.又∵x 2010+y 2015=1, 3x 20+2(-16x 0)2=30,∴x 0=±3,点Q 的坐标为(3,-62)或(-3,62). 12.(15分)(2020·北京高考)已知椭圆G :x 24+y 2=1.过点(m,0)作圆x 2+y 2=1的切线l 交椭圆G 于A ,B 两点.(1)求椭圆G 的核心坐标和离心率;(2)将|AB|表示为m 的函数,并求|AB|的最大值.解:(1)由已知得a =2,b =1,因此c =a 2-b 2= 3.因此椭圆G 的核心坐标为(-3,0),(3,0),离心率为e =c a =32. (2)由题意知,|m|≥1.当m =1时,切线l 的方程为x =1,点A ,B 的坐标别离为(1,32),(1,-32). 现在|AB|= 3.当m =-1时,同理可得|AB|=3. 当|m|>1时,设切线l 的方程为y =k(x -m).由⎩⎪⎨⎪⎧ y =k x -m ,x 24+y 2=1,得(1+4k 2)x 2-8k 2mx +4k 2m 2-4=0.设A ,B 两点的坐标别离为(x 1,y 1),(x 2,y 2),那么x 1+x 2=8k 2m 1+4k 2,x 1x 2=4k 2m 2-41+4k 2. 又由l 与圆x 2+y 2=1相切,得|km|k 2+1=1,即m 2k 2=k 2+1. 因此|AB|=x 2-x 12+y 2-y 12 =1+k 2[x 1+x 22-4x 1x 2] =1+k 2[64k 4m 21+4k 22-44k 2m 2-41+4k 2] =43|m|m 2+3. 由于当m =±1时,|AB|=3,因此|AB|=43|m|m 2+3,m∈(-∞,-1]∪[1,+∞). 因为|AB|=43|m|m 2+3=43|m|+3|m|≤2, 且当m =±3时,|AB|=2,因此|AB|的最大值为2.。
人教A版高中数学选修2-1课件【12】椭圆的定义及标准方程的应用
答案:D
3.已知 P 为椭圆 C 上一点,F1,F2 为椭圆的焦点,且|F1F2| =2 3,若|PF1|与|PF2|的等差中项为|F1F2|,则椭圆 C 的标准方程 为( ) x2 y2 A. + =1 12 9 x2 y2 x2 y2 B.12+ 9 =1 或 9 +12=1 x2 y2 C. 9 +12=1 x2 y2 x2 y2 D. + =1 或 + =1 48 45 45 48
解:由已知 a=2,b= 3, 所以 c= a2-b2= 4-3=1,|F1F2|=2c=2. 在△PF1F2 中,由余弦定理,得 |PF2|2=|PF1|2+|F1F2|2-2|PF1||F1F2|cos120° , 即|PF2|2=|PF1|2+4+2|PF1|,① 由椭圆定义,得|PF1|+|PF2|=4, 即|PF2|=4-|PF1|.②
5 答案:4
8.椭圆的两焦点为 F1(-4,0)、F2(4,0),点 P 在椭圆上,若 △PF1F2 的面积最大为 12,则椭圆方程为__________.
解析:如图,当 P 在 y 轴上时△PF1F2 面积最大, 1 ∴2×8b=12,∴b=3, 又∵c=4, ∴a2=b2+c2=25. x2 y2 ∴椭圆的标准方程为25+ 9 =1.
第二章
圆锥曲线与方程
2. 2
椭
圆
课时作业(12)
椭圆的定义及标准方程的应用
①能利用椭圆的定义求轨迹方程; 作业 ②能利用相关点法求与椭圆有关 目标 的轨迹方程;③掌握与焦点有关的 三角形问题的方法技巧. 作业 设计 限时:40 分钟 满分:90 分
一、选择题:每小题 5 分,共 30 分. 1.到两定点 F1(-4,0),F2(4,0)的距离之和为 8 的点的轨迹 是( ) A.椭圆 C.圆 B.线段 D.直线
人教版数学高二选修2-1课后训练 2-2-1 椭圆及其标准方程

04课后课时精练一、选择题1.命题甲:动点P 到两定点A 、B 的距离之和|PA |+|PB |=2a (a >0且a 为常数);命题乙:P 点的轨迹是椭圆,则命题甲是命题乙的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件 解析:∵乙⇒甲且甲D ⇒/乙, ∴甲是乙的必要不充分条件. 答案:B2.已知△ABC 的顶点B 、C 在椭圆x 23+y 2=1上,顶点A 是椭圆的一个焦点,且椭圆的另一个焦点F 在BC 上,则△ABC 的周长是( )A. 23B. 6C. 4 3D. 12解析:可知a =3,由椭圆的定义得|BF |+|BA |=|CF |+|CA |=2a =23,∴(|BF |+|CF |)+|BA |+|CA |=|BA |+|CA |+|BC |=43,即△ABC 的周长为43,故选C.答案:C3. 焦点在坐标轴上,且a 2=13,c 2=12的椭圆的标准方程为( )A. x 213+y 212=1B. x 213+y 225=1或x 225+y 213=1 C. x 213+y 2=1D. x 213+y 2=1或x 2+y213=1解析:显然,此题中并没有讲明椭圆的焦点在哪个轴上,题中也没有条件能够得出相应的信息,所以本题中的标准方程应有两种情况,所以排除A 和C ,又由于a 2=13,c 2=12,∴b 2=1.答案:D4.点A (a,1)在椭圆x 24+y 22=1的内部,则a 的取值范围是( ) A .-2<a < 2 B .a <-2或a > 2 C .-2<a <2D .-1<a <1解析:由已知可得a 24+12<1,∴a 2<2,即-2<a < 2. 答案:A5.设F 1、F 2是椭圆x 216+y 212=1的两个焦点,P 是椭圆上一点,且P 到F 1、F 2的距离之差为2,则△PF 1F 2是( )A .钝角三角形B .锐角三角形C .斜三角形D .直角三角形解析:由椭圆的定义,知|PF 1|+|PF 2|=2a =8. 由题可得|PF 1|-|PF 2|=2,则|PF 1|=5,|PF 2|=3.又|F 1F 2|=2c =4, ∴△PF 1F 2为直角三角形. 答案:D6.若方程x 2+ky 2=2表示焦点在y 轴上的椭圆,那么实数k 的取值范围是( )A .(0,+∞)B .(0,2)C .(1,+∞)D .(0,1)解析:将方程x 2+ky 2=2变形为x 22+y 22k=1.∵焦点在y 轴上,∴2k >2且k >0,∴0<k <1.答案:D 二、填空题7.椭圆x 212+y 23=1的两个焦点为F 1、F 2,点P 在椭圆上.如果线段PF 1的中点在y 轴上,那么|PF 1|是|PF 2|的________倍.解析:由已知椭圆的方程得a =23,b =3,c =3,F 1(-3,0),F 2(3,0).由于焦点F 1和F 2关于y 轴对称, ∴PF 2必垂直于x 轴.∴P (3,32)或P (3,-32),|PF 2|=32, |PF 1|=2a -|PF 2|=732. ∴|PF 1|=7|PF 2|.答案:78.已知F 1、F 2为椭圆x 225+y 29=1的两个焦点,过F 1的直线交椭圆于A 、B 两点.若|F 2A |+|F 2B |=12,则|AB |=________.解析:|AB |=|F 1A |+|F 1B |=(2a -|F 2A |)+(2a -|F 2B |)=4a -(|F 2A |+|F 2B |)=20-12=8.答案:89.M 是椭圆x 29+y 24=1上的任意一点,F 1、F 2是椭圆的左、右焦点,则|MF 1|·|MF 2|的最大值是________.解析:|MF 1|+|MF 2|=2a .|MF 1|·|MF 2|≤(|MF 1|+|MF 2|2)2=a 2=9. 答案:9 三、解答题10.已知圆A :x 2+(y +6)2=400,圆A 内一定点B (0,6),圆C 过B 点且与圆A 内切,求圆心C 的轨迹方程.解:设动圆C 的半径为r ,则|CB |=r . ∵圆C 与圆A 内切,∴|CA |=20-r . ∴|CA |+|CB |=20.又|AB |=12,∴|CA |+|CB |=20>|AB |.∴点C 的轨迹是以A 、B 两点为焦点的椭圆. ∵2a =20,2c =12,∴a =10,c =6,b 2=64. 又∵A 、B 在y 轴上,∴C 点的轨迹方程为y 2100+x 264=1. 11.求适合下列条件的椭圆的方程. (1)焦点在x 轴上,且经过点(2,0)和点(0,1);(2)焦点在y 轴上,与y 轴的一个交点为P (0,-10),P 到它较近的一个焦点的距离等于2.解:(1)因为椭圆的焦点在x 轴上,所以可设它的标准方程为x 2a 2+y 2b 2=1(a >b >0). ∵椭圆经过点(2,0)和(0,1)∴⎩⎪⎨⎪⎧22a 2+0b 2=1,0a 2+1b 2=1,∴⎩⎨⎧a 2=4,b 2=1,故所求椭圆的标准方程为x 24+y 2=1.(2)∵椭圆的焦点在y 轴上,所以可设它的标准方程为y 2a 2+x 2b 2=1(a >b >0).∵P (0,-10)在椭圆上,∴a =10.又∵P 到它较近的一个焦点的距离等于2, ∴-c -(-10)=2,故c =8,∴b 2=a 2-c 2=36,∴所求椭圆的标准方程是y 2100+x 236=1.12. 设F 1,F 2分别为椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点. (1)若椭圆C 上的点A (1,32)到F 1,F 2两点的距离之和等于4,写出椭圆C 的方程和焦点坐标;(2)设点K 是(1)中所得椭圆上的动点,求线段F 1K 的中点的轨迹方程.解:(1)椭圆C 的焦点在x 轴上,由椭圆上的点A 到F 1,F 2两点的距离之和是4,得2a =4,即a =2.又点A (1,32)在椭圆上,因此122+(32)2b 2=1,得b 2=3,则c 2=a 2-b 2=1.所以椭圆C 的方程为x 24+y 23=1,焦点为F 1(-1,0),F 2(1,0).(2)设椭圆C 上的动点K (x 1,y 1),线段F 1K 的中点Q (x ,y ),则x =-1+x 12,y =y 12,即x 1=2x +1,y 1=2y .因为点K (x 1,y 1)在椭圆x 24+y 23=1上,所以(2x +1)24+(2y )23=1,即(x +12)2+4y 23=1,此即为所求的轨迹方程.。
2.2.1椭圆及其标准方程-数学选修2-1

由椭圆的定义知
5 3 2 5 3 2 2 2 2a ( 2) ( ) ( 2) ( ) 2 10 2 2 2 2
所以
a 10.
例 题 演 练
又因为 c 2,所以
b a c 10 4 6.
2 2 2
因此, 所求椭圆的标准方程为
x y 1 . 10 6
2
y
b
观察左图, 和同桌讨论你们能从中找 出表示c 、 a 的线段吗?
a c
o
x
a2-c2 有什么几何意义?
令 | OP | a c b
2 2
则方程可化为
x y 2 1 a b 0 2 a b
2
2
思考:当焦点在y轴上时,椭圆方程是什么?
x2 y 2 1.我们把形如 2 + 2 = 1(a > b > 0)叫做椭圆的标准方程 a b
结论:若常数大于|F1F2|,则点M的轨迹是( 椭圆
)
若常数等于|F1F2|,则点M的轨迹是( 线段F1F2) 若常数小于|F1F2|,则点M的轨迹( 不存在 )
椭圆的方程的推导
独立思考轨迹方程的一般步骤,并按其方法及提示独立 逐步求椭圆的一般方程。 y 以经过椭圆焦点 F1,F2 的直 建 线为 x 轴,线段F1F2的中垂线为y 轴,建立直角坐标系xoy。
y
数 学 归 纳
它表示焦点在x轴上的椭圆
o
x
y2 x2 2.也把形如 2 + 2 = 1(a > b > 0)叫做椭圆的标准方程 a b
y
F2 M
它表示焦点在y轴上的椭圆
o
F1
x
椭圆的标准方程有哪些特征呢?
20212022高中数学人教版选修21作业221椭圆及其标准方程系列一.docx
2. 2. 1椭圆及其标准方程基础巩固—、选择题1-椭圆2^ + 3/=12的两焦点之间的距离是( )A.2拆B. y[\0C. «D. 2^2[答案]D[详细分析]椭圆方程2^ + 3/=12可化为:f+ f =1,a2 = 6,胪=4, <? = 6-4 = 2, :.2c = 2\fi.2.(2015-广东文)已知椭圆§ + 4=l(m>0)的左焦点为丹(-4,0),则〃7 =()A. 2B. 3C. 4D. 9[答案】B[详细分析]..•椭圆|| + 5=1(^>0)的左焦点为乩(-4,。
),:.c = 4 = yl25-m2, :.m2 =9,m = 3,选B .3.(2015•海南中学期中考试)已知Fi,形是椭圆+ f =1的两个焦点,过点儿的直线交椭圆于点A, B,若|AB| = 5,则|时i| + |BFi| = ()A. 11B. 10C. 9D. 16[答案〕A[详细分析]由方程知«2=16,...2a = 8,由椭圆定义知,|*肝|奶| = 8, \BF!\ + \BF2\ =8, .\|AFi| + |AF2| + |BFi| + \BF2\ = |AFi| + |BFi| + \AB\ = 16,.•.|AFi| + |BFi|=ll,故选A.4.设定点Fi(0, - 3), F2(0,3),动点F满足条件|职| + |华| =。
+戋?>0),则点F的轨迹是()A.椭圆B.线段C.不存在D.椭圆或线段[答案]D9[详细分析]I« + ->6, AlPFil + \PF2\>6 =|F I F2|,.••选D.5.设P是椭圆法+书=1上一点,P到两焦点F5 的距离之差为2,则△尸皿是( )A.锐角三角形B.直角三角形C.钝角三角形D.等腰直角三角形[答案]B[详细分析]由椭圆定义,知|PF I|+|PF2|=2“=8.又|PF I|-|PF2|=2,...|PF I|=5,\PF2\ = 3.又|HF2| = 2c = 2 寸16 - 12 = 4,△PF1F2为直角三角形.6.已知椭圆的两个焦点分别是Fi、F2, P是椭圆上的一个动点,如果延长FiP到Q, 使得\PQ\ = \PF2\,那么动点。
课时作业10:2.1.1 椭圆及其标准方程(一)
§2.1椭圆2.1.1椭圆及其标准方程(一)一、选择题1.设椭圆x2m2+y2m2-1=1(m>1)上一点P到其左、右焦点的距离分别为3和1,则m等于()A.6 B.3 C.2 D.4考点椭圆的标准方程题点给条件确定椭圆方程中的参数(或其范围) 答案 C解析∵m2>m2-1,∴椭圆焦点在x轴上,∴a=m,则2m=3+1=4,∴m=2.2.设P是椭圆x216+y212=1上一点,P到两焦点F1,F2的距离之差为2,则△PF1F2是()A.锐角三角形B.直角三角形C.钝角三角形D.等腰直角三角形考点椭圆的定义题点焦点三角形中的问题答案 B解析由椭圆定义知|PF1|+|PF2|=2a=8,不妨设|PF1|>|PF2|,∵|PF1|-|PF2|=2,∴|PF1|=5,|PF2|=3,又∵|F 1F 2|=2c =4,∴△PF 1F 2为直角三角形.3.已知椭圆5x 2+ky 2=5的一个焦点坐标是(0,2),那么k 的值为( )A .1B .-1 C. 5 D .- 5 考点 椭圆的标准方程 题点 给条件确定椭圆方程中的参数(或其范围) 答案 A 解析 原方程可化简为x 2+y 25k =1, 由c 2=5k-1=4,得k =1. 4.椭圆x 225+y 29=1上的一点M 到左焦点F 1的距离为2,N 是MF 1的中点,则|ON |等于( ) A .2B .8C .4D.32考点 椭圆的定义题点 椭圆定义的应用答案 C解析 如图,F 2为椭圆右焦点,连接MF 2,则ON 是△F 1MF 2的中位线,∴|ON |=12|MF 2|,又|MF 1|=2,|MF 1|+|MF 2|=2a =10,∴|MF 2|=8, ∴|ON |=4.5.已知P 为椭圆C 上一点,F 1,F 2为椭圆的焦点,且|F 1F 2|=23,若|PF 1|与|PF 2|的等差中项为|F 1F 2|,则椭圆C 的标准方程为( )A.x 212+y 29=1 B.x 212+y 29=1或x 29+y 212=1 C.x 29+y 212=1 D.x 248+y 245=1或x 245+y 248=1 考点 椭圆标准方程的求法题点 定义法求椭圆的标准方程答案 B解析 由已知2c =|F 1F 2|=23,所以c = 3.因为2a =|PF 1|+|PF 2|=2|F 1F 2|=43,所以a =23,所以b 2=a 2-c 2=9.故椭圆C 的标准方程是x 212+y 29=1或x 29+y 212=1. 6.曲线x 225+y 29=1与x 29-k +y 225-k=1(0<k <9)的关系是( ) A .有相等的焦距,相同的焦点B .有相等的焦距,不同的焦点C .有不等的焦距,不同的焦点D .以上都不对考点 椭圆的标准方程题点 由椭圆的标准方程求焦点、焦距答案 B解析 曲线x 225+y 29=1焦点在x 轴上.对于曲线x 29-k +y 225-k =1,∵0<k <9,∴25-k >9-k >0,∴焦点在y 轴上,故两者的焦点不同.∵25-9=(25-k )-(9-k )=16=c 2,∴2c =8,故两者焦距相等.故选B.7.方程x 24+m +y 22-m =1表示椭圆的必要不充分条件是() A .m ∈(-1,2)B .m ∈(-4,2)C .m ∈(-4,-1)∪(-1,2)D .m ∈(-1,+∞)考点 椭圆的标准方程题点 给条件确定椭圆方程中的参数(或其范围)答案 B解析 方程x 24+m +y 22-m =1表示椭圆的充要条件是⎩⎪⎨⎪⎧ 4+m >0,2-m >0,4+m ≠2-m ,即m ∈(-4,-1)∪(-1,2).由题意可得,所求m 的取值范围包含集合(-4,-1)∪(-1,2).观察选项,故选B.8.已知椭圆x 24+y 2=1的焦点为F 1,F 2,点M 在该椭圆上,且MF 1→·MF 2→=0,则点M 到x 轴的距离为( ) A.233B.263C.33D. 3考点 椭圆的定义题点 焦点三角形中的问题答案 C解析 ∵MF 1→·MF 2→=0,∴MF 1→⊥MF 2→,由|MF 1|+|MF 2|=4,①又|MF 1|2+|MF 2|2=(23)2=12,②由①与②可得,|MF 1|·|MF 2|=2,设M 到x 轴的距离为h ,则|MF 1|·|MF 2|=|F 1F 2|·h ,h =223=33. 9.已知椭圆x 2100+y 264=1的左焦点为F ,一动直线与椭圆交于M ,N 两点,则△FMN 的周长的最大值为( )A .16B .20C .32D .40考点 椭圆的定义题点 焦点三角形中的问题答案 D解析 设右焦点为A ,一动直线与椭圆交于M ,N 两点,则△FMN 的周长l =|MN |+|MF |+|NF |=|MN |+2a -|MA |+2a -|NA |=4a +(|MN |-|MA |-|NA |),由于|MA |+|NA |≥|MN |,所以当M ,A ,N 三点共线时,△FMN 的周长取得最大值4a =40.二、填空题10.椭圆x 2m +y 24=1的焦距是2,则m 的值是________. 考点 椭圆的标准方程题点 给条件确定椭圆方程中的参数(或其范围)答案 3或5解析 当椭圆的焦点在x 轴上时,a 2=m ,b 2=4,c 2=m -4,又2c =2,∴c =1.∴m -4=1,m =5.当椭圆的焦点在y 轴上时,a 2=4,b 2=m ,∴c 2=4-m =1,∴m =3,∴m =3或5.11.已知椭圆C 经过点A (2,3),且点F (2,0)为其右焦点,则椭圆C 的标准方程为________. 考点 椭圆标准方程的求法题点 待定系数法求椭圆的标准方程答案 x 216+y 212=1 解析 方法一 依题意,可设椭圆C 的方程为x 2a 2+y 2b 2=1(a >b >0),且可知左焦点为F ′(-2,0). 从而有⎩⎪⎨⎪⎧ c =2,2a =|AF |+|AF ′|=3+5=8, 解得⎩⎪⎨⎪⎧c =2,a =4. 又a 2=b 2+c 2,所以b 2=12,故椭圆C 的标准方程为x 216+y 212=1. 方法二 依题意,可设椭圆C 的方程为x 2a 2+y 2b 2=1(a >b >0), 则⎩⎪⎨⎪⎧4a 2+9b 2=1,a 2-b 2=4,解得b 2=12或b 2=-3(舍去),从而a 2=16.所以椭圆C 的标准方程为x 216+y 212=1. 12.已知F 1,F 2是椭圆C :x 2a 2+y 2b 2=1(a >b >0)的两个焦点,P 为椭圆C 上一点,且PF 1→⊥PF 2→.若△PF 1F 2的面积为9,则b =________.考点 椭圆的定义题点 焦点三角形中的问题答案 3解析 由椭圆定义,得|PF 1|+|PF 2|=2a ,∴|PF 1|2+|PF 2|2+2|PF 1|·|PF 2|=4a 2.又∵PF 1→⊥PF 2→,∴|PF 1|2+|PF 2|2=|F 1F 2|2=(2c )2=4c 2,即4c 2+2|PF 1|·|PF 2|=4a 2,∴|PF 1|·|PF 2|=2b 2,∴12PF F S =12·|PF 1|·|PF 2|=12×2b 2=b 2=9, 又∵b >0,∴b =3.三、解答题13.求过点(0,4)且与椭圆9x 2+4y 2=36有相同焦点的椭圆的方程.考点 椭圆标准方程的求法题点 待定系数法求椭圆的标准方程解 由9x 2+4y 2=36,得x 24+y 29=1, 则c =9-4=5,焦点在y 轴上,设所求椭圆方程为y 2a 2+x 2b 2=1, 则a =4,∴b 2=a 2-c 2=11,∴所求椭圆方程为x 211+y 216=1. 四、探究与拓展14.已知点P 在椭圆上,且P 到椭圆的两个焦点的距离分别为5,3.过P 且与椭圆的长轴垂直的直线恰好经过椭圆的一个焦点,求椭圆的标准方程.考点 椭圆标准方程的求法题点 待定系数法求椭圆的标准方程解 方法一 设所求的椭圆方程为x 2a 2+y 2b 2=1(a >b >0)或y 2a 2+x 2b 2=1(a >b >0), 由已知条件得⎩⎪⎨⎪⎧ 2a =5+3,(2c )2=52-32, 解得⎩⎪⎨⎪⎧a =4,c =2,所以b 2=a 2-c 2=12. 于是所求椭圆的标准方程为x 216+y 212=1或y 216+x 212=1. 方法二 设所求的椭圆方程为x 2a 2+y 2b 2=1(a >b >0)或y 2a 2+x 2b 2=1(a >b >0),两个焦点分别为F 1,F 2. 由题意知2a =|PF 1|+|PF 2|=3+5=8,所以a =4.在方程x 2a 2+y 2b 2=1中,令x =±c ,得|y |=b 2a; 在方程y 2a 2+x 2b 2=1中,令y =±c ,得|x |=b 2a. 依题意有b 2a=3,得b 2=12. 于是所求椭圆的标准方程为x 216+y 212=1或y 216+x 212=1.15.已知椭圆y 2a 2+x 2b2=1(a >b >0)的焦点分别为F 1(0,-1),F 2(0,1),且3a 2=4b 2. (1)求椭圆的方程;(2)设点P 在这个椭圆上,且|PF 1|-|PF 2|=1,求∠F 1PF 2的余弦值. 考点 椭圆的定义题点 焦点三角形中的问题解 (1)由题意得椭圆焦点在y 轴上,且c =1. 又∵3a 2=4b 2,∴a 2-b 2=14a 2=c 2=1, ∴a 2=4,b 2=3,∴椭圆的标准方程为y 24+x 23=1. (2)如图所示,|PF 1|-|PF 2|=1.又由椭圆定义知,|PF 1|+|PF 2|=4,∴|PF 1|=52,|PF 2|=32,|F 1F 2|=2, ∴cos ∠F 1PF 2=⎝⎛⎭⎫522+⎝⎛⎭⎫322-222×52×32=35.。
高中数学选修2-1课时作业7:2.2.2 椭圆的简单几何性质(一)
2.2.2 椭圆的简单几何性质(一)1.椭圆x 2m +y 24=1的焦距是2,则m 的值为( ) A .5 B .8C .5或3 D .8或5[解析] 当焦点在x 轴上时,m =4+1=5;当焦点在y 轴上时,4=m +1,∴m =3,综上知,m =5或3.[答案] C2.椭圆x 225+y 29=1与x 29-k +y 225-k=1(0<k <9)的关系为( ) A .有相等的长轴B .有相等的短轴C .有相同的焦点D .有相等的焦距[解析] 当0<k <9时,(25-k )-(9-k )=25-9=16=c 2,∴c =4,而焦点一个在x 轴上,一个在y 轴上,∴两椭圆的焦点不同,因此,有相同的焦距,故选D.[答案] D3.已知椭圆的长轴长是短轴长的2倍,则椭圆的离心率等于( )A.13B.33C.12D.32[解析] 依题意2a =4b ,即a =2b ,又a 2=b 2+c 2,∴a 2=14a 2+c 2,即34a 2=c 2,∴c 2a 2=34, ∴e =c a =32. [答案] D4.若椭圆x 216+y 2m =1的离心率为13,则m 的值为( ) A.1289B.1289或18C .18 D.1283或6 [解析] 当焦点在x轴上时,a 2=16,b 2=m ,∴c 2=a 2-b 2=16-m ,∴e 2=c 2a 2=16-m 16=⎝⎛⎭⎫132,∴m =1289,当焦点在y 轴上时,同理可求得m =18.综上知m 的值为1289或18. [答案] B5.直线y =x +1被椭圆x 2+2y 2=4所截得的弦的中点坐标是________.[解析] 把y =x +1代入x 2+2y 2=4得,x 2+2(x 2+2x +1)=4,即3x 2+4x -2=0.设直线与椭圆的两个交点为A (x 1,y 1),B (x 2,y 2),则x 1+x 2=-43,y 1+y 2=(x 1+x 2)+2=-43+2=23. ∴x 1+x 22=-23,y 1+y 22=13.因此得弦AB 中点的坐标为⎝⎛⎭⎫-23,13.[答案] (-23,13) 6.人造地球卫星的运行轨道是以地心为一个焦点的椭圆,设地球半径为R ,卫星近地点、远地点离地面的距离分别为r 1、r 2,则卫星远行轨道的离心率是__________.[解析] 由题意得⎩⎪⎨⎪⎧a +c =r 2+R ,a -c =r 1+R ,∴2a =2R +r 1+r 2,2c =r 2-r 1.∴e =c a =r 2-r 12R +r 1+r 2. [答案] r 2-r 12R +r 1+r 27.在平面直角坐标系xOy 中,设椭圆x 2a 2+y 2b 2=1(a >b >0)的焦距为2c .以点O 为圆心,a 为半径作圆M ,若过点P (a 2c,0)所作圆M 的两条切线互相垂直.则该椭圆的离心率为________.[解析] 如图,切线P A ,PB 互相垂直,又半径OA 垂直于P A ,所以△OAP 为等腰直角三角形.∴a 2c =2a ∴e =c a =22. [答案]228.椭圆y 2a 2+x 2b 2=1(a >b >0)的两焦点为F 1(0,-c ),F 2(0,c )(c >0),离心率e =32,焦点到椭圆上点的最短距离为2-3,求椭圆的方程.解 ∵椭圆的长轴的一个端点到焦点的距离最短,∴a -c =2- 3.又e =c a =32, ∴a =2,c = 3.∴b 2=1.∴椭圆的方程为y 24+x 2=1. 9.设集合A ={(x ,y )|x 24+y 216=1},B ={(x ,y )|y =3x },则A ∩B 的子集的个数是( ) A .4 B .3C .2 D .1[解析] 画出示意图知,两曲线有两个交点,∴A ∩B 含有2个元素,子集有4个.[答案] A10.若一个椭圆的长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是( ) A.45B.35C.25D.15[解析] 依题意得2b =a +c ,又b 2=a 2-c 2,∴4(a 2-c 2)=(a +c )2.∴5c 2+2ac -3a 2=0.∴5e 2+2e -3=0.解得e =35,或e =-1(舍去). [答案] B11.直线l 过点M (1,1),与椭圆x 24+y 23=1相交于A ,B 两点,若AB 的中点为M ,求直线l 的方程.解 设A (x 1,y 1),B (x 2,y 2),则x 214+y 213=1,① x 224+y 223=1,② ①-②得x 1-x 2x 1+x 24+y 1-y 2y 1+y 23=0,∴y 1-y 2x 1-x 2=-34·x 1+x 2y 1+y 2. 又M (1,1)为AB 的中点,∴x 1+x 2=2,y 1+y 2=2.∴直线l 的斜率为-34. ∴直线l 的方程为y -1=-34(x -1),即3x +4y -7=0. 12.椭圆过点(3,0)点,离心率e =63,求椭圆的标准方程. 解 当椭圆焦点在x 轴上时,则a =3,c a =63,∴c = 6.∴b 2=a 2-c 2=3. 故椭圆的方程为x 29+y 23=1. 当椭圆的焦点在y 轴上时,则b =3,又c a =63,∴a 2-b 2a =63,∴a 2=27, 故椭圆的方程为x 29+y 227=1.∴所求椭圆的方程为x 29+y 23=1或x 29+y 227=1.。
高中数学2.2.1椭圆及其标准方程课时作业含解析人教A版选修2_1.doc
第二章 2.2 2.2.1请同学们认真完成练案[11]A 级 基础巩固一、选择题1.设F 1、F 2为定点,|F 1F 2|=6,动点M 满足|MF 1|+|MF 2|=6,则动点M 的轨迹是( D ) A .椭圆 B .直线 C .圆D .线段[解析] ∵|MF 1|+|MF 2|=6,|F 1F 2|=6, ∴|MF 1|+|MF 2|=|F 1F 2|, ∴点M 的轨迹是线段F 1F 2.2.过点(-3,2)且与x 29+y 24=1有相同焦点的椭圆的方程是( A )A .x 215+y 210=1B .x 2225+y 2100=1C .x 210+y 215=1D .x 2100+y 2225=1[解析] 将点(-3,2)代入验证,只有A 的方程满足,故选A .3.中心在原点,焦点在坐标轴上,且过两点(4,0)、(0,2)的椭圆方程为( D ) A .x 24+y 22=1B .y 24+x 22=1C .y 216+x 24=1D .x 216+y 24=1[解析] 解法一:验证排除:将点(4,0)代入验证可排除A 、B 、C ,故选D . 解法二:设椭圆方程为mx 2+ny 2=1(m >0,n >0),∴⎩⎪⎨⎪⎧16m =14n =1,∴⎩⎨⎧m =116n =14,故选D .4.已知椭圆x 225+y 29=1上的点M 到该椭圆一个焦点F 的距离为2,N 是MF 的中点,O为坐标原点,那么线段ON 的长是( B )A .2B .4C .8D .32[解析] 设椭圆左焦点F ,右焦点F 1,∵2a =10,|MF |=2,∴|MF 1|=8,∵N 为MF 中点,O 为FF 1中点,∴|ON |=12|MF 1|=4.5.(2019-2020学年房山区期末检测)“方程mx 2+ny 2=1表示焦点在y 轴上的椭圆”的充要条件是( A )A .m >n >0B .n >m >0C .mn >0D .mn <0[解析] 若方程表示椭圆,则m ,n ≠0,则方程等价为x 21m +y 21n =1,若方程表示焦点在y 轴上椭圆,则等价为1n >1m>0,解得:m >n >0,故选A .6.(2019-2020学年湖南省长沙市湖南师大附中高二期中)设F 1,F 2为椭圆C :x 236+y 220=1的两个焦点,M 为C 上一点且在第一象限,若△MF 1F 2为等腰三角形,则△MF 1F 2的面积为( D )A .53B .103C .215D . 415[解析] 设M (m ,n ),m ,n >0,则m ∈(0,6),n ∈(0,25), 椭圆C :x 236+y 220=1的a =6,b =25,c =4.设F 1,F 2分别为椭圆C 的左右焦点,由于M 为C 上一点且在第一象限,可得|MF 1|>|MF 2|,|F 1F 2|=2c =8, 因为|MF 1|+|MF 2|=2a =12,所以|MF 1|>6,|MF 2|<6, △MF 1F 2为等腰三角形,只能|MF 2|=2c =8,则|MF 2|=4, 由勾股定理得|MF 2|2=(4-m )2+n 2=16, 又m 236+n 220=1,联立并消去n 得 m 2-18m +45=0,且m ∈(0,6),解得m =3,则n =15. 则△MF 1F 2的面积为12×8×15=415.故选D .二、填空题7.已知椭圆中心在坐标原点,焦点在x 轴上,椭圆与x 轴的一个交点到两焦点的距离分别为3和1,则椭圆的标准方程为__x 24+y 23=1__.[解析] 由题意可得⎩⎪⎨⎪⎧ a +c =3a -c =1,∴⎩⎪⎨⎪⎧a =2c =1.故b 2=a 2-c 2=3,所以椭圆方程为x 24+y 23=1. 8.(福州市2019-2020学年高二期末)若以椭圆上一点和椭圆的两个焦点为顶点的三角形面积的最大值为1,则该椭圆长轴长的最小值为[解析] 由题意可知,因为椭圆上一点和两个焦点为顶点的三角形的最大面积为1,即可知bc =1,因为a 2=b 2+c 2=b 2+1b2≥2,所以a ≥2,故长轴长的最小值为22,答案为2 2.三、解答题9.求满足下列条件的椭圆的标准方程: (1)焦点在y 轴上,焦距是4,且经过点M (3,2);(2)a :c =13:5,且椭圆上一点到两焦点的距离的和为26.[解析] (1)由焦距是4可得c =2,且焦点坐标为(0,-2),(0,2).由椭圆的定义知,2a =32+(2+2)2+32+(2-2)2=8,所以a =4,所以b 2=a 2-c 2=16-4=12. 又焦点在y 轴上,所以椭圆的标准方程为y 216+x 212=1.(2)由题意知,2a =26,即a =13,又a c =135,所以c =5,所以b 2=a 2-c 2=132-52=144, 因为焦点所在的坐标轴不确定,所以椭圆的标准方程为x 2169+y 2144=1或y 2169+x 2144=1.10.已知点A (-12,0),B 是圆F :(x -12) 2+y 2=4(F 为圆心)上一动点,线段AB 的垂直平分线交BF 于P ,求动点P 的轨迹方程.[解析] 如图所示,由题意知,|P A |=|PB |,|PF |+|BP |=2, ∴|P A |+|PF |=2,且|P A |+|PF |>|AF |, ∴动点P 的轨迹是以A 、F 为焦点的椭圆, ∴a =1,c =12,b 2=34.∴动点P 的轨迹方程为x 2+y 234=1,即x 2+43y 2=1. B 级 素养提升一、选择题1.已知椭圆x 225+y 29=1,F 1、F 2分别在其左、右焦点,椭圆上一点M 到F 1的距离是2,N是MF 1的中点,则|ON |的长为( D )A .1B .2C .3D .4[解析] 由椭圆定义得|MF 2|+|MF 1|=2a =10, 因为|MF 1|=2,所以|MF 2|=8. 因为N 是MF 1的中点,所以|ON |=|MF 2|2=4.故选D . 2.若△ABC 的两个焦点坐标为A (-4,0)、B (4,0),△ABC 的周长为18,则顶点C 的轨迹方程为( D )A .x 225+y 29=1B .y 225+x 29=1(y ≠0)C .x 216+y 29=1(y ≠0)D .x 225+y 29=1(y ≠0)[解析] ∵|AB |=8,△ABC 的周长为18,∴|AC |+|BC |=10>|AB |,故点C 轨迹为椭圆且两焦点为A 、B ,又因为C 点的纵坐标不能为零,所以选D .3.(多选题)若方程x 2a 2+y 2a +6=1表示焦点在x 轴上的椭圆,则实数a 的取值范围可以是( AD )A .a >3B .a <-2C .-2<a <3D .-6<a <-2[解析] 由题意得a 2>a +6>0, 解得a >3或-6<a <-2,故选AD .4.(多选题)直线2x +by +3=0过椭圆10x 2+y 2=10的一个焦点,则b 的值可以为( AB ) A .-1 B .1 C .-12D .12[解析] 椭圆方程化为标准形式为x 2+y 210=1,∴焦点坐标为(0,±3),当直线过焦点(0,3)时,b =-1;当直线过焦点(0,-3)时,b =1.故选AB .二、填空题5.下列命题是真命题的是__③__.①已知定点F 1(-1,0),F 2(1,0),则满足|PF 1|+|PF 2|=2的点P 的轨迹为椭圆;②到定点F 1(-3,0),F 2(3,0)距离相等的点的轨迹为椭圆;③若点P 到定点F 1(-4,0),F 2(4,0)的距离之和等于点M (5,3)到定点F 1(-4,0),F 2(4,0)的距离之和,则点P 的轨迹为椭圆.[解析] ①2<2,故点P 的轨迹不存在;②到定点F 1(-3,0),F 2(3,0)距离相等的点的轨迹是线段F 1F 2的垂直平分线(y 轴);③点M (5,3)到定点F 1(-4,0),F 2(4,0)的距离之和为410>8,故点P 的轨迹为椭圆.故填③.6.设F 1、F 2分别是椭圆x 225+y 216=1的左、右焦点,P 为椭圆上任意一点,点M 的坐标为(6,4),则|PM |+|PF 1|的最大值为__15__.[解析] 由椭圆的方程可得a =5,b =4,c =3. ∴F 1(-3,0),F 2(3,0),如图所示,由椭圆的定义可得,|PF 1|+|PF 2|=2a =10,∴|PM |+|PF 1|=|PM |+2a -|PF 2|=10+(|PM |-|PF 2|)≤10+|MF 2|=10+32+42=15,∴|PM |+|PF 1|的最大值为15. 三、解答题7.已知椭圆的中心在原点,且经过点P (3,0),a =3b ,求椭圆的标准方程.[解析] 当焦点在x 轴上时,设其方程为x 2a 2+y 2b 2=1(a >b >0).由椭圆过点P (3,0),知9a 2+0b2=1,又a=3b,解得b2=1,a2=9,故椭圆的方程为x29+y2=1.当焦点在y轴上时,设其方程为y2a2+x2b2=1(a>b>0).由椭圆过点P(3,0),知0a2+9b2=1,又a=3b,联立解得a2=81,b2=9,故椭圆的方程为y281+x29=1.故椭圆的标准方程为y281+x29=1或x29+y2=1.8.如图所示,在圆C:(x+1)2+y2=25内有一点A(1,0).Q为圆C上一点,AQ的垂直平分线与C,Q的连线交于点M,求点M的轨迹方程.[解析]如图所示,连接MA,由题知点M在线段CQ上,从而有|CQ|=|MQ|+|MC|.又点M在AQ的垂直平分线上,所以|MA|=|MQ|,故|MA|+|MC|=|CQ|=5.又A(1,0),C(-1,0),故点M的轨迹是以(1,0),(-1,0)为焦点的椭圆,且2a=5,c=1,故a=52,b2=a2-c2=254-1=214.故点M的轨迹方程为x2254+y2214=1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时作业9 椭圆及其标准方程
时间:45分钟 满分:100分
一、选择题(每小题5分,共30分)
1.椭圆2x2+3y2=12的两焦点之间的距离是( )
A.210 B.10
C.2 D.22
【答案】 D
【解析】 将椭圆方程化为标准方程为x26+y24=1,则a2=6,b
2
=4,c2=2,
∴两焦点间距离为22.故选D.
2.(2013·全国卷大纲文)已知F1(-1,0),F2(1,0)是椭圆C的两个
焦点,过F2且垂直于x轴的直线交C于A、B两点,且|AB|=3,则C
的方程为( )
A.x22+y2=1 B.x23+y22=1
C.x24+y23=1 D.x25+y24=1
【答案】 C
【解析】 设椭圆方程为x2a2+y2b2=1(a>b>0),则a2=b2+1,当x
=1时,y=±b2a,∴|AB|=2b2a=3,∴a2=32a+1,即2a2-3a-2=0.
∴a=-12(舍去)或a=2,∴b2=3,∴方程为x24+y23=1.
3.椭圆的两个焦点坐标分别为F1(-8,0),F2(8,0),且椭圆上一点
到两个焦点的距离之和为20,则此椭圆的标准方程为( )
A.x236+y2100=1 B.x2400+y2336=1
C.x2100+y236=1 D.x220+y212=1
【答案】 C
【解析】 由题意知椭圆的焦点在x轴上,所以可设椭圆的标准
方程为x2a2+y2b2=1(a>b>0),由题意知2a=20,所以a=10,又c=8,
所以b2=a2-c2=36.
4.若△ABC的两个顶点坐标为A(-4,0),B(4,0),△ABC的周长
为18,则顶点C的轨迹方程为( )
A.x225+y29=1 B.y225+x29=1(y≠0)
C.x216+y29=1(y≠0) D.x225+y29=1(y≠0)
【答案】 D
【解析】 因为|AB|=8,所以|CA|+|CB|=18-8=10>8,所以点
C在以A、B为焦点的椭圆上,但由于A、B、C三点不共线,所以点
C的纵坐标y≠0,所以顶点C 的轨迹方程为x225+y29=1(y≠0).
5.两个焦点的坐标分别为(-2,0),(2,0),并且经过P52,-32的
椭圆的标准方程是( )
A.x210+y26=1 B.y210+x26=1
C.x294+y2254=1 D.y294+x2254=1
【答案】 A
【解析】 设F1(-2,0),F2(2,0),
设椭圆方程为x2a2+y2b2=1(a>b>0),由题意得,
|PF1|+|PF2|=52+22+94+52-22+94
=210=2a,
∴a=10,
又c=2,∴b2=6,椭圆的方程为x210+y26=1.
6.AB为过椭圆x2a2+y2b2=1中心的弦,F(c,0)为椭圆的右焦点,则
△AFB的面积最大值是( )
A.b2 B.bc
C.ab D.ac
【答案】 B
【解析】 ∵S△ABF=S△AOF+S△BOF=12|OF|·|yA-yB|,
当A、B为短轴两个端点时,|yA-yB|最大,最大值为2b.
∴△ABF面积的最大值为bc.
二、填空题(每小题10分,共30分)
7.若点P在椭圆x22+y2=1上,F1,F2分别是椭圆的两个焦点,
且∠F1PF2=90°,则△F1PF2的面积是________.
【答案】 1
【解析】 由题意得|PF1|+|PF2|=22,|PF1|2+|PF2|2=(2c)2=4,
所以|PF1|·|PF2|=2,所以S△F1PF2=12|PF1|·|PF2|=1.
8.椭圆x212+y23=1的一个焦点为F1,点P在椭圆上,如果线段
PF1的中点M在y轴上,那么点M的纵坐标是________.
【答案】 ±34
【解析】 设F1(-3,0),P(x,y),M(0,y0),则得-3+x2=0,∴
x=3,将x=3代入x212+y23=1,得y=±32,∴y0=y+02=±34.
9.椭圆x225+y29=1上的一点M到左焦点F1的距离为2,N是MF
1
的中点,则|ON|等于________.
【答案】 4
【解析】 设椭圆的右焦点为F2,则由|MF1|+|MF2|=10,知MF
2
=10-2=8.
又因为点O为F1F2的中点,点N为MF1的中点,所以|ON|=12|MF2|
=4.
三、解答题(本题共3小题,共40分.解答应写出必要的文字说
明、证明过程或演算步骤)
10.(13分)设0≤α≤2π,若方程x2sinα-y2cosα=1表示焦点在y
轴上的椭圆,则α的取值范围是多少?
【解析】 ∵x2sinα-y2cosα=1,
∴x21sinα+y2-1cosα=1.
∵焦点在y轴上,∴a2=-1cosα,b2=1sinα,
∴ 1sinα>0,-1cosα>1sinα,即 sinα>0,-1cosα>1sinα,
∴-tanα>1,∴tanα<-1,
又α∈(0,π),∴α∈(π2,3π4).
11.(13分)△ABC的三边a>b>c成等差数列,A、C两点的坐标
分别是(-1,0),(1,0),求顶点B的轨迹方程.
【分析】 由题意2b=a+c,即|BC|+|BA|=2|AC|=4,结合椭圆
的定义求解.
【解析】 设点B的坐标为(x,y),
∵a,b,c成等差数列,
∴a+c=2b,即|BC|+|AB|=2|AC|,
∴|BC|+|BA|=4.根据椭圆的定义知,点B的轨迹方程为x24+y23=1.
又∵a>b>c,∴a>c,即|BC|>|AB|,
∴(x-1)2+y2>(x+1)2+y2,∴x<0,
∴点B的轨迹是椭圆的一半,方程为
x24+y
2
3
=1(x<0).
又当x=-2时,点B、A、C在同一直线上,不能构成△ABC,∴
x≠-2.
∴顶点B的轨迹方程为x24+y23=1(-2
是不能构成△ABC的情况应给予考虑,从而排除不能构成△ABC的点
B(-2,0).
12.(14分)已知P是椭圆x24+y2=1上的一点,F1,F2是椭圆上的
两个焦点.
(1)当∠F1PF2=60°时,求△F1PF2的面积;
(2)当∠F1PF2为钝角时,求点P横坐标的取值范围.
【解析】 (1)由椭圆的定义,点P的轨迹是以F1,F2为焦点,
长轴长2a=4的椭圆,且b=1,c=3,所以|PF1|+|PF2|=4.①
在△F1PF2中,由余弦定理,得
|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|cos60°.②
由①②得|PF1|·|PF2|=43.所以S△PF1F2=33.
(2)设点P(x,y),由已知∠F1PF2为钝角,得PF1→·PF2→<0,
即(x+3,y)·(x-3,y)<0,所以-263
