圆环截面惯性矩
材料力学第六章 截面的几何性质惯性矩
IP
2dA
A
(y2
A
z2 )dA
IZ
Iy.
返回 下一张 上一张 小结
第三节 惯性矩和惯性积的 y1dA (y a)2 dA A
y2dA 2a ydA a2 dA
I z1 z a2 A; y1 y b2 A;
2dA
A
(y2
A
z2 )dA
IZ
Iy.
Izy
z y dA;
A
五、平行移轴公式:
I z1 z a2 A; y1 y b2 A;
I z1y1 I zy abA;
返回 下一张 上一张 小结
六、主惯性轴和主惯性矩: 主惯性轴(主轴)—使 I zoyo 0 的这对正交坐标轴; 主惯性矩(主惯矩)—截面对主惯性轴的惯性矩; 形心主惯性轴(形心主轴)—通过形心的主惯性轴; 形心主惯性矩(形心主惯矩)—截面对形心主轴的惯性矩。
I z1y1 I zy abA;
注意: y、z轴必须是形心轴。
二、转轴公式:
Iz1
A y12dA
( y cos z sin)2 dA;
A
I z1
Iz
Iy 2
Iz
Iy 2
cos 2
I zy
sin 2;
I y1
Iz
2
Iy
Iz
2
Iy
cos 2
I zy
sin 2;
I z1y1
Iz
Iy 2
三、惯性积:
定义:平面图形内, 微面积dA与其两个坐 标z、y的乘积zydA在整个图形内的积分称为 该图形对z、y轴的惯性积。
Izy
z y dA;
A
特点: ①惯性积是截面对某两个正交
惯性矩的计算方法

第1节静矩和形心4.1静矩和形心任何受力构件的承载能力不仅与材料性能和加载方式有关.而口与构件截面的几何形状和尺寸有关.如:计算杆的拉伸与压缩变形时用到截面而积A ,计算圆轴扭转变形时用到横截面的极惯性矩I?等.A、1?等是从不同角度反映了截而的几何特性,因此称它们为截而图形的几何性质.4.1静矩和形心设有一任意截而图形如图4 一1所示,其面积为A .选収直角坐标系yoz ,在坐标为(y,z)处取一微小而积dA ,定义微而积dA乘以到y轴的距离z ,沿整个截面的积分,为图形对y轴的静矩S?,其数学表达式(4 -la )同理,图形对z轴的静矩为□4-1图41截面静矩与坐标轴的选取有关•它随坐标轴y、z的不同而不同.所以静矩的数值可能足正,也可能足负或定零.静矩的虽纲为长度的三次方.确定截面图形的形心位置(图4-1中C点):A (4-2b)第1页共30页式中T、"为截而图形形心的坐标值.若把式(4-2)改写成心"•儿,為"•乙(4 3)性质:・若截面图形的静矩等于零,则此坐标轴必定通过截面的形心.・若坐标轴通过截而形心,则截而对此轴的静矩必为零.・山于截而图形的对称轴必定通过截而形心,故图形对其对称轴的静矩恒为零。
4 )工程实际中,有些构件的截面形状比较复杂,将这些复杂的截面形状看成是山若干简单图形(如矩形、圆形等)组合g而成的.对于这样的组合截而图形,计算静矩(S»‘ r)与形心坐标(y*、z ')时,可用以下公式1-1 2-1式中A— y i , z i分别表示第,个简单图形的面积及其形心坐标值,n为组成组合图形的简单图形个数.即:组合图形对某一轴的静矩等于组成它的简单图形对同一轴的静矩的代数和.组合图形的形心坐标值等于组合图形对相应坐标轴的静矩除以组合图形的面积.组合截面图形有时还可以认为是山一种简单图形减去另一种简单图形所组成的.例4J己知T形截面尺寸如图4-2所示,试确定此截面的形心坐标值.i-1 i-1 (4-5)图4-2解:(1)选参考轴为y 轴,z 轴为对称轴,(2)将图形分成I 、口两个矩形,则= 20 x 100加朋 S 右=(10 + 140)^^34 = 2Q X 14%/,22 二注型(3)代入公式(4・5)20x100x150+20x140x70 20x100 + 20x140此=°4.2惯性矩、惯性积和惯性半径设任一截面图形(图4-3),其而积为A ・选取直角坐标系yoz ,在坐标为(y 、z)处取一微小面积dA ,定义此微2面积dA 乘以到坐标原点o 的距离的平方Q ,沿整个截面积分,为截而图形的极惯性矩I?.做而积dA 乘以到坐标轴y 的2距离的平方2 ,沿整个截而积分为截面图形对y 轴的惯性矩I 》•极惯性矩、惯性矩常简称极惯矩、惯矩.j.l ~2Z4数学表达式为打=f p^dA极惯性矩“俎(4-6)对y轴惯性矩图4-3山图4-3看到“ =y +Z 9所以有打=\A^dA= £cy2 +/)曲二必+加必即;? (4-8)式(4-8)说明截面对任一对正交轴的惯性矩之和恒等于它对该两轴交点的极惯性矩。
挠度计算
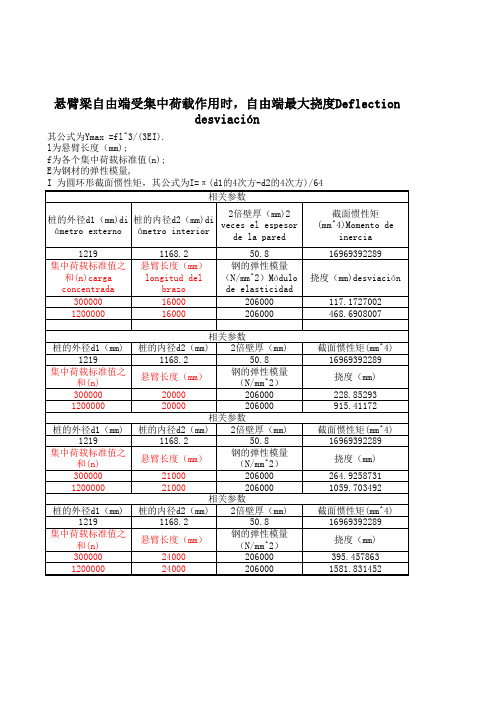
其公式为Ymax =fl^3/(3EI). l为悬臂长度(mm); f为各个集中荷载标准值(n); E为钢材的弹性模量, I 为圆环形截面惯性矩,其公式为I=π (d1的4次方-d2的4次方)/64 相关参数 2倍壁厚(mm)2 桩的外径d1(mm)di 桩的内径d2(mm)di veces el espesor ámetro externo ámetro interior de la pared 1219 集中荷载标准值之 和(n)carga concentrada 300000 1200000 1168.2 悬臂长度(mm) longitud del brazo 16000 16000 50.8 钢的弹性模量 (N/mm^2)Módulo de elasticidad 206000 206000 截面惯性矩 (mm^4)Momento de inercia 16969392289 挠度(mm)desviación 117.1727002 468.6908007
桩的外径d1(mm) 1219 集中荷载标准值之 和(n) 300000 1200000 桩的外径d1(mm) 1219 集中荷载标准值之 和(n) 300000 1200000 桩的外径d1(mm) 1219 集中荷载标准值之 和(n) 300000 1200000
相关参数 桩的内径d2(mm) 2倍壁厚(mm) 1168.2 50.8 钢的弹性模量 悬臂长度(mm) (N/mm^2) 20000 206000 20000 206000 相关参数 桩的内径d2(mm) 2倍壁厚(mm) 1168.2 50.8 钢的弹性模量 悬臂长度(mm) (N/mm^2) 21000 206000 21000 206000 相关参数 桩的内径d2(mm) 2倍壁厚(mm) 1168.2 50.8 钢的弹性模量 悬臂长度(mm) (N/mm^2) 24000 206000 24000 206000
圆形截面面积矩

圆形截面面积矩什么是圆形截面面积矩?圆形截面面积矩是描述圆形截面几何特性的物理量。
它可以通过求解圆形截面的面积、质心、惯性矩和转动惯量来计算。
圆形截面面积矩在工程、物理学和力学中有广泛应用,特别是在结构设计、材料力学和机械工程等领域。
圆形截面面积矩的计算公式圆形截面面积矩有三个常用参数,分别是面积、质心和转动惯量。
下面是基于圆形截面的计算公式:1.圆形截面的面积(A)公式:A=π×r2,其中,π是圆周率,r是圆形的半径。
2.圆形截面的质心(x c,y c)公式:x c=0, y c=0,其中,x c和y c分别表示质心在 x 轴和 y 轴上的坐标。
3.圆形截面的惯性矩(I x,I y)公式:I x=I y=14πr4,其中,I x和I y分别表示围绕 x 轴和 y 轴的惯性矩。
4.圆形截面的转动惯量(I z)公式:I z=12πr4,表示围绕截面法线轴的转动惯量。
圆形截面面积矩的应用圆形截面面积矩在工程设计和物理学中有广泛的应用,以下分别介绍不同方面的应用:结构设计圆形截面的面积矩在结构设计中起到了至关重要的作用,它可以帮助工程师计算出结构件的质心和转动惯量。
这些参数对于结构件的稳定性和受力分析至关重要。
例如,在建筑设计中,圆形截面的柱子通常承受来自上层结构的压力。
通过计算圆形截面的质心,工程师可以确定柱子的最佳支撑点,从而保证结构的稳定性。
材料力学圆形截面面积矩在材料力学中的应用主要涉及材料的弯曲和扭转行为。
通过计算圆形截面的转动惯量,可以得到材料的抗弯强度和抗扭强度。
这些参数对于材料的强度和刚度分析非常重要。
例如,在金属加工中,圆材料的曲率半径和材料的性质可以通过圆形截面的转动惯量推导出来,从而帮助工程师选择合适的材料和工艺参数。
机械工程在机械工程中,圆形截面面积矩被广泛应用于机械零件的设计和制造。
通过计算圆形截面的转动惯量,可以得到机械零件的惯性特性和运动稳定性。
这些参数对于机械系统的设计和性能评估非常重要。
截面惯性矩和截面抵抗矩

截面惯性矩和截面抵抗矩
梁的截面惯性矩和截面抗矩是有力学原理由力学原理计算得出,对于工程计算和设计十分重要。
截面惯性矩是指梁截面在任意方向和平面围绕其中心点,旋转一周所产生的力矩;而抗矩则
来源于求取梁截面在一起受力时所抵抗偏转作用的力矩。
简言之,截面惯性矩和抗矩表示了梁所能承受的偏转能力有多大。
梁的截面惯性矩计算时,需根据所使用的梁截面的几何形状不同,综合考虑其面积、外接图形的面积以及距离质心的距离大小等因素,综合计算所得结果是根据梁的几何形状所得的结果逐步的减小的。
抗矩的计算与计算惯性矩相同,也需要根据梁截面的形状来计算,不过抗矩采用的是恒压梁横向剖面质心与中心线距离来计算,这是因为梁蒙受的外力及其作用的方向改变时,偏转力也会改变,因此梁的抗矩会发生变化。
总的来说,梁的截面惯性矩和抗矩是非常重要的参数,在工程设计和分析中起着举足轻重的作用。
精确计算梁截面惯性矩及抗矩有助于更加准确地分析梁的偏转能力,从而降低设计梁容易出现破坏情况。
截面的静矩和形心位置及惯性矩的计算
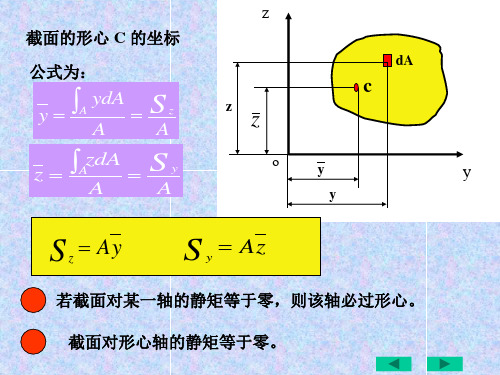
y1 60mm
矩形 2
A2 10 70 700mm2
x2
10
70 2
45mm
y2 5mm
y 10
1 x1
y1
o
2 y2
10
x2
x
80
所以
x
A1 x1 A 2 x2 A1 A2
37500 1900
20mm
y
A1 y1 A1
A2 y2 A2
75500 1900
40mm
y 10
1 x1
求形心主惯性矩的步骤
确定形心 的位置
x
Ai x i
,
y
Ai
yi
Ai
Ai
选择一对通过形心且便于计算惯性矩(积)的坐 标轴 x ,y, 计算 Ix , Iy , Ixy
I x I xi I y I yi
I xy I xyi
确定主惯性轴的位置
I 1 2 xy
2 0
tg
(
)
Ix Iy
y
80
c
x
10
y
Ix
1 12
120 103 152 120 10
1 12
703
10
(25)2
70
10
100.4 104 mm 4
Iy 278.4 104 mm4
70 20 10
120
y
80
c
x
10
y
I xy 0 15 20 120 10 0 (25) (35) 70 10
yc
C(a,b)
xc
b
x
Ix , Iy , Ixy _____ 截面对 x , y 轴的惯性矩和惯性积。
材料力学B精选题12

动 载 荷1. 重量为P 的物体,以匀速v 下降,当吊索长度为l 时,制动器刹车,起重卷筒以等减速在t 秒后停止转动,如图示。
设吊索的横截面积为A ,弹性模量为E ,动荷因数K d 有四种答案: (A) gPl EA v; (B) gPlEA t v; (C) gt v ; (D) gt v+1。
答:D2. 图示一起重机悬吊一根工字钢,由高处下降。
如在时间间隔t 内下降速度由v 1均匀地减小到v 2 (v 2<v 1),则此问题的动荷因数为: (A) gtv v 2121+-; (B) gt v v 2121++;(C) gt v v 211--; (D) gtv v 211-+。
答:C3. 长度为l 的钢杆AB ,以匀角速度绕铅垂轴OO ′旋转,若钢的密度为ρ,许用应力为[σ ],则此杆的最大许可角速度ω 为(弯曲应力不计):(A) ρσ][1l ; (B) ρσ][21l ;(C) ρσ][21l ; (D) ρσ][22l 。
答:D4. 长度为l 的钢杆AB 以匀角速度绕铅垂轴OO ′旋转。
已知钢的密度ρ和弹性模量E 。
若杆AB 的转动角速度为ω,则杆的绝对伸长∆l 为(弯曲应力不计): (A) ρω2 l 3 / 12E ; (B) ρω2 l 3 / 8E ; (C) ρω2 l 3 / 4E ; (D) ρω2 l 3 / 3E 。
答:A5. 图示钢质圆盘有一偏心圆孔。
圆盘以匀角速度ω 旋转,密度为ρ。
由圆盘偏心圆孔引起的轴内横截面上最大正应力m ax σ为: (A) 3218)(d a d ωρδ;(B)3214)(da d ωρδ;(C) 321)(4d a d ωρδ; (D) 321)(8da d ωρδ。
答:C6. 直径为d 的轴上,装有一个转动惯量为J 的飞轮A 。
轴的速度为n 转/秒。
当制动器B 工作时,在t 秒内将飞轮刹停(匀减速),在制动过程中轴内最大切应力为: (A)3π16d ntJ ; (B) 3πtd J n ; (C) 332td nJ ; (D) 3π32td Jn 。
不对称工字钢惯性矩计算公式

钢结构工字钢的惯性矩公式:(t*h*h*h/12)+2*{a*b*[(t+b)/2][(a*b)/2]}
对横轴:工字型钢的翼缘长a、腹板长b、板厚t
简单来说,算腹板、翼缘对横轴的惯性矩,腹板的惯性矩是宽乘以高的三次方再除以十二,翼缘是翼缘的面积乘以翼缘中心到横轴的距离的平方。
惯性矩的注意事项:
1、惯性矩没有总和不总的区别。
2、惯性矩是对某一轴的距。
3、型钢的惯性矩是型钢对于形心轴,或者说表面的某一轴的距。
扩展资料:
各种截面的惯性矩的计算公式如下:
常见截面的惯性矩公式
1、矩形:b*h^3/12 其中:b-宽;h-高
2、三角形:b*h^3/36 其中:b-底长;h-高
3、圆形:π*d^4/64其中:d-直径
4、圆环形:π*D^4*(1-α^4)/64; α=d/D 其中:d-内环直径;D-外环直径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆环截面惯性矩
圆环截面惯性矩是物理学中一种常见的物理概念,它指的是一个圆形截面的物体的转动惯性的总和,而圆形截面的物体是指圆环截面的物体。
与其它形状的截面不同,圆环截面惯性矩具有较大的转动惯性。
圆环截面惯性矩可以计算出来,其计算方法是圆环截面的半径R,重量ρ,密度rho和厚度t,可以使用下面的公式计算出圆环截面惯性矩:J=1/2ρrt。
数学公式可以告诉人们,圆环截面惯性矩越大,则物体越能抵抗外力带来的转动,因此,这也是为什么圆环截面的物体会具有较大的转动惯性的原因。
圆环截面惯性矩的应用非常广泛,它可以用于机械、电子、通信等不同领域。
在机械工程中,圆环截面惯性矩是摆动物体的最佳参数之一,可以用于计算摆线轮的齿数和齿宽;在电子领域,圆环截面惯性矩可以用于计算电子元件的响应时间;在通信领域,圆环截面惯性矩可以用于计算振荡电路中振荡元件的响应频率等。
总之,圆环截面惯性矩是物理学中一种重要的概念,它可以用于不同领域,因此,研究它的重要性及其应用是十分必要的。
例如,可以通过实验研究圆环截面的惯性矩系数,针对不同的材料进行不同的设计,以提高圆环截面的转动惯性,从而达到更好的应用效果。
- 1 -。
