分式混合运算练习题(30题)
分式混合运算练习题及答案

分式混合运算练习题及答案1. 小明需要将墙上的一段长方体装饰条剪成相等的三段,已知该长方体装饰条的长度为5/6米。
请问每段装饰条的长度是多少?解答:将装饰条剪成三段,每段长度为x。
根据题意,有以下等式:x + x + x = 5/63x = 5/6x = (5/6) ÷ 3x = 5/6 × 1/3x = 5/18答案:每段装饰条的长度为5/18米。
2. 小华将两个相同的大理石板用副伪币P贴在一起,已知每个大理石板的面积为3/5平方米。
请问贴在一起的两个大理石板的总面积是多少平方米?解答:将两个大理石板贴在一起,总面积为x。
根据题意,有以下等式:2 × (3/5) = x6/5 = x答案:贴在一起的两个大理石板的总面积为6/5平方米。
3. 假设一个圆形花坛的半径为2/3米,已知小明想在花坛中种上一圈半径为1/6米的小花。
请问小明一共需要准备多少米的小花?解答:花坛的半径为2/3米,小花的半径为1/6米。
需要计算一圈小花的周长,即2πr,其中r表示小花的半径。
周长= 2 × (π × 1/6)周长= π/3答案:小明一共需要准备π/3米的小花。
4. 小红前一天用2/5的时间完成了数学作业,剩下的时间用来做英语作业。
如果她共用了1小时做完这两门科目的作业,请问她用多长时间做完了英语作业?解答:小红前一天用2/5的时间完成了数学作业,剩下的时间用来做英语作业。
总时间为1小时。
假设小红用x小时完成了英语作业。
根据题意,有以下等式:2/5 + x = 1x = 1 - 2/5x = 3/5答案:小红用3/5小时完成了英语作业。
5. 小明将一条长绳剪成了3段,已知第一段长1/2米,第二段比第一段长1/3米,第三段比第二段长1/4米。
请问原始的长绳一共有多长?解答:将原始的长绳的长度设为x。
根据题意,有以下等式:x = 1/2 + (1/2 + 1/3) + (1/2 + 1/3 + 1/4)x = 1/2 + 3/6 + 4/12x = 6/12 + 6/12 + 4/12x = 16/12x = 4/3答案:原始的长绳一共有4/3米长。
初二分式的混合运算练习题

初二分式的混合运算练习题
首先,让我们来回顾一下初二分式的混合运算。
在分式的混合运算中,我们需要进行加、减、乘、除等运算,并且考虑到分式的化简和
约分。
下面是一些练习题,帮助你巩固这方面的知识。
1. 计算以下各式的值:
a) 3/4 + 1/2
b) 5/6 - 1/3
c) 2/3 × 4/5
d) 3/4 ÷ 1/2
2. 化简以下各式:
a) (2/3) × (6/10)
b) (1/2) ÷ (2/4)
c) 4/6 + 2/3 - 1/2
d) (3/8) ÷ (1/4) × (2/5)
3. 解决以下问题:
a) 如果一个苹果馅饼有16块,你吃了其中的3/4块,还剩下多少块?
b) 你用1/3小时跑完了1/2公里的距离,以相同的速度再跑2/3小时,你总共跑了多少公里?
c) 小明有1/4公斤的巧克力,他分给了3个朋友,每人得到多少公
斤的巧克力?
d) 如果12本书总共有3/4公斤,每本书的重量是多少?
4. 填空:
a) 5/6 + 3/4 = ___
b) 2/3 - 1/5 = ___
c) 2/5 × 3/4 = ___
d) 3/4 ÷ 2/5 = ___
以上就是初二分式的混合运算的练习题。
希望通过这些题目的练习,你能够更好地理解和掌握分式的混合运算。
如果有任何疑问,请随时
向老师或同学寻求帮助。
加油!。
八年级数学—分式的混合运算习题

4a 8a a 1 a 1 4).(a 2) (a 1 ) a 1 a 1
5.拓展思维: 你能很快计算出
20022003 2 2 20022002 20022004 2
的值吗?
2
4.答案1).解法一:
a 1 4 a a2 2 2 2 a 2a a 4a 4 a 2a
a 4 a(a 1) a 2a 2 a ( a 2) 4a
2 2
a4 a ( a 2) 2 a ( a 2) 4a
1 a2
1).解法二:
a 1 4 a a2 2 2 2 a 2a a 4a 4 a 2a
1 a2
x3 5 2).解: ( x 2) 2x 4 x 2 x 3 5 ( x 2)( x 2) 2x 4 x2
1 2( 3 x )
x2 x 3). 解: 2 2 x x 4x 4 x 2x
4 x
1 ( x 2)( x 2) 1 x 2 x 2 x
1 ( x 2)( x 2) 1 ( x 2)( x 2) ( x 2) x ( x 2) x
x2 x2 x x
4 x
4).解:
16.2 分式的混合运算习题课 分式的加减法(二)
1.计算:
3x x y 7y 1 x 4y 4y x x 4y x 2 x 1 x 1
2
(1) 2
3 3 2 2 x 2x x 4x 4
1 (2) x 1 x3 (3) x2 x ( x 2)
a 1 3. a 1
四年级数学分式混合运算练习题

四年级数学分式混合运算练习题在数学学习中,分式混合运算是一个重要的知识点,它是将整数、分数以及四则运算相结合的运算方式。
通过练习分式混合运算题,可以提高我们的计算能力和解决问题的能力。
下面,我将为你提供一些适合四年级学生的分式混合运算练习题。
练习题一:1. 将3和1/4与2/3相加。
2. 将5/8减去1/4。
3. 将2和3/5乘以2/7。
4. 将4/9除以1/3。
5. 将1/2与2/3相加再减去3/4。
练习题二:1. 将2和1/3与3/4相加。
2. 将7/8减去3/5。
3. 将1和3/4乘以2/3。
4. 将2/5除以1/2。
5. 将3/4与2/3相加再减去1/2。
练习题三:1. 将3和2/5与1/2相加。
2. 将9/10减去2/5。
3. 将4和3/8乘以3/7。
4. 将3/7除以1/4。
5. 将2/3与3/4相加再减去1/5。
练习题四:1. 将2和3/4与1/3相加。
2. 将3/5减去1/4。
3. 将3和1/2乘以4/7。
4. 将5/6除以2/3。
5. 将1/2与5/6相加再减去2/3。
练习题五:1. 将4和1/3与2/5相加。
2. 将7/8减去2/5。
3. 将2和1/2乘以3/4。
4. 将3/7除以1/3。
5. 将2/3与1/2相加再减去1/4。
以上是一些适合四年级学生的数学分式混合运算练习题。
希望通过这些练习题,能够让你更好地掌握分式混合运算的方法和技巧。
同时也希望你能够在解题过程中注意计算的准确性和步骤的清晰性。
加油!。
分式混合运算专题目练习(经典集合)

合用标准文案分式的乘除乘方运算一、基础知识点:1.约分把一个分式的分子与分母的公因式约去,叫做约分.约分的依照是分式的根本性质 .假设分式的分子、分母是多项式,必定先把分子、分母分解因式,尔后才能约去公因式.分子与分母没有公因式的分式,叫做最简分式,又叫做既约分式.分式的运算结果必然要化为最简分式.2.分式的乘法乘法法测:a·c=ac.b d bd3.分式的除法除法法那么:a÷c=a · d = adb d bc bc4.分式的乘方求 n 个相同分式的积的运算就是分式的乘方,用式子表示就是a n () . b分式的乘方,是把分子、分母各自乘方.用式子表示为:(a n a n) =n (n 为正整数 ) b b二、典型例题例 1、以下分式15bc,3( a b) 2 a 2 b 2a2b2). 12a b,2(a,a中最简分式的个数是 (a b)b例 2. 计算:(1)4xy(2)a212a(3)3xy 26y2 3y 2x3 a 2a2x(4)a 2a 1 a 21例3、假设x y zxy yz zx的值 . 4a 4 a24 2 34,求x 2y 2z2例 4、计算〔 1〕〔2a2b 3x2)2(y23(y4 c3〕〔2〕())y x x〔 3〕( 2a2bc)3(3a3b2x 2y 2)2( x2xy)3(xy2 )〔4〕()例5计算:11248x 1 x 1 x2 1 x4 1 x81112x 4 x38x7练习: 1.计算:2x 2 a 4x 4a8x8a x a x a例 6.计算:11111324351719182011111练习 1、x 2 x 3x 3 x 4x 100 x 101 x 1 x 2例 7、2x 1A B( x 1)( x 2)x 1x 2,求 A. B 的值。
针对性练习: 1. 计算以下各题 :〔 1〕x 3yx 2 y 2x 3 y〔2〕 a23a11. x2y 2x 2y2y 2x2 a 2 1a1(3)16(4)x2- x- 1(5)a-a6+3 ,a 3 9 a2x 1 a 3 a23a a(6)2xy x y2b2⑻313 2⑺ a b211x 2 y 2 ⑽x 2x 1〕 ( a aa 24⑼xy2-2 〔 11).x y x yx 2x x 4 x 4a 2 a 2a2. x 为整数,且2 22 x 18为整数,求所有的吻合条件的 x 的值的和.x 3 3 x x 293、混杂运算:⑴ (2x 3 x 293x x 2x a 1a11)⑵x 2 x 2x 24⑶a 2 2a 1axxa 1⑷ ( a 25a 2 1)a 24 ⑸x 2 2x 1(1 x 3)a 2a 24a 4x 2 1x 1⑹x3 (x 2 5 ) ⑺1 1 x 1x 2x 2x 1 x 2 1 x 2 2x 1x 2 4x 4 x 22x 11⑼xy 1 1⑻24x 2x 2 y 2x y x yxx⑽ (a 2b 2a 2b 2x x 3 x 2 2x 1+2) ÷⑾x 21x 3ab a bx 1⑿ ( x2 x 1 ) x 2 16(13)、 (x 2)2 ( y 2 )3 ( y ) 4 x 22x x 2 4x 4 x 24xy x x〔 14 〕、3 m(m 25 ) 〔 15〕、2x 6 ( x 3)x 2x 6 2m 4m 24 4x x 23 x1 a 1b 2213b 2 c〔 16〕、22b 3〔 17〕、2x 2 18 3 x2a4 4xx22 x4. 算:( x 2x 1)4 x,并求当 x3 原式的 .x 2 2x x 2 4x 4 x5、先化 ,3xxx 21再取一个你喜 的数代入求 :x 1 x 1 xx 22x 1÷x 1 6、有 一道 : “ 算21x 2 x x-x 的 ,其中 x=2 004 〞甲同学把“ x=2 004 〞 抄成“ x=2 040 〞,但他的 算 果也正确,你 是怎么回事?11+117、 算、++⋯+。
分式混合运算专题练习(经典集合)
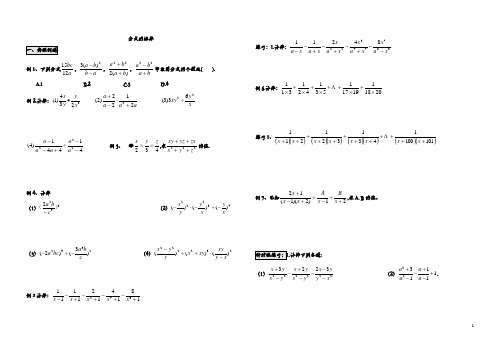
分式的运算一、典型例题例1、下列分式a bc 1215,a b b a --2)(3,)(222b a b a ++,b a b a +-22中最简分式的个数是( ).A.1B.2C.3D.4例2.计算:3234)1(x y y x ∙ a a a a 2122)2(2+⋅-+ x y xy 2263)3(÷41441)4(222--÷+--a a a a a 例3、 若432z y x ==,求222zy x zxyz xy ++++的值.例4、计算(1)3322)(c b a - (2)43222)()()(xy x y y x -÷-⋅-(3)2332)3()2(c b a bc a -÷- (4)232222)()()(xy xy xy x y y x -⋅+÷-例5计算:1814121111842+-+-+-+--x x x x x练习:1.计算:8874432284211x a x x a x x a x x a x a --+-+-+--例6.计算:2018119171531421311⨯+⨯++⨯+⨯+⨯练习1、()()()()()()()()1011001431321211++++++++++++x x x x x x x x例7、已知21)2)(1(12++-=+-+x Bx A x x x ,求A. B 的值。
针对性练习:1.计算下列各题:(1)2222223223xy yx y x y x y x y x ----+--+ (2)1111322+-+--+a a a a .(3)29631a a --+ (4) 21x x --x -1 (5)3a a --263a a a +-+3a ,(6)xy yy x x y x xy --++-222 ⑺b a b b a ++-22 ⑻293261623x x x -+--+⑼xy y x y x y x 2211-⋅⎪⎪⎭⎫ ⎝⎛+-- ⑽ 222x x x +--2144x x x --+(11)a a a a a a 4)22(2-⋅+--.2.已知x 为整数,且918232322-++-++x x x x 为整数,求所有的符合条件的x 的值的和.3、混合运算:⑴2239(1)x x x x ---÷ ⑵232224xx x x x x ⎛⎫-÷ ⎪+--⎝⎭⑶ a a a a a a 112112÷+---+⑷ 444)1225(222++-÷+++-a a a a a a ⑸ )1x 3x 1(1x 1x 2x 22+-+÷-+-⑹ )252(23--+÷--x x x x ⑺ 221111121x x x x x +-÷+--+⑻2224421142x x x x x x x -+-÷-+-+ ⑼2211xy x y x y x y ⎛⎫÷- ⎪--+⎝⎭⑽ (ab b a 22++2)÷ba b a --22 ⑾22321113x x x x x x x +++-⨯--+⑿ x x x x x x x x x 416)44122(2222+-÷+----+ (13)、22234()()()x y y y x x-⋅-÷-(14)、)252(423--+÷--m m m m (15)、x x x x xx x --+⋅+÷+--36)3(446222(16)、 ()3212221221------⎪⎭⎫ ⎝⎛ba cb b a (17)、⎪⎭⎫ ⎝⎛---÷⎪⎪⎭⎫ ⎝⎛+--x x x x x 23441823224.计算:x xx x x x x x -÷+----+4)44122(22,并求当3-=x 时原式的值.5、先化简,x x x x x x11132-⋅⎪⎭⎫ ⎝⎛+--再取一个你喜欢的数代入求值:6、有这样一道题:“计算22211x x x -+-÷21x x x -+-x 的值,其中x=2 004”甲同学把“x=2 004”错抄成“x=2 040”,但他的计算结果也正确,你说这是怎么回事?7、计算、)1(1+a a +)2)(1(1++a a +)3)(2(1++a a +…+)2006)(2005(1++a a 。
八年级下册分式混合运算练习题

分式练习题一.解答题1.计算:(1)(2)(﹣2m2n﹣2)2•(3m﹣1n3)﹣32.计算:3.化简:.4.(2007•双柏县)化简:5.(2006•襄阳)计算:.6.(2005•XX)化简•(x2﹣9)7.(2007•)计算:.8.(2005•宜昌)计算:+.9.(2001•XX)计算:(1);(2).10.(2001•常州).11.计算:12.计算:﹣a﹣1.13.计算:(1)(2)14.计算:a ﹣2+15.计算:.(2)()31031624π--⎛⎫⎛⎫-⋅-÷- ⎪ ⎪⎝⎭⎝⎭(3)2211y x xy y x y x -÷⎪⎪⎭⎫ ⎝⎛++-16.化简:,并指出x 的取值范围.17.已知ab=1,试求分式:的值. 18.计算:﹣19.(2010•XX )计算:20.(2009•太原)化简:21.(2009•XX)计算:.22.(2009•眉山)化简:23.(2009•XX)计算:(1);(2).24.(2009•东营)化简:25.(2008•白银)化简:.26.(2007•XX )化简:27.(2007•巴中)计算:28.(2006•宜昌)计算:()÷.29.(2006•十堰)化简:.30.(2006•XX )计算:﹣x ﹣2)18.先化简代数式1121112-÷⎪⎭⎫ ⎝⎛+-+-+x x x x x x ,然后选取一个使你喜欢的x的值代入求值.分式方程练习题一、填空、选择题:1.以下是方程211x x x-=-去分母的结果,其中正确的是 A .2(1)1x x --= B .2221x x --= C .2222x x x x --=- D .2222x x x x -+=- 2.在下列方程中,关于x的分式方程的个数有.①0432212=+-x x ②.4=a x ③;4=x a ④.;1392=+-x x ⑤;621=+x ⑥211=-+-ax a x . A.2个 B.3个 C.4个 D.5个 3.分式25m +的值为1时,m 的值是. A .2 B .-2 C .-3 D .3 4.不解下列方程,判断下列哪个数是方程21311323x x x x =+++--的解. A .x=1 B .x=-1 C .x=3 D .x=-3 6.若分式x 2-12(x+1) 的值等于0,则x 的值为.A 、1B 、±1C 、12D 、-18.关于x的方程2354ax a x +=-的根为x=2,则a应取值 . A.1 B.3 C.-2D.-37.赵强同学借了一本书,共280页,要在两周借期内读完,当他读了一半时,发现平时每天要多读21页才能在借期内读完.他读了前一半时,平均每天读多少页?如果设读前一半时,平均每天读x 页,则下列方程中,正确的是. A 、1421140140=-+x xB 、1421280280=++x x C 、1211010=++x x D 、1421140140=++x x8.关于x 的方程2354ax a x+=-的根为x =2,则a 应取值.A.1B .3 C.-2D.-310.“五一”江北水城文化旅游节期间,几名同学包租一辆面包车前去旅游,面包车的租价为180元,出发时又增加了两名同学,结果每个同学比原来少摊了3元钱车费,设参加游览的同学共x 人,则所列方程为. A .32180180=+-x xB .31802180=-+x x C .32180180=--x x D .31802180=--xx 一、填空题: 13.若分式11--x x 的值为0,则x 的值等于14.若分式方程xmx x -=--2524无解,那么m 的值应为 16.阅读材料: 方程1111123x x x x -=-+--的解为1x =, 方程1111134x x x x -=----的解为x=2, 方程11111245x x x x -=-----的解为3x =,… 请写出能反映上述方程一般规律的方程,并直接写出这个方程的解是. 二、解答题:17.解方程)2)(1(311+-=--x x x x19.若方程122-=-+x ax 的解是正数,求a 的取值范围。
分式混合运算练习题(

分式的加减乘除混合运算
1.计算:
(1) (2)(﹣2m2n﹣2)2•(3m﹣1n3)﹣3
2.计算: 3.化简:
4.计算: 5.计算:
6.计算:+. 7.计算:
8.. 9.计算:﹣a﹣1.
10.计算:(1) (2)
11.计算:a﹣2+ 12.计算:.
13.化简:,并指出x的取值范围.
14.已知ab=1,试求分式:的值. 15.计算
16.. 17.
18.计算:. 19.化简:
20.计算:(1); (21).
22.化简: ﹣x﹣2).
