基于点云几何与形状特征的曲面重构算法
表面重建算法

表面重建算法概述表面重建算法是计算机图形学中的一个重要研究领域,其主要目的是从点云数据中生成连续、光滑的曲面模型。
表面重建算法应用广泛,如三维扫描、医学成像、地形建模等领域。
本文将介绍表面重建算法的基本原理、分类以及常用算法。
基本原理表面重建算法的基本原理是从离散的点云数据中生成连续、光滑的曲面模型。
点云数据通常由三维扫描仪或激光雷达等设备获取。
对于一个给定的点云,表面重建算法需要确定每个点在曲面上的位置和法向量。
分类表面重建算法可以分为两类:基于网格和基于隐式函数。
1. 基于网格基于网格的表面重建算法将点云转换为一个三角网格,然后通过对网格进行平滑处理来生成曲面模型。
其中最常用的方法是Poisson重构算法。
Poisson重构算法基于Poisson方程,该方程描述了曲面上任意一点处梯度向量与曲面法向量之间的关系。
该算法首先计算每个点在曲面上的法向量,然后通过对点云进行重采样得到一个规则的网格,最后利用Poisson方程求解得到曲面模型。
2. 基于隐式函数基于隐式函数的表面重建算法将点云转换为一个隐式函数,然后通过等值面提取算法生成曲面模型。
其中最常用的方法是Moving Least Squares (MLS)算法。
MLS算法首先对点云进行平滑处理,然后对每个点构建一个局部加权多项式函数。
该函数表示了该点附近的曲面形状,然后通过等值面提取算法生成曲面模型。
常用算法1. Marching Cubes算法Marching Cubes算法是一种基于网格的表面重建算法。
该算法将三维空间划分为一系列小立方体,并在每个立方体中确定等值面的位置和拓扑结构。
最终将所有立方体中的等值面拼接起来形成曲面模型。
2. Poisson重构算法Poisson重构算法是一种基于网格的表面重建算法。
该算法首先计算每个点在曲面上的法向量,然后通过对点云进行重采样得到一个规则的网格,最后利用Poisson方程求解得到曲面模型。
3. MLS算法MLS算法是一种基于隐式函数的表面重建算法。
基于海量点云的复杂曲面重构及误差分析

构设计 , 建立精确 的光顺 的 C D数 字模 型 , A 并应 用 3 D点 云
对齐的 方式对 重 构模 型进 行 误差 分 析 , 以达 到 最佳 的 重构
效果。
数据 获取 的方法虽然多样 , 在实 际 的测 量过程 中受到 但 人 为或随机 因素 的影 响 , 不可 避 免会 引入 不合 理 的 噪音 都
造 , 点高 , 起 周期短 , 成效快。 在海量点 云采 集 的基 础 上 , 应用 曲面重 构基本 理 论 , 结
合 正 逆 向工 程 软 件 , 长 补 短 , 复 杂 曲 面 进 行 逆 向三 维 重 取 对
面的反射特性和传感器 噪声 等的影 响 , 测量 数据还 会存在 大
量无用的数据 , 即所 谓 “ 噪声 ” , 些数 据 的存 在对 零件 的 点 这 造型有害无益 , 要将 其剔 除 。通常 , 原 始点 云数据 的预 对
引入数据误差 , 尤其 是尖 锐边 和边 界 附近 的测量 数据 , 量 测
数据 中的坏点 , 能使该 点及 其周 围 的 曲面片偏 离原 曲面 ; 可 还有 , 由于测量采用的是光学原 理 , 光照条 件 、 量工 件表 受 测
体模 型和设 计模 型之 问 的比较 差 异 , 新产 品 的设计 与 制 使
讨研 究 , 并应 用 3 D点云对 重构模型进行 了误 差分析。将该方法应用 于工业产品复 杂曲面的 实际制造 中, 高了设 计 提 精度 , 缩短 了生产周期 , 实际生产具有重要 意义。 对
关键 词 : 向工 程 ; 云 处 理 ; 面 重构 ; 差 分 析 逆 点 曲 误 中 图分 类 号 : P9 . 1 T 3 14 文献 标 识 码 : A 文章 编 号 :6 1 6 4 2 1 )4— 0 3— 3 17 —4 4 (0 0 0 0 1 0
基于散乱点云数据的曲面重构方法

重构 , 与通 用 C D C M 系统 中的四边域重构 不兼容 。本 文提 出一种在 三角域上对 散乱点 云数据进 行 N R S曲 A /A UB
面重构 的方法 , 结合 了三角 面片重 构的灵 活性与 N R S曲面重构 的通用性 。首先对 测量 点云数 据进 行 D l ny UB e u a a 三角剖分 , 然后针对三角 网格模 型的数据组织 特点 采用基 于特征 的块边 界扩展 生长 数据分 块方法 进行 网格分块 , 最后通过构造 C os 曲面进行 曲面插值 , 到了 G 连续 的 N R S曲面。 on 基 得 UB
Jn 20 u .0 8
文章编号 :0 6— 4 6 2 0 ) 2— 14— 10 0 5 ( 08 0 0 5 0 4
基 于散 乱 点 云数 据 的 曲面 重构 方 法
吴 禄 慎 , 慧 何
( 昌大学 机 电工程学院 , 西 南昌 303 ) 南 江 30 1
摘要 : 散乱点 云的三维 重构 有广阔的应用前景 , 通用 高效 的重构算法是研究 重点之一 , 目前 大多采用 三角面 片
Ke o ds:u a e r c n t ci n;t a g l t n;NURBS yW r s r c e o sr to f u i r n uai o
基 于散乱点 云数据 的曲面重构技术是逆 向工 程技
术 关注 的主要对 象 , 是逆 向工程 中最重要 和最 困难 也
维普资讯
第3 0卷第 2期
20 0 8年 6月
南 昌 大 学 学 报 ・工科 版
Junl f aca gU i ri ( nier g& T cnlg ora o nhn n esy E g e n N v t n i ehooy
从点云创建曲面
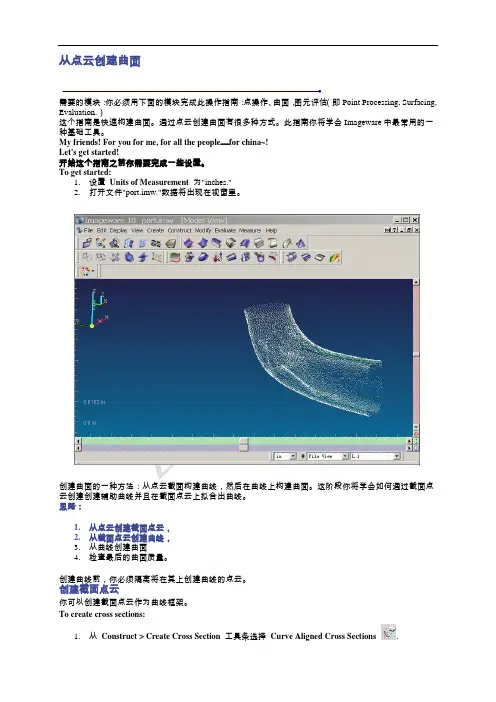
从点云创建曲面需要的模块:你必须用下面的模块完成此操作指南:点操作、曲面,图元评估(即Point Processing, Surfacing, Evaluation.)这个指南是快速构建曲面。
通过点云创建曲面有很多种方式。
此指南你将学会Imageware中最常用的一种基础工具。
My friends! For you for me, for all the people—for china~!Let's get started!开始这个指南之前你需要完成一些设置。
To get started:1.设置Units of Measurement为"inches."2.打开文件"port.imw."数据将出现在视窗里。
创建曲面的一种方法:从点云截面构建曲线,然后在曲线上构建曲面。
这阶段你将学会如何通过截面点云创建创建辅助曲线并且在截面点云上拟合出曲线。
思路:1.从点云创建截面点云,2.从截面点云创建曲线,3.从曲线创建曲面4.检查最后的曲面质量。
创建曲线前,你必须隔离将在其上创建曲线的点云。
创建截面点云你可以创建截面点云作为曲线框架。
To create cross sections:1.从Construct > Create Cross Section工具条选择Curve Aligned Cross Sections.确信数据显示在最佳视角。
本人推荐使用对齐视图到点云:View|Align View To|Cloud. 3. 指定截面类型为 View Aligned (使截面垂直于当前视图,而截面中心在曲线上) 4. 设置截面数为20.(将可能得到20条截面点云)5. 设置截面宽度为 1.65. 接受默认的neighborhood size.(相邻点间的尺寸)6. 点击 Apply 创建了新点云CrvAlignSectCld.1 – 曲线"Seam"2 – 从点云创建的截面点云 "port" 和曲线 "seam"从截面点云创建曲线从点云创建曲线有许多方法,这里将使用Uniform Curve 功能。
面向点云的特征模型重构及其关键算法研究

;b aioar e e ni en df u o poutei i t tnadt a o icl o yr tnle r g ergs iclts w td i v se n i i f t h i o r cds nn ie i , ’ l f u fr: d g gn no n i sdf t i
… … … … ~ … … ~ ■ ^ 1 、 斤 1 . . 、 M ' . ” 、 , ’、 - … 一 喜 ’ .^ ’ . 、 、 ’ … … ● ’、 ^ ● -
【 要】 摘 针对传统逆向工程技术所重构的Br 模型信息表达层次低、 体现设计意图、 -p e 无法 难以 ;
利用随机抽样一致性算法并结合最小二乘法实现拉伸方向
和旋转轴的估算 , 其基本思路是 : 首先估算 点云中各点处的微 分
3点 的微分几何性质估算
1( ) 然后在法矢集合中 点 的微分几何性质估算处于上述特征模型重构策 略的第一 几何 性质并建立如式( )2所示的 目标 函数 ; 反复随机抽取足量 的样本 , 利用最小二乘法来估算 目标函数各参 步, 其下游的点云分区 、 曲面特征重建 、 特征识别等大都依赖于微 即拉伸方 向和旋转轴 ) 的初始值 , 并利用这 些估 算的参数初 分几何性质 的计算结果 , 因此其计算精度尤为重要 。法矢量 和曲 数( 根据是否能满足精度要求, 把法矢集合划分为两个 子集 : 内点 率是点 的两个重要的微 分几何性质 , 目前 , 关于它们 的估算常用 值 ,
★ 来稿 日 :0 0 — 3 ★ 期 2 1- 6 1 基金项 目: 1 华北水利水电学 院青年科研基金资助( S J0 9 2 ) H Q 2 0 0 2
20 2
闫雒 恒 : 面向点云 的特征模型 重构及其 关键 算 法研 究
激光扫描点云数据的NURBS曲面重构技术研究

( U R )方法克服了传统样条 曲线无法完善表达二 NBS 次 曲线 的缺陷 , 能以统一的形式表达二次曲线和 自由 曲线 ,已被广泛应用于复杂曲面造型领域. 作者利用 激光扫描系统获得实物表面原始点云数据 , 利用其数
据特 点 , 出了 N R S曲面 的重构 方 法. 提 UB
激光扫描系统提供 的数据是一个 多行 3列的矩 阵, 为了后续对数据处理 的方便 , 要将提供的数据整
表 面 进 行 高 质 量 的 曲 面 重 构 .非 均 匀 有 理 B样 条
量来计算实物各点的高度分布, 再通过一维步进扫描 测量 , 获取被测实物表面的三维轮廓信息. 因此 , 在测 量时 , 每次投影到实物 表面上 的光刀 , 都将在一个平 面内,采集到 的三维数据有一维是不变的. 这里采用 的激光线结构光扫描系统 ,每次测量时光刀都在 y
收稿 日期 :0 6 0 — 6 2 0 - 2 2
是将 坐标值相 同的数据保存在 同一个数据矩阵 中. 排序是 将拼 接后 的数据 矩 阵 中的元 素顺序 按 照 Y的坐 标值升序排列. 由于激光扫描系统的 C D视场范围有 C
基金项目:塞自 K 垦助项目( 资 签 学基金资助项目 525 0, 南省杰出青年 (0 1 )湖 72 基金资助项目 0J B0) (2YO9, J 机械没 备健康维护湖南省重点实验室开放基金
参7 .
关 键词 : 求 工 程 ; 面重 构 ; 光扫 描 ; 反 曲 激 NURB S
中图分类号 : P 9 T 31
文献标识 码: A
文章编号 :6 2 9 0 ( 06 0 — 0 1 0 17 — 12 2 0 )3 0 3 — 4
近年来 , 随着计 算机视觉 、 数字 图像处理 以及计 算机辅助几何设计技术的不断发展 , 反求工程作为快 速设计与制造 的主要技术之一 , 成为了研究与应用的 热点. 已广泛地应用于飞机 、 车 、 它 汽 船舶 、 具等领 模 域. 依据测量所获得 的海量点云数据重构实物模型是 反求工程的关键技术 , 几何形状反求 , 首先要求快速 、 准确地获取实物表 面的原始数据 , 即实物表面的数字 化 , 后 在 获 得 实 物 表 面 原 始 数 据 的基 础 上 , 实 物 然 对
几何特征形状匹配算法在三维视觉中的应用
几何特征形状匹配算法在三维视觉中的应用近年来随着科技的不断进步,人们在计算机视觉方面的研究也变得越来越深入。
其中,几何特征形状匹配算法在三维视觉中的应用受到了广泛的关注。
本文将着重探讨这一算法在三维视觉领域中的特点及应用。
一、几何特征形状匹配算法几何特征形状匹配算法主要是基于几何属性而非图像属性进行模型匹配。
该算法可以用于三维模型中几何特征的比对和匹配,常见的例子包括基于点、线、面、曲面等几何特征的匹配。
该算法不依赖于视角、光照等因素,可以实现较为鲁棒的匹配,是三维视觉领域中的重要算法之一。
由于三维模型存在多种表示方法,如点云、网格、B样条曲线等,几何特征形状匹配算法的实现也各不相同。
例如点云匹配算法主要是基于距离度量的,而网格匹配算法则是基于曲面拓扑特性的。
具体而言,点云匹配算法主要包括ICP算法、PCA算法等;网格匹配算法则包括基于手工特征、特征描述子、特征级联等方法。
二、几何特征形状匹配算法在三维视觉中的应用几何特征形状匹配算法在三维视觉领域中的应用非常广泛,下面将以几个典型的应用场景为例。
1、三维重建三维重建是利用多张2D图像或基于点云数据,生成一个三维模型的过程。
几何特征形状匹配算法可以通过点云匹配实现不同视角下点云数据的融合,进而得到更为准确的三维重建结果。
例如,在建筑物测绘、文物保护等领域经常使用该算法实现三维重建。
2、物体检测与识别在物体检测和识别方面,几何特征形状匹配算法可以通过模板匹配实现不同形状物体的检测和识别。
例如,在工业领域可以通过对机器零部件、轮廓、边缘等几何特征进行匹配,实现不同类工件的分类和识别。
3、机器人视觉在机器人视觉领域,几何特征形状匹配算法可以帮助机器人识别周围环境的几何特征,从而进行路径规划、定位以及姿态控制等任务。
例如,在视觉引导、物品抓取等方面经常将该算法作为视觉导引的重要手段。
三、几何特征形状匹配算法的应用前景随着计算机视觉技术的不断深入和发展,几何特征形状匹配算法的应用前景也越来越广泛。
web环境下三维点云数据轻量化处理与模型重构方法
web环境下三维点云数据轻量化处理与模型重构方法汇报人:2023-12-12•三维点云数据概述•三维点云数据的轻量化处理•三维点云模型的重构方法目录•三维点云数据轻量化处理与模型重构的挑战与未来发展•应用案例分析01三维点云数据概述特点数据量大:通常包含成千上万个点。
结构复杂:点云数据结构复杂,需要专业的处理和分析方法。
高维度:每个点具有x、y、z三个坐标值,以及颜色、反射强度等附加信息。
定义:三维点云数据是指通过三维扫描、激光雷达等技术获取的物体表面空间坐标点的集合。
三维点云数据的定义与特点使用专业的三维扫描设备对物体进行扫描,获取物体表面的空间坐标。
三维扫描仪激光雷达图像三维重建利用激光雷达技术,对物体进行照射并分析反射光束,从而获取物体表面的空间坐标。
通过多视角图像获取物体表面信息,利用三维重建算法生成点云数据。
030201工业制造用于检测、测量、建模等工业生产流程中的质量控制和生产管理。
文化传承对历史文物和文化遗产进行数字化保存和保护,以及进行三维重建和虚拟展示。
游戏娱乐在游戏开发中用于角色建模、场景渲染等,提高游戏的真实感和沉浸感。
智能感知用于机器视觉、自动驾驶等领域,进行物体识别、跟踪和姿态估计等任务。
02三维点云数据的轻量化处理压缩算法采用无损压缩算法,如LZMA、Deflate等,对三维点云数据进行压缩,以减小数据大小和存储空间。
压缩效果通过比较压缩前后的数据大小和重构模型的质量评估压缩效果,通常以压缩比、重构模型误差等指标进行评价。
采用表面重建算法,如Poisson表面重建、Ball Pivoting等,将三维点云数据简化为更小的数据集,以减小数据大小和存储空间。
通过比较简化前后的数据大小和重构模型的质量评估简化效果,通常以数据量减少率、重构模型误差等指标进行评价。
简化效果数据简化算法采用编码算法,如Run-length encoding、Delta encoding 等,对三维点云数据进行编码,以减小数据大小和存储空间。
基于GeomagicStudio的曲面重构过程
曲面重构处理流程学号:班级:11材型(卓越)-1班时间:2014年12月目录一、点处理阶段 (2)二、多边形处理阶段 (7)三、参数化曲面 (11)、点处理阶段1. 打开素材文件。
启动Geomagic studio12软件后,点击I【打开】选择“swug3-1 ”文件如图图12. 着色点击点工具栏的也,系统将自动计算点云的法向量,赋予点云颜色3. 断开组件连接点击点工具栏的断开组件连接图标,弹出选择非连接选项的对话框,在“分隔”选择“低”,然后点击确定。
退出对话框后按Delete删除选中的非连接点云4. 选择体外孤点。
点击点工具栏的体外孤点图标,弹出体外孤点对话框,将敏感性设置为100图5点击应用后确定,按Delete删除选中的红色点云,该命令使用3次。
5. 手动删除。
点击矩形选择工具图标,进入矩形工具的选择状态,改变模型的视图(按住中间旋转),在视窗点击一个点,按住鼠标左键进行拖动框选,如图所示。
按Delete 删除选中的红色杂点許.jiitt ril t—.fUAHPM ]■ Mt i z ・ r-M IJU -I -MV P ■* V z ; 1」 'V I >R 3 Uu|F6. 减少噪音弓"J I定。
该命令有助于减少在扫描中的噪音点到最小,更好地表现真实的物体形状造成噪音点的原因可能是扫描设备轻微震动、物体表面较差、光线变化。
统一采样。
点击点工具栏的统一采样图标也■,进入统一采样对话框,在输入中选择绝对间距里输入0.2mm,曲率优先拉到中间,点击应用后确定。
在保留物体原来面貌的同时减少点云数量,便于删除重叠点云、稀释点云点击点工具栏的减少噪音图标,进入减少噪音对话框,点击应用后确:=A* n Ai^iEia.««图98. 封装。
点击点工具栏的封装图标,进入封装对话框,直接点击确定,软件将自动计算。
该命令将点转换成三角面。
图10、多边形处理阶段1.打开素材文件。
alpha_shape算法原理文献
Alpha_shape算法原理简介一、概述1.1 算法概述Alpha_shape算法是一种用于处理多维点云数据的几何算法,它可以用来构建点云的凸壳或非凸壳,并且在三维空间中可以用来构建曲面。
1.2 发展历史Alpha_shape算法最早由Edelsbrunner等人于1983年提出,最初被应用于计算凸多面体的体积和表面积。
随后,在几何建模、CAD、地理信息系统等领域得到了广泛的应用。
二、算法原理2.1 Delaunay三角剖分在介绍Alpha_shape算法之前,我们需要了解一下Delaunay三角剖分。
Delaunay三角剖分是对给定的点云进行连接构成的三角形网络,满足以下性质:任意一个三角形的外接圆内不包含其他点。
Delaunay三角剖分的性质决定了其在构建Alpha_shape时的重要性。
2.2 Alpha_shape构建Alpha_shape通过调整参数alpha,从而构建不同形状的凸壳。
当alpha为正无穷时,得到的凸壳即为点云的凸包;当alpha为负无穷时,得到的凸壳即为点云的凸壳。
通过不同的alpha值,可以得到点云的不同形状的凸壳。
2.3 四面体化Alpha_shape算法还涉及到四面体化的概念,其作用是构建点云的三维曲面。
四面体化的目标是找到一组四面体,这些四面体的外接球没有包含点云中的其他点,从而形成点云的几何模型。
三、算法实现3.1 使用现有库实现目前,Alpha_shape算法已经有很多成熟的开源库可以进行实现,如CGAL库、Open3D库等。
通过这些库,可以很方便地实现Alpha_shape算法,从而应用于实际的点云数据处理中。
3.2 自行实现如果需要根据具体业务需求对Alpha_shape进行定制化,也可以选择自行实现该算法。
通常采用C++、Python等语言进行实现,并且需要对Delaunay三角剖分、四面体化等基础算法有一定的了解。
四、应用领域4.1 地理信息系统在地理信息系统中,Alpha_shape算法被广泛用于地形分析、地下水模拟等领域,用来构建地理空间数据的三维曲面模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3 6卷 第 1 期 3
L3 6
计
算
机
工
程
21 0 0年 7月
J y 01 ul 2 0
No 13 .
C o pu e m t rEng ne r ng i ei
・图形 图像 处理 ・
文章 编号:l ( 2( 1 l— l4 3 文献 0 卜 8 00 3 09 0 4 2 ) — 标识码: A
理想 。
否 则 P 可 能 是 边 界 点 。判 断 点 P 是 内 部点 还 是 边界 点 的方 法 如 下 : 先 将 K Pp) 的点 投 影 到 由这 些 点 确 定 的最 小 二 乘 首 N ( 中 平 面 pae 上 , q为 点 p 在 pae f上 的 投 影 , N ( ) 】l ( ) 记 i np , l () np K Pq 为 K Pp) 平 面 上 的投 影 。 失 一 般性 , N ( 在 不 假定 gl K Pq) f 为 N( f
[ ywod lp i lu ; s c nt cin cas ct n g o ti sa efa r Ke r s on c d mehr o s ut ; l i ai ; e me c h p t e to e r o sf o i r; eu
1 概述
在计算机 图形学、计算机辅助设计及 计算机视觉 中的大 量应用涉及 曲面重构问题。 目前 ,学者们 已经提 出很多 曲面 重构 的算法 ,大致分为 以下 3类 :() 1基于 D l ny的算法 : e ua a 该类算法首先建立点云 D lu a 三 角化 , ean y 然后抽取表示模型 形状三角面片 ,如 Ⅱsae rs 一hp 、cut算法等 。() 2基于隐函数的 算法 :该类算法使用隐函数来表示 曲面 。通过泊松公式得到 隐函数, 通过移动最小二乘法计算隐函数 J () 区域增 。。 3基于 长的算法 :该类算法首先构造种子三角形 ,然后从种子三角 形开始,逐渐添加新 的三角形到部分重构的网格 中。 文献[] 3算法根据点云的固有特性来选择新 的点。 文献[] 4 算法首先根据点的局部几何分布把 点云分成几类 ,然后对 不 同 的点 采 用 不 同 的方 法 进 行 重 构 。它 们 在 平 滑 的 区 域 能取 得 很好的效果 ,但在形状特征 比较复杂的一些区域效果不是很
形状特征进行分类 ,对每类点进行局部网格重构 ,并进行后续处理以修补拓扑和几何错误 。实验 结果表 明,该算法强健 有效 ,能生成高质 量 的网格 ,并能较好地保持模型 的几何与形状特征。
关健诃 :点云;曲面重构 ;分类 ;几何 ;形状特征
M e h Re o s r to g rt m s d o o e rca s c n t uc i n Al o ih Ba e n Ge m t i nd S peFe t eo i tCl ud ha a ur fPo n o
中圈分类号l P 15 31 2 T .
基 于 点云 几何 与形 状 特Байду номын сангаас 的 曲面 重构 算 法
肖 华 ,张三元 ,张 引
( 江 大 学 计 算 机 科 学 与 技 术 学 院 ,杭 州 3 0 2 ) 浙 10 7
擅
妥 :提出一种新 的利用点云进行曲面重构 的算法 ,该算法基于点 云的几何与形状特征 , 根据点云 的几何分布进行分类和按照点的局部
X I O ua A H ,ZH AN G n— uan, Sa y ZH A NG i Y n
( ol eo mp t c neadT cn lg, hj n nv ri , a gh u3 2 ) C l g f e Co ue S i c n ehoo yZ ei gU iesy H n zo 10 7 r e a t 0 [ b tat o e mehrcnt cinag rh s gp it lu rsne h rpsdag rh ae ngo tcadsaefa r A src]An v l s o s ut loi m ui on o dipee td T epo o e loi m ib sdo e me i n p t e e r o t n c s t s r h eu
