北京市西城区2011年高三一模数学文参考答案
2024年北京市西城区高三一模数学答案

2024.4 第1页(共6页)西 城 区 高 三 统 一 测 试 试 卷数学答案及评分参考 2024.4一、选择题(共10小题,每小题4分,共40分) ( 1 )B ( 2 )D ( 3 )A ( 4 )C ( 5 )C( 6 )A( 7 )A( 8 )B( 9 )D(10)C二、填空题(共5小题,每小题5分,共25分)(11(12)π3 π3(答案不唯一) (13)y =(14)6−n 13−(15)① ③ ④三、解答题(共6小题,共85分) (16)(共14分) 解:(Ⅰ)连接1A B ,设11A BAB E =,连接DE .………1分因为在三棱柱111ABC A B C −中,四边形11A ABB 是平行四边形, 所以E 为1A B 的中点.………2分因为D 为BC 的中点, 所以1//DE A C .………3分又因为1A C ⊄平面1AB D ,⊂DE 平面1AB D , 所以1//AC 平面1AB D . ………5分(Ⅱ)因为1AB AC ⊥,AB AC ⊥,所以AB ⊥平面11A ACC .………6分所以1AB AA ⊥.又1AA AC ⊥,所以1,,AB AC AA 两两相互垂直. 如图建立空间直角坐标系A x yz −.………7分 则(0,0,0)A ,1(2,0,2)B ,(1,1,0)D ,(0,2,0)C . 所以1(,,)202AB =,(,,)110AD =.2024.4 第2页(共6页)设平面1AB D 的法向量为(,,)x y z =m ,则10,0,AB AD =⎧⎪⎨=⎪⎩⋅⋅m m 即220,0.x z x y +=⎧⎨+=⎩令1x =−,则1y =,1z =.于是(1,1,1)=−m . ………10分因为AC ⊥平面11A ABB ,所以(0,2,0)AC =是平面11A ABB 的一个法向量. ………11分 所以3cos ,3||||AC AC AC 〈〉==⋅m m m .………13分由题设,二面角11D ABA −−的平面角为钝角, 所以二面角11D AB A −−的余弦值为 ………14分(17)(共13分)解:(Ⅰ)由tan 2sin a B b A =,得sin 2sin cos a B b A B =.………1分 在ABC △中,由正弦定理得sin sin 2sin sin cos A B A B B =.………3分因为sin 0,sin 0A B >>, 所以1cos 2B =. ………4分 又0πB <∠<, ………5分 所以π3B ∠=.………6分 (Ⅱ)选条件①:BC………7分设BC 边中点为M ,连接AM ,则AM =,4BM =.在ABM △中,由余弦定理得2222cos AM AB BM AB BM B =+−⋅⋅,………9分 即2π21168cos3AB AB =+−⋅. 整理得2450AB AB −−=. 解得5AB =或1AB =−(舍).………11分 所以ABC △的面积为1sin 2ABC S AB BC B =⋅⋅=△.………13分2024.4 第3页(共6页)选条件③:7b =.………7分 在ABC △中,由余弦定理得2222cos b a c ac B =+−,………9分即222π7816cos3c c =+−⋅. 整理得28150c c −+=. 解得3c =或5c =.………11分当3c =时,ABC △的面积为1sin 2ABC S ac B ==△ 当5c =时,ABC △的面积为1sin 2ABC S ac B ==△.………13分(18)(共13分)解:(Ⅰ)甲进入决赛,理由如下:丙射击成绩的总环数为26471081892610542⨯+⨯+⨯+⨯+⨯=,甲射击成绩的总环数为16171082492410549⨯+⨯+⨯+⨯+⨯=. 因为549542>,所以甲进入决赛.………3分(Ⅱ)根据题中数据,“甲命中9环”的概率可估计为242605=; “甲命中10环” 的概率可估计为242605=; “乙命中9环” 的概率可估计为301602=; “乙命中10环” 的概率可估计为151604=.………5分所以这4次射击中出现2个“9环”和2个“10环”的概率可估计为:222212122212121113()()()()C ()C ()5452524100⨯+⨯+⨯⨯=. ………10分 (Ⅲ)7a =和8.(写出一个即可)………13分2024.4 第4页(共6页)(19)(共15分)解:(Ⅰ)由题设,2222,1,2.a c a abc =⎧⎪⎪=⎨⎪⎪−=⎩………3分解得224,3a b ==.所以椭圆G 的方程为22143x y +=. ………5分(Ⅱ)由题设,直线l 的斜率存在,设其方程为y kx m =+.则(2,2)E k m +,直线OE 的方程为()2my k x =+. ………6分 由22,3412,y kx m x y =+⎧⎨+=⎩ 得222(43)84120k x kmx m +++−=.………7分由2248(43)0=−+>Δk m ,得2243<+m k .设11(,)C x y ,22(,)D x y ,则122843kmx x k +=−+,212241243m x x k −=+. ………8分直线AC 的方程为11(2)2yy x x =++. ………9分联立直线AC 和OE 得11(2)()22y mx k x x +=++. 解得1111111244()44()(2)2M y y kx m x mmx k mx kk x y +===++++−.………11分同理可得224()4N kx m x mx k +=+.所以122112()(4)()(4)4(4)(4)M N kx m mx k kx m mx k x x mx k mx k ++++++=⨯++.………12分因为1221()(4)()(4)+++++kx m mx k kx m mx k22121222222222(4)()82(412)8(4)8(43)4343430kmx x k m x x kmkm m km k m km k k k k =++++−++=−++++=,所以0M N x x +=,即点M 和点N 关于原点O 对称. 所以||||=OM ON .………15分2024.4 第5页(共6页)(20)(共15分)解:(Ⅰ)当1a =时,()ln e =++x f x x x x ,所以1()1(1)e '=+++x f x x x. ………2分所以(1)2e 2f '=+.所以曲线()y f x =在点(,())11f 处切线的斜率为2e 2+.………4分(Ⅱ)当1a =−时,()ln()e =+−−x f x x x x ,()f x 的定义域为(,0)−∞.11()1(1)e (1)(e )'=+−+=+−x x f x x x x x. ………6分因为1e 0xx−<, 所以(,1)x ∈−∞−时,()0f x '>;(1,0)x ∈−时,()0f x '<.所以()f x 的单调递增区间为(,1)−∞−;单调递减区间为(1,0)−. ………9分 (Ⅲ)1e ()(1)()'=++xf x x x a.当0a >时,()f x 的定义域为(0,)+∞. 所以()0'>f x ,()f x 在(0,)+∞上单调递增.因为1()0>f a ,所以0a >不合题意.………11分当0a <时,()f x 的定义域为(,0)−∞.因为(,1)x ∈−∞−时,()0f x '>;(1,0)x ∈−时,()0f x '<. 所以()f x 的单调递增区间为(,1)−∞−;单调递减区间为(1,0)−. 所以max 1()(1)1ln()e=−=−+−−f x f a a . ………13分设1()1ln()e =−+−−g x x x ,则2211e 1()e e +'=+=x g x x x x , 因为1(,)e ∈−∞−x 时,()0'<g x ;1(,0)e∈−x 时,()0'>g x ,所以()g x 的单调递减区间为1(,)e −∞−;单调递增区间为1(,0)e −.所以min 1()()1e=−=−g x g .所以集合{|()1}−≥x f x 有且只有一个元素时1ea =−.………15分2024.4 第6页(共6页)(21)(共15分) 解:(Ⅰ)记1122i i i n in t a b a b a b =+++.因为1233,2,0t t t ===, ………3分 所以2=K .………4分(Ⅱ)(ⅰ)B 不满足3m r =,理由如下:假设B 满足3m r =.因为B 的每行恰有三个1,故B 中满足1==i p i q b b 的(,,)i p q 的个数共有3m 个. 另一方面,从B 中任选两列共有2C n 种可能,且对任意两列,都恰有r 行使得 这两列的数均为1,故B 中满足1==i p i q b b 的(,,)i p q 的个数共有2C n r 个. 所以23C n m r =.当3m r =时,得2C 9n =,此方程无解. 所以B 不满足3m r =.………9分(ⅱ)由(ⅰ)可得23C nm r =,即2C 3nr m =.下面考虑满足1==i p i q b b ,但p q a a ≠的(,,)i p q 的个数:对B 中满足0≠i t 和3的−m K 行,每行恰有两组(,)p q 使1==i p i q b b 且p q a a ≠,所以满足1==i p i q b b ,但p q a a ≠的(,,)i p q 的个数为2C 2()2()3−=−n r m K K .………11分设数列A 中有x 项为1,−n x 项为0.满足1==i p i q b b ,但p q a a ≠的(,)p q 的个数为()−x n x . 所以满足1==i p i q b b ,但p q a a ≠的(,,)i p q 的个数为()−rx n x .………13分所以2C ()2()3−=−n r rx n x K .所以222C ()(33)326−=−=−+−nr rx n x r K x nx n n 22222331()()(4)6426424−+−=−−≥≥r n n r n n n n n n . ………15分。
北京市西城区高三一模(数学理)(西城一模)
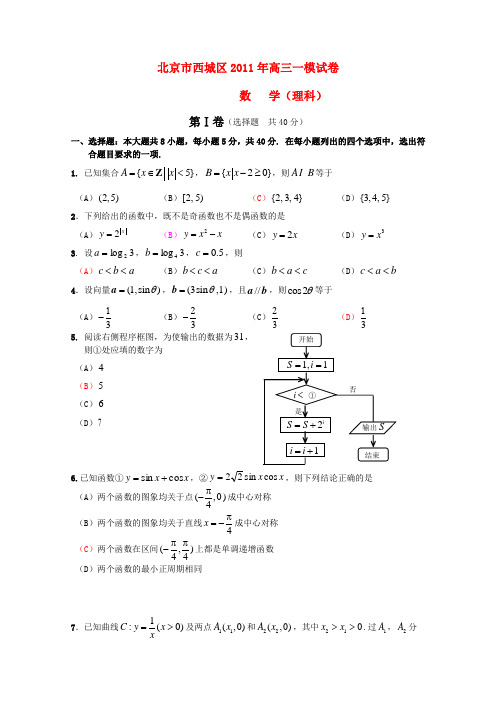
北京市西城区2011年高三一模试卷数 学(理科) 第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分. 在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知集合{5}A x x =∈<Z ,{20}B x x =-≥,则AB 等于 (A )(2,5) (B )[2,5) (C ){2,3,4}(D ){3,4,5} 2.下列给出的函数中,既不是奇函数也不是偶函数的是(A )2x y = (B )2y x x =- (C )2y x = (D )3y x =3. 设3log 2=a ,3log 4=b ,5.0=c ,则(A )a b c << (B )b c a << (C )c a b << (D )b a c <<4.设向量(1,sin )θ=a ,(3sin ,1)θ=b ,且//a b ,则cos 2θ等于(A )31- (B )32- (C )32 (D )31 5. 阅读右侧程序框图,为使输出的数据为31,则①处应填的数字为(A )4(B )5(C )6(D )76.已知函数①x x y cos sin +=,②x x y cos sin 22=,则下列结论正确的是(A )两个函数的图象均关于点(,0)4π-成中心对称 (B )两个函数的图象均关于直线4x π=-成中心对称 (C )两个函数在区间(,)44ππ-上都是单调递增函数 (D )两个函数的最小正周期相同7.已知曲线1:(0)C y x x=>及两点11(,0)A x 和22(,0)A x ,其中210x x >>.过1A ,2A 分别作x 轴的垂线,交曲线C 于1B ,2B 两点,直线12B B 与x 轴交于点33(,0)A x ,那么(A )312,,2x x x 成等差数列 (B )312,,2x x x 成等比数列 (C )132,,x x x 成等差数列 (D )132,,x x x 成等比数列8.如图,四面体OABC 的三条棱OC OB OA ,,两两垂直,2==OB OA ,3=OC ,D 为四面体OABC 外一点.给出下列命题.①不存在点D ,使四面体ABCD 有三个面是直角三角形②不存在点D ,使四面体ABCD 是正三棱锥③存在点D ,使CD 与AB 垂直并且相等④存在无数个点D ,使点O 在四面体ABCD 的外接球面上其中真命题的序号是(A )①② (B )②③ (C )③ (D )③④第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.9. 在复平面内,复数2i 1i -对应的点到原点的距离为_____. 10.如图,从圆O 外一点P 引圆O 的切线PA 和割线PBC ,已知PA =4PC =,圆心O 到BC圆O 的半径为_____.11.已知椭圆:C cos ,()2sin x y θθθ=⎧∈⎨=⎩R 经过点1(,)2m ,则m =______,离心率e =______. 12.一个棱锥的三视图如图所示,则这个棱锥的体积为_____.13.某展室有9个展台,现有3件展品需要展出,要求每件展品独自占用1个展台,并且3件展品所选用的展台既不在两端又不相邻,则不同的展出方法有______种;如果进一步要求3O A B DC 正(主)视图 俯视图侧(左)视图件展品所选用的展台之间间隔不超过两个展位,则不同的展出方法有____种.14.已知数列{}n a 的各项均为正整数,对于⋅⋅⋅=,3,2,1n ,有1135,2n n n n n n kk a a a a a a +++⎧⎪=⎨⎪⎩为奇数为偶数.其中为使为奇数的正整数,, 当111a =时,100a =______;若存在*m ∈N ,当n m >且n a 为奇数时,n a 恒为常数p ,则p 的值为______.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(本小题满分13分)设ABC ∆中的内角A ,B ,C 所对的边长分别为a ,b ,c ,且54cos =B ,2=b . (Ⅰ)当35=a 时,求角A 的度数; (Ⅱ)求ABC ∆面积的最大值.16.(本小题满分13分) 甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为11,,23p .且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为14. (Ⅰ)求甲乙二人中至少有一人破译出密码的概率;(Ⅱ)求p 的值;(Ⅲ)设甲、乙、丙三人中破译出密码的人数为X ,求X 的分布列和数学期望EX .17.(本小题满分13分)如图, ABCD 是边长为3的正方形,DE ⊥平面ABCD ,DE AF //,AF DE 3=,BE 与平面ABCD 所成角为060.(Ⅰ)求证:AC ⊥平面BDE ;(Ⅱ)求二面角D BE F --的余弦值;(Ⅲ)设点M 是线段BD 上一个动点,试确定点M 的位置,使得//AM 平面BEF ,并证明你的结论.18. (本小题满分14分) 已知函数2(1)()a x f x x -=,其中0a >. A B C D F E(Ⅰ)求函数()f x 的单调区间;(Ⅱ)若直线10x y --=是曲线()y f x =的切线,求实数a 的值;(Ⅲ)设2()ln ()g x x x x f x =-,求()g x 在区间[1,e ]上的最大值.(其中e 为自然对数的底数)19. (本小题满分14分)已知抛物线22(0)y px p =>的焦点为F ,过F 的直线交y 轴正半轴于点P ,交抛物线于,A B 两点,其中点A 在第一象限.(Ⅰ)求证:以线段FA 为直径的圆与y 轴相切;(Ⅱ)若1FA AP λ=,2BF FA λ=,1211[,]42λλ∈,求2λ的取值范围.20.(本小题满分13分)定义=),,,(21n a a a τ12231||||||n n a a a a a a --+-++-为有限项数列{}n a 的波动强度.(Ⅰ)当(1)n n a =-时,求12100(,,,)a a a τ;(Ⅱ)若数列,,,a b c d 满足()()0a b b c -->,求证:(,,,)(,,,)a b c d a c b d ττ≤; (Ⅲ)设{}n a 各项均不相等,且交换数列{}n a 中任何相邻两项的位置,都会使数列的波动强度增加,求证:数列{}n a 一定是递增数列或递减数列.。
2011年北京市各区一模数学试题分类解析(17):几何证明选讲

A 十七、几何证明选讲
1(2011西城一模理10).如图,从圆O 外一点P 引圆O 的切线PA 和割线PBC ,
已知PA =4PC =,圆心O 到BC
则圆O 的半径为__2___. 2(2011东城一模理12)如图,已知圆O 的半径为3,从圆O 外一点A 引切线AD 和
割线
ABC ,圆心O 到AC 的距离为22,3AB =,则切线AD 的长为
4.(
2011朝阳一模理13)如下图,在圆内接四边形ABCD 中, 对角线, AC BD 相交于
点E .已知BC CD ==2
AE EC =,30CBD ∠=, 则CAB ∠= 30 ,AC 的长是 6 .
5(2011丰台一模理12).如图所示,过⊙O 外一点A 作一条直线与⊙O 交于C ,D 两点,AB 切⊙O 于B ,弦MN 过CD 的中点P .已知AC =4,AB =6,则MP ·NP = 25
4
.
6(2011海淀一模理11).如图,A ,B ,C 是⊙O 上的三点,BE 切⊙O 于点B , D 是CE 与
⊙O 的交点.若︒
=∠70BAC ,则=∠CBE __70____;若2=BE ,4
=CE ,
则=CD
3
.
B
7(2011门头沟一模理11).如上右图:AB 是
O 的直径,点P 在AB 的延长线上,且2PB OB ==,PC
切O 于点C ,CD AB ⊥于点D ,则PC =
CD =
8(2011石景山一模理12).如图,圆O 的直径8=AB ,C 为圆周上一点,4=BC ,过C 作圆的切线l ,
过A 作直线l 的垂线AD ,D 为垂足,AD 与圆O 交于点E ,则线段AE 的长为 4
.
A
P。
(全优试卷)北京市西城区高三一模考试数学(文)试题 Word版含答案

西城区高三统一测试数学(文科) 2017.4第Ⅰ卷(选择题 共40分)一、 选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知全集{1,2,3,4,5,6}U =,集合{1,3,5}A =,{1,4}B =,那么U A B =ð(A ){3,5} (B ){2,4,6} (C ){1,2,4,6} (D ){1,2,3,5,6}2.在复平面内,复数1ii+的对应点位于 (A )第一象限 (B )第二象限 (C )第三象限(D )第四象限3.双曲线2213x y -=的焦点坐标是(A ),(0, (B ),( (C )(0,2),(0,2)-(D )(2,0),(2,0)-4.函数21()()log 2x f x x =-的零点个数为 (A )0(B )1(C )2 (D )35.函数()f x 定义在(,)-∞+∞上.则“曲线()y f x =过原点”是“()f x 为奇函数”的 (A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件(D )既不充分也不必要条件6.在ABC △中,点D 满足3BC BD −−→−−→=,则(A )1233AD AB AC −−→−−→−−→=+(B )1233AD AB AC −−→−−→−−→=-(C )2133AD AB AC −−→−−→−−→=+ (D )2133AD AB AC −−→−−→−−→=-7.在正方形网格中,某四面体的三视图如图所示.如果小 正方形网格的边长为1,那么该四面体最长棱的棱长为 (A) (B )6 (C) (D)8.函数()f x 的图象上任意一点(,)A x y 的坐标满足条件||||x y ≥,称函数()f x 具有性 质P .下列函数中,具有性质P 的是 (A )2()f x x = (B )21()1f x x =+ (C )()sin f x x = (D )()ln(1)f x x =+第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9.函数()f x 的定义域为____. 10.执行如图所示的程序框图. 当输入1ln 2x =时,输出的y 值为____.11.圆22:2210C x y x y +--+=的圆心坐标是____;直线 :0l x y -=与圆C 相交于,A B 两点,则||AB =____. 12.函数sin4()1cos4xf x x=+的最小正周期是____.13.实数,x y 满足1,2,220,x y x y ⎧⎪⎨⎪+-⎩≤≤≥则22x y +的最大值是____;最小值是____.14. 如图,正方体1111ABCD A B C D -的棱长为2,点P 在正方形ABCD 的边界及其内部运动.平面区域W 由所有满足1A P P 组成,则W 的面积是____.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤.15.(本小题满分13分)已知{}n a 是等比数列,13a =,424a =.数列{}n b 满足11b =,48b =-,且{}n n a b +是等差数列.(Ⅰ)求数列{}n a 和{}n b 的通项公式; (Ⅱ)求数列{}n b 的前n 项和.16.(本小题满分13分)在△ABC 中,角,,A B C 的对边分别为,,a b c ,且tan 2sin a C c A =. (Ⅰ)求角C 的大小;(Ⅱ)求sin sin A B +的最大值. 17.(本小题满分13分)在测试中,客观题难度的计算公式为ii R P N=,其中i P 为第i 题的难度,i R 为答对该题的人数,N 为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:题号 1 2 3 4 5 考前预估难度i P0.90.80.70.60.4测试后,从中随机抽取了10名学生,将他们编号后统计各题的作答情况,如下表所示(“√”表示答对,“×”表示答错):学生编号 题号123 4 5 1 ×√ √ √ √2 √ √ √ √ ×3 √ √ √ √× 4 √ √ √ ××5 √ √√√ √6 √××√ × 7 ×√√√× 8 √ ×× × × 9 √ √ ××× 10√√√√×(Ⅰ)根据题中数据,将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表,并估计这120名学生中第5题的实测答对人数;题号 1 2 3 4 5 实测答对人数 实测难度(Ⅱ)从编号为1到5的5人中随机抽取2人,求恰好有1人答对第5题的概率; (Ⅲ)定义统计量22211221[()()()]n n S P P P P P P n'''=-+-++-,其中i P '为第i 题的实测难度,i P 为第i 题的预估难度(1,2,,)i n =.规定:若0.05S <,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.18.(本小题满分14分)如图,在四棱锥P ABCD -中,底面ABCD 为正方形,PA ⊥底面ABCD ,PA AC =.过点A 的平面与棱,,PB PC PD 分别交于点,,E F G (,,E F G 三点均不在棱的端点处).(Ⅰ)求证:平面PAB ⊥平面PBC ;(Ⅱ)若PC ⊥平面AEFG ,求PFPC的值; (Ⅲ)直线AE 是否可能与平面PCD 平行?证明你的结论.19.(本小题满分14分)如图,已知椭圆2222:1(0)x y C a b a b +=>>的离心率为12,F 为椭圆C 的右焦点.(,0)A a -, ||3AF =.(Ⅰ)求椭圆C 的方程;(Ⅱ)设O 为原点,P 为椭圆上一点,AP 的中点为M .直线OM 与直线4x =交于点D ,过O 作OE DF ⊥,交直线4x =于点E .求证://OE AP .20.(本小题满分13分)已知函数21()e 2xf x x =-.设l 为曲线()y f x =在点00(,())P x f x 处的切线,其中0[1,1]x ∈-.(Ⅰ)求直线l 的方程(用0x 表示);(Ⅱ)求直线l 在y 轴上的截距的取值范围;(Ⅲ)设直线y a =分别与曲线()y f x =和射线1([0,))y x x =-∈+∞交于,M N 两点,求||MN 的最小值及此时a 的值.西城区高三统一测试高三数学(文科)参考答案及评分标准2017.4一、选择题:本大题共8小题,每小题5分,共40分.1.A 2.D 3.C 4.B 5.B 6.C 7.B 8.C二、填空题:本大题共6小题,每小题5分,共30分.9.{|0x x ≥,且1}x ≠ 10.1211.(1,1);212.π2 13.5;4514.π44-注:第11,13题第一空2分,第二空3分.三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分)解:(Ⅰ)设等比数列{}n a 的公比为q ,由题意得3418a q a ==, 解得 2q =. [ 2分]所以 11132(1,2,)n n n a a q n --=⋅=⋅=. [ 4分]设等差数列{}n n a b +的公差为d ,由题意得4411()()1644413a b a b d +-+-===-. [ 6分]所以 11()(1)4n n a b a b n d n +=++-=. [ 8分]从而 1432(1,2,)n n b n n -=-⋅=. [ 9分](Ⅱ)由(Ⅰ)知1432(1,2,)n n b n n -=-⋅=.数列{4}n 的前n 项和为2(1)n n +;数列1{32}n -⋅的前n 项和为3(21)n ⋅-.[12分]所以,数列{}n b 的前n 项和为 222323n n n +-⋅+. [13分]16.(本小题满分13分)解:(Ⅰ) 由 tan 2sin a C c A =,得sin 2sin cos a CA c C⋅=. [ 1分]由正弦定理得sin sin 2sin sin cos A CA C C⋅=. [ 3分]所以 1cos 2C =. [ 4分]因为 (0,π)C ∈, [ 5分]所以 π3C =. [ 6分](Ⅱ) sin sin A B +2πsin sin()3A A =+- [ 7分]3sin 2A A = [ 9分]π)6A +. [11分]因为 π3C =,所以 2π03A <<, [12分]所以 当π3A =时,sin sin A B +取得最大值. [13分]17.(本小题满分13分)解:(Ⅰ)每道题实测的答对人数及相应的实测难度如下表:题号 1 2 3 4 5 实测答对人数 8 8 7 7 2 实测难度0.80.80.70.70.2[4分]所以,估计120人中有1200.224⨯=人答对第5题.[ 5分] (Ⅱ)记编号为i 的学生为(1,2,3,4,5)i A i =,从这5人中随机抽取2人,不同的抽取方法有10种.其中恰好有1人答对第5题的抽取方法为12(,)A A ,13(,)A A ,14(,)A A ,25(,)A A ,35(,)A A ,45(,)A A ,共6种. [ 9分]所以,从抽样的10名学生中随机抽取2名答对至少4道题的学生,恰好有1人答对第5题的概率为63105P ==. [10分](Ⅲ)i P '为抽样的10名学生中第i 题的实测难度,用i P '作为这120名学生第i 题的实测难度.222221[(0.80.9)(0.80.8)(0.70.7)(0.70.6)(0.20.4)]5S =-+-+-+-+-0.012=. [12分]因为 0.0120.05S =<,所以,该次测试的难度预估是合理的. [13分]18.(本小题满分14分)解:(Ⅰ)因为PA ⊥平面ABCD ,所以PA BC ⊥. [ 1分] 因为ABCD 为正方形,所以AB BC ⊥, [ 2分] 所以BC ⊥平面PAB . [ 3分] 所以平面PAB ⊥平面PBC . [ 4分](Ⅱ)连接AF . [ 5分]因为 PC ⊥平面AEFG ,所以 PC AF ⊥. [ 7分] 又因为 PA AC =,所以 F 是PC 的中点. [ 8分]所以12PF PC =.[ 9分] (Ⅲ)AE 与平面PCD 不可能平行. [10分]证明如下:假设//AE 平面PCD ,因为 //AB CD ,AB ⊄平面PCD .所以 //AB 平面PCD . [12分] 而 AE AB ⊂,平面PAB ,所以 平面//PAB 平面PCD ,这显然矛盾! [13分] 所以假设不成立,即AE 与平面PCD 不可能平行.[14分]19.(本小题满分14分)解:(Ⅰ)设椭圆C 的半焦距为c .依题意,得12c a =,3a c +=. [ 2分] 解得 2a =,1c =.所以 2223b a c =-=,所以椭圆C 的方程是 22143x y +=. [ 5分](Ⅱ)解法一:由(Ⅰ)得 (2,0)A -.设AP 的中点00(,)M x y ,11(,)P x y .设直线AP 的方程为:(2)(0)y k x k =+≠,将其代入椭圆方程,整理得2222(43)1616120k x k x k +++-=, [ 7分]所以 21216243k x k --+=+. [ 8分]所以 202843k x k -=+,0026(2)43k y k x k =+=+,即 22286(,)4343k kM k k -++. [ 9分]所以直线OM 的斜率是22263438443k k k k k +=--+, [10分]所以直线OM 的方程是 34y x k =-.令4x =,得3(4,)D k-. [11分] 由(1,0)F ,得直线DF 的斜率是 3141k k-=--, [12分]因为OE DF ⊥,所以直线OE 的斜率为k , [13分] 所以直线//OE AP . [14分] 解法二:由(Ⅰ)得 (2,0)A -.设111(,)(2)P x y x ≠±,其中221134120x y +-=. 因为AP 的中点为M ,所以 112(,)22x y M -.[ 6分] 所以直线OM 的斜率是 112OM y k x =-, [ 7分]所以直线OM 的方程是 112y y x x =-.令4x =,得114(4,)2y D x -. [ 8分] 由(1,0)F ,得直线DF 的斜率是 1143(2)DF y k x =-. [ 9分]因为直线AP 的斜率是 112AP y k x =+, [10分]所以 2121413(4)DF APy k k x ⋅==--, [12分] 所以 AP DF ⊥. [13分]因为 OE DF ⊥,所以 //OE AP . [14分]20.(本小题满分13分)解:(Ⅰ) 对()f x 求导数,得()e x f x x '=-, [ 1分]所以切线l 的斜率为000()e x x f x '=-, [ 2分]由此得切线l 的方程为:000002(1(e 2))e ()x x x x x y x ----=,即 000020(e )(1)1e 2x x x x y x x =+-+-. [ 3分](Ⅱ) 由(Ⅰ)得,直线l 在y 轴上的截距为0020(1)1e 2x x x +-. [ 4分]设 2()(1)1e 2x g x x x +=-,[1,1]x ∈-. 所以 ()(1e )x g x x '=-,令()0g x '=,得0x =. ()g x ,()g x '的变化情况如下表:全优试卷所以函数()g x 在[1,1]-上单调递减, [ 6分]所以max 21[()](1)e 2g x g =-=+,min 1[()](1)2g x g ==, 所以直线l 在y 轴上的截距的取值范围是121[,]2e 2+. [ 8分](Ⅲ)过M 作x 轴的垂线,与射线1y x =-交于点Q ,所以△MNQ 是等腰直角三角形. [ 9分] 所以 21|||||()()||e 1|2x MN MQ f x g x x x ==-=--+. [10分]设 21()e 12x h x x x =--+,[0,)x ∈+∞, 所以 ()e 1x h x x '=--.令 ()e 1x k x x =--,则()e 10(0)x k x x '=->>, 所以 ()()k x h x '=在[0,)+∞上单调递增, 所以 ()(0)0h x h ''=≥,从而 ()h x 在[0,)+∞上单调递增, [12分]所以 min [()](0)2h x h ==,此时(0,1)M ,(2,1)N .所以 ||MN 的最小值为2,此时1a =. [13分]。
北京市西城区高三下学期4月统一测试(一模)数学(文)试题Word版含答案

北京市西城区高三下学期 4 月统一测试(一模)数学(文)试题Word 版含答案数学(文科)第I卷(选择题共40分)选择题:本大题共8小题,每小题5分,共40分.在每小题列出的选出符合题目要求的一项.1.若集合2018. 4四个选项中,[KS5UKS5U] )(2.若复数的实部与虚部相等,则实数A )(B )(C )(D )3执行如图所示的程序框图值为(A)B)C) D)是奇函数,则■I ■宙・柵5 •正三棱柱的三视图如图所示,该正三棱柱的表面积是B) C)D)6.已知二次函数恒成立 ”的B )必要而不充分条件 (D )既不充分也不必要条件是正方形(A )充分而不必要条件 (C )充分必要条件已知的中心^ 若D)8.如图,在长方体中,占八、、在侧面上. 满足到直线的距离相等的点( A )不存在、填空题:本大题共(B)恰有1个(C)恰有2个第n卷(非选择题共no分)D )有无数个6小题,每小题5分,共30 分.9.函数的定义域是10满足条件的最小值为11 .已知抛物线的焦点与双曲线个焦点重合___,双曲线的渐近线方程是 _____.12则13 .能够说明“ 存在不相等的正数使得是真命题的的值为14.某班共有学生40 名,在乒乓球、篮球、排球三项运动中每人至少会其中的一项,有些人会其中的两项,没有人三项均会.若该班18 人不会打乒乓球,24 人不会打篮球,16 人不会打排球,则该班会其中两项运动的学生人数是 _______ .三、解答题:本大题共 6 小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤.15.(本小题满分13 分)设等差数列且成等比数列.(I)求的通项公式;(n ) 设数列16.(本小题满分13 分)的部分图象如图所示.的最小值.函数17.(本小题满分13分)某企业2017年招聘员工,其中A、B、C、D、E五种岗位的应聘人数、录用人数和录用(I)从表中所有应聘人员中随机选择1人,试估计此人被录用的概率;(H)从应聘E岗位的6人中随机选择1名男性和1名女性,求这2人均被录用的概率; (川)表中A、B、C、D、E各岗位的男性、女性录用比例都接近(二者之差的绝对值不大于5%),但男性的总录用比例却明显高于女性的总录用比例•研究发现,若只考虑其中某四种岗位,则男性、女性的总录用比例也接近,请写出这四种岗位.(只需写出结论)18.(本小题满分14分)分另为使得平面平面的中点,如图2.(n ) 求证:平面平面(川)线上是否存在点19.(本小题满分14分)已知椭圆的任意三个顶点为顶点的三角形的面积是(I)求椭圆的方程;的右顶点,点轴上. 若椭圆20.(本小题满分13 分)已知函数横坐标的取值范围.其中( I ) 若曲线处的切线与直线的值;的导函数为占八、、且西城区高三统一测试数学(文科)参考答案及评分标准2018.4一、选择题:本大题共8 小题,每小题5 分,共40 分.1.D2.B3.C4.A 5.D6.B7.A8.D二、填空题:本大题共6 小题,每小题 5 分,共30 分.910111213.(答案不唯一)14.22注:第11题第一空 3 分,第二空2 分.三、解答题:本大题共6小题,共80 分. 其他正确解答过程,请参照评分标准给分15.(本小题满分13 分)的公差为解:(I )设等差数列成等比数列。
北京西城区2011届高三第一学期期末考试数学(理)试题及答案

北京市西城区2010—2011学年度高三第一学期期末考试数学(理)试题第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分. 在每小题列出的四个选项中,选出符合题目要求的一项. 1.已知全集U =R ,集合{10}A x x =+<,{30}B x x =-<,那么集合()U C A B =( )A .{13}x x -≤<B .{13}x x -<<C .{1}x x <-D .{3}x x >2.已知点(1,1)A -,点(2,)B y ,向量=(1,2)a ,若//ABa ,则实数y 的值为 ( )A .5B .6C .7D .8 3.已知ABC ∆中,1,a b =45B =,则角A 等于 ( )A .150B .90C .60D .304.在极坐标系中,过点(1,0)并且与极轴垂直的直线方程是( )A .cos ρθ=B .sin ρθ=C .cos 1ρθ=D .sin 1ρθ=5.阅读右面程序框图,如果输出的函数值在区间11[,]42内,则输入的实数x 的取值范围是( ) A .(,2]-∞-B .[2,1]--C .[1,2]-D .[2,)+∞6.设等比数列{}n a 的前n 项和为n S ,若0852=+a a ,则下列式子中数值不能确定的是( )A .35a a B .35S S C .nn a a 1+ D .nn S S 1+ 7.如图,四边形ABCD 中,1AB AD CD ===,BD =BD CD ⊥.将四边形ABCD 沿对角线BD 折成四面体A BCD '-,使平面A BD '⊥平面BCD ,则下列结论正确的是( ) A .A C BD '⊥B .90BA C'∠=C .CA '与平面A BD '所成的角为30D .四面体A BCD '-的体积为138.对于函数①1()45f x x x =+-,②21()log ()2xf x x =-,③()cos(2)cos f x x x =+-, 判断如下两个命题的真假:命题甲:()f x 在区间(1,2)上是增函数;命题乙:()f x 在区间(0,)+∞上恰有两个零点12,x x ,且121x x <. 能使命题甲、乙均为真的函数的序号是A .①B .②C .①③D .①②第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9.i 为虚数单位,则22(1i)=+______.10.在5(2)x +的展开式中,2x 的系数为_____.AB CD11.若实数,x y 满足条件10,2,1,x y x y x -+≥⎧⎪+≥⎨⎪≤⎩则2x y +的最大值为_____.12.如图所示,过圆C 外一点P 做一条直线与圆C 交于A B ,两点,2BA AP =,PT 与圆C 相切于T 点.已知圆C 的半径为2,30CAB ∠= ,则PT =_____.13.双曲线22:1C x y -=的渐近线方程为_____;若双曲线C 的右顶点为A ,过A 的直线l 与双曲线C 的两条渐近线交于,P Q 两点,且2PA AQ =,则直线l 的斜率为_____.14.在平面直角坐标系中,定义1212(,)d P Q x x y y =-+-为两点11(,)P x y ,22(,)Q x y 之间的“折线距离”.则坐标原点O与直线20x y +-=上一点的“折线距离”的最小值是____;圆221x y +=上一点与直线20x y +-上一点的“折线距离”的最小值是____.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数2()22sin f x x x =-.(Ⅰ)若点(1,P 在角α的终边上,求()f α的值;(Ⅱ)若[,]63x ππ∈-,求()f x 的值域.16.(本小题满分13分)如图,在三棱柱111ABC A B C -中,侧面11ABB A ,11ACC A 均为正方形,∠=90BAC,点D 是棱11B C 的中点. (Ⅰ)求证:1A D ⊥平面11BB C C ;(Ⅱ)求证:1//AB 平面1A DC ; (Ⅲ)求二面角1D AC A --的余弦值.17.(本小题满分13分) 一个袋中装有6个形状大小完全相同的小球,球的编号分别为1,2,3,4,5,6. (Ⅰ)若从袋中每次随机抽取1个球,有放回的抽取2次,求取出的两个球编号之和为6的概率;(Ⅱ)若从袋中每次随机抽取2个球,有放回的抽取3次,求恰有2次抽到6号球的概率;(Ⅲ)若一次从袋中随机抽取3个球,记球的最大编号为X ,求随机变量X 的分布列. 18.(本小题满分13分)已知椭圆12222=+by a x (0>>b a )的右焦点为2(3,0)F ,离心率为e .A BC C 1B 1A 1D(Ⅰ)若2e =,求椭圆的方程;(Ⅱ)设直线y kx =与椭圆相交于A ,B 两点,,M N 分别为线段22,AF BF 的中点.若坐标原点O 在以MN 为直径的圆上,且2322≤<e ,求k 的取值范围.19.(本小题满分14分) 已知函数21()(21)2ln ()2f x ax a x x a =-++∈R . (Ⅰ)若曲线()y f x =在1x =和3x =处的切线互相平行,求a 的值; (Ⅱ)求()f x 的单调区间;(Ⅲ)设2()2g x x x =-,若对任意1(0,2]x ∈,均存在2(0,2]x ∈,使得12()()f x g x <,求a 的取值范围.20.(本小题满分14分) 已知数列}{n a ,{}n b 满足n n n a a b -=+1,其中1,2,3,n = . (Ⅰ)若11,n a b n ==,求数列}{n a 的通项公式;(Ⅱ)若11(2)n n n b b b n +-=≥,且121,2b b ==.(ⅰ)记)1(16≥=-n a c n n ,求证:数列}{n c 为等差数列; (ⅱ)若数列}{na n中任意一项的值均未在该数列中重复出现无数次.求首项1a 应满足的条件.参考答案(理科) 2011.1一、选择题:本大题共8小题,每小题5分,共40分.题号1 2 3 4 5 6 7 8 答案A C D CB D B D二、填空题:本大题共6小题,每小题5分,共30分. 9.i - 10.80 11.412.3 13.0x y ±=,3± 142注:13、14题第一问2分,第二问3分. 三、解答题:(本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分.) 15.(本小题满分13分)解:(Ⅰ)因为点(1,P 在角α的终边上,所以sin 2α=-,1cos 2α=, ………………2分所以22()22sin cos 2sin f αααααα=-=- ………………4分21(2(3222=-⨯-⨯-=-. ………………5分(Ⅱ)2()22sin f x x x =-cos21x x =+- ………………6分2sin(2)16x π=+-, ………………8分因为[,]63x ππ∈-,所以65626πππ≤+≤-x , ………………10分所以1sin(2)126x π-≤+≤, ………………11分所以()f x 的值域是[2,1]-. ………………13分16.(本小题满分13分)(Ⅰ)证明:因为侧面11ABB A ,11ACC A 均为正方形, 所以11,AA AC AA AB ⊥⊥,所以1AA ⊥平面ABC ,三棱柱111ABC A B C -是直三棱柱. ………………1分 因为1A D ⊂平面111A B C ,所以11CC A D ⊥, ………………2分又因为1111A B AC =,D 为11B C 中点, 所以111A D B C ⊥. ……………3分 因为1111CC B C C = ,所以1A D ⊥平面11BB C C . ……………4分 (Ⅱ)证明:连结1AC ,交1AC 于点O ,连结OD , 因为11ACC A 为正方形,所以O 为1AC 中点,又D 为11B C 中点,所以OD 为11ABC ∆中位线, 所以1//AB OD , ………………6分 因为OD ⊂平面1A DC ,1AB ⊄平面1A DC , 所以1//AB 平面1A DC . ………………8分(Ⅲ)解: 因为侧面11ABB A ,11ACC A 均为正方形, 90BAC ∠=, 所以1,,AB AC AA 两两互相垂直,如图所示建立直角坐标系A xyz -.设1AB =,则111(0,10),(1,0,0),(0,0,1),(,,1)22C B AD ,.1111(,,0),(0,11)22A D AC ==- ,, ………………9分 设平面1A DC 的法向量为=()x,y,z n ,则有1100A D A C ⋅=⎧⎨⋅=⎩n n ,00x y y z +=⎧⎨-=⎩, x y z =-=-, 取1x =,得(1,1,1)=--n . ………………10分 又因为AB ⊥平面11ACC A ,所以平面11ACC A 的法向量为(1,00)AB =,,………11分cos ,AB AB AB⋅〈〉===n n n , ………………12分 因为二面角1D AC A --是钝角, 所以,二面角1D AC A --的余弦值为 ………………13分 17.(本小题满分13分) 解:(Ⅰ)设先后两次从袋中取出球的编号为,m n ,则两次取球的编号的一切可能结果),(n m 有6636⨯=种, ………………2分其中和为6的结果有(1,5),(5,1),(2,4),(4,2),(3,3),共5种, 则所求概率为536. ………………4分 (Ⅱ)每次从袋中随机抽取2个球,抽到编号为6的球的概率152613C p C ==.………………6分所以,3次抽取中,恰有2次抽到6号球的概率为2223122(1)3()()339C p p -=⨯=. ………………8分(Ⅲ)随机变量X 所有可能的取值为3,4,5,6. (9)分33361(3)20C P X C ===, 23363(4)20C P X C ===,243663(5)2010C P X C ====,2536101(6)202C P X C ====. ………………12分所以,随机变量X 的分布列为:X 3 45 6P120 320 310 12………………13分18、(本小题满分13分)解:(Ⅰ)由题意得3c c a=⎧⎪⎨=⎪⎩a = (2)分结合222a b c =+,解得212a =,23b =. ………………3分所以,椭圆的方程为131222=+y x . ………………4分 (Ⅱ)由22221,,x y a b y kx ⎧+=⎪⎨⎪=⎩得222222()0b a k x a b +-=.设1122(,),(,)A x y B x y .所以2212122220,a b x x x x b a k -+==+, ………………6分依题意,OM ON ⊥,易知,四边形2OMF N 为平行四边形,所以22AF BF ⊥, ………………7分因为211(3,)F A x y =- ,222(3,)F B x y =-,所以222121212(3)(3)(1)90F A F B x x y y k x x ⋅=--+=++=. ………………8分 即 222222(9)(1)90(9)a a k a k a --++=+-, ………………9分将其整理为 4222424218818111818a a k a a a a -+==---+-. ………………10分因为2322≤<e ,所以a ≤<21218a ≤<. ………………11分所以218k ≥,即(,](]44k ∈-∞-+∞ . ………………13分 19.(本小题满分14分)解:2()(21)f x ax a x'=-++(0)x >. ………………2分(Ⅰ)(1)(3)f f ''=,解得23a =. ………………3分 (Ⅱ)(1)(2)()ax x f x x--'=(0)x >. (5)分①当0a ≤时,0x >,10ax -<,在区间(0,2)上,()0f x '>;在区间(2,)+∞上()0f x '<,故()f x 的单调递增区间是(0,2),单调递减区间是(2,)+∞. ………………6分②当102a <<时,12a >, 在区间(0,2)和1(,)a +∞上,()0f x '>;在区间1(2,)a上()0f x '<,故()f x 的单调递增区间是(0,2)和1(,)a +∞,单调递减区间是1(2,)a.…………7分③当12a =时,2(2)()2x f x x-'=, 故()f x 的单调递增区间是(0,)+∞.………8分④当12a >时,102a <<, 在区间1(0,)a 和(2,)+∞上,()0f x '>;在区间1(,2)a上()0f x '<,故()f x 的单调递增区间是1(0,)a 和(2,)+∞,单调递减区间是1(,2)a. ………9分(Ⅲ)由已知,在(0,2]上有max max ()()f x g x <. ………………10分 由已知,max ()0g x =,由(Ⅱ)可知,①当12a ≤时,()f x 在(0,2]上单调递增, 故max ()(2)22(21)2ln 2222ln 2f x f a a a ==-++=--+, 所以,222ln 20a --+<,解得ln 21a >-,故1ln 212a -<≤.……………11分 ②当12a >时,()f x 在1(0,]a 上单调递增,在1[,2]a上单调递减, 故max 11()()22ln 2f x f a a a==---. 由12a >可知11ln ln ln 12ea >>=-,2ln 2a >-,2ln 2a -<,所以,22ln 0a --<,max ()0f x <, ………………13分 综上所述,ln 21a >-. ………………14分20.(本小题满分14分)解:(Ⅰ)当2≥n 时,有121321()()()n n n a a a a a a a a -=+-+-++- 1121n a b b b -=++++ …………2分2(1)11222n n n n -⨯=+=-+. ………………3分又因为11=a 也满足上式,所以数列}{n a 的通项为2122n n na =-+.………………4分(Ⅱ)(ⅰ)因为对任意的n ∈*N 有5164321n n n n n n n b b b b b b b ++++++====,………………5分所以 1656161661626364n n n n n n n n n n c c a a b b b b b b ++--++++-=-=+++++111221722=+++++=(1)n ≥, 所以数列}{n c 为等差数列. ………………7分 (ⅱ)设)0(6≥=+n a c i n n ,(其中i 为常数且}6,5,4,3,2,1{∈i ),所以1666661626364657(0)n n n i n i n i n i n i n i n i n i c c a a b b b b b b n +++++++++++++++-=-=+++++=≥所以数列}{6i n a +均为以7为公差的等差数列. ………………9分设6777(6)7766666666i i k i i k i i i k a a a a k f k i i k i k i k+++--+====+++++, (其中i k n +=6)0(≥k ,i 为}6,5,4,3,2,1{中的一个常数),当76i i a =时,对任意的i k n +=6有n a n 76=; ………………10分 当76i ia ≠时, 17771166()()6(1)666(1)6i i k k ii ia a i f f a k i k i k i k i+---=-=--++++++ 76()()6[6(1)](6)i i a k i k i -=-+++………………11分①若76i ia >,则对任意的k ∈N 有k k f f <+1,所以数列}6{6i k a i k ++为单调减数列; ②若76i ia <,则对任意的k ∈N 有k k f f >+1,所以数列}6{6ik a i k ++为单调增数列; ………………12分综上:设集合741111{}{}{}{}{}{}632362B =-- 74111{,,,,}63236=--,当B a ∈1时,数列}{na n中必有某数重复出现无数次. 当B a ∉1时,}6{6ik a ik ++ )6,5,4,3,2,1(=i 均为单调数列,任意一个数在这6个数列中最 多出现一次,所以数列}{na n中任意一项的值均未在该数列中重复出现无数次……14分。
2011年北京市石景山区高考一模数学(文)试题及答案 - 副本
北京石景山区2011年高三统一测试数学试题(文科)第Ⅰ卷 选择题一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设2{|4},{|4}M x x N x x =<=<,则( )A .MNB .NMC .R M C N ⊆D .R N C M ⊆2.若17(,),2i a bi a b R i i+=+∈-是虚数单位,则乘积a b 的值是( )A .-15B .3C .-3D .53.已知等差数列{}n a 的前n 项和为n S ,若45818,a a S =-=则 ( ) A .54 B .68 C .90D .72 4.一个空间几何体的三视图及部分数据如图所示(单位:cm ),则这个几何的表面积是 ( )A .29cm πB .122cm πC .152cm πD .242cm π5.已知O 是A B C ∆所在平面内一点,D 为BC 边中点,且20OA OB OC ++=,那么 ( ) A .AO OD = B .2AO OD =C .3AO OD =D .2AO OD =6.已知α是第二象限角,且3sin(),tan 25παα+=-则的值为( )A .45B .237-C .247-D .83-7.已知椭圆2214xy +=的焦点为12,F F ,在长轴A 1A 2上任取一点M ,过M 作垂直于A 1A 2的直线交椭圆于点P ,则使得120PF PF ⋅<的点M 的概率为( )A3B3C3D .128.定义在R 上的函数()f x 满足(4)1,()()f f x f x '=为的导函数,已知()y f x '=的图象如图所示,若两个正数,a b 满足1(2)1,1b f a b a ++<+则的取值范围是( )A .11(,)53B .1(,)(5,)3-∞⋃+∞C .1(,5)3D .(,3)-∞第Ⅱ卷 非选择题二、填空题:本大题共6个小题,每小题5分,共30分. 9.在A B C ∆中,角A ,B ,C 所对应的边分别为222,,,a b c b c bc a +=+且,则角A 的大小为 .10.阅读如图所示的程序框图,运行该程序后输出的k 的值是 . 11.已知命题2:,20p x R x a x a ∃∈++≤,则命题p 的否定是 ;若命题p 为假命题,则实数a 的取值范围是 .12.已知向量(1,),(1,),2a n b n a b b ==-+若与垂直,则n = .13.已知函数22,(,1)(),[1,)x x f x x x -⎧∈-∞⎪=⎨∈+∞⎪⎩,那么(1)f -= ,若()4f x >则x 的取值范围是 .14.函数2(0)y x x =>的图象在点2(,)n n a a 处的切线与x 轴交点的横坐标为1n a +,*135,16,n N a a a ∈=+=若则 ,数列{}n a 的通项公式为 .三、解答题:本磊题共6小题,共80分.解答题应写出文字说明,证明过程或演算步骤. 15.(本小题满分13分)在A B C ∆中,角A ,B ,C 所对应的边分别为27,,,4sin cos 2.22A B a b c C +-=且(Ⅰ)求角C 的大小;(Ⅱ)求sin sin A B +的最大值.16.(本小题满分13分)为预防H 1N 1病毒爆发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:(Ⅰ)求x 的值;(Ⅱ)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C 组抽取多少个? (Ⅲ)已知465,30y z ≥≥,求不能通过测试的概率.17.(本小题满分14分) 在棱长为1的正方体ABCD —A 1B 1C 1D 1中,E ,F ,G 分别为棱BB 1,DD 1和CC 1的中点. (Ⅰ)求证:C 1F//平面DEG ;(Ⅱ)求三棱锥D 1—A 1AE 的体积;(Ⅲ)试在棱CD 上求一点M ,使1D M ⊥平面DEG .18.(本小题满分13分)已知函数()2ln .k f x kx x x=--(Ⅰ)若(2)0,()f y f x '==求函数的解析式;(Ⅱ)若函数()f x 在其定义域内为增函数,求实数k 的取值范围.19.(本小题满分13分)已知椭圆)0(12222>>=+b a by ax 经过点1)22P ,离心率为2,动点(2,)(0).M t t > (Ⅰ)求椭圆的标准方程;(Ⅱ)求以OM 为直径且被直线3450x y --=截得的弦长为2的圆的方程;(Ⅲ)设F 是椭圆的右焦点,过点F 作OM 的垂线与以OM 为直径的圆交于点N ,证明线段ON 的长为定值,并求出这个定值.20.(本小题满分14分)已知定义在R 上的函数()f x 和数列121{},,n a a a a a =≠,当*2n N n ∈≥且时,111(),()()()n n n n n n a f a f a f a k a a ---=-=-且,其中,a k 均为非零常数.(Ⅰ)若数列{}n a 是等差数列,求k 的值;(Ⅱ)令*11(),1n n n b a a n N b +=-∈=若,求数列{}n b 的通项公式;(Ⅲ)若数列{}n a 为等比数列,求函数()f x 的解析式.。
北京市西城区高三一模试卷数学理参考答案
北京市西城区2011年高三一模试卷参考答案及评分标准数学(理科) 2011.4一、选择题:本大题共8小题,每小题5分,共40分.二、填空题:本大题共6小题,每小题5分,共30分.9. 2 10. 2 11. 415±,212. 12 13. 60,48 14.62;1或5 注:11题,13题,14题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分.15.(本小题满分13分) 解:(Ⅰ)因为54cos =B ,所以53sin =B . ……………………2分 因为35=a ,2=b ,由正弦定理B b A a sin sin =可得21sin =A . …………………4分因为b a <,所以A 是锐角,所以o30=A . ……………………6分(Ⅱ)因为ABC ∆的面积ac B ac S 103sin 21==, ……………………7分 所以当ac 最大时,ABC ∆的面积最大.因为B ac c a b cos 2222-+=,所以ac c a 58422-+=. ……………………9分 因为222a c ac +≥,所以8245ac ac -≤, ……………………11分所以10≤ac ,(当a c == ……………………12分 所以ABC ∆面积的最大值为3. ……………………13分16.(本小题满分13分)解:记“甲、乙、丙三人各自破译出密码”分别为事件1,A 12311(),(),(),23P A P A P A p ===且321,,A A A (Ⅰ)甲、乙二人中至少有一人破译出密码的概率为121()P A A -⋅1221233=-⨯= (Ⅱ)设“三人中只有甲破译出密码”为事件B ,则有()P B =123()P A A A ⋅⋅=121(1)233p p -⨯⨯-=,分 所以1134p -=,14p =. ……………………7分(Ⅲ)X 的所有可能取值为3,2,1,0. ……………………8分所以1(0)4P X ==, (1)P X ==P 123()A A A ⋅⋅+P 123()A A A ⋅⋅+P 123()A A A ⋅⋅111312111423423424=+⨯⨯+⨯⨯=, (2)P X ==P 123()A A A ⋅⋅+P 123()A A A ⋅⋅+P 123()A A A ⋅⋅11312111112342342344=⨯⨯+⨯⨯+⨯⨯=, (3)P X ==P 123()A A A ⋅⋅=111123424⨯⨯= . ……………………11分X ……………………12分所以,1111113()012342442412E X =⨯+⨯+⨯+⨯=. ……………………13分17.(本小题满分13分)(Ⅰ)证明: 因为DE ⊥平面ABCD ,所以AC DE ⊥. ……………………2分 因为ABCD 是正方形, 所以BD AC ⊥,从而AC ⊥平面BDE . ……………………4分 (Ⅱ)解:因为DE DC DA ,,两两垂直,所以建立空间直角坐标系xyz D -如图所示.因为BE 与平面ABCD 所成角为060,即60DBE ∠=, ………………5分 所以3=DBED. 由3=AD可知DE =AF =………………6分则(3,0,0)A,F,E ,(3,3,0)B ,(0,3,0)C ,所以(0,BF =-,(3,0,EF =-, ………………7分设平面BEF 的法向量为=n (,,)x y z ,则00BF EF ⎧⋅=⎪⎨⋅=⎪⎩n n,即3030y x ⎧-+=⎪⎨-=⎪⎩,令z =则=n (4,2,. …………………8分因为AC ⊥平面BDE ,所以CA 为平面BDE 的法向量,(3,3,0)CA =-,所以cos ,1332CA CA CA⋅〈〉===n n n . …………………9分 因为二面角为锐角,所以二面角D BE F --的余弦值为1313. ………………10分 (Ⅲ)解:点M 是线段BD 上一个动点,设(,,0)M t t .则(3,,0)AM t t =-, 因为//AM 平面BEF ,所以AM ⋅n 0=, …………………11分 即4(3)20t t -+=,解得2=t . …………………12分 此时,点M 坐标为(2,2,0),13BM BD =,符合题意. …………………13分18. (本小题满分14分) 解:(Ⅰ)3(2)()a x f x x -'=,(0x ≠), ……………3分 在区间(,0)-∞和(2,)+∞上,()0f x '<;在区间(0,2)上,()0f x '>.所以,()f x 的单调递减区间是(,0)-∞和(2,)+∞,单调递增区间是(0,2). ………4分(Ⅱ)设切点坐标为00(,)x y ,则002000030(1)10(2)1a x y x x y a x x -⎧=⎪⎪⎪--=⎨⎪-⎪=⎪⎩ ……………7分(1个方程1分)解得01x =,1a =. ……………8分 (Ⅲ)()g x =ln (1)x x a x --,则()ln 1g x x a '=+-, …………………9分 解()0g x '=,得1e a x -=,所以,在区间1(0,e)a -上,()g x 为递减函数,在区间1(e ,)a -+∞上,()g x 为递增函数. ……………10分当1e1a -≤,即01a <≤时,在区间[1,e]上,()g x 为递增函数,所以()g x 最大值为(e)e e g a a =+-. ………………11分当1ee a -≥,即2a ≥时,在区间[1,e]上,()g x 为递减函数,所以()g x 最大值为(1)0g =. ………………12分当11<e<e a -,即12a <<时,()g x 的最大值为(e)g 和(1)g 中较大者;(e)(1)e e 0g g a a -=+->,解得ee 1a <-, 所以,e1e 1a <<-时,()g x 最大值为(e)e e g a a =+-, …………………13分e2e 1a ≤<-时,()g x 最大值为(1)0g =. …………………14分 综上所述,当e 0e 1a <<-时,()g x 最大值为(e)e e g a a =+-,当ee 1a ≥-时,()g x 的最大值为(1)0g =.19. (本小题满分14分) 解:(Ⅰ)由已知(,0)2pF ,设11(,)A x y ,则2112y px =, 圆心坐标为112(,)42x p y +,圆心到y 轴的距离为124x p+, …………………2分圆的半径为1121()2224FA x p px +=⨯--=, …………………4分 所以,以线段FA 为直径的圆与y 轴相切. …………………5分 (Ⅱ)解法一:设022(0,),(,)P y B x y ,由1FA AP λ=,2BF FA λ=,得111101(,)(,)2p x y x y y λ-=--,22211(,)(,)22p px y x y λ--=-, …………………6分 所以1111101,()2px x y y y λλ-=-=-,221221(),22p px x y y λλ-=-=-, …………………8分 由221y y λ=-,得222221y y λ=. 又2112y px =,2222y px =,所以 2221x x λ=. …………………10分代入221()22p p x x λ-=-,得22121()22p p x x λλ-=-,2122(1)(1)2px λλλ+=+, 整理得122p x λ=, …………………12分代入1112px x λ-=-,得122222p p p λλλ-=-, 所以12211λλλ=-, …………………13分 因为1211[,]42λλ∈,所以2λ的取值范围是4[,2]3. …………………14分 解法二:设),(),,(2211y x B y x A ,:2pAB x my =+, 将2p x my =+代入22y px =,得2220y pmy p --=, 所以212y y p =-(*), …………………6分由1FA AP λ=,2BF FA λ=,得111101(,)(,)2p x y x y y λ-=--,22211(,)(,)22p px y x y λ--=-, …………………7分所以,1111101,()2px x y y y λλ-=-=-, 221221(),22p px x y y λλ-=-=-, …………………8分 将122y y λ-=代入(*)式,得2212p y λ=, …………………10分所以2122p px λ=,122p x λ=. …………………12分代入1112px x λ-=-,得12211λλλ=-. …………………13分因为1211[,]42λλ∈,所以2λ的取值范围是4[,2]3. …………………14分 20.(本小题满分13分)(Ⅰ)解:12100122399100(,,,)||||||a a a a a a a a a τ=-+-++- ………………1分222299198=+++=⨯=. ………………3分(Ⅱ)证明:因为(,,,)||||||a b c d a b b c c d τ=-+-+-,(,,,)||||||a c b d a c c b b d τ=-+-+-,所以(,,,)(,,,)||||||||a b c d a c b d a b c d a c b d ττ-=-+-----. ……………4分 因为()()0a b b c -->,所以a b c >>,或a b c <<. 若a b c >>,则(,,,)(,,,)||||a b c d a c b d a b c d a c b d ττ-=-+--+--||||c b c d b d =-+---当b c d >>时,上式()2()0c b c d b d c b =-+---=-<, 当b d c ≥≥时,上式()2()0c b d c b d d b =-+---=-≤, 当d b c >>时,上式()0c b d c d b =-+---=,即当a b c >>时,(,,,)(,,,)0a b c d a c b d ττ-≤. ……………………6分若a b c <<,则(,,,)(,,,)||||a b c d a c b d b a c d c a b d ττ-=-+--+--,||||0b c c d b d =-+---≤.(同前)所以,当()()0a b b c -->时,(,,,)(,,,)a b c d a c b d ττ≤成立. …………………7分(Ⅲ)证明:由(Ⅱ)易知对于四个数的数列,若第三项的值介于前两项的值之间,则交换第二项与第三项的位置将使数列波动强度减小或不变.(将此作为引理)下面来证明当12a a >时,{}n a 为递减数列.(ⅰ)证明23a a >.若231a a a >>,则由引理知交换32,a a 的位置将使波动强度减小或不变,与已知矛盾. 若2a a a >>31,则1212212121(,,)||||||||(,,)a a a a a a a a a a a a a a ττ=-+->-+-=3333,与已知矛盾.所以,321a a a >>. ………………………9分 (ⅱ)设12(32)i a a a i n >>>≤≤-,证明1i i a a +>.若i i i a a a >>+-11,则由引理知交换1,+i i a a 的位置将使波动强度减小或不变,与已知矛盾. 若i i i a a a >>-+11,则211211(,,,)(,,,)i i i i i i i i a a a a a a a a ττ--+--+=,与已知矛盾.所以,1+>i i a a . …………………11分 (ⅲ)设121n a a a ->>>,证明1n n a a ->.若1n n a a ->,考查数列121,,,,n n a a a a -,则由前面推理可得122n n n a a a a -->>>>,与121n a a a ->>>矛盾.所以,1n n a a ->. …………………12分 综上,得证.同理可证:当12a a <时,有{}n a 为递增数列. ……………………13分。
(优辅资源)北京市西城区高三一模考试数学(文)试题 Word版含答案
西城区高三统一测试数学(文科) 2017.4第Ⅰ卷(选择题 共40分)一、 选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知全集{1,2,3,4,5,6}U =,集合{1,3,5}A =,{1,4}B =,那么U A B =ð(A ){3,5} (B ){2,4,6} (C ){1,2,4,6} (D ){1,2,3,5,6}2.在复平面内,复数1ii+的对应点位于 (A )第一象限 (B )第二象限 (C )第三象限(D )第四象限3.双曲线2213x y -=的焦点坐标是(A ),(0, (B ),( (C )(0,2),(0,2)-(D )(2,0),(2,0)-4.函数21()()log 2x f x x =-的零点个数为 (A )0(B )1(C )2 (D )35.函数()f x 定义在(,)-∞+∞上.则“曲线()y f x =过原点”是“()f x 为奇函数”的 (A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件(D )既不充分也不必要条件6.在ABC △中,点D 满足3BC BD −−→−−→=,则(A )1233AD AB AC −−→−−→−−→=+(B )1233AD AB AC −−→−−→−−→=-(C )2133AD AB AC −−→−−→−−→=+ (D )2133AD AB AC −−→−−→−−→=-7.在正方形网格中,某四面体的三视图如图所示.如果小 正方形网格的边长为1,那么该四面体最长棱的棱长为 (A) (B )6 (C) (D)8.函数()f x 的图象上任意一点(,)A x y 的坐标满足条件||||x y ≥,称函数()f x 具有性 质P .下列函数中,具有性质P 的是 (A )2()f x x = (B )21()1f x x =+ (C )()sin f x x = (D )()ln(1)f x x =+第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9.函数()f x 的定义域为____. 10.执行如图所示的程序框图. 当输入1ln 2x =时,输出的y 值为____.11.圆22:2210C x y x y +--+=的圆心坐标是____;直线 :0l x y -=与圆C 相交于,A B 两点,则||AB =____. 12.函数sin4()1cos4xf x x=+的最小正周期是____.13.实数,x y 满足1,2,220,x y x y ⎧⎪⎨⎪+-⎩≤≤≥则22x y +的最大值是____;最小值是____.14. 如图,正方体1111ABCD A B C D -的棱长为2,点P 在正方形ABCD 的边界及其内部运动.平面区域W 由所有满足1A P P 组成,则W 的面积是____.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤.15.(本小题满分13分)已知{}n a 是等比数列,13a =,424a =.数列{}n b 满足11b =,48b =-,且{}n n a b +是等差数列.(Ⅰ)求数列{}n a 和{}n b 的通项公式; (Ⅱ)求数列{}n b 的前n 项和.16.(本小题满分13分)在△ABC 中,角,,A B C 的对边分别为,,a b c ,且tan 2sin a C c A =. (Ⅰ)求角C 的大小;(Ⅱ)求sin sin A B +的最大值. 17.(本小题满分13分)在测试中,客观题难度的计算公式为ii R P N=,其中i P 为第i 题的难度,i R 为答对该题的人数,N 为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:题号 1 2 3 4 5 考前预估难度i P0.90.80.70.60.4测试后,从中随机抽取了10名学生,将他们编号后统计各题的作答情况,如下表所示(“√”表示答对,“×”表示答错):学生编号 题号123 4 5 1 ×√ √ √ √2 √ √ √ √ ×3 √ √ √ √× 4 √ √ √ ××5 √ √√√ √6 √××√ × 7 ×√√√× 8 √ ×× × × 9 √ √ ××× 10√√√√×(Ⅰ)根据题中数据,将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表,并估计这120名学生中第5题的实测答对人数;题号 1 2 3 4 5 实测答对人数 实测难度(Ⅱ)从编号为1到5的5人中随机抽取2人,求恰好有1人答对第5题的概率; (Ⅲ)定义统计量22211221[()()()]n n S P P P P P P n'''=-+-++-,其中i P '为第i 题的实测难度,i P 为第i 题的预估难度(1,2,,)i n =.规定:若0.05S <,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.18.(本小题满分14分)如图,在四棱锥P ABCD -中,底面ABCD 为正方形,PA ⊥底面ABCD ,PA AC =.过点A 的平面与棱,,PB PC PD 分别交于点,,E F G (,,E F G 三点均不在棱的端点处).(Ⅰ)求证:平面PAB ⊥平面PBC ;(Ⅱ)若PC ⊥平面AEFG ,求PFPC的值; (Ⅲ)直线AE 是否可能与平面PCD 平行?证明你的结论.19.(本小题满分14分)如图,已知椭圆2222:1(0)x y C a b a b +=>>的离心率为12,F 为椭圆C 的右焦点.(,0)A a -, ||3AF =.(Ⅰ)求椭圆C 的方程;(Ⅱ)设O 为原点,P 为椭圆上一点,AP 的中点为M .直线OM 与直线4x =交于点D ,过O 作OE DF ⊥,交直线4x =于点E .求证://OE AP .20.(本小题满分13分)已知函数21()e 2xf x x =-.设l 为曲线()y f x =在点00(,())P x f x 处的切线,其中0[1,1]x ∈-.(Ⅰ)求直线l 的方程(用0x 表示);(Ⅱ)求直线l 在y 轴上的截距的取值范围;(Ⅲ)设直线y a =分别与曲线()y f x =和射线1([0,))y x x =-∈+∞交于,M N 两点,求||MN 的最小值及此时a 的值.西城区高三统一测试高三数学(文科)参考答案及评分标准2017.4一、选择题:本大题共8小题,每小题5分,共40分.1.A 2.D 3.C 4.B 5.B 6.C 7.B 8.C二、填空题:本大题共6小题,每小题5分,共30分.9.{|0x x ≥,且1}x ≠ 10.1211.(1,1);212.π2 13.5;4514.π44-注:第11,13题第一空2分,第二空3分.三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分)解:(Ⅰ)设等比数列{}n a 的公比为q ,由题意得3418a q a ==, 解得 2q =. [ 2分]所以 11132(1,2,)n n n a a q n --=⋅=⋅=. [ 4分]设等差数列{}n n a b +的公差为d ,由题意得4411()()1644413a b a b d +-+-===-. [ 6分]所以 11()(1)4n n a b a b n d n +=++-=. [ 8分]从而 1432(1,2,)n n b n n -=-⋅=. [ 9分](Ⅱ)由(Ⅰ)知1432(1,2,)n n b n n -=-⋅=.数列{4}n 的前n 项和为2(1)n n +;数列1{32}n -⋅的前n 项和为3(21)n ⋅-.[12分]所以,数列{}n b 的前n 项和为 222323n n n +-⋅+. [13分]16.(本小题满分13分)解:(Ⅰ) 由 tan 2sin a C c A =,得sin 2sin cos a CA c C⋅=. [ 1分]由正弦定理得sin sin 2sin sin cos A CA C C⋅=. [ 3分]所以 1cos 2C =. [ 4分]因为 (0,π)C ∈, [ 5分]所以 π3C =. [ 6分](Ⅱ) sin sin A B +2πsin sin()3A A =+- [ 7分]3sin 2A A = [ 9分]π)6A +. [11分]因为 π3C =,所以 2π03A <<, [12分]所以 当π3A =时,sin sin A B +取得最大值. [13分]17.(本小题满分13分)解:(Ⅰ)每道题实测的答对人数及相应的实测难度如下表:题号 1 2 3 4 5 实测答对人数 8 8 7 7 2 实测难度0.80.80.70.70.2[4分]所以,估计120人中有1200.224⨯=人答对第5题.[ 5分] (Ⅱ)记编号为i 的学生为(1,2,3,4,5)i A i =,从这5人中随机抽取2人,不同的抽取方法有10种.其中恰好有1人答对第5题的抽取方法为12(,)A A ,13(,)A A ,14(,)A A ,25(,)A A ,35(,)A A ,45(,)A A ,共6种. [ 9分]所以,从抽样的10名学生中随机抽取2名答对至少4道题的学生,恰好有1人答对第5题的概率为63105P ==. [10分](Ⅲ)i P '为抽样的10名学生中第i 题的实测难度,用i P '作为这120名学生第i 题的实测难度.222221[(0.80.9)(0.80.8)(0.70.7)(0.70.6)(0.20.4)]5S =-+-+-+-+-0.012=. [12分]因为 0.0120.05S =<,所以,该次测试的难度预估是合理的. [13分]18.(本小题满分14分)解:(Ⅰ)因为PA ⊥平面ABCD ,所以PA BC ⊥. [ 1分] 因为ABCD 为正方形,所以AB BC ⊥, [ 2分] 所以BC ⊥平面PAB . [ 3分] 所以平面PAB ⊥平面PBC . [ 4分](Ⅱ)连接AF . [ 5分]因为 PC ⊥平面AEFG ,所以 PC AF ⊥. [ 7分] 又因为 PA AC =,所以 F 是PC 的中点. [ 8分]所以12PF PC =.[ 9分] (Ⅲ)AE 与平面PCD 不可能平行. [10分]证明如下:假设//AE 平面PCD ,因为 //AB CD ,AB ⊄平面PCD .所以 //AB 平面PCD . [12分] 而 AE AB ⊂,平面PAB ,所以 平面//PAB 平面PCD ,这显然矛盾! [13分] 所以假设不成立,即AE 与平面PCD 不可能平行.[14分]19.(本小题满分14分)解:(Ⅰ)设椭圆C 的半焦距为c .依题意,得12c a =,3a c +=. [ 2分] 解得 2a =,1c =.所以 2223b a c =-=,所以椭圆C 的方程是 22143x y +=. [ 5分](Ⅱ)解法一:由(Ⅰ)得 (2,0)A -.设AP 的中点00(,)M x y ,11(,)P x y .设直线AP 的方程为:(2)(0)y k x k =+≠,将其代入椭圆方程,整理得2222(43)1616120k x k x k +++-=, [ 7分]所以 21216243k x k --+=+. [ 8分]所以 202843k x k -=+,0026(2)43k y k x k =+=+,即 22286(,)4343k kM k k -++. [ 9分]所以直线OM 的斜率是22263438443k k k k k +=--+, [10分]所以直线OM 的方程是 34y x k =-.令4x =,得3(4,)D k-. [11分] 由(1,0)F ,得直线DF 的斜率是 3141k k-=--, [12分]因为OE DF ⊥,所以直线OE 的斜率为k , [13分] 所以直线//OE AP . [14分] 解法二:由(Ⅰ)得 (2,0)A -.设111(,)(2)P x y x ≠±,其中221134120x y +-=. 因为AP 的中点为M ,所以 112(,)22x y M -.[ 6分] 所以直线OM 的斜率是 112OM y k x =-, [ 7分]所以直线OM 的方程是 112y y x x =-.令4x =,得114(4,)2y D x -. [ 8分] 由(1,0)F ,得直线DF 的斜率是 1143(2)DF y k x =-. [ 9分]因为直线AP 的斜率是 112AP y k x =+, [10分]所以 2121413(4)DF APy k k x ⋅==--, [12分] 所以 AP DF ⊥. [13分]因为 OE DF ⊥,所以 //OE AP . [14分]20.(本小题满分13分)解:(Ⅰ) 对()f x 求导数,得()e x f x x '=-, [ 1分]所以切线l 的斜率为000()e x x f x '=-, [ 2分]由此得切线l 的方程为:000002(1(e 2))e ()x x x x x y x ----=,即 000020(e )(1)1e 2x x x x y x x =+-+-. [ 3分](Ⅱ) 由(Ⅰ)得,直线l 在y 轴上的截距为0020(1)1e 2x x x +-. [ 4分]设 2()(1)1e 2x g x x x +=-,[1,1]x ∈-. 所以 ()(1e )x g x x '=-,令()0g x '=,得0x =. ()g x ,()g x '的变化情况如下表:优质文档优质文档所以函数()g x 在[1,1]-上单调递减, [ 6分]所以max 21[()](1)e 2g x g =-=+,min 1[()](1)2g x g ==, 所以直线l 在y 轴上的截距的取值范围是121[,]2e 2+. [ 8分](Ⅲ)过M 作x 轴的垂线,与射线1y x =-交于点Q ,所以△MNQ 是等腰直角三角形. [ 9分] 所以 21|||||()()||e 1|2x MN MQ f x g x x x ==-=--+. [10分]设 21()e 12x h x x x =--+,[0,)x ∈+∞, 所以 ()e 1x h x x '=--.令 ()e 1x k x x =--,则()e 10(0)x k x x '=->>, 所以 ()()k x h x '=在[0,)+∞上单调递增, 所以 ()(0)0h x h ''=≥,从而 ()h x 在[0,)+∞上单调递增, [12分]所以 min [()](0)2h x h ==,此时(0,1)M ,(2,1)N .所以 ||MN 的最小值为2,此时1a =. [13分]。
北京市各区2011届高三一模考试试题汇总
北京市各区2011届高三一模考试试题汇总试题精粹05-18 0802:北京市各区2011届高三一模考试试题汇总北京市海淀区2011届高三第二学期期中练习--语文(扫描版)北京市海淀区2011年高三年级第二学期期中练习数学文北京市海淀区2011年高三年级第二学期期中练习数学理北京市海淀区2011届高三第二学期期中练习--英语(扫描版)北京市海淀区2011届高三一模考试(理综)北京市海淀区2011届高三第二学期期中练习--文综(扫描版)北京市海淀区2011届高三第二学期期中练习(全科6套)扫描版北京市海淀区2011高三第二学期期中练习(文科全套)扫描版北京市海淀区2011高三第二学期期中练习(理科全套)扫描版北京市西城区2011届高三一模试题(语文)Word版北京市西城区2011届高三一模试题(数学文)Word版北京市西城区2011届高三一模试题(数学理)Word版北京市西城区2011届高三一模试题(英语)Word版北京市西城区2011届高三一模试题(文综)Word版北京市西城区2011届高三下学期4月模拟考试(理综)扫描版北京市西城区2011届高三4月一模试题(文科全套)北京市西城区2011届高三4月一模试题(理科全套)北京市西城区2011届高三4月一模试题(全科)北京市东城区2011年高三第二学期综合练习(一):语文北京市东城区2011学年度综合练习(一)数学文北京市东城区2011学年度综合练习(一)数学理北京市东城区2011年高三第二学期综合练习(一):英语北京市东城区2011年高三第二学期综合练习(一):文综北京市东城区2011年高三第二学期综合练习(一):理综北京市东城区2011届高三下学期综合练习(一)(文科全套)北京市东城区2011届高三下学期综合练习(一)(理科全套)北京市东城区2011届高三下学期综合练习(一)(全科)北京市丰台区2011高三下学期统一练习(一)语文(无答案)北京市丰台区2011年高三下学期统一练习(一):数学文北京市丰台区2011年高三下学期统一练习(一)(数学理)北京市丰台区2011年高三下学期统一练习(一)(英语)北京市丰台区2011年高三下学期统一练习(一):理综北京市丰台区2011年高三下学期统一练习(一):文综北京市丰台区2011年高三下学期统一练习(一)(文科全套)北京市丰台区2011年高三下学期统一练习(一)(理科4套)北京市丰台区2011年高三下学期统一练习(一)(文理科6套)北京市石景山区2011届高三统一测试扫描版(语文)北京市石景山区2011届高三统一测试扫描版(数学文)北京市石景山区2011届高三统一测试试题(word版):数学理北京市石景山区2011届高三统一测试扫描版(英语)北京市石景山区2011届高三统一测试试题(word版):文综北京市石景山区2011届高三统一测试扫描版(理综)北京市石景山区2011届高三3月统一测试(文科4套)word版北京市石景山区2011届高三3月统一测试(理科4套)word版北京市石景山区2011届高三3月统一测试(全科6套)word版北京市朝阳区2011届高三第一次综合练习(语文)北京市朝阳区高三第一次综合练习试卷(word版):数学文北京市朝阳区高三第一次综合练习试卷(word版):数学理北京市朝阳区高三4月第一次综合练习试卷(英语)扫描版北京市朝阳区高三第一次综合练习试卷(word版):文综北京市朝阳区届高三第一次综合练习试卷(word版):理综北京市朝阳区2011高三4月第一次综合练习(文科全套)北京市朝阳区2011高三4月第一次综合练习(理科全套)北京市朝阳区2011高三4月第一次综合练习(全科)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市西城区2011年高三一模试卷数学(文科)参考答案 第1页(共4页)
北京市西城区2011年高三一模试卷
参考答案及评分标准
数学(文科)
2011.4
一、选择题:本大题共8小题,每小题5分,共40分.
题号 1 2 3 4 5 6 7 8
答案 B A C D B D C A
二、填空题:本大题共6小题,每小题5分,共30分.
9. 1 10. 45 11.62,2 12. 8 13.31 14. 5,910
注:11题,14题第一问2分,第二问3分.
三、解答题:本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分.
15.(本小题满分13分)
解:(Ⅰ)因为54cosB,所以53sinB . ……………………2分
由正弦定理BbAasinsin,可得10sin303a. ……………………4分
所以35a. ……………………6分
(Ⅱ)因为ABC的面积1sin2SacB,53sinB,
所以3310ac,10ac. ……………………8分
由余弦定理Baccabcos2222, ……………………9分
得165842222caacca,即2022ca. ……………………10分
所以2()220acac,2()40ac, ……………………12分
所以,102ca. …………13分
16.(本小题满分13分)
(Ⅰ)证明:因为平面ABCD平面ADEF,90ADE,
所以DE平面ABCD,………2分 所以ACDE.………3分
因为ABCD是正方形,所以BDAC,
所以AC平面BDE. …………………4分
(Ⅱ)证明:设ACBDO,取BE中点G,连结OGFG,,
所以,OG//12DE. ……5分因为DEAF//,AFDE2,所以AF//OG,……6分
从而四边形AFGO是平行四边形,AOFG//. ……………………7分
因为FG平面BEF,AO平面BEF, ……………………8分
A
B
C
G
F
E
D
O
北京市西城区2011年高三一模试卷数学(文科)参考答案 第2页(共4页)
所以//AO平面BEF,即//AC平面BEF. ……………………9分
(Ⅲ)解:因为平面ABCD平面ADEF,ABAD,所以AB平面ADEF. ………11分
因为DEAF//,90ADE,22AFDADE,
所以DEF的面积为122EDAD, ……………………12分
所以四面体BDEF的体积ABSDEF3143. ……………………13分
17.(本小题满分13分)
解:(Ⅰ)由已知可得211123aaqaq, ……………………2分
因为{}na是等比数列,所以23210qq. ……………………3分
解得1q或13q. ……………………5分
(Ⅱ)①当1q时,1nbn,232nnnT, ……………………7分
所以,当2n时,2202nnnnTb.
即当1q时,(2)nnTbn. ……………………8分
②当13q时,72(1)()33nnbn, ……………………9分
2
132(1)()236nnnnTnn
, ……………………10分
(1)(14)6nnnnTb
, ……………………12分
所以,当14n时,nnTb;当14n时,nnTb;当214n时,nnTb.…13分
综上,当1q时,(2)nnTbn.当13q时,若14n,nnTb;若14n,nnTb;若214n,
nn
Tb
.
18.(本小题满分14分)
解:(Ⅰ)()ln1fxx,0x, ……………………2分
由()0fx得1ex, ……………………3分
所以,()fx在区间1(0,)e上单调递减,在区间1(,)e上单调递增. ………………4分
所以,1ex是函数()fx的极小值点,极大值点不存在. …………………5分
(Ⅱ)设切点坐标为00(,)xy,则000lnyxx, …………………6分
北京市西城区2011年高三一模试卷数学(文科)参考答案 第3页(共4页)
切线的斜率为0ln1x,
所以,0001ln1yxx, …………………7分
解得01x,00y, …………………8分
所以直线l的方程为10xy. …………………9分
(Ⅲ)()gxln(1)xxax,
则()ln1gxxa, …………………10分
解()0gx,得1eax,
所以,在区间1(0,e)a上,()gx为递减函数,
在区间1(e,)a上,()gx为递增函数. …………………11分
当1e1a,即1a时,在区间[1,e]上,()gx为递增函数,
所以()gx最小值为(1)0g. …………………12分
当11
所以()gx最小值为(e)eegaa. ………………14分
综上,当1a时,()gx最小值为0;当12a时,()gx的最小值1eaa;当2a时,()gx的最小
值为eeaa.
19.(本小题满分14分)
解:(Ⅰ)由已知,4x不合题意.设直线l的方程为(4)ykx,
由已知,抛物线C的焦点坐标为(1,0), …………………1分
因为点F到直线l的距离为3,所以2331kk, …………………3分
解得22k,所以直线l的斜率为22 . …………………5分
(Ⅱ)设线段AB中点的坐标为00(,)Nxy,),(),,(2211yxByxA,
因为AB不垂直于x轴,
则直线MN的斜率为004yx,直线AB的斜率为004xy, …………………7分
直线AB的方程为00004()xyyxxy, …………………8分
北京市西城区2011年高三一模试卷数学(文科)参考答案 第4页(共4页)
联立方程000024(),4,xyyxxyyx
消去x得2200000(1)(4)04xyyyyxx, …………………10分
所以012044yyyx, …………………11分
因为N为AB中点,所以1202yyy,即00024yyx, …………………13分
所以02x.即线段AB中点的横坐标为定值2. …………………14分
20. (本小题满分13分)
解:(Ⅰ)3n时,排列321,,aaa的所有可能为1,2,3;1,3,2;2,1,3;2,3,1;3,1,2;3,2,1.
………………2分
2)3,2,1(;3)2,3,1(;3)3,1,2(
;
3)1,3,2(;3)2,1,3(;2)1,2,3(
. ………………4分
(Ⅱ)1210(,,,)aaa1223910||||||aaaaaa
上式转化为1223910aaaaaa,
在上述18个中,有9个选正号,9个选负号,其中110,aa出现一次,239,,,aaa各出现两次.
………………6分
所以1210(,,,)aaa可以表示为9个数的和减去9个数的和的形式,
若使1210(,,,)aaa最大,应使第一个和最大,第二个和最小.
所以1210(,,,)aaa最大为:
(10109988776)(112233445)49
. ……………8分
所对应的一个排列为:5,7,1,8,2,9,3,10,4,6.(其他正确的排列同等给分) ………9分
(Ⅲ)不可以.
例如排列10,9,8,7,1,2,3,4,5,6,除调整1,2外,其它调整都将使波动强度增加,调整1,2波动强度不
变. ……………11分
所以只能将排列10,9,8,7,1,2,3,4,5,6调整为排列10,9,8,7,2,1,3,4,5,6.
对于排列10,9,8,7,2,1,3,4,5,6,仍然是除调整2,1外,其它调整都将使波动强度增加,所以仍只能调
整1,2两个数字.
如此不断循环下去,不可能经过有限次调整使其波动强度降为9. ……………13分
