《有余数除法的初步认识》精品课件
合集下载
有余数的除法PPT课件
课件contents•引入与概念•运算方法与步骤目录•实例分析与计算•应用场景与拓展•练习题与答案解析引入与概念01如何分配物品，使得每个人得到的数量不同？在日常生活中，遇到不能整除的情况怎么办？有余数除法在实际问题中的应用有哪些？引入问题有余数除法定义有余数除法的概念两个整数相除，不能整除时，商为整数，余数为非零整数的除法运算。
余数的定义在整数除法中，被除数减去除数与商的乘积后所得的数。
有余数除法表示方法a ÷b =c …… r，其中a为被除数，b 为除数，c为商，r为余数。
无余数除法中，被除数能被除数整除，商为整数；有余数除法中，被除数不能被除数整除，商为整数，余数为非零整数。
结果差异无余数除法满足结合律和交换律；有余数除法不满足这些运算性质。
运算性质无余数除法常用于等分、计算比例等问题；有余数除法常用于解决分配、周期等问题。
应用场景与无余数除法区别运算方法与步骤02将被除数、除数和商按照竖式格式排列。
列竖式如果余数大于除数，说明试商偏小，需要调大；如果余数小于除数，说明试商偏大，需要调小。
调整根据被除数和除数的大小，估计一个接近的商。
试商将试商与除数相乘，得到积。
相乘将被除数减去积，得到余数。
相减0201030405竖式运算方法运算步骤详解观察被除数和除数的大小关系，确定商的位数。
从被除数的最高位开始，依次与除数相除，得到每一位的商和余数。
将每一位的商相加，得到最终的商。
根据被除数的最高位和除数的最高位进行试商，确定商的最高位。
010204注意事项在列竖式时，要保证被除数、除数和商的位数对齐。
在试商时，要根据被除数和除数的大小关系进行估计，避免过大或过小的试商。
在相乘和相减时，要注意运算顺序和符号问题。
在得到最终的商后，要检查余数是否为零，以确保运算的正确性。
03实例分析与计算03例子1：23 ÷5 = 4...3计算过程：23 -5 ×4 = 3被除数为17，除数为3，商为5，余数为2。
数学下册《有余数的除法》课件
在其他学科中的应用
01 02
物理学
在物理学中，常常需要将一定量的能量、物质等分成若干个相同的小部 分，这时就可以使用有余数的除法来确定每一部分的大小和剩余部分的 大小。
化学
在化学中，常常需要将一定量的化学物质进行反应，如果反应不完全， 就可以使用有余数的除法来确定剩余的化学物质的数量。
03
经济学
在经济学中，常常需要将一定量的资源分配给一定量的人或组织，如果
02
除法运算可以用以下符号表示：被 除数÷除数=商，其中被除数是待 分配的数，除数是每份的数量，商 是能整除被除数的最大整数。
余数的概念
余数是在除法运算中，被除数除以除 数后剩下的部分。
余数的取值范围是0到除数减一，即当 被除数能被除数整除时，余数为0；否 则，余数为非负整数。
有余数除法的定义
有余数除法是一种特殊的除法运算，被除数、除数和商都是非负整数，且商和余 数满足一定的关系。
有余数除法可以用以下符号表示：被除数=商×除数+余数，其中余数的取值范围是 0到除数减一。
03
有余数除法的性质
余数的性质
余数的定义
当一个数被另一个数除时， 不能整除的部分称为余数。
余数的取值范围
余数的取值范围是0到除数 -1，即0≤余数<除数。
余数的唯一性
一个数被另一个数除，如 果有两个余数，则这两个 余数是相同的。
果？
题目6
计算：10个橘子平均分 给5个人，每人分得多少 个橘子，还剩下多少个
橘子？
题目7
计算：15个糖果平均分 给10个人，每人分得多 少个糖果，还剩下多少
个糖果？
题目8
计算：24个香蕉平均分 给12个人，每人分得多 少个香蕉，还剩下多少
数学下册《有余数的除法》课件
等。
通过这类题目，培养学生的综 合运用能力和思维灵活性，提 高其解决复杂问题的能力。
06
总结与回顾
本节课的总结
重点内容
本节课主要学习了有余数的除法，包括余数的概念、有余数除法 的计算方法以及余数在现实生活中的应用。
难点解析
通过例题和练习，深入理解了有余数除法的原理，掌握了计算方法 和技巧，能够正确运用余数解决实际问题。
小数除法
除数、被除数和商都是小 数，且商的小数点位置与 被除数的小数点位置对齐。
分数除法
除数、被除数和商都是分 数，且商的分子与被除数 的分子相除，分母与被除 数的分母相除。
余数运算规则
余数的定义
在整数除法中，被除数减 去除数与商的乘积后的剩 余部分即为余数。
余数的取值范围
余数的取值范围在0到除数 -1之间，即0≤余数<除数。
下节课预告
• 下节课我们将继续学习《分数的运算》，主要内容包括分数的 加、减、乘、除以及分数的混合运算。通过学习，我们将进一 步掌握分数的运算方法和技巧，为后续学习打下坚实的基础。
感谢您的观看
THANKS
当被除数不能被除数整除时，进行的除法运算称为有余数除法。
有余数除法的性质
在有余数除法中，商和余数是唯一确定的，并且商和余数之间有一定的关系。例 如，在$a div b = c ... d$中，$a = b times c + d$。
03
有余数除法的运算规则
除法运算规则
01
02
03
整数除法
除数、被除数和商都是整 数，且商的最高位在被除 数的整数部分。
提升练习
针对知识应用的提高练习题目
•·
设计一些稍有难度的题目，如 “23÷5=？余数是多少？”等， 要求学生不仅会计算商和余数， 还要理解余数的意义和作用。
通过这类题目，培养学生的综 合运用能力和思维灵活性，提 高其解决复杂问题的能力。
06
总结与回顾
本节课的总结
重点内容
本节课主要学习了有余数的除法，包括余数的概念、有余数除法 的计算方法以及余数在现实生活中的应用。
难点解析
通过例题和练习，深入理解了有余数除法的原理，掌握了计算方法 和技巧，能够正确运用余数解决实际问题。
小数除法
除数、被除数和商都是小 数，且商的小数点位置与 被除数的小数点位置对齐。
分数除法
除数、被除数和商都是分 数，且商的分子与被除数 的分子相除，分母与被除 数的分母相除。
余数运算规则
余数的定义
在整数除法中，被除数减 去除数与商的乘积后的剩 余部分即为余数。
余数的取值范围
余数的取值范围在0到除数 -1之间，即0≤余数<除数。
下节课预告
• 下节课我们将继续学习《分数的运算》，主要内容包括分数的 加、减、乘、除以及分数的混合运算。通过学习，我们将进一 步掌握分数的运算方法和技巧，为后续学习打下坚实的基础。
感谢您的观看
THANKS
当被除数不能被除数整除时，进行的除法运算称为有余数除法。
有余数除法的性质
在有余数除法中，商和余数是唯一确定的，并且商和余数之间有一定的关系。例 如，在$a div b = c ... d$中，$a = b times c + d$。
03
有余数除法的运算规则
除法运算规则
01
02
03
整数除法
除数、被除数和商都是整 数，且商的最高位在被除 数的整数部分。
提升练习
针对知识应用的提高练习题目
•·
设计一些稍有难度的题目，如 “23÷5=？余数是多少？”等， 要求学生不仅会计算商和余数， 还要理解余数的意义和作用。
有余数的除法教学课件ppt
2. 23个 ，3个3个地圈。
圈了（ 7 ）组，剩下（ 2 ）个。 23÷3＝ 7（组）…… 2（个）
在整堂课 的教学 中，刘 教师总 是让学 生带着 问题来 学习， 而问题 的设置 具有一 定的梯 度，由 浅入深 ，所提 出的问 题也很 明确
拓展延伸
A ÷6 ﹦5……（ ） （ ）里都可以填几
分的物品 几个一份
分的结果
算式表达
6个
每2个一盘 分了3盘，恰好分完 6÷2＝3(盘)
7个
每2个一盘 分了3盘，还剩一个 7÷2＝3(盘)……1(个)
有余数的除法
圈一圈，填一填，及时巩固
1. 17个 ，2个2个地圈。
圈了（ 8 ）组，剩下（ 1 ）个。 17÷2＝ 8（组）…… 1（个）
圈一圈，填一填，及时巩固
把下面这些 每2个摆一盘，摆一摆。
6÷2＝3(盘)
把下面这些 每2个摆一盘，摆一摆。
7÷2＝3(，初步感知有余数除法的意义。
把下面这些 每2个摆一盘，摆一摆。
6÷2＝3（盘） 7÷2＝3（盘）……1（个）
比较：有什么相同？有什么不同？
把下面这些 每2个摆一盘，摆一摆。
圈了（ 7 ）组，剩下（ 2 ）个。 23÷3＝ 7（组）…… 2（个）
在整堂课 的教学 中，刘 教师总 是让学 生带着 问题来 学习， 而问题 的设置 具有一 定的梯 度，由 浅入深 ，所提 出的问 题也很 明确
拓展延伸
A ÷6 ﹦5……（ ） （ ）里都可以填几
分的物品 几个一份
分的结果
算式表达
6个
每2个一盘 分了3盘，恰好分完 6÷2＝3(盘)
7个
每2个一盘 分了3盘，还剩一个 7÷2＝3(盘)……1(个)
有余数的除法
圈一圈，填一填，及时巩固
1. 17个 ，2个2个地圈。
圈了（ 8 ）组，剩下（ 1 ）个。 17÷2＝ 8（组）…… 1（个）
圈一圈，填一填，及时巩固
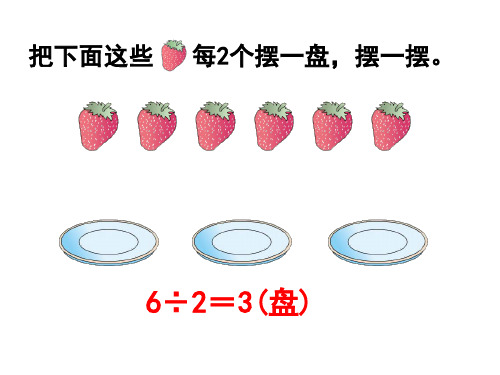
把下面这些 每2个摆一盘，摆一摆。
6÷2＝3(盘)
把下面这些 每2个摆一盘，摆一摆。
7÷2＝3(，初步感知有余数除法的意义。
把下面这些 每2个摆一盘，摆一摆。
6÷2＝3（盘） 7÷2＝3（盘）……1（个）
比较：有什么相同？有什么不同？
把下面这些 每2个摆一盘，摆一摆。
有余数的除法课件(21张PPT)
（ 6）个。
20÷7= 2（人）……6（个）
余数必须
（5）拿出21个小圆片每人）拿出22个小圆片每人分7个，可以分给（ 3）人，还剩
（1）个。
22÷7= 3（人）……1（个）
返回
平均每筒可以装几个？还剩几个？
例4
求57里面有几个9，还 剩几，用除法计算。
剩下的4个不 够分1份。
18÷7= 2（人）……4（个）
…
… … …
被除 商
余
除数
数
数
返回
（2）拿出18个小圆片每人分7个，可以分给（2）人，还剩
（4）个。
18÷7= 2（人）……4（个）
（3）拿出19个小圆片每人分7个，可以分给（ 2）人，还剩
（ 5）个。
19÷7= 2（人）……5（个）
（4）拿出20个小圆片每人分7个，可以分给（2）人，还剩
57÷9=
(个)…… （个）
返回
57÷9= 6 (个)…… 3 （个） 6
9 57 54
3 ……余数 答：平均每筒可以装（ 6 ）个， 还剩（ 3 ）个。
返回
计算。 50÷6=（ ）……（ ） 例 5 哪位同学的计算是正确的？为什么？
7
8
6 50
6 50
42
48
8 余数
2
返回
计算。 50÷6=（ ）……（ ）
返回
试一试。
27÷4= 6……3 58÷7= 8……2
6 4 27
24
3
8 7 58
56
2
返回
说说错在哪里，再改正。
余数要比除数小。
7 7 49
49
08
商要写在个位上。
《有余数的除法》示范课PPT课件
列式表达
9 ÷ 4= 2 …… 1 10÷4= 2 …… 2 11 ÷4= 2 …… 3 12÷4= 3 13÷4= 3 …… 1
1、计算有余数的除法，（余数）一定要比（除数）小。
2、46 ÷ 9 ＝5……1中，被除数是（ ）46，除
数是（ ）9 ，商是（ ）5，余数是（ ）。1 3、一个数除以8，余数可能是（7、6、5、4、）3、2、1
圈了（ 8）组， 剩下（ 1）个。
17÷2＝ 8（组）…… 1（个）
圈了（ 7）组， 剩下（ 2）个。
23÷3＝ 7（组）…… 2（个）
摆一摆，探究余数、除数大小关系
摆一摆，探究余数、除数大小关系
问题：1. 用9根小棒，你能摆几个这样的 正方形？请你动手摆一摆。 2. 能用除法算式表示你摆的意思吗？ 3. 如果用10根小棒来摆呢？ 4. 11根、12根呢? 5. 余数和谁有很密切的关系？ 是什么关系？
复习巩固除数意义，引出课题
4 ÷ 2= 9 ÷ 3=
35 ÷ 7= 12÷5= ？
学习目标
1、在平均分的活动中认识余数，理解有余数除法 的意义。 2、能根据平均分有剩余的活动写出除法算式，正确表达
商和余数。
创设情境 ，初步感知
把下面这些
每ห้องสมุดไป่ตู้个摆一盘，摆一摆。
6÷2＝3(盘)
创设情境 ，初步感知
总结
①剩下不能再分的数叫做余数。 ②计算有余数的除法，余数要比 除数小。
谢 谢！
把下面这些
每2个摆一盘，摆一摆。
7÷2＝3(盘)……1(个)
比一比，感知有余数除法的意义
6÷2＝3（盘） 7÷2＝3（盘）……1（个）
比较：有什么相同？有什么不同？
有余数的除法课件PPT
余数处理不当
学生可能未能正确处理余 数，导致余数与商的位数 不一致。
运算顺序错误
在复杂的除法运算中，学 生可能未能依照正确的运 算顺序进行计算，导致结 果错误。
错误原因分析
概念理解不清楚
学生对除法的概念理解不 清楚，无法准确判断商的 位数和余数的处理方式。
运算能力不足
学生的运算能力不足，无 法在复杂的除法运算中正 确处理余数和商的位数。
余数的性质
总结词
余数具有一些重要的性质，包括余数的唯独性、余数的取值范围以及余数的符 号。
详细描写
余数的唯独性是指在一个除法中，余数是唯独的。余数的取值范围取决于除数 的大小，例如，如果除数是a，那么余数的取值范围是0到a-1。余数的符号与被 除Biblioteka 和除数的符号相同。余数的范围
总结词
余数的取值范围受到除数的限制，具体的范围取决于除数的 大小。
余数的取值范围是0到除数-1， 当余数为0时，表示被除数能被
除数整除。
有余数除法的计算方法
01
02
03
04
确定被除数和除数
第一确定要进行除法运算的被 除数和除数。
确定商
将被除数除以除数，得到商。
确定余数
用被除数减去商乘以除数的结 果，得到余数。
写出答案
将商和余数写出，即为有余数 除法的结果。
03
详细描写
如果除数是正数或零，余数的取值范围是0到除数减一。如果 除数是负数，余数的取值范围是负除数到0。例如，如果除数 是5，那么余数的取值范围是0到4；如果除数是-3，那么余 数的取值范围是-3到0。
02
有余数的除法运算
除法的基本概念
除法是一种数学运算，表示将一个数（被除数）平均分成若干等份（除数），求每 一份的数值（商）和剩余的部分（余数）。
《有余数除法的认识》PPT-完美版
《有余数除法的认识》PPT-完美版
《有余数除法的认识》PPT-完美版
情景导入
课件PPT
生活中这样的事情可多 了，你能举出几件吗
《有余数除法的认识》PPT-完美版
《有余数除法的认识》PPT-完美版
情景导入
三个人分三支铅笔，每 个人分三支，还剩一支
课件PPT
《有余数除法的认识》PPT-完美版
《有余数除法的认识》PPT-完美版
•
1、学生自读。指名读。
•
2、理解重点词语：
•
3、有感情地朗读、背诵。
•
课外再搜集一些鲁迅先生的名言。
•
趣味语文
•
1、过渡：鲁迅先生的童年发生过许多 故事， 这节课 我们就 来读一 个鲁迅 巧对先 生的故 事。
•
2、学生自读。指名读。
•
周樟寿的对子妙在哪里？他为什么对 得好？
•
文人巧对对联的故事还有很多，课后 搜集此 类故事 ，与同 学们交 流。
•
联系上下文；联系生活实际；结合时 代背景 ；展开 丰富联 想。……
•
师：希望同学们在以后的学习过程中 ，继 运用我 们总结 的这些 体会句 子的方 法去学 习课文 ，一定 会有更 多的收 获。
•
日积月累
•
过渡：鲁迅先生的文章无疑是人类文 化宝库 中的一 笔财富 ，这节 课我们 一起细 细品读 鲁迅先 生文章 中的脍 炙人口 、发人 深省的 名言警 句。
典题精讲
分画片 21 5=4（个）……1（张）
余数
课件PPT
21 5=4……1读作：21除以5商4余1
《有余数除法的认识》PPT-完美版
《有余数除法的认识》PPT-完美版 《有余数除法的认识》PPT-完美版
《有余数的除法》优质课件
详细描述
有余数除法是一种特殊的除法运算，其中被除数不能被除数整除，商和余数都 不为零。例如，当我们将7除以3时，商为2，余数为1，这表明7除以3有余数。
有余数除法的性质
总结词
有余数除法具有以下性质：余数小于除数，余数可以为0，余数的符号与商的符号相同。
详细描述
首先，余数总是小于除数。例如，当我们将9除以4时，余数为1，因为1小于4。其次，余数可以为0，表示被除 数正好能被除数整除。最后，如果商为正数，则余数也为正数；如果商为负数，则余数也为负数。这意味着余数 的符号与商的符号相同。
在科学计算中的应用
物理学
在物理学中，有余数的除法可以 用来计算速度、加速度和力等物 理量，例如计算物体的运动轨迹
或者力的合成与分解。
化学
在化学中，有余数的除法可以用 来计算化学反应的速率和平衡常 数，例如计算化学反应的速率或
者反应产物的浓度。
天文学
在天文学中，有余数的除法可以 用来计算天体的轨道和位置，例 如计算行星或者卫星的轨道参数
反馈建议
学生提出自己的学习感受和建议，帮 助教师更好地改进教学方法和课件内 容。
下节课预告
下节课主题
介绍下节课的主题和重点内容，让学生提前预习和准备。
预告内容
简要介绍下节课的教学内容和目标，激发学生的好奇心和学 习动力。
THANKS
谢谢提升学生的计算能力和对余数的理解
详细描述
设计一些涉及多个步骤的除法题目，例如连续除法、除法的逆运算等，以加强学 生对余数在复杂计算中的运用。
综合练习题
总结词
培养学生解决实际问题的能力
详细描述
设计一些与实际生活相关的题目，例如购物时找零、分配物品等，让学生在实际情境中运用有余数的 除法知识。
有余数除法是一种特殊的除法运算，其中被除数不能被除数整除，商和余数都 不为零。例如，当我们将7除以3时，商为2，余数为1，这表明7除以3有余数。
有余数除法的性质
总结词
有余数除法具有以下性质：余数小于除数，余数可以为0，余数的符号与商的符号相同。
详细描述
首先，余数总是小于除数。例如，当我们将9除以4时，余数为1，因为1小于4。其次，余数可以为0，表示被除 数正好能被除数整除。最后，如果商为正数，则余数也为正数；如果商为负数，则余数也为负数。这意味着余数 的符号与商的符号相同。
在科学计算中的应用
物理学
在物理学中，有余数的除法可以 用来计算速度、加速度和力等物 理量，例如计算物体的运动轨迹
或者力的合成与分解。
化学
在化学中，有余数的除法可以用 来计算化学反应的速率和平衡常 数，例如计算化学反应的速率或
者反应产物的浓度。
天文学
在天文学中，有余数的除法可以 用来计算天体的轨道和位置，例 如计算行星或者卫星的轨道参数
反馈建议
学生提出自己的学习感受和建议，帮 助教师更好地改进教学方法和课件内 容。
下节课预告
下节课主题
介绍下节课的主题和重点内容，让学生提前预习和准备。
预告内容
简要介绍下节课的教学内容和目标，激发学生的好奇心和学 习动力。
THANKS
谢谢提升学生的计算能力和对余数的理解
详细描述
设计一些涉及多个步骤的除法题目，例如连续除法、除法的逆运算等，以加强学 生对余数在复杂计算中的运用。
综合练习题
总结词
培养学生解决实际问题的能力
详细描述
设计一些与实际生活相关的题目，例如购物时找零、分配物品等，让学生在实际情境中运用有余数的 除法知识。