MATLAB入门教程(2) 二维绘图
实验二MATLAB绘图帽子哥版

实验二MATLAB绘图一、实验目的1 掌握绘制二维图形的常用函数。
2 掌握绘制三维图形的常用函数。
3 熟悉利用图形对象进行绘图操作的方法。
4 掌握绘制图形的辅助操作。
二、实验设备及预备材料:实验设备:MATLAB7.0;预备材料:(一)曲线图:Matlab作图是通过描点、连线来实现的,故在画一个曲线图形之前,必须先取得该图形上的一系列的点的坐标(即横坐标和纵坐标),然后将该点集的坐标传给Matlab函数画图。
命令格式为:plot(x,y,s)其中x,y分别表示所取点集的横纵坐标,s指定线型及颜色。
缺省时表示画的是蓝色实线。
Plot(X,Y1,S1,X,Y2,S2,……,X,Yn,Sn)表示将多条线画在一起。
例在[0,2*pi]用红线画sin(x),用绿圈画cos(x)。
解:x=linspace(0,2*pi,30);y=sin(x);z=cos(x);plot(x,y,’r’,x,z,’go’)所得图形如下图所示(二)符号函数(显函数、隐函数和参数方程)画图(1) ezplotezplot(‘f(x)’,[a,b])表示在a<x<b 绘制显函数f=f(x)的函数图;ezplot(‘f(x,y)’,[xmin,xmax,ymin,ymax])表示在区间xmin<x<xmax 和 ymin<y<ymax 绘制隐函数f(x,y)=0的函数图; ezplot(‘x(t)’,’y(t)’,[tmin,tmax])表示在区间tmin<t<tmax 绘制参数方程x=x(t),y=y(t)的函数图。
例 在[0,pi]上画y=cos(x)的图形解 输入命令:ezplot(‘sin(x)’,[0,pi])例 在[0,2*pi]上画t x 3cos =,t y 3sin =星形图解 输入命令:ezplot(‘cos(t).^3’,’sin(t).^3’,[0,2*pi])例 在[-2,0.5],[0,2]上画隐函数0)sin(=+xy e x 的图解 输入命令:ezplot('exp(x)+sin(x.*y)',[-2,0.5,0,2])(2) fplot格式:fplot(‘fun ’,lims)表示绘制字符串fun 指定的函数在lims=[xmin,xmax]的图形。
MATLAB4二维图形绘制

y3=cos(t);y4=cos(t+0.25);y5=cos(t+0.5); plot(t,y3);hold on; plot(t,y4); plot(t,y5);
1 0.8 0.6 0.4 0.2 0 -0.2 -0.4 -0.6 -0.8 -1 0 1 2 3 4 5 6 7
0
figure(1) title('\fontsize{16}y(\omega)=\int^{\infty }_{0}y(t)e^{-j\omegat}dt')
二、绘制曲线的一般步骤
步骤 1 表 4.1 绘制二维、三维图形的一般步骤 内容 曲线数据准备: 对于二维曲线,横坐标和纵坐标数据变量; 对于三维曲面,矩阵参变量和对应的函数值。 指定图形窗口和子图位置: 默认时,打开 Figure No.1 窗口或当前窗口、当前子图; 也可以打开指定的图形窗口和子图。 设置曲线的绘制方式: 线型、色彩、数据点形。 设置坐标轴: 坐标的范围、刻度和坐标分格线 图形注释: 图名、坐标名、图例、文字说明 着色、明暗、灯光、材质处理(仅对三维图形使用) 视点、三度(横、纵、高)比(仅对三维图形使用) 图形的精细修饰(图形句柄操作): 利用对象属性值设置; 利用图形窗工具条进行设置。
x=peaks;plot(x) x=1:length(peaks);y=peaks;plot(x,y)
10 8 6 4 2 0 -2 -4 -6 -8
0
5
10
15
20
25
30
35
40
45
50
3. 单窗口多曲线分图绘图 subplot(1,3,1); plot(t,y) subplot(1,3,2); plot(t,y3) subplot(1,3,3); plot(t,y2)
第3章 MATLAB绘图

第3章 MATLAB绘图
例3-5:用红颜色、点连线、叉号画 出正弦曲线
clear clc x=0:0.2:8; y=sin(x); plot(x,y,’r:x’)
第3章 MATLAB绘图
3.1 二维绘图
一、plot函数 Plot函数有以下几种常用形式: 1.plot(x) ★若x为向量,则绘制出一个x元素和x元素排列 号之间关系的线性坐标图。 ★若x为矩阵,则绘制出x的列向量相对于行号的 一组二维图形
第3章 MATLAB绘图
例3-1:单矢量绘图(如图3-1)
第3章 MATLAB绘图
三、图形控制
4.图形的填充
fill函数用于填充二维封闭多边形。 函数:fill (x,y,‘颜色参数’) 功能:在由数据所构成的多边形内,用所指定的颜色 填充。如果该多边形不是封闭的,则用初始点 和终点的连线将其封闭。颜色参数三维控制符
同plot函数。
第3章 MATLAB绘图
Clear Clc x=[0 0.2 0.5 0.7 0.6 0.7 1.2 1章 MATLAB绘图
例3-2:二维矩阵绘图(如图3-2)
clear clc x=[1 2 3;7 8 9; 13 14 15];
plot(x)
auto
ij
square
将图形设置为正方形图形
xy
使用笛卡儿坐标系
equal
将图形的x,y坐标轴的单位刻 on 度设置为相等 关闭axis(square)和axis(equal) 函数的作用
打开所有轴标注、标记和背景
第5章matlab绘制二维图形及三维图形的方法
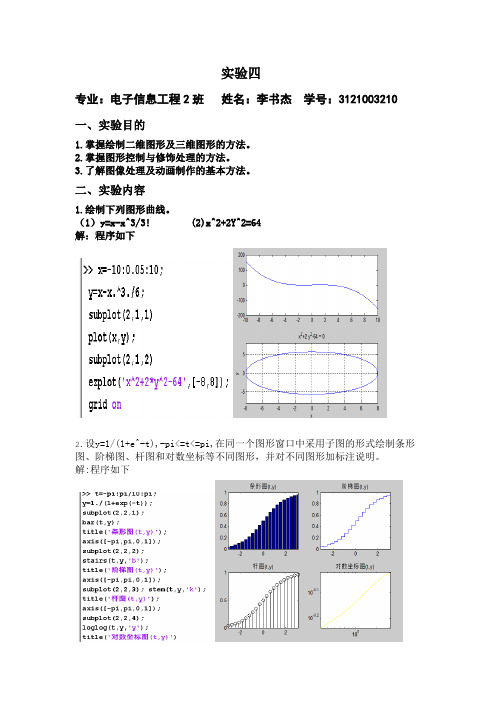
实验四
专业:电子信息工程2班姓名:李书杰学号:3121003210
一、实验目的
1.掌握绘制二维图形及三维图形的方法。
2.掌握图形控制与修饰处理的方法。
3.了解图像处理及动画制作的基本方法。
二、实验内容
1.绘制下列图形曲线。
(1)y=x-x^3/3! (2)x^2+2Y^2=64
解:程序如下
2.设y=1/(1+e^-t),-pi<=t<=pi,在同一个图形窗口中采用子图的形式绘制条形图、阶梯图、杆图和对数坐标等不同图形,并对不同图形加标注说明。
解:程序如下
3.绘制下列极坐标图。
(1)ρ=5cosθ+4 (2)γ=5sin^2φ/cosφ,-π/3<φ<π/3 解:程序如下
思考练习:
2.绘制下列曲线
(1)y=1/2πe^(-x^2/2) (2)x=tsint y=tcost
解:程序如下
(1)
结果如下:
(2)
结果如下:
3.在同一坐标中绘制下列两条曲线并标注两曲线交叉点。
(1)y=2x-0.5
(2)x=sin(3t)cost
Y=sin(3t)sint
解:程序如下
4.分别用plot和fplot函数绘制y=sin(1/x)的曲线,分析两曲线的差别。
解:程序如下
结果如下:
5.绘制下列极坐标图:
(1)p=12/sqrt(θ) (2)γ=3asinφcosφ/(sin^3φ+cos^3φ)解:程序如下
结果如下:。
matlab:画二维正态分布密度函数图

matlab:画⼆维正态分布密度函数图⾸先,把⼆维正态分布密度函数的公式贴这⾥这只图好⼤啊~~但是上⾯的那个是多维正态分布的密度函数的通式,那个n阶是对称正定⽅阵叫做协⽅差矩阵,其中的x,pi,u都是向量形式。
虽然这个式⼦很酷,但是⽤在matlab⾥画图不太⽅⾯,下⾯换⼀个这个公式与上⾯的等价,只不过把向量和矩阵展开,计算出来。
我们可以⽤这个式⼦画图。
因为⼆维函数的形式是:z=f(x,y)所以必须先选择⼀些点,然后计算出f(x,y)。
这些点分布在⼀个平⾯上,⽽z则在三维空间。
如何选择平⾯上的点阵?[x,y]=meshgrid(a,b)meshgrid就是这样⼀个⽣成点阵的函数,这个meshgrid理解起来有点绕,不过举个例⼦就马上能⼒明⽩了。
下⾯是matlab⾥⾯的⼀段截图:我们可以看到meshgrid⽣成了两个同样⼤⼩的矩阵,第⼀个矩阵是通过把第⼀个参数[1:3]顺着⾏的⽅向复制了4次,4是第⼆个参数的长度,同样第⼆个矩阵是第⼆个参数顺着列的⽅向复制了三次,3是第⼀个参数向量的长度。
⽽这个点阵就是:(1,2) (2,2) (3,2)(1,3) (2,3) (3,3)...看出什么意思了吧?就这个意思。
⾄于这两个参数到底怎么选,这样根据你的正态分布的均值,尽量使点阵的中⼼与分布的均值靠近。
好了,有了平⾯上的点,就来算这些点对应的函数值。
往函数⾥套就⾏,下⾯是代码:function Z=drawGaussian(u,v,x,y)% u,vector,expactation;v,covariance matrix%x=150:0.5:190;%y=35:110;[X,Y]=meshgrid(x,y);DX=v(1,1); %X的⽅差dx=sqrt(DX);DY=v(2,2); %Y的⽅差dy=sqrt(DY);COV=v(1,2); %X Y的协⽅差r=COV/(dx*dy);part1=1/(2*pi*dx*dy*sqrt(1-r^2));p1=-1/(2*(1-r^2));px=(X-u(1)).^2./DX;py=(Y-u(2)).^2./DY;pxy=2*r.*(X-u(1)).*(Y-u(2))./(dx*dy);Z=part1*exp(p1*(px-pxy+py));mesh(x,y,Z); 最后⼀句mesh(x,y,Z) 是画图函数,画出的图⾏⼤概是下⾯这个样⼦:。
MATLAB入门教程

用户可以尝试点击MATLAB界面上的各个按钮,看看它们的功能。如果不小心关闭了当前路径窗口、命令历史记录窗口或命令窗口,可以通过菜单栏的“Desktop”菜单中“DesktopLayoutDefault”恢复,如图1.1.3所示:
图1.1.3把MATLAB界面窗口恢复为默认状态
1.2.1
在命令窗口中的>>后面输入:
[1]李继成,《数学实验》,高等教育出版社,2006年10月,第1版。
[2]罗建军,《MATLAB教程》,电子工业出版社,2005年07月,第1版。
[3]徐金明等,《MATLAB实用教程》,清华大学出版社,2005年7月,第1版。
[4]张圣勤,《MATLAB7.0实用教程》,机械工业出版社,2006年7月,第1版。
数学实验简明教程
MATLAB入门
2东南大学数学系
007.10.10
Matlab是美国MathWorks公司自20世纪80年代中期推出的数学软件,优秀的数值计算能力和卓越的数据可视化能力使其很快在数学软件中脱颖而出。到目前为止,其最高版本7.0版已经推出。随着版本的不断升级,它在数值计算及符号计算功能上得到了进一步完善。Matlab已经发展成为多学科、多种工作平台的功能强大的大型软件。在欧美等高校,Matlab已经成为线性代数、自动控制理论、概率论及数理统计、数字信号处理、时间序列分析、动态系统仿真等高级课程的基本教学工具,是攻读学位的大学生、硕士生、博士生必须掌握的基本技能。
图2.1.3智能ABC输入法5.0版的几种输入状态
图2.1.4MATLAB提示
因此,应该在“半角”及“英文标点”格式 下输入标点符号,如逗号(,),分号(;),句号/小数点(.)。
2
1.全零阵。
matlab里的plot的功能与用法(二)

matlab里的plot的功能与用法(二)MATLAB中plot函数的功能与用法简介plot函数是MATLAB中最常用的绘图函数之一,它用于绘制一维和二维图形。
通过plot函数,我们可以方便地绘制曲线、散点图、柱状图等各种图形。
本文将介绍plot函数的一些常用用法。
绘制基本曲线使用plot函数,可以绘制基本的曲线。
下面是一个简单的示例代码:x = linspace(0, 2*pi, 100);y = sin(x);plot(x, y)参数说明•x:表示x轴上的数据点的取值,可以是向量或矩阵。
在上述示例代码中,我们使用了linspace函数生成了一个包含100个点的向量。
•y:表示y轴上的数据点的取值,也可以是向量或矩阵。
在示例代码中,我们计算了对应于x轴取值的正弦函数值。
绘制结果运行上述代码,可以绘制出一个以x为自变量,y为因变量的曲线图。
修改曲线样式plot函数允许我们修改绘图的样式,包括曲线的颜色、线型、标记等。
下面是一个示例代码:x = linspace(0, 2*pi, 100);y = sin(x);plot(x, y, 'r--o')参数说明通过在plot函数的第三个参数位置传入一个字符串,我们可以控制绘图的样式: - 'r':表示曲线的颜色为红色。
- '--':表示曲线的线型为虚线。
- 'o':表示在每个数据点处绘制圆形标记。
绘制结果通过修改样式参数,我们可以得到一条红色的虚线,且在每个数据点处都有圆形标记的曲线图。
绘制多个曲线除了绘制单个曲线外,我们还可以在同一个图中绘制多个曲线。
下面是一个示例代码:x = linspace(0, 2*pi, 100);y1 = sin(x);y2 = cos(x);plot(x, y1, 'r')hold on % 开启绘图保持功能plot(x, y2, 'b--')legend('sin', 'cos')参数说明•y1和y2:分别表示两条曲线的因变量取值。
第二讲 MATLAB 绘图

绘制y=1-exp(0.3*t).*cos(0.7*t)
t=6*pi*(0:100)/100; y=1-exp(-0.3*t).*cos(0.7*t); tt=t(find(abs(y-1)>0.05)); ts=max(tt); plot(t,y,'r-'); grid on; axis([0,6*pi,0.6,max(y)]); title('y=1-exp(-\alpha*t)*cos(\omega*t)'); hold on; plot(ts,0.95,'bo'); hold off; set(gca,'xtick',[2*pi,4*pi,6*pi],'ytick',[0.95,1,1.05,max(y)]); grid on;
绘制曲线
x t cos(3t ) , t 2 y t sin t
t = -pi:pi/100:pi; x = t.*cos(3*t); y = t.*sin(t).^2; plot(x,y)
2015-5-14 10
图形标识
图形标识包括:
图名(title) 坐标轴名(xlabel、ylabel) 图形文本注释(text) 图例(legend)
2015-5-14 22
双纵坐标:plotyy指令
plotyy指令调用格式:
plotyy(x1, y1, x2, y2)
x1-y1曲线y轴在左, x2-y2曲线y轴在右。
例3.7:
x = 0:0.01:20; y1 = 200*exp(-0.05*x).*sin(x); y2 = 0.8*exp(-0.5*x).*sin(10*x); plotyy(x,y1,x,y2);
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MATLAB 的二维绘图基础了解了MATLAB 的矩阵和向量概念与输入方法之后,MATLAB 的二维绘图再简单也不过了。
假设有两个同长度的向量 x 和y, 则用plot(x,y) 就可以自动绘制画出二维图来。
如果打开过图形窗口,则在最近打开的图形窗口上绘制此图,如果未打开窗口,则开一个新的窗口绘图。
〖例〗正弦曲线绘制:>> t=0:.1:2*pi;%生成横坐标向量,使其为0,0.1,0.2,...,6.2y=sin(t); % 计算正弦向量plot(t,y) %绘制图形这样立即可以得出如图所示的二维图[4.1(a)]plot() 函数还可以同时绘制出多条曲线,其调用格式和前面不完全一致,但也好理解。
>> y1=cos(t); plot(t,y,t,y1); %或plot(t,[y; y1]), 即输出为两个行向量组成的矩阵。
图形见 4.1(b)。
plot() 函数最完整的调用格式为:>> plot(x1,y1,选项1, x2,y2, 选项2, x3,y3, 选项3, ...)其中所有的选项如表 4.1 所示。
一些选项可以连用,如'-r' 表示红色实线。
由MATLAB 绘制的二维图形可以由下面的一些命令简单地修饰。
如>> xlabel('字符串') % 给横坐标轴加说明>> ylabel('字符串') % 给纵坐标轴加说明,%并自动旋转90度>> title('字符串') % 给整个图形加图题得出的图形如右图所示。
axis() 函数可以手动地设置x,y 坐标轴范围还可以使用plotyy() 函数绘制具有两个纵坐标刻度的图形。
坐标系的分割在MATLAB 图形绘制中是很有特色的,比较规则的分割方式是用subplot() 函数定义的,其标准调用格式为subplot(n,m,k)其中,n 和m 为将图形窗口分成的行数和列数,而k 为相对的编号。
例如在标准的Bode 图绘制中需要将窗口分为上下两个部分(即n=2, m=1), 分割后上部编号为1,下部编号为2。
MATLAB 的图形对象简介MATLAB 从4.0 版本开始就提出了句柄图形学(Handle Graphics) 的概念,为面向对象的图形处理提供了十分有用的工具。
和早期版本的MATLAB 相比较,其最大区别在于,它在图形绘制时其中每个图形元素(比如其坐标轴或图形上的曲线、文字等) 都是一个独立的对象。
用户可以对其中任何一个图形元素进行单独地修改,而不影响图形的其他部分,具有这样特点的图形称为向量化的绘图。
这种向量化的绘图要求给每个图形元素分配一个句柄(handle), 以后再对该图形元素做进一步操作时,则只需对该句柄进行操作即可。
MATLAB 5.0 版进一步加强了图形绘制的功能,而5.3 版绘图又具有自己的新特色。
例如它提供了新的图形编辑程序,并定义了一些新的三维绘图函数等。
本章将主要介绍MATLAB 5.3 版本的应用与特性,并介绍部分有关句柄图形学的内容。
其余有关句柄图形学的问题,如窗口特性设置、图形界面设计等项内容将在第 6 章中讲述图形界面设计内容时详细介绍。
MATLAB 6 也在图形显示,特别是三维图形显示与照相机参数设置等方面引入了新鲜的内容。
MATLAB 定义的各种图形对象及其关系如下图所示。
获取和改变对象的属性可以采用get() 和set() 函数对来实现。
>> set(句柄, 属性1,属性值1, 属性2,属性值2,...)>> 属性值=get(句柄,属性)坐标轴对象时MATLAB 图形中常用的对象,坐标轴对象可以用MATLAB 5.3 上的菜单项添加。
添加之后,可以用鼠标改变其大小和形状,其他一些属性说明如下:∙Box 属性: 表示是否需要坐标轴上的方框,选项可以为'on' 和'off', 默认的值为'on'。
本书中在后面介绍属性值时,将把默认的属性值列在前面。
∙ColorOrder 属性: 设置多条曲线的颜色顺序,应该为一个n x 3 矩阵,可以由colormap() 函数来设置。
∙GridLineStyle 属性: 网格线类型,如实线、虚线等,其设置类似于plot() 函数的选项,默认值为':',见前面的表格。
∙NextPlot 属性: 表示坐标轴图形的更新方式,'replace' 是默认的选项,表示重新绘制,而'add' 选项表示在原来的图形上叠印,它相当于直接使用hold on 命令的效果。
∙Title 属性: 本坐标轴标题的句柄。
而其具体内容由title() 函数设定,由此句柄就可以访问到原来的标题了。
∙XLabel 属性: x 轴标注的句柄,其内容由xlabel() 函数设定。
此外,类似地还有YLabel 和ZLabel 属性等。
∙XDir 属性: x 轴方向,可以选择'normal' (正向) 和'rev' (逆向), 此外YDir 和ZDir 属性也是类似的。
∙XGrid 属性: 表示x 轴是否加网格线,可选值为'off' 和'on', 此外还类似地有YGrid 和ZGrid 选项。
∙XLim 属性: x 轴上下限,以向量[xm,xM] 形式给出。
此外,还有YLim 和ZLim 属性,前面介绍的axis() 函数实际上是对这些属性的直接赋值。
∙XScale 属性: x 轴刻度类型设置,可以为'linear' (线性的) 和'log' (对数的)。
此外还有YScale 和ZScale 属性。
XTick 和XTickLabel 属性: XTick 属性将给出x 轴上标尺点值的向量,而XTickLabel 将存放这些标尺点上的标记字符串。
对y 和z 轴也将有相应的标尺属性,如ZTick 等。
MATLAB 图形上的文字修饰字符对象及其属性文字标注是图形修饰中的重要因素,它可以是用户在窗口上随意添加的字符说明,还可以是坐标轴对象中所用到的刻度标志等。
字符对象的常用属性如下:∙Color 属性: 字符的颜色。
该属性的属性值是一个1x3 颜色向量。
∙FontAngle 属性: 字体倾斜形式。
如正常'normal' 和斜体'italic' 等。
∙FontName 属性: 字体的名称。
如'Times New Roman' 与'Courier' 等。
∙FontSize 属性: 字号大小。
默认以pt 为单位,属性值应该为实数。
∙FontWeight 属性: 字体是否加黑。
可以选择'light'、'normal' (默认值)、'demi' 和'bold' 4 个选项, 其颜色逐渐变黑。
∙HorizontalAlignment 属性: 表示文字的水平对齐方式。
可以有'left' (按左边对齐)、'center' (居中对齐)、'right'(按右边对齐) 三种选择。
类似地,对字符矩阵的位置还有VerticalAlignment 属性。
∙FontUnits 属性: 字体大小的单位。
如'points' (磅数,即pt) 为默认的值,此外,还可以使用如下单位'inches' (英寸)、'centimeters' (厘米)、'normalized' (归一值) 与'pixels' (像素) 等。
∙Rotation 属性: 字体旋转角度。
可以为任何数值。
∙Editing 属性: 是否允许交互式修改。
选项可以为'on' 和'off'。
∙String 属性: 构成本字符对象的字符串。
可以是字符串矩阵。
∙Interpreter 属性: 是否允许TeX 格式。
选项为'tex' (允许TeX 格式) 和'none' (不允许) 两种,前者显示的效果好,而后者速度快。
∙Extent 属性: 字符串所在的位置范围,是只读型的,1x4 向量,前两个值表示字符串所在位置的左下角坐标,而后两个分量分别为字符对象的长和高。
MATLAB 字符串中可以直接使用的一些TeX 命令见表4-3。
〖例〗给出下面的MATLAB命令>> t=['\partial(f_ip)/\partialt=-\Sigma_{i=1}^n\partial(f_ip)/',...'\partialx_i + 0.5\Sigma_{i=1}^n\Sigma_{j=1}^n',...'\partial^2(b_{ij}p)/\partialx_i\partialx_j'];tt=str2mat(t,'Y(\omega)=\int_0^\infty y(t)e^{-j\omegat}dt');[x,y]=ginput(1); text(x,y,tt);则将得出如下图所示的结果。
看见较复杂的数学公式也可以在MATLAB 窗口中显示出来。
例〗分形理论是一个很有趣的领域,在这里我们给出一个简单的例子。
任意选定一个二维平面上的初始点坐标(x0, y0),假设我们可以生成一个在[0,1] 区间上均匀分布的随机数γi,那么根据其取值的大小,可以按下面的公式生成一个新的坐标点(x1,y1):从新坐标再根据随机数计算下一个点,如此类推。
可以将上面的算法编写出下面的MATLAB 函数function [x,y]=frac_tree(x0,y0,v,N)x=[x0; zeros(N-1,1)]; y=[y0; zeros(N-1,1)];for i=2:Nvv=v(i);if vv<0.05, y(i)=0.5*y(i-1);elseif vv<0.45,x(i)=0.42*(x(i-1)-y(i-1)); y(i)=0.2+0.42*(x(i-1)+y(i-1));elseif vv<0.85,x(i)=0.42*(x(i-1)+y(i-1)); y(i)=0.2-0.42*(x(i-1)-y(i-1));else,x(i)=0.1*x(i-1); y(i)=0.1*y(i-1)+0.2;endend调用此函数,我们可以由下面的MATLAB 命令生成10,000 个这样的点,并将这些点在MATLAB 图形窗口中用点的形式表示出来,如图所示。
