2019年秋浙教版初中数学八年级上册《一次函数》单元测试(含答案) (72)
2019年秋浙教版初中数学八年级上册《一次函数》单元测试(含答案) (84)

浙教版初中数学试卷2019-2020年八年级数学上册《一次函数》测试卷学校:__________ 姓名:__________ 班级:__________ 考号:__________题号 一 二 三 总分 得分评卷人 得分一、选择题1.(2分) 如图,点A 、B 、C 在一次函数2y x m =-+的图象上,它们的横坐标依次为-1、1、2,分别过这些点作x 轴与y 轴的垂线. 则图中阴部分的面积之和是( ) A .1B . 3C .3(1)m -D .3(2)2m -2.(2分)根据右边流程图中的程序,当输入数值x 为2-时,输出数值y 为( ) A .4B .6C .8D .103.(2分)下列函数(1)y x π=,(2)y=2x 一1,(3)1y x=,(4)123y x -=-,(5)21y x =-是一次函数的有( )A .4个B . 3个C . 2个D .1个4.(2分)弹簧的长度与所挂物体的质量关系为一次函数,如图所示,由图可知不挂物体时弹簧的长度为( ) A .7 cmB .8 cmC .9 cmD .10 cm5.(2分)如图,某电信公司提供了A B ,两种方案的移动通讯费用y (元)与通话时间x (元)之间的关系,则以下说法错误..的是( ) A .若通话时间少于120分,则A 方案比B 方案便宜20元 B .若通话时间超过200分,则B 方案比A 方案便宜12元 C .若通讯费用为60元,则B 方案比A 方案的通话时间多 D .若两种方案通讯费用相差10元,则通话时间是145分或185分 6.(2分)一次函数y=kx+b 中,k<0,b>0.那么它的图像不经过( ) A .第一象限B .第二象限C .第三象限D .第四象限7.(2分)如图是某蓄水池的横断面示意图,分为深水池和浅水池,如果这个蓄水池以固定的流量注水,下面能大致表示水的最大深度h 与时间t 之间的关系的图象是( )A .B .C .D .8.(2分)下列函数中,自变量x 的取值范围是x ≥2的是( ) A .2y x =--B .2xy -=C .2y x =-D .24y x =-9.(2分)在△ABC 中,它的底边为a ,底边上的高为h ,则三角形的面积12S ah =,若h 为定长,则此式中( ) A .S 、a 是变量,12、h 是常量 B .S 、h 、a 是变量,12是常量 C .S 、12是常量,a,h 是变量 D .以上答案均不对评卷人 得分二、填空题10.(3分)已知梯形的面积为10,底边上的高为x ,上底为2,下底为y ,则y 与x 之间的函数解析式为 .11.(3分)若点(-4,m ),(3,n )都在直线14y x t =-+上,则m 与n 的大小关系是 . 12.(3分)如图,已知函数y ax b =+和y kx =的图象交于点P ,则根据图象,可得关于y ax by kx=+⎧⎨=⎩的二元一次方程组的的解是 .13.(3分)根据图中的程序,当输入x =3时,输出的结果y = .14.(3分)直线4y kx =+与两坐标轴围成的直角三角形面积为2,则这条直线与x 轴的交点 为 .15.(3分)把直线y=-2x 一2向上平移3个单位的直线是 .16.(3分)一次函数y kx b =+的图象经过点A(0,2),B(3,0),则此函数的解析式为 ;若将该图象沿x 轴向左平移4个单位,则新图象对应的函数解析式是 . 17.(3分)如图,OB ⊥OA 于点0,以 OA 为半径画弧,交OB 于点B ,P 是半径OA 上的动点.已知0A=2cm .设0P=xcm ,阴影部分的面积为ycm 2,则y(cm 2)关于x(cm)的函数解析式为 .18.(3分)直线2y x b =+经过点(13),,则b = .19.(3分)物体沿一个斜坡下滑,它的速度v(m /s)与其下滑时间t(s)的关系如图所示: (1)下滑2s 时物体的速度为 .(2)v(m /s)与t(s)之间的函数解析式为 . (3)下滑3s 时物体的速度为 .20.(3分)弧长的计算公式180n rl π=中,常量是 ,变量是 . 21.(3分)某中学购买一种数学参考书,每本书售价12元,该校有学生x 人,需总金额y元,则y=12x ,这三个量中,常量为 ,变量为 .22.(3分)某居民所在区域电的单价为0.53元/度,所付电费y(元)与用电度数x(度)之间的关系 式是y=0.53x ,其中常量是 ,变量是 .23.(3分)钢筋的横截面面积是0.25π,长度为h ,则钢筋的体积V=0.257πh ,这里常量是 ,变量是 .24.(3分)仓库里现有粮食l200 t ,每天运出60 t ,x 天后仓库里剩余粮食y(t),则y 与x 之间的函数解析式为 ,自变量x 的取值范围是 . 25.(3分)已知函数21xy x =+,当x=-2时,对应的函数值为 .三、解答题26.(6分)在同一直角坐标系中画出一次函数121y x =-+与223y x =+的图象,并根据图象解答下 列问题:(1)直线121y x =-+、223y x =+与y 轴分别交于A 、B .求A 、B 两点的坐标; (2)求直线121y x =-+与223y x =+的交点P 的坐标; (3)△PAB 的面积为多少?27.(6分)若y 是x 的一次函数,当x=2时,y=2,当x=一6时,y=6. (1)求这个一次函数的关系式; (2)当x=8时,函数y 的值;(4)当1≤y<4时,自变量x 的取值范围.28.(6分)一池塘内有水2000 m 3,现用抽水机抽水,每小时可抽水200 m 3. (1)求池塘中余水量y(m 3)与抽水时间x(h)之间的函数解析式; (2)求自变量x 的取值范围; (3)画出它的图象.29.(6分)一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱用,按市场价售出一些后,又降价出售,售出土豆千克数与他手中持有钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:(1)农民自带的零钱是多少?(2)降价前他每千克土豆出售的价格是多少?(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少kg土豆?30.(6分)用总长为20 m的篱笆围成一长方形场地.(1)写出长方形面积S(m2)与一边x(m)之间的函数解析式和自变量X的取值范围;(2)分别求当x=2,5,8时,函数S的值.【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题1.B2.B3.B4.D5.D6.C7.C 8.B 9.A二、填空题10.202y x=-11.m n > 12.42x y =-⎧⎨=-⎩13.214.(-1,0)或(1,O) 15.y=-2x+116.223y x =-+,223y x =-- 17.y x π=-(0≤x ≤2) 18.119.(1)5 m /s ;(2)u=2.5t ;(3)7.5 m /s 20.180、π;l 、n 、r 21.12;x ,y 22.0.53;x 、y 23.0.25π;V,h24.y=1200-60x ,0≤x ≤20 25.4三、解答题26.图象略.(1)A(0,1),B(0,3); (2)P(12-,2); (3)111(31)222⨯-⨯-= .27.(1)132y x =-+;(2)-1;(3)-2<x ≤428.(1)y=2000-200x;(2)0≤x≤10;(3)图略29.(1)5元;(2)0.5元;(3)45 kg30.(1)210=-+(0<x<10);(2)16,25,16S x x。
2019年秋浙教版初中数学八年级上册《一次函数》单元测试(含答案) (125)

y=-x+6 上的点是
,在直线 y=3x 一 4 上的点是 ..
17.(3 分)等腰三角形底角的度数为 70°,则顶角的度数为 .若设等腰三角形底角的
度数为 x,顶角的度数为 y,则 y 关于 x 的函数解析式为
,其中常量是 .
18.(3 分)已知正比例函数 y=kx(k≠0)的图象经过原点、第二象限与第四象限,请写出
x+3
x−2
【参考答案】***试卷处理标记,请不要删除
评卷人 得分
一、选择题
1.B 2.D 3.B 4.C 5.A 6.C 7.A
评卷人
得分
二、填空题
8.2 9.平行
10. y = − 1 x + 8 ( 0 x 8) 2
11.如 y = −x +1(答案不唯一)
12.1 13.<2 14.y=-2x+1 15.-2 16.点 C,点 B 17.40°;y=180°-2x,180°,2 18.例如:“-1”
1、2,分别过这些点作 x 轴与 y 轴的垂线. 则图中阴部分的面积之和是( )
A.1
B. 3
C. 3(m −1)
D. 3 (m − 2) 2
2.(2 分)一次函数的图象如图所示,这个一次函数的解析式是( )
A. y = −x +1
B. y = x −1
C. y = −x −1
D. y = x +1
锻炼和在新华书店买书共用去的时间是( )
A.35min
B.45min
C.50min
D.60min
5.(2 分)若直线 y = − 1 x 沿 y 轴向上平移 3 个单位,则所得的函数图象的解析式为( ) 2
2019年秋浙教版初中数学八年级上册《一次函数》单元测试(含答案) (393)

A. y=3x
B.y=3x-2
C.y=3+2x
5.(2 分)下列各曲线中不表示 y 是 x 的函数的是( )
D.y=-3x-2
A.
B.
C.
D.
6.(2 分)下列函数中,自变量 x 的取值范围是 x 2 的函数是( )
A. y = x − 2
B. y = 1 x−2
C. y = 2x −1
D. y = 1 2x −1
22.(6 分)一池塘内有水 2000 m3,现用抽水机抽水,每小时可抽水 200 m3. (1)求池塘中余水量 y(m3)与抽水时间 x(h)之间的函数解析式; (2)求自变量 x 的取值范围; (3)画出它的图象.
23.(6 分)已知一次函数的图象过点(-1,5),且与正比例函数 y = − 1 x 的图象交于点(2, 2
标.
,点 B 的坐
10.(3 分)直线 y = kx + 4 与两坐标轴围成的直角三角形面积为 2,则这条直线与 x 轴的交点
为.
11.(3 分)已知一次函数 y = kx + b (k≠0)的图象经过点(0,1),而且 y 随 x 的增大而增大,请
你写出一个符合上述条件的函数解析式
.
12.(3 分)地面气温是 20℃,若每升高 100 m,气温下降 6℃,则气温 t(℃)与高度 h(m)的
21.(6 分)某学校要印刷一批资料,甲印刷公司提出收制版费 900 元,另外每份材料收印刷 费 0.5 元;乙印刷公司提出不收制版费,每从头材料收印刷费 0.8 元. (1)分别写出两家印刷公司的收费 y(元)与印刷材料 x(份)之间的函数解析式; (2)若学校预计要印刷 2500 份宣传材料,请问学校应选择哪一家印刷公司更合算?
2019年秋浙教版初中数学八年级上册《一次函数》单元测试(含答案) (218)

浙教版初中数学试卷2019-2020年八年级数学上册《一次函数》测试卷学校:__________题号 一 二 三 总分 得分评卷人 得分一、选择题1.(2分) 如图,点A 、B 、C 在一次函数2y x m =-+的图象上,它们的横坐标依次为-1、1、2,分别过这些点作x 轴与y 轴的垂线. 则图中阴部分的面积之和是( ) A .1B . 3C .3(1)m -D .3(2)2m -2.(2分)如果点M 在直线1y x =-上,则点M 的坐标可以是( ) A .(-1,O )B .(0,1)C .(1,0)D .(1,-1)3.(2分)一次函数1y kx b =+与2y x a =+的图象如图,则下列结论①k<0;③a>0;③当3x <时,12y y <中,正确的个数是( )A .0个B .1个C . 2个D .3个4.(2分)在某次实验中,测得两个变量m 和v 之间的4组对应数据如下表:m 1 2 3 4 v0.012.98.0315.1则m 与v 之间的关系最接近于下列各关系式中的( )A .v =2m 一2B .v =m 2一1C .v =3m 一3D .v =m 十15.(2分)如图,在光明中学学生耐力测试比赛中,甲、乙两学生测试的路程s (m )与时间t (s )之间的函数关系图象分别为折线OABC 和线段OD ,下列说法正确的是( )A .乙比甲先到达终点B .乙测试的速度随时间增加而增大C .比赛进行到29.4 S 时,两人出发后第一次相遇D .比赛全程甲的测试速度始终比乙的测试速度快6.(2分)无论m 取何实数,直线y=x-2m 与y=-2x+3的交点不可能在( ) A .第一象限B .第二象限C .第三象限D .第四象限7.(2分)在一次函数y=kx+3中,当x=3时,y=6,则k 的值为 ( ) A .-1B .1C .5D .-58.(2分)下列函数中是一次函数的是( ) A .y=kx+bB .2y x-=C .2331y x x =-++D .112y x =-+9.(2分)函数y=3x-6的图象是( ) A .过点(0,-6),(0,-2)的直线 B .过点(0,2),(1,-3)的直线 C .过点(2,O ),(1,3)的直线 D .过点(2,0),(0,-6)的直线 10.(2分)如图,直线12xy =与23y x =-+相交于点A ,若12y y <,那么( ) A .2x >B .2x <C .1x >D .1x <11.(2分)一次函数y kx b =+的图象如图所示,当0y <时,x 的取值范围是( ) A .0x >B .0x <C .2x >D .2x <12.(2分)下列函数中,自变量x 的取值范围是x ≥2的是( ) A .2y x =--B .2xy -=C .2y x =-D .24y x =-评卷人 得分二、填空题13.(3分)若直线5y x =--与x 轴交于点A ,直线上有一点M ,若△AOM 的面积为l0,则点M 的坐标为 . 解答题14.(3分)如图,OB ⊥OA 于点0,以 OA 为半径画弧,交OB 于点B ,P 是半径OA 上的动点.已知0A=2cm .设0P=xcm ,阴影部分的面积为ycm 2,则y(cm 2)关于x(cm)的函数解析式为 .15.(3分)直线4y ax =-与直线3y bx =+交于x 轴上一点,则ab等于 . 16.(3分)已知直线y=kx+2(k 为常数,且k≠0),则k= 时,该直线与坐标轴所围成的三角形的面积等于1.17.(3分)若点(-4,m ),(3,n )都在直线14y x t =-+上,则m 与n 的大小关系是 . 18.(3分)已知某一次函数的图象经过点(-1,2),且函数y 的值随自变量x 减小,请写出一个符合上述条件的函数解析式: .19.(3分)若x=一2,y=3满足一次函数y=kx-3,则k= .20.(3分)等腰三角形底角的度数为70°,则顶角的度数为 .若设等腰三角形底角的度数为x ,顶角的度数为y ,则y 关于x 的函数解析式为 ,其中常量是 . 21.(3分)随着海拔高度的升高,大气压强下降,空气中的含氧量也随之下降,即含氧量3(g /m )y 与大气压强(kPa)x 成正比例函数关系.当36(kPa)x =时,3108(g /m )y =,请写出y 与x 的函数关系式 .22.(3分)仓库里现有粮食l200 t ,每天运出60 t ,x 天后仓库里剩余粮食y(t),则y 与x 之间的函数解析式为 ,自变量x 的取值范围是 .23.(3分)某汽车每小时耗油6 kg ,该车在行驶t(h)后耗去了Q(kg)油,即Q=6t ,其中常量是,变量是 .24.(3分)平行四边形的面积为S ,边长为5,该边上的高为h ,则S 与h 的关系为 ;当h=2时,S= ;当S=40时,h= .评卷人得分三、解答题25.(6分)如图,直线l经过A(1,3),B(-2,0)两点,点P(a,0)在x轴上.(1)求直线l的解析式;(2)若以点A,B,P为顶点的三角形是直角三角形,求点 P的坐标;(3)当a在什么范围射,使以点 A.B、P为顶点的三角形是钝角三角形(直接写出答案即可).26.(6分)某学校要印刷一批资料,甲印刷公司提出收制版费900元,另外每份材料收印刷费0.5元;乙印刷公司提出不收制版费,每从头材料收印刷费0.8元.(1)分别写出两家印刷公司的收费y(元)与印刷材料x(份)之间的函数解析式;(2)若学校预计要印刷2500份宣传材料,请问学校应选择哪一家印刷公司更合算?27.(6分)某城市在1990年为了尽快改善职工住房条件,积极鼓励个人购买和积累住房基金,决定住公房的职工按基本工资的高低交纳住房公积金,办法如下表:每月基本工资交纳公积金比率(%)100元以下(含100元)不交纳100元至200元(含200元)交纳超过l00元部分的5%200元至300元(含300元)100元至200元部分交纳5%,超过200元以上部分交纳10%300元以上100元至200元部分交纳5%,200元至300元部分交纳10%,超过300元以上部分交纳15%’(1)设每月基本工资为x元,交纳公积金的金额为y元.试写出当l00<x≤200时,y与x之间的关系式;(2)若小军的妈妈每月基本工资为200元,问她每月交纳公积金为多少元?(3)若小明的妈妈每月交纳公积金为4元,问她每月基本工资为多少元?28.(6分)已知y-2与x成正比例,且当x=1时,y=-6.(1)求y与x之间的函数解析式;(2)如果点(b,1)在这个函数图象上,求b的值.29.(6分)从2005年9月起,中国的鞋号已“变脸”,新的国家标准要求鞋号用毫米数标注。
2019年秋浙教版初中数学八年级上册《一次函数》单元测试(含答案) (281)
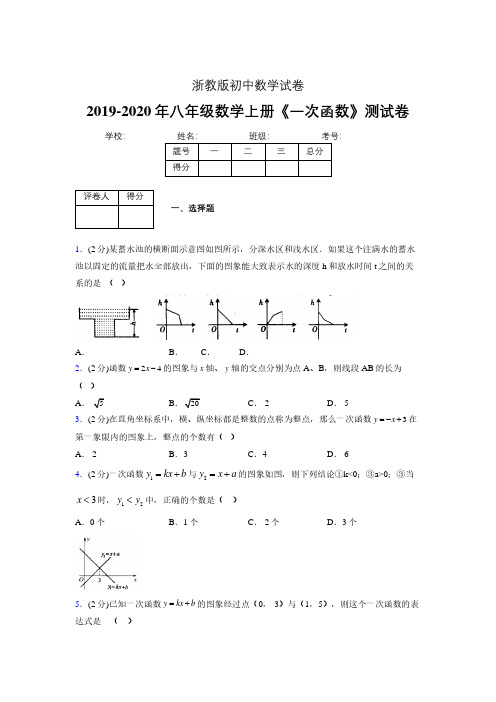
解得 k = −2 .
27.(1)30
t,10
min;(2)
Q1
=
29 10
t
+
40
(
t≥0);(3)够用,理由略
28.(1)2280 元,2040 元;(2)y2=1800x+5600;(3)9 月份
29.(1)y=50-2x(12.5<x<25);(2)20
30.(1)常量:2;变量 a、b、c;(2)常量:120°;变量:α、β;(3)常量:30,变量;
12.(2 分)如图,某电信公司提供了 A,B 两种方案的移动通讯费用 y (元)与通话时间 x
(元)之间的关系,则以下说法错.误.的是( )
A.若通话时间少于 120 分,则 A 方案比 B 方案便宜 20 元
B.若通话时间超过 200 分,则 B 方案比 A 方案便宜 12 元
C.若通讯费用为 60 元,则 B 方案比 A 方案的通话时间多
x、y;(4)常量:10、150;变量:T、h
时,x 的取值范围是( )
A.x<-1
B.x>-1
C.x>2
D.x<2
8.(2 分)当 x=3 时,函数 y=px-1 与函数 y=x+p 的值相等,则 p 的值为( )
A.1
B.2
C.3
D.4
9.(2 分)如果函数 y=ax+b(a<0,b<O)和 y=kx(k>0)的图象交于点 P,那么点 P 应该位
29.(6 分)已知等腰△ABC 的周长为 50 cm,底边 BC 长为 y(cm),腰 AB 长为 x(cm).求: (1)y 与 x 之间的函数解析式及自变量 x 的取值范围; (2)求当 x=15 时的函数值.
2019年秋浙教版初中数学八年级上册《一次函数》单元测试(含答案) (228)

x o y浙教版初中数学试卷2019-2020年八年级数学上册《一次函数》测试卷学校:__________题号 一 二 三 总分 得分评卷人 得分一、选择题1.(2分)函数24y x =-的图象与x 轴、y 轴的交点分别为点A 、B ,则线段AB 的长为( ) A . 5B .20C . 2D . 52.(2分)下列一次函数中,y 随x 的增大而减小的有( ) ①21y x =-+;②6y x =-;③13xy +=-;④(12)y x =- . A .1个B .2个C .3个D . 4个3.(2分)一次函数1y kx b =+与2y x a =+的图象如图,则下列结论①k<0;③a>0;③当3x <时,12y y <中,正确的个数是( )A .0个B .1个C . 2个D .3个4.(2分)已知:一次函数(1)y a x b =-+的图象如图所示,那么,a 的取值范围是( ) A . 1a >B . 1a <C . 0a >D . 0a <5.(2分)如果点M 在直线1y x =-上,则M 点的坐标可以是( ) A .(-1,0)B .(0,1)C .(1,0)D .(1,-1)6.(2分)下列函数(1)y x π=,(2)y=2x 一1,(3)1y x=,(4)123y x -=-,(5)21y x =-是一次函数的有( )A .4个B . 3个C . 2个D .1个7.(2分)“高高兴兴上学来,开开心心回家去.”小王某天放学后,l7时从学校出发,回家途中离家的路程s (km )与所走的时间t (min )之间的函数关系如图所示,那么这天小明到家的时间为( ) A .17 h15 minB .17 h14 minC .17 h12 minD .17 h11 min8.(2分)无论m 取何实数,直线y=x-2m 与y=-2x+3的交点不可能在( ) A .第一象限B .第二象限C .第三象限D .第四象限9.(2分)下列函数中是一次函数的是( ) A .y=kx+bB .2y x-=C .2331y x x =-++D .112y x =-+10.(2分)2007年我国铁路进行了第六次大提速,一列火车由甲市匀速驶往相距600 km 的乙市,火车的速度是200 km /h ,火车离乙市的距离S (单位:km )随行驶时间t (单位:h )变化的函数关系用图象表示正确的是( )A .B .C .D .11.(2分)函数11y x =+中自变量x 的取值范围是( ) A .x ≠-lB .x>-1C .x=-lD .x<-112.(2分)下列变化过程中存在函数关系的是( ) A .人的身高与年龄 B .y=k-3xC .3x+y+1D .速度一定,汽车行驶的路程与时间13.(2分)如图,某电信公司提供了A B ,两种方案的移动通讯费用y (元)与通话时间x (元)之间的关系,则以下说法错误..的是( ) A .若通话时间少于120分,则A 方案比B 方案便宜20元 B .若通话时间超过200分,则B 方案比A 方案便宜12元 C .若通讯费用为60元,则B 方案比A 方案的通话时间多 D .若两种方案通讯费用相差10元,则通话时间是145分或185分14.(2分)设路程为s (km ),速度为v (km /h ),时间为t (h ),当s=100(km )时,在时间的关系式s t v= 中,以下说法正确的是( ) A .路程是常量,时间、速度都是变量 B .路程、时间、速度都是变量 C .时间是常量,路程、速度都是变量 D .速度是常量,路程、时间都是变量 评卷人 得分二、填空题15.(3分)若直线5y x =--与x 轴交于点A ,直线上有一点M ,若△AOM 的面积为l0,则点M 的坐标为 . 解答题16.(3分)两直线3y x =-、5y x =-+与y 轴围成的三角形的面积是 . 17.(3分)直线2y x b =-+经过点M(3,2),则b 的值是 .18.(3分)已知 A ,B 的坐标分别为(-2,0),(4,0),点P 在直线2y x =+上,如果△ABP 为等腰三角形,这样的 P 点共有 个.19.(3分)如图,已知函数y ax b =+和y kx =的图象交于点P, 则根据图象可得,关于y ax by kx=+⎧⎨=⎩的二元一次方程组的解是 .20.(3分)一水池有2个进水速度相同的进水口,l 个出水口,单开一个进水口每小时可进水2 m 3,单开一个出水口每小时可出水3m 2.某天0 h 到6 h 水池的蓄水量与放水时间的关系如图所示(至少打开一个进水口),给出以下3个论断:①O h 到3 h 只进水不出水;②3 h 到4 h 时不进水只出水;③4 h 到6 h 不进水不出水. 则错误的论断是 (填序号).21.(3分)某商店买入一批货,每件l5元,售出时每件加利润3元,若售出x 件,应得货款y 元,则y 与x 之间的函数解析式为 ,当x=112时,y= . 22.(3分)直线2y x b =+经过点(13),,则b = .23.(3分)市场上出售一种大豆,大豆的总售价与所售大豆的数量之间的关系如下表:所售大豆数量(kg ) O 1 1.5 2 2.5 3 总售价(元)34.567.59(1)上表中所反映的变量是 ;(2)如果出售2.5 kg 大豆,那么总售价应为 元; (3)出售 kg 大豆,可得总售价为45元.24.(3分)平行四边形的面积为S ,边长为5,该边上的高为h ,则S 与h 的关系为 ;当h=2时,S= ;当S=40时,h= .25.(3分)平行四边形的面积为S ,边长为5,该边上的高为h ,则S 与h 的关系为 ;当h=2时,S= ;当S=40时,h= . 评卷人 得分三、解答题26.(6分)如图,1l 反映了某个体服装老板的销售收入与销售量之间的关系,2l 反映了该老板的销售成本与销售量的关系,根据图象回答下列问题:(1)分别求出1l 、2l 对应的函数解析式(不要求写出自变量的取值范围); (2)当销售量为30件时,销售收入为 元,销售成本为 元; (3)当销售量为60件时,销售收入为 元,销售成本为 元; (4)当销售量为 件时,销售收入等于销售成本;(5)当销售量 件时,该老板赢利.当销售量 件时.该老板亏本.27.(6分)某学校要印刷一批资料,甲印刷公司提出收制版费900元,另外每份材料收印刷费0.5元;乙印刷公司提出不收制版费,每从头材料收印刷费0.8元.(1)分别写出两家印刷公司的收费y(元)与印刷材料x(份)之间的函数解析式;(2)若学校预计要印刷2500份宣传材料,请问学校应选择哪一家印刷公司更合算?28.(6分)在正常情况下,一个人在运动时所能承受的每分钟心跳的最高次数S(次/分)是这个人年龄n(岁)的一次函数.(1)根据以上信息,求在正常情况下,S关于n的函数解析式;(2)若一位66岁的老人在跑步时,医生在途中给他测得l0秒心跳为25次,问:他是否有危险?为什么?29.(6分)一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱用,按市场价售出一些后,又降价出售,售出土豆千克数与他手中持有钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:(1)农民自带的零钱是多少?(2)降价前他每千克土豆出售的价格是多少?(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少kg 土豆?30.(6分)指出下列事例中的常量与变量: (1)长方形的长和宽分别是a 与b ,周长为c=2(a+b).(2)△ABC 的其中一个内角度数为60°,另两个内角的度数分别为、β,则β=120°-α. (3)某种储蓄的月利率为0.3%,存入l0000元本金后,利息y(元)与所求月数x(月)之间的关系式为y=30x .(4)某地温度T(℃)与海拔高度h(m)之间的关系可用10150hT =-来近似估计.【参考答案】***试卷处理标记,请不要删除评卷人 得分一、选择题1.B 2.D 3.B 4.A 5.C 6.B 7.C 8.C 9.D10.D 11.A 12.D 13.D 14.A二、填空题15.(-9,4)或(-1,-4) 16.16 17.8 18.419.42x y =-⎧⎨=-⎩20.②21.y=18x ,2016 22.123.(1)总售价、所售大豆的数量;(2)7.5;(3)15 24.S=5h ,10,8 25.S=5h ,10,8三、解答题26.(1)1l :100t x =,2l :751000t x =+; (2)3000,3250; (3)6000,5500; (4)40;(5)大于40,小于4027.(1)0.5900y x =+甲,0.8y x =乙;(2)选择乙印刷公司 28.(1)21743S n =-+;(2)有危险29.(1)5元;(2)0.5元;(3)45 kg30.(1)常量:2;变量 a 、b 、c ;(2)常量:120°;变量:α、β;(3)常量:30,变量;x、y;(4)常量:10、150;变量:T、h。
2019年秋浙教版初中数学八年级上册《一次函数》单元测试(含答案) (77)
(1)在 y 轴括号内填入相应的数值; (2)沙尘暴从发生到结束,共经过多少时间? (3)求出当 x≥25 时,风速 y(km/h)与时间 x(h)之间的函数解析式.
27.(6 分)求直线 y=x+1,y=-x+3 与 x 轴所围成的三角形的面积.
28.(6 分)某市自来水公司为限制单位用水,每月只给某单位计划内用水 2500m3,计划内
评卷人 得分
一、选择题
1.B 2.A 3.B
4.B 5.B 6.D 7.D 8.C 9.C
评卷人
得分
二、填空题
10. − 4
3
11. y = −x + 2
12.2
13. − 1
2 14.(-1,0)或(1,O)
15. y = − 2 x + 2 , y = − 2 x − 2
3
3
16. x 5
2 17.a>b
相距 m.
22.(3 分)某汽车每小时耗油 6 kg,该车在行驶 t(h)后耗去了 Q(kg)油,即 Q=6t,其中常量
是
,变量是 .
评卷人 得分
三、解答题
23.(6 分) 已知关于 x 的一次函数 y = (2m − 2)x + m +1的图象与 y 轴的交点在 x 轴的上
方,且 y 随 x 的增大而减小,求整数 m 的值.
.
21.(3 分)音速表示声音在空气中传播的速度,实验测得音速与气温的一些数据如下表: 气温(℃) O 5 10 15 20 … 音速(m/s) 331 334 337 340 343 …
(1)此表反映的是变量 随 而变化;
(2)当气温为 25℃时,某人看到烟花燃放 6 秒后才听到声响,那么此人与燃放烟花所在地约
2019年秋浙教版初中数学八年级上册《一次函数》单元测试(含答案) (159)
A.R
B. l
C.S、R
D.S、 l 、R
评卷人 得分
二、填空题
14.(3 分)如图,OB⊥OA 于点 0,以 OA 为半径画弧,交 OB 于点 B,P 是半径 OA 上的动 点.已知 0A=2cm.设 0P=xcm,阴影部分的面积为 ycm2,则 y(cm2)关于 x(cm)的函数解析 式为 .
所售大豆数 量(kg) O 1
1.5 2
2.5 3
总售价(元) 0 3 4.5 6 7.5 9
(1)上表中所反映的变量是 ; (2)如果出售 2.5 kg 大豆,那么总售价应为 元; (3)出售 kg 大豆,可得总售价为 45 元. 27.(3 分)钢筋的横截面面积是 0.25 ,长度为 h,则钢筋的体积 V=0.257 h,这里常 量是 ,变量是 .
4.(2 分)如果点 M 在直线 y = x −1 上,则点 M 的坐标可以是( )
A.(-1,O)
B.(0,1)
C.(1,0)
D.(1,-1)
5.(2 分)一次函数 y = −2x +1的图象与两坐标轴所围成的三角形的面积为( )
A.1
B. 1 2
C. 1 4
D. 1 8
6.(2分)已知:一次函数 y = (a −1)x + b 的图象如图所示,那么,a的取值范围是( )
A. y = x − 2
B. y = 1 x−2
C. y = 2x −1
D. y = 1 2x −1
11.(2 分)为悼念四川汶川地震中遇难同胞,在全国哀悼日第一天,某校升旗仪式中,先把 国旗匀速升至旗杆顶部,停顿 3 秒钟后再把国旗匀速下落至旗杆中部.能正确反映这一过 程中,国旗高度 h(米)与升旗时间 t(秒)的函数关系的大致图象是
2019年秋浙教版初中数学八年级上册《一次函数》单元测试(含答案) (192)
求: (1)第四个“巨”字需要的棋子数; (2)按以上规律继续摆下去,求第 n 个“巨”字所需的棋子数 m.
28.(6
分)已知直线 l1 :
y
=
−4x + 5和直线 l2 ::
y
=
1 2
x
−
4 ,求两条直线 l1 和 l2
(1) y = x2 + 2x ; (2) y = x ;(3) y = 3x + 3 ;(4) y = x −1 + x + 2 .
x+3
x−2
【参考答案】***试卷处理标记,请不要删除
评卷人 得分
一、选择题
1.B 2.C 3.D 4.C 5.B 6.D 7.D
评卷人
得分
二、填空题
8.
x y
= =
21.(1)总售价、所售大豆的数量;(2)7.5;(3)15
22.6;Q、t
评卷人 得分
三、解答题
23.解(1)解析式为 y=2x+1;(2)点 P(-l,1)不在直线 y=2x+1 上 24.(1)y=2x,y=2.6x-12;(2)53 m3 25.(1)8,32;(2)57 h;(3)y=-x+57(25≤x≤57) 26.(1)m=2;(2)m< 1
12.(3 分)已知一次函数 y = −x + a 与 y = x + b 的图象相交于点(m,8),则 a+b= .
13.(3 分)已知一次函数 y = kx + b (k≠0)的图象经过点(0,1),而且 y 随 x 的增大而增大,请
2019年秋浙教版初中数学八年级上册《一次函数》单元测试(含答案) (265)
,当 x=112 时,y= .
24.(3 分)已知正比例函数 y=kx(k≠0)的图象经过原点、第二象限与第四象限,请写出
符合上述条件的 k 的一个值:_________.
解答题
25.(3 分)钢筋的横截面面积是 0.25 ,长度为 h,则钢筋的体积 V=0.257 h,这里常
量是 ,变量是 .
锻炼和在新华书店买书共用去的时间是( )
A.35min
B.45min
C.50min
D.60min
7.(2 分)编织一副手套收费 3.5 元,则加工费 y(元)与加工件数 x(副)之间的函数解
析式为 ( )
A.y=3.5+x
B.y=3.5-x
C.y=3.5x
D. y = 3.5 x
8.(2 分)如图,射线 l甲 、 l乙 分别表示甲、乙两名运动员在竞走比赛中所走路程 s(km)与
15. y = −x + 2
16.12
17.16
18.<2
19. t = 20 − 0.06h
20.y=15-x,O<x<7.5
21.3
22.-l
23.y=18x,2016
24.例如:“-1”
25. 0.25 ;V,h
评卷人 得分
三、解答题
26.(1) y = x + 2 (2)AP⊥PB 时,P1(1,O);AP⊥AB 时,P2(4,0) (3) a −2或
16.(3 分)如图是我市 2 月份某天 24 小时内的气温变化图,则该天的最大温差是 ℃.
17.(3 分)已知一次函数 y = −x + a 与 y = x + b 的图象相交于点(m,8),则 a+b= .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙教版初中数学试卷
2019-2020年八年级数学上册《一次函数》测试卷
学校:__________ 姓名:__________ 班级:__________ 考号:__________
题号 一 二 三 总分
得分
评卷人 得分
一、选择题
1.(2分)在直角坐标系中,横、纵坐标都是整数的点称为整点,那么一次函数3yx=−+在
第一象限内的图象上,整点的个数有( )
A. 2 B.3 C.4 D. 6
2.(2分)如果点M在直线1yx=−上,则点M的坐标可以是( )
A.(-1,O) B.(0,1) C.(1,0) D.(1,-1)
3.(2分)已知一次函数y=kx+b,当-3≤x≤l时,对应的y值为l≤y≤9,则kb的值为
( )
A. 14 B.-6 C.-4或21 D.-6或14
4.(2分)如果一次函数ykxb=+的图象经过第一象限,且与y轴负半轴相交,那么( )
A.k>0,b>O B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
5.(2分)若直线12yx=−沿y轴向上平移3个单位,则所得的函数图象的解析式为( )
A.132yx=−+ B.132yx=−− C.1(3)2yx=−+ D.
1
(3)2yx=−−
6.(2分)如图,射线l甲、l乙分别表示甲、乙两名运动员在竞走比赛中所走路程s(km)与
时间t(h)的函数关系,则他们行进的速度关系是( )
A.甲比乙快 B.乙比甲快 C.甲、乙速度相同 D.不能确定
7.(2分)在函数1yx=−中,自变量x的取值范围是( )
A.x≥-l B.x≠1 C.x≥1 D.x≤1
8.(2分)如图,直线AB对应的函数表达式是( )
A.3yx32=−+ B.3yx32=+ C.2yx33=−+ D.
2
yx33=+
评卷人 得分
二、填空题
9.(3分)直线23yx=−+关于y轴对称的图象的函数解析式是 .
10.(3分)等腰三角形的周长为 16,则腰长y关于底边x 的函数解析式是: .
11.(3分)已知一次函数24yx=+的图象经过点(m,8),则m= .
12.(3分)一次函数ykxb=+的图象经过点A(0,2),B(3,0),则此函数的解析式
为 ;若将该图象沿x轴向左平移4个单位,则新图象对应的函数解析式是 .
13.(3分)已知m是整数,且一次函数y=(m+4)x+m+2的图象不经过第二象限,那么
m= .
14.(3分)直线y=kx+b经过点A(-2,0)和y轴正半轴上的一点B,若△ABO(0为坐标原点)
的面积为2,则b的值为 .
15.(3分)已知一次函数y=kx-k+4的图象与y轴的交点坐标是(0,-2),那么这个一次函数
的表达式是 .
16.(3分)已知铁的质量m与体积V成正比例,已知当V=5cm3时,m=39g,则铁的质量m
关于体积V的函数解析式是 .
17.(3分)已知函数3()2fxx=+,则(1)f= .
18.(3分)直线2yxb=+经过点(13),,则b= .
19.(3分)在加油站,加油机显示器上显示的某一种油的单价为每升4.75元,总价从0元
开始随着加油量的变化而变化,总价y(元)与加油量x(升)的函数解析式是 .
20.(3分)多边形的内角和的度数y与边数n之间的关系为y=(n-2)·180°,其中常量
为 ,变量为 .
21.(3分)某汽车每小时耗油6 kg,该车在行驶t(h)后耗去了Q(kg)油,即Q=6t,其中常量
是
,变量是 .
22.(3分)平行四边形的面积为S,边长为5,该边上的高为h,则S与h的关系为 ;当
h=2时,S= ;当S=40时,h= .
评卷人 得分
三、解答题
23.(6分)如图,在平面直角坐标系中,一次函数162yx=−+的图象分别交x,y轴于点
A,B,与一次函数yx=的图象交于第一象限内的点 C.
(1)分别求出A,B,C的坐标;
(2)求出△AOC的面积.
24.(6分)已知一次函数物图象经过A(-2,-3),B(1,3)两点.
(1)求这个一次函数的解析式;
(2)试判断点P(-1,1)是否在这个一次函数的图象上?
25.(6分)设关于x的一次函数11yaxb=+与22yaxb=+,则称函数
1122
()()ymaxbnaxb=+++
(其中m+n=1)为此两个函数的生成函数.
(1)当x=1时,求函数y=x+1与y=2x的生成函数的值;
(2)若函数11yaxb=+与22yaxb=+的图象的交点为P,判断点P是否在这两个函数的生成函
数的图象上,并说明理由.
26.(6分)某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费:月
用水量不超过20 m3时,按2元/m3计费;月用水量超过20 m3时,其中的20 m3仍按2元
/m3收费,
超过部分按2.6元/m3计费.设每户家庭月用水量为x(m3)时,应交水费y元.
(1)分别求出0≤x≤20和x>20时,y与x的函数表达式;
(2)小明家第二季度交纳水费的情况如下:
月份 四月份 五月份 六月份
交费金额 30元 34元 42.6元
小明家这个季度共用水多少m3 ?
27.(6分)某气象研究中心观测一场沙尘暴从发生到结束的全过程,开始时风速平均增加2
km/h,4 h后,沙尘暴经过开阔的荒漠地,风速平均增加4 km/h,一段时间风速保持不
变.当沙尘暴遇到绿色植被区时,其风速平均减少l km/h,最终停止.结合风速与时间
的图象(如图所示)回答下列问题:
(1)在y轴括号内填入相应的数值;
(2)沙尘暴从发生到结束,共经过多少时间?
(3)求出当x≥25时,风速y(km/h)与时间x(h)之间的函数解析式.
28.(6分)已知直线y=2x-1.
(1)求已知直线与x轴、y轴交点A、B的坐标;
(2)若直线y=kx+b与已知直线关于x轴对称,求其解析式,并在同一坐标系内画出两条直
线的图象.
29.(6分)已知y-2与x+1成正比,且当x=l时,y=-6.
(1)求y与x之间的函数解析式;
(2)求当x=-l时,y的值.
30.(6分)求下列函数的自变量的取值范围:
(1)22yxx=+; (2)3xyx=+;(3)332xyx+=−;(4)12yxx=−++.
【参考答案】***试卷处理标记,请不要删除
评卷人 得分
一、选择题
1.A
2.C
3.D
4.B
5.A
6.B
7.C
8.A
评卷人 得分
二、填空题
9.23yx=+
10.182yx=−+(
08)x
11.2
12.223yx=−+,
2
23yx=−−
13.-3或-2
14.2
15.y=6x-2
16.M=7.8v
17.1
18.1
19.4.75yx=
20.2、180°;y、n
21.6;Q、t
22.S=5h,10,8
评卷人 得分
三、解答题
23.(1) A(12,0), B(0,6), C(4,4) (2) 24
24.解(1)解析式为y=2x+1;(2)点P(-l,1)不在直线y=2x+1上
25.(1)2;(2)在
26.(1)y=2x,y=2.6x-12;(2)53 m3
27.(1)8,32;(2)57 h;(3)y=-x+57(25≤x≤57)
28.(1)A(12,0),B(0,-l);(2)y=-2x+1,图象略
29.(1)y=-4x-2;(2)2
30.(1)任何实数;(2)x≠-3;(3)x≥-l且x≠2;(4)x≥1
