高考数学理科必考题型：第28练-三视图及表面积与体积(含答案)

合集下载

2022版新高考数学总复习专题试题--空间几何体的三视图、表面积和体积(解析版)

2022版新高考数学总复习--第八章立体几何§8.1 空间几何体的三视图、表面积和体积— 专题检测 —一、单项选择题1.(2021北京朝阳二模,5)某四棱锥的三视图如图所示,已知网格纸上小正方形的边长为1,则该四棱锥的5个面的面积中,最大的是 ( )A.2B.√5C.√6D.3 答案 D三视图所对应的四棱锥如图所示,PD ⊥平面ABCD ,PD =2,四边形ABCD 是直角梯形,AD ∥BC ,AD ⊥DC ,AD =DC =2,BC =1,S △PAD=12×2×2=2,S △PDC =12×2×2=2,S △PBC =12PC ×BC =12×2√2×1=√2, S四边形ABCD =12×(2+1)×2=3.△PAB 中,PA =2√2,PB =3,AB =√5,cos ∠APB =√2)22√5)22×2√2×3=√22,∴sin∠APB =√22,∴S △PAB=12×2√2×3×√22=√3. 综上,四棱锥P -ABCD 的5个面的面积中,最大的是3,故选D .2.(2021北京房山一模,10)祖暅是我国南北朝时代伟大的科学家,他在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”.意思是:如果两个等高的几何体在同高处截得的截面面积恒等,那么这两个几何体的体积相等.此即祖暅原理.利用这个原理求球的体积时,需要构造一个满足条件的几何体,已知该几何体三视图如图所示,用一个与该几何体的下底面平行,且相距为h (0<h <2)的平面截该几何体,则截面面积为 ( )A.4πB.4πh 2C.π(2-h 2) D.π(4-h 2)答案 D 由三视图得到该几何体为一个圆柱挖去一个圆锥,该几何体的底面圆的半径为2,高为2,截面为圆环,大圆半径为2,设小圆半径为r ,则r 2=ℎ2,所以r =h ,所以截面圆环的面积为4π-πh 2=π(4-h 2).故选D.3.(2021天津和平一模,6)已知正方体ABCD -A 1B 1C 1D 1的棱长为2,则三棱锥A -B 1CD 1的体积为 ( )A.43B.83C.4D.6答案 B 易知,三棱锥A -B 1CD 1是棱长为2√2的正四面体,如图,设D 1在底面内的射影为O ,AO =23√(2√2)2-(√2)2=2√63,∴D 1O =√(2√2)2-(2√63)2=4√33.∴三棱锥A -B 1CD 1的体积为13×12×2√2×2√2×√32×4√33=83.故选B .4.(2021天津十二区二模,6)已知三棱锥S -ABC 外接球的球心O 在线段SA 上,若△ABC 与△SBC 均为面积是4√3的等边三角形,则三棱锥S -ABC 外接球的体积为 ( ) A.8√2π3 B.16√2π3C.32√2π3D.64√2π3答案 D由题意得AB =SB =4, ∴△ABS 是等腰三角形, ∵O 是球心,∴OB =OS =OA =12AS , ∴△ABS 是直角三角形,SB ⊥AB , ∴△ABS 是等腰直角三角形,∴OA =AB √2=2√2,∴三棱锥S -ABC 外接球的体积V =43π×(2√2)3=64√2π3. 5.(2021浙江金华十校4月模拟,6)某几何体的三视图如图所示,则该几何体的体积是 ( )A .20-2πB .19-23π C .20-23π D .20-12π答案 D 根据三视图可得几何体为一个长方体截去两个小长方体和半个圆柱后剩余部分,如图所示.所以其体积V =5×5×1-1×1×1-2×2×1-12×1×π×12=20-12π,故选D .6.(2021浙江新高考研究卷(五),9)已知四棱锥P -ABCD ,底面是边长为2的菱形ABCD ,其中一个内角为π3,则侧棱PA 、PB 、PC 、PD 的长度可以是 ( )A .√3、2、1、2B .1、1、2、2C .2、1、2、3D .3、1、2、√2 答案 A 不妨设∠ABC =π3,连接AC ,BD ,交于点O ,连接PO ,易知AC =2,BD =2√3,且满足:2(PA 2+PC 2)=4PO 2+AC 2,2(PB 2+PD 2)=4PO 2+BD 2,且PA +PC >2,PB +PD >2√3,代入四个选项数据知只有A 选项满足条件,故选A . 7.(2021安徽六安一中3月月考,7)中国古代建筑结构中的木构架结构的固定通常在衔接处通过外力作用增加一个“塞”,简称“加塞”,这种“加塞”能使结构非常稳固,使整体上能承受巨大的压力.如图所示的巢车是木构架结构,为使其在作战中经久耐用,制作过程中在衔接处“加塞”,如图所示的为某个“加塞”的五面体的三视图,则该“加塞”几何体的侧面积为 ( )A.4√3B.5√3C.6√3D.8√3答案 D 由三视图可知该几何体为如图所示的五面体EF -ABCD ,其中底面ABCD 为矩形,AB =4,BC =EF =EB =EC =FA =FD =2,EF ∥平面ABCD ,侧面ABEF 与CDFE 为上底边长为2,下底边长为4的等腰梯形,△BCE 与△ADF 是边长为2的等边三角形,S 等腰梯形ABEF =(2+4)×√32=3√3,S △BCE =√34×22=√3,所以S =2S 等腰梯形ABEF +2S △BCE=6√3+2√3=8√3.故选D .8.(2021河南重点中学3月联考,8)若用平行于某圆锥底面的平面去截该圆锥,得到的小圆锥与圆台的母线长相等,则该小圆锥与该圆台的侧面积的比值为 ( )A.14B.13C.12D.34答案 B 设圆锥的底面半径为r ,母线长为2l ,则该圆锥的侧面积S =12×2πr ×2l =2πrl ,截得的小圆锥的底面半径为r2,母线长为l ,其侧面积S 1=12×πr ×l =12πrl ,从而圆台的侧面积S 2=S -S 1=2πrl -12πrl =32πrl ,故S1S 2=12πrl 32πrl =13. 9.(2021黑龙江大庆重点中学3月联考,9)已知四棱锥P -ABCD ,底面ABCD 为矩形,点P 在平面ABCD 上的射影为AD 的中点O.若AB =2,AD =6,PO =4,则四棱锥P -ABCD 的表面积等于 ( )A.34+6√5B.34+4√3C.6+6√5+4√3D.6+6√3+4√13答案 A 连接OB ,OC ,因为PO ⊥平面ABCD ,AD ⊂平面ABCD ,所以PO ⊥AD ,同理PO ⊥CD ,PO ⊥OB ,PO ⊥OC ,PO ⊥AB , 又CD ⊥AD ,AD ∩PO =O ,AD ,PO ⊂平面PAD ,所以CD ⊥平面PAD ,因为PD ⊂平面PAD ,所以CD ⊥PD ,同理AB ⊥PA ,因为PO ⊥AD ,O 是AD 的中点,所以PA =PD =5,所以S △PCD =12CD ·PD =12×2×5=5,S △PAB =5,S 四边形ABCD =2×6=12,PC =√PO 2+OC 2=√PO 2+OD 2+DC 2=√42+32+22=√29,同理PB =√29,则△PCB 是等腰三角形,其底边CB 上的高为h =√PC 2-(BC2)2=√29-9=2√5,∴S △PBC =12×6×2√5=6√5,又S △PAD =12AD ·PO =12×6×4=12,所以所求几何体的表面积为S =12+5+5+12+6√5=34+6√5,故选A .10.(2021山西顶级名校4月联考,10)已知三棱锥P -ABC 的顶点P ,A ,B ,C 均在球O 的球面上,且AB ⊥BC ,AB =8,BC =6,若此三棱锥体积的最大值为40√5,则球O 的表面积为 ( ) A.90π B.120π C.160π D.180π答案 D 因为三棱锥P -ABC 的底面积一定,所以当球心在三棱锥P -ABC 的高上时,此三棱锥的体积最大.设球O 的半径为R ,顶点P 在底面内的射影为O 1, 因为AB ⊥BC ,所以O 1为斜边AC 的中点,则AO 1=AC 2=√82+622=5,如图所示,由三棱锥P -ABC 的体积V =13S △ABC ·PO 1得40√5=13×12×8×6×PO 1,解得PO 1=5√5.在Rt △AOO 1中,有AO 2=A O 12+O O 12,即R 2=52+(5√5-R )2,解得R =3√5,故球O 的表面积S 球=4πR 2=4π(3√5)2=180π,故选D .11.(2021山西晋中二模,5)如图,一个直四棱柱形容器中盛有水,在底面ABCD 中,AB ∥CD ,AB =3,CD =1,侧棱AA 1=4,若侧面AA 1B 1B 水平放置时,水面恰好过AD ,BC ,B 1C 1,A 1D 1的中点,那么当底面ABCD 水平放置时,水面高为 ( )A.2B.52C.3D.72答案 B 设四棱柱的底面梯形的高为2a ,AD ,BC 的中点分别为F ,E ,所求水面的高为h ,则水的体积V 水=S 四边形ABEF·AA 1=(2+3)a 2·4=S 四边形ABCD ·h =(1+3)2a2·h ,所以h =52,故选B .12.(2021豫北名校联盟5月联考,12)在直三棱柱ABC -A 1B 1C 1中,∠BAC =π2,AB =AC =√2,AA 1=2.以A 为球心,√3为半径的球面与该直三棱柱的三个侧面的交线长之和为( )(取cos72°=13)A.3√3π5+√2π2B.2√3π5+√2π2C.√3π5+√2π2D.4√3π5+√2π2答案 A 如图①所示,PQ⏜为球面与侧面BCC 1B 1的交线,则AP =AQ =√3.又在直三棱柱ABC -A 1B 1C 1中,AB =AC =√2,所以BP =CQ =1.取BC 的中点D ,连接AD ,易得AD ⊥BC.因为侧面BCC 1B 1⊥平面ABC ,侧面BCC 1B 1∩平面ABC =BC ,所以AD ⊥侧面BCC 1B 1,所以可求得PD =QD ,所以D 为PQ⏜所在圆的圆心.连接PD ,DQ ,PQ ,易知BD =CD =1,则PD =QD =√2,又PQ =BC =2,所以PD 2+QD 2=PQ 2,所以∠PDQ =90°,所以PQ⏜的长=π2×√2=√2π2.图①图②将侧面ABB 1A 1,侧面ACC 1A 1展开到同一平面内,如图②.易知MN =2√2.在△AMN 中,由余弦定理的推论可得cos ∠MAN =√3)2√3)2√2)22×√3×√3=-13,所以∠MAN =108°=3π5,所以MN ⏜的长=3π5×√3=3√3π5.所以球面与该直三棱柱的三个侧面的交线长之和为3√3π5+√2π2.二、多项选择题13.(2020山东潍坊期末,10)等腰直角三角形的直角边长为1,现将该三角形绕其某一边旋转一周,则所形成的几何体的表面积可以为()A.√2πB.(1+√2)πC.2√2πD.(2+√2)π答案AB如果绕直角边所在直线旋转,那么形成圆锥,圆锥底面半径为1,高为1,母线长就是直角三角形的斜边长√2,所以所形成的几何体的表面积S=πrl+πr2=π×1×√2+π×12=(√2+1)π.如果绕斜边所在直线旋转,那么形成,两个圆锥的母线长都是1,所以形成的几何体的表的是同底的两个圆锥,圆锥的底面半径是直角三角形斜边的高√22面积S=2×πrl=2×π×√2×1=√2π.2综上可知,形成几何体的表面积是(√2+1)π或√2π.故选AB.三、填空题14.(2021天津部分区一模,13)已知正方体的所有顶点在一个球面上,若这个球的表面积为12π,则这个正方体的体积为.答案8解析正方体的所有顶点在一个球面上,则正方体的体对角线长等于球的直径,设正方体的棱长为a,则体对角线长为√3a,设球的半径为R,由球的表面积为12π,得4πR2=12π,即R2=3,则R=√3,则√3a=2R=2√3,则a=2,则正方体的体积V=a3=23=8,故答案为8.15.(2021天津河北一模,13)在长方体ABCD-A1B1C1D1中,已知AB=√5,BC=√7,AA1=2,则三棱锥D1-ACD的体积为,长方体的外接球的表面积为.答案√353;16π解析如图,三棱锥D 1-ACD 的体积为13×12×AD ×DC ×DD 1=13×12×√7×√5×2=√353.外接球的半径为12√5+7+4=2,所以外接球的表面积为4π×22=16π.故答案为√353;16π.16.(2021河南新乡二模,14)一个棱长为4的正方体被挖去一个高为4的正四棱柱后得到如图所示的几何体,若该几何体的体积为60,则该几何体的表面积为 . 答案 110解析设正四棱柱的底面边长为m ,则4(42-m 2)=60,解得m =1,则该几何体的表面积为42×4+(42-12)×2+4×1×4=110.17.(2021浙江新高考研究卷(一),14)已知矩形ABCD 中,AB =2,BC =4,E 是AD 的中点,沿直线BE 将△ABE 翻折成△A'BE ,则三棱锥A'-BDE 的体积的最大值为 . 答案2√23解析如图,在矩形ABCD 中,过A 作AF ⊥BE 于F ,则AF =√2,在翻折过程中,点A'到平面BDE 的距离d 满足0≤d ≤AF , 故d max =√2,则V A'-BDE =13S △BDE d =23d ≤2√23.故三棱锥A'-BDE的体积的最大值为2√2.3。

高考数学(理科)-空间几何体表面积或体积的求解 -专题练习(含答案与解析)

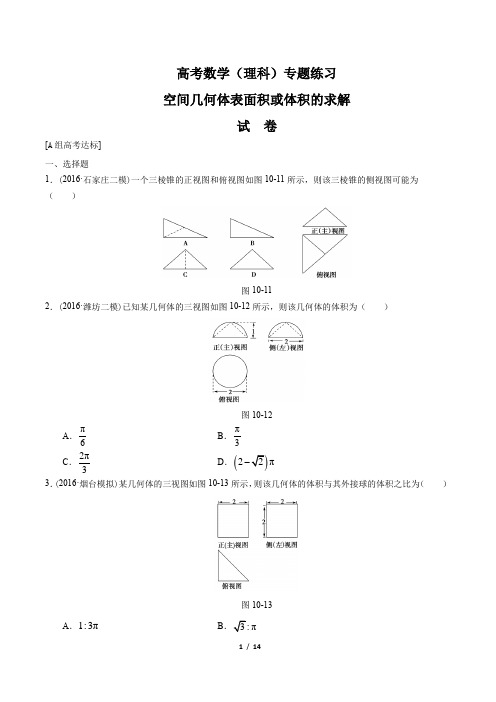
高考数学（理科）专题练习空间几何体表面积或体积的求解试卷[A组高考达标]．(石家庄二模)一个三棱锥的正视图和俯视图如图所示，则该三棱锥的侧视图可能为（）．(潍坊二模)已知某几何体的三视图如图所示，则该几何体的体积为（）3．(2016·烟台模拟)某几何体的三视图如图10-13所示，则该几何体的体积与其外接球的体积之比为（）DEFG平面ABB水平放置时，求液面的高。

M CD PMB⊥PCD．(唐山二模)某几何体的三视图如图所示，则该几何体的体积为（）⊥．BE DFAC平面MDFABCD的体积．中，△BCD是等边三角形，AB⊥OM平面ABDBC=，求三棱锥2高考数学（理科）专题练习空间几何体表面积或体积的求解答案[A 组高考达标] 一、选择题 1~5．DBDBA 二、填空题6．3+7．148．(16π三、解答题9．解：(1)证明：取PA 的中点F ，连接EF ，BF ，则EF AD BC ，即EF ，BC 共面．∵PB ⊥平面ABCD ，∴PB BC ⊥，又BC AB ⊥且PB AB B =，∴BC ⊥平面PAB ，∴.BC PA ⊥ ∵PB AB =，∴BF PA ⊥，又BC BF B =，∴PA ⊥平面EFBC ，∴PA CE ⊥． (2)设四棱锥P ABCD -的表面积为S ，∵PB ABCD ⊥平面，∴PB CD ⊥，又CD BC ⊥，PBBC B =，∴CD PBC ⊥平面，∴CD PC ⊥，即△PCD 为直角三角形，由(1)知BC PAB ⊥平面，而AD BC ，∴AD PAB ⊥平面，故AD PA ⊥，即△P AD 也为直角三角形．224ABCD S ==⨯=，12222PBC PAB PDA S S S ===⨯⨯=△△△，122PCDS=⨯= ∴ABCD PBC PDA PAB PCD S S S S S S ==++++△△△△表10=+10．解：．(1)证明：因为D ，E 分别为棱AC ，BC 的中点，所以DE 是△ABC 的中位线，所以DEAB又11DE ABB A ⊄平面，AB ⊂平面11ABB A ，所以DE 平面11ABB A ．同理DG 平面11ABB A ，又DE DG D =，所以平面DEFG 平面11ABB A ．(2)当直三棱柱111ABC A B C -容器的侧面11AA B B 水平放置时，由(1)可知，液体部分是直四棱柱，其高即为原直三棱柱111ABC A B C -容器的高，即侧棱长l ，当底面ABC 水平放置时，设液面的高为h ，ABC △的面积为S ，则由已知条件可知，CDE ABC △∽△，且14CDE S S =△，所以34ABED S S =四边形．由于两种状态下液体体积相等，所以34ABED V Sh S l Sl ===液体四边形，即34h l =．因此，当底面ABC 水平放置时，液面的高为34l ． [B 组名校冲刺] 一、选择题 1~4．ABDC 二、填空题5 6．83π2三、解答题7．解：(1)证明：设EC 与DF 交于点N ，连接MN ，在矩形CDEF 中，点N 为EC 中点，因为M 为EA 中点，所以MNAC ．又因为AC MDF ⊄平面，MN MDF ⊂平面，所以AC MDF 平面．(2)取CD 中点为G ，连接1A BG ，EG ，CDEF ABCD ⊥平面平面，CDEF ABCD CD =平面平面，AD ABCD ⊂平面，AD CD ⊥，所以AD CDEF ⊥平面，同理ED ABCD ⊥平面，所以ED 的长即为四棱锥E-ABCD 的高. 在梯形ABCD 中，12AB CD DG ==，AB DG ，所以四边形ABGD 是平行四边形，BGAD ，所以BG CDEF ⊥平面．又DF ⊂平面CDEF ，所以BG DF ⊥，又BE DF ⊥，BE BG B =，所以DF BEG ⊥平面，DF EG ⊥．注意到Rt DEG Rt EFD △∽△，所以28DE DG EF ==，DE = 所以1423E ABCD ABCD V S ED -==梯形． 8．解：(1)证明：∵△CMD 是等腰直角三角形，90CMD ∠=︒，点O 为CD 的中点，∴OM CD ⊥．∵CMD BCD ⊥平面平面，CMD BCD CD =平面平面，OM CMD ⊂平面，∴OM BCD ⊥平面． ∵AB ⊥平面BCD ，∴OMAB .∵AB ABD ⊂平面，OM ABD ⊄平面，∴OM ABD 平面．(2)法一：由(1)知OMABD 平面，∴点M 到平面ABD 的距离等于点O 到平面ABD 的距离．过点O 作OH BD ⊥，垂足为点H ．∵AB BCD ⊥平面，OH BCD ⊂平面，∴OH AB ⊥． ∵AB ABD ⊂平面，BD ABD ⊂平面，AB BD B =，∴OH ABD ⊥平面．∵2AB BC ==，△BCD 是等边三角形，∴2BD =，1OD =，sin60=OH OD =︒． ∴A BDM M ABD V V --=三棱锥三棱锥1132AB BD OH =⨯⨯11223223=⨯⨯⨯⨯=．∴三棱锥A -BDM ．法二：由(1)知OMABD 平面，∴点M 到平面ABD 的距离等于点O 到平面ABD 的距离. ∵2AB BC ==，△BCD 是等边三角形，∴21BD OD ==，．连接OB ，则OB CD ⊥，sin60=3OB BD =︒． ∴A BDM M ABD O ABD A BDO V V V V ----===三棱锥三棱锥三棱锥三棱锥1132OD OB AB =⨯⨯111232=⨯⨯=．∴三棱锥A -BDM ．山东省2017年高考数学（理科）专题练习空间几何体表面积或体积的求解解析[建议A 、B 组各用时：45分钟] [A 组高考达标] 一、选择题 1.D[分析三视图可知，该几何体为如图所示的三棱锥，其中平面ACD ⊥平面BCD ，故选D.] 2．B[由三视图可知该几何体由半球内挖去一个同底的圆锥得到，所以该几何体的体积为V ＝12×43π×13－13π×12×1＝π3.]3．D[由三视图可知，几何体是一个三棱柱，体积V 1＝12×2×2×2＝4，设外接球的半径为R ，则4R 2＝22＋22＋22＝12，所以R ＝3.所以球的体积V 2＝43πR 3＝43π，体积比V 1∶V 2＝4∶43π＝1∶3π.] 4．B[分析题意可知，该几何体是由如图所示的三棱柱ABC -A 1B 1C 1截去四棱锥A -BEDC 得到的，故其体积V ＝34×22×3－13×1＋22×2×3＝23，故选B.] 5．A[在正方体中还原出该四面体C -A 1EC 1如图所示，可求得该四面体的表面积为8＋82＋4 6.] 二、填空题6．3＋2 2[依题意，边长是3的等边△ABC 的外接圆半径r ＝12·3sin 60°＝1.∵球O 的表面积为36π＝4πR 2，∴球O 的半径R ＝3，∴球心O 到平面ABC 的距离d ＝R 2－r 2＝22，∴球面上的点P 到平面ABC 距离的最大值为R ＋d ＝3＋2 2.]7．14[如图，设S △ABD ＝S 1，S △PAB ＝S 2，E 到平面ABD 的距离为h 1，C 到平面PAB 的距离为h 2，则S 2＝2S 1，h 2＝2h 1，V 1＝13S 1h 1，V 2＝13S 2h 2，所以V 1V 2＝S 1h 1S 2h 2＝14．] 8．16(π－2)[设内接正四棱柱底边长为a ，高为h ，那么16＝2a 2＋h 2≥22ah ，正四棱柱的侧面积S ＝4ah ≤162，球的表面积与该正四棱柱的侧面积之差是16(π－2)．]三、解答题9．解：(1)证明：取P A 的中点F ，连接EF ，BF ，则EF ∥AD ∥BC ，即EF ，BC 共面．∵PB ⊥平面ABCD ，∴PB ⊥BC ，又BC ⊥AB 且PB ∩AB ＝B ，∴BC ⊥平面P AB ，∴BC ⊥P A ．3分∵PB ＝AB ，∴BF ⊥P A ，又BC ∩BF ＝B ，∴P A ⊥平面EFBC ，∴P A ⊥CE ．6分(2)设四棱锥P -ABCD 的表面积为S ，∵PB ⊥平面ABCD ，∴PB ⊥CD ，又CD ⊥BC ，PB ∩BC ＝B ，∴CD ⊥平面PBC ，∴CD ⊥PC ，即△PCD 为直角三角形，8分由(1)知BC ⊥平面P AB ，而AD ∥BC ，∴AD ⊥平面P AB ，故AD ⊥P A ，即△P AD 也为直角三角形．S ▱ABCD ＝2×2＝4，S △PBC ＝S △P AB ＝S △PDA ＝12×2×2＝2， S △PCD ＝12×2×22＋22＝22，10分 ∴S 表＝S ▱ABCD ＋S △PBC ＋S △PDA ＋S △P AB ＋S △PCD＝10＋22．12分10．解：(1)证明：因为D ，E 分别为棱AC ，BC 的中点，所以DE 是△ABC 的中位线，所以DE ∥AB .又DE ⊄平面ABB 1A 1，AB ⊂平面ABB 1A 1，所以DE ∥平面ABB 1A 1.同理DG ∥平面ABB 1A 1，又DE ∩DG ＝D ，所以平面DEFG ∥平面ABB 1A 1．6分(2)当直三棱柱ABC -A 1B 1C 1容器的侧面AA 1B 1B 水平放置时，由(1)可知，液体部分是直四棱柱，其高即为原直三棱柱ABC -A 1B 1C 1容器的高，即侧棱长l ，当底面ABC 水平放置时，设液面的高为h ，△ABC 的面积为S ，则由已知条件可知，△CDE ∽△ABC ，且S △CDE ＝14S ，所以S 四边形ABED ＝34S ．9分由于两种状态下液体体积相等，所以V 液体＝Sh ＝S 四边形ABED l ＝34Sl ，即h ＝34l . 因此，当底面ABC 水平放置时，液面的高为34l ．12分 [B 组名校冲刺]一、选择题1．A[过点D 在平面PCD 内作DN ⊥PM 于点N ，又平面PMB ⊥平面PCD ，平面PMB ∩平面PCD ＝PM ，所以DN ⊥平面PMB ，所以DN ⊥BM .又由PD ⊥平面ABCD ，得PD ⊥BM ，又PD 与DN 是平面PDC 内的两条相交直线，所以BM ⊥平面PDC ，则BM ⊥CD .又点M 是CD 的中点，BC ＝CD ，所以∠BCD ＝60°，所以底面菱形ABCD 的面积为2×2×sin 60°＝23，故该四棱锥的体积为13×23×2＝433．] 2．B[根据三视图可知，几何体是由一个直三棱柱与一个三棱锥所组成的，其中该直三棱柱的底面是一个直角三角形(直角边长分别为1,2，高为1)；该三棱锥的底面是一个直角三角形(腰长分别为1,2，高为1)，因此该几何体的体积为12×2×1×1＋13×12×2×1×1＝43，选B ．] 3．D[由三视图知，该几何体为一个底面半径为1，高为1的圆柱体，与底面半径为1，高为2的半圆柱体构成，所以该三视图的体积为π×12×1＋12π×12×2＝2π，故选D ．] 4．C[设OP 交平面ABC 于O ′，由题得△ABC 和△P AB 为正三角形，所以O ′A ＝33AB ＝33AP .因为AO ′⊥PO ，OA ⊥P A ，所以OP OA ＝AP AO ′，AO ′AB＝33，AO ′AP ＝33，所以OA ＝OP ·O ′A AP ＝3×33＝1，即球的半径为1，所以其体积为43π×13＝43π．选C ．]二、填空题5．55π6[由题意知六棱柱的底面正六边形的外接圆半径r ＝1, 其高h ＝1，∴球半径为R ＝r 2＋⎝⎛⎭⎫h 22＝1＋14＝54，∴该球的体积V ＝43πR 3＝43×⎝⎛⎭⎫543π＝55π6．] 6．832π [由题可知，△ABC 中AC 边上的高为15－32＝6，球心O 在底面ABC 的投影即为△ABC的外心D ，设DA ＝DB ＝DC ＝x ，∴x 2＝32＋(6－x )2，解得x ＝546，∴R 2＝x 2＋⎝⎛⎭⎫PC 22＝758＋1＝838(其中R 为三棱锥外接球的半径)，∴外接球的表面积S ＝4πR 2＝832π．] 三、解答题7．解：(1)证明：设EC 与DF 交于点N ，连接MN ，在矩形CDEF 中，点N 为EC 中点，因为M 为EA 中点，所以MN ∥AC ．2分又因为AC ⊄平面MDF ，MN ⊂平面MDF ，所以AC ∥平面MDF ．4分(2)取CD 中点为G ，连接BG ，EG ，平面CDEF ⊥平面ABCD ，平面CDEF ∩平面ABCD ＝CD ，AD ⊂平面ABCD ，AD ⊥CD ，所以AD ⊥平面CDEF ，同理ED ⊥平面ABCD ，7分所以ED 的长即为四棱锥E -ABCD 的高．8分在梯形ABCD 中，AB ＝12CD ＝DG ，AB ∥DG ，所以四边形ABGD 是平行四边形，BG ∥AD ，所以BG ⊥平面CDEF .又DF ⊂平面CDEF ，所以BG ⊥DF ，又BE ⊥DF ，BE ∩BG ＝B ，所以DF ⊥平面BEG ，DF ⊥EG ．10分注意到Rt △DEG ∽Rt △EFD ，所以DE 2＝DG ·EF ＝8，DE ＝22，所以V E -ABCD ＝13S 梯形ABCD ·ED ＝42．12分 8．解：(1)证明：∵△CMD 是等腰直角三角形，∠CMD ＝90°，点O 为CD 的中点，∴OM ⊥CD ．1分∵平面CMD ⊥平面BCD ，平面CMD ∩平面BCD ＝CD ，OM ⊂平面CMD ，∴OM ⊥平面BCD ．2分∵AB⊥平面BCD，∴OM∥AB．3分∵AB⊂平面ABD，OM⊄平面ABD，∴OM∥平面ABD．4分(2)法一：由(1)知OM∥平面ABD，∴点M到平面ABD的距离等于点O到平面ABD的距离．5分过点O作OH⊥BD，垂足为点H.∵AB⊥平面BCD，OH⊂平面BCD，∴OH⊥AB．6分∵AB⊂平面ABD，BD⊂平面ABD，AB∩BD＝B，∴OH⊥平面ABD．7分∵AB＝BC＝2，△BCD是等边三角形，∴BD＝2，OD＝1，OH＝OD·sin 60°＝32．9分∴V三棱锥A-BDM＝V三棱锥M-ABD＝13×12×AB·BD·OH＝13×12×2×2×32＝33．11分∴三棱锥A-BDM的体积为33．12分法二：由(1)知OM∥平面ABD，∴点M到平面ABD的距离等于点O到平面ABD的距离．5分∵AB＝BC＝2，△BCD是等边三角形，∴BD＝2，OD＝1．6分连接OB，则OB⊥CD，OB＝BD·sin 60°＝3．7分∴V三棱锥A-BDM＝V三棱锥M-ABD＝V三棱锥O-ABD＝V三棱锥A-BDO＝13×12×OD·OB·AB＝13×12×1×3×2＝33．11分∴三棱锥A-BDM的体积为33．12分。

高考数学(理科)总复习 8.1 空间几何体的三视图、表面积和体积

考向突破
考向一空间几何体的表面积例1 (2018广东广州3月调研,7)如图,网格纸上小正方形的边长为1,粗线画出的是某个几何体的三视图,则该几何体的表面积为 ( )
A.4+4 2 +2 3 C.10+4 2 +2 3
B.14+4 2 D.4
解析如图,该几何体是一个底面为直角梯形,有一条侧棱垂直于底面
(1)当小球与正方体一顶点处的三个面都相切时,球面与该顶点处的三
个面之间形成的空隙小球始终无法经过,其体积为13-1 × 4 ×13=1- .正
83
6
方体有8个顶点,共形成8个无法经过的空隙,总体积为8×1
6
=8-
4.
3
(2)小球只与正方体过同一条棱的两个面相切时,在该棱处能形成一个
高为2的小柱体,其体积为1
2
(2)正方体的外接球、内切球及与各条棱都相切的球:
①外接球:球心是正方体的中心,半径r= 3 a(a为正方体的棱长);
2
②内切球:球心是正方体的中心,半径r= a (a为正方体的棱长);
2
③与各条棱都相切的球:球心是正方体的中心,半径r= 2 a(a为正方体的
2
棱长).
(3)正四面体的外接球与内切球(正四面体可以看作是正方体的一部分):
头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合
时带卯眼的木构件的俯视图可以是 ( )
解析本题考查空间几何体的三视图. 两个木构件咬合成长方体时,小长方体(榫头)完全嵌入带卯眼的木构件, 易知俯视图可以为A.故选A.
答案 A
考向二由空间几何体的三视图还原直观图例2 (2018课标Ⅰ,7,5分) 某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为 ( )

同步配套练习28 三视图与表面展开图

课后强化训练28三视图与表面展开图一、选择题1．如图，一个放置在水平桌面上的圆柱，它的主视图是(C)(第1题)A.B.C. D.【解析】圆柱的主视图是长方形．2．如图所示的几何体的左视图是(A)(第2题)A.B.C. D.【解析】该几何体由两个圆锥组合而成，根据圆锥的三视图就可以得到该几何体的左视图为A.3．有3块积木，每一块的各面都涂上不同的颜色，3块的涂法完全相同，现把它们摆放成不同的位置(如图)，请你根据图形判断涂成绿色一面的对面的颜色是(C)(第3题)A．白B．红C．黄D．黑【解析】∵涂有绿色一面的邻面的颜色是白色，红色，蓝色，黑色，∴涂成绿色一面的对面的颜色是黄色．4．若一个圆锥的主视图是腰长为13，底边长为10的等腰三角形，则该圆锥的侧面积是(B)A. 60πB. 65πC. 120πD. 130π【解析】根据题意，得圆锥底面圆的半径为5，母线长为13， ∴该圆锥的侧面积＝π×5×13＝65π.故选B. 5．如图所示的三视图所对应的几何体是(B)（第5题）【解析】选项A ，C ，D 的主视图与题图中的主视图都不对应，故选B.6．如图，圆柱体中挖去一个小圆柱，那么这个几何体的主视图和俯视图分别为(B)A.B.C.D.(第6题)【解析】由主视方向可得主视图和俯视图分别为和.二、填空题7．如图，这是一个长方体的主视图和俯视图，由图示数据(单位： cm)可以得出该长方体的体积是__18__cm 3.(第7题)【解析】观察其视图可知该长方体的长为3，宽为2，高为3，故其体积为3×2×3＝18(cm 3)．8．由棱长为1的立方体搭成的积木的三视图如图所示，则图中棱长为1的立方体的个数是__6__．(第8题)【解析】在俯视图中标注个数如解图，故有6个．(第8题解)(第9题)9．如图是一个上、下底密封纸盒的三视图，根据图中数据，计算这个密封纸盒的表面积为(753＋360)cm 2(结果可保留根号)．【解析】根据该几何体的三视图知道其是一个正六棱柱，高为12 cm ，底面正六边形的边长为5 cm ，∴其侧面积为6×5×12＝360(cm 2)，两个底面积为2×6×12×5×5×32＝753(cm 2)．∴其全面积为(753＋360)cm 2.10．如图，观察由棱长为1的小立方体摆成的图形，寻找规律：如图①中，共有1个小立方体，其中1个看得见，0个看不见；如图②中，共有8个小立方体，其中7个看得见，1个看不见；如图③中，共有27个小立方体，其中19个看得见，8个看不见……则图⑥中，看得见的小立方体有__91__个．（第10题）【解析】观察后得规律：图中看得见的小立方体有[n 3－(n －1)3]个，故图⑥中看得见的小立方体有63－53＝91(个)．三、解答题11．如图是由两个相同的小立方体和一个圆锥组成的立体图形，画出该图形的三视图．(第11题) (第11题解)【解析】画图如解图．(第12题)12．一个几何体的三视图如图所示，它的俯视图为菱形．请写出该几何体的形状，并根据图中所给的数据求出它的侧面积和体积．【解析】该几何体是直四棱柱．由三视图知，棱柱底面菱形的对角线长分别为4cm ，3cm ，∴菱形的边长为52cm ，∴棱柱的侧面积为52×8×4＝80(cm 2)，棱柱的体积为12×3×4×8＝48(cm 3)．13．将一直径为17 cm 的圆形纸片(图①)剪成如图②所示形状的纸片，再将纸片沿虚线折叠得到立方体(图③)形状的纸盒，则这样的纸盒体积最大是多少？（第13题）【解析】如解图，当AB 长等于圆的直径时，立方体棱长最长，设立方体的棱长为a .（第13题解）此时a 2＋(4a )2＝172，17a 2＝172，∴a ＝17. ∴纸盒的最大体积为a 3＝(17)3＝1717(cm 3)．14．如图，以边长为20 cm 的正三角形纸板的各顶点为端点，在各边上分别截取4 cm 长的六条线段，过截得的六个端点作所在边的垂线，形成三个有两个直角的四边形．把它们沿图中虚线剪掉，用剩下的纸板折成一个底为正三角形的无盖柱形盒子，求它的容积．(第14题)【解析】如解图，连结AO .由题意，得△ABC 与△PQO 都为等边三角形，AD ＝AK ＝BE ＝BF ＝CG ＝CH ＝4 cm ， ∠DAK ＝∠B ＝∠C ＝60°，AB ＝BC ＝AC ＝20 cm. 易得四边形DOPE 是矩形，(第14题解)∴OP ＝DE ＝AB －AD －BE ＝12 cm ，∴S △OPQ ＝34OP 2＝36 3 cm 2. 易得AO 平分∠DAK ，∴∠DAO ＝12∠DAK ＝30°.又∵AD ＝4 cm ， ∴DO ＝433cm.∴无盖盒子的容积＝363×433＝144(cm 3)．(第15题)15．如图是一个几何体的三视图． (1)写出这个几何体的名称．(2)根据图示数据计算这个几何体的表面积． (3)如果一只蚂蚁要从这个几何体中的点B 出发，沿表面爬到AC 的中点D ，请求出这个路线的最短路程．【解析】 (1)圆锥．(2)∵S 圆锥侧＝πrl ＝π×2×6＝12π(cm 2)， S 底面＝πr 2＝π×22＝4π(cm 2)，∴S 表＝S 圆锥侧＋S 底面＝12π＋4π＝16π(cm 2)．(第15题解)(3)如解图．∵圆锥侧面扇形圆心角θ＝r l ·360°＝26×360°＝120°，∴∠BAC ＝60°.又∵AB ＝AC ，∴△ABC 是正三角形．∵D 是AC 的中点，∴BD ⊥AC ， ∴BD ＝AB ·sin ∠BAD ＝6×32＝33(cm)．课后强化训练16 统计的应用一、选择题(第1题)1．某校学生参加体育兴趣小组情况的统计图如图所示．若参加人数最少的小组有25人，则参加人数最多的小组有(C )A. 25人B. 35人C. 40人D. 100人【解析】根据总数＝部分量÷对应百分比可求出，总人数＝25÷25%＝100(人)，∴参加人数最多的小组有100×40%＝40(人)．2．为了支援地震灾区同学，某校开展捐书活动，九(1)班40名同学积极参与．现将捐书数量绘制成频数直方图如图所示，则捐书数量在5.5～6.5组别的频率是(B )(第2题)A ．0.1B ．0.2C ．0.3D ．0.4【解析】捐书数量在5.5～6.5组别的频数是8，其频率是840＝0.2.3．小明统计了他家今年5月打电话的次数及通话时间，并列出了频数分布表：通话时间x (min) 0＜x ≤5 5＜x ≤10 10＜x ≤1515＜x ≤20频数(通话次数)201695则通话时间不超过15 min 的频率为(D ) A. 0.1 B. 0.4 C. 0.5 D. 0.9【解析】不超过15 min 的通话次数共有20＋16＋9＝45(次)，总共通话次数为45＋5＝50(次)，∴通话时间不超过15 min 的频率为4550＝0.9.4．某企业2016年1～5月利润的变化情况如图所示，以下说法与图中反映的信息相符的是(C )(第4题)A. 1～2月利润的增长快于2～3月利润的增长B. 1～5月利润的平均数为120万元C. 1～5月利润的众数是130万元D. 1～5月利润的中位数为120万元【解析】2～3月利润的增长快于1～2月；1～5月利润的平均数为117万元；1～5月利润的众数是130万元，中位数是115万元，只有C正确．5．下面是甲、乙两人10次射击成绩(环数)的条形统计图，则下列说法正确的是(B)(第5题)A．甲比乙的成绩稳定B．乙比甲的成绩稳定C．甲、乙两人的成绩一样稳定D．无法确定谁的成绩更稳定【解析】x甲＝110×(8×4＋9×2＋10×4)＝9，S甲2＝110×[4×(8－9)2＋2×(9－9)2＋4×(10－9)2]＝0.8.x乙＝110×(8×3＋9×4＋10×3)＝9，S乙2＝110×[3×(8－9)2＋4×(9－9)2＋3×(10－9)2]＝0.6.∵S甲2>S乙2，∴乙比甲的成绩稳定．6．某学校将为七年级学生开设A，B，C，D，E，F这6门选修课，现选取若干名学生进行了“我最喜欢的一门选修课”调查，将调查结果绘制成了如下不完整的统计图表：选修课 A B C D E F人数4060100根据图表提供的信息，下列结论错误的是(D)(第6题)A ．这次被调查的学生人数为400人B ．扇形统计图中E 部分扇形的圆心角为72°C ．被调查的学生中喜欢选修课E ，F 的人数分别为80人，70人D ．喜欢选修课C 的人数最少【解析】 ∵被调查的学生人数为60÷15%＝400(人)，∴A 选项正确． ∵扇形统计图中D 的圆心角为100400×360°＝90°，A 的圆心角为40400×360°＝36°，360°×(17.5%＋15%＋12.5%)＝162°，∴扇形统计图中E 的圆心角为360°－162°－90°－36°＝72°，∴B 选项正确．喜欢选修课E 的人数为400×72°360°＝80(人)，喜欢选修课F 的人数为400×17.5%＝70(人)，∴C 选项正确．∵12.5%＞10%，∴喜欢选修课A 的人数最少，∴D 选项错误．二、填空题7．在开展“国学诵读”活动中，某校为了了解全校1300名学生课外阅读的情况，随机调查了50名学生一周的课外阅读时间，并绘制成如图所示的条形统计图．根据图中数据，估计该校1300名学生中一周的课外阅读时间不少于7 h 的人数是__520__．(第7题)【解析】该校1300名学生中一周的课外阅读时间不少于7 h 的人数是1300×15＋550＝520.8．小亮对60名同学进行节水方法选择的问卷调查(每人选择一项)，人数统计如图所示，如果绘制成扇形统计图，那么表示“一水多用”的扇形的圆心角度数是__240°__．(第8题)【解析】表示“一水多用”的扇形的圆心角度数＝4060×360°＝240°. 9．为监测某河道水质，进行了6次水质检测，绘制了如图所示的氨氮含量折线统计图．若这6次水质检测氨氮含量的平均数为1.5 mg/L ，则第3次检测得到的氨氮含量是__1__mg/L.水质检测中氨氮含量统计图（第9题）【解析】设第三次的检测结果为x (mg/L)，则由题意，得 16(1.6＋2＋x ＋1.5＋1.4＋1.5)＝1.5，解得x ＝1. 10．某单位若干名职工参加普法知识竞赛，将成绩制成如图所示的扇形统计图和条形统计图．根据图中提供的信息，这些职工成绩的中位数是__96__分，平均数是__96.4__分．(第10题)【解析】 ∵总人数为6÷10%＝60(人)，∴94分的有60×20%＝12(人)，98分的有60－6－12－15－9＝18(人)． ∵按从小到大的顺序排列后第30与31名的成绩都是96分， ∴这些职工成绩的中位数是(96＋96)÷2＝96(分)．这些职工成绩的平均数是(92×6＋94×12＋96×15＋98×18＋100×9)÷60＝96.4(分)．三、解答题11．某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图如图所示．某汽车厂去年每个季度汽车销售数量占当季汽车产量百分比统计图(第11题)根据统计图回答下列问题：(1)若第一季度的汽车销售数量为2100辆，求该季度的汽车产量．(2)圆圆同学说：“因为第二，第三这两个季度汽车销售数量占当季汽车产量的百分比从75%降到50%，所以第二季度的汽车产量一定高于第三季度的汽车产量”．你觉得圆圆说的对吗？为什么？【解析】(1)2100÷0.7＝3000(辆)．答：第一季度的汽车产量为3000辆．(2)圆圆的说法不对．因为百分比仅能够表示所要考察的数据在总量中所占的比例，并不能反映总量的大小．12．为了让书籍开拓学生的视野，陶冶学生的情操，某中学开展了“五个一”课外阅读活动，为了解全校学生课外阅读情况，抽样调查了50名学生平均每天课外阅读时间(单位：min)，将抽查得到的数据分成5组，下面是尚未完成的频数表：组别分组频数频率110≤t＜300.16230≤t＜5020350≤t＜700.28470≤t＜906590≤t＜110(1)将表中空格处的数据补全．(2)请画出相应的频数直方图．(3)如果该校有1500名学生，请你估计该校共有多少名学生平均每天阅读时间不少于50 min?【解析】(1)根据题意填表如下：组别分组频数频率110≤t＜3080.16230≤t＜50200.40350≤t＜70140.28470≤t＜9060.12590≤t＜11020.04(2)作出频数直方图如解图．平均每天课外阅读时间频数直方图（第12题解）(3)1500×(0.28＋0.12＋0.04)＝660(人)．答：估计该校共有660名学生平均每天阅读时间不少于50 min.13．班主任张老师为了了解学生课堂发言情况，对前一天本班男、女生的发言次数进行了统计，并绘制成如下频数折线图(如图①)．前一天男、女生发言次数频数折线图第二天全班发言次数变化人数扇形统计图(第13题)(1)请根据图①，回答下列问题：①这个班共有__40__名学生，发言次数是5次的男生有__2__人、女生有__5__人．②男、女生发言次数的中位数分别是__4__次和__5__次．(2)通过张老师的鼓励，第二天的发言次数比前一天明显增加，全班发言次数变化的人数的扇形统计图如图②所示．求第二天发言次数增加3次的学生人数和全班增加的发言总次数．【解析】(1)①∵男生有2＋1＋6＋4＋2＋3＋2＝20(人)，女生有1＋2＋3＋2＋5＋4＋3＝20(人)，∴这个班共有40名学生．从图中可知，发言次数是5次的男生有2人，女生有5人．②∵男、女生发言次数分别从小到大排列后，男生数据的第10，11个都是4次，女生数据的第10，11个都是5次，∴男、女生发言次数的中位数分别是4次，5次．(2)发言次数增加3次的学生有40×(1－20%－30%－40%)＝4(人)．全班增加的发言总次数有40%×40×1＋30%×40×2＋4×3＝16＋24＋12＝52(次)．。

2020届高考数学复习备考-空间几何体的三视图、表面积及体积

2020届高考数学复习备考-空间几何体的三视图、表面积及体积高考考点聚焦高考考点考点解读空间几何体的三视图与直观图的关系1.根据某几何体的部分三视图，判断该几何体的其他三视图；或者已知某几何体的三视图，判断该几何体的形状2．考查三视图的画法以及数量关系空间几何体的表面积与体积的计算1.以三视图为命题背景，考查空间几何体体积、表面积的计算方法2．以空间几何体为命题背景考查空间几何体体积、表面积的计算方法多面体与球的切、接问题以球与多面体为背景，考查球的截面性质高考真题体验1．某几何体的三视图如图所示(单位：cm)，则该几何体的体积(单位：cm3)是()A．π2＋1B．π2＋3C．3π2＋1 D．3π2＋32．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为()A．90πB．63πC．42πD．36π3．某三棱锥的三视图如图所示，则该三棱锥的体积为()A．60 B．30C．20 D．104．某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为()A．3 2 B．2 3C．2 2 D．25．体积为8的正方体的顶点都在同一球面上，则该球的表面积为()A．12πB．32 3πC．8πD．4π6．已知三棱锥S－ABC的所有顶点都在球O的球面上，SC是球O的直径．若平面SCA⊥平面SCB，SA＝AC，SB＝BC，三棱锥S－ABC的体积为9，则球O的表面积为____.命题热点突破热点1空间几何体的三视图例1(1)某几何体的三视图如图所示，且该几何体的体积是3，则正(主)视图中的x的值是()A．2B．9 2C．32D．3（2）一只蚂蚁从正方体ABCD－A1B1C1D1的顶点A处出发，经正方体的表面，按最短路线爬行到顶点C1处，则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图的是()A ．(1)(2)B ．(1)(3)C ．(2)(4)D ．(3)(4)热点2 空间几何体的表面积与体积例2 (1)某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形．该多面体的各个面中有若干个是梯形，这些梯形的面积之和为 ( )A ．10B ．12C ．14D ．16（2）一个正方体被一个平面截去一部分后，剩余部分的三视图如下图，则截去部分体积与剩余部分体积的比值为 ( )A ．18 B ．17 C ．16D ．15(3)由一个长方体和两个14圆柱体构成的几何体的三视图如下，则该几何体的体积为 _____热点3多面体与球例3(1)已知正四棱锥P－ABCD内接于一个半径为R的球，则正四棱锥P－ABCD体积的最大值是()A．16R381B．32R381C．64R381D．R3(2)设三棱柱的侧棱垂直于底面，所有棱的长都为a，顶点都在一个球面上，则该球的表面积为______.强化训练提升1.已知三棱锥P－ABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，PC为球O的直径，该三棱锥的体积为26，则球O的表面积为()A．4πB．8πC．12πD．16π．2．已知三棱锥D－ABC中，AB＝BC＝1，AD＝2，BD＝5，AC＝2，BC⊥AD，则该三棱锥的外接球的表面积为()3.若某棱锥的三视图(单位：cm)如图所示，则该棱锥的体积等于()A．10 cm3B．20 cm3C．30 cm3D．40 cm34．某几何体的三视图如图所示，则该几何体的表面积为()A ．18＋2πB ．20＋πC ．20＋π2 D ．16＋π5．某四面体的三视图如图所示，正视图、俯视图都是腰长为2的等腰直角三角形，侧视图是边长为2的正方形，则此四面体的四个面中面积最大的为 ( )A ．2 2B ．2 3C ．4D ．2 66．三棱锥S －ABC 及其三视图中的正视图和侧视图如图所示，则棱SB 的长为 ( )A ．211B ．4 2C ．38D ．16 37．三棱锥P －ABC 中，P A ⊥平面ABC 且P A ＝2，△ABC 是边长为3的等边三角形，则该三棱锥外接球的表面积为 ( )A ．4π3B ．4πC ．8πD ．20π8．如图，正方体ABCD －A 1B 1C 1D 1的棱长为1，E ，F 分别为线段AA 1，B 1C 上的点，则三棱锥D 1－EDF 的体积为______.9．已知E ，F 分别是矩形ABCD 的边BC 与AD 的中点，且BC ＝2AB ＝2，现沿EF 将平面ABEF 折起，使平面ABEF ⊥平面EFDC ，则三棱锥A －FEC 外接球的体积为______10．甲、乙两个圆柱的底面积分别为S 1，S 2，体积分别为V 1，V 2.若它们的侧面积相等且V 1V 2＝32，则S 1S 2的值是_____.11．已知在直角梯形ABCD 中，AB ⊥AD ，CD ⊥AD ，AB ＝2AD ＝2CD ＝2，将直角梯形ABCD 沿AC 折叠成三棱锥D －ABC ，当三棱锥D －ABC 的体积取最大值时，其外接球的体积为_____.。

高考理科数学考前培优练习三视图与几何体的体积、表面积

专题五立体几何5.1三视图与几何体的体积、表面积命题角度1空间几何体三视图的识别与画法高考真题体验·对方向1.(2018全国Ⅲ·3)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是(),从上往下看,看不见的线画虚线,则A正确.2.(2018全国Ⅰ·7)某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()A.2√17B.2√5C.3D.2⏜的中点,将圆柱的侧面沿母线MC剪开,展平为矩形MCC'M',易知CC'=4,MC=2,从M到N的路程中最短路径为MN.CN=14在Rt△MCN中,MN=√MC2+NC2=2√5.3.(2017北京·7)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为()A.3√2B.2√3C.2√2D.2,直观图为四棱锥A-BCDE(如图所示),最长的棱为正方体的体对角线AE=√22+22+22=2√3.故选B.4.(2014全国Ⅰ·12)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为()A.6√2B.6C.4√2D.4如图所示的正方体ABCD-A1B1C1D1的棱长为4.取B1B的中点G,即三棱锥G-CC1D1为满足要求的几何体,其中最长棱为D1G,D1G=√(4√2)2+22=6.5.(2013全国Ⅰ·7)一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到的正视图可以为(),该四面体在空间直角坐标系O-xyz的图象为下图:则它在平面zOx上的投影即正视图为,故选A.典题演练提能·刷高分1.某几何体的正视图与俯视图如图,则其侧视图可以为(),因此其侧视图为矩形内有一条虚线,虚线靠近矩形的左边部分,只有选项B符合题意,故选B.2.如图,O1,O2为棱长为a的正方体的上、下底面中心,若正方体以O1O2为轴顺时针旋转,则该正方体的所有正视图中最大面积是()A.a2B.√2a2C.√3a2D.2a2√2a,宽为a的矩形,面积为√2a2,故选B.3.已知一几何体的正视图、侧视图如图所示,则该几何体的俯视图不可能是(),选项D对应的几何体为长方体与三棱柱的组合,其侧视图中间的线不可视,应为虚线,故选D.4.(2019湖南六校联考)一个几何体的三视图如图所示,这个几何体的体积为8,则俯视图中三角形的高x等于()A.2B.3C.4D.1,该几何体为四棱锥,体积为V=13×12×(2+4)×2·x=8,解得x=4.5.(2019陕西第二次质检,理9)某三棱锥的三视图如图所示,其俯视图是一个等腰直角三角形,在此三棱锥的六条棱中,最长棱的长度为()A.2B.2√2C.√6D.√2,由题意,可知PA⊥底面ABC,△ABC是等腰直角三角形,AB⊥BC,则PC是最长的棱,PC=√4+4=2√2.故选B.6.在正方体ABCD-A1B1C1D1中,E是棱A1B1的中点,用过点A,C,E的平面截正方体,则位于截面以下部分的几何体的侧(左)视图为(),取B1C1的中点F,则EF∥AC,即平面ACFE亦即平面ACE截正方体所得的截面,据此可得位于截面以下部分的几何体的侧(左)视图如选项A所示.7.已知三棱柱HIG-EFD的底面为等边三角形,且侧棱垂直于底面,该三棱柱截去三个角(如图①所示,A,B,C分别是△GHI三边的中点)后得到的几何体如图②,则该几何体的侧视图为()DEHG⊥平面EFD,所以几何体的侧视图为直角梯形,且直角腰在侧视图的左侧,故选A.命题角度2空间几何体的体积、表面积高考真题体验·对方向1.(2019全国Ⅲ·16)学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD-A1B1C1D1挖去四棱锥O-EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6 cm,AA1=4 cm.3D打印所用原料密度为0.9 g/cm3.不考虑打印损耗,制作该模型所需原料的质量为g..8×2×3=12(cm2),点O到平面BB1C1C的距离为,四棱锥O-EFGH的底面积为4×6-4×123 cm,则此四棱锥的体积为V1=1×12×3=12(cm3).3又长方体ABCD-A1B1C1D1的体积为V2=4×6×6=144(cm3),则该模型的体积为V=V2-V1=144-12=132(cm3).故其质量为0.9×132=118.8(g).2.(2015全国Ⅰ·6)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( ) A .14斛 B .22斛C .36斛D .66斛R ,米堆高为h.∵米堆底部弧长为8尺, ∴14·2πR=8,∴R=16π.∴体积V=14×13·πR 2h=112×π×(16π)2×5. ∵π≈3,∴V ≈3209(尺3). ∴堆放的米约为3209×1.62≈22(斛).3.(2018全国Ⅱ·16)已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45°.若△SAB 的面积为5√15.则该圆锥的侧面积为 .√2πO 为底面圆圆心,∵cos ∠ASB=78,∴sin ∠ASB=√1-(78)2=√158.∴S △ASB =1×|AS|·|BS|·√15=5√15. ∴SA 2=80. ∴SA=4√5.∵SA 与圆锥底面所成的角为45°,∠SOA=90°.∴SO=OA=√2SA=2√10.∴S 圆锥侧=πrl=4√5×2√10×π=40√2π.典题演练提能·刷高分1.我国古代数学名著《增删算法统宗》中有如下问题:“有个金球里面空,球高尺二厚三分,一寸自方十六两,试问金球几许金?”意思是:有一个空心金球,它的直径12寸,球壁厚0.3寸,1立方寸金重1斤,试问金球重是多少斤?(注π≈3)( ) A.125.77 B.864 C.123.23 D.369.69,大球半径R=6,空心金球的半径r=6-0.3=5.7,则其体积V=43π(63-5.73)≈123.23(立方寸).因为1立方寸金重1斤,所以金球重123.23斤,故选C .2.我国古代数学名著《孙子算经》中有如下问题:“今有筑城,上广二丈,下广五丈四尺,高三丈八尺,长五千五百五十尺,秋程人功三百尺.问:须工几何?”意思是:“现要筑造底面为等腰梯形的直棱柱的城墙,其中底面等腰梯形的上底为2丈、下底为5.4丈、高为3.8丈,直棱柱的侧棱长为5 550尺.如果一个秋天工期的单个人可以筑出300立方尺,问:一个秋天工期需要多少个人才能筑起这个城墙?”(注:一丈等于十尺)( )A.24 642B.26 011C.52 022D.78 033,可得城墙所需土方为20+542×38×5 550=7 803 300(立方尺),一个秋天工期所需人数为7 803 300300=26 011,故选B . 3.三棱锥D-ABC 中,CD ⊥底面ABC ,△ABC 为正三角形,若AE ∥CD ,AB=CD=AE=2,则三棱锥D-ABC 与三棱锥E-ABC 的公共部分构成的几何体的体积为( )A.√39 B.√33 C.13D.√3:∴三棱锥D-ABC 与三棱锥E-ABC 的公共部分构成的几何体为三棱锥F-ABC. ∵△ABC 为正三角形,AB=2,∴S △ABC =12×2×2×√32=√3.∵CD ⊥底面ABC ,AE ∥CD ,CD=AE=2,∴四边形AEDC 为矩形,则F 为EC 与AD 的中点,∴三棱锥F-ABC 的高为12CD=1,∴三棱锥F-ABC 的体积为V=13×√3×1=√33.故选B .4.《九章算术》是我国古代的数学名著,书中提到一种名为“刍甍”的五面体,如图所示,四边形ABCD 是矩形,棱EF ∥AB ,AB=4,EF=2,△ADE 和△BCF 都是边长为2的等边三角形,则这个几何体的体积是( )A.203B.83+2√3C.10√2D.8√2E 作EG ⊥平面ABCD ,垂足为点G ,过点F 作FH ⊥平面ABCD ,垂足为点H ,过点G 作PQ ∥AD ,交AB 于点Q ,交CD 于点P ,过点H 作MN ∥BC ,交AB 于点N ,交CD 于点M ,如图所示:∵四边形ABCD 是矩形,棱EF ∥AB ,AB=4,EF=2,△ADE 和△BCF 都是边长为2的等边三角形,∴四边形PMNQ 是边长为2的正方形,EG=√(√3)2-12=√2,∴这个几何体的体积为V=V E-AQPD +V EPQ-FMN +V F-NBCM =13×1×2×√2×2+12×2×√2×2=4√23+2√2=10√23.故选C . 5.已知M ,N 是三棱锥P-ABC 的棱AB ,PC 的中点,记三棱锥P-ABC 的体积为V 1,三棱锥N-MBC 的体积为V 2,则V2V 1等于 .如图,设三棱锥P-ABC 的底面积为S ,高为h.∵M 是AB 的中点, ∴S △BMC =12S. ∵N 是PC 的中点, ∴三棱锥N-MBC 的高为12h ,则V 1=13Sh ,V 2=13×12S×12h=112Sh ,∴V 2V 1=112Sℎ13Sℎ=14.故填14.6.在四棱锥S-ABCD 中,SD ⊥底面ABCD ,底面ABCD 是正方形,SD=AD=2,三棱柱MNP-M 1N 1P 1的顶点都位于四棱锥S-ABCD 的棱上,已知M ,N ,P 分别是棱AB ,AD ,AS 的中点,则三棱柱MNP-M 1N 1P 1的体积为 .M 1是BC 中点,N 1是DC 中点,P 1是SC 中点,PN=1,MN=√2,且PN ⊥MN ,所以三棱柱MNP-M 1N 1P 1的底面积为12×1×√2=√22.由题得正方形的对角线长2√2,三棱柱MNP-M 1N 1P 1的高为12×2√2=√2,所以三棱柱MNP-M 1N 1P 1的体积为√22×√2=1,故填1.命题角度3三视图还原与几何体的体积、表面积高考真题体验·对方向1.(2019浙江·4)祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V 柱体=Sh ,其中S 是柱体的底面积,h 是柱体的高.若某柱体的三视图如图所示(单位:cm),则该柱体的体积(单位:cm 3)是( )A.158B.162C.182D.324解析由三视图得该棱柱的高为6,底面五边形可以看作是由两个直角梯形组合而成,其中一个上底为4,下底为6,高为3,另一个的上底为2,下底为6,高为3,则该棱柱的体积为2+62×3+4+62×3×6=162.2.(2017全国Ⅰ·7)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )A .10B .12C .14D .16.该五面体中有两个侧面是全等的直角梯形,且该直角梯形的上底长为2,下底长为4,高为2,则S梯=(2+4)×2÷2=6,所以这些梯形的面积之和为12.3.(2017全国Ⅱ·4)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为()A.90πB.63πC.42πD.36π,可知该几何体由两部分组成,这两部分分别是高为6的圆柱截去一半后的图形和高为×π×32×6+π×32×4=63π,故选B.4的圆柱,且这两个圆柱的底面圆半径都为3,故其体积为V=124.(2016全国Ⅰ·6)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3,则它的表面积是( )A.17πB.18πC.20πD.28π由三视图可知该几何体是球截去18后所得几何体,则78×4π3×R 3=28π3,解得R=2,所以它的表面积为78×4πR 2+34×πR 2=14π+3π=17π.5.(2019北京·11)某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为 .,如图所示.该几何体的体积V=43-1×(2+4)×2×4=40.典题演练提能·刷高分1.(2019甘肃兰州一中高三冲刺模拟)榫卯是我国古代工匠极为精巧的发明,它是在两个构件上采用凹凸部位相结合的一种连接方式。

高考数学复习：空间几何体的三视图、表面积及体积

V＝13×3×6×3＝18.
返回导航
专题五立体几何
空间几何体的三视图与直观图的对应关系
典题例析例 1 (1)下列三视图所对应的直观图是
二轮复习
(C )
数学
[解析] 由题意可知，几何体的直观图下部是长方体，上部是圆柱，并且高相等，所以C选项符合题意．
返回导航
专题五立体几何
(2)如图是一个空间几何体的正视图和俯视图，则它的侧视图为
学
习
(r，r′为底面半径，h 为高)
球 V 球＝__43_π_R_3_____(R 为球的半径) S 球＝___4_π_R_2___(R 为球的半径)
返回导航
专题五立体几何
2．空间几何体的三视图和直观图
(1)空间几何体的三视图
三视图的正视图、侧视图、俯视图分别是从物体的正前方、正左方、正上
方看到的物体轮廓线的正投影围成的平面图形，三视图的画法规则为“长对
＝π4.
返回导航
专题五立体几何
7．(2019·北京卷，11)某几何体是由一个正方体去掉一个四棱柱所得，其三视图如图所示．如果网格纸上小正方形的边长为1，那么该几何体的体积为__4_0___.
数学
二轮复习
[解析 ] 由题意知去掉的四棱柱的底面为直角梯形，底面积S＝(2＋4) ×2÷2＝6，高为正方体的棱长4，所以去掉的四棱柱的体积为6×4＝24.又正方体的体积为43＝64，所以该几何体的体积为64－24＝40.
(1)加强对空间几何体结构特征的理解，掌握各种几何体的体积、表面积公式．
(2)掌握空间几何三视图的画法规则，掌握几何直观图中各个元素之间的关系以
及三视图中长宽之间的关系．
数

八立体几何第二十二讲空间几何体的三视图、表面积和体积答案【文.2010-2018.高考真题分类】

专题八立体几何第二十二讲空间几何体的三视图、表面积和体积答案部分1．B 【解析】∵过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形，所以圆柱的高为2212ππ⨯⨯+⨯=．故选B ．2．B 【解析】由三视图可知，该几何体为如图①所示的圆柱，该圆柱的高为2，底面周长16．画出该圆柱的侧面展开图，如图②所示，连接MN ，则2=MS ，4=SN ，则从M 到N==B ．图① 图②3．C 【解析】连接1BC ，因为AB ⊥平面11BB C C ，所以130AC B ∠=o，1AB BC ⊥，所以1ABC ∆为直角三角形．又2AB =，所以1BC =，又112B C =，所以1BB ==22V =⨯⨯=4．A 【解析】由题意知，在咬合时带卯眼的木构件中，从俯视方向看，榫头看不见，所以是虚线，结合榫头的位置知选A ．5．B 【解析】设等边三角形ABC 的边长为x，则21sin 602x =o 6x =．设ABC ∆的外接圆半径为r ，则62sin 60r =o，解得r =，所以球心到ABC ∆所在平面的距离2d ==，则点D 到平面ABC 的最大距离146d d =+=，所以三棱锥D ABC -体积的最大值max 116633ABC V S ∆=⨯=⨯=故选B ． 6．C 【解析】由三视图可知，该几何体是一个底面为直角梯形的直四棱柱，所以该几何体的体积1(12)2262V =⨯+⨯⨯=．故选C ． SNM7．C 【解析】解法一将三视图还原为直观图，几何体是底面为直角梯形，且一条侧棱和底面垂直的四棱锥，如图所示，易知，BC AD ∥，1BC =，2AD AB PA ===，AB AD ⊥，PA ⊥平面ABCD ，故PAD ∆，PAB ∆为直角三角形，∵PA ⊥平面ABCD ，BC ⊂平面ABCD ，PA BC ⊥，又BC AB ⊥，且PA AB A =I ，∴BC ⊥平面PAB ，又PB ⊂平面PAB ．BC PB ⊥，∴PBC ∆为直角三角形，容易求得3PC =，CD =，PD =，故PCD ∆不是直角三角形，故选C ．解法二在正方体中作出该几何体的直观图，记为四棱锥P ABCD -，如图，由图可知在此四棱锥的侧面中，直角三角形的个数为3，故选C ．8．B 【解析】圆柱的轴截面如图，1AC =，12AB =，所以圆柱底面半径r BC ==，那么圆柱的体积是22314V r h πππ==⨯⨯=，故选B ．DBA PPDCBACBA9．D 【解析】借助立方体可知所求三棱锥为下图粗线部分该几何体的体积为11(35)41032V =⨯⨯⨯=．选D ． 10．A 【解析】该几何体是由一个高为3的圆锥的一半，和高为3的三棱锥组成（如图），其体积为：21111(13)(213)132322ππ⨯⨯⨯+⨯⨯⨯=+．选A ．11．B 【解析】由题意，该几何体是由高为6的圆柱截取一半后的图形加上高为4的圆柱，故其体积为221π36π3463π2V =⋅⋅⋅+⋅⋅=，故选B ． 12．C 【解析】由三视图可知，四棱锥的底面是边长为1的正方形，高为1，其体积21111133V =⨯⨯=．设半球的半径为R，则2R =2R =，所以半球的体积32142326V π=⨯⨯=．故该几何体的体积12136V V V =+=+．故选C ． 13．A 【解析】由三视图可得此几何体为一个球切割掉18后剩下的几何体，设球的半径为r ，故37428833r ππ⨯=，所以2r =，表面积227341784S r r πππ=⨯+=，选A ．14．C 【解析】该几何体是圆锥与圆柱的组合体，设圆柱底面圆半径为r ，周长为c ，圆锥母线长为l ，圆柱高为h ．由图得2r =，2π4πc r ==，由勾股定理得：4l =，421π2S r ch cl =++表4π16π8π=++28π=，故选C ．15．B 【解析】由三视图可得该几何体是平行六面体，上下底面是边长为3的正方形，故面积都是9，前后两个侧面是平行四边形，一边长为3、该边上的高为6，故面积都为18，左右两个侧面是矩形，边长为3，故面积都为2(9+18+16．C 【解析】由题意得，该几何体为一立方体与四棱锥的组合，∴体积，故选C ． 17．D 【解析】由三视图知：该几何体是半个圆柱，其中底面圆的半径为，母线长为，所以该几何体的表面积是，故选D ． 18．A 【解析】这是一个三棱锥与半个圆柱的组合体，，选A ．19．D 【解析】如图，设正方形的棱长为1，则截取部分为三棱锥111A A B D -，其体积为16，又正方体的体积为1，则剩余部分的体积为56，故所求比值为15．20．B 【解析】在长、宽、高分别为2、1、1的长方体中，该四面体是如图所示的三棱锥P ABC -，表面积为21122222⨯⨯⨯+⨯=+．3322231223=⨯⨯+=V 12()1211222342ππ⨯⨯⨯++⨯=+2111112(12)12323V ππ=⨯⨯+⨯⨯⨯⨯⨯=+A 1AC21．A 【解析】由圆锥的对称性可知，要使其内接长方体最大，则底面为正方形，令此长方体底面对角线长为2x ，高为h ，则由三角形相似可得，212x h -=，所以22h x =-，(0,1)x ∈，长方体体积2232216)2(22)2()327x x x V h x x ++-==-=长方体≤，当且仅当22x x =-，即23x =时取等号，2121233V ππ=⨯⨯=圆锥，故材料利用率为16827293ππ=，选A ． 22．B 【解析】由三视图可知，此组合体是由半个圆柱与半个球体组合而成，其表面积为22222422016r r r r ππππ+++=+，所以2r =．23．B 【解析】如图，设辅助正方体的棱长为4，三视图对应的多面体为三棱锥A BCD -，最长的棱为6AD ==，选B ．24．C 【解析】原毛坯的体积2(3)654V ππ=⨯⨯=，由三视图可知该零件为两个圆柱的组合体，其体积2212(2)4(3)234V V V πππ'=+=⨯⨯+⨯⨯=，故所求比值为10127V V '-=． 25．A 【解析】如图，将边长为2的正方体截去两个角，∴21226112212S =⨯⨯-⨯⨯+=+表26．A 【解析】圆柱的正视图是矩形，∴选A ．27．D 【解析】由三视图画出几何体的直观图，如图所示，则此几何体的表面积1232S S S S S S =-+++正方形斜面，其中1S 是长方体的表面积，2S 是三棱柱的水平放置的一个侧面的面积，3S 是三棱柱的一个底面的面积，可求得2138()S cm =，选D ．28．C 【解析】由题意可知AD BC ⊥，由面面垂直的性质定理可得AD ⊥平面11DB C ，又2sin 60AD =⋅=o，所以111111121332A B DC B DC V AD S -∆=⋅=⨯=，故选C ．29．A 【解析】圆柱的底面半径为1，母线长为1，2112S ππ=⨯⨯=侧． 30．B 【解析】直观图为棱长为2的正方体割去两个底面半径为l 的14圆柱，所以该几何体的体积为321221284ππ-⨯⨯⨯⨯=-． 31．C 【解析】由几何体的形成过程知所得几何体为圆柱，底面半径为1，高为1，其侧面积22S rh ππ==．32．B 【解析】由直观图可知，该几何体由一个长方体和一个截角三棱柱组成．从上往下看，外层轮廓线是一个矩形，矩形内部有一条线段连接的两个三角形．33．A 【解析】由三视图知，该几何体为放到的半个圆柱底面半径为2高为4，上边放一个长为4宽为2高为2长方体，故其体积为=，故选A ． 34．A 【解析】还原后的直观图是一个长宽高依次为10，6 ，5的长方体上面是半径为3高为2的半个圆柱．35．C 【解析】几何体是圆柱与圆锥叠加而成它的体积为221353573V πππ=⨯⨯+⨯=36．B 【解析】由三视图可知该几何体的体积：221121232V πππ=⨯⨯+⨯⨯⨯=． 37．D 【解析】通过正视图及俯视图可看出该几何体为半个圆锥和一个三棱锥的组合体，故侧视图可以为D ．21244222π⨯⨯+⨯⨯168π+38．C 【解析】由三视图可知该几何体是底面为等腰梯形的放倒的一个直四棱柱，如图，所以该四棱柱的表面积12(24)444242S =⨯⨯+⨯+⨯+⨯24+48=+39．D 【解析】选项A 正确，∵SD ⊥平面ABCD ，而AC 在平面ABCD 内，所以AC SD ⊥．因为ABCD 为正方形，所以AC BD ⊥，而BD 与SD 相交，所以AC ⊥平面SBD ，所以AC SB ⊥；选项B 正确，因为AB CD P ，而CD 在平面SCD 内，AB 不在平面SCD 内，所以AB P 平面SCD ；选项C 正确，设AC 与BD 的交点为O ，连结SO ，则SA 与平面SBD 所成的角ASO ∠，SC 与平面SBD 所成的角CSO ∠，易知这两个角相等；选项D 错误，AB 与SC 所成的角等于SCD ∠，而DC 与SA 所成的角等于SAB ∠，易知这两个角不相等．40．C 【解析】该几何体由两个长方体组合而成，其表面积等于下面长方体的全面积加上面长方体的4个侧面积之和．2(10810282)2(6882)360S =⨯+⨯+⨯+⨯+⨯=． 41．B 【解析】该几何体上半部是底面边长为4cm ，高为2cm ，的正四棱柱，其体积为344232()cm ⨯⨯=；下半部分是上、下底面边长分别为4cm ，8cm ，高为2cm 的正四棱台，其体积为1224(164864)233⨯+⨯+⨯=，故其总体积为2243203233+=．42．13【解析】解法一连接11A C ，交11B D 于点E ，则111A E B D ⊥，11A E BB ⊥，则1A E ⊥ 平面11BB D D ，所以1A E 为四棱锥111A BB D D -的高，且12A E =11BB D D ，1，故111111323A BB D D V -=⨯=．解法二连接1BD ，则四棱锥111A BB D D -分成两个三棱锥111B A DD -和111B A B D -111111111111111111132323A BB D D B A DD B A B D V V V ---=+=⨯⨯⨯⨯+⨯⨯⨯⨯=．43．43【解析】正方体的棱长为2，以其所有面的中心为顶点的多面体是正八面体，其中正，则该正八面体的体积为214233⨯⨯=． 44．36π【解析】取SC 的中点O ，连接,OA OB ，因为,SA AC SB BC ==，所以,OA SC OB SC ⊥⊥．因为平面SAC ⊥平面SBC ，所以OA ⊥平面SBC ．设OA r =，3111123323A SBC SBC V S OA r r r r -∆=⨯⨯=⨯⨯⨯⨯=所以31933r r =⇒=，所以球的表面积为2436r ππ=．45．14π【解析】球的直径是长方体的体对角线，设球O 的半径为R ，所以224π14π.R S R ====46．9π2【解析】设正方体边长为a ，则226183a a =⇒= ，外接球直径为34427923,πππ3382R V R ====⨯=.47．22π+【解析】由三视图可知,长方体的长、宽、高分别为2,1,1,圆柱的高为1,底面圆半径为1,所以2π1π21121242V ⨯=⨯⨯+⨯⨯=+． 48．32【解析】设球的半径为r ，则213223423V r r V r ππ⨯==． 49．【解析】通过俯视图可知该四棱柱的底面为等腰梯形，则四棱柱的底面积(12)1322S +⨯==，通过侧视图可知四棱柱的高1h =，所以该四棱柱的体积32V Sh ==．50．80 ；40【解析】由三视图知该组合体是一个长方体上面放置了一个小正方体，，．3.222262244242280S =⨯+⨯+⨯⨯-⨯=表3244240V =+⨯⨯=51．83π【解析】由三视图可知，该几何体是中间为一个底面半径为1，高为2的圆柱，两端是底面半径为1，高为1的圆锥，所以该几何体的体积22181221133V πππ=⨯⨯+⨯⨯⨯⨯=．52．12【解析】由题意知，该六棱锥是正六棱锥，设该六棱锥的高为h ，则21623h ⨯⨯=，解得1h =，底面正六边形的中心到其边的距离为2=，该六棱锥的侧面积为1122122⨯⨯=． 53．结合三视图有PA ⊥平面ABC ，2PA =，AB BC ==2CA =，所以PB ==，PC ==∴三棱锥最长棱的棱长为54．32【解析】设甲、乙两个圆柱的底面半径分别是12,r r ，母线长分别是12,l l ．则由1294S S =，可得1232r r =．又两个圆柱的侧面积相等，即112222rl r l ππ=，则112223l r l r ==，所以111222923432V S l V S l ==⨯=． 55，即球半a 2r =径．若球的体积为，即，解得56．1：24【解析】三棱锥与三棱锥的相似比为1：2，故体积之比为1：8．又因三棱锥与三棱柱的体积之比为1：3．所以，三棱锥与三棱柱的体积之比为1：24．另：，所以．57．38【解析】由三视图知，此几何体为一个长为4，宽为3，高为1的长方体中心，去除一个半径为1的圆柱，所以表面积为． 58．92【解析】该几何体是底面是直角梯形，高为4的直四棱柱几何体的表面积是12(25)4(2544922S =⨯⨯+⨯+++⨯=．59． 60．13【解析】由圆锥底面面积是这个球面面积的316，得223416r R ππ=，所以2r R =，则小圆锥的高为2R，大圆锥的高为32R ，所以比值为13．61．【解析】(1)由已知可得，BAC ∠=90°，BA AC ⊥．又BA ⊥AD ，所以AB ⊥平面ACD ．又AB ⊂平面ABC ，所以平面ACD ⊥平面ABC ．(2)由已知可得，3===DC CM AB ，=DA ．r =92π349)32ππ=a =ADE F -ABC A -1ABC A -1ABC C B A -111ADE F -ABC C B A -111112211111334224ADE ABC V S h S h V ==⨯⨯=121:24V V =()243+41+31+2-2=38ππ⨯⨯⨯⨯111322sin 60332ABC V PA S ∆=⋅=⋅⋅⋅⋅⋅=o EMP Q DCBA又23BP DQ DA ==，所以BP = 作QE ⊥AC ，垂足为E ，则QE =P 13DC ．由已知及(1)可得DC ⊥平面ABC ，所以QE ⊥平面ABC ，1=QE ．因此，三棱锥Q ABP -的体积为11113451332-=⨯⨯=⨯⨯⨯⨯︒=△Q ABP ABP V QE S ． 62．【解析】（1）由已知90BAP CDP ==︒∠∠，得AB AP ⊥，CD PD ⊥．由于AB CD ∥，故AB PD ⊥，从而AB ⊥平面PAD ．又AB ⊂平面PAB ，所以平面PAB ⊥平面PAD ．（2）在平面PAD 内作PE AD ⊥，垂足为E ．由（1）知，AB ⊥平面PAD ，故AB PE ⊥，可得PE ⊥平面ABCD ．设AB x =，则由已知可得AD =，2PE x =．故四棱锥P ABCD -的体积 31133P ABCD V AB AD PE x -=⋅⋅=．由题设得31833x =，故2x =．从而2PA PD ==，AD BC ==PB PC ==．可得四棱锥P ABCD -的侧面积为21111sin 6062222PA PD PA AB PD DC BC ⋅+⋅+⋅+︒=+ 63．【解析】（Ⅰ）证明：PD ⊥平面,,ABCD PD PCD ⊂∴平面PCD ⊥平面ABCD ，平面PCD I 平面,ABCD CD MD =⊂平面ABCD ，MD CD ⊥，PAC DE∴MD ⊥平面PCD ，,,,,,CF PCD CF MD CF MF MD MF MDF ⊂∴⊥⊥⊂平面又平面MD MF M =I ，∴CF MDF ⊥平面．（Ⅱ）00,,60,30,CF MDF CF DF PCD CDF ⊥∴⊥∠=∴∠=Q 平面又易知11==,22CF CD 从而12,,,244DE CF EF DC DE PE DP CP ∴=∴=∴=Q ∥12CDE S CD DE ∆=⋅=，2MD ====11.338216M CDE CDE V S MD -∆∴=⋅=⋅⋅= 64．【解析】（Ⅰ）由已知得ABC DBC ∆≅∆，因此AC DC =，又G 为AD 的中点，CG AD ⊥；同理BG AD ⊥；因此AD ⊥平面BCG ,又EF AD ∥,∴EF ⊥平面BCG ．（Ⅱ）在平面ABC 内，做AO CB ⊥，交CB 的延长线于O ，由平面ABC ⊥平面BCD ，知AO ⊥平面BCD ，又G 为AD 的中点，因此G 到平面BCD 的距离h 是AO 的一半，在AOB ∆中，sin 60AO AB =⋅=o 1132D BCG G BCD DBG V V S h --∆==⨯⨯=． 65．【解析】（Ⅰ）连结，交于点O ，连结DO ，则O 为的中点，因为D 为AB的中点，所以OD ∥，又因为OD 平面，平面，CD 1AC 1A C 1AC 1BC ⊂1A CD 1BC ⊄1A CD所以 //平面；（Ⅱ）由题意知 CD ⊥平面11ABB A ．再由，90ACB∠=o ，CD =1A D ，DE =13A E =．故22211A D DE A E +=，即1DE A D ⊥所以111132C A DE V -=⨯=． 66．【解析】（Ⅰ）证明：连接AC ，交于BD 于O 点，连接PO ．因为底面ABCD 是菱形，所以，由知，．再由PO AC O ⋂=知， BD ⊥面APC ，因此BD PC ⊥．（Ⅱ）解：因为E 是P A 的中点，所以由知，因为,所以. 又.故. 由（1）知，． 67．【解析】（1）由已知可得AE =3，BF =4，则折叠完后EG =3，GF =4，又因为EF =5，所以可得，又因为,可得，即所以平面1BC 1A CD 12AA AC CB ===AB =,AC BD BO DO ⊥=PB PD =PO BD ⊥1122P BCE C PEB C PAB B APC V V V V ----===2PB PD AB AD ====ABD PBD ≅V V 60BAD ∠=o 1PO AO AC BO ====222,PA PO AO PA PO AC =+=⊥即132APC S PO AC =•=V 1111,2232P BCE B APC APC BO APC V V BO S --⊥==•••=V 面因此EG GF ⊥CF EGF ⊥底面CF EG ⊥EG CFG ⊥面DEG ⊥平面CFG .（2）过G 作GO 垂直于EF ，GO 即为四棱锥G -EFCD 的高，所以所求体积为11124516335CDEF S GO ⋅=⨯⨯⨯=． 68．【解析】（I ）由条件知PDAQ 为直角梯形因为QA ⊥平面ABCD ，所以平面PDAQ ⊥平面ABCD ，交线为AD ．又四边形ABCD 为正方形，DC ⅡAD ，所以DC ⊥平面PDAQ ，可得PQ ⊥DC ．在直角梯形PDAQ 中可得DQ =PQ =2PD ，则PQ ⊥QD所以PQ ⊥平面DCQ .（II ）设AB =a .由题设知AQ 为棱锥Q —ABCD 的高，所以棱锥Q —ABCD 的体积311.3V a =由（I ）知PQ 为棱锥P —DCQ 的高，而PQ ，ⅡDCQ 的面积为22a ，所以棱锥P —DCQ 的体积为321.3V a =故棱锥Q —ABCD 的体积与棱锥P —DCQ 的体积的比值为1．。

2018届高三理科数学答题模板根据三视图求几何体的表面积与体积

根据三视图求几何体的表面积与体积【空间几何体的三视图】光线从几何体的前面向后面正投影，得到投影图，叫做几何体的正视图；光线从几何体的左面向右面正投影，得到投影图，叫做几何体的侧视图；从几何体的上面向下面正投影，得到投影图，叫做几何体的俯视图。

几何体的正视图、侧视图、俯视图统称为几何体的三视图。

【柱、锥、台和球的侧面积和体积】【几何体的表面积】(1)棱柱、棱锥、棱台的表面积就是各面面积之和． (2)圆柱、圆锥、圆台的侧面展开图分别是矩形、扇形、扇环形；它们的表面积等于侧面积与底面面积之和【求组合体的两种方法】(1)解与球有关的组合体问题的方法，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径．球与旋转体的组合，通常作它们的轴截面进行解题，球与多面体的组合，通过多面体的一条侧棱和球心或“切点”、“接点”作出截面图． (2)等积法：等积法包括等面积法和等体积法．等积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到，利用等积法可以用来求解几何图形的高或几何体的高，特别是在求三角形的高和三棱锥的高．这一方法回避了具体通过作图得到三角形(或三棱锥)的高，而通过直接计算得到高的数值。

【多面体的面积和体积公式】【旋转体的面积和体积公式】【2017年高考全国II卷,理4】如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为A．B．C．D．【答案】B【考点】三视图、组合体的体积【点拨】求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,在由三视图还原为空间几何体的实际形状时,要从三个视图综合考虑,根据三视图的规则,空间几何体的可见轮廓线在三视图中为实线,不可见轮廓线在三视图中为虚线．在还原空间几何体实际形状时,一般是以正视图和俯视图为主,结合侧视图进行综合考虑．答题思路【命题意图】高考对本部分内容的考查以读图、识图能力以及空间想象能力为主,重点考查根据几何体的三视图确定其体积或表面积,在考查三视图的同时,又考查了学生的空间想象能力及运算与推理能力．【命题规律】从近几年的高考试题来看,三视图是高考的热点,题型多为选择题、填空题,难度中、低档．高考对三视图的考查主要考查由三视图得出几何体的直观图,求其表面积、体积或由几何体的表面积、体积得出某些量；试题难度逐年有所增加,近几年组合体、几何体的切割及非正常状态下放置的棱锥的三视图成为高考考查的热点.【答题模板】解答本类题目,以2017年试题为例,一般考虑如下三步：第一步：观察三视图,确定几何体形状观察三视图,确定该几何体是一个组合体,下半部分是一个圆柱,上半部分是圆柱的一半；第二步：由三视图确定相关数据根据三视图,可知圆柱的底面半径为3,下半高为4,上半部分高为6；第三步：利用公式求表面积体积借助圆柱的体积计算公式,分别求出两部分的体积,再相加.【方法总结】1.空间几何体的三视图三视图是观测者从不同位置观察同一个几何体,画出的空间几何体的图形.他具体包括：（1）正视图：物体前后方向投影所得到的投影图；它能反映物体的高度和长度；（2）侧视图：物体左右方向投影所得到的投影图；它能反映物体的高度和宽度；（3）俯视图：物体上下方向投影所得到的投影图；它能反映物体的长度和宽度.2.三视图画法规则高平齐：主视图与左视图的高要保持平齐长对正：主视图与俯视图的长应对正宽相等：俯视图与左视图的宽度应相等3．由三视图还原几何体时,要遵循以下三步：(1)看视图,明关系；(2)分部分,想整体；(3)综合起来,定整体．4.画三视图应注意的问题(1)若相邻两物体的表面相交,表面的交线是它们的分界线,在三视图中,要注意实、虚线的画法．(2)确定正视、侧视、俯视的方向,观察同一物体方向不同,所画的三视图也不同．5.解答三视图题目时：(1)可以从熟知的某一视图出发,想象出直观图,再验证其他视图是否正确；(2)视图中标注的长度在直观图中代表什么,要分辨清楚；(3)视图之间的数量关系：正俯长对正,正侧高平齐,侧俯宽相等．6.由三视图求几何体体积的步骤(1)应先根据三视图得到几何体的直观图；(2) 若所给定的几何体是可直接用公式求解的柱体、锥体或台体，则可直接利用公式进行求解．若所给定的几何体的体积不能直接利用公式得出，则常用转换法、分割法、补形法等方法进行求解．7.由三视图求几何体表面积应注意的问题以三视图为载体的几何体的表面积问题，关键是分析三视图确定几何体中各元素之间的位置关系及数量．注意多面体的表面积是各个面的面积之和；组合体的表面积注意衔接部分的处理．旋转体的表面积问题注意其侧面展开图的应用．8．从能力上来看,三视图着重考查空间想象能力,即空间形体的观察分析和抽象的能力,要求是“四会”：①会画图——根据题设条件画出适合题意的图形或画出自己想作的辅助线(面),作出的图形要直观、虚实分明；②会识图——根据题目给出的图形,想象出立体的形状和有关线面的位置关系；③会析图——对图形进行必要的分解、组合；④会用图——对图形或其某部分进行平移、翻折、旋转、展开或实行割补术；考查逻辑思维能力、运算能力和探索能力.9.易错警示(1)不能正确把握投影方向、角度致误；不能正确确定点、线的投影位置；不能正确应用实虚线区分可见线与非可见线．是解决三视图问题常出现的错误(2) 求组合体的表面积时,要忽视重叠部分不再是组合体表面积的一部分．(3)底面是梯形的四棱柱侧放时,容易和四棱台混淆．(4)当三视图都在全等的正方形内时,常通过构造正方体,把几何体放到正方体内求解.1.【2017年高考全国Ⅰ卷，理7】某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形、该多面体的各个面中有若干是梯形，这些梯形的面积之和为A．10B．12C．14D．16【答案】B【解析】由三视图可画出立体图该立体图平面内只有两个相同的梯形的面()S=+⨯÷=24226梯S=⨯=6212全梯故选B2.【2017年高考北京卷，理7】某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为（A）（B）C）（D）2【答案】B【解析】试题分析：几何体是四棱锥，如图l==，红色线为三视图还原后的几何体，最长的棱长为正方体的对角线，故选B.【考点】三视图【点拨】本题考查了空间想象能力，由三视图还原几何体的方法:或者也可根据三视图的形状，将几何体的顶点放在正方体或长方体里面，便于分析问题.3．【2017年高考浙江卷，理3】某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 3）是A ．12+πB ．32+πC ．123+πD ．323+π 【答案】A【解析】【考点】三视图【点拨】思考三视图中·华.资*源%库还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽．由三视图画出直观图的步骤和思考方法：1、首先看俯视图，根据俯视图画出几何体地面的直观图；2、观察正视图和侧视图找到几何体前、后、左、右的高度；3、画出整体，然后再根据三视图进行调整．4.【2017年高考山东卷，理13】由一个长方体和两个圆柱体构成的几何体的三视图如右图，则该几何体的体积为.【答案】【解析】试题分析：该几何体的体积为．【考点】1.三视图.2.几何体的体积.【点拨】1.解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图．2．三视图中“正侧一样高、正俯一样长、俯侧一样宽”，因此，可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据．3.利用面积或体积公式计算.5.【2017黑龙江大庆三模】已知某几何体的三视图如图所示,则该几何体的表面积为A. B. C. D.【答案】D【解析】由三视图可知,该几何体为三棱锥,如下图所示,根据上图计算可得三棱锥的表面积为.故选择D.6．【2017辽宁省实验中学考前模拟】某几何体的三视图如图所示,其体积为A. B. C. D.【答案】B7．【2017吉林吉大附中6月模考】圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16＋20π,则r＝A. B. C. D.【答案】B8．【2017黑龙江虎林最后冲刺】如图所示,这是一个几何体的三视图,则该几何体的体积为A. B. C. D.【答案】A【解析】由三视图可知：该几何体分为上下两部分,下半部分是长、宽、高分别为的长方体,上半部分为底面半径为1,高为2的两个半圆柱,故其体积为,故选A.9．【2017辽宁鞍山最后一次模】如图是某四棱锥的三试图,且该四棱锥的顶点都在同一球面上,则该四棱锥的外接球的表面积为A. B. C. D.【答案】C【解析】如图四棱锥就是题中的几何体,它是正方体中的一部分,正方体棱长为10.记正方体棱长为,四棱锥外接球半径为,则,解得,所以,故选C．11.【2017辽宁沈阳三模】已知一个三棱锥的三视图如右图所示,则该三棱锥的体积为A. 9B. 21C. 25D. 34【答案】B12．【2017内蒙古鄂尔多斯三拟】某三棱锥的三视图如图所示,则该三棱锥的体积为A. 1B.C.D.【答案】D8．【2017甘肃省肃南5月联考】若某几何体的三视图（单位：）如图所示,则此几何体的侧面积等于A. B. C. D.【答案】C【解析】由三视图知：几何体是圆锥,其中圆锥的母线长为5,底面直径为6,∴圆锥的侧面积（cm2）,故选C.9．【2017黑龙江哈尔滨三模】北宋数学家沈括的主要数学成就之一为隙积术,所谓隙积,即“积之有隙”者,如累棋、层坛之类,这种长方台形状的物体垛积．设隙积共n层,上底由个物体组成,以下各层的长、宽依次各增加一个物体,最下层（即下底）由个物体组成,沈括给出求隙积中物体总数的公式为．已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为A. B. C. D.【答案】A【解析】由题意知：,故选A.13．【2017青海西宁二模】某四棱锥的三视图如图所示,其中正(主)视图是等腰直角三角形,侧(左)视图是等腰三角形,俯视图是正方形,则该四棱锥的体积是A. 8B.C. 4D.【答案】D14.【2016年高考全国Ⅱ卷,理6】如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为A.20B.24C.28D.32【答案】C【考点】三视图,空间几何体的表面积【点拨】空间几何体表面积的求法(1)以三视图为载体的几何体的表面积问题,关键是分析三视图确定几何体中各元素之间的位置关系及数量．(2)多面体的表面积是各个面的面积之和；组合体的表面积要注意各几何体重叠部分的处理．(3)旋转体的表面积问题注意其侧面展开图的应用．【方法】三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图．注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示．(2)由几何体的部分视图画出剩余的部分视图．先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式．当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合．(3)由几何体的三视图还原几何体的形状．要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图．15.【2016年高考全国Ⅰ卷,理6】如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3，则它的表面积是（A ）17π （B ）18π （C ）20π （D ）28π【答案】A 【解析】由三视图知，该几何体的直观图如图所示：是一个球被切掉左上角的18,即该几何体是78个球，设球的半径为R ，则37428ππR 833V =⨯=，解得R 2=，所以它的表面积是78的球面面积和三个扇形面积之和,即22734π2π217π84⨯⨯+⨯⨯=，故选A ．【考点】三视图及球的表面积与体积【点拨】由于三视图能有效地考查学生的空间想象能力,所以以三视图为载体的立体几何题基本上是高考每年必考内容,高考试题中三视图一般与几何体的表面积与体积相结合.由三视图还原出原几何体是解决此类问题的关键.16.【2016年高考全国Ⅲ卷,理9】如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为(A)18+54+【答案】B【解析】试题分析：由三视图知该几何体是一个斜四棱柱，所以该几何体的表面积为2362332354S =⨯⨯+⨯⨯+⨯⨯=+，故选B ．【考点】空间几何体的三视图及表面积．17.【2016年高考四川卷,理13】已知三棱锥的四个面都是腰长为2的等腰三角形，该三棱锥的正视图如图所示，则该三棱锥的体积是.【解析】试题分析：由三棱锥的正视图知，三棱锥的高为1，底面边长为2,2，所以，该三棱锥的体积为1122132V =⨯⨯⨯=. 【考点】三视图，几何体的体积【点拨】本题考查三视图和几何体的体积，考查学生的识图能力．解题时要求我们根据三视图想象出几何体的形状，由三视图得出几何体的尺寸，为此我们必须掌握基本几何体（柱、锥、台、球）的三视图以及各种组合体的三视图．。

2015届高考数学二轮复习检测：专题6.28 空间几何体的三视图及表面积与体积

专题6.28 空间几何体的三视图及表面积与体积 1．(2013·四川)一个几何体的三视图如图所示，则该几何体的直观图可以是( ) 答案　D 解析　由三视图可知上部是一个圆台，下部是一个圆柱，选D. 2．如图，网格纸上正方形小格的边长为1(表示1 cm)，图中粗线画出的是某零件的三视图，该零件由一个底面半径为3 cm，高为6 cm的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为( ) A. B. C. D. 答案　C 解析　由三视图可知几何体是如图所示的两个圆柱的组合体．其中左面圆柱的高为4 cm，底面半径为2 cm，右面圆柱的高为2 cm，底面半径为3 cm，则组合体的体积V1＝π×22×4＋π×32×2＝16π＋18π＝34π(cm3)，原毛坯体积V2＝π×32×6＝54π(cm3)，则所求比值为＝. 3．(2014·浙江)某几何体的三视图(单位：cm)如图所示，则此几何体的表面积是( ) A．90 cm2 B．129 cm2 C．132 cm2 D．138 cm2 答案　D 解析　该几何体如图所示，长方体的长、宽、高分别为6 cm,4 cm，3 cm，直三棱柱的底面是直角三角形，边长分别为3 cm,4 cm,5 cm，所以表面积S＝[2×(4×6＋4×3)＋3×6＋3×3]＋＝99＋39＝138(cm2)． 4．(2014·重庆)某几何体的三视图如图所示，则该几何体的表面积为( ) A．54 B．60 C．66 D．72 答案　B 解析　由俯视图可以判断该几何体的底面为直角三角形，由正视图和侧视图可以判断该几何体是由直三棱柱(侧棱与底面垂直的棱柱)截取得到的．在长方体中分析还原，如图(1)所示，故该几何体的直观图如图(2)所示．在图(1)中，直角梯形ABPA1的面积为×(2＋5)×4＝14，计算可得A1P＝5.直角梯形BCC1P的面积为×(2＋5)×5＝.因为A1C1⊥平面A1ABP，A1P?平面A1ABP，所以A1C1⊥A1P，故Rt△A1PC1的面积为×5×3＝. 又Rt△ABC的面积为×4×3＝6，矩形ACC1A1的面积为5×3＝15，故几何体ABC－A1PC1的表面积为14＋＋＋6＋15＝60. 5．两球O1和O2在棱长为1的正方体ABCD－A1B1C1D1的内部，且互相外切，若球O1与过点A的正方体的三个面相切，球O2与过点C1的正方体的三个面相切，则球O1和球O2的表面积之和的最小值为( ) A．(6－3)πB．(8－4)π C．(6＋3)πD．(8＋4)π 答案　A 解析　设球O1，O2的半径分别为r1，r2，由题意知O1A＋O1O2＋O2C1＝，而O1A＝r1，O1O2＝r1＋r2，O2C1＝r2， ∵r1＋r1＋r2＋r2＝.∴r1＋r2＝，从而S1＋S2＝4πr＋4πr＝4π(r＋r) ≥4π·＝(6－3)π. 6．已知球的直径SC＝4，A，B是该球球面上的两点，AB＝，∠ASC＝∠BSC＝30°，则棱锥S—ABC的体积为( ) A．3 B．2 C. D．1 答案　C 解析　如图，过A作AD垂直SC于D，连接BD. 由于SC是球的直径，所以∠SAC＝∠SBC＝90°，又∠ASC＝∠BSC＝30°，又SC为公共边，所以△SAC≌△SBC. 由于AD⊥SC，所以BD⊥SC. 由此得SC⊥平面ABD. 所以VS—ABC＝VS—ABD＋VC—ABD＝S△ABD·SC. 由于在Rt△SAC中，∠ASC＝30°，SC＝4，所以AC＝2，SA＝2，由于AD＝＝. 同理在Rt△BSC中也有BD＝＝. 又AB＝，所以△ABD为正三角形，所以VS—ABC＝S△ABD·SC＝××()2·sin 60°×4＝，所以选C. 7．(2014·辽宁)某几何体三视图如图所示，则该几何体的体积为( ) A．8－2πB．8－π C．8－D．8－答案　B 解析　这是一个正方体切掉两个圆柱后得到的几何体，如图，几何体的高为2， V＝23－×π×12×2×2＝8－π. 8．已知某几何体的三视图如图所示，其中正视图、侧视图均由直角三角形与半圆构成，俯视图由圆与内接三角形构成，根据图中的数据可得几何体的体积为( )A.＋B.＋C.＋D.＋答案　C 解析　由三视图确定该几何体是一个半球体与三棱锥构成的组合体，如图，其中AP，AB，AC两两垂直，且AP＝AB＝AC＝1，故AP⊥平面ABC，S△ABC＝AB×AC＝，所以三棱锥P－ABC的体积V1＝×S△ABC×AP＝××1＝，又Rt△ABC是半球底面的内接三角形，所以球的直径2R＝BC ＝，解得R＝，所以半球的体积V2＝××()3＝，故所求几何体的体积V＝V1＋V2＝＋. 9．(2014·北京)某三棱锥的三视图如图所示，则该三棱锥最长棱的棱长为________．答案　2 解析　根据三视图还原几何体，得如图所示的三棱锥P－ABC. 由三视图的形状特征及数据，可推知PA⊥平面ABC，且PA＝2. 底面为等腰三角形，AB＝BC，设D为AC的中点，AC＝2，则AD＝DC＝1，且BD＝1，易得AB＝BC＝，所以最长的棱为PC， PC＝＝2. 10．已知正三棱锥P－ABC，点P，A，B，C都在半径为的球面上，若PA，PB，PC两两相互垂直，则球心到截面ABC的距离为________．答案解析　如图，作PM⊥平面ABC，设PA＝a，则AB＝a，CM＝a， PM＝a. 设球的半径为R，所以2＋2＝R2，将R＝代入上式，解得a＝2，所以d＝－＝. 11．已知一个圆锥的底面半径为R，高为H，在其内部有一个高为x的内接圆柱． (1)求圆柱的侧面积； (2)x为何值时，圆柱的侧面积最大？解　(1)作圆锥的轴截面，如图所示．因为＝，所以r＝R－x，所以S圆柱侧＝2πrx ＝2πRx－x2(0<x<H)． (2)因为－<0，所以当x＝＝时，S圆柱侧最大．故当x＝，即圆柱的高为圆锥高的一半时，圆柱的侧面积最大． 12．(2014·北京)如图，在三棱柱ABC－A1B1C1中，侧棱垂直于底面，AB⊥BC，AA1＝AC＝2，BC＝1，E，F分别是A1C1，BC的中点． (1)求证：平面ABE⊥平面B1BCC1； (2)求证：C1F∥平面ABE； (3)求三棱锥E－ABC的体积． (1)证明　在三棱柱ABC－A1B1C1中， BB1⊥底面ABC，所以BB1⊥AB. 又因为AB⊥BC，所以AB⊥平面B1BCC1，又因为AB?平面ABE，所以平面ABE⊥平面B1BCC1. (2)证明　取AB的中点G，连接EG，FG. 因为E，F分别是A1C1，BC的中点，所以FG∥AC，且FG＝AC. 因为AC∥A1C1，且AC＝A1C1，所以FG∥EC1，且FG＝EC1，所以四边形FGEC1为平行四边形．所以C1F∥EG. 又因为EG?平面ABE，C1F?平面ABE，所以C1F∥平面ABE. (3)解　因为AA1＝AC＝2，BC＝1，AB⊥BC，所以AB＝＝. 所以三棱锥E－ABC的体积V＝S△ABC·AA1 ＝×××1×2＝.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第28练空间几何体的三视图及表面积与体积 [内容精要] 三视图作为新课标新增加的内容、是多个省市高考的热点和重点：其考查形式多种多样、选择题、填空题和综合解答题都有出现、而这些题目以选择题居多；立体几何中的计算问题考查的知识、涉及到三视图、空间几何体的表面积和体积以及综合解答和证明、

题型一三视图识图例1 将正方体(如图(1)所示)截去两个三棱锥、得到如图(2)所示的几何体、则该几何体的侧(左)视图为( )

破题切入点根据三视图先确定原几何体的直观图和形状、然后再解题、答案 B 解析还原正方体后、将D1、D、A三点分别向正方体右侧面作垂线、D1A的射影为C1B、且为实线、B1C被遮挡应为虚线、题型二空间几何体的表面积和体积例2 如图是某简单组合体的三视图、则该组合体的体积为( ) A、363(π＋2) B、363(π＋2) C、1083π D、108(3π＋2) 破题切入点先根据三视图的结构特征确定几何体的构成——半圆锥与棱锥的组合体、然后把三视图中的数据转化为该组合体的数字特征、分别求出对应几何体的体积、则两者体积之和即该组合体的体积、答案 B 解析由俯视图、可知该几何体的底面由三角形和半圆两部分构成、结合正视图和侧视图可知该几何体是由半个圆锥与一个三棱锥组合而成的、并且圆锥的轴截面与三棱锥的一个侧面重合、两个锥体的高相等、由三视图中的数据、可得该圆锥的底面半径r＝6、三棱锥的底面是一个底边长为12、高为6的等腰三角形、两个锥体的高h＝122－62＝63、故半圆锥的体积V1＝12×13π×62×63＝363π.

三棱锥的底面积S＝12×12×6＝36、三棱锥的体积V2＝13Sh＝13×36×63＝723. 故该几何体的体积V＝V1＋V2＝363π＋723 ＝363(π＋2)、故选B. 题型三立体几何中的综合问题例3 (2014·陕西)四面体ABCD及其三视图如图所示、平行于棱AD、BC的平面分别交四面体的棱AB、BD、DC、CA于点E、F、G、H.

(1)求四面体ABCD的体积； (2)证明：四面体EFGH是矩形、破题切入点由三视图和几何体得知原几何体中各元素的量和性质来求解、 (1)解由该四面体的三视图可知、BD⊥DC、BD⊥AD、AD⊥DC、BD＝DC＝2、AD＝1、 ∴AD⊥平面BDC、

∴四面体ABCD体积V＝13×12×2×2×1＝23. (2)证明 ∵BC∥平面EFGH、平面EFGH∩平面BDC＝FG、平面EFGH∩平面ABC＝EH、 ∴BC∥FG、BC∥EH、∴FG∥EH. 同理EF∥AD、HG∥AD、∴EF∥HG、 ∴四边形EFGH是平行四边形、又∵AD⊥平面BDC、∴AD⊥BC、∴EF⊥FG. ∴四边形EFGH是矩形、总结提高 (1)三视图的正视图、侧视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线、画三视图的基本要求：正俯一样长、俯侧一样宽、正侧一样高、 (2)三视图排列规则：俯视图放在正视图的下面、长度与正视图一样；侧视图放在正视图的右面、高度和正视图一样、宽度与俯视图一样、 (3)立体几何中有关表面积、体积的计算首先要熟悉几何体的特征、其次运用好公式、作好辅助线等、

1、(2013·四川)一个几何体的三视图如图所示、则该几何体的直观图可以是( )

答案 D 解析由三视图可知上部是一个圆台、下部是一个圆柱、选D. 2、如图、网格纸上正方形小格的边长为1(表示1 cm)、图中粗线画出的是某零件的三视图、该零件由一个底面半径为3 cm、高为6 cm的圆柱体毛坯切削得到、则切削掉部分的体积与原来毛坯体积的比值为( ) A.1727 B.59 C.1027 D.13 答案 C 解析由三视图可知几何体是如图所示的两个圆柱的组合体、其中左面圆柱的高为4 cm、底面半径为2 cm、右面圆柱的高为2 cm、底面半径为3 cm、则组合体的体积V1＝π×22×4＋π×32×2＝16π＋18π＝34π(cm3)、原毛坯体积V2＝π×32×6＝54π(cm3)、

则所求比值为54π－34π54π＝1027. 3、(2014·浙江)某几何体的三视图(单位：cm)如图所示、则此几何体的表面积是( )

A、90 cm2 B、129 cm2 C、132 cm2 D、138 cm2 答案 D 解析该几何体如图所示、长方体的长、宽、高分别为6 cm,4 cm、3 cm、直三棱柱的底面是直角三角形、边长分别为3 cm,4 cm,5 cm、所以表面积

S＝[2×(4×6＋4×3)＋3×6＋3×3]＋5×3＋4×3＋2×12×4×3＝99＋39＝138(cm2)、 4、(2014·重庆)某几何体的三视图如图所示、则该几何体的表面积为( ) A、54 B、60 C、66 D、72 答案 B 解析由俯视图可以判断该几何体的底面为直角三角形、由正视图和侧视图可以判断该几何体是由直三棱柱(侧棱与底面垂直的棱柱)截取得到的、在长方体中分析还原、如图(1)所示、故

该几何体的直观图如图(2)所示、在图(1)中、直角梯形ABPA1的面积为12×(2＋5)×4＝14、计

算可得A1P＝5.直角梯形BCC1P的面积为12×(2＋5)×5＝352.因为A1C1⊥平面A1ABP、A1P⊂平面A1ABP、所以A1C1⊥A1P、故Rt△A1PC1的面积为12×5×3＝152.

又Rt△ABC的面积为12×4×3＝6、矩形ACC1A1的面积为5×3＝15、故几何体ABC－A1PC1

的表面积为14＋352＋152＋6＋15＝60. 5、两球O1和O2在棱长为1的正方体ABCD－A1B1C1D1的内部、且互相外切、若球O1与过点A的正方体的三个面相切、球O2与过点C1的正方体的三个面相切、则球O1和球O2的表面积之和的最小值为( ) A、(6－33)π B、(8－43)π C、(6＋33)π D、(8＋43)π 答案 A 解析设球O1、O2的半径分别为r1、r2、由题意知O1A＋O1O2＋O2C1＝3、而O1A＝3r1、O1O2＝r1＋r2、O2C1＝3r2、

∵3r1＋r1＋r2＋3r2＝3.∴r1＋r2＝3－32、从而S1＋S2＝4πr21＋4πr22＝4π(r21＋r22) ≥4π·r1＋r222＝(6－33)π. 6、已知球的直径SC＝4、A、B是该球球面上的两点、AB＝3、∠ASC＝∠BSC＝30°、则棱锥S—ABC的体积为( ) A、33 B、23 C.3 D、1 答案 C 解析如图、过A作AD垂直SC于D、连接BD. 由于SC是球的直径、所以∠SAC＝∠SBC＝90°、又∠ASC＝∠BSC＝30°、又SC为公共边、所以△SAC≌△SBC. 由于AD⊥SC、所以BD⊥SC. 由此得SC⊥平面ABD.

所以VS—ABC＝VS—ABD＋VC—ABD＝13S△ABD·SC. 由于在Rt△SAC中、∠ASC＝30°、SC＝4、所以AC＝2、SA＝23、由于AD＝SA·CASC＝3.

同理在Rt△BSC中也有BD＝SB·CBSC＝3. 又AB＝3、所以△ABD为正三角形、所以VS—ABC＝13S△ABD·SC＝13×12×(3)2·sin 60°×4＝3、所以选C. 7、(2014·辽宁)某几何体三视图如图所示、则该几何体的体积为( )

A、8－2π B、8－π C、8－π2 D、8－π4 答案 B 解析这是一个正方体切掉两个14圆柱后得到的几何体、如图、几何体的高为2、 V＝23－14×π×12×2×2＝8－π. 8、已知某几何体的三视图如图所示、其中正视图、侧视图均由直角三角形与半圆构成、俯视图由圆与内接三角形构成、根据图中的数据可得几何体的体积为( ) A.2π3＋12 B.4π3＋16 C.2π6＋16 D.2π3＋12 答案 C 解析由三视图确定该几何体是一个半球体与三棱锥构成的组合体、如图、其中AP、AB、AC两两垂直、且AP＝AB＝AC＝1、故AP⊥平面ABC、S

△ABC＝12AB×AC＝12、所以三棱锥P－ABC的体积V1＝13×S△ABC×AP＝13×12

×1＝16、又Rt△ABC是半球底面的内接三角形、所以球的直径2R＝BC＝

2、解得R＝22、所以半球的体积V2＝12×4π3×(22)3＝2π6、故所求几何体的体积V＝V1＋V2

＝16＋2π6. 9、(2014·北京)某三棱锥的三视图如图所示、则该三棱锥最长棱的棱长为________、

答案 22 解析根据三视图还原几何体、得如图所示的三棱锥P－ABC. 由三视图的形状特征及数据、可推知PA⊥平面ABC、且PA＝2. 底面为等腰三角形、AB＝BC、设D为AC的中点、AC＝2、则AD＝DC＝1、且BD＝1、易得AB＝BC＝2、所以最长的棱为PC、 PC＝PA2＋AC2＝22. 10、已知正三棱锥P－ABC、点P、A、B、C都在半径为3的球面上、若PA、PB、PC两两相互垂直、则球心到截面ABC的距离为________、答案 33

解析如图、作PM⊥平面ABC、设PA＝a、则AB＝2a、CM＝63a、 PM＝33a. 设球的半径为R、所以33a－R2＋63a2＝R2、将R＝3代入上式、解得a＝2、所以d＝3－233＝33. 11、已知一个圆锥的底面半径为R、高为H、在其内部有一个高为x的内接圆柱、 (1)求圆柱的侧面积； (2)x为何值时、圆柱的侧面积最大？解 (1)作圆锥的轴截面、如图所示、

因为rR＝H－xH、所以r＝R－RHx、所以S圆柱侧＝2πrx ＝2πRx－2πRHx2(0

(2)因为－2πRH<0、所以当x＝2πR4πRH＝H2时、S圆柱侧最大、

故当x＝H2、即圆柱的高为圆锥高的一半时、圆柱的侧面积最大、 12、(2014·北京)如图、在三棱柱ABC－A1B1C1中、侧棱垂直于底面、AB⊥BC、AA1＝AC＝2、BC＝1、E、F分别是A1C1、BC的中点、 (1)求证：平面ABE⊥平面B1BCC1； (2)求证：C1F∥平面ABE； (3)求三棱锥E－ABC的体积、 (1)证明在三棱柱ABC－A1B1C1中、 BB1⊥底面ABC、所以BB1⊥AB. 又因为AB⊥BC、