北师大版七年级数学上第一章复习试题

合集下载

第一章丰富的图形世界同步测试2021-2022学年北师大版七年级数学上册

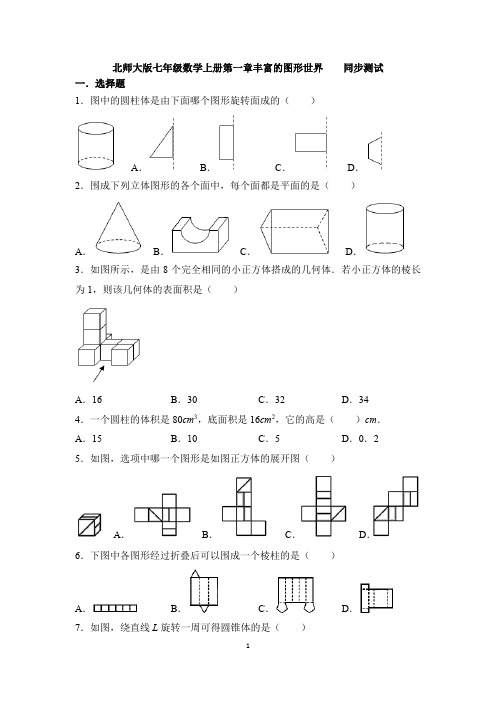
北师大版七年级数学上册第一章丰富的图形世界同步测试一．选择题1．图中的圆柱体是由下面哪个图形旋转面成的（）A．B．C．D．2．围成下列立体图形的各个面中，每个面都是平面的是（）A．B．C．D．3．如图所示，是由8个完全相同的小正方体搭成的几何体．若小正方体的棱长为1，则该几何体的表面积是（）A．16B．30C．32D．344．一个圆柱的体积是80cm3，底面积是16cm2，它的高是（）cm．A．15B．10C．5D．0．25．如图，选项中哪一个图形是如图正方体的展开图（）A．B．C．D．6．下图中各图形经过折叠后可以围成一个棱柱的是（）A．B．C．D．7．如图，绕直线L旋转一周可得圆锥体的是（）A．B．C．D．8．用一个平面去截正方体，截面图形不可能是（）A．B．C．D．9．用一个平面去截一个几何体，如果截面的形状是长方形，那么这个几何体不可能是（）A．圆柱B．圆锥C．五棱柱D．正方体10．如图，是一个底面为等边三角形的正三棱柱，它从正面看是（）A．B．C．D．11．如右图所示的是将正方体切去一个角后形成的几何体，则该几何体的从左面看为（）A．B．C．D．12．有一实物如图，那么它从正面看是（）A．B．C．D．二．填空题13．夜晚的流星划过天空时留下一道明亮的光线，由此说明了的数学事实．14．如图，长方形的长为3cm，宽为2cm，以该长方形的一边所在直线为轴，将其旋转一周，形成圆柱，其体积为cm3．（结果保留π）15．一个无盖的长方形包装盒展开后如图所示（单位：cm），则其容积为cm3．16．用一个平面去截一个正方体，如果截去的几何体是一个三棱柱，那么截面的形状一定是．17．如图，网格图中五个相连的阴影正方形可以折叠成一个无盖的正方体盒子．小荣同学想从网格中余下的正方形中增选一个，折叠为有盖的正方体纸盒，可增选的正方形有（填写序号）．18．如图四个几何体分别是三棱柱，四棱柱，五棱柱和六棱柱，三棱柱有5个面，9条棱，6个顶点，观察图形，填写下面的空．（1）四棱柱有个面，条棱，个顶点；（2）六棱柱有个面，条棱，个顶点；（3）由此猜想n棱柱有个面，条棱，个顶点．三．解答题19．如图是一个长为4cm，宽为3cm的长方形纸片（1）若将此长方形纸片绕长边或短边所在直线旋转一周，能形成的几何体是，这能说明的事实是．（2）求：当此长方形纸片绕长边所在直线旋转一周时（如图1），所形成的几何体的体积．（3）求：当此长方形纸片绕短边所在直线旋转一周时（如图2），所形成的几何体的体积．20．小明学习了“面动成体”之后，他用一个边长为3cm、4cm和5cm的直角三角形，其中一条直角边旋转一周，得到了一个几何体，请计算出几何体的体积．（锥体体积＝底面积×高）21．如图是一个正方体的平面展开图，标注了字母M的是正方体的正面，如果正方体的左面与右面标注的式子相等．（1）求x的值；（2）求正方体的上面和底面的数字和．22．计算如图圆柱的表面积和体积．（单位：厘米）23．如图所示，圆柱的底面半径为3cm，高为4cm．若沿图中的线AB把圆柱的侧面展开，你认为会得到什么图形？请你求出这个侧面展开图的面积．24．如图所示，木工师傅把一个长为1．6米的长方体木料锯成3段后，表面积比原来增加了80cm2，那么这根木料本来的体积是多少？25．如图是一个大正方体切去一个小正方体组成的几何体．（1）下列三个图形中，从上面、左面、正面看到的平面图形分别是、、；（2）若大正方体的边长为20cm，小正方体的边长为10cm，求这个几何体的表面积．北师大版七年级数学上册第一章丰富的图形世界答案提示一．选择题1．图中的圆柱体是由下面哪个图形旋转面成的（）选：B．A．B．C．D．2．围成下列立体图形的各个面中，每个面都是平面的是（）选：C．A．B．C．D．3．如图所示，是由8个完全相同的小正方体搭成的几何体．若小正方体的棱长为1，则该几何体的表面积是（）选：D．A．16B．30C．32D．344．一个圆柱的体积是80cm3，底面积是16cm2，它的高是（）cm．选：C．A．15B．10C．5D．0．25．如图，选项中哪一个图形是如图正方体的展开图（）选：A．A．B．C．D．6．下图中各图形经过折叠后可以围成一个棱柱的是（）选：B．A．B．C．D．7．如图，绕直线L旋转一周可得圆锥体的是（）选：B．A．B．C．D．8．用一个平面去截正方体，截面图形不可能是（）选：D．A．B．C．D．9．用一个平面去截一个几何体，如果截面的形状是长方形，那么这个几何体不可能是（）选：B．A．圆柱B．圆锥C．五棱柱D．正方体10．如图，是一个底面为等边三角形的正三棱柱，它从正面看是（）选：A．A．B．C．D．11．如右图所示的是将正方体切去一个角后形成的几何体，则该几何体的从左面看为（）选：C．A．B．C．D．12．有一实物如图，那么它从正面看是（）选：A．A．B．C．D．二．填空题13．夜晚的流星划过天空时留下一道明亮的光线，由此说明了点动成线的数学事实．14．如图，长方形的长为3cm，宽为2cm，以该长方形的一边所在直线为轴，将其旋转一周，形成圆柱，其体积为12π或18πcm3．（结果保留π）解：由题可得，当以该长方形的长所在直线为轴时V＝π•22×3＝12π，当以该长方形的宽所在直线为轴，V＝π•32×2＝18π，故答案为：12π或18π．15．一个无盖的长方形包装盒展开后如图所示（单位：cm），则其容积为800cm3．16．用一个平面去截一个正方体，如果截去的几何体是一个三棱柱，那么截面的形状一定是长方形．17．如图，网格图中五个相连的阴影正方形可以折叠成一个无盖的正方体盒子．小荣同学想从网格中余下的正方形中增选一个，折叠为有盖的正方体纸盒，可增选的正方形有（1）（10）（11）（12）（填写序号）．18．如图四个几何体分别是三棱柱，四棱柱，五棱柱和六棱柱，三棱柱有5个面，9条棱，6个顶点，观察图形，填写下面的空．（1）四棱柱有6个面，12条棱，8个顶点；（2）六棱柱有8个面，18条棱，12个顶点；（3）由此猜想n棱柱有（n+2）个面，3n条棱，2n个顶点．三．解答题19．如图是一个长为4cm，宽为3cm的长方形纸片（1）若将此长方形纸片绕长边或短边所在直线旋转一周，能形成的几何体是圆柱，这能说明的事实是面动成体．（2）求：当此长方形纸片绕长边所在直线旋转一周时（如图1），所形成的几何体的体积．（3）求：当此长方形纸片绕短边所在直线旋转一周时（如图2），所形成的几何体的体积．解：（1）若将此长方形纸片绕长边或短边所在直线旋转一周，能形成的几何体是圆柱，这能说明的事实是面动成体；（2）绕长边旋转得到的圆柱的底面半径为3cm，高为4cm，体积＝π×32×4＝36πcm3；（3）绕短边旋转得到的圆柱底面半径为4cm，高为3cm，体积＝π×42×3＝48πcm3．故答案为：圆柱；面动成体．36πcm3；48πcm3．20．小明学习了“面动成体”之后，他用一个边长为3cm、4cm和5cm的直角三角形，其中一条直角边旋转一周，得到了一个几何体，请计算出几何体的体积．（锥体体积＝底面积×高）解：以4cm为轴体积为×π×32×4＝12π，以3cm为轴的体积为×π×42×3＝16π．21．如图是一个正方体的平面展开图，标注了字母M的是正方体的正面，如果正方体的左面与右面标注的式子相等．（1）求x的值；（2）求正方体的上面和底面的数字和．解：正方体的表面展开图，相对的面之间一定相隔一个正方形，“M”与“x”是相对面，“﹣2”与“﹣3”是相对面，“4x”与“2x+3”是相对面，（1）∵正方体的左面与右面标注的式子相等，∵4x＝2x+3，解得x＝1．5；（2）∵标注了A字母的是正方体的正面，左面与右面标注的式子相等，∵上面和底面上的两个数字﹣2和﹣3，∵﹣2﹣3＝﹣5．22．计算如图圆柱的表面积和体积．（单位：厘米）解：S表＝2S底+S侧＝2×3．14×（6÷2）2+3．14×6×6＝169．56（平方厘米）；V＝S底h＝3．14×（6÷2）2×6＝169．56（立方厘米）；答：圆柱体的表面积是169．56平方厘米，体积是169．56立方厘米．23．如图所示，圆柱的底面半径为3cm，高为4cm．若沿图中的线AB把圆柱的侧面展开，你认为会得到什么图形？请你求出这个侧面展开图的面积．解：沿图中的线AB把圆柱的侧面展开，得到的是长方形，圆柱的侧面展开图的面积是π×2×3×4＝24π（cm2）．24．如图所示，木工师傅把一个长为1．6米的长方体木料锯成3段后，表面积比原来增加了80cm2，那么这根木料本来的体积是多少？解：∵把长方体木料锯成3段后，其表面积增加了四个截面，因此每个截面的面积为80÷4＝20cm2，∵这根木料本来的体积是：1．6×100×20＝3200（cm3）．25．如图是一个大正方体切去一个小正方体组成的几何体．（1）下列三个图形中，从上面、左面、正面看到的平面图形分别是③、②、①；（2）若大正方体的边长为20cm，小正方体的边长为10cm，求这个几何体的表面积．解：（1）由题可得，从上面、左面、正面看到的平面图形分别是③，②，①；故答案为：③，②，①；（2）∵大正方体的边长为20cm，小正方体的边长为10cm，∴这个几何体的表面积为：2（400+400+400）=2×1200=2400（cm2）．。

北师大版七年级数学上册丰富的图形世界单元测试题及答案

七年级数学第一章《丰富的图形世界》单元测试题时间90分，满分100分一、选择题（每小题4分，共40分，请将答案填写在下面的表格中）题号 1 2 3 4 5 6 7 8 9 10 答案1.下列说法中，正确的个数是（）.①柱体的两个底面一样大；②圆柱、圆锥的底面都是圆；③棱柱的底面是四边形；④长方体一定是柱体；⑤棱柱的侧面一定是长方形.（A）2个（B）3个（C）4个（D）5个2.下面几何体截面一定是圆的是（）(A)圆柱(B)圆锥（C）球(D)圆台3.如图绕虚线旋转得到的几何体是（）.4.某物体的三视图是如图所示的三个图形，那么该物体的形状是（）（A）长方体（B）圆锥体（C）立方体（D）圆柱体5．如图，其主视图是（??）6．如图，是一个几何体的主视图、左视图和俯视图，则这个几何体是（）7.下列各个平面图形中，属于圆锥的表面展开图的是()第10题图（A ）（B ）（C ）（D ）8．如图是由一些相同的小正方体构成的立体图形的三种视图：构成这个立体图形的小正方体的个数是（??）．A ．5?B ．6?C ．7?D ．89．下面每个图形都是由6个全等的正方形组成的，其中是正方体的展开图的是（）A B C D10．如图，是一个正方体纸盒展开图，按虚线折成正方体后，若使相对面上的两数互为相反数，则A 、B 、C 表示的数依次是（）（A ）235、、π--(B)235、、π- （C ）π、、235-(D)235-、、π 二、填空题（每小题3分，共18分）11．正方体与长方体的相同点是_________________，不同点是_______________。

12．点动成_____，线动成_____，_____动成体。

比如：（1）圆规在纸上划过会留下一个封闭的痕迹，这种现象说明_________。

（2）冬天环卫工人使用下部是长方形的木锨推雪时，木锨过处，雪就没了，这种现象说明________。

（3）一个人手里拿着一个绑在一根棍上的半圆面，当这个人把这个半圆面绕着这根棍飞快地旋转起来时就会看到一个球，这种现象说明______________。

北师大版七年级上册数学第一章丰富的图形世界含答案

北师大版七年级上册数学第一章丰富的图形世界含答案一、单选题(共15题，共计45分)1、如图，矩形ABCD，AB=a，BC=b，a＞b；以AB边为轴将矩形绕其旋转一周形成圆柱体甲，再以BC边为轴将矩形绕其旋转一周形成圆柱体乙；记两个圆柱体的体积分别为V甲、V乙，侧面积分别为S甲、S乙，则下列式子正确的是（）A.V甲＞V乙S甲=S乙B.V甲＜V乙S甲=S乙C.V甲=V乙S甲=S乙D.V甲＞V乙S甲＜S乙2、如图，由几个相同的小正方体搭成的一个几何体，它的左视图为（）A. B. C. D.3、下面几何体从正面看得到的平面图形，哪一个和其他有明显的不同( )A. B. C. D.4、用一个平面去截正方体（如图），下列关于截面（截出的面）的形状的结论：①可能是锐角三角形；②可能是直角三角形；③可能是钝角三角形；④可能是平行四边形.其中所有正确结论的序号是（）A.①②B.①④C.①②④D.①②③④5、如图所示的几何体是由5个大小相同的小立方块搭成，它的俯视图是（）A. B. C. D.6、某几何体的示意图如图所示，该几何体的主视图应为（）A. B. C. D.7、下面四个立体图形中，三视图完全相同的是（）A. B. C. D.8、如图是一个几何体的三视图，根据图中所示数据计算这个几何体的侧面积为（）A.10πB.14πC.18πD.20π9、由几个相同的小正方体搭成的一个几何体如图所示，这个几何体的三视图中，是轴对称图形的是（）A.主视图和左视图B.主视图和俯视图C.俯视图和左视图D.三者均是10、一个立体图形由4个相同的正方体组成，如果从左面看到的图形如图所示，那么这个立体图形不可能是（）A. B. C. D.11、如图是某个几何体的展开图，该几何体是（）A.三棱柱B.圆锥C.四棱柱D.圆柱12、如图是正方体的一个表面展开图，则原正方体表面上与“周”相对的面上的字是（）A.七B.十C.华D.诞13、由大小相同的正方体木块堆成的几何体的三视图，如图所示，则该几何体中正方体木块的个数是（）A.8B.7C.6D.514、超市货架上摆放着一些桶装红烧牛肉方便面，它们的三视图如图所示，则货架上的红烧牛肉方便面至多有（）桶．A.8B.9C.10D.1115、下面四个几何体中，主视图与其它几何体的主视图不同的是（）A. B. C. D.二、填空题(共10题，共计30分)16、如图是棱长为2cm的正方体，过相邻三条棱的中点截取一个小正方体，则剩下部分的表面积为________cm2．17、如图是由若干个棱长为1的小正方体组合而成的一个几何体的三视图，则这个几何体的表面积是________．18、如图是一个圆柱体的三视图，由图中数据计算此圆柱体的侧面积为________．（结果保留π）19、一个正方体的棱长2×102毫米，则它的表面积是________.体积是________.20、如图是一个正方体纸盒的展开图，正方体的各面标有数字1，2，3，﹣3，A，B，相对面上是两个数互为相反数，则A=________．21、长方体有________ 个顶点，有________ 个面，有________ 条棱．22、一个圆柱的三视图如图所示，若其俯视图为圆，则这个圆柱的体积为________．23、如图所示的积木是由16块棱长为acm的正方体堆积而成的，则这个几何体的表面积是________ cm2．24、由一些大小相同的小正方体搭成的几何体的主视图和俯视图，如图所示，则搭成该几何体的小正方体最多是________个．25、由5个棱长为1的小正方形组成的几何体如图放置，一面着地，两面靠墙，如果要将露出来的部分涂色，则涂色部分的面积为________.三、解答题(共5题，共计25分)26、我们知道，将一个长方形绕它的一边旋转一周得到的几何体是圆柱，现有一个长是5cm，宽是3cm的长方形，分别绕它的长和宽所在的直线旋转一周，得到不同的圆柱几何体，分别求出它们的体积．27、已知如图是三个方向看到的一个几何体的形状．（1）写出这个几何体的名称；（2）写出它的侧面展开的形状；（3）若从正面看到的高为10cm，从上面看到的三角形的三边长都为4cm，求这个几何体的侧面积．28、把正方体的六个面分别涂上六种不同的颜色，并画上朵数不等的花，各面上的颜色与花的朵数情况见下表：颜色红黄蓝白紫绿花的朵数 1 2 3 4 5 6现将上述大小相同，颜色.花朵分布也完全相同的四个正方体拼成一个水平放置的长方体，如图所示．问：长方体的下底面共有多少朵花?29、如图，是一个由长方体和圆柱组合而成的几何体．已知长方体的底面是正方形，其边长与圆柱底面圆的直径相等，圆柱的高与长方体的高也相等．（1）画出这个几何体的主视图、左视图、俯视图；（2）若圆柱底面圆的直径记为a，高记为b．现将该几何体露在外面的部分喷上油漆，求需要喷漆部分的面积．30、如图是一个正方体的展开图，标注了字母A的面是正方体的正面，如果正方体的左面与右面所标注代数式的值相等，求x的值.参考答案一、单选题(共15题，共计45分)1、A2、A3、B4、B5、C6、A7、B8、A9、C10、B11、A12、C13、A14、C15、C二、填空题(共10题，共计30分)16、17、18、19、20、22、23、24、25、三、解答题(共5题，共计25分)26、28、30、。

北师大版初一(七年级)上册第一章丰富的图形测试试卷汇集版

北师大初一数学上册第一单元测试题（一）班级：姓名：成绩：一、填空题（每空1分，共24分）1．长方体有________个顶点，有_______条棱，______个面，这些面的形状都是_______. 2．圆柱的侧面展开图是__________，圆锥的侧面展开图__________.3．如果一个几何体的视图之一是三角形，这个几何体可能是___________（写出两个即可）. 4．用平行于圆锥的底面的平面去截圆锥，则得到的截面是________形. 5．薄薄的硬币在桌面上转动时，看上去象球，这说明了____ _____________.6．如图所示，将图沿虚线折起来，得到一个正方体，那么“3”的对面是_______（填编号）.7．能展开成如图所示的几何体可能是____________.8．如图中，共有____个三角形的个数，_____个平行四边形，_____个梯形. 9．一个正多面体的面数为12，棱数是30，则其顶点数为_________.10．在乒乓球、橄榄球、足球、羽毛球、冰球中，是球体的有； 11．将下列几何体分类，柱体有：，锥体有（填序号）；12．棱柱的侧面是，分为棱柱和棱柱； 13．如图1-1中的几何体有个面，面面相交成线； 14．把一块学生使用的三角板以一条直角边为轴旋转成的形状是体形状；二、选择题（每小题3分，共36分）第6题第9题第7题1-11．如图，四个三角形均为等边三角形，将图形折叠，得到的立体图形是（） A. 三棱锥 B. 圆锥体 C. 棱锥体 D. 六面体 2. 用一个平面去截一个正方体，截面不可能是 A ．梯形 B.五边形 C.六边形 D ．圆 3.下面的图形中，是三棱柱的侧面展开图的为 ( )A ．B ．C ．D ．4.用一个平面去截①圆锥；②圆柱；③球；④五棱柱，能得到截面是圆的图形是……( ) A ．①②④ B ．①②③ C ．②③④ D ．①③④5.从多边形一条边上的一点（不是顶点）发出发，连接各个顶点得到2003个三角形，则这个多边形的边数为……………………………（） A 、2001 B 、2005 C 、2004 D 、20066.观察下图，请把左边的图形绕着给定的直线旋转一周后可能形成的几何体选出来( )7．下列说法中，正确的是（）A 、棱柱的侧面可以是三角形B 、由六个大小一样的正方形所组成的图形是正方体的展开图C 、正方体的各条棱都相等D 、棱柱的各条棱都相等 8．下列立体图形中，有五个面的是（）A 、四棱锥B 、五棱锥C 、四棱柱D 、五棱柱 9．将一个正方体截去一个角，则其面数（）A 、增加B 、不变C 、减少D 、上述三种情况均有可能 10．直棱柱的侧面都是（）(A)正方形 (B)长方形 (C)菱形 (D)五边形11．如图所示，是一个由小立方体搭成的几何体的俯视图，小正方形中数字表示该位置的小ABCD立方块的个数，则它的主视图为（）12．如图中是正方体的展开图的有（）个 A 、2个 B 、3个 C 、4个 D 、5个三、解答题（每小题5分，共40分）1．下图是由五块积木搭成，这几块积木都是相同的正方体，请画出这个图形的主视图、左视图和俯视图。

北师大版数学七年级上册第一章丰富的图形世界填空题训练很实用

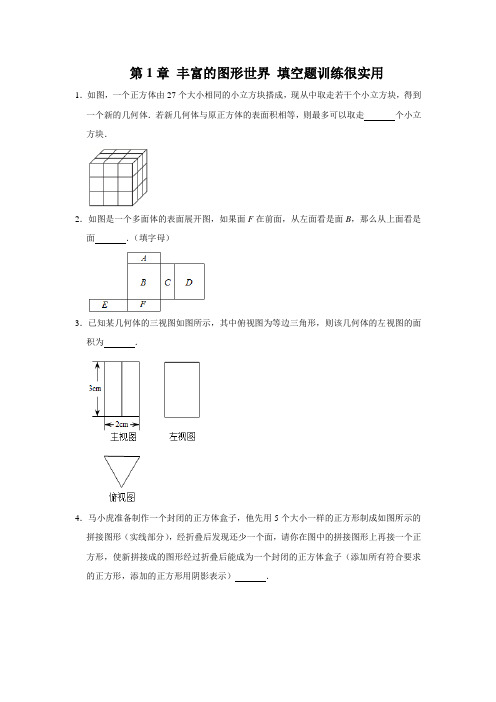
第1章丰富的图形世界填空题训练很实用1．如图，一个正方体由27个大小相同的小立方块搭成，现从中取走若干个小立方块，得到一个新的几何体．若新几何体与原正方体的表面积相等，则最多可以取走个小立方块．2．如图是一个多面体的表面展开图，如果面F在前面，从左面看是面B，那么从上面看是面．（填字母）3．已知某几何体的三视图如图所示，其中俯视图为等边三角形，则该几何体的左视图的面积为．4．马小虎准备制作一个封闭的正方体盒子，他先用5个大小一样的正方形制成如图所示的拼接图形（实线部分），经折叠后发现还少一个面，请你在图中的拼接图形上再接一个正方形，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子（添加所有符合要求的正方形，添加的正方形用阴影表示）．5．在如图所示的几何体中，其三视图中有矩形的是．（写出所有正确答案的序号）6．一个由16个完全相同的小立方块搭成的几何体，其最下面一层摆放了9个小立方块，它的主视图和左视图如图所示，那么这个几何体的搭法共有种．7．三棱柱的三视图如图所示，已知△EFG中，EF＝8cm，EG＝12cm，∠EFG＝45°．则AB的长为cm．8．一个立方体的表面展开图如图所示，将其折叠成立方体后，“你”对面的字是．9．如图是按1：10的比例画出的一个几何体的三视图，则该几何体的侧面积是．10．在一个高与底面直径相等的圆柱内放置一个体积最大的球．已知球的表面积公式为S n ＝4πr2，其中r为球的半径．那么该球与它的外切圆柱的表面积的比为．11．如图，圆柱的侧面是由一张长16πcm、宽3cm的长方形纸条围成（接缝处重叠部分忽略不计），那么该圆柱的体积是cm3．12．一个几何体的三视图如图，根据图示的数据计算该几何体的体积为．（结果保留π）13．用一张边长是10cm的正方形铁皮围成一个圆柱体，这个圆柱的侧面积是cm2．14．如图，一个5×5×5的正方体，先在它的前后方向正中央开凿一个“十字形”的孔（打通），再在它的上下方向正中央也开凿一个“十字形”的孔（打通），最后在它的左右方向正中央开凿一个“十字形”的孔（打通），这样得到一个被凿空了的几何体，则所得几何体的体积为．15．若某几何体从某个方向观察得到的视图是正方形，则这个几何体可以是．16．如图是一个几何体的三视图（图中尺寸单位：cm），根据图中所示数据求得这个几何体的侧面积是cm2．17．如图是某几何体的三视图及相关数据（单位：cm），则该几何体的侧面积为cm2．18．如图为某几何体的展开图，该几何体的名称是．19．如图是由几个相同的小正方体搭建而成的几何体的主视图和俯视图，则搭建这个几何体所需要的小正方体至少为个．20．如图是一个立体图形的三种视图，则这个立体图形的体积（结果保留π）为．21．如图，该正方体的主视图是形．22．已知一个几何体的三视图如图所示，这个几何体是．23．如图是由一些大小相同的小正方体组成的简单几何体的左视图和俯视图，符合条件的几何体有种．24．如图，在边长为12cm的正方形纸片ABCD中，EF∥AD，M、N是线段EF的六等分点，若把该正方形纸片折成一个正六棱柱，使AB与点DC重合，则M、N两点间的距离是cm．25．如图，是用8个大小相同的小正方体搭成的几何体，仅在该几何体中取走一块小正方体，使得到的新几何体同时满足两个要求：（1）从正面看到的形状和原几何体从正面看到的形状相同；（2）从左面看到的形状和原几何体从左面看到的形状也相同．在不改变其它小正方体位置的前提下，可取走的小正方体的标号是．26．一个几何体的三视图如图所示，这个几何体的侧面积为．27．如图是一个包装盒的三视图，则这个包装盒的体积是．28．用硬纸壳做一个如图所示的几何体，其底面是圆心角为300°的扇形，则该几何体的表面积为cm2．29．如图所示是一种棱长分别为3cm，4cm，5cm的长方体积木，现要用若干块这样的积木来搭建大长方体，如果用3块来搭，那么搭成的大长方体表面积最小是cm，如果用4块来搭，那么搭成的大长方体表面积最小是cm，如果用12块来搭，那么搭成的大长方体表面积最小是cm．30．如图，是一个长方体的主视图，左视图与俯视图，根据图中数据计算这个长方体的表面积是．31．如图是一个几何体的三视图，根据图中标注的数据可求得该几何体的侧面积为．32．如图是正方体的一个表面展开图，在这个正方体中，与“晋”字所在面相对的面上的汉字是．33．如图是由一些完全相同的小正方体搭成的几何体的俯视图和左视图，组成这个几何体的小正方体的个数最少是．34．如图，在四个小正方体搭成的几何体中，每个小正方体的棱长都是1，则该几何体的三视图的面积之和是．35．如图所示，是一个简单几何体的三视图，则这个几何体的侧面积等于．36．一个长方体的三视图如图所示，若其俯视图为正方形，则这个长方体的体积为．37．一个油桶靠在墙边（其俯视图如图所示），量得AC＝0.65米，并且AC⊥BC，这个油桶的底面半径是米．38．一个长方体的主视图和左视图如图所示，则这个长方体的俯视图的面积是．第1章丰富的图形世界填空题训练参考答案与试题解析1．【分析】根据表面积不变，只需留11个，分别是正中心的3个和四角上各2个．【解答】解：若新几何体与原正方体的表面积相等，最多可以取走16个小正方体，只需留11个，分别是正中心的3个和四角上各2个，如图所示：故答案为：16【点评】本题主要考查了几何体的表面积．2．【分析】由面F在前面，从左面看是面B知上面是E，左侧面是B，前面是F，后面是A，右侧面是D，下面是C．【解答】解：由题意知，上面是E，左侧面是B，前面是F，后面是A，右侧面是D，下面是C，故答案为：E．【点评】考查了几何体的展开图，注意正方体的空间图形，从相对面入手，分析及解答问题．3．【分析】由三视图想象几何体的形状，首先，应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，然后综合起来考虑整体形状．【解答】解：该几何体是一个三棱柱，底面等边三角形边长为2cm，高为cm，三棱柱的高为3，所以，其左视图的面积为3×＝3（cm2），故答案为3cm2．【点评】本题考查了三视图，三视图是中考经常考查的知识内容，难度不大，但要求对三视图画法规则要熟练掌握，对常见几何体的三视图要熟悉．4．【分析】由平面图形的折叠及正方体的展开图解题．【解答】解：，故答案为：．【点评】本题通过考查正方体的侧面展开图，展示了这样一个教学导向，教学中要让学生确实经历活动过程，而不要将活动层次停留于记忆水平．我们有些老师在教学“展开与折叠”时，不是去引导学生动手操作，而是给出几种结论，这样教出的学生肯定遇到动手操作题型时就束手无策了．5．【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形，据此作答．【解答】解：长方体主视图，左视图，俯视图都是矩形，圆柱体的主视图是矩形，左视图是矩形，俯视图是圆，圆锥的主视图、左视图是等腰三角形，俯视图是带有圆心的圆，故答案为：①②．【点评】本题主要考查三视图的知识，熟练掌握常见几何体的三视图是解题的关键．6．【分析】先根据主视图确定每一列最大分别为4，2，3，再根据左视确定每一行最大分别为4，3，2，总和要保证为16，还要保证俯视图有9个位置．【解答】解：由题意和主视图、左视图可知俯视图必定由9个正方形组成，并设这9个位置分别如图所示：由主视图和左视图知：①第1个位置一定是4，第6个位置一定是3；②一定有2个2，其余有5个1；③最后一行至少有一个2，当中一列至少有一个2；根据2的排列不同，这个几何体的搭法共有10种：如下图所示：故答案为：10．【点评】本题考查几何体的三视图．由几何体的主视图、左视图及小立方块的个数，可知俯视图的列数和行数中的最大数字．7．【分析】根据三视图的对应情况可得出，△EFG中FG上的高即为AB的长，进而求出即可．【解答】解：过点E作EQ⊥FG于点Q，由题意可得出：EQ＝AB，∵EF＝8cm，∠EFG＝45°，∴EQ＝AB＝×8＝4（cm）．故答案为：4．【点评】此题主要考查了由三视图解决实际问题，根据已知得出EQ＝AB是解题关键．8．【分析】正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．【解答】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，“你”对面的字是顺．故答案为：顺．【点评】本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．9．【分析】首先判断出该几何体，然后计算其面积即可．【解答】解：观察三视图知：该几何体为圆柱，高为2，底面直径为1，侧面积为：πdh＝2×π＝2π，∵是按1：10的比例画出的一个几何体的三视图，∴原几何体的侧面积＝100×2π＝200π，故答案为：200πcm2【点评】本题考查了由三视图判断几何体及圆柱的计算，解题的关键是首先判断出该几何体．10．【分析】设球的半径为r，根据球的表面积＝4πr2，圆柱的表面积＝2×πr2+2πr×2r＝6πr2，即可得到该球与它的外切圆柱的表面积的比．【解答】解：设球的半径为r，依题意得球的表面积＝4πr2，圆柱的表面积＝2×πr2+2πr×2r＝6πr2，∴该球与它的外切圆柱的表面积的比为2：3，故答案为：2：3．【点评】本题主要考查了几何体的表面积，几何体的表面积＝侧面积+底面积（上、下底的面积和）．11．【分析】由圆柱的侧面展开图的特点可知：圆柱的侧面展开后，是一个长方形，长方形的长等于底面周长，宽等于圆柱的高，长方形的长已知，从而可以求出底面积半径，进一步求得该圆柱的体积．【解答】解：16π÷（2×π）＝8（cm）π×82×3＝192π（cm3）故该圆柱的体积是192πcm3．故答案为：192π．【点评】本题主要考查了立体图形，解答此题的关键是明白：圆柱的侧面展开后，是一个长方形，长方形的长等于底面周长，宽等于圆柱的高．12．【分析】根据圆锥侧面积公式首先求出圆锥的侧面积，再求出底面圆的面积，即可得出表面积．【解答】解：∵如图所示可知，圆锥的高为4，底面圆的直径为6，∴圆锥的体积为π×32×4＝12π，故答案为：12π．【点评】此题主要考查了圆锥侧面积公式，根据已知得母线长，再利用圆锥侧面积公式求出是解决问题的关键．13．【分析】易得此几何体为圆柱，那么侧面积＝底面周长×高，依此即可求解．【解答】解：10×10＝100（cm2）．答：这个圆柱的侧面积是100cm2．故答案：100．【点评】考查了展开图折叠成几何体，本题难点是确定几何体的形状，关键是找到等量关系里相应的量．14．【分析】从5×5×5的正方体的8个顶点进行分割，可得8个2×2×2的正方体，再加上12条棱中间的12个小正方体，依此求得小正方体的个数，再乘以1个小正方体的体积即可求解．【解答】解：如图所示：该正方体可按如图方式分割，则体积为（1×1×1）×（8×8+12）＝1×76＝76故所得几何体的体积为76．故答案为：76．【点评】考查了截一个几何体，正方体的体积，关键是得到小正方体的个数．15．【分析】根据主视图是从正面看到的图形直接回答即可．【解答】解：主视图是正方形的几何体可以是正方体，故答案为：正方体（答案不唯一）．【点评】本题考查由三视图确定几何体的形状，主要考查学生空间想象能力及对立体图形的认识．16．【分析】根据三视图确定该几何体是圆柱体，再计算圆柱体的侧面积．【解答】解：先由三视图确定该几何体是圆柱体，底面半径是2÷2＝1cm，高是3cm．所以该几何体的侧面积为2π×1×3＝6π（cm2）．故答案为：6π．【点评】此题主要考查了由三视图确定几何体和求圆柱体的侧面积，关键是根据三视图确定该几何体是圆柱体．17．【分析】根据三视图易得此几何体为圆锥，再根据圆锥侧面积公式＝（底面周长×母线长）÷2 可计算出结果．【解答】解：由题意得底面直径为10cm，母线长为＝13cm，∴几何体的侧面积为×10π×13＝65πcm2．故答案为65π．【点评】此题主要考查了由三视图判断几何体，以及圆锥的侧面积公式的应用，关键是找到等量关系里相应的量．18．【分析】展开图为两个圆，一个长方形，易得是圆柱的展开图．【解答】解：∵圆柱的展开图为两个圆和一个长方形，∴展开图可得此几何体为圆柱．故答案为：圆柱．【点评】此题主要考查了由展开图得几何体，关键是考查同学们的空间想象能力．19．【分析】主视图、俯视图是分别从物体正面、上面看，所得到的图形．【解答】解：综合主视图和俯视图，底层最少有5个小立方体，第二层最少有2个小立方体，第三层至少有1个，因此搭成这个几何体的小正方体的个数最少是8个．故答案为：8．【点评】考查了由三视图判断几何体的知识，根据题目中要求的以最少的小正方体搭建这个几何体，可以想象出左视图的样子，然后根据“俯视图打地基，正视图疯狂盖，左视图拆违章”很容易就知道小正方体的个数．20．【分析】从三视图可以看正视图以及左视图为矩形，而俯视图为圆形，故可以得出该立体图形为圆柱．由三视图可以圆柱的半径，长和高，易求体积．【解答】解：该立体图形为圆柱，∵圆柱的底面半径r＝5，高h＝10，∴圆柱的体积V＝πr2h＝π×52×10＝250π（立方单位）．答：所以立体图形的体积为250π立方单位，故答案为：250π．【点评】考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查；圆柱体积公式＝底面积×高．21．【分析】根据主视图为正面所看到的图形进而得出答案．【解答】解：正方形的主视图为正方形，故答案为：正方．【点评】本题考查了三视图的知识，主视图即为从正面所看到的图形．22．【分析】由主视图和左视图确定是柱体，锥体还是球体，再由俯视图确定具体形状．【解答】解：由该几何体的三视图知，这个几何体是正三棱柱，故答案为：正三棱柱．【点评】考查了由三视图判断几何体．主视图和左视图的大致轮廓为长方形的几何体为柱体，俯视图为几边形就是几棱柱．23．【分析】从俯视图中可以看出最底层小正方体的个数及形状，从左视图可以看出每一层小正方体的层数和个数，从而得出答案．【解答】解：该几何体中小正方体的分布情况有如下7种可能结果，故答案为：7．【点评】本题主要考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就更容易得到答案．24．【分析】根据正六边形的性质解答即可．【解答】解：如图所示：∵正六边形的周长为12cm，∴MQ＝QN＝2cm，∠MQN＝120°，连接MN，过Q作QP⊥MN，在Rt△MQP中，MP＝，同理可得PN＝，∴MN＝2，故答案为：2【点评】此题考查几何体的展开图，关键是根据正六边形的性质解答．25．【分析】若要使从正面看到的形状和原几何体从正面看到的形状相同，则可取走的小正方体是3号或5号或7号；若要使从左面看到的形状和原几何体从左面看到的形状也相同，则可取走的小正方体是1号或3号或5号；据此可得．【解答】解：若要使从正面看到的形状和原几何体从正面看到的形状相同，则可取走的小正方体是3号或5号或7号，若要使从左面看到的形状和原几何体从左面看到的形状也相同，则可取走的小正方体是1号或3号或5号，故答案为：3号或5号．【点评】本题主要考查由三视图判断几何体，根据题意正确掌握三视图的观察角度是解题关键．26．【分析】俯视图为圆的只有圆锥，圆柱，球，根据主视图和左视图都是三角形可得到此几何体为圆锥，那么侧面积＝底面周长×母线长÷2．【解答】解：此几何体为圆锥；∵直径为2cm，母线长为4cm，∴侧面积＝2π×4÷2＝4π（cm2）．故答案为4πcm2．【点评】本题考查了由三视图判断几何体，圆锥的有关计算，由该三视图中的数据确定圆锥的底面直径和母线长是解本题的关键；本题体现了数形结合的数学思想，熟记圆锥的侧面积公式是解题的关键．27．【分析】根据三视图，易判断出该几何体是圆柱．已知底面半径和高，根据圆柱的体积公式可求．【解答】解：综合三视图，可以得出这个几何体应该是个圆柱体，且底面半径为10，高为20．因此它的体积应该是：π×10×10×20＝2000π．故答案为2000π．【点评】本题主要考查了由三视图确定几何体的形状以及圆柱的体积的求法．28．【分析】求得该几何体的侧面积以及底面积，相加即可得到表面积．【解答】解：侧面积为10×（6+）＝60+50π，底面积之和为：2×＝15π，∴该几何体的表面积为60+50π+15π＝60+65π，故答案为：60+65π．【点评】本题主要考查了几何体的表面积，由三视图想象几何体的形状，首先，应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，然后综合起来考虑整体形状．29．【分析】如果用3块来搭，那么搭成的大长方体表面积最小是长3×3＝9cm，宽4cm，高5cm的长方体的表面积，根据长方体的表面积公式即可求解；如果用4块来搭，那么搭成的大长方体表面积最小是长4×2＝8cm，宽3×2＝6cm，高5cm的长方体的表面积，根据长方体的表面积公式即可求解；如果用12块来搭，那么搭成的大长方体表面积最小是长3×3＝9cm，宽4×2＝8cm，高5×2＝10cm的长方体的表面积，根据长方体的表面积公式即可求解．【解答】解：长3×3＝9cm，宽4cm，高5cm，（9×4+9×5+4×5）×2＝（36+45+20）×2＝101×2＝202（cm2）．答：如果用3块来搭，那么搭成的大长方体表面积最小是202cm2．长4×2＝8cm，宽3×2＝6cm，高5cm，（8×6+8×5+6×5）×2＝（48+40+30）×2＝118×2＝236（cm2）．答：如果用4块来搭，那么搭成的大长方体表面积最小是236cm2．长3×3＝9cm，宽4×2＝8cm，高5×2＝10cm，（9×8+9×10+8×10）×2＝（72+90+80）×2＝242×2＝484（cm2）．答：如果用12块来搭，那么搭成的大长方体表面积最小是484cm2．故答案为：202；258；484．【点评】考查了几何体的表面积，关键是熟练掌握长方体的表面积公式，难点是得到搭成的大长方体的长宽高．30．【分析】根据三视图我们可以得出这个几何体应该是个长方体，进而得出其表面积．【解答】解：该几何体的主视图以及左视图都是相同的矩形，俯视图也为一个矩形，可确定这个几何体是一个长方体，依题意可求出该几何体的表面积为：2×（2×3+3×4+2×4）＝52．故答案为：52．【点评】此题考查了由三视图判断几何体，本题要先判断出几何体的形状，然后根据其表面积公式进行计算即可．31．【分析】易得此几何体为圆柱，圆柱的侧面积＝底面周长×高．【解答】解：由主视图和左视图为长方形可得此几何体为柱体，由俯视图为圆形可得此几何体为圆柱；易得圆柱的底面直径为2，高为1，∴侧面积＝2π×1＝2π，故答案为：2π．【点评】本题考查圆柱的侧面积计算公式，关键是得到该几何体的形状．32．【分析】正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．【解答】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，“晋”与“祠”是相对面，“汾”与“酒”是相对面，“恒”与“山”是相对面．故答案为：祠．【点评】本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．33．【分析】首先根据几何体的左视图，可得这个几何体共有3层；然后从俯视图中可以看出最底层小正方体的个数及形状；最后从左视图判断出第二层、第三层的个数，进而求出组成这个几何体的小正方体的个数是多少即可．【解答】解：根据几何体的左视图，可得这个几何体共有3层，从俯视图可以可以看出最底层的个数是4个，（1）当第一层有1个小正方体，第二层有1个小正方体时，组成这个几何体的小正方体的个数是：1+1+4＝6（个）；（2）当第一层有1个小正方体，第二层有2个小正方体时，或当第一层有2个小正方体，第二层有1个小正方体时，组成这个几何体的小正方体的个数是：1+2+4＝7（个）；（3）当第一层有2个小正方体，第二层有2个小正方体时，组成这个几何体的小正方体的个数是：2+2+4＝8（个）．综上，可得组成这个几何体的小正方体的个数是6或7或8．所以组成这个几何体的小正方体的个数最少是6故答案为：6【点评】此题主要考查了由三视图判断几何体，考查了空间想象能力，解答此题的关键是要明确：由三视图想象几何体的形状，应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状．34．【分析】根据三视图的定义求解即可．【解答】解：主视图是第一层是三个小正方形，第二层右边一个小正方形，主视图的面积是4，俯视图是三个小正方形，俯视图的面积是3，左视图是下边一个小正方形，第二层一个小正方形，左视图的面积是2，几何体的三视图的面积之和是4+3+2＝9，故答案为：9．【点评】本题考查了简单组合体的三视图，利用三视图的定义是解题关键．35．【分析】由几何体的三视图可知，该几何体是底面边长为2的等边三角形、高为3的三棱柱，再根据侧面积公式可得．【解答】解：由几何体的三视图可知，该几何体是底面边长为2的等边三角形、高为3的三棱柱，∴这个几何体的侧面积等于3×2×3＝18，故答案为：18．【点评】本题考查了由三视图求几何体的侧面积，根据三视图判断几何体的形状是关键．36．【分析】由主视图所给的图形可得到俯视图的对角线长为2，利用勾股定理可得俯视图的面积，乘以高即为这个长方体的体积．【解答】解：设俯视图的正方形的边长为a．∵其俯视图为正方形，正方形的对角线长为2，∴a2+a2＝（2）2，解得a2＝4，∴这个长方体的体积为4×3＝12．【点评】解决本题的关键是理解长方体的体积公式为底面积乘高，难点是利用勾股定理得到长方体的底面积．37．【分析】圆的圆心为O，连接OA、OB，可得四边形OBCA为正方形，从而求得这个油桶的底面半径．【解答】解：连接OA、OB，如图，∵BC⊥AC，OA⊥AC，OB⊥BC，OB＝OA，∴四边形OBCA为正方形，∴OB＝AC，∵AC＝0.65m，∴这个油桶的底面半径是0.65m．故答案为：0.65【点评】本题考查了切线的性质，是基础知识比较简单．38．【分析】通过观察长方体的主视图和左视图可以得到，这个长方体的高4厘米，长3厘米，宽2厘米，因此俯视图是长3厘米，宽2厘米的长方形，因此得解．【解答】解：3×2＝6（平方厘米）；答：则其俯视图的面积是6平方厘米．故答案为：6．【点评】此题考查了从不同方向观察问题和几何体，锻炼了学生的空间想象力和抽象思维能力．北师版七年级上册第一章丰富的图形世界1.2.2棱柱、圆柱、圆锥的展开与折叠同步测试一．选择题（共10小题，3*10=30）1．如图由7个小正方体组合而成的几何体，从物体正面看所得到的是( )2．将五个相同的小正方体堆成如图所示的物体，从上面看到的是( )3．如图所示的几何体是由五个小正方体组成的，从左面看到的是( )4．如图，几何体上半部分为正三棱柱，下半部为圆柱，其从上面看的形状图是( )5．下列四个几何体从上面看到的图形中与众不同的是( )6．下列四个几何体：其中从左面看与从上面看得到的形状图相同的几何体共有( )A．1个B．2个C．3个D．4个7．图中的两个圆柱体底面半径相同而高度不同，关于这两个圆柱体的从三个方向看的形状图说法正确的是( )A．从正面看的形状图相同。

2014----2015学年度上学期北师大版七年级第一章测试题

北师大版2014----2015学年度上学期七年级数学第一章测试题一、单选题1、能把表面依次展开成如图所示的图形的是（）A ．球体、圆柱、棱柱B ．球体、圆锥、棱柱C ．圆柱、圆锥、棱锥 D ．圆柱、球体、棱锥2、水平放置的正方体的六面分别用“前面、后面、上面、下面、左面、右面”表示，如图是一个正方体的表面展开图，若图中“2”在正方体的前面，则这个正方体的后面是 ( ) A ．O B ．6 C ．快 D ．乐3、如图，长方体的面有（）A ．4个 B ．5个 C ．6个 D ．7个4、一张坐凳的形状如图所示，以箭头所指的方向为主视方向，则他的左视图可以是( )5、一个物体由多个完全相同的小正方体组成，它的三视图如图所示，那么组成这个物体的小正方体的个数为[ ]A ．2个B ．3个C ．5个D ．10个6、如图是一个几何体的三视图，则这个几何体的侧面积是[ ]A ．12πcm 2B ．8πcm 2C ．6πcm 2D ．3πcm 27、如图所示，将平面图形绕轴旋转一周，得到的几何体是（）A ．B ．C ．D ．8、如图为从正面看到的图形的几何体，它从上面看到的图形是（）A ．B ．C ．D ．A． B． C． D．9、如图是由几个相同的小立方块组成的三视图，小立方块的个数是[ ] A．3个 B．4个 C．5个 D．6个10、骰子是一种特别的数字立方体（如图），它符合规则：相对两面的点数之和总是7．下面四幅图中可以折成符合规则的骰子的是（）A． B．C． D．11、用平面去截下图中的正方体，截面形状不可能是（）A． B． C． D．12、如图，模块①﹣⑤均由4个棱长为1的小正方体构成，模块⑥由15个棱长为1的小正方体构成．现从模块①﹣⑤中选出三个放到模块⑥上，使得模块⑥成为一个棱长为3的大正方体．则下列选择方案中，能够完成任务的为（）A．模块①，②，⑤B．模块①，③，⑤C．模块②，④，⑤D．模块③，④，⑤下的几何体面的个数和棱的条数分别为（）A．6，14 B．7，14 C．7，15 D．6，1514、如图是一个立体图形的二视图，根据图示的数据求出这个立体图形的体积是（）A．24cm3 B．48cm3 C．72cm3 D．192cm315、如图所示的平面图形中，不可能围成圆锥的是（）A． B．C． D．二、填空题(注释)16. 如图，长方体中，与棱AA′平行的面是________________．17、一个五棱柱有____个面，用一个平面去截五棱柱，则得到的截面的形状不可能是____（填“七边形“或“八边形“）18、展开图：几何体名称：_______，_______，_______，_______．19、如图是正方体的一种平面展开图，它的每个面上都有一个汉字，那么在原正方体的表面上，与汉字“香”相对的面上的汉字是____．20、如图，正方体每个侧面的面积为2平方米，用经过A，B，C三点的平面截这个正方体，则所得的切面的周长是____米．21、一个矩形绕着它的一边旋转一周，所得到的立体图形是________________．22、三棱柱的三视图如图所示，△EFG中，EF=8cm，EG=12cm，∠EGF=30°，则AB的长为 cm．23、一个物体的外形是长方体，其内部构造不详．用一组水平的平面截这个物体时，得到了一组（自下而上）截面，截面形状如图所示，这个长方体的内部构造可能是________．三、解答题24、如图1，大正方体上截去一个小正方体后，可得到图2的几何体．（1）设原大正方体的表面积为S，图2中几何体的表面积为S′，那么S′与S的大小关系是（）A、S′＞SB、S′=SC、S′＜SD、不确定（2）小明说：“设图1中大正方体各棱的长度之和为c，图2中几何体各棱的长度之和为c′，那么c′比c正好多出大正方体3条棱的长度．”若设大正方体的棱长为1，小正方体的棱长为x，请问x为何值时，小明的说法才正确？（3）如果截去的小正方体的棱长为大正方体棱长的一半，那么图3是图2中几何体的表面展开图吗？如有错误，请在图3中修正．25、一个正方体，截掉一个角，剩余部分还有几个角？26、将一个正方体的表面涂上颜色．如图把正方体的棱2等分，然后沿等分线把正方体切开，能够得到8个小正方体，通过观察我们可以发现8个小正方体全是3个面涂有颜色的．如果把正方体的棱三等分，然后沿等分线把正方体切开，能够得到27个小正方体，通过观察我们可以发现这些小正方体中有8个是3个面涂有颜色的，有12个是2个面涂有颜色的，有6个是1个面涂有颜色的，还有1个各个面都没有涂色．（1）如果把正方体的棱4等分，所得小正方体表面涂色情况如何呢？把正方体的棱n等分27.如图，这6个图形虽然形状各异，但是可以将它们各剪一刀，各自能拼成一个正方形，你会做到吗？28、把图中的几何体分类，并简要说明理由．29、如图所示，用1、2、3、4标出的四块正方形，以及由字母标出的八块正方形中任意一块，一共要用5块连在一起的正方形折成一个无盖方盒，共有几种不同的方法？请选择合适的方法．30、指出下列平面图形是什么几何体的展开图：。

北师大版七年级上册数学第一章易错题训练

北师大版七年级上册数学第一章易错题训练一、单选题1．如图是一个正方体被截去一个正三棱锥得到的几何体，从上面看这个几何体，得到的形状图是（）A．B．C．D．2．如图所示是某一正方体的表面展开图，则该正方体是（）A．B．C．D．3．如图所示是一个正方体的表面展开图，这个正方体是（）A．B．C．D．二、解答题4．如图所示是一个长方体的表面展开图，每个面都标柱了字母，请回答：如果F在前面，从左面看是B，那么哪一面会在上面？5．从正面、左面、上面观察如图所示的几何体，分别画出你所看到的几何体的形状图.6．如图所示是由若干个相同的小立方块堆成的几何体从上面看到的形状图，小正方形中的数字表示在该位置上小立方块的个数，请你画出从正面、左面看到的这个几何体的形状图.三、填空题7．由若干个相同的小立方块搭成的一个几何体从正面和上面看到的形状图如图所示，小正方形中的字母或数字表示该位置上小立方块的个数，则x=______，y=______.8．如图，在一次数学活动课上，张明用17个边长为1的小正方形搭成了一个几何体，然后他请王亮用其他同样的小正方体在旁边再搭一个几何体，使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体（不改变张明所搭几何体的形状），那么王亮至少还需要个小立方体，王亮所搭几何体的表面积为．参考答案1．B【解析】【分析】根据从上边看得到的图形是俯视图，可得答案．【详解】解：从上边看，故选：B．【点睛】本题考查了简单组合体的三视图，从上边看的到的图形是俯视图．2．D【解析】【分析】认真观察展开图，可知实心圆和空心圆相对，实心圆与白色三角形的边相邻，据此即可判断应选D.【详解】由正方体的平面展形图可知，实心圆和空心圈在相对面，空心圈与黑色三角形的直角边相邻，实心圆与白色三角形的直角边相邻.故：D【点睛】本题考查了正方体的平面展开图，掌握正方体的展形图是解题的关键.3．D【解析】【分析】根据展开图折叠成几何体，四个小正方形组合成一个正方体的面，可得答案【详解】解：把展开图围起来，我们可以发现表面是阴影的面与有12阴影的面相对，而12阴影的面中的两小正方形阴影是在对角线上，显然只有D符合题意.故：D.【点睛】本题考查了几何体的展开图，利用四个小正方形组合成一个正方体的面是解题关键．4．E【解析】【分析】从图上可以看出：A和F、B和D、C和E都是对面，进一步由位置确定每一个面的位置解决问题．【详解】解：如果A在前面，则F在后面，从左面看是B，则D是右面，那么C一定在下面，在上面的是E．【点睛】此题考查多面体展开图各个面的位置情况，动手操作验证一下，效果会更好．5．见解析【解析】【分析】由简单几何体的三视图的定义即可画出.【详解】从正面看：从左面看从上面看：【点睛】此题主要考查简单几何体的三视图，解题的关键是从各方向直接观察即可画出.6．见详解.【解析】【分析】由已知条件可知，从正面看有3列，每列小正方数形数目分别为4，2，3；从左面看有3列，每列小正方形数目分别为2，4，3．据此可画出图形．【详解】解：如图所示：【点睛】考查几何体的三视图画法．由几何体的俯视图及小正方形内的数字，可知主视图的列数与俯视图的列数相同，且每列小正方形数目为俯视图中该列小正方形数字中的最大数字．左视图的列数与俯视图的行数相同，且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字．7．1或23【解析】【分析】从上面看的图中的每个数字是该位置小立方体的个数，结合从正面看2列中的个数，分析其中的数字，从而求解．【详解】解：由从上面看可知，该组合体有两行两列，左边一列前一行有两个正方体，结合从正面看可知左边一列叠有2个正方体，故x=1或2；由从正面看右边一列可知，右边一列最高可以叠3个正方体，故y=3，【点睛】本题考查了根据三视图判断几何体的构成及对几何体三种视图的空间想象能力．注意找到该几何体的主视图中每列小正方体最多的个数．8．19，48．【解析】试题分析：首先确定张明所搭几何体所需的正方体的个数，然后确定两人共搭建几何体所需小立方体的数量，求差即可．解：∵王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体，∴该长方体需要小立方体4×32=36个，∵张明用17个边长为1的小正方形搭成了一个几何体，∴王亮至少还需36﹣17=19个小立方体，表面积为：2×（9+7+8）=48，故答案为19，48．考点：由三视图判断几何体．。

北师大版七年级上册数学配套练习(带答案)+同步练习全套

北师大版七年级上册数学配套练习(带答案)+同步练习全套北师大七年级上第一章丰富的图形世界第1.1.1课时家庭作业生活中的立体图形1）学习目标：1．经历从现实世界中抽象出几何图表的过程，感受图形世界的丰富多彩。

2．在具体情境中认识圆柱、圆锥、正方体、长方体、棱柱、棱台、球，并能用自已的语言描述它们的某些特征。

一．填空题：1．立体图形的各个面都是__________的面，这样的立体图形称为多面体.；2．图形是由________，_________，________构成的；3．物体的形状似于圆柱的有________________，类似于圆锥的有_____________________，类似于球的有__________________；（各举一例）4．围成几何体的侧面中，至少有一个是曲面的是______________；（举一例）5．正方体有_____个顶点，经过每个顶点有_________条棱，这些棱都____________；6．圆柱、圆锥、球的共同点是_____________________________；7．假如我们把笔尖看作一个点,当笔尖在纸上移动时，就能画出线,说明了______________,时钟秒针旋转时，形成一个圆面，这说明了_______________，三角板绕它的一条直角边旋转一周，形成一个圆锥体，这说明了___________________；8．圆可以分割成_____ 个扇形，每个扇形都是由___________________；9．从一个七边形的某个顶点出发，分别连结这个点与其余各顶点，可以把七边形分割成__________个三角形；10．在乒乓球、橄榄球、足球、羽毛球、冰球中，是球体的有；11．将下列几何体分类，柱体有：，锥体有（填序号）；12．长方体由_______________个面_______________条棱_______________个顶点；13．半圆面绕直径旋转一周形成__________；二．选择题14．观察下图，请把左边的图形绕着给定的直线旋转一周后可能形成的几何体选出来（）A B C D15．从一个十边形的某个点出发，分别连接这个顶点与其余各顶点，可以把这个多边形分割成三角形（）（A） 10个（B） 9个（C） 8个（D） 7个16．如图的几何体是下面（）平面图形绕轴旋转一周得到的（）（A）（B）（C）（D）18．下面图形不能围成封闭几何体的是（）（A）（B）（C）（D）三．解答题：19．指出下列平面图形是什么几何体的展开图：A CB20. ⑴.下面这些基本图形和你很熟悉，试一试在括号里写出它们的名称.( ) ( ) ( ) ( ) ( )⑵. 将这些几何体分类，并写出分类的理由.第1.1.1课时家庭作业参考答案一、1．平；2．点、线、面；3．略；4．略；5．8，3，相等；6．都有一个面是曲面； 7．点动成线，线动成面，面动成体；8．无数，一条弧和两条半径组成的；9．5； 10．乒乓球、足球；11．（1）（2）（3），（5）（6）；12．6，12，8；13．球体；二、14．D ；15．C ；16．B ； 17．A ；三、18．长方体（四棱柱），圆锥，圆柱；19．（1）（从左至右）球、圆柱、圆锥、长方体、三棱柱；（2）按面分：曲面：球、圆柱、圆锥；平面：长方体、三棱柱；按柱体分：圆柱、长方体、三棱柱；球；圆锥；北师大七年级上第一章丰富的图形世界第1.1.2课时家庭作业（平面内的立体图形2）姓名学习目标：1．通过丰富的实例，进一步认识点、线、面、初步感受点、线、面之间的关系.2．进一步经历从现实世界中抽象出图形的过程，从构成图形的基本元素的角度认识常见图形；二．填空题：1．围成球的面有个；2．圆柱有_____ 个面组成，这些面相交共得____ 条线，圆锥的侧面展开图是____ ；3．圆锥是由_ __个面围成，其中__ _个平面，___ _个曲面，圆锥的侧面与底面相交成条线，是线；4．圆柱的表面展开图是________________________ (用语言描述)； 5．图形所表示的各个部分不在同一个平面内，这样的图形称为图形； 6．图形所表示的各个部分都在同一个平面内，称为图形；二．选择题：7．圆锥的侧面展开图是（）（A ）长方形（B ）正方形（C ）圆（D ）扇形 8．将半圆绕它的直径旋转一周形成的几何体是（）（A ）圆柱（B ）圆锥（C ）球（D ）正方体9．如图所示的图形绕虚线旋转一周，所形成的几何体是（）新知识点要小心呦！（）10．以下立体图形中是棱柱的有（）（A）①⑤ （B）①②③ （C）①②④⑤ （D）①②⑤[11．下列说法中，正确的是（）（A）正方体不是棱柱（B）圆锥是由3个面围成（C）正方体的各条棱都相等（D）棱柱的各条棱都相等12．将一个直角三角形绕它的最长边旋转一周，得到的几何体是（）（A）（B）（C）（D）13．按组成面的平或曲划分，与圆锥为同一类几何体的是（）（A）正方体（B）长方体（C）球（D）棱柱14．如图，沿着虚线旋转一周得到的图形为（）（A）（B）（C）（D）15．一个正方体锯掉一个角后，顶点的个数是（）（A） 7个（B） 8个（C） 9个（D） 7个或8个或9个或10个三、解答题16．请写出下列几何体的名称( ) ( ) ( ) ( )( ) ( ) ( ) ( )17．如图，第二行的图形绕点划线旋转一周，便形成第一行的某个图形(几何体)，将对应的两个图形用线联结起来．第1.1.2课时家庭作业参考答案一、1．一个；2．三，二，扇形；3．二，一，一，一，曲；4．由一个长方形和两个相等的圆形组成；5．平面； 6．立体；[二、7．D；8．C；9．B；10．A；11．C；12．D；13．C；14．C；15．D；三、16．略；17．略；截一个几何体练习卷(1)一、填空题1．用一个平面去截一个球体所得的截面图形是__________．2．如图1，长方体中截面BB1D1D是长方体的对角面，它是__________．3．在正方体中经过从一个顶点出发的三条棱的中点的截面是_________．4．一座大楼，小明只看到了楼顶，则小明的看到的图叫__________．5．现有一张长52cm，宽28cm的矩形纸片，要从中剪出长15cm，宽12cm的矩形小纸片（不能粘贴），则最多能剪出__________张．6．一个正方体的主视图、左视图及俯视图都是__________．二、选择题7．用一个平面去截一个正方体，截面图形不可能是（）A．长方形; B．梯形; C．三角形; D．圆8．用一个平面去截一个几何体，如果截面的形状是圆，则这个几何体不可能是（）A．圆柱; B．圆锥; C．正方体; D．球9．小明看到了“实验楼”三个字，而且能看到该楼所有的门窗，则小明看到的图是（）A．俯视图; B．左视图; C．主视图; D．都有可能10．截去四边形的一个角，剩余图形不可能是（）A．三角形; B．四边形; C．五边形; D．圆三、解答题11．如图2，将等腰三角形对折沿着中间的折痕剪开，得到两个形状和大小都相同的直角三角形，将这两个直角三角形拼在一起，使得它有一条相等的边是公有的，你能拼出多少种不同的几何图形？并请你分别说出所拼的图形的名称．12．用火柴棒拼搭等边三角形（1）用火柴棒拼搭出两个边长等于棒长的等边三角形，你有几种拼法，最少需要几根火柴棒？（2）拼6个边长等于棒长的等边三角形，看谁用的棒最少？（3）用6根火柴棒拼搭等边三角形，若允许搭成的等边三角形不在同一平面内，那么可以搭多少个？13．选择你所熟悉的实物模型作出它的俯视图、主视图及左视图．14．用一个平面去截圆锥，可以得到几种不同的图形？动手试一试．参考答案一、1．圆2．矩形3．三角形4．俯视图5．7 6．正方形二、7．D 8．C 9．C 10．D三、11．共可以拼出以下六种图形（（1）～（6））（1）、（3）是等腰三角形；（2）、（4）是平行四边形；（5）是长方形；（6）可以称它为筝形．12．（1）2、5 （2）12 （3）4（1）有两种情况，至少要用5根火柴棒，如图（2）；而图（1）则用6根火柴棒．（2）最少要12根火柴棒，如图（4）；图（3）用了13根．（3）若可以不在同一个平面内拼搭，可以搭4个等边三角形，如图（5）．13．略14．略截一个几何体练习卷(2)一、判断题1．用一个平面去截一个正方体，截出的面一定是正方形或长方形. （）2．用一个平面去截一个圆柱，截出的面一定是圆. （）3．用一个平面去截圆锥，截出的面一定是三角形. （）4．用一个平面去截一个球，无论如何截，截面都是一个圆. （）二、选择题1．用一个平面去截圆锥，得到的平面不可能是（）2．用一个平面去截一个圆柱，得到的图形不可能是（）三、用平面去截一个正方体，截面的形状可能是平行四边形吗？截一截，想一想.四、指出下列几何体的截面形状.___________ ___________*自我陶醉编写一道自己感兴趣并与本节内容相关的题，解答出来.参考答案一、1．×2．×3．×4．√二、1．C 2．D三、可能四、五边形圆形1.3 截一个几何体一、选择题1、有下列几何体：（1）圆柱；（2）正方体；（3）棱柱；（4）球；（5）圆锥；（6）长方体。

北师大版七年级数学上第一章复习试题

第一章丰富的图形世界 同步测试2021-2022学年北师大版七年级数学上册

北师大版七年级数学上册 丰富的图形世界单元测试题及答案

北师大版七年级上册数学第一章 丰富的图形世界 含答案