上海市长宁区2008年第一学期初三年级数学期末考试试卷
2008年上海市中考数学试题及答案

2008年上海市中考数学试卷(满分150分,考试时间100分钟)考生注意:1.本试卷含三个大题,共25题:第一大题选择题含Ⅰ、Ⅱ两组选做题,Ⅰ组供使用一期课改教材的考生完成,Ⅱ组供使用二期课改教材的考生完成;其余大题为共做题;一、选择题:(本大题含Ⅰ、Ⅱ两组,每组各6题,每题4分,满分24分) 考生注意:1.请从下列Ⅰ、Ⅱ两组中选择一组,并在答题纸的相应位置填涂选定的组号,完成相应的1—6题.若考生没有填涂任何组号或将两个组号全部填涂,默认考生选择了Ⅰ组;2.下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.Ⅰ组:供使用一期课改教材的考生完成1.计算23a a 的结果是( ) A .5aB .6aC .25aD .26a2.如果2x =是方程112x a +=-的根,那么a 的值是( ) A .0B .2C .2-D .6-3.在平面直角坐标系中,直线1y x =+经过( ) A .第一、二、三象限 B .第一、二、四象限 C .第一、三、四象限D .第二、三、四象限4.在平面直角坐标系中,抛物线21y x =-与x 轴的交点的个数是( ) A .3B .2C .1D .05.如果12x x ,是一元二次方程2620x x --=的两个实数根,那么12x x +的值是( ) A .6-B .2-C .6D .26.如图1,从圆O 外一点P 引圆O 的两条切线PA PB ,,切点分别为A B ,.如果60APB ∠=,8PA =,那么弦AB 的长是( ) A .4B .8C.D.Ⅱ组:供使用二期课改教材的考生完成1.计算23a a 的结果是( ) A .5aB .6aC .25aD .26a2.如果2x =是方程112x a +=-的根,那么a 的值是( ) A .0B .2C .2-D .6-P图13.在平面直角坐标系中,直线1y x =+经过( ) A .第一、二、三象限 B .第一、二、四象限 C .第一、三、四象限D .第二、三、四象限4.计算32a a -的结果是( )A .aB .aC .a -D .a -5.从一副未曾启封的扑克牌中取出1张红桃,2张黑桃的牌共3张,洗匀后,从这3张牌中任取1张牌恰好是黑桃的概率是( ) A .12B .13C .23D .16.如图2,在平行四边形ABCD 中,如果AB a = ,AD b =, 那么a b +等于( )A .BDB .ACC .DBD .CA二、填空题:(本大题共12题,每题4分,满分48分) [请将结果直接填入答题纸的相应位置]7.不等式30x -<的解集是 . 8.分解因式:24x -= . 9.用换元法解分式方程21221x x x x --=-时,如果设21x y x-=,并将原方程化为关于y 的整式方程,那么这个整式方程是 . 102=的根是 . 11.已知函数()f x =(2)f = .12.在平面直角坐标系中,如果双曲线(0)ky k x=≠经过点(21)-,,那么k = .13.在图3中,将直线OA 向上平移1个单位,得到一个一次函数的图像,那么这个一次函数的解析式是 . 14.为了了解某所初级中学学生对2008年6月1日起实施的“限塑令”是否知道,从该校全体学生1200名中,随机抽查了80名学生,结果显示有2名学生“不知道”.由此,估计该校全体学生中对“限塑令”约有 名学生“不知道”.15.如图4,已知a b ∥,140∠=,那么2∠的度数等于 .图2x12a b图416.如果两个相似三角形的相似比是1:3,那么这两个三角形面积的比是 .17.如图5,平行四边形ABCD 中,E 是边BC 上的点,AE 交BD 于点F ,如果23BE BC =,那么BFFD= .18.在ABC △中,5AB AC ==,3cos 5B =(如图6).如果圆O且经过点B C ,,那么线段AO 的长等于 . 三、解答题(本大题共7题,满分78分) 19.(本题满分10分)++ 20.(本题满分10分) 解方程:2654111x x x x x ++=--+ 21.(本题满分10分,第(1)小题满分3分,第(2)小题满分7分)“创意设计”公司员工小王不慎将墨水泼在一张设计图纸上,导致其中部分图形和数据看不清楚(如图7所示).已知图纸上的图形是某建筑物横断面的示意图,它是以圆O 的半径OC 所在的直线为对称轴的轴对称图形,A 是OD 与圆O 的交点.(1)请你帮助小王在图8中把图形补画完整;(2)由于图纸中圆O 的半径r 的值已看不清楚,根据上述信息(图纸中1:0.75i =是坡面CE 的坡度),求r 的值.E 图5B图6图7 图822.(本题满分10分,第(1)小题满分3分,第(2)小题满分4分,第(3)小题满分3分)某人为了了解他所在地区的旅游情况,收集了该地区2004至2007年每年的旅游收入及入境旅游人数(其中缺少2006年入境旅游人数)的有关数据,整理并分别绘成图9,图10.根据上述信息,回答下列问题:(1)该地区2004至2007年四年的年旅游收入的平均数是 亿元;(2)据了解,该地区2006年、2007年入境旅游人数的年增长率相同,那么2006年入境旅游人数是 万;(3)根据第(2)小题中的信息,把图10补画完整. 23.(本题满分12分,每小题满分各6分)如图11,已知平行四边形ABCD 中,对角线AC BD ,交于点O ,E 是BD 延长线上的点,且ACE △是等边三角形.(1)求证:四边形ABCD 是菱形;(2)若2AED EAD ∠=∠,求证:四边形ABCD 是正方形.24.(本题满分12分,第(1)小题满分5分,第(2)小题满分7分)如图12,在平面直角坐标系中,O 为坐标原点.二次函数23y x bx =-++的图像经过点(10)A -,,顶点为B .(1)求这个二次函数的解析式,并写出顶点B 的坐标;年旅游收入 (亿元)图9 旅游收入图 图10 EB A图11(2)如果点C 的坐标为(40),,AE BC ⊥,垂足为点E ,点D 在直线AE 上,1DE =,求点D 的坐标.25.(本题满分14分,第(1)小题满分5分,第(2)小题满分4分,第(3)小题满分5分) 已知24AB AD ==,,90DAB ∠=,AD BC ∥(如图13).E 是射线BC 上的动点(点E 与点B 不重合),M 是线段DE 的中点.(1)设BE x =,ABM △的面积为y ,求y 关于x 的函数解析式,并写出函数的定义域;(2)如果以线段AB 为直径的圆与以线段DE 为直径的圆外切,求线段BE 的长;(3)联结BD ,交线段AM 于点N ,如果以A N D ,,为顶点的三角形与BME △相似,求线段BE 的长.B A D M E C图13 B A D C 备用图x2008年上海市中考数学试卷答案要点与评分标准说明:1.解答只列出试题的一种或几种解法.如果考生的解法与所列解法不同,可参照解答中评分标准相应评分;2.第一、二大题若无特别说明,每题评分只有满分或零分;3.第三大题中各题右端所注分数,表示考生正确做对这一步应得分数;4.评阅试卷,要坚持每题评阅到底,不能因考生解答中出现错误而中断对本题的评阅.如果考生的解答在某一步出现错误,影响后继部分而未改变本题的内容和难度,视影响的程度决定后继部分的给分,但原则上不超过后继部分应得分数的一半;5.评分时,给分或扣分均以1分为基本单位. 一、选择题:(本大题含Ⅰ,Ⅱ两组,每组各6题,满分24分) 1.D ; 2.C ; 3.A ; 4.B ; 5.C ; 6.B . 二、填空题:(本大题共12题,满分48分) 7.3x <; 8.(2)(2)x x -+; 9.2210y y --=;10.1x =-;12.2-; 13.21y x =+; 14.30;15.40;16.1:9;17.23; 18.3或5.三、解答题:(本大题共7题,满分78分)19.解:原式13=+-·················· (8分) 4=. ································ (2分)20.解:去分母,得65(1)(4)(1)x x x x ++=+-. ······················ (3分)整理,得2890x x --=. ······················· (2分)11x ∴=-,29x =. ·························· (4分)经检验,11x =-是增根,29x =是原方程的根. ·············· (1分) 所以,原方程的根是9x =. 21.(1)(图形正确); ························· (3分)(2)解:由已知OC DE ⊥,垂足为点H ,则90CHE ∠=.1:0.75i = ,43CH EH ∴=. ······················ (1分) 在Rt HEC △中,222EH CH EC +=.设4CH k =,3(0)EH k k =>,又5CE = ,得222(3)(4)5k k +=,解得1k =.3EH ∴=,4CH =. ········· (3分)7DH DE EH ∴=+=,7OD OA AD r =+=+,4OH OC CH r =+=+.在Rt ODH △中,222OH DH OD +=,222(4)7(7)r r ∴++=+. 解得83r =.······························ (3分) 22.(1)45; ····························· (3分) (2)220; ······························ (4分) (3)(图正确). ···························· (3分) 23.证明:(1) 四边形ABCD 是平行四边形,AO CO ∴=. ······· (2分) 又ACE △是等边三角形,EO AC ∴⊥,即DB AC ⊥. ········· (2分)∴平行四边形ABCD 是菱形;······················ (2分) (2)ACE △是等边三角形,60AEC ∴∠=. ············· (1分)EO AC ⊥ ,1302AEO AEC ∴∠=∠= . ················ (1分) 2AED EAD ∠=∠ ,15EAD ∴∠= .45ADO EAD AED ∴∠=∠+∠= . · (1分)四边形ABCD 是菱形,290ADC ADO ∴∠=∠= . ··········· (2分)∴四边形ABCD 是正方形.······················· (1分) 24.解:(1) 二次函数23y x bx =-++的图像经过点(10)A -,, 013b ∴=--+,得2b =, ······················ (2分)所求二次函数的解析式为223y x x =-++. ················ (1分)则这个二次函数图像顶点B 的坐标为(14),; ················ (2分)(2)过点B 作BF x ⊥轴,垂足为点F .在Rt BCF △中,4BF =,3CF =,5BC =,4sin 5BCF ∴∠=.在Rt ACE △中,sin AEACE AC∠=,又5AC =, 可得455AE =.4AE ∴=. ······················· (2分) 过点D 作DH x ⊥轴,垂足为点H .由题意知,点H 在点A 的右侧,易证ADH ACE △∽△.AH DH ADAE CE AC∴==. 其中3CE =,4AE =.设点D 的坐标为()x y ,,则1AH x =+,DH y =, ①若点D 在AE 的延长线上,则5AD =.得15435x y +==,3x ∴=,3y =,所以点D 的坐标为(33),; ②若点D 在线段AE 上,则3AD =.得13435x y +==,75x ∴=,95y =,所以点D 的坐标为7955⎛⎫⎪⎝⎭,. 综上所述,点D 的坐标为(33),或7955⎛⎫⎪⎝⎭,. ················ (5分)25.解:(1)取AB 中点H ,联结MH ,M 为DE 的中点,MH BE ∴∥,1()2MH BE AD =+. ········· (1分) 又AB BE ⊥ ,MH AB ∴⊥. ····················· (1分)12ABM S AB MH ∴=△,得12(0)2y x x =+>; ··········· (2分)(1分)(2)由已知得DE =. ·················· (1分)以线段AB 为直径的圆与以线段DE 为直径的圆外切, 1122MH AB DE ∴=+,即11(4)222x ⎡+=+⎣. ······· (2分)解得43x =,即线段BE 的长为43; ··················· (1分)(3)由已知,以A N D ,,为顶点的三角形与BME △相似,又易证得DAM EBM ∠=∠. ······················ (1分) 由此可知,另一对对应角相等有两种情况:①ADN BEM ∠=∠;②ADB BME ∠=∠. ①当ADN BEM ∠=∠时,AD BE ∥,ADN DBE ∴∠=∠.DBE BEM ∴∠=∠. DB DE ∴=,易得2BE AD =.得8BE =; ··············· (2分) ②当ADB BME ∠=∠时,AD BE ∥,ADB DBE ∴∠=∠. DBE BME ∴∠=∠.又BED MEB ∠=∠,BED M EB ∴△∽△.DE BEBE EM∴=,即2BE EM DE = ,得2x =解得12x =,210x =-(舍去).即线段BE 的长为2. ··········· (2分) 综上所述,所求线段BE 的长为8或2.。
2008年上海市中考数学试卷及答案解析

图 13
备用图
2008 年上海市中考数学试卷
答案要点与评分标准 说明: 1.解答只列出试题的一种或几种解法.如果考生的解法与所列解法不同,可参照解答中评 分标准相应评分;
2.第一、二大题若无特别说明,每题评分只有满分或零分; 3.第三大题中题右端所注分数,表示考生正确做对这一步应得分数; 4.评阅试卷,要坚持每题评阅到底,不能因考生解答中出现错误而中断对本题的评阅.如 果考生的解答在某一步出现错误,影响后继部分而未改变本题的内容和难度,视影响的程 度决定后继部分的给分,但原则上不超过后继部分应得分数的一半; 5.评分时,给分或扣分均以 1 分为基本单位. 一、选择题: (本大题含Ⅰ,Ⅱ两组,每组各 6 题,满分 24 分) 1.D; 2.C; 3.A; 4.B; 5.C; 6.B. 二、填空题: (本大题共 12 题,满分 48 分) 7. x 3 ; 11. 3 ; 15.40; 8. ( x 2)( x 2) ; 12. 2 ; 16. 1: 9 ; 9. y 2 y 1 0 ;
2
10. x 1 ;
13. y 2 x 1 ; 17.
14.30; 18.3 或 5.
2 ; 3
三、解答题: (本大题共 7 题,满分 78 分) 19.解:原式
2 1 3 3 2 2 2 ·························································(8 分)
.
B
图6
C
1 3( 3 6) 8 . 2 1
20. (本题满分 10 分) 解方程:
6x 5 x4 2 x 1 x 1 x 1
21. (本题满分 10 分,第(1)小题满分 3 分,第(2)小题满分 7 分) “创意设计” 公司员工小王不慎将墨水泼在一张设计图纸上, 导致其中部分图形和数据看不 清楚 (如图 7 所示) . 已知图纸上的图形是某建筑物横断面的示意图, 它是以圆 O 的半径 OC 所在的直线为对称轴的轴对称图形, A 是 OD 与圆 O 的交点.
08年九年级质量检测数学卷答案

2008年九年级复习教学质量检测 数学试题参考答案及评分标准一、选择题(每小题3分,共30分)二、填空题(每小题4分,共24分) 11. 4x = 12. 213.14. 54 15. 0.5 16. 168三. 解答题(8小题共66分) 17.(本题6分)解:2211()2ab a b a ab b -⋅-+2()b a ab ab a b -=⋅-1b a =-. ……2分 01)s i n 302a =︒=,3b =︒=,……2分∴ 原式121532==-. ……2分 18.(本题6分)解:四边形1111A B C D 如图所示.……3分(画图2分,顶点表示2分)四边形2222A B C D 即为放大后的图形.……2分(顶点或结论的表示不扣分)19.(本题6分)证明:∵ AB =BD ,BM =BM ,∴ Rt △ABM ≌Rt △DBM . ……2分 ∴ AM =DM ,即M 是AD 的中点. ……1分 又∵ N 是AC 的中点,∴ MN 是△ADC 的中位线. ……1分 ∴ 2MN =DC . ……2分(第18题)ABCNDM(第19题)20.(本题8分)解:参加本次活动的总人数是25÷50%=50(人).……2分 乙组的人数是50-(25+15)=10(人).……1分 补全条形统计图如图所示. ……2分甲组所占的比例是 15÷50=30%,在扇形图中表示甲组的扇形的圆心角度数是30%×360º=108º,……1分 补全扇形统计图如图所示. ……2分21.(本题8分)解:选出的两张牌构成点P 的各种可能情况如下表:……4分求点P 在函数x y 6=图象上的概率,就是求两张牌的牌面数字之积是6的概率.……2分积是6共有4种情况,因此所求的概率是41164=.……2分22.(本题10分)解:(1) 射线OA 上整数的排列规律是56-n ;……1分 射线OB 上整数的排列规律是46-n ; ……1分 射线OC 上整数的排列规律是36-n ;……1分(2) 射线OD 上整数的排列规律是26-n; 射线OE 上整数的排列规律是16-n ; 射线OF 上整数的排列规律是n 6. ……1分 在6条射线上的整数排列规律中,只有008226=-n 有整数解,解为335=n . ……2分 因此“2 008”在射线OD 上,……2分 该射线上共有335个整数.……2分(第20题)人数(报名人数扇形统计图23.(本题10分)解:(1) 分配给甲店的A ,B 两种玩具分别为8箱和12箱,销售利润为20×8+24×12=448(元). ……1分 分配给乙店的A ,B 两种玩具分别为12箱和8箱,销售利润为26×12+28×8=536(元). ……1分 所以玩具经销商获得的销售利润为448+536=984(元). ……1分 (2) 解法1:因为乙店销售A ,B 两种玩具的利润都要比甲店高,所以当甲店配货最少时,经销商获利最大. ……2分 在甲店A ,B 两种玩具按2︰3配货的条件下,给甲店配A 种玩具2箱,B 种玩具3箱,给乙店配A 种玩具18箱, B 种玩具17箱时,玩具经销商获利最大. ……2分 其最大销售利润为:2×20+3×24+18×26+17×28=1 056(元). ……3分 解法2:设分配给甲店的A 种玩具为x (2≤x ≤18)箱,则分配给甲店的B 种玩具为x 23箱,分配给乙店的A 种玩具为(20-x )箱, B 种玩具为(20-x 23)箱. ……1分 设玩具经销商获得的利润为y 元,则y =20 x +24×x 23+26×(20-x )+28×(20-x 23) ……2分= -12 x +1 080. ……1分 因为y 是x 的一次函数,y 的值随x 的增大而减小,所以当x =2时,y 取得最大值,最大值为1 056元, ……1分 即给甲店配A 种玩具2箱,B 种玩具3箱,给乙店配A 种玩具18箱, B 种玩具17箱时,玩具经销商获利最大,最大利润为1 056元. ……2分 24.(本题12分)解:(1) 分两种情况讨论:① 当4≤x <8时,此时点Q 在矩形内部(包括边上),∵点Q 是点C 关于直线PD的对称点,∴△PDQ ≌△PDC ,∴1624)8(2121+-=⨯-⨯=⋅=x x CD PC S .……1分 即 162+-=x S (4≤x <8). ……1分 ② 当0<x <4时,此时点Q 在矩形外部,如图甲(其中E 是PQ 与AD 的交点,PF ⊥AD 于F ),∵ ∠CPD =∠QPD =∠EDP ,∴ EP =ED . ∴ )(8ED x EF +-=. ∵ 222PE PF EF =+, ∴ 2224)8(ED ED x =+--.(甲)解得 )8(280162x x x ED -+-=.……1分∴ 当0<x <4时,xx x S -+-=880162.……1分 当2=x 时,326288021628801622=-+⨯-=-+-=x x x S .……1分(2) 由(1)知,当4≤x <8时,162+-=x S 的最大值是8,而541>8,∴162541+-≠x .于是,令x x x -+-=880165412,(其中0<x <4)解得31=x ,5242=x (舍去).即得点P 坐标为P (3,0). ……1分另一方面,当3=x 时,1041)8(280162=-+-=x x x ED ,10398=-=ED AE .因此点E 的坐标为E (1039,4). ……1分 ∵ 求直线PQ 的函数解析式就是求经过P ,E 两点的直线函数解析式,设为 b kx y +=,将P ,E 两点的坐标代入,解得940=k ,340-=b .……1分∴ 所求函数解析式为:340940-=x y . ……1分 (3) 作QG ⊥x 轴于点G ,H 是QG 与PD 的交点(如图乙).∵ 点G 是PC 的中点,GH ∥CD ,∴ H 是PD 的中点.∴ HQ =HP . 从而∠HQP =∠HPQ =∠HPG ,∴ ∠HPG =30°. ……1分 ∴ 3430tan 4=︒=PC .∴ 点P 的横坐标为348-. 故348-=a ,……1分将a 值代入x x x S -+-=880162,得3316=S .(或4sin60ED =︒331621=⨯⨯=CD ED S )……1分(乙)。
南汇2008年第一学期初三测试卷
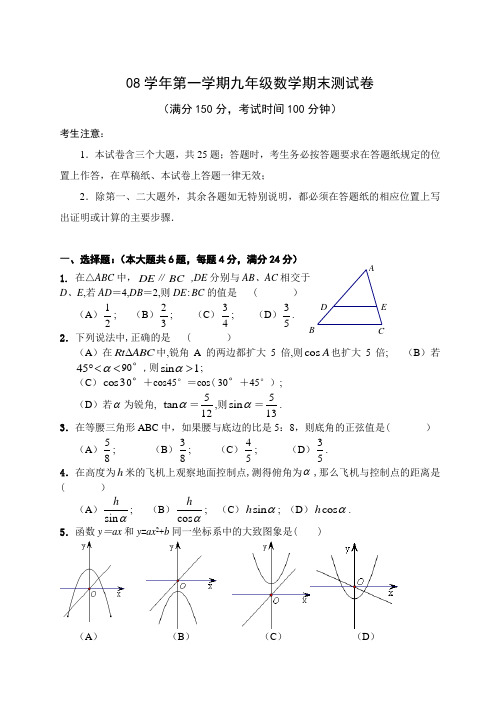
08学年第一学期九年级数学期末测试卷(满分150分,考试时间100分钟)考生注意:1.本试卷含三个大题,共25题;答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分) 1. 在△ABC 中,DE ∥BC ,DE 分别与AB 、AC 相交于D 、E ,若AD =4,DB =2,则DE :BC 的值是 ( ) (A )12; (B )23; (C )34; (D )35. 2.下列说法中,正确的是 ( )(A )在Rt ABC ∆中,锐角A 的两边都扩大5倍,则cos A 也扩大5倍; (B )若45α︒<<90°,则sin 1α>;(C )cos30°+cos45°=cos ( 30°+45°); (D )若α为锐角, tan α=512,则sin α=513. 3.在等腰三角形ABC 中,如果腰与底边的比是5:8,则底角的正弦值是( )(A )85; (B )83; (C )54; (D )53. 4.在高度为h 米的飞机上观察地面控制点,测得俯角为α,那么飞机与控制点的距离是( ) (A )sin h α; (B )cos h α; (C )sin h α; (D )cos h α. 5.函数y =ax 和y =ax 2+b 同一坐标系中的大致图象是( )(A ) (B ) (C ) (D )E D CBA6.若A (-2, 1y ), B (-1, 2y ), C (53,3y )为二次函数245y x x =--+图像上的三点,则123,,y y y 的大小关系是( )(A )123y y y <<; (B )321y y y <<;(C )312y y y <<;(D )213y y y <<. 二、填空题(本大题共12题,每题4分,满分48分)7. 己知a =2,cm b =3,cm c =4,cm 则a 、b 、c 的第四比例项d = cm .8. 如图,梯形A B C D 对角线AC 、BD 交于点O ,若AOD S ∆∶ACD S ∆=1∶4,则AOD S ∆∶BOC S ∆= .9. 化简:⎪⎭⎫ ⎝⎛---b a a 2323= .第8题图 10.计算:tan 45︒—sin 45︒= . 11. 在△ABC 中,AB =AC ,又cos B =15,则BC AB= . 12.一个钢球沿着坡比为3:1=i 的斜坡向上滚动了5米,此时钢球距地面的高度是米.13.如图,在Rt ABC ∆中, ∠ACB =90°, B ∠=30°, AD 是BAC ∠的平分线,己知AB=AD = .14.用长为20米的篱笆,一面靠墙(墙的长度是10米),围成一个长方形花圃,如图,设AB 边的长为x 数,花圃的面积为y 平方米,写出y 与x 的函数关系式及函数的定义域 .第13题图 第14题图 第15题图O AD CB DC B AD C BA15.二次函数y =2()a x m -的图像如图,己知a =12,OA =OC ,则该抛物线的解析式为 .16. 抛物线y =22(1)3x -++向左平移1个单位,再向下平移5个单位,得到的抛物线解析式为 .17. 已知二次函数2y ax bx c =++则点()P a bc ,在第 象限.18.己知抛物线y ()229x a x =-++的顶点在x 轴上,则a = . 三、解答题(本大题共7题,满分78分) 19.(本题满分10分)己知四边形ABCD 是正方形, CE ∶DE =1∶2,线段AE 、BC 的延长线交于点F .求ECF ∆与ABF ∆的周长比.20.(本题满分10分)在ABC ∆和AED ∆中, AB ·AD =AC ·AE ,CAE ∠=BAD ∠,ADE S ∆=4ABC S ∆. 求证∶DE =2BC .F EDC B A EDCBA21.(本题满分10分)在Rt ABC ∆中,己知C ∠=90°, B ∠=60°, b =4.解这个直角三角形.22.(本题满分10分,4分+ 4分+ 2分)二次函数的图像经过三点A (1, 0 )、B (2, 0 )、C (3, 4 ). (1 )求二次函数的函数解析式;(2 )求抛物线的对称轴方程和顶点坐标; (3 )求点C 关于对称轴的对称点1C 的坐标.23.(本题满分12分, 6分+6分)在Rt ABC ∆中, ∠ACB =90°, CD AB ⊥,垂足为D . E 、F 分别是AC 、BC 边上一点,且CE =13AC ,BF =13BC . (1 )求证∶AC BC =CDBD.(2 )求EDF ∠的度数.24.(本题满分12分, 4分+8分)去年某省将地处A 、B 两地的两所大学合并成了一所综合大学.为了方便A 、B两地师生的交往, 学校准备在相距2km 的A 、B 两地之间修筑一条笔直公路AB .经测量,在A 地的北偏东60°方向, B 地的北偏西45°方向的C 处有一个半径为0.7km 的公园.(1 ) 在图中画出点C .(2 )问计划修筑的这条公路会不会穿过公园,为什么?FEDC BA BA25.(本题满分14分,5分+ 5分+ 4分)已知抛物线经过)2,1(),2,0(),0,1(---C B A ,且与x 轴的另一个交点为E . (1)求抛物线的解析式;(2)用配方法求抛物线的顶点D 的坐标和对称轴; (3)求四边形ABDE 的面积A BCDOExy参考答案及评分标准1.B2.D3.D4.A5.C6.B7.68.91 9.2325+- 10. 222- 11.5212. 210 13.4 14.)105(2022<≤+-=x x x y 15. ()2221-=x y 16. ()2222-+-=x y 17.三 18.4或-819.∵四边形ABCD 是正方形∴ CE ∥AB -----------------------------------3′ ∴ ⊿ABF ∽⊿ECF ----------------------------2′ 设k DC AB k DE k CE 3,2,====则------------2′∴313===∆∆k k AB EC ABF ECF 的周长的周长----------------3′20.证明:∵AE AC AD AB ⋅=⋅ ∴ADAEAC AB = ----------------------------2′ 又 ∵∠CAE =∠BAD∴ ∠CAE+∠DAC =∠BAD+∠DAC即 ∠DAE =∠CAB ----------------------------2′ ∴ ⊿ADE ∽⊿ACB ----------------------------1′ 又 ∵ACB ADE S S ∆∆=4 ∴4=∆∆ACBADES S ----------------------------2′∴ 42==⎪⎭⎫⎝⎛∆∆ACB ADE S S BC DE ∴2=BCDE∴ BC DE 2= ----------------------------3′21.解:∵ ∠B=60°∴ ∠A=90°-60°=30°-------------------------3′ 33433430tan 4tan =⨯=︒⨯=⋅=A b a --------4′ 3382==a c -------------------------3′ 22.解:(1)设函数解析式为 ()()21--=x x a y 将点C(3,4)代入得 a =2所以其解析式为 ()()212--=x x y ------------------4′ (或4622+-=x x y )(2)将解析式写为顶点式为 212322-⎪⎭⎫ ⎝⎛-=x y所以对称轴方程为 x =23 ,顶点坐标为(21,23-). ----------4′ (3)由对称性知点C 1在y 轴上,当x=0时,y=4∴C 1(0,4) -------------------------2′ 23.(1)证明:∵CD ⊥AB , ∴∠A+∠ACD=90° 又∵∠A+∠B=90°∴∠B=∠ACD ----------------------------3′ ∴ Rt ⊿ADC ∽Rt ⊿CDB∴BDCDBC AC =----------------------------3′ (2) ∵BDCDBC AC BC ACBF CE ===3131 又∵∠ACD =∠B∴ ⊿CED ∽⊿BFD --------------------------3′ ∴ ∠CDE =∠BDF∴ ∠EDF =∠EDC+∠CDF=∠BDF+∠CDF=∠CDB=90°-----------3′ 24.(1)图略.(2)过点C 作CD ⊥AB 于D.设CD 为x ﹒km ,则BD 为x ﹒km ,AD 为x 3﹒km ,则有7.07321.01323>≈-=⇒=+x x x答:这条公路不会穿过公园.25.解:(1)因为2(0)y ax bx c a =++≠经过)2,1(),2,0(),0,1(---C B A 三点,∴ ⎪⎩⎪⎨⎧-=-==⎪⎩⎪⎨⎧-=++-==+-2,1,122,0c b a c b a c c b a 解得 --------------------------3′ ∴抛物线解析式为 22--=x x y . --------------------------2′(2)4921222-⎪⎭⎫ ⎝⎛-=--=x x x y --------------------------3′所以,顶点坐标D (21,49-),对称轴:x =21. -------------------1′+1′ (3) 联结OD,由2,102212=-==--x x x x 解得,所以OE=2. ---------2′ ∴ 41549221212212121=⨯⨯+⨯⨯+⨯⨯=++=∆∆∆OED OBD AOB ABDE S S S S 四边形 ---------2′。
上海市长宁区2019年中考一模(即期末)数学试题及答案

长宁区九年级数学学科期末练习卷(2019年1月)(考试时间:100分钟,满分:150分)一、 选择题(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】1.下列说法中,结论错误的是( ▲ )A .直径相等的两个圆是等圆;B .长度相等的两条弧是等弧;C .圆中最长的弦是直径;D .一条弦把圆分成两条弧,这两条弧可能是等弧. 2.已知非零向量,,a b c ,下列条件中,不能..判定//a b 的是( ▲ ) A .a b =; B . a b =-; C .//,//a c b c ; D .2,4a c b c ==. 3.抛物线2(1)3y x =-++的顶点坐标是( ▲ )A .(1,3)--;B .(1,3)-;C .(1,3)-;D .(1,3).4.抛物线241y x x =++可以通过平移得到2y x =,则下列平移过程正确的是( ▲ )A .先向左平移2个单位,再向上平移3个单位;B .先向左平移2个单位,再向下平移3个单位;C .先向右平移2个单位,再向下平移3个单位;D .先向右平移2个单位,再向上平移3个单位.5.在△ABC 中,∠ACB = 90°,CD ⊥AB 于D ,下列各组边的比不能..表示sin B 的( ▲ ) A .AC AB ; B .DC AC ; C .DC BC ; D .ADAC.6.如图,P 是平行四边形ABCD 的对称中心,以P 为圆心作圆,过P 的任意直线与圆相交于点M 、N .则线段BM 、DN 的大小关系是( ▲ ) A .BM > DN ; B .BM < DN ; C .BM = DN ; D .无法确定.二、填空题(本大题共12题,每题4分,满分48分)7.已知两个相似三角形的面积比是 4 : 1,则这两个三角形的周长比是 ▲ .8.如图,直线////a b c ,直线m n 、与a b c 、、分别交于点A 、C 、E 、B 、D 、F ,已知AC=4,CE = 6,BD = 3,则BF 等于 ▲ .9.将二次函数224y x x =-配方成2()y a x m k =++的形式,配方后的解析式为 ▲ . 10.如图,望大伯屋后有一块长12米,宽8米的矩形空地ABCD ,他在以较长边BC 为直径的半圆形内中菜,他家养的羊平时栓在A 处的一棵树上,为了不让羊吃到菜,栓羊的绳长应小于 ▲ .11.已知抛物线24(2)y mx x m m =++-经过坐标原点,则实数m 的值是 ▲ .12.已知抛物线22y x bx c =++经过点A (0 , 3)、B (4 , 3),则此抛物线的对称轴是 ▲ . 13.已知⊙A 的半径为5,圆心A (3 , 4),坐标原点O 与⊙A 的位置关系是 ▲ .14.印刷厂10月份印刷一畅销小说书5万册,因购买此书人数激增,印刷厂需加印,若设印书量每月的增长率为x ,12月印书量y 万册,写出y 关于x 的函数解析式 ▲ .15.在Rt △ABC 中,∠C =90°,中线AF 和中线BE 交于点G ,若AB = 3,则CG = ▲ . 16.某一山坡,坡长200米,山坡的高度100米,则此山坡的坡度是 ▲ .17.已知点123(0,)(1,)(3,)A y B y C y 、、在抛物线221(0)y ax ax a =-+<上,则123y y y 、、的大小关系是 ▲ .18.如图,△ABC 是面积为3的等边三角形,△ADE ∽△ABC ,AB = 2AD ,∠BAD = 45°,AC与DE 相交于点F ,则△AEF 的面积是 ▲ . 三、解答题(本大题共7题,满分78分) 19.(本题满分10分)计算:2013(tan 45)cos60|cot 301|-︒-︒+︒-.20.(本题满分10分)如图,在梯形ABCD 中,AD // BC ,AD = 2,BC = 3,EF 是梯形的中位线,EF 与BD 交于点M .设AD a =,试用a 表示BC 与FM21.(本题满分10分)已知⊙O 的半径为12cm ,弦122AB cm =. (1)求圆心O 到弦AB 的距离;(2)若弦AB 恰好是△OCD 的中位线,以CD 中点E 为圆心,R 为半径作⊙E ,当⊙O 和⊙E 相切时,求R 的值.22.(本题满分10分)为了开发利用海洋资源,需要测量某岛屿两端A 、B 的距离.如图,勘测飞机在距海平面垂直高度为100米的点C 处测得点A 的俯角为60°,然后沿着平行于AB 的方向飞行了500米至D 处,在D 处测得点B 的俯角为45°,求岛屿两端A 、B 的距离.(结果精确到0.1米) 说明:①A 、B 、C 、D 在与海平面垂直的同一平面上;②参考数据:3 1.732,2 1.414≈≈.23.(本题满分12分,第(1)小题满分5分,第(2)小题满分7分) 如图,△ABC 中,AC = BC ,F 为底边AB 上一点,(,0)BF mm n AF n=>,D 是CF 中点,联结AD 并延长交BC 于E .(1)求BEEC的值;(2)若BE = 2EC,求证:CF⊥AB.24.(本题满分12分)如图,在直角坐标平面上,点A、B在x轴上(A点在B点左侧),点C在y轴正半轴上,若A(– 1 , 0),OB = 3OA,且tan∠CAO = 2.(1)求点B、C的坐标(2)求经过点A、B、C三点的抛物线解析式;(3)P是(2)中所求抛物线的顶点,设Q是此抛物线上一点,若△ABQ与△ABP的面积相等,求P点的坐标.25.(本题满分14分)在△ABC中,∠BAC = 90°,AB < AC,M是BC边的中点,MN⊥BC交AC于点N.动点P 从点B出发,沿射线BA以每秒3个长度单位运动,联结MP,同时Q从点N出发,沿射线NC 以一定的速度运动,且始终保持MQ⊥MP,设运动时间为x秒(x > 0).(1)求证:△BMP∽△NMQ;AB ,设△APQ的面积为y,求y与x的函数关系式;(2)若∠B = 60°,43(3)判断BP、PQ、CQ之间的数量关系,并说明理由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008学年第一学期初三数学期终抽测试卷 (考试时间100分钟,满分150分) 2009.1
考生注意: 1.本试卷含三个大题,共25题; 2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效; 3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.
一、选择题(4分6=24分) 【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】 1.在ABCRt中,已知90C,AC=4,BC=3,则Acos等于( ) A.43 B.34 C.54 D.53 2.在直角坐标平面上,将函数2yx的图象向上平移2个单位,得到新的图象的函数表达式是( ) A.22yx B.2(2)yx C.22yx D.2(2)yx 3.如图,已知一坡面的坡度1:3i,则坡角为( ) A.15 B.30 C.45 D.60 4. 如图,直线123lll∥∥,另两条直线分别交1l,2l,3l于 点ABC,,及点DEF,,,且3AB,4DE,2EF, 则( ) A. BC:DE=1:2 B. BC:DE=2:3 C. BC×DE=8 D. BC×DE=6 5.已知非零向量nm,和单位向量e,则下列等式中正确的是( ) .
第4题
A D
1l
2l 3l E B
F C
C B A 1:3i
第3题 A.mem B.emm1 C.nne D. mm1nn1 6. 如图,在平面直角坐标系中,点P在第一象限,⊙P与x轴相切于 点Q,与y轴交于(02)M,,(08)N,两点,则点P的坐标是( ) A.(53), B.(35), C.(54), D.(45),
二、填空题(4分12=48分) 【请将结果直接填入答题纸的相应位置上】 7.已知抛物线12xaxy的对称轴在y轴的右边,则这个抛物线的开口方向是向 . 8.已知线段AB=1,C是线段AB的黄金分割点,且AC9. 已知二次函数2(1)yaxbxc(0a),则它的的图象经过原点的条件是 . 10.如图,ABC△和EBD△中,53ABBCACEBBDED,若 ABC△与EBD△的周长之差为10cm,则ABC△的周长是
cm.
11.已知G是ABC△的重心,设bACaAB,,用向量ba, 表示向量AG,则AG= . 12. 如图, 在Rt△ABC中,∠ACB=90°,CD⊥AB于D, 若AD=1,BD=4,则CD= . 13. 已知点P是⊙O外一点,PA切⊙O于点A,PO 与⊙O交
于点B,PA=52,PB=2,则⊙O的半径r= . 14. 如图,点AB,是⊙O上两点,10AB,点P是⊙O上 的动点(P与AB,不重合),连结APPB,,过点O分别作 OEAP于E,OFPB于F,则EF .
15. 已知:平行四边形ABCD中,点E是AB的中点,在直线 AD上截取2AFFD,EF交AC于G,则AGAC .
16. 如图,D,E分别是ABC△的边CA、BA的延长线上的点, 请你添加一个条件,使ADE△与ABC△相似.你添加的条件是
Q P O
N
x
y
M 第 6
题
A D B C 第12题 A B O
F P
E
第14题
ED
CBA第
16 题
_ E_ D _ C _ B
_ A第10题 OED
CBA
17.如图,已知AB是⊙O的直径,CD是弦且CD⊥AB,BC=6, AC=8.则sin∠ABD= .
18.如图,梯形ABCD中,ABCD∥,对角线ACBD、相交 于O,下面四个结论:①AOBCOD△∽△; ②AODBOC△∽△; ③::DOCBOASSDCAB△△; ④AODBOCSS△△. 其中结论始终正确的序号是 .
三、解答题(本大题共7题,满分78分,19题10分, 20题10分,21题10分,22题10分, 23题12分,24题12分,25题14分)
19.(10分)计算:45sin230cot45cos60sin2
20.(10分) 已知抛物线322mxxy,且当x > 3时,y随x的增大而增大,当x < 3时,y随x的增大而减小.请用配方法求抛物线的顶点坐标.
21.(10分) 如图,点O是ABC△的垂心(垂心即三角形三条高所在直线的交点),联结AO交CB的延长线于点D,联结CO交AB的延长线于点E,联结DE.求证:ODE~OCA.
OD
CBA第
17 题
A B C D
O 第18题 DCBA
22. (10分) 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴交于A、B两点,点A在x轴负半轴,点B在x轴正半轴,与y轴交于点C,且tan∠ACO=12,CO=BO,AB=3,求这条抛物线的函数解析式.
23. (12分)如图,梯形ABCD中,已知AD//BC,90A,AB=7,AD=2,102cosC. (1)求BC的长;(2)试在边AB上确定点P的位置,使PAD~PBC.
24.(12分)如图,为某小区的两幢10层住宅楼,由地面向上依次为第1层、第2层、…、第10层,每层的高度为3m,两楼间的距离30ACm.现需了解在某一时段内,甲楼对乙楼的采光的影响情况.假设某一时刻甲楼楼顶B落在乙楼的影子长ECh,太7阳光线与水平线的夹角为. (1)用含的式子表示h; (2)当30时,甲楼楼顶B的影子落在乙楼的第几层?从此时算起,若每小时增加10,约几小时后,甲楼的影子刚好不影响乙楼采光.(结果精
A
B C D
E
太阳光 甲楼 乙
楼 确到0.01) 25.(14分)如图1,已知:在直角坐标系中,点E从坐标原点O出发,以1个单位/秒的速度沿x轴正方向运动,点F从坐标原点O出发,以2个单位/秒的速度沿y轴正方向运动。 B(4,2),以BE为直径做⊙M. (1)若点E、F同时出发,设线段EF与线段OB交于点G,试判断点 G 与⊙M的位置关系,并证明你的结论; (2)在(1)的条件下,联结FB,几秒时FB与⊙M相切; (3)如图2,若点E提前2秒出发,点F再出发,当点F出发后,E点在A点左侧时,设BA⊥x轴于点A,联结AF交⊙M于点P,请问AP·AF的值是否会发生变化?若不变,请说明理由,并求其值;若变化,请求其值的变化范围.
2008学年第一学期初三数学期终抽测试卷参考答案 2009.1 一、选择题(4分6=24分) 说明:选对得4分,错选或多选得0分. 题号 1 2 3 4 5 6 答案 C C B D C D
二、填空题(3分12=36分) 说明:填对得4分,填错得0分. 题号 7 8 9 10 11 12 答案 下 215 a+c=0 25 ba3131 2
. 题号 13 14 15 16 17 18 答案 4 5 72或52 ∠ADE=∠ABC 或AD:AC=AE:AB等(答案不唯一) 54 ①④
三、解答题(本大题共7题,满分78分,19题10分, 20题10分,21题10分,22题10分, 23题12分,24题12分,25题14分) 19.(10分)解:原式=222322223 4分(写出一个三角比的值得1分)
=32123 2分 =343 2分 = 435 2分
20. (10分)解:(1)据题意得 抛物线的对称轴是直线x =3 ∴322m 3分 解得m =12. 2分 (2)3122y2xx 1分 =3)996(22xx =318)96(22xx O
E
D
CBA EDCB
A
= 15)3(22x 2分 ∴抛物线的顶点坐标是(3,-15). 2分
21. (10分)证明:∵O是垂心 ∴AO⊥CD ∴∠CDO=90° 同理 ∠AEO=90° ∴∠AEO=∠CDO 3分
在△AEO和△CDO中 OOCDOAEO ∴△AEO~△CDO 3分 ∴OCOAODOE ∴OCODOAOE 2分 在△ODE和△OCA中 OOCODOAOEO ∴△ODE~△OCA 2分
22. (10分) 解:据题意 设CO = BO = t (t > 0) 1分 在Rt△OCA中,tan∠ACO =COAO=21 ∴AO = 21CO = 21t ∵AB = 3 ∴ AO + BO = 21t + t =3 解得 t = 2 2分 ∴A(-1,0),B(2,0),C(0,-2) 3分
代入y=ax2+bx+c 得 -2c0c2b4a0cb-a 解得211cba 3分 ∴所求函数解析式为22yxx. 1分 23. (12分) 解:(1) 过D作BC的垂线,垂足为E.设EC = x (x >0). 1分 ∵梯形ABCD中 AD // BC 且 90A ∴ABED是矩形 ∴AB = DE = 7 AD = BE = 2
在Rt△CDE中 102249cosxxDCECC 2分 解得 x = 1 即 EC = 1 ∴ BC = BE + EC = 3 2分
