上海市浦东新区2017年初三数学二模考试试题及答案
精品解析：2017年上海市青浦区中考数学二模试题(解析版)
2017年上海市青浦区中考数学二模试卷一、单项选择题1. 下列运算中，正确的是（）A. 2a﹣a＝1B. a+a＝2aC. （a3）3＝a6D. a8÷a2＝a4【答案】B【解析】【分析】分别利用合并同类项法则以及结合幂的乘方运算法则以及同底数幂的除法运算法则化简求出答案．【详解】A、2a﹣a＝a，故此选项错误；B、a+a＝2a，故此选项正确；C、（a3）3＝a9，故此选项错误；D、a8÷a2＝a6，故此选项错误．故选B．【点睛】此题主要考查了合并同类项以及幂的乘方运算、同底数幂的除法运算等知识，正确掌握相关运算法则是解题关键．2. 不等式组23120xx+≥⎧⎨-<⎩的解集在数轴上可表示为（）A. B.C. D.【答案】B【解析】【分析】利用不等式的性质求出不等式组的解集，然后在数轴上表示出来即可.【详解】解不等式2x+3≥1，得：x≥﹣1，解不等式x﹣2＜0，得：x＜2，∴不等式组的解集为﹣1≤x＜2，故选B．【点睛】本题考查解一元一次不等式组，熟练掌握不等式的性质和一元一次不等式组求解集是解题关键.3. 二次根式()23-的值是（ ） A. ﹣3B. 3或﹣3C. 9D. 3【答案】D【解析】【分析】 本题考查二次根式的化简， 2(0)(0)a a a a a ⎧=⎨-<⎩． 【详解】2(3)|3|3-=-=．故选D ．【点睛】本题考查了根据二次根式的意义化简．二次根式2a 化简规律：当a ≥0时，2a ＝a ；当a ≤0时，2a ＝﹣a ．4. 在正方形网格中，△ABC 的位置如图所示，则cos ∠B 的值为（ ）A. 2B. 3C. 3D. 1【答案】A【解析】【分析】作AD ⊥BC ，可得AD=BD=5，利用勾股定理求得AB ，再由余弦函数的定义求解.【详解】作AD ⊥BC 于点D ，则AD=5，BD=5，∴AB=22BD AD +=2255+=52，∴cos ∠B=BD AB =52= 2. 故选A .【点睛】本题考查锐角三角函数的定义.5. 某集团公司有9个子公司，各个子公司所创年利润的情况如下表所示．各子公司所创年利润的众数和中位数分别是（ ）A. 4千万元，3千万元B. 6千万元，4千万元C. 6千万元，3千万元D. 3千万元，3千万元【答案】D【解析】【分析】 找中位数要把数据按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数；众数是一组数据中出现次数最多的数据，注意众数可以不只一个．【详解】这组数据按照从小到大的顺序排列为：6，4，4，3，3，3，3，2，2，3出现次数最多，则众数为：3千万元，中位数为：3千万元．故选D ．【点睛】本题考查了众数和中位数的概念：一组数据中出现次数最多的数据叫做众数；将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．6. 如图，在四边形ABCD 中，动点P 从点A 开始沿A B C D →→→的路径匀速前进到D 为止，在这个过程中，APD ∆的面积S 随时间t 的变化关系用图象表示正确的是（ ）A. B. C. D.【答案】C【解析】【分析】根据点P 的运动过程可知：APD ∆的底边为AD ，而且AD 始终不变，点P 到直线AD 的距离为APD ∆的高，根据高的变化即可判断S 与t 的函数图象．【详解】解：设点P 到直线AD 的距离为h ，APD ∴∆的面积为：1·2S AD h =， 当P 在线段AB 运动时，此时h 不断增大，S 也不端增大当P 线段BC 上运动时，此时h 不变，S 也不变，当P 在线段CD 上运动时，此时h 不断减小，S 不断减少，又因为匀速行驶且CD AB >，所以在线段CD 上运动的时间大于在线段AB 上运动的时间故选C ．【点睛】本题考查函数图象，解题的关键是根据点P 到直线AD 的距离来判断s 与t 的关系，本题属于基础题型．二、填空题7. 若x ∶y ＝2∶3，那么x ∶（x ＋y ）＝_____________．【答案】2∶5．【解析】【分析】试题分析：∵x∶y ＝2∶3，设，x=2k ，则y=3k ，∴x∶（x ＋y ）=2k:(2k+3k ）=2：5．故答案为2：5． 考点：比例的性质．【详解】请在此输入详解！8. 在实数范围内分解因式：x 2﹣3＝_____．【答案】((x x +-【解析】【分析】把3【详解】解：x 2﹣3＝x 22＝（x （x ．【点睛】本题考查平方差公式分解因式，把39. 已知函数1x f x x，那么1f _____． 【答案】2+【解析】【分析】根据题意可知1x =，代入原函数即可解答. 【详解】因为函数1x f x x， 所以当1x =时， 211()2221f x ．【点睛】本题主要考查了代数式求值问题，熟练掌握相关知识点以及二次根式的运算是解题关键. 10. 已知反比例函数1k y x-=的图象经过一、三象限，则实数k 的取值范围是_____． 【答案】k ＞1．【解析】【分析】 根据反比例函数1k y x-=的图象经过一、三象限得出关于k 的不等式，求出k 的取值范围即可． 【详解】∵反比例函数1k y x -=的图象经过一、三象限， ∴k ﹣1＞0，即k ＞1．故答案为k ＞1．【点睛】本题考查的是反比例函数的性质，熟知反比例函数的图象与系数的关系是解答此题的关键． 11. 已知关于x 的方程220x x a -+=有两个实数根，则实数a 的取值范围是_____．【答案】a≤1．【解析】试题分析：∵方程220x x a -+=有两个实数根，∴△=4﹣4a≥0，解得：a≤1，故答案为a≤1．考点：根的判别式．12. 1=的解为_____．【答案】x=2【解析】【分析】1=两边同时乘方，即可解答.【详解】方程两边平方得：x ﹣1＝1，解得：x ＝2，经检验x ＝2是原方程的解，故答案为x ＝2【点睛】本题考点为无理方程求解，熟练掌握相关知识点是解题关键.13. 抛物线y ＝﹣ax 2+2ax +3（a ≠0）的对称轴是_____．【答案】直线x ＝1．【解析】【分析】直接利用抛物线对称轴公式求出答案．【详解】抛物线y ＝﹣ax 2+2ax +3（a ≠0）的对称轴是：直线2a 12(a)x． 故答案为直线x ＝1．【点睛】此题主要考查了二次函数的性质，正确记忆对称轴公式是解题关键．14. 布袋中装有3个红球和n 个白球，它们除颜色外其它都相同，如果从布袋里随机摸出一个球，所摸到球恰好是红球的概率是13，那么布袋中白球有_____个． 【答案】6.【解析】【分析】根据概率的概念建立等量关系：1133n，解方程即可．【详解】∵布袋中有n个白球，∴11 33n，解得：n＝6，则布袋中白球有6个；故答案为6．【点睛】本题考查了概率的概念：所有等可能的结果有n个，其中某事件占m个，则这个事件的概率mPn =．15. 化简：1233a a b_____．【答案】3a b+【解析】【分析】先利用去括号法则将整式去括号，再合并同类项即可完成.【详解】1233a a b，23a a b，3a b．故答案为3a b+．【点睛】本题考查整式的加减运算，熟练掌握去括号法则以及合并同类项是解题关键.16. 如图，在菱形ABCD中，EF∥BC，AE1BE3，EF＝3，则CD的长为_____．【答案】12 【解析】【分析】根据题意可知△AEF∽△ABC，可得14AEAB，进而求得BC＝12，再根据菱形的性质，即可解答.【详解】∵EF∥BC，13AEBE，EF＝3，∴△AEF∽△ABC，14 AEAB，∴EF AE BC AB，∴314 BC，解得，BC＝12，∵四边形ABCD是菱形，∴CD＝BC＝12，故答案为12．【点睛】本题考点涉及三角形相似、菱形的性质等知识点，熟练掌握相关性质定理是解题关键.17. 在△ABC中，已知BC＝4cm，以边AC的中点P为圆心1cm为半径画⊙P，以边AB的中点Q为圆心x cm 长为半径画⊙Q，如果⊙P与⊙Q相切，那么x＝_____cm．【答案】1或3【解析】【分析】根据三角形的中位线的性质得到122PQ BC cm，①当⊙P与⊙Q相外切时，②当⊙P与⊙Q相内切时，列方程即可得出结论.【详解】∵BC＝4cm，点P是AC的中点，点Q是AB的中点，∴122PQ BC cm，①当⊙P与⊙Q相外切时，PQ＝1+x＝2，∴x＝1cm，②当⊙P与⊙Q相内切时，PQ＝|x﹣1|＝2，∴x＝3cm（负值舍去），∴如果⊙P与⊙Q相切，那么x＝1cm或3cm，故答案为1或3．【点睛】本题考查了三角形中位线定理以及相切两圆的性质，熟练掌握相关性质定理是解题关键.18. 如图，在Rt△ABC中，AB＝AC，D、E是斜边BC上两点，且∠DAE＝45°，将△ADC绕点A顺时针旋转90°后，得到△AFB．设BE＝a，DC＝b，那么AB＝_____．（用含a、b的式子表示AB）【答案】2222a b a b【解析】【分析】 只要证明△F AE ≌△DAE ，推出EF ＝ED ，∠ABF ＝∠C ＝45°，由∠EBF ＝∠ABF +∠ABE ＝90°，推出22ED EF a b ，可得22BC a b a b ，根据AB ＝BC •cos45°即可解决问题．【详解】证明：如图，∵△DAC ≌△F AB ，∴AD ＝AF ，∠DAC ＝∠F AB，∴∠F AD ＝90°，∵∠DAE ＝45°，∴∠DAC +∠BAE ＝∠F AB +∠BAE ＝∠F AE ＝45°，在△F AE 和△DAE 中，DA FA DAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩，∴△F AE ≌△DAE ，∴EF ＝ED ，∠ABF ＝∠C ＝45°，∵∠EBF ＝∠ABF +∠ABE ＝90°，∴22ED EF a b ，∴BC ＝a +b 22a b +∴222cos 45()2AB BC a b a b ．故答案为222a b a b ．【点睛】本题考查旋转变换、等腰直角三角形的性质、全等三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．三、解答题：19. 计算： 10120176cos30232． 【答案】1【解析】【分析】首先计算乘方和乘法，然后从左向右依次计算，求出算式的值是多少即可． 【详解】10120176cos30|23|2 312623233323143 【点睛】此题主要考查了实数的运算，要熟练掌握，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．另外，有理数的运算律在实数范围内仍然适用．20. 解方程： 24211422xx x x ． 【答案】x ＝1．【解析】分析】分式方程去分母转化为整式方程，求出整式方程的解得到x 的值，经检验即可得到分式方程的解．【详解】去分母得：4x ﹣2x ﹣4＝x 2﹣4﹣x +2，即x 2﹣3x +2＝0，解得：x ＝1或x ＝2，经检验x ＝2是增根，所以，分式方程的解为x ＝1．【点睛】此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验． 21. 已知直线132y x =-+与x 轴、y 轴分别交于A 、B 两点，设O 为坐标原点． （1）求∠ABO 的正切值；（2）如果点A 向左平移12个单位到点C ，直线l 过点C 且与直线132y x =-+平行，求直线l 的解析式． 【答案】（1）tan 2ABO ；（2）132y x =--． 【解析】 【分析】（1）根据已知条件得到A （6，0），B （0，3），求得OA ＝6，OB ＝3，根据三角函数的定义即可得到结论； （2）将点A 向左平移12个单位到点C ，于是得到C （﹣6，0），设直线l 的解析式为12y x b =-+，把C （﹣6，0）代入12y x b =-+即可得到结论． 【详解】（1）∵直线132y x =-+与x 轴、y 轴分别交于A 、B 两点，∴A （6，0），B （0，3）， ∴OA ＝6，OB ＝3， ∵∠AOB ＝90°， ∴6tan 23OAABOOB ；（2）将点A 向左平移12个单位到点C ， ∴C （﹣6，0），∵直线l 过点C 且与直线132y x =-+平行， 设直线l 的解析式为12y x b =-+， 把C （﹣6，0）代入12y x b =-+得1(6)2b ，∴b ＝﹣3，∴直线l 的解析式为132y x =--． 【点睛】本题考查了两直线平行或相交问题，坐标与图形变换﹣平移，解直角三角形，正确的理解题意是解题的关键．22. 小明在海湾森林公园放风筝．如图所示，小明在A 处，风筝飞到C 处，此时线长BC 为40米，若小明双手牵住绳子的底端B 距离地面1.5米，从B 处测得C 处的仰角为60°，求此时风筝离地面的高度CE.(计算结果精确到0.1米，3≈1.732)【答案】此时风筝离地面的高度CE是36.1米．【解析】【分析】过点B作BD⊥CE于点D，由锐角三角函数的定义求出CD的长，根据CE=CD+DE即可得出结论．【详解】过点B作BD⊥CE于点D，∵AB⊥AE，DE⊥AE，BD⊥CE，∴四边形ABDE是矩形，∴DE=AB=1.5米．∵BC=40米，∠CBD=60°，∴CD=BC·sin 60°=40×3=203，∴CE=CD＋DE=203＋1.5≈20×1.73＋1.5≈36.1(米)．答：此时风筝离地面的高度CE是36.1米．【点睛】本题考查的是解直角三角形的应用-仰角俯角问题，根据题意作出辅助线，构造出直角三角形是解答此题的关键．23. 如图，在△ABC中，点P是AC边上的一点，过点P作与BC平行的直线PQ，交AB于点Q，点D在线段BC上，连接AD交线段PQ于点E，且CP QECD BD，点G在BC延长线上，∠ACG的平分线交直线PQ于点F．（1）求证：PC ＝PE ；（2）当P 是边AC 的中点时，求证：四边形AECF 是矩形． 【答案】(1)见解析；(2)见解析 【解析】 【分析】（1）根据相似三角形的性质得出,QEAE PE AE BD AD CD AD ，等量代换得到PEQE CD BD ，推出CPPECD CD，于是得出结论；（2）根据平行线的性质得到∠PFC ＝∠FCG ，根据角平分线的性质得到∠PCF ＝∠FCG ，等量代换得到∠PFC ＝∠FCG ，根据等腰三角形的性质得到PF=PC ，得到PF=PE ，由已知条件得到AP=CP ，推出四边形AECF 是平行四边形，再证得∠ECF ＝90°，于是得出结论. 【详解】（1）证明：∵PQ ∥BC ， ∴△AQE ∽△ABD ，△AEP ∽△ADC ，∴,QE AE PE AEBD AD CD AD， ∴PE QECD BD ， ∵CP QECD BD ， ∴CP PECDCD， ∴PC ＝PE ； （2）∵PF ∥DG ， ∴∠PFC ＝∠FCG ， ∵CF 平分∠PCG ， ∴∠PCF ＝∠FCG ， ∴∠PFC ＝∠FCG ， ∴PF ＝PC ， ∴PF ＝PE ，∵P 是边AC 的中点，∴AP ＝CP ，∴四边形AECF 是平行四边形， ∵PQ ∥CD ， ∴∠PEC ＝∠DCE ， ∴∠PCE ＝∠DCE ， ∴1()902PCEPCFPCD PCG ，∴∠ECF ＝90°，∴平行四边形AECF 是矩形．【点睛】本题考查相似三角形的判定及性质以及矩形的判定，还涉及了平行线的性质、角平分线的性质、等腰三角形的性质、平行四边形的判定等知识点，属于综合题，难度适中，熟练掌握相关性质定理是解题关键.24. 已知△OAB 在直角坐标系中的位置如图，点A 在第一象限，点B 在x 轴正半轴上，OA ＝OB ＝6，∠AOB ＝30°．（1）求点A 、B 的坐标；（2）开口向上的抛物线经过原点O 和点B ，设其顶点为E ，当△OBE 为等腰直角三角形时，求抛物线的解析式；（3）设半径为2的⊙P 与直线OA 交于M 、N 两点，已知23MN =P （m ，2）（m ＞0），求m 的值． 【答案】（1）A 点坐标为(33,3)，B 点坐标为（6，0）；（2）2123y x x ；（3）m 的值为232或232- 【解析】 【分析】（1）根据30°角所对的直角边是斜边的一半，可得AC 的长，再根据锐角三角函数，可得OC ，根据点的坐标，可得答案；（2）根据等腰直角三角形，可得E 点坐标，再根据待定系数法，可得答案；（3）根据30°角所对的直角边是斜边的一半，可得∠CNP=30°，再根据勾股定理求得OE 的长，根据点的坐标，可得N 点坐标，根据点的左右平移，可得点P 坐标.【详解】（1）如图1，作 AC ⊥OB 于C 点，由OB ＝OA ＝6，得B 点坐标为（6，0）， 由OB ＝OA ＝6，∠AOB ＝30°，得133,cos 3322ACOA OC OA AOCOA ，∴A 点坐标为(33,3)；（2）如图2，由其顶点为E ，当△OBE 为等腰直角三角形，得132OC BC CEOB ，即E 点坐标为（3，﹣3）．设抛物线的解析式为y ＝a （x ﹣3）2﹣3，将B 点坐标代入，解得13a =， 抛物线的解析式为21(3)33y x化简得2123yx x ；（3）如图3，PN ＝2， 3CN =PC ＝1，∠CNP ＝∠AOB ＝30°， NP ∥OB ，NE ＝2，得ON ＝4， 由勾股定理，得2223OEON NE ，即23,2N ．N 向右平移2个单位得232,2P ， N 向左平移2个单位，得232,2P ，m 的值为232+或232-．【点睛】本题为二次函数综合题，难度较大，考点涉及含30°角的直角三角形、锐角三角形函数、等腰直角三角形的性质、待定系数法求函数解析式以及勾股定理等知识点，熟练掌握各个知识点是解题关键. 25. 如图，△ABC 的边AB 是⊙O 的直径，点C 在⊙O 上，已知AC ＝6cm ，BC ＝8cm ，点P 、Q 分别在边AB 、BC 上，且点P 不与点A 、B 重合，BQ ＝k •AP （k ＞0），联接PC 、PQ ．（1）求⊙O 的半径长；（2）当k ＝2时，设AP ＝x ，△CPQ 的面积为y ，求y 关于x 的函数关系式，并写出定义域； （3）如果△CPQ 与△ABC 相似，且∠ACB ＝∠CPQ ，求k 的值． 【答案】（1）5；（2）y=234224(04)55x x x ;（3）720k【解析】 【分析】（1）首先证明∠ACB ＝90°，然后利用勾股定理即可解决问题； （2）如图2中，作PH ⊥BC 于H ．由PH ∥AC ，，推出PH PB AC AB ，推出10610PHx，得出3(10)5PH x ，根据12yCQ PH 计算即可； （3）因为△CPQ 与△ABC 相似，∠CPQ ＝∠ACB ＝90°，又因为∠CQP ＞∠B ， 所以只有∠PCB ＝∠B ，推出PC ＝PB ，由∠B +∠A ＝90°，∠ACP +∠PCB ＝90°，推出∠A ＝∠ACP ，得出P A ＝PC ＝PB ＝5，由△COQ ∽△BCA ，推出CO CQBC AB， 推出585810k，即可解决问题. 【详解】（1）∵AB 是直径， ∴∠ACB ＝90°，∵AC ＝6，BC ＝8， ∴22226810ABAC BC ，∴⊙O 的半径为5．（2）如图2中，作PH ⊥BC 于H ．∵PH ∥AC ，∴PH PBAC AB ， ∴10610PH x， ∴3(10)5PH x ， ∴2113342(82)(10)24(04)22555y CQ PH x x x x x ．（3）如图2中，∵△CPQ 与△ABC 相似，∠CPQ ＝∠ACB ＝90°， 又∵∠CQP ＞∠B ， ∴只有∠PCB ＝∠B ， ∴PC ＝PB ，∵∠B +∠A ＝90°，∠ACP +∠PCB ＝90°，∴∠A＝∠ACP，∴P A＝PC＝PB＝5，∴△COQ∽△BCA，∴CO CQ BC AB，∴585 810k，∴720 k．【点睛】本题为圆的综合题，难度较大，考点涉及圆的性质、相似三角形的性质与判定等知识点，熟练掌握各个性质定理是解题关键.。
精品解析：2017年上海市青浦区中考数学二模试题(解析版)
2017年上海市青浦区中考数学二模试卷一、单项选择题1. 下列运算中，正确的是（）A. 2a﹣a＝1B. a+a＝2aC. （a3）3＝a6D. a8÷a2＝a4【答案】B【解析】【分析】分别利用合并同类项法则以及结合幂的乘方运算法则以及同底数幂的除法运算法则化简求出答案．【详解】A、2a﹣a＝a，故此选项错误；B、a+a＝2a，故此选项正确；C、（a3）3＝a9，故此选项错误；D、a8÷a2＝a6，故此选项错误．故选B．【点睛】此题主要考查了合并同类项以及幂的乘方运算、同底数幂的除法运算等知识，正确掌握相关运算法则是解题关键．2. 不等式组23120xx+≥⎧⎨-<⎩的解集在数轴上可表示为（）A. B.C. D.【答案】B【解析】【分析】利用不等式的性质求出不等式组的解集，然后在数轴上表示出来即可.【详解】解不等式2x+3≥1，得：x≥﹣1，解不等式x﹣2＜0，得：x＜2，∴不等式组的解集为﹣1≤x＜2，故选B．【点睛】本题考查解一元一次不等式组，熟练掌握不等式的性质和一元一次不等式组求解集是解题关键.3. 二次根式()23-的值是（ ） A. ﹣3B. 3或﹣3C. 9D. 3【答案】D【解析】【分析】 本题考查二次根式的化简， 2(0)(0)a a a a a ⎧=⎨-<⎩． 【详解】2(3)|3|3-=-=．故选D ．【点睛】本题考查了根据二次根式的意义化简．二次根式2a 化简规律：当a ≥0时，2a ＝a ；当a ≤0时，2a ＝﹣a ．4. 在正方形网格中，△ABC 的位置如图所示，则cos ∠B 的值为（ ）A. 2B. 3C. 3D. 1【答案】A【解析】【分析】作AD ⊥BC ，可得AD=BD=5，利用勾股定理求得AB ，再由余弦函数的定义求解.【详解】作AD ⊥BC 于点D ，则AD=5，BD=5，∴AB=22BD AD +=2255+=52，∴cos ∠B=BD AB =52= 2. 故选A .【点睛】本题考查锐角三角函数的定义.5. 某集团公司有9个子公司，各个子公司所创年利润的情况如下表所示．各子公司所创年利润的众数和中位数分别是（ ）A. 4千万元，3千万元B. 6千万元，4千万元C. 6千万元，3千万元D. 3千万元，3千万元【答案】D【解析】【分析】 找中位数要把数据按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数；众数是一组数据中出现次数最多的数据，注意众数可以不只一个．【详解】这组数据按照从小到大的顺序排列为：6，4，4，3，3，3，3，2，2，3出现次数最多，则众数为：3千万元，中位数为：3千万元．故选D ．【点睛】本题考查了众数和中位数的概念：一组数据中出现次数最多的数据叫做众数；将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．6. 如图，在四边形ABCD 中，动点P 从点A 开始沿A B C D →→→的路径匀速前进到D 为止，在这个过程中，APD ∆的面积S 随时间t 的变化关系用图象表示正确的是（ ）A. B. C. D.【答案】C【解析】【分析】根据点P 的运动过程可知：APD ∆的底边为AD ，而且AD 始终不变，点P 到直线AD 的距离为APD ∆的高，根据高的变化即可判断S 与t 的函数图象．【详解】解：设点P 到直线AD 的距离为h ，APD ∴∆的面积为：1·2S AD h =， 当P 在线段AB 运动时，此时h 不断增大，S 也不端增大当P 线段BC 上运动时，此时h 不变，S 也不变，当P 在线段CD 上运动时，此时h 不断减小，S 不断减少，又因为匀速行驶且CD AB >，所以在线段CD 上运动的时间大于在线段AB 上运动的时间故选C ．【点睛】本题考查函数图象，解题的关键是根据点P 到直线AD 的距离来判断s 与t 的关系，本题属于基础题型．二、填空题7. 若x ∶y ＝2∶3，那么x ∶（x ＋y ）＝_____________．【答案】2∶5．【解析】【分析】试题分析：∵x∶y ＝2∶3，设，x=2k ，则y=3k ，∴x∶（x ＋y ）=2k:(2k+3k ）=2：5．故答案为2：5． 考点：比例的性质．【详解】请在此输入详解！8. 在实数范围内分解因式：x 2﹣3＝_____．【答案】((x x +-【解析】【分析】把3【详解】解：x 2﹣3＝x 22＝（x （x ．【点睛】本题考查平方差公式分解因式，把39. 已知函数1x f x x，那么1f _____． 【答案】2+【解析】【分析】根据题意可知1x =，代入原函数即可解答. 【详解】因为函数1x f x x， 所以当1x =时， 211()2221f x ．【点睛】本题主要考查了代数式求值问题，熟练掌握相关知识点以及二次根式的运算是解题关键. 10. 已知反比例函数1k y x-=的图象经过一、三象限，则实数k 的取值范围是_____． 【答案】k ＞1．【解析】【分析】 根据反比例函数1k y x-=的图象经过一、三象限得出关于k 的不等式，求出k 的取值范围即可． 【详解】∵反比例函数1k y x -=的图象经过一、三象限， ∴k ﹣1＞0，即k ＞1．故答案为k ＞1．【点睛】本题考查的是反比例函数的性质，熟知反比例函数的图象与系数的关系是解答此题的关键． 11. 已知关于x 的方程220x x a -+=有两个实数根，则实数a 的取值范围是_____．【答案】a≤1．【解析】试题分析：∵方程220x x a -+=有两个实数根，∴△=4﹣4a≥0，解得：a≤1，故答案为a≤1．考点：根的判别式．12. 1=的解为_____．【答案】x=2【解析】【分析】1=两边同时乘方，即可解答.【详解】方程两边平方得：x ﹣1＝1，解得：x ＝2，经检验x ＝2是原方程的解，故答案为x ＝2【点睛】本题考点为无理方程求解，熟练掌握相关知识点是解题关键.13. 抛物线y ＝﹣ax 2+2ax +3（a ≠0）的对称轴是_____．【答案】直线x ＝1．【解析】【分析】直接利用抛物线对称轴公式求出答案．【详解】抛物线y ＝﹣ax 2+2ax +3（a ≠0）的对称轴是：直线2a 12(a)x． 故答案为直线x ＝1．【点睛】此题主要考查了二次函数的性质，正确记忆对称轴公式是解题关键．14. 布袋中装有3个红球和n 个白球，它们除颜色外其它都相同，如果从布袋里随机摸出一个球，所摸到球恰好是红球的概率是13，那么布袋中白球有_____个． 【答案】6.【解析】【分析】根据概率的概念建立等量关系：1133n，解方程即可．【详解】∵布袋中有n个白球，∴11 33n，解得：n＝6，则布袋中白球有6个；故答案为6．【点睛】本题考查了概率的概念：所有等可能的结果有n个，其中某事件占m个，则这个事件的概率mPn =．15. 化简：1233a a b_____．【答案】3a b+【解析】【分析】先利用去括号法则将整式去括号，再合并同类项即可完成.【详解】1233a a b，23a a b，3a b．故答案为3a b+．【点睛】本题考查整式的加减运算，熟练掌握去括号法则以及合并同类项是解题关键.16. 如图，在菱形ABCD中，EF∥BC，AE1BE3，EF＝3，则CD的长为_____．【答案】12 【解析】【分析】根据题意可知△AEF∽△ABC，可得14AEAB，进而求得BC＝12，再根据菱形的性质，即可解答.【详解】∵EF∥BC，13AEBE，EF＝3，∴△AEF∽△ABC，14 AEAB，∴EF AE BC AB，∴314 BC，解得，BC＝12，∵四边形ABCD是菱形，∴CD＝BC＝12，故答案为12．【点睛】本题考点涉及三角形相似、菱形的性质等知识点，熟练掌握相关性质定理是解题关键.17. 在△ABC中，已知BC＝4cm，以边AC的中点P为圆心1cm为半径画⊙P，以边AB的中点Q为圆心x cm 长为半径画⊙Q，如果⊙P与⊙Q相切，那么x＝_____cm．【答案】1或3【解析】【分析】根据三角形的中位线的性质得到122PQ BC cm，①当⊙P与⊙Q相外切时，②当⊙P与⊙Q相内切时，列方程即可得出结论.【详解】∵BC＝4cm，点P是AC的中点，点Q是AB的中点，∴122PQ BC cm，①当⊙P与⊙Q相外切时，PQ＝1+x＝2，∴x＝1cm，②当⊙P与⊙Q相内切时，PQ＝|x﹣1|＝2，∴x＝3cm（负值舍去），∴如果⊙P与⊙Q相切，那么x＝1cm或3cm，故答案为1或3．【点睛】本题考查了三角形中位线定理以及相切两圆的性质，熟练掌握相关性质定理是解题关键.18. 如图，在Rt△ABC中，AB＝AC，D、E是斜边BC上两点，且∠DAE＝45°，将△ADC绕点A顺时针旋转90°后，得到△AFB．设BE＝a，DC＝b，那么AB＝_____．（用含a、b的式子表示AB）【答案】2222a b a b【解析】【分析】 只要证明△F AE ≌△DAE ，推出EF ＝ED ，∠ABF ＝∠C ＝45°，由∠EBF ＝∠ABF +∠ABE ＝90°，推出22ED EF a b ，可得22BC a b a b ，根据AB ＝BC •cos45°即可解决问题．【详解】证明：如图，∵△DAC ≌△F AB ，∴AD ＝AF ，∠DAC ＝∠F AB，∴∠F AD ＝90°，∵∠DAE ＝45°，∴∠DAC +∠BAE ＝∠F AB +∠BAE ＝∠F AE ＝45°，在△F AE 和△DAE 中，DA FA DAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩，∴△F AE ≌△DAE ，∴EF ＝ED ，∠ABF ＝∠C ＝45°，∵∠EBF ＝∠ABF +∠ABE ＝90°，∴22ED EF a b ，∴BC ＝a +b 22a b +∴222cos 45()2AB BC a b a b ．故答案为222a b a b ．【点睛】本题考查旋转变换、等腰直角三角形的性质、全等三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．三、解答题：19. 计算： 10120176cos30232． 【答案】1【解析】【分析】首先计算乘方和乘法，然后从左向右依次计算，求出算式的值是多少即可． 【详解】10120176cos30|23|2 312623233323143 【点睛】此题主要考查了实数的运算，要熟练掌握，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．另外，有理数的运算律在实数范围内仍然适用．20. 解方程： 24211422xx x x ． 【答案】x ＝1．【解析】分析】分式方程去分母转化为整式方程，求出整式方程的解得到x 的值，经检验即可得到分式方程的解．【详解】去分母得：4x ﹣2x ﹣4＝x 2﹣4﹣x +2，即x 2﹣3x +2＝0，解得：x ＝1或x ＝2，经检验x ＝2是增根，所以，分式方程的解为x ＝1．【点睛】此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验． 21. 已知直线132y x =-+与x 轴、y 轴分别交于A 、B 两点，设O 为坐标原点． （1）求∠ABO 的正切值；（2）如果点A 向左平移12个单位到点C ，直线l 过点C 且与直线132y x =-+平行，求直线l 的解析式． 【答案】（1）tan 2ABO ；（2）132y x =--． 【解析】 【分析】（1）根据已知条件得到A （6，0），B （0，3），求得OA ＝6，OB ＝3，根据三角函数的定义即可得到结论； （2）将点A 向左平移12个单位到点C ，于是得到C （﹣6，0），设直线l 的解析式为12y x b =-+，把C （﹣6，0）代入12y x b =-+即可得到结论． 【详解】（1）∵直线132y x =-+与x 轴、y 轴分别交于A 、B 两点，∴A （6，0），B （0，3）， ∴OA ＝6，OB ＝3， ∵∠AOB ＝90°， ∴6tan 23OAABOOB ；（2）将点A 向左平移12个单位到点C ， ∴C （﹣6，0），∵直线l 过点C 且与直线132y x =-+平行， 设直线l 的解析式为12y x b =-+， 把C （﹣6，0）代入12y x b =-+得1(6)2b ，∴b ＝﹣3，∴直线l 的解析式为132y x =--． 【点睛】本题考查了两直线平行或相交问题，坐标与图形变换﹣平移，解直角三角形，正确的理解题意是解题的关键．22. 小明在海湾森林公园放风筝．如图所示，小明在A 处，风筝飞到C 处，此时线长BC 为40米，若小明双手牵住绳子的底端B 距离地面1.5米，从B 处测得C 处的仰角为60°，求此时风筝离地面的高度CE.(计算结果精确到0.1米，3≈1.732)【答案】此时风筝离地面的高度CE是36.1米．【解析】【分析】过点B作BD⊥CE于点D，由锐角三角函数的定义求出CD的长，根据CE=CD+DE即可得出结论．【详解】过点B作BD⊥CE于点D，∵AB⊥AE，DE⊥AE，BD⊥CE，∴四边形ABDE是矩形，∴DE=AB=1.5米．∵BC=40米，∠CBD=60°，∴CD=BC·sin 60°=40×3=203，∴CE=CD＋DE=203＋1.5≈20×1.73＋1.5≈36.1(米)．答：此时风筝离地面的高度CE是36.1米．【点睛】本题考查的是解直角三角形的应用-仰角俯角问题，根据题意作出辅助线，构造出直角三角形是解答此题的关键．23. 如图，在△ABC中，点P是AC边上的一点，过点P作与BC平行的直线PQ，交AB于点Q，点D在线段BC上，连接AD交线段PQ于点E，且CP QECD BD，点G在BC延长线上，∠ACG的平分线交直线PQ于点F．（1）求证：PC ＝PE ；（2）当P 是边AC 的中点时，求证：四边形AECF 是矩形． 【答案】(1)见解析；(2)见解析 【解析】 【分析】（1）根据相似三角形的性质得出,QEAE PE AE BD AD CD AD ，等量代换得到PEQE CD BD ，推出CPPECD CD，于是得出结论；（2）根据平行线的性质得到∠PFC ＝∠FCG ，根据角平分线的性质得到∠PCF ＝∠FCG ，等量代换得到∠PFC ＝∠FCG ，根据等腰三角形的性质得到PF=PC ，得到PF=PE ，由已知条件得到AP=CP ，推出四边形AECF 是平行四边形，再证得∠ECF ＝90°，于是得出结论. 【详解】（1）证明：∵PQ ∥BC ， ∴△AQE ∽△ABD ，△AEP ∽△ADC ，∴,QE AE PE AEBD AD CD AD， ∴PE QECD BD ， ∵CP QECD BD ， ∴CP PECDCD， ∴PC ＝PE ； （2）∵PF ∥DG ， ∴∠PFC ＝∠FCG ， ∵CF 平分∠PCG ， ∴∠PCF ＝∠FCG ， ∴∠PFC ＝∠FCG ， ∴PF ＝PC ， ∴PF ＝PE ，∵P 是边AC 的中点，∴AP ＝CP ，∴四边形AECF 是平行四边形， ∵PQ ∥CD ， ∴∠PEC ＝∠DCE ， ∴∠PCE ＝∠DCE ， ∴1()902PCEPCFPCD PCG ，∴∠ECF ＝90°，∴平行四边形AECF 是矩形．【点睛】本题考查相似三角形的判定及性质以及矩形的判定，还涉及了平行线的性质、角平分线的性质、等腰三角形的性质、平行四边形的判定等知识点，属于综合题，难度适中，熟练掌握相关性质定理是解题关键.24. 已知△OAB 在直角坐标系中的位置如图，点A 在第一象限，点B 在x 轴正半轴上，OA ＝OB ＝6，∠AOB ＝30°．（1）求点A 、B 的坐标；（2）开口向上的抛物线经过原点O 和点B ，设其顶点为E ，当△OBE 为等腰直角三角形时，求抛物线的解析式；（3）设半径为2的⊙P 与直线OA 交于M 、N 两点，已知23MN =P （m ，2）（m ＞0），求m 的值． 【答案】（1）A 点坐标为(33,3)，B 点坐标为（6，0）；（2）2123y x x ；（3）m 的值为232或232- 【解析】 【分析】（1）根据30°角所对的直角边是斜边的一半，可得AC 的长，再根据锐角三角函数，可得OC ，根据点的坐标，可得答案；（2）根据等腰直角三角形，可得E 点坐标，再根据待定系数法，可得答案；（3）根据30°角所对的直角边是斜边的一半，可得∠CNP=30°，再根据勾股定理求得OE 的长，根据点的坐标，可得N 点坐标，根据点的左右平移，可得点P 坐标.【详解】（1）如图1，作 AC ⊥OB 于C 点，由OB ＝OA ＝6，得B 点坐标为（6，0）， 由OB ＝OA ＝6，∠AOB ＝30°，得133,cos 3322ACOA OC OA AOCOA ，∴A 点坐标为(33,3)；（2）如图2，由其顶点为E ，当△OBE 为等腰直角三角形，得132OC BC CEOB ，即E 点坐标为（3，﹣3）．设抛物线的解析式为y ＝a （x ﹣3）2﹣3，将B 点坐标代入，解得13a =， 抛物线的解析式为21(3)33y x化简得2123yx x ；（3）如图3，PN ＝2， 3CN =PC ＝1，∠CNP ＝∠AOB ＝30°， NP ∥OB ，NE ＝2，得ON ＝4， 由勾股定理，得2223OEON NE ，即23,2N ．N 向右平移2个单位得232,2P ， N 向左平移2个单位，得232,2P ，m 的值为232+或232-．【点睛】本题为二次函数综合题，难度较大，考点涉及含30°角的直角三角形、锐角三角形函数、等腰直角三角形的性质、待定系数法求函数解析式以及勾股定理等知识点，熟练掌握各个知识点是解题关键. 25. 如图，△ABC 的边AB 是⊙O 的直径，点C 在⊙O 上，已知AC ＝6cm ，BC ＝8cm ，点P 、Q 分别在边AB 、BC 上，且点P 不与点A 、B 重合，BQ ＝k •AP （k ＞0），联接PC 、PQ ．（1）求⊙O 的半径长；（2）当k ＝2时，设AP ＝x ，△CPQ 的面积为y ，求y 关于x 的函数关系式，并写出定义域； （3）如果△CPQ 与△ABC 相似，且∠ACB ＝∠CPQ ，求k 的值． 【答案】（1）5；（2）y=234224(04)55x x x ;（3）720k【解析】 【分析】（1）首先证明∠ACB ＝90°，然后利用勾股定理即可解决问题； （2）如图2中，作PH ⊥BC 于H ．由PH ∥AC ，，推出PH PB AC AB ，推出10610PHx，得出3(10)5PH x ，根据12yCQ PH 计算即可； （3）因为△CPQ 与△ABC 相似，∠CPQ ＝∠ACB ＝90°，又因为∠CQP ＞∠B ， 所以只有∠PCB ＝∠B ，推出PC ＝PB ，由∠B +∠A ＝90°，∠ACP +∠PCB ＝90°，推出∠A ＝∠ACP ，得出P A ＝PC ＝PB ＝5，由△COQ ∽△BCA ，推出CO CQBC AB， 推出585810k，即可解决问题. 【详解】（1）∵AB 是直径， ∴∠ACB ＝90°，∵AC ＝6，BC ＝8， ∴22226810ABAC BC ，∴⊙O 的半径为5．（2）如图2中，作PH ⊥BC 于H ．∵PH ∥AC ，∴PH PBAC AB ， ∴10610PH x， ∴3(10)5PH x ， ∴2113342(82)(10)24(04)22555y CQ PH x x x x x ．（3）如图2中，∵△CPQ 与△ABC 相似，∠CPQ ＝∠ACB ＝90°， 又∵∠CQP ＞∠B ， ∴只有∠PCB ＝∠B ， ∴PC ＝PB ，∵∠B +∠A ＝90°，∠ACP +∠PCB ＝90°，∴∠A＝∠ACP，∴P A＝PC＝PB＝5，∴△COQ∽△BCA，∴CO CQ BC AB，∴585 810k，∴720 k．【点睛】本题为圆的综合题，难度较大，考点涉及圆的性质、相似三角形的性质与判定等知识点，熟练掌握各个性质定理是解题关键.。
上海市浦东新区2017年中考二模数学试题(含答案)
浦东新区2017年中考二模数学试卷 （2017.4.21）考生注意：1．本试卷含三个大题，共25题；2．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效；3．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．一、选择题：（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】 1．下列等式成立的是（A ）2222-=-； （B ）236222=÷； （C ）5232)2(=； （D ）120=．2．下列各整式中，次数为5次的单项式是 （A ）xy 4；（B ）xy 5；（C ）x+y 4；（D ）x+y 5． 3．如果最简二次根式2+x 与x 3是同类二次根式，那么x 的值是 （A ）－1；（B ）0；（C ）1；（D ）2．4．如果正多边形的一个内角等于135度，那么这个正多边形的边数是 （A ）5；（B ）6；（C ）7；（D ）8．5．下列说法中，正确的个数有①一组数据的平均数一定是该组数据中的某个数据； ②一组数据的中位数一定是该组数据中的某个数据； ③一组数据的众数一定是该组数据中的某个数据． （A ）0个；（B ）1个；（C ）2个；（D ）3个．6．已知四边形ABCD 是平行四边形，对角线AC 与BD 相交于点O ，那么下列结论中正确 的是（A ）当AB =BC 时，四边形ABCD 是矩形； （B ）当AC ⊥BD 时，四边形ABCD 是矩形； （C ）当OA =OB 时，四边形ABCD 是矩形； （D ）当∠ABD =∠CBD 时，四边形ABCD 是矩形．二、填空题：（本大题共12题，每题4分，满分48分） 【请将结果直接填入答题纸的相应位置上】 7．计算：23-= ▲ ． 8．分解因式：x x 43-= ▲ ． 9．方程43+=x x 的解是 ▲ ．10．已知分式方程312122=+++x xx x ，如果设x x y 12+=，那么原方程可化为关于y 的整式方程是 ▲ ．11．如果反比例函数的图像经过点（3,－4），那么这个反比例函数的比例系数是 ▲ ． 12．如果随意把各面分别写有数字“1”、“2”、“3”、“4”、“5”、“6”的骰子抛到桌面上，那 么正面朝上的数字是合数的概率是 ▲ ．13．为了解某山区金丝猴的数量，科研人员在该山区不同的地方捕获了15只金丝猴，并在它们的身上做上标记后放回该山区．过段时间后，在该山区不同的地方又捕获了32只 金丝猴，其中4只身上有上次做的标记，由此可以估计该山区金丝猴的数量约有 ▲ 只． 14．已知点G 是△ABC 的重心，=，=，那么向量用向量、表示为 ▲ ． 15．如图，已知AD ∥EF ∥BC ，AE=3BE ，AD =2，EF =5，那么BC = ▲ ．16．如图，已知小岛B 在基地A 的南偏东30°方向上，与基地A 相距10海里，货轮C 在基地A 的南偏西60°方向、小岛B 的北偏西75°方向上，那么货轮C 与小岛B 的距离 是 ▲ 海里．17．对于函数()2b ax y +=，我们称[a ,b ]为这个函数的特征数．如果一个函数()2b ax y +=的特征数为[2,－5]，那么这个函数图像与x 轴的交点坐标为 ▲ ．18．如图，已知在Rt △ABC 中，D 是斜边AB 的中点，AC =4，BC=2，将△ACD 沿直线CD折叠，点A 落在点E 处，联结AE ，那么线段AE 的长度等于 ▲ ．三、解答题：（本大题共7题，满分78分） 19．（本题满分10分）化简并求值：12)111(22+-÷-+x x x x ，其中12+=x ．20．（本题满分10分）解不等式组：⎪⎩⎪⎨⎧->--≥+,1262,6325x x x x 并写出它的非负整数解．已知：如图，在△ABC 中，D 是边BC 上一点，以点D 为圆心、CD 为半径作半圆，分别与边AC 、BC 相交于点E 和点F ．如果AB =AC =5，cos B =54，AE =1．求：（1）线段CD 的长度； （2）点A 和点F 之间的距离．22．（本题满分10分）小张利用休息日进行登山锻炼，从山脚到山顶的路程为12千米．他上午8时从山脚出发，到达山顶后停留了半小时，再原路返回，下午3时30分回到山脚．假设他上山与下山时都是匀速行走，且下山比上山时的速度每小时快1千米，求小张上山时的速度．C（第21题图）如图，已知在平行四边形ABCD中，AE⊥BC，垂足为点E，AF⊥CD，垂足为点F．（1）如果AB=AD，求证：EF∥BD；（2）如果EF∥BD，求证：AB=AD．AB CD F（第23题图）已知：如图，直线y =kx +2与x 轴的正半轴相交于点A （t ,0）、与y 轴相交于点B ，抛物线c bx x y ++-=2经过点A 和点B ，点C 在第三象限内，且AC ⊥AB ，tan ∠ACB =21．（1）当t =1时，求抛物线的表达式； （2）试用含t 的代数式表示点C 的坐标；（3）如果点C 在这条抛物线的对称轴上，求t 的值．（第24题图）如图，已知在△ABC 中，射线AM ∥BC ，P 是边BC 上一动点，∠APD =∠B ，PD 交射线AM 于点D ，联结CD ．AB =4，BC =6，∠B =60°． （1）求证：BP AD AP ⋅=2；（2）如果以AD 为半径的圆A 与以BP 为半径的圆B 相切，求线段BP 的长度； （3）将△ACD 绕点A 旋转，如果点D 恰好与点B 重合，点C 落在点E 的位置上，求此时∠BEP 的余切值．。
上海市浦东新区2017年中考数学二模试卷(含解析)
2017年上海市浦东新区中考数学二模试卷一、选择题：（本大题共6题.每题4分.满分24分）【下列各题的四个选项中.有且只有一个选项是正确的.选择正确项的代号并填涂在答题纸的相应位置上】1．下列实数中.是无理数的为（）A．3.14 B．C．D．2．下列二次根式中.与是同类二次根式的是（）A． B．C． D．3．函数y=kx﹣1（常数k＞0）的图象不经过的象限是（）A．第一象限 B．第二象限 C．第三象限 D．第四象限4．某幢楼10户家庭每月的用电量如下表所示：用电量（度）140 160 180 200户数 1 3 4 2那么这10户家庭该月用电量的众数和中位数分别是（）A．180.180 B．180.160 C．160.180 D．160.1605．已知两圆的半径分别为1和5.圆心距为4.那么两圆的位置关系是（）A．外离 B．外切 C．相交 D．内切6．如图.已知△ABC和△DEF.点E在BC边上.点A在DE边上.边EF和边AC相交于点G．如果AE=EC.∠AEG=∠B.那么添加下列一个条件后.仍无法判定△DEF与△ABC一定相似的是（）A． = B． = C． = D． =二、填空题：（本大题共12题.每题4分.满分48分）【请将结果直接填入答题纸的相应位置上】7．计算：a•a2= ．8．因式分解：x 2﹣2x= ．9．方程=﹣x 的根是 ．10．函数f （x ）=的定义域是 ． 11．如果方程x 2﹣2x+m=0有两个实数根.那么m 的取值范围是 ．12．计算：2+（+） ．13．将抛物线y=x 2+2x ﹣1向上平移4个单位后.所得新抛物线的顶点坐标是 ．14．一个不透明的袋子里装有3个白球、1个红球.这些球除了颜色外无其他的差异.从袋子中随机摸出1个球.恰好是白球的概率是 ．15．正五边形的中心角的度数是 ．16．如图.圆弧形桥拱的跨度AB=16米.拱高CD=4米.那么圆弧形桥拱所在圆的半径是 米．17．如果一个三角形一边上的中线的长与另两边中点的连线段的长相等.我们称这个三角形为“等线三角形”.这条边称为“等线边”．在等线三角形ABC 中.AB 为等线边.且AB=3.AC=2.那么BC= ．18．如图.矩形ABCD 中.AB=4.AD=7.点E.F 分别在边AD 、BC 上.且B 、F 关于过点E 的直线对称.如果以CD 为直径的圆与EF 相切.那么AE= ．三、解答题：（本大题共7题.满分78分）19．计算：|2﹣|﹣8+2﹣2+．20．解不等式组：．21．已知：如图.在平面直角坐标系xOy 中.点A 在x 轴的正半轴上.点B 、C 在第一象限.且四边形OABC是平行四边形.OC=2.sin∠AOC=.反比例函数y=的图象经过点C以及边AB的中点D．求：（1）求这个反比例函数的解析式；（2）四边形OABC的面积．22．某文具店有一种练习簿出售.每本的成本价为2元.在销售的过程中价格有些调整.按原来的价格每本8.25元.卖出36本；经过两次涨价.按第二次涨价后的价格卖出了25本．发现按原价格和第二次涨价后的价格销售.分别获得的销售利润恰好相等．（1）求第二次涨价后每本练习簿的价格；（2）在两次涨价过程中.假设每本练习簿平均获得利润的增长率完全相同.求这个增长率．（注：利润增长率=×100%）23．已知：如图.在直角梯形ABCD中.AD∥BC.∠C=90°.BC=CD.点E、F分别在边BC、CD上.且BE=DF=AD.联结DE.联结AF、BF分别与DE交于点G、P．（1）求证：AB=BF；（2）如果BE=2EC.求证：DG=GE．24．已知：抛物线y=ax2+bx﹣3经过点A（7.﹣3）.与x轴正半轴交于点B（m.0）、C（6m、0）两点.与y轴交于点D．（1）求m的值；（2）求这条抛物线的表达式；（3）点P在抛物线上.点Q在x轴上.当∠PQD=90°且PQ=2DQ时.求点P、Q的坐标．25．如图所示.∠MON=45°.点P是∠MON内一点.过点P作PA⊥OM于点A、PB⊥ON于点B.且PB=2．取OP的中点C.联结AC并延长.交OB于点D．（1）求证：∠ADB=∠OPB；（2）设PA=x.OD=y.求y关于x的函数解析式；（3）分别联结AB、BC.当△ABD与△CPB相似时.求PA的长．2017年上海市浦东新区中考数学二模试卷参考答案与试题解析一、选择题：（本大题共6题.每题4分.满分24分）【下列各题的四个选项中.有且只有一个选项是正确的.选择正确项的代号并填涂在答题纸的相应位置上】1．下列实数中.是无理数的为（）A．3.14 B．C．D．【考点】26：无理数．【分析】A、B、C、D根据无理数的概念“无理数是无限不循环小数.其中有开方开不尽的数”即可判定选择项．【解答】解：A、B、D中3.14.. =3是有理数.C中是无理数．故选：C．2．下列二次根式中.与是同类二次根式的是（）A． B．C． D．【考点】77：同类二次根式．【分析】根据二次根式的性质把各个二次根式化简.根据同类二次根式的概念判断即可．【解答】解：A、与不是同类二次根式；B、=a与不是同类二次根式；C、=a与是同类二次根式；D、=a2与不是同类二次根式；故选：C．3．函数y=kx﹣1（常数k＞0）的图象不经过的象限是（）A．第一象限 B．第二象限 C．第三象限 D．第四象限【考点】F7：一次函数图象与系数的关系．【分析】一次函数y=kx﹣1（常数k＞0）的图象一定经过第一、三.四象限.不经过第二象限．【解答】解：∵一次函数y=kx﹣1（常数k＞0）.b=﹣1＜0.∴一次函数y=kx﹣1（常数k＞0）的图象一定经过第一、三.四象限.不经过第二象限．故选：B．4．某幢楼10户家庭每月的用电量如下表所示：用电量（度）140 160 180 200户数 1 3 4 2那么这10户家庭该月用电量的众数和中位数分别是（）A．180.180 B．180.160 C．160.180 D．160.160【考点】W5：众数；W4：中位数．【分析】根据众数和中位数的定义求解可得．【解答】解：由表可知180出现次数最多.故众数为180.∵共有1+3+4+2=10个数据.∴中位数为第5、6个数据的平均数.即=180.故选：A．5．已知两圆的半径分别为1和5.圆心距为4.那么两圆的位置关系是（）A．外离 B．外切 C．相交 D．内切【考点】MJ：圆与圆的位置关系．【分析】由两圆半径分别是1和5.圆心距为4.两圆位置关系与圆心距d.两圆半径R.r的数量关系间的联系即可得出两圆位置关系．【解答】解：∵两圆半径分别是1和5.圆心距为4.又∵5﹣1=4.∴这两个圆的位置关系内切．故选D．6．如图.已知△ABC和△DEF.点E在BC边上.点A在DE边上.边EF和边AC相交于点G．如果AE=EC.∠AEG=∠B.那么添加下列一个条件后.仍无法判定△DEF与△ABC一定相似的是（）A． = B． = C． = D． =【考点】S8：相似三角形的判定．【分析】利用两组对应边的比相等且夹角对应相等的两个三角形相似可由=得到△ABC∽△EDF；利用=或=可根据两组对应边的比相等且夹角对应相等的两个三角形相似先判断△DEF∽△AEG.再利用有两组角对应相等的两个三角形相似判定△AEG∽△ABC.从而得到△ABC∽△EDF.于是可对各选项进行判断．【解答】解：当=时.则=.而∠B=∠AEG.所以△ABC∽△EDF；当=.则=.而∠DEF=∠AEG.所以△DEF∽△AEG.又因为AE=EC.所以∠EAG=∠C.而∠AEG=∠B.所以△AEG∽△ABC.所以△ABC∽△EDF；当=.则=.而∠DEF=∠AEG.所以△DEF∽△AEG.又因为AE=EC.所以∠EAG=∠C.而∠AEG=∠B.所以△AEG∽△ABC.所以△ABC∽△EDF．故选C．二、填空题：（本大题共12题.每题4分.满分48分）【请将结果直接填入答题纸的相应位置上】7．计算：a•a2= a3．【考点】46：同底数幂的乘法．【分析】根据同底数幂的乘法法则.同底数幂相乘.底数不变.指数相加.即a m•a n=a m+n计算即可．【解答】解：a•a2=a1+2=a3．故答案为：a3．8．因式分解：x2﹣2x= x（x﹣2）．【考点】53：因式分解﹣提公因式法．【分析】原式提取x即可得到结果．【解答】解：原式=x（x﹣2）.故答案为：x（x﹣2）9．方程=﹣x的根是x=﹣4 ．【考点】AG：无理方程．【分析】方程两边平方转化为整式方程.求出整式方程的解得到x的值.经检验即可得到无理方程的解．【解答】解：两边平方得：8﹣2x=x2.整理得：（x+4）（x﹣2）=0.可得x+4=0或x﹣2=0.解得：x=﹣4或x=2.经检验x=2是增根.无理方程的解为x=﹣4．故答案为：x=﹣410．函数f（x）=的定义域是x≠﹣2 ．【考点】E4：函数自变量的取值范围．【分析】根据分式有意义的条件分母不为0计算即可．【解答】解：由x+2≠0得.x≠﹣2；故答案为x≠﹣2．11．如果方程x2﹣2x+m=0有两个实数根.那么m的取值范围是m≤1 ．【考点】AA：根的判别式．【分析】由方程x2﹣2x+m=0有两个实数根.即可得判别式△≥0.继而可求得m的取值范围．【解答】解：∵方程x2﹣2x+m=0有两个实数根.∴△=b2﹣4ac=（﹣2）2﹣4×1×m=4﹣4m≥0.解得：m≤1．故答案为：m≤1．12．计算：2+（+） + ．【考点】LM ：*平面向量． 【分析】根据向量的加法运算法则进行计算即可得解．【解答】解：2+（+）.=2++.=+．故答案为： +．13．将抛物线y=x 2+2x ﹣1向上平移4个单位后.所得新抛物线的顶点坐标是 （﹣1.2） ．【考点】H6：二次函数图象与几何变换．【分析】将抛物线解析式整理成顶点式形式.求出顶点坐标.再根据向上平移纵坐标加求解即可．【解答】解：∵y=x 2+2x ﹣1=（x+1）2﹣2.∴原抛物线的顶点坐标为（﹣1.﹣2）.∵向上平移4个单位后.∴平移后抛物线顶点横坐标不变.纵坐标为﹣2+4=2.∴所得新抛物线的顶点坐标是（﹣1.2）．故答案为：（﹣1.2）．14．一个不透明的袋子里装有3个白球、1个红球.这些球除了颜色外无其他的差异.从袋子中随机摸出1个球.恰好是白球的概率是 ．【考点】X4：概率公式．【分析】根据不透明的袋子里装有3个白球、1个红球.共有4个球.再根据概率公式即可得出答案．【解答】解：∵不透明的袋子里装有3个白球、1个红球.共有4个球.∴从袋子中随机摸出1个球.恰好是白球的概率是．故答案为：．15．正五边形的中心角的度数是72°．【考点】MM：正多边形和圆．【分析】根据正多边形的圆心角定义可知：正n边形的圆中心角为.则代入求解即可．【解答】解：正五边形的中心角为：=72°．故答案为：72°．16．如图.圆弧形桥拱的跨度AB=16米.拱高CD=4米.那么圆弧形桥拱所在圆的半径是10 米．【考点】M3：垂径定理的应用．【分析】根据题意构造直角三角形.进而利用勾股定理求出答案．【解答】解：设圆弧形桥拱所在圆心为O.连接BO.DO.可得：AD=BD.OD⊥AB.∵AB=16米.拱高CD=4米.∴BD=AD=8m.设BO=xm.则DO=（x﹣4）m.根据题意可得：BD2+DO2=BO2.即82+（x﹣4）2=x2.解得：x=10.即圆弧形桥拱所在圆的半径是10m．故答案为：10．17．如果一个三角形一边上的中线的长与另两边中点的连线段的长相等.我们称这个三角形为“等线三角形”.这条边称为“等线边”．在等线三角形ABC中.AB为等线边.且AB=3.AC=2.那么BC= ．【考点】KX：三角形中位线定理．【分析】由三角形的中位线定理证得EF=AB.根据题意得出CD=AB.从而证得△ABC是直角三角形.再利用勾股定理得出BC的长．【解答】解：∵E.F分别是AC.BC的中点.∴EF=AB.∵CD=EF.∴CD=AB.∵AD=BD.∴△ABC是直角三角形.∠ACB=90°.∵AB=3.AC=2.∴BC===.故答案为：．18．如图.矩形ABCD中.AB=4.AD=7.点E.F分别在边AD、BC上.且B、F关于过点E的直线对称.如果以CD为直径的圆与EF相切.那么AE= 3 ．【考点】MC：切线的性质；LB：矩形的性质；P2：轴对称的性质．【分析】设⊙O与EF相切于M.连接EB.作EH⊥BC于H．由题意易知四边形AEHB是矩形.设AE=BH=x.由切线长定理可知.ED=EM.FC=FM.由B、F关于EH对称.推出HF=BH=x.ED=EM=7﹣x.FC=FM=7﹣2x.EF=14﹣3x.在Rt△EFH中.根据EF2=EH2+HF2.列出方程即可解决问题．【解答】解：如图.设⊙O与EF相切于M.连接EB.作EH⊥BC于H．由题意易知四边形AEHB是矩形.设AE=BH=x.由切线长定理可知.ED=EM.FC=FM.∵B、F关于EH对称.∴HF=BH=x.ED=EM=7﹣x.FC=FM=7﹣2x.EF=14﹣3x.在Rt△EFH中.∵EF2=EH2+HF2.∴42+x2=（14﹣3x）2.解得x=3或（舍弃）.∴AE=3.故答案为3．三、解答题：（本大题共7题.满分78分）19．计算：|2﹣|﹣8+2﹣2+．【考点】2C：实数的运算；2F：分数指数幂；6F：负整数指数幂．【分析】首先计算乘方.然后从左向右依次计算.求出算式的值是多少即可．【解答】解：|2﹣|﹣8+2﹣2+=2﹣﹣2+++1=120．解不等式组：．【考点】CB：解一元一次不等式组．【分析】先求出各不等式的解集.再求其公共解集即可．【解答】解：.解不等式①得x＞﹣1.解不等式②得x≤1.所以不等式组的解集为﹣1＜x≤1．21．已知：如图.在平面直角坐标系xOy中.点A在x轴的正半轴上.点B、C在第一象限.且四边形OABC是平行四边形.OC=2.sin∠AOC=.反比例函数y=的图象经过点C以及边AB的中点D．求：（1）求这个反比例函数的解析式；（2）四边形OABC的面积．【考点】G7：待定系数法求反比例函数解析式；G5：反比例函数系数k的几何意义；L5：平行四边形的性质；T7：解直角三角形．【分析】（1）过C作CM⊥x轴于M.则∠CMO=90°.解直角三角形求出CM.根据勾股定理求出OM.求出C的坐标.即可求出答案；（2）根据D为中点求出DN的值.代入反比例函数解析式求出ON.求出OA.根据平行四边形的面积公式求出即可．【解答】解：（1）过C作CM⊥x轴于M.则∠CMO=90°.∵OC=2.sin∠AOC==.∴MC=4.由勾股定理得：OM==2.∴C的坐标为（2.4）.代入y=得：k=8.所以这个反比例函数的解析式是y=；（2）过B作BE⊥x轴于E.则BE=CM=4.AE=OM=2.过D作DN⊥x轴于N.∵D为AB的中点.∴DN==2.AN==1.把y=2代入y=得：x=4.即ON=4.∴OA=4﹣1=3.∴四边形OABC的面积为OA×CM=3×4=12．22．某文具店有一种练习簿出售.每本的成本价为2元.在销售的过程中价格有些调整.按原来的价格每本8.25元.卖出36本；经过两次涨价.按第二次涨价后的价格卖出了25本．发现按原价格和第二次涨价后的价格销售.分别获得的销售利润恰好相等．（1）求第二次涨价后每本练习簿的价格；（2）在两次涨价过程中.假设每本练习簿平均获得利润的增长率完全相同.求这个增长率．（注：利润增长率=×100%）【考点】AD：一元二次方程的应用．【分析】（1）设第二次涨价后每本练习簿的价格为x元.根据总利润=单本利润×数量结合两次销售总利润相等.即可得出关于x的一元一次方程.解之即可得出结论；（2）设每本练习簿平均获得利润的增长率为y.根据涨价前单本利润已经连续两次涨价后的单本利润.即可得出关于y的一元二次方程.解之取其正值即可．【解答】解：（1）设第二次涨价后每本练习簿的价格为x元.根据题意得：（8.25﹣2）×36=（x﹣2）×25.解得：x=11．答：第二次涨价后每本练习簿的价格为11元．（2）设每本练习簿平均获得利润的增长率为y.根据题意得：（8.25﹣2）（1+y）2=11﹣2.解得：y1=0.2=20%.y2=﹣2.2（舍去）．答：每本练习簿平均获得利润的增长率为20%．23．已知：如图.在直角梯形ABCD中.AD∥BC.∠C=90°.BC=CD.点E、F分别在边BC、CD上.且BE=DF=AD.联结DE.联结AF、BF分别与DE交于点G、P．（1）求证：AB=BF；（2）如果BE=2EC.求证：DG=GE．【考点】S9：相似三角形的判定与性质；KD：全等三角形的判定与性质；LI：直角梯形．【分析】（1）先证△BCF≌△DCE.再证四边形ABED是平行四边形.从而得AB=DE=BF．（2）延长AF交BC延长线于点M.从而CM=CF.又由AD∥BC可以得到==1.从而DG=GE．【解答】证明：（1）∵BC=CD.BE=DF.∴CF=CE.在△BCF与△DCE中..∴△BCF≌△DCE.∴BF=DE.∵AD∥BC.BE=AD.∴四边形ABED是平行四边形；∴AB=DE.∴AB=BF．（2）延长AF交BC延长线于点M.则CM=CF；∵AD∥BC.∴=.∵BE=2EC.∴==1.∴DG=GE．24．已知：抛物线y=ax2+bx﹣3经过点A（7.﹣3）.与x轴正半轴交于点B（m.0）、C（6m、0）两点.与y轴交于点D．（1）求m的值；（2）求这条抛物线的表达式；（3）点P在抛物线上.点Q在x轴上.当∠PQD=90°且PQ=2DQ时.求点P、Q的坐标．【考点】HF：二次函数综合题．【分析】（1）先求得点D的坐标.然后设抛物线的解析式为y=a（x﹣m）（x﹣6m）.把点D和点A的坐标代入可求得m的值；（2）由6am2=﹣3.m=1可求得a的值.然后代入抛物线的解析式即可；（3）过点P作PE⊥x轴.垂足为E．设点Q的坐标为（a.0）则OQ=﹣a.然后证明△ODQ∽△EQP.依据相似三角形的性质可求得QE=6.PE=﹣2a．.则P的坐标为（a+6.﹣2a）.将点P的坐标代入抛物线的解析式可求得a的值．【解答】解：（1）当x=0时.y=﹣3.∴D（0.﹣3）．设抛物线的解析式为y=a（x﹣m）（x﹣6m）．把点D和点A的坐标代入得：6am2=﹣3①.a（7﹣m）（7﹣6m）=﹣3②.∴a（7﹣m）（7﹣6m）=6am2．∵a≠0.∴（7﹣m）（7﹣6m）=m2．解得：m=1．（2）∵6am2=﹣3.∴a=﹣=﹣．将a=﹣.m=1代入得：y=﹣x2+x﹣3．∴抛物线的表达式为y=﹣x2+x﹣3．（3）如图所示：过点P作PE⊥x轴.垂足为E．设点Q的坐标为（a.0）则OQ=﹣a﹣∵∠DQP=90°.∴∠PQO+∠OQD=90°．又∵∠ODQ+∠DQO=90°.∴∠PQE=∠ODQ．又∵∠PEQ=∠DOQ=90°.∴△ODQ∽△EQP．∴===.即==.∴QE=6.PE=﹣2a．∴P的坐标为（a+6.﹣2a）将点P的坐标代入抛物线的解析式得：﹣（a+6）2+（a+6）﹣3=﹣2a.整理得：a2+a=0. 解得a=﹣1或a=0．当a=﹣1时.Q（﹣1.0）.P（5.2）；当a=0时.Q（0.0）.P（6.0）．综上所述.Q（﹣1.0）.P（5.2）或者Q（0.0）.P（6.0）．25．如图所示.∠MON=45°.点P是∠MON内一点.过点P作PA⊥OM于点A、PB⊥ON于点B.且PB=2．取OP的中点C.联结AC并延长.交OB于点D．（1）求证：∠ADB=∠OPB；（2）设PA=x.OD=y.求y关于x的函数解析式；（3）分别联结AB、BC.当△ABD与△CPB相似时.求PA的长．【考点】SO：相似形综合题．【分析】（1）先判断出∠DAE=∠POB.再利用等角的余角相等即可得出结论；（2）先利用等腰直角三角形的性质得出OB=BF=（x+2）.同理得出OA=x+4.即可得出AE.OE.进而得出DE.最后用△ADE∽△OPB的比例式建立方程化简即可得出结论；（3）先利用直角三角形斜边的中线等于斜边的一半和三角形外角的性质判断出△ABC是等腰直角三角形.即可得出∠OBC+∠ABP=45°.再用△ABD与△CPB得出.∠ABD=∠PBC.即∠OBC=∠ABP=×45°=22.5°.进而得出OP是∠MON的平分线即可得出结论．【解答】解：（1）证明：如图.∵PA⊥OM.CO=CP.∴CO=CP=CA.∴∠CAO=∠COA.过A作AE⊥OB于E.∵∠MON=45°.∴∠AOE=∠OAE=45°.∴∠POB=∠DAE.∵PB⊥OB.∴∠ADB=∠OPB；（2）如图1.延长BP交OM于F.∵BP⊥ON.PA⊥OM.∴∠OBP=∠OAP=90°.∵∠MON=45°.∴∠AFB=45°.在Rt△APF中.AP=x.∠OFB=45°.∴PF=x.∴BF=PF+PB=x+2=（x+2）.在Rt△OBF中.OB=BF=（x+2）延长AP交ON于G.同理：PG=PB=4.∴OA=AG=AP+PG=x+4.过点A作AE⊥ON.∴OE=AE=OA=（x+4）.∴DE=OE﹣OD=（x+4）﹣y由（1）知.∠ADE=∠OPB.∵∠AED=∠OBP=90°.∴△ADE∽△OPB.∴.∴.∴y=（3）如图2.在Rt△OAP中.点C是OP中点.∴AC=OC=OP.在Rt△OBP中.点C是OP中点.∴BC=OC=OP.∴AC=BC.∵AC=OC.∴∠ACP=2∠AOP.∵OC=BC.∴∠BCP=2∠BOP.∴∠ACB=∠ACP+∠BCP=2（∠AOP+∠BOP）=2∠AOB=90°. ∴∠BAC=∠CAB=45°.∵∠OBP=90°.∴∠OBC+∠ABP=45°∵当△ABD与△CPB相似时.∵∠ADB=∠CPB.∴∠ABD=∠PBC.∴∠OBC=∠ABP=×45°=22.5°.∵OC=BC.∴∠BOC=∠OBC=22.5°.∴∠AOP=∠BOP.∴OP是∠MON的角平分线.∵PA⊥OM.PB⊥ON.∴PA=PB=2．。
中考数学 二模 25题
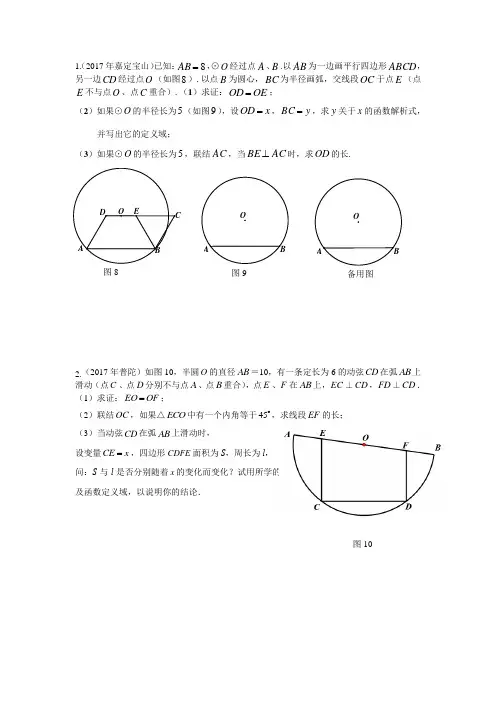
1.（2017年嘉定宝山）已知：8=AB ，⊙O 经过点A 、B .以AB 为一边画平行四边形ABCD ，另一边CD 经过点O （如图8）.以点B 为圆心，BC 为半径画弧，交线段OC 于点E （点E 不与点O 、点C 重合）.（1）求证：OE OD =；（2）如果⊙O 的半径长为5（如图9），设x OD =，y BC =，求y 关于x 的函数解析式，并写出它的定义域；（3）如果⊙O 的半径长为5，联结AC ，当AC BE ⊥时，求OD 的长.2.（2017年普陀）如图10，半圆O 的直径AB ＝10，有一条定长为6的动弦CD 在弧AB 上滑动（点C 、点D 分别不与点A 、点B 重合），点E 、F 在AB 上，EC ⊥CD ，FD ⊥CD ． （1）求证：EO OF =；（2）联结OC ，如果△ECO 中有一个内角等于45 ，求线段EF 的长； （3）当动弦CD 在弧AB 上滑动时，设变量CE x =，四边形CDFE 面积为S ，周长为l ，问：S 与l 是否分别随着x 的变化而变化？试用所学的函数知识直接写出它们的函数解析式及函数定义域，以说明你的结论．图9 B O A 备用图 B OA 图8 E CB A O D 图103.（2017年崇明）如图，梯形ABCD 中，AB CD ∥，90ABC ∠=︒，6AB =，8BC =，tan 2D =，点E 是射线CD 上一动点（不与点C 重合），将BCE ∆沿着BE 进行翻折，点C 的对应点记为点F ． （1）如图1，当点F 落在梯形ABCD 的中位线MN 上时，求CE 的长；（2）如图2，当点E 在线段CD 上时，设CE x =，BFC EFCS y S ∆∆=，求y 与x 之间的函数关系式，并写出定义域；（3）如图3，联结AC ，线段BF 与射线CA 交于点G ，当CBG ∆是等腰三角形时，求CE 的长．ABCDEFM NEDCFABEDC FAB GD CAB（第25题图1）（第25题图2）（第25题图3）（第25题备用图）4.（2017年杨浦）已知：以O 为圆心的扇形AOB 中，∠AOB =90°，点C 为»AB 上一动点，射线AC 交射线OB 于点D ，过点D 作OD 的垂线交射线OC 于点E ，联结AE . （1） 如图1，当四边形AODE 为矩形时，求∠ADO 的度数； （2） 当扇形的半径长为5，且AC =6时，求线段DE 的长；（3） 联结BC ，试问：在点C 运动的过程中，∠BCD 的大小是否确定？若是，请求出它 的度数；若不是，请说明理由.5.（2017年奉贤）已知：如图9，线段AB =4，以AB 为直径作半圆O ，点C 为弧AB 的中点，点P 为直径AB 上一点，联结PC ，过点C 作CD //AB ，且CD =PC ，过点D 作DE//PC ，交射线PB 于点E ，PD 与CE 相交于点Q ． （1）若点P 与点A 重合，求BE 的长； （2）设PC = x ，y CEPD，当点P 在线段AO 上时，求y 与x 的函数关系式及定义域； （3）当点Q 在半圆O 上时，求PC 的长．图9ACPOBD E Q备用图AO BCA OBCD E（备用图） A O B CD E （图1）6.（2017年闵行）如图，在梯形ABCD 中，AD // BC ，∠B = 90°，AB = 4，BC = 9，AD = 6．点E 、F 分别在边AD 、BC 上，且BF = 2DE ，联结FE ．FE 的延长线与CD 的延长线相交于点P ．设DE = x ，PEy EF ． （1）求y 关于x 的函数解析式，并写出函数的定义域；（2）当以ED 为半径的⊙E 与以FB 为半径的⊙F 外切时，求x 的值；（3）当△AEF ∽△PED 时，求x 的值．7.（2017年长宁金山）如图，△ABC 的边AB 是⊙O 的直径，点C 在⊙O 上，已知AC =6 cm ，BC =8 cm ，点P 、Q 分别在边AB 、BC 上，且点P 不与点A 、B 重合，BQ =k ·AP （k >0），连接PC 、PQ ． （1）求⊙O 的半径长； （2）当k =2时，设AP =x ，△CPQ 的面积为y ，求y 关于x 的函数关系式，并写出定义域； （3）如果△CPQ ∽△ABC ，且∠ACB =∠CPQ ，求k 的值.第25题图A B CDE F P （第25题图）A B C D （备用图）EP 第25题图 C AB D8.（2017年虹口）如图，在△ABC 中，AB=AC =5，cos B =45，点P 为边BC 上一动点，过点P 作射线PE 交射线BA 于点D ，∠BPD=∠BAC ．以点P 为圆心，PC 长为半径作⊙P 交射线PD 于点E ，联结CE ，设BD=x ，CE=y ． （1）当⊙P 与AB 相切时，求⊙P 的半径；（2）当点D 在BA 的延长线上时，求y 关于x 的函数解析式，并写出定义域； （3）如果⊙O 与⊙P 相交于点C 、E ，且⊙O 经过点B ，当OP=54时，求AD 的长．9.（2017年浦东新区）如图所示，︒=∠45MON ，点P 是MON ∠内一点，过点P 作OM PA ⊥于点A 、ON PB ⊥于点B ，且22=PB ．取OP 的中点C ，联结AC 并延长，交OB 于点D ．（1）求证：OPB ADB ∠=∠；（2）设x PA =，y OD =，求y 关于x 的函数解析式；（3）分别联结AB 、BC ，当ABD △与CPB △相似时，求PA 的长．（第25题图）（备用图）10.（2016年崇明）如图，已知BC 是半圆O 的直径，8BC =，过线段BO 上一动点D ，作AD BC ⊥交半圆O 于点A ，联结AO ，过点B 作BH AO ⊥，垂足为点H ，BH 的延长线交半圆O 于点F ． （1）求证：AH BD =；（2）设BD x =，BE BF y ⋅=，求y 关于x 的函数关系式；（3）如图2，若联结FA 并延长交CB 的延长线于点G ，当FAE ∆与FBG ∆相似时，求BD 的长度．11.（2016年宝山嘉定）如图8，⊙O 与过点O 的⊙P 相交于AB ，D 是⊙P 的劣弧OB 上一点，射线OD 交⊙O 于点E ，交AB 的延长线于点C .如果AB =24，32tan =∠AOP . (1) 求⊙P 的半径长；(2) 当△AOC 为直角三角形时，求线段OD 的长； (3) 设线段OD 的长度为x ，线段CE 的长度为y ，求y 与x 之间的函数关系式及其定义域．（第25题图1）ABDOE HFC（第25题图2） CO D B G A F H E 图8_C _ E _B _O_P_A_ D12.（2016年长宁金山）如图, 已知在Rt △ABC 中, ∠ACB =90°, AB =5, 4sin 5A, P 是边BC 上的一点, PE ⊥AB , 垂足为E , 以点P 为圆心, PC 为半径的圆与射线PE 相交于点Q , 线段CQ 与边AB 交于点D . （1）求AD 的长;（2）设CP =x , △PCQ 的面积为y , 求y 关于x 的函数解析式, 并写出定义域;（3）过点C 作CF ⊥AB , 垂足为F , 联结PF 、QF , 如果△PQF 是以PF 为腰的等腰三角形, 求CP 的长.13.（2016年闸北）如图，在△ABC 中，AB=AC=6，BC=4，⊙B 与边AB 相交于点D ，与边BC 相交于点E ，设⊙B 的半径为x ． （1）当⊙B 与直线AC 相切时，求x 的值；（2）设DC 的长为y ，求y 关于x 的函数解析式，并写出定义域； （3）若以AC 为直径的⊙P 经过点E ，求⊙P 与⊙B 公共弦的长．BCAP EQDBCACB ADE （第25题图）14.（2016年闵行）如图，已知在△ABC 中，AB = AC = 6，AH ⊥BC ，垂足为点H ．点D 在边AB 上，且AD = 2，联结CD 交AH 于点E ．（1）如图1，如果AE = AD ，求AH 的长；（2）如图2，⊙A 是以点A 为圆心，AD 为半径的圆，交线段AH 于点F ．设点P 为边BC 上一点，如果以点P 为圆心，BP 为半径的圆与⊙A 外切，以点P 为圆心，CP 为半径的圆与⊙A 内切，求边BC 的长；（3）如图3，联结DF ．设DF = x ，△ABC 的面积为y ，求y 关于x 的函数解析式，并写出自变量x 的取值范围．15.（2016年松江）已知：如图1，在梯形ABCD 中，AD //BC ，∠BCD =90º， BC=11，CD=6，tan ∠ABC =2，点E 在AD 边上，且AE=3ED ，EF //AB 交BC 于点F ，点M 、N 分别在射线FE 和线段CD 上．（1）求线段CF 的长； （2）如图2，当点M 在线段FE 上，且AM ⊥MN ，设FM ·cos ∠EFC =x ，CN =y ，求y 关于x 的函数解析式，并写出它的定义域；（3）如果△AMN 为等腰直角三角形，求线段FM 的长．AB C H D （第25题图1) E AB C H D E（第25题图3) F P AB C H D E（第25题图2) F （第25题图1）AC B DE F（第25题图2）AC B DE FNM （备用图）A CBDE F16.（2016年黄埔）如图7，在Rt △ABC 中，90ACB ∠=︒，1AC =，BC =7，点D 是边CA 延长线上的一点，AE ⊥BD ，垂足为点E ，AE 的延长线交CA 的平行线BF 于点F ，联结CE 交AB 于点G ．（1）当点E 是BD 的中点时，求tan AFB ∠的值；（2）CE AF 的值是否随线段AD 长度的改变而变化，如果不变，求出CE AF 的值；如果变化，请说明理由；（3）当BGE ∆与BAF ∆相似时，求线段AF 的长．19.（2016年杨浦）已知：半圆O 的直径AB =6，点C 在半圆O 上，且tan 22ABC ∠=，点D 为AC 上一点，联结DC （如图）．（1）求BC 的长；（2）若射线DC 交射线AB 于点M ，且△MBC 与△MOC 相似，求CD 的长； （3）联结OD ，当OD//BC 时，作∠DOB 的平分线交线段DC 于点N ，求ON 的长．图7AB C DEF G （第25题备用图） A B O C A B O C D（第25题图）20.（2016年奉贤） 已知：如图，在边长为5的菱形ABCD 中，cos A =35，点P 为边AB 上一点，以A 为圆心、AP 为半径的⊙A 与边AD 交于点E ，射线CE 与⊙A 另一个交点为点F ． （1）当点E 与点D 重合时，求EF 的长；（2）设AP =x ，CE =y ，求y 关于x 的函数关系式及定义域；（3）是否存在一点P ，使得 2EF PE =⋅，若存在，求AP 的长，若不存在，请说明理由．21.（2016年普陀）如图9，在Rt △ABC 中，90C ∠= ，14AC =，3tan 4A =，点D 是边AC 上的一点，8AD =．点E 是边AB 上一点，以点E 为圆心，EA 为半径作圆，经过点D ．点F 是边AC 上一动点（点F 不与A 、C 重合），作FG EF ⊥，交射线BC 于点G ． （1）用直尺圆规作出圆心E ，并求圆E 的半径长（保留作图痕迹）；（2）当点G 在边BC 上时，设AF x =，CG y =，求y 关于x 的函数解析式，并写出它的定义域；（3）联结EG ，当△EFG 与△FCG 相似时，推理判断以点G 为圆心、CG 为半径的圆G 与圆E 可能产生的各种位置关系．DCBA E F第25题图P DCBA备用图DCBA图9DCBA图9备用图22.(2016年浦东）如图，Rt △ABC 中，90ACB ∠= ，6BC =，点D 为斜边AB 的中点，点E 为边AC 上的一个动点．联结DE ，过点E 作DE 的垂线与边BC 交于点F ，以,DE EF 为邻边作矩形DEFG ．（1）如图1，当8AC =，点G 在边AB 上时，求DE 和EF 的长； （2）如图2，若12DE EF =，设AC x =，矩形DEFG 的面积为y ，求y 关于x 的函数解析式； （3）若23DE EF =，且点G 恰好落在Rt △ABC 的边上，求AC 的长．23.(2015年黄埔）如图8，Rt △ABC 中，90C ︒∠=，30A ︒∠=，BC =2，CD 是斜边AB 上的高，点E 为边AC 上一点（点E 不与点A 、C 重合），联结DE ，作CF ⊥DE ，CF 与边AB 、线段DE 分别交于点F 、G ．（1）求线段CD 、AD 的长；（2）设CE x =，DF y =，求y 关于x 的函数解析式，并写出它的定义域； （3）联结EF ，当△EFG 与△CDG 相似时，求线段CE 的长．GFED C BA 第25题 图2A BC D EFG 第25题 图1 ABCD备用图DCBA(备用图）图8GFDCB A E23.(2015年奉贤）已知：如图，线段AB =8，以A 为圆心，5为半径作圆A ，点C 在⊙A 上，过点C 作CD //AB 交⊙A 于点D （点D 在C 右侧），联结BC 、AD ． （1）若CD=6，求四边形ABCD 的面积；（2）设CD =x ，BC =y ，求y 与x 的函数关系式及自变量x 的取值范围；（3）设BC 的中点为M ，AD 的中点为N ，线段MN 交⊙A 于点E ，联结CE ，当CD 取何值时，CE //AD ．23.(2015年松江区）如图，已知在直角梯形ABCD 中，AD ∥BC ，∠ABC =90º，AB =4，AD=3，552sin =∠BCD ，点P 是对角线BD 上一动点，过点P 作PH ⊥CD ，垂足为H ． （1）求证：∠BCD =∠BDC ；（2）如图1，若以P 为圆心、PB 为半径的圆和以H 为圆心、HD 为半径的圆外切时，求DP 的长；（3）如图2，点E 在BC 延长线上，且满足DP =CE ，PE 交DC 于点F ，若△ADH 和△ECF 相似，求DP 的长．DCB （第25题图）AB（备用图）AABCHPD （第25题图1）ABCHPD EF（第25题图2）23.(2015年闵行区）如图，已知在梯形ABCD 中，AD // BC ，AB = DC = 5，AD = 4．M 、N 分别是边AD 、BC 上的任意一点，联结AN 、DN ．点E 、F 分别在线段AN 、DN 上，且ME // DN ，MF // AN ，联结EF ．（1）如图1，如果EF // BC ，求EF 的长；（2）如果四边形MENF 的面积是△ADN 的面积的38，求AM 的长；（3）如果BC = 10，试探索△ABN 、△AND 、△DNC 能否两两相似？如果能，求AN 的长；如果不能，请说明理由．23.(2015年嘉定）在Rt △ABC 中，︒=∠90C ，2=BC ，Rt △ABC 绕着点B 按顺时针方向旋转，使点C 落在斜边AB 上的点D ，设点A 旋转后与点E 重合，联结AE ，过点E 作直线EM 与射线CB 垂直，交点为M ．（1）若点M 与点B 重合如图10，求BAE ∠cot 的值；（2）若点M 在边BC 上如图11，设边长x AC =，y BM =，点M 与点B 不重合，求y 与x 的函数关系式，并写出自变量x 的取值范围； （3）若EBM BAE ∠=∠，求斜边AB 的长．A B C D M N E F（图1）A B C D M NE F （第25题图）A CB (M )ED 图10ACBMED图11。
2017年初三数学二模25题
专题：2017年二模25题1.已知：以O 为圆心的扇形AOB 中，90AOB ∠=，点C 为 AB 上一动点，射线AC 交射线OB 于点D ，过点D 作OD 的垂线交射线OC 于点E ，联结AE ．（1）如图1，当四边形AODE 为矩形时，求ADO ∠的度数；（2）当扇形的半径长为5，且6AC =时，求线段DE 的长；（3）联结BC ，试问：在点C 运动的过程中，BCD ∠的大小是否确定？若是，请求出它的度数；若不是，请说明理由．2.如图，在梯形ABCD 中，AD ∥BC ，∠B =90°，AB =4，BC =9,AD =6，点E 、F 分别在边AD 、BC 上，且BF =2DE ，联结FE 。
FE 的延长线与CD 的延长线相交于点P 。
设DE =x ,EFPE =y .（1）求y 关于x 的函数解析式，并写出函数的定义域；（2）当以ED 为半径的○E 与以FB 为半径的○F 外切时，求x 的值；（3）当△AEF ∽△PED 时，求x 的值。
3.已知：如图9，线段4AB =，以AB 为直径作半圆O ，点C 为弧AB 的中点，点P 为直径AB 上一点，联结PC ，过点C 作CD //AB ，且CD PC =，过点D 作DE //PC ，交射线PB 于点E ，PD 与CE 交于点Q .（1）若点P 与点A 重合，求BE 的长；（2）设PC x =，PD y CE=，当点P 在线段AO 上时，求y 关于x 的函数关系式及定义域；（3）当点Q 在半圆O 上时，求PC 的长.4.如图11，已知△ABC 中，，6,5===BC AC AB 点O 是边BC 上的动点，以点O 为圆心，OB 为半径作圆O ，交AB 边于点D ，过点D 作∠ODP =∠B ，交边AC 于点P ，交圆O 与点E 。
设x OB =。
（1）当点P 与点C 重合时，求PD 的长；（2）设y EP AP =-，求y 关于x 的解析式及定义域；（3）联结OP ，当OD OP ⊥时，试判断以点P 为圆心，PC 为半径的圆P 与圆O 的位置关系。
201705浦东初三数学二模试卷
文档（完卷时间：100分钟，满分：150分）2017.5一、选择题：（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】1．下列实数中，是无理数的是（ ）（A ）3.14； （B ）31； （C ）3； （D ）9．2．下列二次根式中，与a 是同类二次根式的是（ ）（A ）a 3； （B ）22a ； （C ）3a ； （D ）4a ．3．函数1-=kx y （常数0>k ）的图像不经过的象限是（ ）（A ）第一象限； （B ）第二象限； （C ）第三象限； （D ）第四象限．4．某幢楼10那么这10 （A ）180，180； （B ）180，160； （C ）160，180； （D ）160，160．5．已知两圆的半径分别为1和5，圆心距为4，那么两圆的位置关系是（ ）（A ）外离 ； （B ）外切； （C ）相交； （D ）内切．6．如图，已知ABC △和DEF △，点E 在BC 边上，点A 在DE 边上，边EF 和边AC 交于点G ．如果AE =EC ，B AEG ∠=∠．那么添加下列一个条件后，仍无法判定DEF △与ABC △一定相似的是（A ）EF DE BC AB =； （B ）GEGF AE AD =； （C ）EF EG AC AG =； （D ）EA EG EF ED =． 二、填空题：（本大题共12题，每题4分，满分48分） 7． 计算：=⋅2a a ．8． 因式分解：=-x x 22 ．9． 方程x x -=-28的根是 ．10．函数23)(+=x x x f 的定义域是 ． 11．如果关于x 的方程022=+-m x x 有两个实数根，那么m 的取值范围是 ．（第6题图）文档12．计算：()=++b a a 312 ． 13．将抛物线122-+=x x y 向上平移4个单位后，所得新抛物线的顶点坐标是 ．14．一个不透明的袋子里装有3个白球、1个红球，这些球除颜色外无其他的差异，从袋子中随机摸出1个球，恰好是白球的概率是 ．15．正五边形的中心角是 ．16．如图，圆弧形桥拱的跨度16=AB 米，拱高4=CD 米，那么圆弧形桥拱所在圆的半径是 米．17．如果一个三角形一边上的中线的长与另两边中点的连线段的长相等，我们称这个三角形为“等线三角形”，这条边称为“等线边”．在等线三角形ABC 中，AB 为等线边，且AB =3，AC =2，那么BC = ．18．如图，矩形ABCD 中，AB =4，AD =7．点E 、F 分别在边AD 、BC 上，且点B 、F 关于过点E 的直线对称．如果以CD 为直径的圆与EF 相切，那么AE = ．三、解答题：（本大题共7题，满分78分）19．（本题满分10分） 计算：1212822231+++---．20．（本题满分10分） （第18题图）（第16题图）文档 （第21题图） 解不等式组：32145,311.22x x x x ->-⎧⎪⎨-≤⎪⎩（）21．（本题满分10分，每小题各5分）已知：如图，在平面直角坐标系xOy 中，点A 在x 轴正半轴上，点B 、C 在第一象限，且四边形OABC 是平行四边形，52=OC ，552sin =∠AOC ．反比例函数xk y =的图像经过点C 以及边AB 的中点D ．求：（1）这个反比例函数的解析式；（2）四边形OABC 的面积．22．（本题满分10分，其中第（1）小题4分，第（2）小题6分）某文具店有一种练习簿出售，每本的成本价为2元．在销售的过程中价格有调整，按原价格每本8.25元，卖出36本；后经两次涨价，按第二次涨价后的价格卖出了25本．发现按原价格和第二次涨价后的价格销售，分别获得的销售利润恰好相等．① ②文档（第23题图）（1）求第二次涨价后每本练习簿的价格；（2）在两次涨价过程中，假设每本练习簿平均获得利润的增长率完全相同，求这个增长率．（注：100%-=⨯（后一次的利润前一次的利润）利润增长率前一次的利润）23．（本题满分12分，每小题各6分）已知：如图，在直角梯形ABCD 中，AD ∥BC ，︒=∠90C ，BC =CD ，点E 、F 分别在边BC 、CD 上，且BE =DF =AD ，联结DE ，联结AF 、BF 分别与DE 交于点G 、P ．（1）求证：AB =BF ；（2）如果BE =2EC ，求证：DG =GE ．文档24．（本题满分12分，其中第（1）小题3分，第（2）小题4分，第（3）小题5分）已知抛物线32-+=bx ax y 经过点A ）（3,7-，与x 轴正半轴交于B ）（0,m 、C ）（0,6m 两点，与y 轴交于点D ．（1）求m 的值；（2）求这条抛物线的表达式；（3）点P 在抛物线上，点Q 在x 轴上，当∠PQD =90°且PQ =2DQ 时，求点P 、Q 的坐标．（第24题图）文档25．（本题满分14分，其中第（1）小题5分，第（2）小题5分，第（3）小题4分）如图所示，︒=∠45MON ，点P 是MON ∠内一点，过点P 作OM PA ⊥于点A 、ON PB ⊥于点B ，且22=PB ．取OP 的中点C ，联结AC 并延长，交OB 于点D ．（1）求证：OPB ADB ∠=∠；文档（2）设x PA =，y OD =，求y 关于x 的函数解析式；（3）分别联结AB 、BC ，当ABD △与CPB △相似时，求PA 的长．浦东新区2016学年第二学期初三教学质量检测数学参考答案及评分说明（第25题图） （备用图）文档一、选择题：（本大题共6题，每题4分，满分24分）1．C ； 2．C ； 3．B ； 4．A ； 5．D ； 6．C ．二、填空题：（本大题共12题，每题4分，满分48分）7．3a ； 8．()2-x x ； 9．4-=x ； 10．2-≠x ； 11．1≤m ； 12．b a 3137+； 13．()2,1-； 14．43； 15． 72； 16．10； 17．5； 18．3．三、解答题：（本大题共7题，满分78分）19．（本题满分10分）解：原式=1241222-++--．………………………………………………………各2分 = 43-．………………………………………………………………………………2分 20．（本题满分10分）解：由①得:5436->-x x ．…………………………………………………………………2分 22->x ．……………………………………………………………………2分 1->x ．……………………………………………………………………1分 由②得:x x ≤-23．………………………………………………………………………2分 22≤x ．………………………………………………………………………1分 1≤x ．………………………………………………………………………1分 ∴原不等式组的解集是11≤<-x ．……………………………………………………2分21．（本题满分10分，每小题各5分）解：（1）过点C 作CH ⊥OA 于点H ．………………………………………………………1分 在△COH 中，∠CHO=90°, ∴sin ∠AOC=552=OC CH ． ………………………1分 ∵52=OC ，∴CH=4．………………………………………………………………1分 在△COH 中，∠CHO=90°, ∴222=-=CH OC OH ．文档∵点C 在第一象限，∴点C 的坐标是（2，4）．………………………………………1分 ∵反比例函数x k y =的图像过点C （2，4），∴k =8．即x y 8=．…………………1分（2）过点D 作DG ⊥OA 于点G ．……………………………………………………………1分∵四边形ABCD 是平行四边形，∴AB =OC =52．……………………………………1分 ∵点D 是边AB 的中点，∴AD =5． …………………………………………………1分 在△DAG 中，∠DGA=90°, ∴sin ∠DAG =sin ∠AOC=552=DA DG ． ∴DG=2，AG =1．∴设点D 的坐标为（a ，2）．∵反比例函数xy 8=的图像过点D （a ，2），∴a =4．即OG =4．…………………1分 ∴OA =OG －AG =3．∴四边形OABC 的面积为12．……………………………………1分22．（本题满分10分，其中第（1）小题4分，第（2）小题6分）解：（1）设第二次涨价后每本练习簿的价格为x 元．………………………………………1分 由题意得：()()25236225.8⨯-=⨯-x ．…………………………………………2分 解得：11=x ．答：第二次涨价后每本练习簿的价格为11元．……………………………………1分（2）设每本练习簿平均获得利润的增长率为y ．………………………………………1分 由题意得：()()2111225.82-=+⨯-y ．…………………………………………2分 解得：2.0=y 或2.2-=y （不合题意，舍去）．…………………………………2分 答：每本练习簿平均获得利润的增长率为20%．…………………………………1分23．（本题满分12分，每小题各6分）证明：（1）∵ AD ∥BC ，AD=BE ，∴四边形ABED 是平行四边形．………………………1分∴AB =DE ．………………………………………………………………………………1分 ∵BE =DF ，BC =CD ，∴ CE =CF ．……………………………………………………1分 又∵∠BCF=∠DCE=90º，BC =CD ．∴△BCF ≌△DCE ．……………………………2分 ∴ DE =BF ．………………………………………………………………………………1分 ∴ AB =BF ．（2）延长AF 与BC 延长线交于点H ．………………………………………………………1分∵BE =2CE ，BE =DF=AD ，CE =CF ，文档 ∴ DF =2CF ，AD=2CE ．…………………………………………………………………1分∵ AD ∥BC ，∴CFDF CH AD =．……………………………………………………………1分 ∴AD =2CH ．………………………………………………………………………………1分 ∴AD=2CE =2CH ．又∵EH =CE +CH ．∴AD=EH ．…………………………………………………………1分 ∵ AD ∥BC ，∴EHAD GE DG =．……………………………………………………………1分 ∴DG=GE ．文档 24．（本题满分12分，其中第（1）小题3分，第（2）小题4分，第（3）小题5分） 解：（1）抛物线32-+=bx ax y 与y 轴的交点D （0，3-）．……………………………1分∵抛物线经过点A （7，3-），∴抛物线的对称轴为直线27=x ．…………………1分 ∴2726=+m m ．解得1=m ．…………………………………………………………1分 （2）由1=m 得B （1，0）．将A （7，3-）、B （1，0）代入抛物线解析式得：⎩⎨⎧=-+-=-+.03,33749b a b a ……………2分 解得：⎪⎪⎩⎪⎪⎨⎧=-=.27,21b a …………………………………………………………………………1分 ∴这条抛物线的表达式为：327212-+-=x x y ．……………………………………1分 （3） ①当点Q 在原点时，抛物线与x 轴的交点）（0,6即为点P ， 90=∠PQD 且PQ =2DQ ．∴）（0,6P ，）（0,0Q ．…………………………………………………………1分 ②当点Q 不在原点时，过点P 作轴x PH ⊥于点H ．∵ 90=∠=∠QHP DOQ ，QPH DQO ∠=∠，∴△DOQ ∽△QHP ．…………………………………………………………………1分 ∵PQ =2DQ ，∴21===QP DQ PH OQ QH OD ． ∴62==OD QH ，OQ PH 2=．………………………………………………………1分由题意，设）（0,k Q ，那么)26(k k P -+，． ∵点)26(k k P -+，在抛物线327212-+-=x x y 上， ∴k k k 23)6(27)6212-=-+++-（解得01=k ，12-=k ．………………………………………………………………1分文档当0=k 时，点Q 与点O 重合，舍去．∴）（2,5P ，）（0,1-Q ．………………………………………………………………1分∴）（0,6P ，）（0,0Q 或）（2,5P ，）（0,1-Q ．文档25．（本题满分14分，其中第（1）小题5分，第（2）小题5分，第（3）小题4分）（1）证明：记COA α∠=∵PA OM ⊥，C 是OP 的中点，∴PC OC AC ==．……………………………1分∴COA CAO α∠=∠=．……………………………………………………………1分 又∵︒=∠45MON ，∴45ADB AOD CAO α∠=∠+∠=+o ．……………………………………………1分 45POB MON COA α∠=∠-∠=-o ．……………………………………………1分又∵PB ON ⊥，∴在△POB 中，∠PBO=90°,∴9045OPB POB α∠=-∠=+o o ．……………1分 ∴ADB OPB ∠=∠．（2）解：延长AP ，交ON 于点E ，过点A 作AF ON ⊥于点F ．……………………1分 ∵PA OM ⊥，∠MON=45°, PB ON ⊥，∴∠AEO=45°．即△AOE 、△PBE 均为等腰直角三角形．又PA =x ，PB=PE =4，AO =AE =4x +．…………………………………1分 ∴OE+∴OF=EF=AF+OB+DF =y x -+2222．………1分 ∵ADB OPB ∠=∠，∴cot cot ADB OPB ∠=∠．∴DF PB AF OB =．………………1分y += ∴422422++=x x x y ．………………………………………………………………1分 （3）∵PB ON ⊥，C 是OP 的中点，∴CB CP =．∴CBP CPB ∠=∠，即△CBP 为等腰三角形．又∵△ABD 与△CBP 相似，且ADB CPB ∠=∠．∴ADB ABD ∠=∠或ADB DAB ∠=∠．即AD AB =或BD AB =．…………………………………………………………1分 ∵CA CO CP CB ===，∴2ACP COA ∠=∠，2BCP BOC ∠=∠．∴︒=∠=∠902AOB ACB ．又∵CA CB =，∴︒=∠45DAB ．………………………………………………1分① 如果AB AD =，那么1804567.52ADB ABD -∠=∠==o oo ． ∴67.5OPB ∠=o ．∴22.5AOP BOP ∠=∠=o ．文档 又∵OM PA ⊥于点A 、ON PB ⊥于点B ，∴22==PB PA ．……………………………………………………………1分 ② 如果BA BD =，那么90ABD ∠=o ．∵︒=∠90PBD ，∴点A 在直线PB 上．又∵OM PA ⊥于点A ，∴点P 与点A 重合．而点P 是MON ∠内一点，∴点P 与点A 不重合．此情况不成立．………1分综上所述，当△ABD 与△CBP 相似时，22=PA ．。
2017年上海中考二模24题专练(学生版)
1、（宝山）如图，已知直线221-=x y 与x 轴交于点B ，与y 轴交于点C ，抛物线2212-+=bx x y 与x 轴交于A 、B 两点（A 在B 的左侧），与y 轴交于点C ． （1）求抛物线的解析式；（2）点M 是上述抛物线上一点，如果△ABM 和△ABC 相似，求点M 的坐标；（3）连接AC ，求顶点D 、E 、F 、G 在△ABC 各边上的矩形DEFG 面积最大时，写出该矩形在AB 边上的顶点的坐标．2、（崇明）如图，已知抛物线c x ax y +-=22经过△ABC 的三个顶点，其中点A （0，1），点B （9，10），AC ∥x 轴． （1）求这条抛物线的解析式； （2）求tan ∠ABC 的值；（3）若点D 为抛物线的顶点，点E 是直线AC 上一点，当△CDE 与△ABC 相似时，求点E 的坐标．3、（奉贤）如图，在平面直角坐标系xOy 中，抛物线c bx x y ++-=2经过点A （3，0）和点B （2，3），过点A 的直线与y 轴的负半轴相交于点C ，且31tan =∠CAO ． （1）求这条抛物线的表达式及对称轴； （2）联结AB 、BC ，求∠ABC 的正切值；（3）若点D 在x 轴下方的对称轴上，当S △DBC=S △ADC 时，求点D 的坐标．4、（虹口）如图，在平面直角坐标系xOy 中，抛物线c bx x y ++=241经过点A （－2，0）和原点，点B 在抛物线上且21tan =∠BAO ，抛物线的对称轴与x 轴相交于点P . （1）求抛物线的解析式，并直接写出点P 的坐标；（2）点C 为抛物线上一点，若四边形AOBC 为等腰梯形且AO ∥BC ，求点C 的坐标； （3）点D 在AB 上，若△ADP 相似于△ABP ，求点D 的坐标．5、（黄浦）如图，点A 在函数)0(4>=x xy 图像上，过点A 作x 轴和y 轴的平行线分别交函数xy 1=图像于点B 、C ，直线BC 与坐标轴的交点为D 、E. （1）当点C 的横坐标为1时，求点B 的坐标； （2）试问：当点A 在函数)0(4>=x xy 图像上运动时，△ABC 的面积是否发生变化？若不变，请求出△ABC 的面积；若变化，请说明理由； （3）试说明：当点A 在函数)0(4>=x xy 图像上运动时，线段BD 与CE 的长始终相等.EBC A DxyO6、（嘉定）在平面直角坐标系xOy （如图7）中，已知点A 的坐标为)1,3(，点B 的坐标为），（56，点C 的坐标为)5,0(；某二次函数的图像经过点A 、点B 与点C . （1）求这个二次函数的解析式；（2）假如点Q 在该函数图像的对称轴上，且△ACQ 是等腰三角形，直接写出点Q 的坐标； （3）如果第一象限内的点P 在（1）中求出的二次函数 的图像上，且21tan =∠PCA ，求PCB ∠的正弦值.图77、（静安）已知二次函数c bx x y ++-=221的图像与x 轴的正半轴相交于点A （2，0）和点B 、与y 轴相交于点C ，它的顶点为M 、对称轴与x 轴相交于点N ． （1） 用b 的代数式表示顶点M 的坐标； （2） 当tan ∠MAN=2时，求此二次函数的解析式 及∠ACB 的正切值．8、（闵行）如图，在平面直角坐标系xOy 中, 抛物线m x m x y 3)1(2+--=经过点)0,1(-A ，且与y 轴相交于点B .（1）求这条抛物线的表达式及点B 的坐标；（2）设点C 是所求抛物线上一点，线段BC 与x 轴正半轴相交于点D ，如果53=CD BD ，求点C 的坐标；（3）在（2）条件下，联结AC ，求ABC ∠的度数.9、（浦东）已知：抛物线32-+=bx ax y 经过点A （7，﹣3），与x 轴正半轴交于点B （m ，0）、C （6m 、0）两点，与y 轴交于点D ． （1）求m 的值；（2）求这条抛物线的表达式；（3）点P 在抛物线上，点Q 在x 轴上，当∠PQD=90°且PQ=2DQ 时，求点P 、Q 的坐标．10、（普陀）如图，在平面直角坐标系xOy 中，二次函数)0(22>+-=m m x x y 的对称轴与比例系数为5的反比例函数图象交于点A ，与x 轴交于点B ，抛物线的图象与y 轴交于点C ，且OB OC 3=． （1）求点A 的坐标； （2）求直线AC 的表达式；（3）点E 是直线AC 上一动点，点F 在x 轴上方的平面内，且使以A 、B 、E 、F 为顶点的四边形是菱形，直接写出点F 的坐标．11、（青浦）已知OAB ∆在直角坐标系中的位置如图，点A 在第一象限，点B 在x 轴正半轴上，6OA OB ==，30AOB ∠=︒.（1）求点A 、B 的坐标；（2）开口向上的抛物线经过原点O 和点B ，设其顶点为E ，当OBE ∆为等腰直角三角形时，求抛物线的解析式；（3）设半径为2的EP 与直线OA 交于M N 、两点，已知MN ()2P m ，（0m >），求m 的值.12、（松江）已知抛物线c bx x y ++-=2与x 轴交于点A 和点B （3，0），与y 轴交于点C （0，3），P 是线段BC 上一点，过点P 作PN ∥y 轴交x 轴于点N ，交抛物线于点M ．（1）求该抛物线的表达式；（2）如果点P 的横坐标为2，点Q 是第一象限抛物线上的一点，且△QMC 和△PMC 的面积相等，求点Q 的坐标；（3）如果PN PM 23=，求tan ∠CMN 的值．13、（徐汇）如图，已知抛物线)0(42≠+=a ax y 与x 轴交于点A 和点B （2，0），与y 轴交于点C ，点D 是抛物线在第一象限的点．（1）当△ABD 的面积为4时，①求点D 的坐标；②联结OD ，点M 是抛物线上的点，且∠MDO=∠BOD ，求点M 的坐标；（2）直线BD 、AD 分别与y 轴交于点E 、F ，那么OE+OF 的值是否变化，请说明理由．14、（杨浦）如图，已知抛物线c x ax y +-=2的对称轴为直线x=1，与x 轴的一个交点为A （﹣1，0），顶点为B ．点C （5，m ）在抛物线上，直线BC 交x 轴于点E ．（1）求抛物线的表达式及点E 的坐标；（2）联结AB ，求∠B 的正切值；（3）点G 为线段AC 上一点，过点G 作CB 的垂线交x 轴于点M （位于点E 右侧），当△CGM 与△ABE 相似时，求点M 的坐标．15、（长宁金山）已知△OAB在直角坐标系中的位置如图，点A在第一象限，点B在x轴正半轴上，OA=OB=6，∠AOB=30°．（1）求点A、B的坐标；（2）开口向上的抛物线经过原点O和点B，设其顶点为E，当△OBE为等腰直角三角形时，求抛物线的解析式；2，P（m，2）（m＞0），（3）设半径为2的⊙P与直线OA交于M、N两点，已知MN=3求m的值．。
2017年上海青浦中考数学二模--2017.04.20
青浦区2016学年九年级第二次学业质量调研测试数学试卷2017.4一、单项选择题（本大题共6题，每题4分，满分24分） 1. 下列运算中，正确的是（ ）A. 21a a −=B. 2a a a +=C. 336()a a =D. 824a a a ÷=2. 不等式组23120x x +≥−< 的解集在数轴上可表示为（ ）3. ）A. 3−B. 3或3−C. 9D. 3 4. 在正方形网格中，△ABC 的位置如图所示，则cos B ∠的值为（ ）A.B.C.D. 15. 某集团公司有9个子公司，各个子公司所创年利润的情况如下表所示.各子公司所创年利润的众数和中位数分别是（ ） A. 4千万元，3千万元 B. 6千万元，4千万元 C. 6千万元，3千万元 D. 3千万元，3千万元6.如图，在四边形ABCD 中，动点P 从点A 开始沿A B C D →→→的路径匀速前进到D 为止. 在这个过程中，△APD 的面积S 随时间t 的变化关系用图像表示正确的是（ ）二、填空题（本大题共12题，每题4分，满分48分） 7. 若23x y =，则x x y=+________________. 8. 在实数范围内因式分解：23x −=________________. 110. 已知反比例函数1k y x−=的图像经过一、三象限，则实数k 的取值范围是________________. 11. 已知关于x 的方程220x x m −+=有实数根，那么实数m 的取值范围是________________.12. 1=的解为________________.13. 抛物线223(0)y ax ax a =−++≠的对称轴是________________.14. 布袋中装有3个红球和n 个白球，它们除颜色外其它都相同，如果从布袋里随机摸出一个球，所摸到的球恰好是红球的概率是13，那么布袋中白球有________________个.15. 化简：2aa⃗−3(13aa ⃗−bb �⃗)=________________. 16. 如图，在菱形ABCD 中，//EF BC ，13AE BE =，3EF =，则CD 的长为________________.17. 在△ABC 中，已知4BC =cm ，以边AC 的中点P 为圆心1cm 为半径画⊙P ，以边AB 的中点Q 为圆心x cm 长为半径画⊙Q ，如果⊙P 与⊙Q 相切，那么x =________________cm.18. 如图，在Rt △ABC 中，AB AC =，D 、E 是斜边BC 上两点，且45DAE ∠=°，将△ADC 绕点A 顺时针旋转90°后，得到△AFB . 设BE a =，DC b =，那么AB =________________.（用含a 、b 的式子表示AB ）三、解答题（本大题共7题，满分78分） 19. （本题满分10分）计算：1120176cos30|2|2−++°−.20. （本题满分10分）解方程：24211422x x x x −=−−−+.21. （本题满分10分，第（1）小题5分，第（2）小题5分） 已知直线132y x =−+与x 轴、y 轴分别交于A 、B 两点，设O 为坐标原点. （1）求ABO ∠的正切值；（2）如果点A 向左平移12个单位到点C ，直线l 过点C 且与直线132y x =−+平行，求直线l 的解析式.22. （本题满分10分）小明在海湾社林公园放风筝. 如图所示，小明在A处，风筝飞到C处，此时线长BC为40米，若小明双手牵住绳子的底端B距离地面1.5米，从B处测得C处的仰角为60°，求此时风筝离地面的高度.（计算结果精确到0.1 1.732≈）23. （本题满分12分，第（1）小题4分，第（2）小题8分）如图，在△ABC中，点P是AC边上的一点，过点P作与BC平行的直线PQ，交AB于点Q，点D在线段BC上，联接AD交线段PQ于点E，且CP QECD BD=，点G在BC延长线上，ACG∠的平分线交直线PQ于点F.（1）求证：PC PE=；（2）当P是边AC的中点时，求证：四边形AECF是矩形.24. （本题满分12分，第（1）小题3分，第（2）小题4分，第（3）小题5分）已知△OAB 在直角坐标系中的位置如图，点A 在第一象限，点B 在x 轴正半轴上，6OA OB ==，30AOB ∠=°. （1）求点A 、B 的坐标； （2）开口向上的抛物线经过原点O 和点B ，设其顶点为E ，当△OBE 为等腰直角三角形时，求抛物线的解析式；（3）设半径为2的⊙P 与直线OA 交于M 、N 两点，已知MN =，(,2)P m (0)m >，求m 的值.25. （本题满分14分，第（1）小题4分，第（2）小题5分，第（3）小题5分）如图，△ABC 的边AB 是⊙O 的直径，点C 在⊙O 上，已知6AC =cm ，8BC =cm ，点P 、Q 分别在边AB 、BC 上，且点P 不与点A 、B 重合，(0)BQ k AP k =⋅>，联接PC 、PQ . （1）求⊙O 的半径长；（2）当2k =时，设AP x =，△CPQ 的面积为y ，求y 关于x 的函数关系式，并写出定义域； （3）如果△CPQ 与△ABC 相似，且ACB CPQ ∠=∠，求k 的值.参考答案1-6:BBDADC 7、258、(x x +9、10、1k > 11、1m ≤ 12、2x = 13、1x = 14、6 15、3a b +16、12 17、1或318a b ++ 19、1+20、1x =21、（1）2；（2）132y x =−−；22、36.123、（1）证明略；（2）证明略.24、（1）(6,0)B ,()A ;（2）2123y x x =−；（3）2−或2+ 25、（1）5；（2）234224,(04)55y x x x =−+<<；（3）720。
2017年上海市浦东新区中考数学、语文、英语二模试卷
三、解答题：（本大题共 7 题，满分 78 分）
19．计算：|2﹣ |﹣8 +2﹣2+
．
20．解不等式组：
．
21．已知：如图，在平面直角坐标系 xOy 中，点 A 在 x 轴的正半轴上，点 B、C 在第一象限，且四边形 OABC 是平行四边形，OC=2 ，sin∠AOC= ，反比例
函数 y= 的图象经过点 C 以及边 AB 的中点 D． 求：（1）求这个反比例函数的解析式； （2）四边形 OABC 的面积．
【考点】M3：垂径定理的应用． 【分析】根据题意构造直角三角形，进而利用勾股定理求出答案． 【解答】解：设圆弧形桥拱所在圆心为 O，连接 BO，DO， 可得：AD=BD，OD⊥AB， ∵AB=16 米，拱高 CD=4 米， ∴BD=AD=8m，
12．计算：2 + （ + ） ．
13．将抛物线 y=x2+2x﹣1 向上平移 4 个单位后，所得新抛物线的顶点坐标是 ． 14．一个不透明的袋子里装有 3 个白球、1 个红球，这些球除了颜色外无其他的 差异，从袋子中随机摸出 1 个球，恰好是白球的概率是 ． 15．正五边形的中心角的度数是 ． 16．如图，圆弧形桥拱的跨度 AB=16 米，拱高 CD=4 米，那么圆弧形桥拱所在圆 的半径是 米．
14．一个不透明的袋子里装有 3 个白球、1 个红球，这些球除了颜色外无其他的
差异，从袋子中随机摸出 1 个球，恰好是白球的概率是
．
【考点】X4：概率公式． 【分析】根据不透明的袋子里装有 3 个白球、1 个红球，共有 4 个球，再根据概 率公式即可得出答案． 【解答】解：∵不透明的袋子里装有 3 个白球、1 个红球，共有 4 个球，
11．如果方程 x2﹣2x+m=0 有两个实数根，那么 m 的取值范围是 m≤1 ．
2017年上海市各区数学二模压轴题——图文解析
2017 年上海市浦东新区中考模拟第 24、25 题 / 34 2017 年上海市普陀区中考模拟第 24、25 题 / 38 2017 年上海市松江区中考模拟第 24、25 题 / 42 2017 年上海市徐汇区中考模拟第 24、25 题 / 47 2017 年上海市杨浦区中考模拟第 24、25 题 / 52 2017 年上海市长宁区青浦区金山区中考模拟第 24、25 题 / 55 2017 年上海市宝山区中考模拟第 18 题 / 59 2017 年上海市崇明区中考模拟第 18 题 / 60 2017 年上海市奉贤区中考模拟第 18 题 / 61 2017 年上海市虹口区中考模拟第 18 题 / 62 2017 年上海市黄浦区中考模拟第 18 题 / 63 2017 年上海市嘉定区中考模拟第 18 题 / 64 2017 年上海市静安区中考模拟第 18 题 / 65 2017 年上海市闵行区中考模拟第 18 题 / 66 2017 年上海市浦东新区中考模拟第 18 题 / 67 2017 年上海市普陀区中考模拟第 18 题 / 68 2017 年上海市松江区中考模拟第 18 题 / 69 2017 年上海市徐汇区中考模拟第 18 题 / 70 2017 年上海市杨浦区中考模拟第 18 题 / 71 2017 年上海市长宁区青浦区金山区中考模拟第 18 题 / 72 2015 年上海市中考第 24、25 题 / 73 2016 年上海市中考第 24、25 题 / 77
心从点 C 出发，沿着 CB 方向以 1 个单位长度/秒的速度匀速运动，同时动点 P 从点 B 出发， 沿着 BA 方向也以 1 个单位长度/秒的速度匀速运动，设运动时间为 t 秒（0＜t≤5） ，以 P 为 圆心、PB 为半径的⊙P 与 AB、BC 的另一个交点分别为 E、D，联结 ED、EQ． （1）判断并证明 ED 与 BC 的位置关系，并求当 点 Q 与点 D 重合时 t 的值； （2）当⊙P 和 AC 相交时，设 CQ 为 x，⊙P 被 AC 解得的弦长为 y，求 y 关于 x 的函数解析式，并求 当⊙Q 过点 B 时⊙P 被 AC 截得的弦长； （3）若⊙P 与⊙Q 相交，写出 t 的取值范围． 图1
2017初三数学二模汇编24题
（长宁青浦）24.（本题满分12分）已知△OAB在直角坐标系中的位置如图，点A在第一象限，点B在x轴正半轴上，OA=OB=6，∠AOB=30°.（1）求点A、B的坐标；等腰直角三角形时，求抛物线的解析式；（3）设半径为2的⊙P与直线OA交于M、N两点，已知MN=P(m，2）（m>0),求m的值.第24题图（杨浦）24．（本题满分12分，第（1）小题4分，第（2）小题3分，第（3）小题5分）如图，已知抛物线2y ax x c =-+的对称轴为直线x =1，与x 轴的一个交点为A （-1，0），顶点为B . 点C （5，m ）在抛物线上，直线BC 交x 轴于点E . （1） 求抛物线的表达式及点E 的坐标； （2） 联结AB ，求∠B 的正切值；（3） 点G 为线段AC 上一点，过点G 作CB 的垂线交x 轴于点M （位于点E 右侧），当△CGM 与△ABE 相似时，求点M 的坐标.x yA BE C O （第24题图）（徐汇）24．（本题满分12分）如图10，已知抛物线)0(42≠+=a ax y 与x 轴交于点A 和点)0,2(B ，与y 轴交于点C ，点D 是抛物线在第一象限的点． （1）当ABD ∆的面积为4时，① 求点D 的坐标； （4分）② 联结OD ，点M 是该抛物线上的点，且BOD MDO ∠=∠，求点M 的坐标；（4分）（2）直线BD 、AD 分别交y 轴于点E 、F ，那么OF OE +的值是否变化，请说明理由． （4分）（松江）24．（本题满分12分，第（1）小题3分，第（2）小题4分，第（3）小题5分）已知抛物线c bx x y ++-=2与x 轴交于点A 和点B （3，0），与y 轴交于点C （0，3），P 是线段BC 上一点，过点P 作PN ∥y 轴交x 轴于点N ，交抛物线于点M ． （1）求该抛物线的表达式；（2）如果点P 的横坐标为2，点Q 是第一象限抛物线上的一点，且△QMC 和△PMC 的面积相等，求点Q 的坐标； （3）如果PN PM 23=，求tan ∠CMN 的值．（第24题图）（普陀）24．（本题满分12分）如图9，在平面直角坐标系xOy 中，二次函数22y x x m =-+（m ＞0）的对称轴与比例系数为5的反比例函数图像交于点A ，与x 轴交于点B ，抛物线的图像与y 轴交于点C ，且3OC OB =． （1）求点A 的坐标；（2）求直线AC 的表达式；（3）点E 是直线AC 上一动点，点F 在x 轴上方的平面内，且使以A 、B 、E 、F 为顶点的四边形是菱形，直接写出点F 的坐标．图9（闵行）24．（本题共3小题，其中每小题各4分，满分12分）如图，在平面直角坐标系xOy中，抛物线2(1)3y x m x m=--+经过点A（1-，0），且与y轴相交于点B．（1）求这条抛物线的表达式及点B的坐标；（2）设点C是所求抛物线上一点，线段BC与x轴正半轴相交于点D．如果35BDCD=，求点C的坐标；（3）在（2）条件下，联结AB．求∠ABC的度数．O xy（第24题图）（静安）24．（本题满分12分，第（1）小题满分5分，第（2）小题满分7分）已知二次函数c bx x y ++-=221的图像与x 轴的正半轴相交于点A （2，0）和点B 、 与y 轴相交于点C ，它的顶点为M 、对称轴与x 轴相交于点N ． （1） 用b 的代数式表示顶点M 的坐标； （2） 当tan ∠MAN =2时，求此二次函数的解析式 及∠ACB 的正切值．（嘉定）24．（本题满分12分，每小题4分）在平面直角坐标系xOy （如图7）中，已知点A 的坐标为（3,1），点B 的坐标为（6，5），点C 的坐标为（0,5）；某二次函数的图像经过点A 、点B 与点C . （1）求这个二次函数的解析式；（2）假如点Q 在该函数图像的对称轴上，且△ACQ 是等腰三角形，直接．．写出点Q 的坐标； （3）如果第一象限内的点P 在（1）中求出的二次函数 的图像上，且21tan =∠PCA ，求PCB ∠的正弦值.图7（黄浦）24．（本题满分12分）如图，点A 在函数()40y x x =>图像上，过点A 作x 轴和y 轴的平行线分别交函数xy 1=图像于点B 、C ，直线BC 与坐标轴的交点为D 、E .（1）当点C 的横坐标为1时，求点B 的坐标； （2）试问：当点A 在函数()40y x x=>图像上运动时，△ABC 的面积是否发生变化？若不变，请求出△ABC 的面积；若变化，请说明理由；（3）试说明：当点A 在函数()40y x x=>图像上运动时，线段BD 与CE 的长始终相等.E BCA DxyO图8（奉贤）24．（本题满分12分，每小题4分）如图8，在平面直角坐标系xOy 中，抛物线y 2经过点A (3，0)和点B (2，3)，过点A 的直线与y 轴的负半轴相交于点C ，且（1）求这条抛物线的表达式及对称轴； （2）联结AB 、BC ，求∠ABC 的正切值；（3）若点D 在x 轴下方的对称轴上，当ABC S ∆= 求点D 的坐标．（崇明）24．（本题满分12分，其中每小题各4分）如图，已知抛物线22y ax x c =-+经过ABC ∆AC x ∥轴．（1）求这条抛物线的解析式；（2）求tan ABC ∠的值；（3）若点D 为抛物线的顶点，点E 是直线AC 上一点，当CDE ∆与ABC ∆相似时，求点E 的坐标．（第24题图）（宝山）24. （本题满分12分，每小题满分各4分)如图7，已知直线221-=x y 与x 轴交于点B ，与y 轴交于点C ，抛物线2212-+=bx x y 与x 轴交于A 、B 两点（A 在B 的左侧），与y 轴交于点C.（1）求抛物线的解析式；（2）点M 是上述抛物线上一点，如果△ABM 和△ABC 相似，求点M 的坐标；（3）连接AC ，求顶点D 、E 、F 、G 在△ABC 各边上的矩形DEFC面积最大时，写出该矩形在AB 边上的顶点的坐标．图7（浦东）24.(本题满分12分，其中第（1）小题3分，第（2）小题4分，第（3）小题5分)已知抛物线23y ax bx =+-经过点(7,3)A -，与x 轴正半轴交于()(,0)6,0B m C m 、两点，与y 轴交于点D .（1）求m 的值；（2）求这条抛物线的表达式；（3）点P 在抛物线上，点Q 在x 轴上，当90PQD ∠=,且2PQ DQ =时，求点P Q 、的坐标。
上海市浦东新区2017年中考数学二模试卷(含解析)
2017年上海市浦东新区中考数学二模试卷、选择题：（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】1 •下列实数中，是无理数的为（）A. 3.14 B •一 C.二D.-2 •下列二次根式中，与—是同类二次根式的是（）A—B • ： C 7 D• 73•函数y=kx - 1 （常数k > 0）的图象不经过的象限是（）A.第一象限B •第二象限C •第三象限D •第四象限4.某幢楼10户家庭每月的用电量如下表所示：用电量（度）140 160 180 200户数1342那么这10户家庭该月用电量的众数和中位数分别是（）A. 180, 180 B • 180, 160 C • 160, 180 D • 160, 1605•已知两圆的半径分别为1和5，圆心距为4,那么两圆的位置关系是（）A.外离B .外切C .相交D .内切6.如图，已知△ ABC^D^ DEF点E在BC边上，点A在DE边上，边EF和边AC相交于点G.如果AE=EC / AEG=/ B,那么添加下列一个条件后，仍无法判定△DEF-与^ ABC一定相似的是AB DE D AD GF c AG EG 厂ED EGBC EF AE GE AC EF EF EA、填空题：（本大题共12题，每题4分，满分48分）【请将结果直接填入答题纸的相应位置上】( )7 .计算：a?a 2=&因式分解：x2- 2x= ______ .9.方程=-x的根是 ______________ .10•函数f (x)='的定义域是x+2 -----11. _______________________________________________________ 如果方程X2-2x+m=0有两个实数根，那么m的取值范围是__________________________________ .12. 计算：2「+.： ( + ■) _.13. ___________________________________________________________________ 将抛物线y=x2+2x- 1向上平移4个单位后，所得新抛物线的顶点坐标是______________________ .14. 一个不透明的袋子里装有3个白球、1个红球，这些球除了颜色外无其他的差异，从袋子中随机摸出1个球，恰好是白球的概率是_______ .15. ____________________________ 正五边形的中心角的度数是.16 .如图，圆弧形桥拱的跨度AB=16米，拱高CD=4米,那么圆弧形桥拱所在圆的半径是米.Ann17 .如果一个三角形一边上的中线的长与另两边中点的连线段的长相等，我们称这个三角形为“等线三角形”，这条边称为“等线边”. 在等线三角形ABC中，AB为等线边，且AB=3AC=2,那么BC ____ .18.如图，矩形ABCD中, AB=4, AD=7点E, F分别在边AD BC上，且B F关于过点E三、解答题：(本大题共7题，满分78 分)3(2x-l) >4旷5 ①q 1亍-1<知②19.计算:|2 - "| -8 …+2-2+」.20.解不等式组:21. 已知：如图，在平面直角坐标系xOy中，点A在x轴的正半轴上，点 B C在第一象限,且四边形OABC是平行四边形，OC=2 —, sin / AOC=,.J],反比例函数y=「的图象经过点CJ 5 X以及边AB的中点D.求：(1 )求这个反比例函数的解析式;22. 某文具店有一种练习簿出售，每本的成本价为2元，在销售的过程中价格有些调整，按原来的价格每本8.25元，卖出36本；经过两次涨价，按第二次涨价后的价格卖出了25本•发现按原价格和第二次涨价后的价格销售，分别获得的销售利润恰好相等.(1 )求第二次涨价后每本练习簿的价格;CD上，且BE=DF=AD联结DE联结AF、BF分别与DE交于点G P.24.已知：抛物线y=ax2+bx-3经过点A (乙-3),与x轴正半轴交于点0)两点，与y轴交于点D.(1、求m的值;(2、求这条抛物线的表达式;(3、点P在抛物线上，点Q在x轴上，当/ PQD=90且PQ=2DQ寸，求点P、Q的坐标.(2)在两次涨价过程中，假设每本练习簿平均获得利润的增长率完全相同,(注：利润增长率x 100%)求这个增长率.前一枕的刑润23.已知：如图，在直角梯形ABCD中, AD// BC, / C=90 , BC=CD 点E、F分别在边BCB ( m, 0)、C (6m、(1)求证：AB=BFDG=GEO 125.如图所示，/ M0N=4° ,点P是/ MON内一点，过点P作PA丄0M于点A PB丄ON于点B, 且PB=2三.取0P的中点C,联结AC并延长，交0B于点D.(1 )求证：/ ADB=/ OPB(2 )设PA=x OD=y求y关于x的函数解析式；(3)分别联结AB BC,当厶ABM A CPB相似时，求PA的长.2017年上海市浦东新区中考数学二模试卷参考答案与试题解析一、选择题：（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】1 •下列实数中，是无理数的为（）A. 3.14 B • C - D -【考点】26 :无理数.【分析】A、B、C、D根据无理数的概念“无理数是无限不循环小数，其中有开方开不尽的数”即可判定选择项.【解答】解：A、B、D中3.14 , , - =3是有理数，C中「是无理数.故选：C.2 •下列二次根式中，与 .一是同类二次根式的是（）A. — B •： C 7 D •厂【考点】77:同类二次根式.【分析】根据二次根式的性质把各个二次根式化简，根据同类二次根式的概念判断即可.【解答】解：A、—与—不是同类二次根式；B厂="a与.不是同类二次根式；C』o=a 一与—是同类二次根式；D - =a2与—不是同类二次根式；故选：C.3•函数y=kx - 1 （常数k > 0）的图象不经过的象限是（）A.第一象限B .第二象限C .第三象限D .第四象限【考点】F7: —次函数图象与系数的关系.【分析】一次函数y=kx - 1 （常数k>0）的图象一定经过第一、三，四象限，不经过第二象限. 【解答】解：•一次函数y=kx - 1 （常数k>0）, b=- 1 v0,•••一次函数y=kx - 1 （常数k>0）的图象一定经过第一、三，四象限，不经过第二象限.故选：B.4. 某幢楼10户家庭每月的用电量如下表所示：用电量（度）140 160 180 200户数1342那么这10户家庭该月用电量的众数和中位数分别是（）A. 180, 180 B . 180, 160 C . 160, 180 D . 160, 160【考点】W5众数；W4中位数.【分析】根据众数和中位数的定义求解可得.【解答】解：由表可知180出现次数最多，故众数为180,•••共有1+3+4+2=10个数据,•中位数为第5、6个数据的平均数，即：丿V：=180,2故选：A.5. 已知两圆的半径分别为1和5，圆心距为4,那么两圆的位置关系是（）A.外离B .外切C .相交D .内切【考点】MJ圆与圆的位置关系.【分析】由两圆半径分别是1和5,圆心距为4，两圆位置关系与圆心距d,两圆半径R, r 的数量关系间的联系即可得出两圆位置关系.【解答】解：：•两圆半径分别是1和5,圆心距为4,又T 5-仁4,•这两个圆的位置关系内切.故选D.6. 如图，已知△ ABC^D^ DEF点E在BC边上，点A在DE边上，边EF和边AC相交于点G.如果AE=EC / AEG=/ B,那么添加下列一个条件后，仍无法判定△DEF-与^ ABC一定相似的是AAB _ DE o AD _ GF c AG _ EG n ED _ EGBC EF AE GE AC EF EF BA【考点】S8:相似三角形的判定.【分析】利用两组对应边的比相等且夹角对应相等的两个三角形相似可由—='得到△ ABCBC EFEDF 利用军孕或军=¥2可根据两组对应边的比相等且夹角对应相等的两个三角形AE GE EF EA相似先判断△ DEI A AEG 再利用有两组角对应相等的两个三角形相似判定△ AE3A ABC从而得到厶AB3A EDF ,于是可对各选项进行判断.【解答】解：当二= ._；时则】j ，而/ B=Z AEG 所以△ AB" EDFAD GF DE HF当.一.=一_.，则一=…，而/ DEF=/ AEG 所以△ DEF-A AEG AL vE nE ntj / C,而/ AEG=z B ,所以△ AE3A ABC 所以△ ABC^A EDF 当r <，则.<■，而/ DEF’ AEG 所以"△ AEG 又因为/ C,而/ AEG=z B ,所以△ AE3A ABC 所以△ ABC^A EDF 故选C.二、填空题：（本大题共12题，每题4分，满分48分）【请将结果直接填入答题纸的相应 位置上】7 .计算：a?a 2= a 3.【考点】46:同底数幕的乘法.【分析】根据同底数幕的乘法法则，同底数幕相乘，底数不变，指数相加，即 a m ?a n =a m+n 计算即可.【解答】 解：a?a 2=a 1+2=a 3. 故答案为：a 3.&因式分解：x 2 - 2x= x (x - 2)又因为 AE=EC 所以/ EAG= AE=EC 所以/ EAG=【考点】53:因式分解-提公因式法.【分析】原式提取x即可得到结果.【解答】解：原式=x (x - 2),故答案为：x (x - 2)9. 方程匸二=-x的根是x= - 4 .【考点】AG无理方程.【分析】方程两边平方转化为整式方程，求出整式方程的解得到x的值，经检验即可得到无理方程的解.【解答】解：两边平方得：8-2x=x2,整理得：(x+4) (x - 2) =0,可得x+4=0 或x - 2=0,解得：x= - 4或x=2,经检验x=2是增根，无理方程的解为x=- 4.故答案为：x= - 410. 函数f (x)='的定义域是X M- 2 .x+2 -------------【考点】E4:函数自变量的取值范围.【分析】根据分式有意义的条件分母不为0计算即可.【解答】解：由X+2M 0得，x M- 2;故答案为x M- 2.11. 如果方程x2- 2x+m=0有两个实数根，那么m的取值范围是me 1【考点】AA根的判别式.【分析】由方程x2- 2x+m=0有两个实数根，即可得判别式0，继而可求得m的取值范围.【解答】解：•••方程x2- 2x+m=0有两个实数根，2 2/•△=b - 4ac= (- 2) - 4 X 1 x m=4- 4m> 0,解得：me 1.故答案为：m e 1.【考点】LM *平面向量.【分析】根据向量的加法运算法则进行计算即可得解.【解答】解：2 ( + '),13•将抛物线y=x2+2x - 1向上平移4个单位后，所得新抛物线的顶点坐标是(-1,2)【考点】H6:二次函数图象与几何变换.【分析】将抛物线解析式整理成顶点式形式，求出顶点坐标，再根据向上平移纵坐标加求解即可.【解答】解：•••y=x2+2x- 1= ( x+1) 2- 2,•••原抛物线的顶点坐标为(- 1,- 2),•••向上平移4个单位后，•••平移后抛物线顶点横坐标不变，纵坐标为- 2+4=2,•所得新抛物线的顶点坐标是(- 1, 2).故答案为：(-1, 2).14. 一个不透明的袋子里装有3个白球、1个红球，这些球除了颜色外无其他的差异，从袋3子中随机摸出1个球，恰好是白球的概率是..—4—【考点】X4:概率公式.【分析】根据不透明的袋子里装有3个白球、1个红球，共有4个球，再根据概率公式即可得出答案.【解答】解：•••不透明的袋子里装有3个白球、1个红球，共有4个球，•从袋子中随机摸出1个球，恰好是白球的概率是 ..故答案为：:.415. 正五边形的中心角的度数是72° .【考点】MM正多边形和圆.12.计算: 2 -+「一+)【分析】根据正多边形的圆心角定义可知：正n边形的圆中心角为一，则代入求解即n可.【解答】解：正五边形的中心角为：——=72°.5故答案为：72°.16. 如图，圆弧形桥拱的跨度AB=16米，拱高CD=4米，那么圆弧形桥拱所在圆的半径是_J0米.A n【考点】M3垂径定理的应用.【分析】根据题意构造直角三角形，进而利用勾股定理求出答案.【解答】解：设圆弧形桥拱所在圆心为0,连接BQ DO可得：AD=BD ODL AB•/ AB=16 米，拱高CD=4米,/• BD=AD=8m设BO=xm 贝U D0=( x - 4) m,根据题意可得：BD2+D(Q=BQ),即82+ (x - 4) 2=x2,解得：x=10 ,即圆弧形桥拱所在圆的半径是10m故答案为：10.17. 如果一个三角形一边上的中线的长与另两边中点的连线段的长相等，我们称这个三角形为“等线三角形”，这条边称为“等线边”.在等线三角形ABC中，AB为等线边，且AB=3 AC=2 那么BC= T .【考点】KX三角形中位线定理.【分析】由三角形的中位线定理证得EF=_AB,根据题意得出CD=AB从而证得厶ABC是直角三角形，再利用勾股定理得出BC的长.【解答】解：••• E, F分别是AC, BC的中点，••• EF= AB,2•/ CD=EF•CD= AB,2•/ AD=BD•△ ABC是直角三角形，/ ACB=90 ,•/ AB=3, AC=2•BC=/小乎」:？=；二=., 故答案为：「.18. 如图，矩形ABCD中 , AB=4, AD=7点E , F分别在边AD BC上,且B F关于过点E的直线对称，如果以CD为直径的圆与EF相切，那么AE= 3 .A【考点】MC切线的性质；LB:矩形的性质；P2:轴对称的性质.【分析】设O O与EF相切于M连接EB作EHL BC于H.由题意易知四边形AEHB是矩形，设AE=BH=x由切线长定理可知，ED=EMFC=FM由B、F关于EH对称，推出HF=BH=x ED=EM=7 -x, FC=FM=7- 2x, EF=14-3x，在Rt △ EFH中，根据Eh=EH+HF，列出方程即可解决问题.【解答】解：如图，设O O与EF相切于M连接EB作EH L BC于H.由题意易知四边形AEHB是矩形，设AE=BH=x由切线长定理可知，ED=EM FC=FM••• B、F关于EH对称，••• HF=BH=x ED=EM=- x, FC=FM=- 2x, EF=14- 3x,在Rt△ EFH中，T E F=E H+H F,•42+X2= (14 - 3x) 2,15解得X=3或.(舍弃)，•AE=3,故答案为3.三、解答题：（本大题共7题，满分78分）19•计算：|2 - 7| - 8 +2- 2+——.【考点】2C:实数的运算；2F:分数指数幕；6F:负整数指数幕.【分析】首先计算乘方，然后从左向右依次计算，求出算式的值是多少即可.L ±- 2 1【解答】解：|2 - ,_| - 8 +2 +一=2- 2+ + ~+13(2x-l)>4x-5$20. 解不等式组:【考点】CB解一元一次不等式组.【分析】先求出各不等式的解集，再求其公共解集即可.3(2x7)>4旷5① yx-l<yx@ ，解不等式①得x>- 1,解不等式②得x < 1,所以不等式组的解集为-1v x< 1 .21. 已知：如图，在平面直角坐标系xOy中，点A在x轴的正半轴上，点 B C在第一象限，且四边形OABC是平行四边形，OC=2二,sin / AOC=三，反比例函数y=「的图象经过点C5 K以及边AB的中点D.求：(1 )求这个反比例函数的解析式；【考点】G7:待定系数法求反比例函数解析式；G5:反比例函数系数k的几何意义；L5:平行四边形的性质；T7:解直角三角形.【分析】(1 )过C作CM L x轴于M,则/ CMO=9°，解直角三角形求出CM根据勾股定理求出OM 求出C的坐标，即可求出答案；(2)根据D为中点求出DN的值，代入反比例函数解析式求出ON求出OA根据平行四边形的面积公式求出即可.过C作CML x轴于M 则/ CMO=90 ,•••0C=2「, sin / AOC=_ = ；—,••• MC=4由勾股定理得：0M= ' | ] , ：■■- ?_,;:=2,• C的坐标为（2, 4）,代入y=—得：k=8,所以这个反比例函数的解析式是y=：;过 B 作BEL x轴于E,贝U BE=CM=4 AE=0M=2 过D 作DN L x 轴于N•/ D为AB的中点，•DN= ]=2, AN= 、:=1,把y=2代入y=得：x=4,即0N=4•0A=4-仁3,•四边形0ABC勺面积为0从CM=3< 4=12.22. 某文具店有一种练习簿出售，每本的成本价为2元，在销售的过程中价格有些调整，按原来的价格每本8.25元，卖出36本；经过两次涨价，按第二次涨价后的价格卖出了25本•发现按原价格和第二次涨价后的价格销售，分别获得的销售利润恰好相等.(1 )求第二次涨价后每本练习簿的价格；(2)在两次涨价过程中，假设每本练习簿平均获得利润的增长率完全相同，求这个增长率.(注：利润增长率“ ；」.100%前—次的利润【考点】AD 一元二次方程的应用.【分析】(1)设第二次涨价后每本练习簿的价格为x元，根据总利润=单本利润X数量结合两次销售总利润相等，即可得出关于x的一元一次方程，解之即可得出结论；(2)设每本练习簿平均获得利润的增长率为y，根据涨价前单本利润已经连续两次涨价后的单本利润，即可得出关于y的一元二次方程，解之取其正值即可.【解答】解：(1)设第二次涨价后每本练习簿的价格为x元，根据题意得：(8.25 - 2)X 36= (x - 2)X 25,解得：x=11.答：第二次涨价后每本练习簿的价格为11元.(2)设每本练习簿平均获得利润的增长率为y,根据题意得：(8.25 - 2) ( 1+y) 2=11 - 2,解得：y1=0.2=20%, y2=- 2.2 (舍去).答：每本练习簿平均获得利润的增长率为20%23. 已知：如图，在直角梯形ABCD中，AD// BC, / C=90 , BC=CD点E、F分别在边BGCD上，且BE=DF=AD联结DE联结AF、BF分别与DE交于点G P.(1)求证：AB=BF(2)如果BE=2EC 求证：DG=GE【考点】S9:相似三角形的判定与性质；KD全等三角形的判定与性质；LI :直角梯形.【分析】(1)先证△ BCF^A DCE再证四边形ABED是平行四边形，从而得AB=DE=BF(2)延长AF交BC延长线于点M从而CM=CF又由AD// BC可以得到竺==1,从而DG=GEGE EM【解答】证明：(1 )T BC=CD BE=DF••• CF=CE在厶BCF与厶DCE中，(CF=CEI ZC=ZC=90°,I BC=DC•••△BCF^A DCE•BF=DE•/ AD// BC, BE=AD•四边形ABED是平行四边形；•AB=DE•AB=BF(2)延长AF交BC延长线于点M贝U CM=CF•/ AD// BC,•些型•GE =珈，•/ BE=2EC.DG_AD .= =1 ,「口I224. 已知：抛物线y=ax+bx- 3经过点A (乙-3),与x轴正半轴交于点B( m 0)、C (6m0)两点，与y轴交于点D.(1 )求m的值；(2) 求这条抛物线的表达式；(3) 点P在抛物线上，点Q在x轴上，当/ PQD=90且PQ=2DQ寸，求点P、Q的坐标.【分析】(1)先求得点D的坐标，然后设抛物线的解析式为y=a (x- m) (x-6m),把点D 和点A的坐标代入可求得m的值；(2)由6am=-3, m=1可求得a的值，然后代入抛物线的解析式即可；(3)过点P作PE± x轴，垂足为 E.设点Q的坐标为(a, 0)则OQ- a,然后证明厶ODQEQP依据相似三角形的性质可求得QE=6 PE=- 2a.,则P的坐标为(a+6 , - 2a),将点P的坐标代入抛物线的解析式可求得a的值.【解答】解：(1)当x=0时，y=- 3 ,••• D (0, - 3).设抛物线的解析式为y=a (x- nr) (x- 6m).把点D和点A的坐标代入得：6am=- 3①，a ( 7- n) ( 7- 6n) =- 3②，2• a (7 - nr) (7 - 6mj) =6am.•/ a 丰 0,2••( 7- m) ( 7- 6m) =m.解得：m=1(2 )T 6am =- 3,• a=丄=丄…a= •一6 m22j i 2将a=-=, m=1 代入得：y= - —x + x- 3.1 2 7•抛物线的表达式为y= - —x x - 3.(3)如图所示：过点P作PE L x轴，垂足为E.设点Q的坐标为(a, 0)则0Q= a-DQP=90 ,•••/ PQO y OQD=9° .又•••/ ODQ£ DQO=9° ,•••/ PQE2 ODQ又•••/ PEQ M DOQ=9° ,•△OD©A EQP•鱼=OD=QD = 1 即二二PE = 1•PE -矿丽迈，即可=E迈，•QE=6 PE=- 2a.•P的坐标为(a+6,- 2a)i 2 '' 2将点P的坐标代入抛物线的解析式得：- ,(a+6) 2+ (a+6)- 3=- 2a,整理得：a2+a=0,解得a= - 1或a=0.当a=- 1 时，Q (- 1, 0) , P (5, 2);当a=0 时，Q( 0, 0), P (6, 0).综上所述，Q (- 1 , 0), P (5, 2)或者Q(0, 0), P (6, 0).25. 如图所示，/ MON=4° ,点P是/ MON内一点，过点P作PA L OM于点A PB丄ON于点B,且PB=2二.取OP的中点C,联结AC并延长，交OB于点D.(1 )求证：/ ADB2 OPB(2 )设PA=x OD=y求y关于x的函数解析式；(3)分别联结AB BC,当厶ABMA CPB相似时，求PA的长.【考点】SO相似形综合题.【分析】(1)先判断出/ DAE=/ POB再利用等角的余角相等即可得出结论；(2)先利用等腰直角三角形的性质得出OB=BF=@( x+2),同理得出OA=x+4即可得出AE,OE进而得出DE,最后用△ AD0A OPB的比例式建立方程化简即可得出结论；(3)先利用直角三角形斜边的中线等于斜边的一半和三角形外角的性质判断出△ABC是等腰直角三角形，即可得出/ OBCy ABP=45 ,再用△ ABD与△ CPB得出，/ ABD* PBC即/OBC=/ ABP= X 45° =22.5。
上海市黄浦区2017届九年级学业模拟（二模）考试数学试题（含答案）
上海市黄浦区2017届九年级学业模拟（⼆模）考试数学试题（含答案）黄浦区2017年九年级学业考试模拟卷数学试卷⼀. 选择题1. 下列分数中，可以化为有限⼩数的是（） A.115； B. 118； C. 315； D. 318； 2. 下列⼆次根式中最简根式是（）A.； B. ； C. D.3. 下表是某地今年春节放假七天最低⽓温（C ?）的统计结果A. 4，4；B. 4，5；C. 6，5；D. 6，6；4. 将抛物线2y x =向下平移1个单位，再向左平移2个单位后，所得新抛物线的表达式是（）A. 2(1)2y x =-+； B. 2(2)1y x =-+； C. 2(1)2y x =+-； D. 2(2)1y x =+-；5. 如果两圆的半径长分别为6与2，圆⼼距为4，那么这两个圆的位置关系是（） A. 内含； B. 内切； C. 外切； D. 相交；6. 下列命题中真命题是（）A. 对⾓线互相垂直的四边形是矩形；B. 对⾓线相等的四边形是矩形；C. 四条边都相等的四边形是矩形；D. 四个内⾓都相等的四边形是矩形；⼆. 填空题7. 计算：22()a = ；8. 因式分解：2288x x -+= ； 9. 计算：111x x x +=+- ；10. 1x =-的根是；11. 如果抛物线2(2)3y a x x a =-+-的开⼝向上，那么a 的取值范围是；12. 某校⼋年级共四个班，各班寒假外出旅游的学⽣⼈数如图所⽰，那么三班外出旅游学⽣⼈数占全年级外出旅游学⽣⼈数的百分⽐为；13. 将⼀枚质地均匀的硬币抛掷2次，硬币证明均朝上的概率是； 14. 如果梯形的下底长为7，中位线长为5，那么其上底长为；15. 已知AB 是O e 的弦，如果O e 的半径长为5，AB 长为4，那么圆⼼O 到弦AB 的距离是；16. 如图，在平⾏四边形ABCD 中，点M 是边CD 中点，点N 是边BC 上的点，且12CN BN =，设AB a =uu u r r ，BC b =uu u r r ，那么MN uuu r 可⽤a r 、b r表⽰为；17. 如图，△ABC 是等边三⾓形，若点A 绕点C 顺时针旋转30°⾄点A '，联结A B '，则ABA '∠度数是；18. 如图，点P 是以r 为半径的圆O 外⼀点，点P '在线段OP 上，若满⾜2OP OP r '?=，则称点P '是点P 关于圆O 的反演点，如图，在Rt △ABO 中，90B ∠=?，2AB =，4BO =，圆O 的半径为2，如果点A '、B '分别是点A 、B 关于圆O 的反演点，那么A B ''的长是；三. 解答题19. 计算：1012481)|1-+-+-；20. 解⽅程组：22221x y x y ?-=-?-=?①②；21. 温度通常有两种表⽰⽅法：华⽒度（单位：F ?）与摄⽒度（单位：C ?），已知华⽒度数y 与摄⽒度数x 之间是⼀次函数关系，下表列出了部分华⽒度与摄⽒度之间的对应关系：（2）已知某天的最低⽓温是－5C ?，求与之对应的华⽒度数；22. 如图，在梯形ABCD 中，AD ∥BC ，AB ⊥BC ，已知2AD =，4cot 3ACB ∠=，梯形ABCD 的⾯积是9；（1）求AB 的长；（2）求tan ACD ∠的值；23. 如图，在正⽅形ABCD 中，点E 在对⾓线AC 上，点F 在边BC 上，联结BE 、DF ，DF 交对⾓线AC 于点G ，且DE DG =；（1）求证：AE CG =；（2）求证：BE ∥DF ；24. 如图，在平⾯直⾓坐标系xOy 中，已知点A 的坐标为(,3)a （其中4a >），射线OA 与反⽐例函数12y x =的图像交于点P ，点B 、C 分别在函数12y x=的图像上，且AB ∥x 轴，AC ∥y 轴；（1）当点P 横坐标为6，求直线AO 的表达式；（2）联结BO ，当AB BO =时，求点A 坐标；（3）联结BP 、CP ，试猜想：ABP ACP S S ??的值是否随a 的变化⽽变化？如果不变，求出ABPACPSS ??的值；如果变化，请说明理由；25. 如图，Rt △ABC 中，90C ∠=?，30A ∠=?，2BC =，CD 是斜边AB 上的⾼，点E 为边AC 上⼀点（点E 不与点A 、C 重合），联结DE ，作CF ⊥DE ，CF 与边AB 、线段DE 分别交于点F 、G ；（1）求线段CD 、AD 的长；（2）设CE x =，DF y =，求y 关于x 的函数解析式，并写出它的定义域；（3）联结EF ，当△EFG 与△CDG 相似时，求线段CE 的长；参考答案⼀. 选择题1. C ；2. C ；3. B ；4. D ；5. B ；6. D ；⼆. 填空题7. 4a ； 8. 22(2)x -； 9. 2211x x +-； 10. 3x =； 11. 2a <； 12. 40%；13.14； 14. 3； 15. ； 16.1123a b -； 17. 15?； 18. 5；三. 解答题19. 解：原式12131)11=+-=-=； 20. 解：由②得：1x y =+，代⼊①得：22(1)22y y +-=-，即2230y y --=，∴(1)(3)0y y +-=，∴11y =-，23y =，∴10x =，24x =，∴⽅程组的解为01x y =?? =-?或43x y =??=?；21. 解：设y kx b =+，代⼊(0,32)和(35,95)，即0323595b k b +=??+=?，∴32b =，95k =，∴9325y x =+，当5x =-时，93223y =-+=；22. 解：（1）Rt ABC 中，4cot 3BC ACB AB ∠==，设4BC k =，3AB k =，∴11()(24)3922ABCD S AD BC AB k k =+=+=，∴1k =或32k =-（舍），∴3AB =，4BC =，5AC =；（2）作DH AC ⊥，∵AD ∥BC ，∴DAH ACB ∠=∠，∴Rt ADH ∽Rt CAB ，∴25DH AD AH AB AC BC ===，∴65DH =，85AH =，∴175CH AC AH =-=，∴6tan 17DH ACD CH ∠==； 23. 解：（1）∵DE DG =，∴DEG DGE ∠=∠，∴AED CGD ∠=∠，⼜∵AD CD =，45DAC DCA ∠=∠=?，∴△ADE ≌△CDG ，∴AE CG =（2）∵BC CD =，CE CE =，45BCE DCE ∠=∠=?，∴△BCE ≌△DCE ，∴BEC DEC DGE ∠=∠=∠，∴BE ∥DF ；24. 解：（1）当6x =时，2y =，∴(6,2)P ，设:OA l y kx =，代⼊(6,2)P 得13k =，∴1:3OA l y x =；（2）当3y =时，4x =，∴(4,3)B ，∵AB BO =，∴54a =-，即9a =，∴(9,3)A （3）3:OA l y x a =，联⽴12y x=，得P a ，作PM AB ⊥，PN AC ⊥，当x a =时，12y a =，即12(,)C a a ，当3y =时，4x =，即(4,3)B ，∴1(4)(32ABP S a a =--，112()2ACP S a a=--，∴3121ABP ACP a S S --==； 25. 解：（1）CD =，3AD =；（2）∵90CDE BFC DCF ∠=∠=?-∠，60ECD B ∠=∠=?，∴△CDE ∽△BFC ，∴CE CD BC BF =，即21x y =+，∴1y =，x ≤< （3）90EGF CGD ∠=∠=?①△EGF ∽△DGC 时，GEF GDC ∠=∠，∴EF ∥DC ，∴CE DFAC AD =133y x -==，解得3x =；②△EGF ∽△CGD 时，∴GEF GCD GDF ∠=∠=∠，∴EF DF =，⼜∵CF DE ⊥，∴EG DG =，∴CD CE ==综上，CE =/doc/eca309e048649b6648d7c1c708a1284ac8500507.html。
上海市黄浦区2017届中考数学二模试卷(含解析)
2017年上海市黄浦区中考数学二模试卷一、选择题（本大题共6小题，每小题4分，共24分）1．单项式4xy2z3的次数是（）A．3 B．4 C．5 D．62．下列方程中，无实数解的是（）A．2+x=0 B．2﹣x=0 C．2x=0 D． =03．下列各组数据中，平均数和中位数相等的是（）A．1，2，3，4，5 B．1，3，4，5，6 C．1，2，4，5，6 D．1，2，3，5，6 4．二次函数y=﹣（x﹣2）2﹣3的图象的顶点坐标是（）A．（2，3） B．（2，﹣3）C．（﹣2，3）D．（﹣2，﹣3）5．以一个面积为1的三角形的三条中位线为三边的三角形的面积为（）A．4 B．2 C． D．6．已知点A（4，0），B（0，3），如果⊙A的半径为1，⊙B的半径为6，则⊙A与⊙B的位置关系是（）A．内切 B．相交 C．外切 D．外离二、填空题（本大题共12小题，每小题4分，共48分）7．计算：（x2）3= ．8．因式分解：x2﹣4y2= ．9．不等式组的解集是．10．方程=2的解是．11．关于x的一元二次方程2x2﹣3x+m=0有两个相等的实数根，则实数m= ．12．某个工人要完成3000个零件的加工，如果该工人每小时能加工x个零件，那么完成这批零件的加工需要的时间是小时．13．已知二次函数的图象经过点（1，3）和（3，3），则此函数图象的对称轴与x轴的交点坐标是．14．从1到10这10个正整数中任取一个，该正整数恰好是3的倍数的概率是．15．正八边形一个内角的度数为．16．在平面直角坐标系中，点A（2，0），B（0，﹣3），若=，则点C的坐标为．17．如图，梯形ABCD中，AD∥BC，∠A=90°，它恰好能按图示方式被分割成四个全等的直角梯形，则AB：BC= ．18．如图，矩形ABCD，将它分别沿AE和AF折叠，恰好使点B，C落到对角线AC上点M，N 处，已知MN=2，NC=1，则矩形ABCD的面积是．三、解答题（本大题共7小题，共78分）19．（10分）计算：（﹣1）0+|﹣2|+（）﹣1﹣2sin30°．20．（10分）解分式方程：．21．（10分）如图，在△ABC中，∠ACB=90°，∠A=15°，D是边AB的中点，DE⊥AB交AC 于点E．（1）求∠CDE的度数；（2）求CE：EA．22．（10分）小明家买了一台充电式自动扫地机，每次完成充电后，在使用时扫地机会自动根据设定扫地时间，来确定扫地的速度（以使每次扫地结束时尽量把所储存的电量用完），如图是“设定扫地时间”与“扫地速度”之间的函数图象（线段AB），其中设定扫地时间为x分钟，扫地速度为y平方分米/分钟．（1）求y关于x的函数解析式；（2）现在小明需要扫地机完成180平方米的扫地任务，他应该设定的扫地时间为多少分钟？23．（12分）如图，菱形ABCD，以A为圆心，AC长为半径的圆分别交边BC，DC，AB，AD 于点E，F，G，H．（1）求证：CE=CF；（2）当E为弧中点时，求证：BE2=CE•CB．24．（12分）如图，点A在函数y=（x＞0）图象上，过点A作x轴和y轴的平行线分别交函数y=图象于点B，C，直线BC与坐标轴的交点为D，E．（1）当点C的横坐标为1时，求点B的坐标；（2）试问：当点A在函数y=（x＞0）图象上运动时，△ABC的面积是否发生变化？若不变，请求出△ABC的面积，若变化，请说明理由．（3）试说明：当点A在函数y=（x＞0）图象上运动时，线段BD与CE的长始终相等．25．（14分）已知：Rt△ABC斜边AB上点D，E，满足∠DCE=45°．（1）如图1，当AC=1，BC=，且点D与A重合时，求线段BE的长；（2）如图2，当△ABC是等腰直角三角形时，求证：AD2+BE2=DE2；（3）如图3，当AC=3，BC=4时，设AD=x，BE=y，求y关于x的函数关系式，并写出定义域．2017年上海市黄浦区中考数学二模试卷参考答案与试题解析一、选择题（本大题共6小题，每小题4分，共24分）1．单项式4xy2z3的次数是（）A．3 B．4 C．5 D．6【考点】42：单项式．【分析】单项式的次数是指各字母的指数之和【解答】解：该单项式的次数为：1+2+3=6，故选（D）【点评】本题考查单项式的概念，解题的关键是正确理解单项式的次数概念，本题属于基础题型．2．下列方程中，无实数解的是（）A．2+x=0 B．2﹣x=0 C．2x=0 D． =0【考点】B2：分式方程的解．【分析】根据解方程，可得答案．【解答】解：A、x+2=0，解得x=﹣2，故A正确；B、2﹣x=0，解得x=2，故B正确；C、2x=0，解得x=2，故C正确；D、=0方程无解，故D错误；故选：D．【点评】本题考查了分式方程的解，解方程是解题关键．3．下列各组数据中，平均数和中位数相等的是（）A．1，2，3，4，5 B．1，3，4，5，6 C．1，2，4，5，6 D．1，2，3，5，6 【考点】W4：中位数；W1：算术平均数．【分析】根据平均数和中位数的概念列出算式，再进行计算即可．【解答】解：A、平均数=（1+2+3+4+5）÷5=3；把数据按从小到大的顺序排列：1，2，3，4，5，中位数是3，故选项正确；B、平均数=（1+3+4+5+6）÷5=3.8；把数据按从小到大的顺序排列：1，3，4，5，6，中位数是4，故选项错误；C、平均数=（1+2+4+5+6）÷5=3.6；把数据按从小到大的顺序排列：1，2，4，5，6，中位数是4，故选项错误；D、平均数=（1+2+3+5+6）÷5=3.4；把数据按从小到大的顺序排列：1，2，3，5，6，中位数是3，故选项错误．故选：A．【点评】此题考查了中位数与平均数，平均数是指在一组数据中所有数据之和再除以数据的个数．找中位数的时候一定要先按大小排好顺序，然后再根据奇数和偶数个来确定中位数．如果数据有奇数个，则正中间的数字即为所求；如果是偶数个，则找中间两位数的平均数．4．二次函数y=﹣（x﹣2）2﹣3的图象的顶点坐标是（）A．（2，3） B．（2，﹣3）C．（﹣2，3）D．（﹣2，﹣3）【考点】H3：二次函数的性质．【分析】根据题目中函数的解析式直接得到此二次函数的顶点坐标．【解答】解：∵y=﹣（x﹣2）2﹣3，∴二次函数y=﹣（x﹣2）2﹣3的图象的顶点坐标是（2，﹣3）故选B．【点评】本题考查二次函数的性质，解题的关键是明确题意，找出所求问题需要的条件．5．以一个面积为1的三角形的三条中位线为三边的三角形的面积为（）A．4 B．2 C． D．【考点】KX：三角形中位线定理．【分析】根据三角形的中位线定理得出两个三角形相似，即可得出结果．【解答】解：根据三角形中位线定理得：两个三角形相似，相似比为，面积比为，∴一个面积为1的三角形的三条中位线为三边的三角形的面积为；故选：C．【点评】本题主要考查了三角形中位线定理、相似三角形的判定与性质；熟练掌握三角形中位线定理是解决问题的关键．6．已知点A（4，0），B（0，3），如果⊙A的半径为1，⊙B的半径为6，则⊙A与⊙B的位置关系是（）A．内切 B．相交 C．外切 D．外离【考点】MJ：圆与圆的位置关系；D5：坐标与图形性质．【分析】由点A（4，0），B（0，3），可求得AB的长，又由⊙A与⊙B的半径分别为：1与6，即可根据两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系得出两圆位置关系．【解答】解：∵点A（4，0），B，0，3），∴AB==5，∵⊙A与⊙B的半径分别为：1与6，∴半径差为：6﹣1=5，∴这两圆的位置关系是：内切．故选A．【点评】此题考查了圆与圆的位置关系．注意掌握两圆位置关系与圆心距d，两圆半径R，r 的数量关系间的联系是解此题的关键．二、填空题（本大题共12小题，每小题4分，共48分）7．计算：（x2）3= x6．【考点】47：幂的乘方与积的乘方．【分析】根据幂的乘方，底数不变，指数相乘，进行计算．【解答】解：原式=x2×3=x6．故答案为x6．【点评】此题考查了幂的乘方的性质．8．因式分解：x2﹣4y2= （x+2y）（x﹣2y）．【考点】54：因式分解﹣运用公式法．【分析】直接运用平方差公式进行因式分解．【解答】解：x2﹣4y2=（x+2y）（x﹣2y）．【点评】本题考查了平方差公式分解因式，熟记公式结构是解题的关键．平方差公式：a2﹣b2=（a+b）（a﹣b）．9．不等式组的解集是﹣≤x＜2 ．【考点】CB：解一元一次不等式组．【分析】先求出不等式组中每一个不等式的解集，再求出它们的公共部分就是不等式组的解集．【解答】解：解不等式x﹣2＜0，得：x＜2，解不等式2x+1≥0，得：x≥﹣，∴不等式组的解集为﹣≤x＜2，故答案为：﹣≤x＜2．【点评】本题考查的是一元一次不等式组的解，解此类题目常常要结合数轴来判断．还可以观察不等式的解，若x＞较小的数、＜较大的数，那么解集为x介于两数之间．10．方程=2的解是x=或x=﹣．【考点】AG：无理方程．【分析】方程两边平方，整理后开方即可求出解．【解答】解：两边平方得：x2﹣2=4，解得：x=或x=﹣，经检验x=或x=﹣是原方程的解．故答案为：x=或x=﹣【点评】此题考查了无理方程，无理方程注意要检验．11．关于x的一元二次方程2x2﹣3x+m=0有两个相等的实数根，则实数m= ．【考点】AA：根的判别式．【分析】直接利用根的判别式得出b2﹣4ac=9﹣8m=0，即可得出答案．【解答】解：∵关于x的一元二次方程2x2﹣3x+m=0有两个相等的实数根，∴b2﹣4ac=9﹣8m=0，解得：m=．故答案为：．【点评】此题主要考查了根的判别式，正确掌握判别式的符号是解题关键．12．某个工人要完成3000个零件的加工，如果该工人每小时能加工x个零件，那么完成这批零件的加工需要的时间是小时．【考点】32：列代数式．【分析】根据工作总量=工作时间×工作效率，计算即可得到结果．【解答】解：根据题意得：完成这批零件的加工需要的时间是小时，故答案为：【点评】此题考查了列代数式，弄清题意是解本题的关键．13．已知二次函数的图象经过点（1，3）和（3，3），则此函数图象的对称轴与x轴的交点坐标是（2，0）．【考点】HA：抛物线与x轴的交点．【分析】直接利用二次函数的图象经过点（1，3）和（3，3），得出二次函数的对称轴，进而得出此函数图象的对称轴与x轴的交点坐标．【解答】解：∵二次函数的图象经过点（1，3）和（3，3），∴抛物线的对称轴为：x==2，故此函数图象的对称轴与x轴的交点坐标是：（2，0）．故答案为：（2，0）．【点评】此题主要考查了抛物线与x轴的交点，正确得出对称轴是解题关键．14．从1到10这10个正整数中任取一个，该正整数恰好是3的倍数的概率是．【考点】X4：概率公式．【分析】让1到10中3的倍数的个数除以数的总个数即为所求的概率．【解答】解：1到10中，3的倍数有3，6，9三个，所以正整数恰好是3的倍数的概率是，故答案为：．【点评】本题主要考查了概率公式，用到的知识点为：概率等于所求情况数与总情况数之比．15．正八边形一个内角的度数为135°．【考点】L3：多边形内角与外角．【分析】首先根据多边形内角和定理：（n﹣2）•180°（n≥3且n为正整数）求出内角和，然后再计算一个内角的度数．【解答】解：正八边形的内角和为：（8﹣2）×180°=1080°，每一个内角的度数为×1080°=135°．故答案为：135°．【点评】此题主要考查了多边形内角和定理，关键是熟练掌握计算公式：（n﹣2）•180 （n ≥3）且n为整数）．16．在平面直角坐标系中，点A（2，0），B（0，﹣3），若=，则点C的坐标为（2，﹣3）．【考点】LM：*平面向量；D1：点的坐标．【分析】根据平面向量的平行四边形的法则解答即可得．【解答】解：如图，∵=，∴过点A作y轴的平行线，过点B作x中的平行线，交于点C，则点C（2，﹣3），故答案为：（2，﹣3）．【点评】本题主要考查平面向量，熟练掌握平面向量的平行四边形法则是解题的关键．17．如图，梯形ABCD中，AD∥BC，∠A=90°，它恰好能按图示方式被分割成四个全等的直角梯形，则AB：BC= ：1 ．【考点】LI：直角梯形；LH：梯形．【分析】如图连接EC，设AB=a，BC=b则CD=2b．只要证明∠D=60°，根据sin60°=，即可解决问题．【解答】解：如图连接EC，设AB=a，BC=b则CD=2b．由题意四边形ABCE是矩形，∴CE=AB=a，∠A=∠AEC=∠CED=90°，∵∠BCF=∠DCF=∠D，又∵∠BCF+∠DCF+∠D=180°，∴∠D=60°，∴sinD==，∴=，∴==，∴AB：BC=：1故答案为：1．【点评】本题考查直角梯形的性质，锐角三角函数等知识，解题的关键是理解题意，利用角相等这个信息解决问题，发现特殊角是解题的突破口，属于中考常考题型．18．如图，矩形ABCD，将它分别沿AE和AF折叠，恰好使点B，C落到对角线AC上点M，N 处，已知MN=2，NC=1，则矩形ABCD的面积是9+2 ．【考点】PB：翻折变换（折叠问题）；LB：矩形的性质．【分析】由折叠的性质得，AB=AM，AN=AD，设AB=x，则AD=x+2，AC=x+3，根据勾股定理列方程即可得到结论．【解答】解：由折叠的性质得，AB=AM，AN=AD，∴AD﹣AB=AN﹣AM=MN=2，设AB=x，则AD=x+2，AC=x+3，∵四边形ABCD是矩形，∴∠D=90°，CD=AB，∴AD2+CD2=AC2，即（x+2）2+x2=（x+3）2，∴x=1+（负值舍去），∴AB=1+，AD=3+，∴S矩形ABCD=（1+）（3+）=9+2；故答案为：9+2．【点评】本题主要考查了折叠的性质、矩形的性质、勾股定理等，综合运用各定理是解答此题的关键．三、解答题（本大题共7小题，共78分）19．（10分）（2017•黄浦区二模）计算：（﹣1）0+|﹣2|+（）﹣1﹣2sin30°．【考点】79：二次根式的混合运算；6E：零指数幂；6F：负整数指数幂；T5：特殊角的三角函数值．【分析】利用零指数幂、负整数指数幂和特殊角的三角函数值进行计算．【解答】解：原式=1+2﹣+﹣2×=2﹣++1﹣1=2．【点评】本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．20．（10分）（2017•黄浦区二模）解分式方程：．【考点】B3：解分式方程．【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．【解答】解：去分母得：（x+2）2﹣16=x﹣2，整理得：x2+3x﹣10=0，即（x﹣2）（x+5）=0，解得：x=2或x=﹣5，经检验x=2是增根，分式方程的解为x=﹣5．【点评】此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．21．（10分）（2017•黄浦区二模）如图，在△ABC中，∠ACB=90°，∠A=15°，D是边AB 的中点，DE⊥AB交AC于点E．（1）求∠CDE的度数；（2）求CE：EA．【考点】KO：含30度角的直角三角形；KP：直角三角形斜边上的中线．【分析】（1）根据直角三角形斜边上中线得出CD=AD=BD，求出∠DCA=∠A=15°，求出∠BDC=∠A+∠DCA=30°，即可得出答案；（2）根据线段垂直平分线性质求出BE=AE，求出CE和BE的比，即可得出答案．【解答】解：（1）∵在△ABC中，∠ACB=90°，D是边AB的中点，∴CD=AD=BD，∴∠DCA=∠A，∵∠A=15°，∴∠DCA=15°，∴∠BDC=∠A+∠DCA=30°，∵ED⊥AB，∴∠EDB=90°，∴∠CDE=90°﹣30°=60°；（2）连接BE，∵D为AB中点，DE⊥AB，∴BE=AE，∴∠EBA=∠A=15•，∴∠BEC=15°+15°=30°，∴cos30°=，∵AE=BE，∴=．【点评】本题考查了直角三角形斜边上中线性质，线段垂直平分线性质，解直角三角形等知识点，能综合运用知识点进行推理是解此题的关键．22．（10分）（2017•黄浦区二模）小明家买了一台充电式自动扫地机，每次完成充电后，在使用时扫地机会自动根据设定扫地时间，来确定扫地的速度（以使每次扫地结束时尽量把所储存的电量用完），如图是“设定扫地时间”与“扫地速度”之间的函数图象（线段AB），其中设定扫地时间为x分钟，扫地速度为y平方分米/分钟．（1）求y关于x的函数解析式；（2）现在小明需要扫地机完成180平方米的扫地任务，他应该设定的扫地时间为多少分钟？【考点】FH：一次函数的应用．【分析】（1）设AB的解析式为y=kx+b，把A（20，500），B（100，100）代入解方程组即可．（2）设他应该设定的扫地时间为x分钟．由题意=﹣5x+600，解方程即可．【解答】解：（1）设AB的解析式为y=kx+b，把A（20，500），B（100，100）代入得到，解得，∴y=﹣5x+600．（2）设他应该设定的扫地时间为x分钟．由题意=﹣5x+600，整理得x2﹣120x+3600=0，∴x=60，经检验x=60是分式方程的解．∴他应该设定的扫地时间为60分钟．【点评】本题考查一次函数的应用、分式方程的解等知识，解题的关键是熟练掌握待定系数法确定函数解析式，学会构建方程解决实际问题，注意解分式方程必须检验．23．（12分）（2017•黄浦区二模）如图，菱形ABCD，以A为圆心，AC长为半径的圆分别交边BC，DC，AB，AD于点E，F，G，H．（1）求证：CE=CF；（2）当E为弧中点时，求证：BE2=CE•CB．【考点】S9：相似三角形的判定与性质；L8：菱形的性质；M5：圆周角定理．【分析】（1）连接AE，AF，由四边形ABCD是菱形，得到∠ACB=∠ACF，根据等腰三角形的性质得到∠AEC=∠ACE=∠ACF=∠AFC，推出∠EAC=∠FAC，即可得到结论；（2）由E为弧中点，得到∠CAE=∠BAE，根据等腰三角形的性质和三角形的外角的性质得到∠ACE=∠AEC=∠BAC=∠B+∠BAE，得到BE=AE=AC，根据相似三角形的性质即可得到结论．【解答】（1）证明：连接AE，AF，∵四边形ABCD是菱形，∴∠ACB=∠ACF，∵AE=AC=AF，∴∠AEC=∠ACE=∠ACF=∠AFC，∴∠EA C=180°﹣∠AEC﹣∠ACE，∠CAF=180°﹣∠ACF﹣∠AFC，∴∠EAC=∠FAC，∴，∴CE=CF；（2）解：∵E为弧中点，∴∠CAE=∠BAE，∵AB=BC，AE=AC，∴∠ACE=∠AEC=∠BAC=∠B+∠BAE，∴∠B=∠BAE，∴BE=AE=AC，∴△ABC∽△CAE，∴，∴AC2=BC•CE，即BE2=CE•CB．【点评】本题考查了相似三角形的判定和性质，菱形的性质，圆心角，弧，弦的关系，正确的作出辅助线是解题的关键．24．（12分）（2017•黄浦区二模）如图，点A在函数y=（x＞0）图象上，过点A作x轴和y轴的平行线分别交函数y=图象于点B，C，直线BC与坐标轴的交点为D，E．（1）当点C的横坐标为1时，求点B的坐标；（2）试问：当点A在函数y=（x＞0）图象上运动时，△ABC的面积是否发生变化？若不变，请求出△ABC的面积，若变化，请说明理由．（3）试说明：当点A在函数y=（x＞0）图象上运动时，线段BD与CE的长始终相等．【考点】GB：反比例函数综合题．【分析】（1）由条件可先求得A点坐标，从而可求得B点纵坐标，再代入y=可求得B点坐标；（2）可设出A点坐标，从而可表示出C、B的坐标，则可表示出AB和AC的长，可求得△ABC 的面积；（3）可证明△ABC∽△EFC，利用（2）中，AB和AC的长可表示出EF，可得到BG=EF，从而可证明△DBG≌△CFE，可得到DB=CF．【解答】解：（1）∵点C在y=的图象上，且C点横坐标为1，∴C（1，1），∵AC∥y轴，AB∥x轴，∴A点横坐标为1，∵A点在函数y=（x＞0）图象上，∴A（1，4），∴B点纵坐标为4，∵点B在y=的图象上，∴B点坐标为（，4）；（2）设A（a，），则C（a，），B（，），∴AB=a﹣=a，AC=﹣=，∴S△ABC=AB•AC=××=，即△ABC的面积不发生变化，其面积为；（3）如图，设AB的延长线交y轴于点G，AC的延长线交x轴于点F，∵AB∥x轴，∴△ABC∽△EFC，∴=，即=，∴EF=a，由（2）可知BG=a，∴BG=EF，∵AE∥y轴，∴∠BDG=∠FCE，在△DBG和△CFE中∴△DBG≌△CEF（AAS），∴BD=EF．【点评】本题为反比例函数的综合应用，涉及函数图象的交点、平行线的性质、三角形的面积、相似三角形的判定和性质、全等三角形的判定和性质等知识．要（1）中求得A点坐标是解题的关键，在（2）中用a表示出AB、AC的长是解题的关键，在（3）中证得BG=EF，构造三角形全等是解题的关键．本题考查知识点较多，综合性较强，难度适中．25．（14分）（2017•黄浦区二模）已知：Rt△ABC斜边AB上点D，E，满足∠DCE=45°．（1）如图1，当AC=1，BC=，且点D与A重合时，求线段BE的长；（2）如图2，当△ABC是等腰直角三角形时，求证：AD2+BE2=DE2；（3）如图3，当AC=3，BC=4时，设AD=x，BE=y，求y关于x的函数关系式，并写出定义域．【考点】KY：三角形综合题．【分析】（1）如图1，根据勾股定理得到AB=2，过B作BF∥AC交CE的延长线于F，得到∠F=∠ACE，根据相似三角形的性质即可得到结论；（2）作AF⊥AB，使AF=BE，连接DF，根据SAS证得△CAF≌△CBE和△CDF≌△CDE，再由勾股定理和等量代换即可解答；（3）如图3，作△BCE≌△FCE，△GCD≌△ACD，延长DG交EF于H，由∠HFG=∠B，∠HGF=∠CGD=∠A，∠A+∠B=90°，得到∠DHF=90°，根据勾股定理即可得到结论．【解答】解：（1）如图1，∵∠ACB=90°，BC=，AC=1，∴AB=2，过B作BF∥AC交CE的延长线于F，∴∠F=∠ACE，∵∠BCA=90°，∠DCE=45°，∴∠BCE=∠DCE，∴∠BCE=∠F，∴BF=BC=，∵△BEF∽△AEC，∴=，∴BE=2﹣；（2）证明：过点A作AF⊥AB，使AF=BE，连接DF，CF，∵在△ABC中，AC=BC，∠ACB=90°，∴∠CAB=∠B=45°，∴∠FAC=45°，∴△CAF≌△CBE（SAS），∴CF=CE，∠ACF=∠BCE，∵∠ACB=90°，∠DCE=45°，∴∠ACD+∠BCE=∠ACB﹣∠DCE=90°﹣45°=45°，∵∠ACF=∠BCE，∴∠ACD+∠ACF=45°，即∠DCF=45°，∴∠DCF=∠DCE，又∵CD=CD，∴△CDF≌△CDE（SAS），∴DF=DE，∵AD2+AF2=DF2，∴AD2+BE2=DE2；（3）如图3，作△BCE≌△FCE，△GCD≌△ACD，延长DG交EF于H，∵∠HFG=∠B，∠HGF=∠CGD=∠A，∠A+∠B=90°，∴∠DHF=90°，∵FG=1，∠B=∠F，∴HF=，HG=，∵EH2+HD2=ED2，∴（y﹣）2+（x+）2=（5﹣x﹣y）2，∴y=（0≤x≤）．【点评】本题属于三角形综合题，主要考查了相似三角形的判定与性质，等腰三角形的性质，勾股定理以及解直角三角形的综合应用，解决问题的关键是中辅助线构造直角三角形，根据勾股定理以及面积法进行求解．。
【精选3份合集】2017-2018学年上海市浦东新区中考数学第二次适应性考试题
中考数学模拟试卷一、选择题（本题包括10个小题，每小题只有一个选项符合题意）1．点A（m﹣4，1﹣2m）在第四象限，则m的取值范围是（）A．m＞12B．m＞4C．m＜4 D．12＜m＜4【答案】B【解析】根据第四象限内点的横坐标是正数，纵坐标是负数列出不等式组，然后求解即可．【详解】解：∵点A（m-1，1-2m）在第四象限，∴40120mm-⎧⎨-⎩＞①，＜②解不等式①得，m＞1，解不等式②得，m＞1 2所以，不等式组的解集是m＞1，即m的取值范围是m＞1．故选B．【点睛】本题考查各象限内点的坐标的符号特征以及解不等式，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．2．将函数的图象用下列方法平移后，所得的图象不经过点A（1，4）的方法是（）A．向左平移1个单位B．向右平移3个单位C．向上平移3个单位D．向下平移1个单位【答案】D【解析】A.平移后，得y=(x+1)2，图象经过A点，故A不符合题意；B.平移后，得y=(x−3)2，图象经过A点，故B不符合题意；C.平移后，得y=x2+3，图象经过A点，故C不符合题意；D.平移后，得y=x2−1图象不经过A点，故D符合题意；故选D.3．如图,在△ABC中,点D是AB边上的一点,若∠ACD=∠B,AD=1,AC=2,△ADC的面积为1,则△BCD的面积为（）A．1 B．2 C．3 D．4【答案】C【解析】∵∠ACD=∠B ，∠A=∠A ，∴△ACD ∽△ABC ， ∴12AC AD ABAC ==， ∴2ACDABC S AD SAC ⎛⎫= ⎪⎝⎭， ∴2112ABCS ⎛⎫= ⎪⎝⎭， ∴S △ABC =4， ∴S △BCD = S △ABC - S △ACD =4-1=1．故选C考点：相似三角形的判定与性质.4．如图，在直角坐标系中，有两点A(6，3)、B(6，0)．以原点O 为位似中心，相似比为13，在第一象限内把线段AB 缩小后得到线段CD ，则点C 的坐标为（ ）A ．(2，1)B ．(2，0)C ．(3，3)D ．(3，1)【答案】A 【解析】根据位似变换的性质可知，△ODC ∽△OBA ，相似比是13，根据已知数据可以求出点C 的坐标． 【详解】由题意得，△ODC ∽△OBA ，相似比是13， ∴OD DC OB AB=， 又OB=6，AB=3，∴OD=2，CD=1，∴点C 的坐标为：（2，1），故选A ．【点睛】本题考查的是位似变换，掌握位似变换与相似的关系是解题的关键，注意位似比与相似比的关系的应用．5．如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1=20°，那么∠2的度数是（ ）A ．30°B ．25°C ．20°D ．15°【答案】B 【解析】根据题意可知∠1+∠2+45°=90°，∴∠2=90°﹣∠1﹣45°=25°，6．函数y ＝ax 2与y ＝﹣ax+b 的图象可能是（ ）A ．B ．C ．D ．【答案】B【解析】A 选项中，由图可知：在2y ax =，0a >；在y ax b =-+，0a ->，∴0a <，所以A 错误；B 选项中，由图可知：在2y ax =，0a >；在y ax b =-+，0a -<，∴0a >，所以B 正确；C 选项中，由图可知：在2y ax =，0a <；在y ax b =-+，0a -<，∴0a >，所以C 错误；D 选项中，由图可知：在2y ax =，0a <；在y ax b =-+，0a -<，∴0a >，所以D 错误．故选B ．点睛：在函数2y ax =与y ax b =-+中，相同的系数是“a ”，因此只需根据“抛物线”的开口方向和“直线”的变化趋势确定出两个解析式中“a ”的符号，看两者的符号是否一致即可判断它们在同一坐标系中的图象情况，而这与“b”的取值无关.7．如图，在正方形ABCD 中，E 为AB 的中点，G ，F 分别为AD 、BC 边上的点，若AG=1，BF=2，∠GEF=90°，则GF 的长为( )A ．2B ．3C ．4D ．5【答案】B【解析】∵四边形ABCD是正方形，∴∠A=∠B=90°，∴∠AGE+∠AEG=90°，∠BFE+∠FEB=90°，∵∠GEF=90°，∴∠GEA+∠FEB=90°，∴∠AGE=∠FEB，∠AEG=∠EFB，∴△AEG∽△BFE，∴AE AG，BF BE又∵AE=BE，∴AE2=AG•BF=2，∴（舍负），∴GF2=GE2+EF2=AG2+AE2+BE2+BF2=1+2+2+4=9，∴GF的长为3，故选B.【点睛】本题考查了相似三角形的性质的应用，利用勾股定理即可得解，解题的关键是证明△AEG∽△BFE．8．一、单选题在某校“我的中国梦”演讲比赛中，有7名学生参加了决赛，他们决赛的最终成绩各不相同．其中的一名学生想要知道自己能否进入前3名，不仅要了解自己的成绩，还要了解这7名学生成绩的（）A．平均数B．众数C．中位数D．方差【答案】C【解析】由于其中一名学生想要知道自己能否进入前3名，共有7名选手参加，故应根据中位数的意义分析．【详解】由于总共有7个人，且他们的成绩各不相同，第4的成绩是中位数，要判断是否进入前3名，故应知道中位数的多少．故选C．【点睛】此题主要考查统计的有关知识，主要包括平均数、中位数、众数、方差的意义．反映数据集中程度的统计量有平均数、中位数、众数、方差等，各有局限性，因此要对统计量进行合理的选择和恰当的运用．9．为了支援地震灾区同学，某校开展捐书活动，九（1）班40名同学积极参与．现将捐书数量绘制成频数分布直方图如图所示，则捐书数量在5.5～6.5组别的频率是（）A．0.1 B．0.2 C．0.3 D．0.4 【答案】B【解析】∵在5.5～6.5组别的频数是8，总数是40，∴=0.1．故选B．10．如图，已知线段AB，分别以A，B为圆心，大于12AB为半径作弧，连接弧的交点得到直线l，在直线l上取一点C，使得∠CAB＝25°，延长AC至点M，则∠BCM的度数为( )A．40°B．50°C．60°D．70°【答案】B【解析】解：∵由作法可知直线l是线段AB的垂直平分线，∴AC=BC，∴∠CAB=∠CBA=25°，∴∠BCM=∠CAB+∠CBA=25°+25°=50°．故选B．二、填空题（本题包括8个小题）11．如图，在平面直角坐标系中，⊙P的圆心在x轴上，且经过点A（m，﹣3）和点B（﹣1，n），点C 是第一象限圆上的任意一点，且∠ACB=45°，则⊙P的圆心的坐标是_____．【答案】（2，0）【解析】作辅助线，构建三角形全等，先根据同弧所对的圆心角是圆周角的二倍得：∠APB=90°，再证明△BPE≌△PAF，根据PE=AF=3，列式可得结论．【详解】连接PB、PA，过B作BE⊥x轴于E，过A作AF⊥x轴于F，∵A（m，﹣3）和点B（﹣1，n），∴OE=1，AF=3，∵∠ACB=45°，∴∠APB=90°，∴∠BPE+∠APF=90°，∵∠BPE+∠EBP=90°，∴∠APF=∠EBP，∵∠BEP=∠AFP=90°，PA=PB，∴△BPE≌△PAF，∴PE=AF=3，设P（a，0），∴a+1=3，a=2，∴P（2，0），故答案为（2，0）．【点睛】本题考查了圆周角定理和坐标与图形性质，三角形全等的性质和判定，作辅助线构建三角形全等是关键．12．地球上的海洋面积约为361000000km1，则科学记数法可表示为_______km1．【答案】3.61×2【解析】科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n 是正数；当原数的绝对值＜1时，n 是负数．【详解】将361 000 000用科学记数法表示为3.61×2．故答案为3.61×2．13．若点(),2P m -与点()3,Q n 关于原点对称，则2018()m n +=______．【答案】1【解析】∵点P （m ，﹣2）与点Q （3，n ）关于原点对称，∴m=﹣3，n=2，则（m+n ）2018=（﹣3+2）2018=1，故答案为1．14．若关于x 的分式方程2233x m x x -=--有增根，则m 的值为_____． 【答案】±3【解析】增根是分式方程化为整式方程后产生的使分式方程的分母为0的根．有增根，最简公分母x-3=0，所以增根是x=3，把增根代入化为整式方程的方程即可求出m 的值．【详解】方程两边都乘x-3，得x-2（x-3）=m 2，∵原方程增根为x=3，∴把x=3代入整式方程，得m=±3．【点睛】解决增根问题的步骤：①确定增根的值；②化分式方程为整式方程；③把增根代入整式方程即可求得相关字母的值．15．如图，△ABC 中，AB ＝6，AC ＝4，AD 、AE 分别是其角平分线和中线，过点C 作CG ⊥AD 于F ，交AB 于G ，连接EF ，则线段EF 的长为_____．【答案】1【解析】在△AGF和△ACF中，{GAF CAF AF AF AFG AFC∠=∠=∠=∠，∴△AGF≌△ACF，∴AG=AC=4，GF=CF，则BG=AB−AG=6−4=2.又∵BE=CE，∴EF是△BCG的中位线，∴EF=12BG=1.故答案是：1.16．已知a＜0，那么|2a﹣2a|可化简为_____．【答案】﹣3a【解析】根据二次根式的性质和绝对值的定义解答．【详解】∵a＜0，∴|2a﹣2a|＝|﹣a﹣2a|＝|﹣3a|＝﹣3a．【点睛】本题主要考查了根据二次根式的意义化简．二次根式2a规律总结：当a≥0时，2a＝a；当a≤0时，2a ＝﹣a．解题关键是要判断绝对值符号和根号下代数式的正负再去掉符号．17．如图是一位同学设计的用手电筒来测量某古城墙高度的示意图．点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，测得AB＝2米，BP＝3米，PD＝15米，那么该古城墙的高度CD是_____米．【答案】10【解析】首先证明△ABP∽△CDP，可得ABBP=CDPD，再代入相应数据可得答案．【详解】如图，由题意可得：∠APE=∠CPE，∴∠APB=∠CPD，∵AB⊥BD，CD⊥BD，∴∠ABP=∠CDP=90°，∴△ABP∽△CDP，∴ABBP =CD PD，∵AB=2米，BP=3米，PD=15米，∴23=15 CD，解得：CD=10米.故答案为10.【点睛】本题考查了相似三角形的应用，解题的关键是熟练的掌握相似三角形的应用.18．圆锥的底面半径为3，母线长为5，该圆锥的侧面积为_______．【答案】15【解析】试题分析：利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形的面积公式求解．圆锥的侧面积=12•2π•3•5=15π．故答案为15π．考点：圆锥的计算．三、解答题（本题包括8个小题）19．在一次数学活动课上，老师让同学们到操场上测量旗杆的高度，然后回来交流各自的测量方法．小芳的测量方法是：拿一根高3.5米的竹竿直立在离旗杆27米的C处（如图），然后沿BC方向走到D处，这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上，又测得C、D两点的距离为3米，小芳的目高为1.5米，这样便可知道旗杆的高．你认为这种测量方法是否可行？请说明理由．【答案】这种测量方法可行，旗杆的高为21.1米．【解析】分析：根据已知得出过F作FG⊥AB于G，交CE于H，利用相似三角形的判定得出△AGF∽△EHF，再利用相似三角形的性质得出即可．详解：这种测量方法可行．理由如下：设旗杆高AB=x．过F作FG⊥AB于G，交CE于H（如图）．所以△AGF∽△EHF．因为FD=1.1，GF=27+3=30，HF=3，所以EH=3.1﹣1.1=2，AG=x﹣1.1．由△AGF∽△EHF，得AG GF EH HF=，即1.530 23x-=，所以x﹣1.1=20，解得x=21.1（米）答：旗杆的高为21.1米．点睛：此题主要考查了相似三角形的判定与性质，根据已知得出△AGF∽△EHF是解题关键．20．2018年“植树节”前夕，某小区为绿化环境，购进200棵柏树苗和120棵枣树苗，且两种树苗所需费用相同．每棵枣树苗的进价比每棵柏树苗的进价的2倍少5元，每棵柏树苗的进价是多少元.【答案】15元．【解析】首先设每棵柏树苗的进价是x元，则每棵枣树苗的进价是(2x－5)元，根据题意列出一元一次方程进行求解.【详解】解：设每棵柏树苗的进价是x元，则每棵枣树苗的进价是(2x－5)元.根据题意，列方程得：200=120(25)x x-，解得：x=15答：每棵柏树苗的进价是15元.【点睛】此题考查了一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．21．如图是一副扑克牌中的三张牌，将它们正面向下洗均匀，甲同学从中随机抽取一张牌后放回，乙同学再从中随机抽取一张牌，用树状图（或列表）的方法，求抽出的两张牌中，牌面上的数字都是偶数的概率．【答案】1 3【解析】画树状图展示所有9种等可能的结果数，再找出两次抽取的牌上的数字都是偶数的结果数，然后根据概率公式求解．【详解】画树状图为：共有9种等可能的结果数，其中两次抽取的牌上的数字都是偶数的结果数为2，所以两次抽取的牌上的数字都是偶数的概率＝26＝13．【点睛】本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A 或B的结果数目m，然后利用概率公式求事件A或B的概率．22．某区域平面示意图如图，点O在河的一侧，AC和BC表示两条互相垂直的公路．甲勘测员在A处测得点O位于北偏东45°，乙勘测员在B处测得点O位于南偏西73.7°，测得AC=840m，BC=500m．请求出点O到BC的距离．参考数据：sin73.7°≈2425，cos73.7°≈725，ta n73.7°≈247【答案】点O到BC的距离为480m．【解析】作OM⊥BC于M，ON⊥AC于N，设OM=x，根据矩形的性质用x表示出OM、MC，根据正切的定义用x表示出BM，根据题意列式计算即可．【详解】作OM⊥BC于M，ON⊥AC于N，则四边形ONCM为矩形，∴ON=MC，OM=NC，设OM=x，则NC=x，AN=840﹣x，在Rt△ANO中，∠OAN=45°，∴ON=AN=840﹣x，则MC=ON=840﹣x，在Rt△BOM中，BM==x，由题意得，840﹣x+x=500，解得，x=480，答：点O到BC的距离为480m．【点睛】本题考查的是解直角三角形的应用，掌握锐角三角函数的定义、正确标注方向角是解题的关键．23．先化简，再求值：（1﹣11a+）÷221aa-，其中a=﹣1．【答案】原式=12a-=﹣2．【解析】分析：原式利用分式混合运算顺序和运算法则化简，再将a的值代入计算可得．详解：原式=112()+11(1)(1) a aa a a a+-÷++-=(1)(1)·12a a aa a+-+=1 2a-，当a=﹣1时，原式=312--=﹣2．点睛：本题主要考查分式的化简求值，解题的关键是熟练掌握分式混合运算顺序和运算法则．24．如图，直线y＝﹣x+4与x轴交于点A，与y轴交于点B．抛物线y＝﹣12x2+bx+c经过A，B两点，与x轴的另外一个交点为C填空：b＝，c＝，点C的坐标为．如图1，若点P是第一象限抛物线上的点，连接OP交直线AB于点Q，设点P的横坐标为m．PQ与OQ的比值为y，求y与m的数学关系式，并求出PQ与OQ的比值的最大值．如图2，若点P是第四象限的抛物线上的一点．连接PB与AP，当∠PBA+∠CBO＝45°时．求△PBA的面积．【答案】（3）3，2，C（﹣2，4）；（2）y＝﹣18m2+12m ，PQ与OQ的比值的最大值为12；（3）S△PBA＝3．【解析】（3）通过一次函数解析式确定A、B两点坐标，直接利用待定系数法求解即可得到b，c的值，令y=4便可得C 点坐标．（2）分别过P 、Q 两点向x 轴作垂线，通过PQ 与OQ 的比值为y 以及平行线分线段成比例，找到PQ ED OQ OD =，设点P 坐标为（m ，-12m 2+m+2），Q 点坐标（n ，-n+2），表示出ED 、OD 等长度即可得y 与m 、n 之间的关系，再次利用PE QD OE OD =即可求解． （3）求得P 点坐标，利用图形割补法求解即可．【详解】（3）∵直线y ＝﹣x+2与x 轴交于点A ，与y 轴交于点B ．∴A （2，4），B （4，2）．又∵抛物线过B （4，2）∴c ＝2．把A （2，4）代入y ＝﹣x 2+bx+2得，4＝﹣12×22+2b+2，解得，b ＝3． ∴抛物线解析式为，y ＝﹣12x 2+x+2． 令﹣12x 2+x+2＝4， 解得，x ＝﹣2或x ＝2．∴C （﹣2，4）．（2）如图3，分别过P 、Q 作PE 、QD 垂直于x 轴交x 轴于点E 、D ．设P （m ，﹣12m 2+m+2），Q （n ，﹣n+2）， 则PE ＝﹣12m 2+m+2，QD ＝﹣n+2． 又∵PQ m n OQ n-=＝y ． ∴n ＝1m y +．又∵PE OEQD OD=，即24124mmnmn=-+++把n＝1my+代入上式得，2412411mm mym my++=++-+整理得，2y＝﹣12m2+2m．∴y＝﹣12m2+12m．y max＝210()121248-=⎛⎫⨯ ⎪⎝⎭．即PQ与OQ的比值的最大值为12．（3）如图2，∵∠OBA＝∠OBP+∠PBA＝25°∠PBA+∠CBO＝25°∴∠OBP＝∠CBO此时PB过点（2，4）．设直线PB解析式为，y＝kx+2．把点（2，4）代入上式得，4＝2k+2．解得，k＝﹣2∴直线PB解析式为，y＝﹣2x+2．令﹣2x+2＝﹣12x2+x+2整理得，12x2﹣3x＝4．解得，x＝4（舍去）或x＝5．当x＝5时，﹣2x+2＝﹣2×5+2＝﹣7∴P（5，﹣7）．过P作PH⊥cy轴于点H．则S四边形OHPA＝12（OA+PH）•OH＝12（2+5）×7＝24．S△OAB＝12OA•OB＝12×2×2＝7．S△BHP＝12PH•BH＝12×5×3＝35．∴S△PBA＝S四边形OHPA+S△OAB﹣S△BHP＝24+7﹣35＝3．【点睛】本题考查了函数图象与坐标轴交点坐标的确定，以及利用待定系数法求解抛物线解析式常数的方法，再者考查了利用数形结合的思想将图形线段长度的比化为坐标轴上点之间的线段长度比的思维能力．还考查了运用图形割补法求解坐标系内图形的面积的方法．25．. 在一个不透明的布袋中装有三个小球，小球上分别标有数字﹣1、0、2，它们除了数字不同外，其他都完全相同．随机地从布袋中摸出一个小球，则摸出的球为标有数字2的小球的概率为；小丽先从布袋中随机摸出一个小球，记下数字作为平面直角坐标系内点M的横坐标．再将此球放回、搅匀，然后由小华再从布袋中随机摸出一个小球，记下数字作为平面直角坐标系内点M的纵坐标，请用树状图或表格列出点M所有可能的坐标，并求出点M落在如图所示的正方形网格内（包括边界）的概率．【答案】（1）；（2）列表见解析，.【解析】试题分析：（1）一共有3种等可能的结果总数，摸出标有数字2的小球有1种可能，因此摸出的球为标有数字2的小球的概率为；（2）利用列表得出共有9种等可能的结果数，再找出点M落在如图所示的正方形网格内（包括边界）的结果数，可求得结果.试题解析：（1）P（摸出的球为标有数字2的小球）=；（2）列表如下：小华小丽-1 0 2-1（-1，-1） （-1，0） （-1，2） 0（0，-1） （0，0） （0，2） 2（2，-1） （2，0） （2，2）共有9种等可能的结果数，其中点M 落在如图所示的正方形网格内（包括边界）的结果数为6， ∴P （点M 落在如图所示的正方形网格内）==.考点：1列表或树状图求概率；2平面直角坐标系.26．如图，AB 是⊙O 的直径，BC 交⊙O 于点D ，E 是弧BD 的中点，AE 与BC 交于点F ，∠C=2∠EAB ．求证：AC 是⊙O 的切线；已知CD=4，CA=6，求AF 的长．【答案】（1）证明见解析（2）6【解析】（1）连结AD ，如图，根据圆周角定理，由E 是BD 的中点得到2DAB EAB ∠=∠，由于2ACB EAB ∠=∠，则ACB DAB ∠=∠，，再利用圆周角定理得到90ADB ，∠=︒则90DAC ACB ∠+∠=︒，所以90DAC DAB ∠+∠=︒，于是根据切线的判定定理得到AC 是⊙O 的切线；()2先求出DF 的长，用勾股定理即可求出.【详解】解：（1）证明：连结AD ，如图，∵E 是BD 的中点，∴2DAB EAB ∠=∠，∵2ACB EAB ∠=∠，∴ACB DAB ∠=∠，∵AB 是⊙O 的直径，∴90ADB ，∠=︒∴90DAC ACB ∠+∠=︒，∴90DAC DAB ∠+∠=︒， 即90BAC ∠=︒，∴AC 是⊙O 的切线；（2）∵9090EAC EAB DAE AFD EAD EAB ∠+∠=︒∠+∠=︒∠=∠，，，∴62EAC AFD CF AC DF ，，．∠=∠∴==∴= ∵222226420AD AC CD =-=-=， ∴22220226AF AD DF =+=+=【点睛】本题考查切线的判定与性质，圆周角定理，属于圆的综合题，注意切线的证明方法，是高频考点.中考数学模拟试卷一、选择题（本题包括10个小题，每小题只有一个选项符合题意）1．一组数据：1、2、2、3，若添加一个数据2，则发生变化的统计量是()A．平均数B．中位数C．众数D．方差【答案】D【解析】解：A．原来数据的平均数是2，添加数字2后平均数仍为2，故A与要求不符；B．原来数据的中位数是2，添加数字2后中位数仍为2，故B与要求不符；C．原来数据的众数是2，添加数字2后众数仍为2，故C与要求不符；D．原来数据的方差=222 (12)2(22)(32)4-+⨯-+-=12，添加数字2后的方差=222 (12)3(22)(32)5-+⨯-+-=25，故方差发生了变化．故选D．2．下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（）A．B．C．D．【答案】B【解析】由中心对称图形的定义：“把一个图形绕一个点旋转180°后，能够与自身完全重合，这样的图形叫做中心对称图形”分析可知，上述图形中，A、C、D都不是中心对称图形，只有B是中心对称图形.故选B.3．若一个正比例函数的图象经过A（3，﹣6），B（m，﹣4）两点，则m的值为（）A．2 B．8 C．﹣2 D．﹣8【答案】A【解析】试题分析：设正比例函数解析式为：y=kx，将点A（3，﹣6）代入可得：3k=﹣6，解得：k=﹣2，∴函数解析式为：y=﹣2x，将B（m，﹣4）代入可得：﹣2m=﹣4，解得m=2，故选A．考点：一次函数图象上点的坐标特征．4．在Rt△ABC中∠C＝90°，∠A、∠B、∠C的对边分别为a、b、c，c＝3a，tanA的值为（）A．13B．24C2D．3【答案】B【解析】根据勾股定理和三角函数即可解答.【详解】解：已知在Rt△ABC中∠C=90°，∠A、∠B、∠C的对边分别为a、b、c，c=3a，设a=x,则c=3x,b=229xx-=22x.即tanA=22x =24.故选B.【点睛】本题考查勾股定理和三角函数,熟悉掌握是解题关键.5．若直线y=kx+b图象如图所示，则直线y=−bx+k的图象大致是( )A．B．C．D．【答案】A【解析】根据一次函数y=kx+b的图象可知k＞1，b＜1，再根据k，b的取值范围确定一次函数y=−bx+k 图象在坐标平面内的位置关系，即可判断．【详解】解：∵一次函数y=kx+b的图象可知k＞1，b＜1，∴-b＞1，∴一次函数y=−bx+k的图象过一、二、三象限，与y轴的正半轴相交，故选：A．【点睛】本题考查了一次函数的图象与系数的关系．函数值y随x的增大而减小⇔k＜1；函数值y随x的增大而增大⇔k＞1；一次函数y=kx+b图象与y轴的正半轴相交⇔b＞1，一次函数y=kx+b图象与y轴的负半轴相交⇔b ＜1，一次函数y=kx+b图象过原点⇔b=1．6．如果关于x的分式方程1311a xx x--=++有负数解，且关于y的不等式组2()43412a y yyy---⎧⎪⎨+<+⎪⎩无解，则符合条件的所有整数a的和为（）A．﹣2 B．0 C．1 D．3 【答案】B。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
浦东新区2016学年度第二学期初三质量检测
2017年5月 一、选择题
1．下列实数中，是无理数的是（ ） A 、3.14 B 、
1
3
C
D
2
）
A
B
C
3．函数1y kx =-（常数0k
>）的图像不经过的象限是（ ）
A 、第一象限
B 、第二象限
C 、第三象限
D 、第四象限 4．某幢楼10户家庭某月的用电量如下表所示：
那么这10户家庭该月用电量的众数和中位数分别是（ ）
A 、180,180
B 、180,160
C 、160,180
D 、160，160 5．已知两圆的半径分别为1和5，圆心距为4，那么两圆的位置关系是（ ）
A 、外离
B 、外切
C 、相交
D 、内切
6．如图，已知△ABC 和△DEF ，点E 在BC 边上，点A 在DE 边上，边EF 和边AC 交于点G 。
如果AE=EC,
∠AEG=∠B.那么添加下列一个条件后，仍无法判定△DEF 与△ABC 一定相似的是（ ） A 、
AB DE BC EF = B 、AD GF
AE GE
=
C 、AG EG AC EF =
D 、ED EG EF EA
=
二、填空题
7．计算：2
a a ⋅=_________。
8．因式分解：22x x -=________ 9
x =-的根是_________ 10．函数
3()2
x
f x x =
+的定义域是_________ 11．如果关于x 的方程2
20x x m -+=有两个实根，那么m 的取值范围是_________
12．计算：1
2()3a a b +
+=________ 13．将抛物线2
21y x x =+-向上平移4个单位后，所得新抛物线的顶点坐标是________
14．一个不透明的袋子里装有3个白球、1个红球，这些球除了颜色外无其他的差异，从袋子中随机摸出1个
球，恰好是白球的概率是________ 15．正五边形的中心角是_________
A
D
C
E B
G
6题图
16．如图，圆弧形桥拱的跨度AB=16米，拱高CD=4米，那么圆弧形桥拱所在圆的半径是________米。
17．如果一个三角形一边上的中线的长与另两边中点的连线段的长相等，我们称这个三角形为“等线三角
形”，这条边称为“等线边”。
在等线三角形ABC 中，AB 为等线边，且AB=3，AC=2，那么BC=__________。
18．如图，矩形ABCD 中，AB=4，AD=7.点E 、F 分别在边AD 、BC 上，且点B 、F 关于过点E 的直线对称，
如果以CD 为直径的圆与EF 相切，那么AE=________.
19
．计算：23
282-
-++
20．解不等式组：3(21)4531
12
2x x x x ->-⎧⎪
⎨-≤⎪⎩
21．如图，在平面直角坐标系xOy 中，点A 在x 轴正半轴上，点B 、C 在第一象限，且四边形OABC 是平行
四边形，OC =sin AOC ∠=
.反比例函数k
y x
=的图像经过点C 以及边AB 的中点D 。
求：⑴这个反比例函数的解析式； ⑵四边形OABC 的面积。
18题
C
B
22．(4+6)某文具店有一种练习簿出售，每本的成本价为2元。
在销售的过程中价格有调整，按原价格每本8.25
元，卖出36本；后经两次涨价，按第二次涨价后的价格卖出了25本。
发现按原价格和第二次涨价后的价格销售，分别获得的销售利润恰好相等。
⑴求第二次涨价后每本练习簿的价格；
⑵在两次涨价过程中，假设每本练习簿平均获得利润的增长率完全相同，求这个增长率。
（注：利润增长率=100%⨯（后一次的利润-前一次的利润）前一次的利润
）
23．如图，在直角梯形ABCD 中，AD ∥BC ，∠C=90°，BC=CD ，点E 、F 分别在边BC 、CD 上，且
BE=DF=AD ，联结DE ，联结AF 、BF 分别与DE 交于点G 、P. ⑴求证：AB BF =
⑵如果BE=2CE 时，求证：DG=GE 。
24．（3+4+5）如图，已知抛物线2
3y ax bc =+-经过点A ()7,3-，与x 轴正半轴交于B (),0m 、C ()6,0m 两
点，与
y 轴交于点D 。
⑴求m 的值；
⑵求这条抛物线的表达式；
⑶点P 在抛物线上，点Q 在x 轴上，当∠PQD=90° 且PQ=2DQ 时，求点P 、Q 的坐标。
B E C
F O
x
y
25．(5+5+4)如图所示，∠MON=45°，点P 为∠MON 内一点，过点P 作PA ⊥OM 于点A ，PB ⊥ON 于点B ，
且PB =OP 的中点C ，联结AC 并延长，交OB 于点D 。
⑴求证：∠ADB=∠OPB ； ⑵设PA x =
，OD y =，求y 关于x 的函数解析式；
⑶分别联结AB 、BC ，当△ABD 与△CPB 相似时，求PA 的长。
备用图
O
M
N
B
D C
A
25题图
O
M
N
P
答案
1-6：C C B A D C
7.3
a 8. (2)x x - 9. 4x =- 10. 2x ≠ 11.1x ≤ 12.7133
a b +
13.(1,2)- 14. 3
4
15. 72°19. 34
-
20.11x -<≤ 21.⑴8
y
x
=
； ⑵12OABC
S =
22. ⑴11元； ⑵20%
23. ⑴提示△BCF ≌△DCE ⑵提示：延长AF 交BC 延长线于H 24. ⑴1m =，()2,0E
⑵217
322
y x x =-
-- ⑶当点Q 在原点，()()6,0,0,0P
Q ；Q 不在原点，()()5,2,1,0P Q -
25. ⑴提示：∠ACB=90° ⑵y = ⑶:分类讨论，当AB=AD ；BA=BD ）。