北师大版中考数学微测试系列专题17_相似三角形及应用(含解析)
2021年中考数学 专题汇编:相似三角形及其应用(含答案)

2021中考数学 专题汇编:相似三角形及其应用一、选择题(本大题共10道小题)1. 如图,在△ABC 中,D ,E 分别是AB ,AC 边上的点,DE ∥BC ,若AD=2,AB=3,DE=4,则BC 等于 ( )A .5B .6C .7D .82. (2020·永州)如图,在ABC 中,2//,3AE EF BC EB =,四边形BCFE 的面积为21,则ABC 的面积是( )A. 913B. 25C. 35D. 633. (2020·嘉兴) 如图,在直角坐标系中,△OAB 的顶点为O (0,0),A (4,3),B (3,0).以点O 为位似中心,在第三象限内作与△OAB 的位似比为13的位似图形△OCD ,则点C 坐标为( )A .(﹣1,﹣1)B .(4,13--) C .(41,3--) D .(﹣2,﹣1)4. (2019•巴中)如图ABCD ,F 为BC 中点,延长AD 至E ,使13DE AD =∶∶,连接EF 交DC 于点G ,则:DEG CFG S S △△=A .2∶3B .3∶2C .9∶4D .4∶95. (2020·河南)如图,在△ABC 中,∠ACB=90°,边BC 在x 轴上,顶点A ,B的坐标分别为(-2,6)和(7,0).将正方形OCDE 沿x 轴向右平移,当点E 落在AB 边上时,点D 的坐标为( )A. (32,2)B. (2,2)C. (114,2) D. (4,2)6. (2020·河北) 在图5所示的网格中,以点O 为位似中心,四边形ABCD 的位似图形是A.四边形NPMQB.四边形NPMRC.四边形NHMQD.四边形NHMR7. (2019•贺州)如图,在ABC △中,D E ,分别是AB AC ,边上的点,DE BC ∥,若23AD AB ==,,4DE =,则BC 等于A .5B .6C.7 D.88. 如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB 的垂直平分线,垂足为E.若BC=3,则DE的长为()A. 1B. 2C. 3D. 49. (2020•丽水)如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH.连结EG,BD相交于点O、BD与HC相交于点P.若GO=GP,则ABCDEFGHSS正方形正方形的值是()A.12+B.22+C.52-D.15410. (2020·新疆)如图,在△ABC中,∠A=90°,D是AB的中点,过点D作BC的平行线交AC于点E,作BC的垂线交BC于点F,若AB=CE,且△DFE 的面积为1,则BC的长为·······················································()A.25B.5 C.45D.10二、填空题(本大题共8道小题)11. 如图,在△ABC中,∠ACD=∠B,若AD=2,BD=3,则AC长为.12. 在某一时刻,测得一根高为1.8 m的竹竿的影长为3 m,同时同地测得一栋楼的影长为90 m,则这栋楼的高度为m.13. (2020·郴州)在平面直角坐标系中,将AOB∆以点O为位似中心,32为位似比作位似变换,得到11OBA∆.已知)3,2(A,则点1A的坐标是.14. 如图,在R t△ABC中,∠ACB=90°,AC=3,BC=4,CD⊥AB,垂足为D,E为BC的中点,AE与CD交于点F,则DF的长为_________.FE DBC A15. (2019•泸州)如图,在等腰Rt ABC△中,90C=︒∠,15AC=,点E在边CB上,2CE EB=,点D在边AB上,CD AE⊥,垂足为F,则AD长为__________.16. (2020·杭州)如图是一张矩形纸片,点E在AB边上,把BCE△沿直线CE对折,使点B落在对角线AC上的点F处,连接DF.若点E,F,D在同一条直线上,2AE=,则DF=______,BE=______.FDBEAC17. 如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连接AE,则△ABE的面积等于________.18. (2020·长沙)如图,点P 在以MN 为直径的半圆上运动,(点P 与M ,N 不重合)PQ ⊥MN ,NE 平分∠MNP ,交PM 于点E ,交PQ 于点F . (1)PMPEPQPF +=____________. (2)若MN PM PN •=2,则NQMQ=____________. F E NMP三、解答题(本大题共4道小题) 19. (2020·凉山州)(7分)如图,一块材料的形状是锐角三角形ABC ,边BC =120 mm ,高AD =80mm ,把它加工成正方形零件,使正方形的一边在BC 上,其余两个顶点分别在AB 、AC 上,这个正方形零件的边长是多少?20. 如图,在Rt △ABC 中,∠ACB=90°,AB=10,BC=6,CD ∥AB ,∠ABC 的平分线BD 交AC 于点E ,求DE 的长.HKFEBA21. 已知:在等边△ABC中,D 、E 分别是AC 、BC 上的点,且∠BAE =∠CBD<60°,DH ⊥AB ,垂足为点H .(1)如图①,当点D 、E 分别在边AC 、BC 上时,求证:△ABE ≌△BCD ;(2)如图②,当点D 、E 分别在AC 、CB 延长线上时,探究线段AC 、AH 、BE 的数量关系;(3)在(2)的条件下,如图③,作EK ∥BD 交射线AC 于点K ,连接HK ,交BC 于点G ,交BD 于点P ,当AC =6,BE =2时,求线段BP 的长.22. 已知在△ABC中,AB 边上的动点D 由A 向B 运动(与A ,B 不重合),同时,点E 由点C 沿BC 的延长线方向运动(E 不与C 重合),连接DE 交AC 于点F ,点H 是线段AF 上一点.(1)如图①,若△ABC 是等边三角形,DH ⊥AC ,且D ,E 的运动速度相等,求HFAC的值.(2)如图②,若在△ABC 中,∠ABC=90°,∠ADH=∠BAC=30°,且点D ,E的运动速度之比是:1,求HFAC的值;(3)如图③,若在△ABC 中,AB=AC ,∠ADH=∠BAC=36°,记ACBC=m ,且点D ,E 的运动速度相等,试用含m 的代数式表示HFAC的值.图① 图② 图③2021中考数学 专题汇编:相似三角形及其应用-答案一、选择题(本大题共10道小题) 1. 【答案】B [解析]∵DE ∥BC ,∴△ADE ∽△ABC , ∴=,即=,解得BC=6,故选B .2. 【答案】B【详解】解:∵//EF BC ∴AEF B AFE C ∠=∠∠=∠, ∴AEF ABC ∽ ∵23AE EB = ∴25AE AB = ∴255242AEB ABCS S ⎛⎫==⎪⎝⎭ ∴421AEBBCFESS =四边形 ∵21BCFE S =四边形 ∴AEBS =4∴=25ABCS故选:B .3. 【答案】B【解析】本题考查了在坐标系中,位似图形点的坐标.在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为k ,那么与原图形上的点(x ,y )对应的位似图形上的点的坐标为(kx ,ky )或(–kx ,–ky ).由A (4,3),位似比k =13,可得C (413,--)因此本题选B .4. 【答案】D【解析】设DE x =,∵13DE AD =∶∶,∴3AD x =, ∵四边形ABCD 是平行四边形,∴AD BC ∥,3BC AD x ==, ∵点F 是BC 的中点,∴1322CF BC x ==, ∵AD BC ∥,∴DEG CFG △∽△,∴224()()392DEG CFG S DE x S CF x ===△△,故选D .5. 【答案】B【解析】∵点A ,B 的坐标分别为(-2,6)和(7,0),∴OC=2,AC=6,OB=7, ∴BC=9,正方形的边长为2.将正方形OCDE 沿x 轴向右平移,当点E 落在AB 边上时,设正方形与x 轴的两个交点分别为G 、F ,∵EF ⊥x 轴,EF=GF=DG=2,∴EF ∥AC ,D ,E 两点的纵坐标均为2, ∴EF BF AC BC ,即269BF ,解得BF=3.∴OG=OB-BF-GF=7-3-2=2,∴ D 点的横坐标为2,∴点D 的坐标为 (2,2).6. 【答案】A【解析】解析:连接AO 并延长AO 至点N ,连接BO 并延长PO 至点P, 连接CO 并延长CO 至点M, 连接DO 并延长DO 至Q ,可知12AO BO CO DO NO PO MO QO ====,所以以点O 为位似中心,四边形ABCD 的位似图形是四边形NPMQ ,故答案为A.7. 【答案】B【解析】∵DE BC ∥,∴ADE ABC △∽△, ∴AD DE AB BC=,即243BC =,解得:6BC =,故选B .8. 【答案】A【解析】∵AD 是∠BAC 的平分线,AC ⊥BC ,AE ⊥DE, ∴DC =DE ,AE =AC .又∵DE 是AB 的垂直平分线,∴BE =AE ,即AB =2AE =2AC, ∴∠B =30°.设DE =x ,则BD =3-x .在Rt △BDE 中,x 3-x=12,解得x =1,∴DE的长为1.9. 【答案】C【解析】∵四边形EFGH 为正方形,∴∠EGH =45°,∠FGH =90°,∵OG =GP ,∴∠GOP =∠OPG =67.5°,∴∠PBG =22.5°,又∵∠DBC =45°,∴∠GBC =22.5°,∴∠PBG =∠GBC ,∵∠BGP =∠BG =90°,BG =BG ,∴△BPG ≌△BCG ,∴PG =CG .设OG =PG =CG =x ,∵O为EG,BD的交点,∴EG=2x,FG2=x.∵四个全等的直角三角形拼成“赵爽弦图”,∴BF=CG=x,∴BG=x2+x,∴BC2=BG2+CG2()2222(21)422x x x=++=+,∴()22422222ABCDEFGHxSS x+==+正方形正方形,因此本题选D.10. 【答案】A【解析】本题考查了相似三角形的判定与性质,三角形的中位线定理.如答图,过点E作EG⊥BC于G,过点A作AH⊥BC于H.又因为DF⊥BC,所以DF∥AH∥EG,四边形DEGF是矩形.所以△BDF∽△BAH,DF=EG,所以DFAH=BDBA,因为D为AB中点,所以BDBA=12,所以DFAH =12.设DF=EG=x,则AH=2x.因为∠BAC=90°,所以∠B+∠C=90°,因为EG⊥BC,所以∠C+∠CEG=90°,所以∠B=∠CEG,又因为∠BHA=∠CGE=90°,AB=CE,所以△ABH≌△CEG,所以CG=AH=2x.同理可证△BDF∽△ECG,所以BFEG=BDEC,因为BD=12AB=12CE,所以BF=12EG=12x.在R t△BDF中,由勾股定理得BD=22DF BF+=221()2x x+=5x,所以AD=5x,所以CE=AB=2AD=5x.因为DE∥BC,所以AEAC=ADAB=12,所以AE=12AC=CE=5x.在R t△ADE中,由勾股定理得DE=22AD AE+=225()(5)2x x+=52x.因△DEF的面积为1,所以12DE·DF=1,即12×52x·x=1,解得x=255,所以DE=52×255=5,因为AD=BD,AE=CE,所以BC=2DE=25,因此本题选D.二、填空题(本大题共8道小题)11. 【答案】[解析]∵∠ACD=∠B,∠CAD=∠BAC,∴△ACD∽△ABC,∴=,即=,∴AC=或AC=-(舍去).12. 【答案】5413. 【答案】(,2)【解析】∵将△AOB 以点O 为位似中心,为位似比作位似变换,得到△A 1OB 1,A (2,3),∴点A 1的坐标是:(×2,×3),即A 1(,2).故答案为:(,2).14. 【答案】5485【解析】本题考查平行线分线段成比例定理,相似三角形的判定与性质.已知∠ACB =90°,AC =3, BC =4,由勾股定理,得AB =5.CD ⊥AB ,由三角形的面积,得CD =AC BC AB ⋅=125.易得△ABC ∽△ACD ∽△CBD ,由相似三角形对应边成比例,得AD =AC AC AB ⋅=95,BD =BC BC AB ⋅=165.过点E 作EG ∥AB 交CD于点G ,由平行线分线段成比例,得DG =12CD =65,EG =85,所以DF ADGF EG=,即956855DF DF =-,所以DF =,故答案为5485. GF E DB CA15. 【答案】92【解析】如图,过D 作DH AC ⊥于H ,则∠AHD =90°,∵在等腰Rt ABC △中,90C =︒∠,15AC =, ∴15AC BC ==,45CAD ∠=︒, ∴∠ADH =90°–∠CAD =45°=∠CAD , ∴AH DH =,∴CH =AC –AH =15–DH ,∵CF AE ⊥,∴90DHA DFA ∠=∠=︒,又∵∠ANH =∠DNF ,∴HAF HDF ∠=∠,∴ACE DHC △∽△,∴DH CH AC CE =, ∵2CE EB =,CE +BE =BC =15,∴10CE =, ∴151510DH DH -=, ∴9DH =,∴2292AD AH DH =+=,故答案为:92.16. 【答案】2 5-1【解析】设BE =x ,则AB =AE +BE =2+x .∵四边形ABCD 是矩形,∴CD =AB =2+x ,AB ∥CD ,∴∠DCE =∠BEC .由折叠得∠BEC =∠DEC ,EF =BE =x ,∴∠DCE =∠DEC .∴DE =CD =2+x .∵点D ,F ,E 在同一条直线上,∴DF =DE -EF =2+x -x =2.∵AB ∥CD ,∴△DCF ∽△EAF ,∴DC EA =DF EF .∴22x +=2x ,解得x 1=5-1,x 2=-5-1.经检验,x 1=5-1,x 2=-5-1都是分式方程的根.∵x >0,∴x =5-1,即BE =5-1.17. 【答案】78 【解析】如解图,过A 作AH ⊥BC ,∵AB =15,AC =20,∠BAC =90°,∴由勾股定理得,BC =152+202=25,∵AD =5,∴DC =20-5=15,∵DE ⊥BC ,∠BAC =90°,∴△CDE ∽△CBA ,∴CE CA =CD CB ,∴CE =1525×20=12.法一:BC·AH =AB·AC ,AH =AB·AC BC =15×2025=12,S △ABE =12×12×13=78.法二:DE =152-122=9,由△CDE ∽△CAH 可得,CD CA =ED HA ,∴AH =9×2015=12,S △ABE =12×12×13=78.18. 【答案】1;215- 【解析】本题考查了圆的基本性质,角平分线性质,平行相似,相似判定与性质,(1)作EH ⊥MN ,又∵MN 是直径,NE 平分∠MNP ,PQ ⊥MN ,∴易证出PE =EH =HF =PF ,EH ∥PQ ,∴△EMH ∽△PMQ ,∴PQ PF PQ EH PM ME ==,∴1=+=+PM PE PM ME PM PE PQ PF ; (2)由相似基本图射影型得:解得MN QN PN •=2又∵MN PM PN •=2,∴QN =PM ,设QN =PM =a ,MQ =b ,由相似基本图射影型得:解得MN MQ PM •=2,∴()b a b a +=2解得()251a b +-=或()251a b --=(舍去)∴215-==a b NQ MQ ; 因此本题答案为1;215-. F EQ N M P三、解答题(本大题共4道小题)19. 【答案】解:设这个正方形零件的边长为x mm ,则△AEF 的边EF 上的高AK =(80-x)mm .∵四边形EFHG 是正方形,∴EF ∥GH ,即EF ∥BC .∴△AEF ∽△ABC . ∴EF AK BC AD =,即8012080x x -=.∴x =48.∴这个正方形零件的边长是48 mm .20. 【答案】解:∵BD 平分∠ABC ,∴∠ABD=∠CBD.∵AB ∥CD ,∴∠D=∠ABD ,∴∠CBD=∠D ,∴CD=BC=6.在Rt △ABC 中,AC===8.∵AB ∥CD ,∴△ABE ∽△CDE ,∴====,∴CE=AE ,DE=BE ,即CE=AC=×8=3.在Rt △BCE 中,BE===3, ∴DE=BE=×3=.21. 【答案】(1)证明:∵△ABC 为等边三角形,∴∠ABC =∠C =∠CAB =60°,AB =BC ,在△ABE 和△BCD 中,⎩⎨⎧∠BAE =∠CBDAB =BC∠ABE =∠BCD, ∴△ABE ≌△BCD (ASA);(2)解:∵△ABC 为等边三角形,∴∠ABC =∠CAB =60°,AB =BC ,∴∠ABE =∠BCD =180°-60°=120°.∴在△ABE 和△BCD 中,⎩⎨⎧∠BAE =∠CBDAB =BC∠ABE =∠BCD, ∴△ABE ≌△BCD (ASA),∴BE =CD .∵DH ⊥AB ,∴∠DHA =90°,∵∠CAB =60°,∴∠ADH =30°,∴AD =2AH ,∴AC =AD -CD =2AH -BE ;(3)解:如解图,作DS ⊥BC 延长线于点S ,作HM ∥AC 交BC 于点M ,解图∵AC =6,BE =2,∴由(2)得AH =4,BH =2,与(1)同理可得BE =CD =2,CE =8,∵∠SCD =∠ACB =60°,∴∠CDS =30°,∴CS =1,SD =3,BS =7,∵BD 2=BS 2+SD 2=72+(3)2,∴BD =213,∵EK ∥BD ,∴△CBD ∽△CEK ,∴CB CE =CD CK =BD EK ,∴CK =CD ·CE CB =2×86=83,EK =CE ·BD CB =8×2136=8133. ∵HM ∥AC ,∴∠HMB =∠ACB =60°,∴△HMB 为等边三角形,BM =BH =HM =2, CM =CB -BM =4,又∵HM ∥AC ,∴△HMG ∽△KCG ,∴HM KC =MG CG ,即382=MG 4-MG,∴MG =127,BG =267,EG =407, ∵EK ∥BD ,∴△GBP ∽△GEK ,∴BP EK =GB GE , ∴BP =261315.22. 【答案】(1)过点D 作DG ∥BC 交AC 于点G ,解图①∵△ABC 是等边三角形,∴△AGD 是等边三角形,∴AD =GD ,由题意知CE =AD ,∴CE =GD∵DG ∥BC ,∴∠GDF =∠CEF ,在△GDF 与△CEF 中,GDF CEF GFD EFC CE GD ⎧⎪⎨⎪=∠=∠∠∠⎩=, ∴△GDF ≌△CEF (AAS ),∴CF =GF , ∵DH ⊥AG ,∴AH =GH ,∴AC =AG +CG =2GH +2GF =2(GH +GF )=2HF , ∴AC HF=2; (2)如解图②,过点D 作DG ∥BC 交AC 于点G ,解图②由题意知,点D ,E 3:1, ∴3,AD CE = ∵∠ABC =90°,∠BAC =30°,∴3,AD GD = ∴,AD AD CE GD = ∴GD =CE ,∵DG ∥BC ,∴∠GDF=∠CEF ,在△GDF 和△CEF 中,,GDF CEF GFD EFC GD CE ∠=∠∠=∠⎧⎪⎨⎪⎩=∴△GDF ≌△CEF (AAS ),∴CF =GF ,∵∠ADH =∠BAC =30°,∴AH =HD ,∵∠AGD =∠HDG =60°,∴GH =HD ,∴AH =HG ,∴AC =AG +CG =2GH +2GF =2(GH +GF )=2HF , ∴AC HF=2; (3)如解图③,过点D 作DG ∥BC 交AC 于点G ,解图③∵DG ∥BC ,∴△AGD ∽△ACB ,∴=,GD BC m AG AC = ∵∠ADH =∠BAC =36°,AC=AB ,∴∠GHD =∠HGD =72°,∴GD =HD =AH , ∴=,AH GD m AG AG= ∵AD =CE , ∴==,GD GD GD m AD AG CE = ∵DG ∥BC ,∴△GDF ∽△ECF ,∴=,GD GF m CE CF= ∴GH +FG =m (AH +FC )=m (AC-HF ), 即HF =m (AC-HF ),∴1.=AC m HF m +。
北师大版九年级上册数学 4.6 利用相似三角形测高 同步练习(含解析)
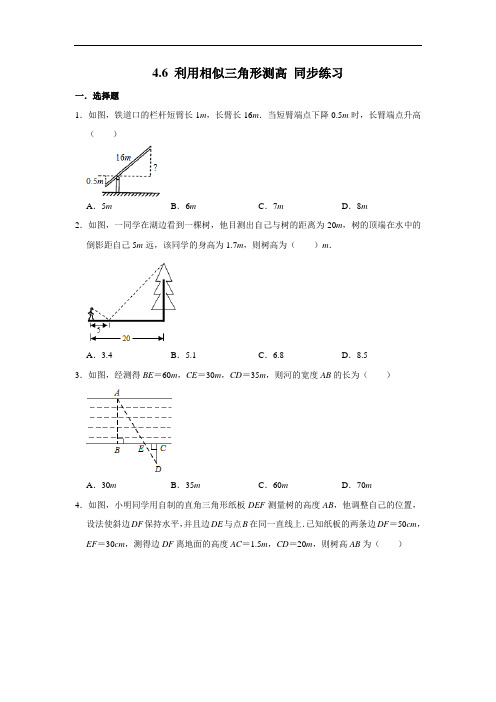
1.解:设长臂端点升高x米,
则 ,
∴x=8.
故选:D.
2.解:由相似三角形的性质,设树高x米,
则 = ,
∴x=5.1m.
故选:B.
3.解:∵AB⊥BC,CD⊥BC,
∴∠ABE=∠DCE=90°,
又∵∠AEB=∠DEC(对顶角相等),
∴△ABE∽△DCE,
∴ = ,
即 = ,
解得:AB=70m.
故选:D.
4.解:∵∠DEF=∠BCD=90°∠D=∠D
∴△DEF∽△DCB
∴ =
∵DF=50cm=0.5m,EF=30cm=0.3m,AC=1.5m,CD=20m,
∴由勾股定理求得DE=40cm,
∴ =
∴BC=15米,
∴AB=AC+BC=1.5+15=16.5米,
故选:D.
5.解:如图所示,过A作AG⊥DE于G,交BC与F,
∴ ,
∴ = ,
∴CD=16.8m,
故答案为:16.8.
14.解:过D作DG⊥AB于G,过C作CH⊥AB于H,
则DG∥CH,
∴△ODG∽△OCH,
∴ = ,
∵栏杆从水平位置AB绕固定点O旋转到位置DC,
∴CD=AB=3.5m,OD=OA=3m,CH=0.3m,
∴OC=0.5m,
∴ = ,
∴DG=1.8m,
∴HF=(10+80 )cm.
故答案为:80 ,(10+80 );
12.解:由题意得:CD∥AB,
∴ = ,
∵AB=3.5cm,BE=5m,DE=3m,
∴ ,
∴CD=2.1cm,
故答案为:2.1cm.
13.解:∵AB⊥BD,CD⊥BD,
相似三角形常考综合题精练(11大题型)(原卷版)—2024-2025学年九年级数学上册(北师大版)

相似三角形常考综合题精练(11大题型)本讲目录链接题型01比例线段的应用题型02黄金分割题型03平行线分线段成比例定理题型04相似多边形的性质题型05相似三角形的性质与判定题型06相似三角形的实际应用题型07图形的位似题型08旋转背景下的相似三角形的性质与判定题型09折叠背景下的相似三角形的性质与判定题型10动点背景下的相似三角形的性质与判定题型11相似三角形的综合问题题型01比例线段的应用1.定义一个运算()()1212121212,,,,0n n n n nx x x H x x x y y y y y y y y y +++=+++¹+++L L L L L ,下列说法正确的有( )个①()1,231H =;②若()()24,41,21H x H x ---=-,则=1x -或2;③()()()()22217511,212,413,6110,20264H H H H ++++=L ;④若()()()(),,,,,,,,H a b c d H b a c d H c a b d H d a b c ===,则1c d a b +=+.A .1B .2C .3D .42.已知代数式x A y z =+,y B x z=+,z C x y =+,下列结论中,正确的个数是( )①若::1:2:3x y z =,则::2:5:10A B C =;②若A B C a ===,则一次函数1y ax =-的图像必过第一、三、四象限;③若x ,y ,z 均为正整数,且x y z <<,则A B C <<;④若1y =,2z =-,且x为方程21m =的一个实数根,则22182023y A B C +=+.A .1B .2C .3D .43.如图,已知在ABC V 中,点D F 分别为边AB BC AC 、、上的点,且AE BF CD 、、相交于点G ,如果2014AG BG CG GE GF GD ++=,那么AG BG CG GE GF GD ××的值为 .4.已知代数式x A y z =+,y B x z=+,z C x y =+,下列结论中,正确的个数是( )①若::1:2:3x y z =,则::2:5:10A B C =;②若()0A B C a a ===¹,则一次函数1y ax =-的图象必定经过第一、三、四象限;③若x ,y ,z 为正整数,且x y z <<,则A B C <<;④若1y =,2z =-,且x为方程21m =的一个实根,则2211A B +与82023C+的值相等;⑤若222x y zx yzxy yz zx z-+-=+++,222y z xy zxxy yz zx x-+-=+++()()()A AB B BC C C A-+-+-的值为28.A.1B.2C.3D.4题型02黄金分割5.我们把宽与长的比等于黄金比的矩形称为黄金矩形.如图,在黄金矩形ABCD()AB BC<中,ABCÐ的平分线交AD边于点E,EF BC^于点F,则下列结论错误的是()A.AE DEAD AE=B.CF BFBF BC=C.AE BEBE BC=D.DE ABEF BC=6.在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连接BE,延长DA至F,使得EF BE=,以AF为边作正方形AFGH,则点H 即是线段AB的黄金分割点.若20AD=,记正方形AFGH的面积为1S,矩形BCIH的面积为2S,则1S与2S 的和为.7.如图①,点C把线段AB分成两部分()AC BC>,若AC BCAB AC=,那么称点C为线段AB的黄金分割点.类似的,可以定义“黄金分割线”:直线l把一个面积为S的图形分成面积为1S和2S的两部分12()S S>,如果121S SS S=,那么称直线l为该图形的黄金分割线.(1)如图②,在ABC V 中,若点D 是线段AB 的黄金分割点()BD AD >,线段CD 所在直线是ABC V 的黄金分割线吗?为什么?(2)在(1)的条件下,如图③,过点C 作一条直线交BD 边于点E ,过点D 作DF EC ∥交ABC V 的一边于点F ,连接EF ,交CD 于点G ,回答问题.①CFG S V ______EDG S △(填“>”“<”或“=”).②EF 是ABC V 的黄金分割线吗?为什么?8.(1)在图①中按下列步骤作图:第一步:过点C 画CD AC ^,使12CD AC =;第二步:连接AD ,以点D 为圆心,DC 的长为半径画弧,交AD 于点E ;第三步:以点A 为圆心,AE 的长为半径画弧,交AC 于点B .(2)在所画图中,点B 是线段AC 的黄金分割点吗?为什么?(3)如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请你在图②中以线段AB 为腰,用直尺和圆规,作一个黄金三角形ABC .(不写作法,保留作图痕迹)9.请阅读下列材料,并完成相应的任务:公元前300著.黄金分割(goldensection )是指把一条线段分割为两部分,使较大部分与全长的比值等于较小部分与较大部分的比值.如图①,在线段AD 上找一个点C ,C 把AD 分为AC 和CD 两段,其中AC 是较小的一段,如果::AC CD CD AD =,那么称线段AD 被C 点黄金分割,点C 叫做线段AD 的黄金分割点,AC 与CD 的比值叫做黄金分割数.为简单起见,设1,AD CD x ==,则1AC x =-.∵::AC CD CD AD =,∴……任务:(1)请根据上面的部分解题过程,求黄金分割数.(2)如图②,采用如下方法可以得到黄金分割点:①设AB 是已知线段,过点B 作BD AB ^且使12BD AB =;②连接DA ,在DA 上截取DE DB =;③在AB 上截取AC AE =;则点C 即为线段AB 黄金分割点.你能说说其中的道理吗?(3)已知线段1AB =,点C ,D 是线段AB 上的两个黄金分割点,则线段CD 的长是 .10.材料一:北师大版数学教材九年级上册第四章,对“黄金分割比”的定义如下:“如图 ,点C 把线段AB 分成两条线段AC 和BC ,如果AC AB =BC AC ,那么称线段AB被点C 黄金分割,点C 叫做线段AB 的黄金分割点,AC AB .”根据定义不难发现,在线段AB 另有一点D 把线段AB 分成两条线段AD 和BD ,满足BD AB =AD BD ,所以点D 也是线段AB 的黄金分割点.材料二:对于实数:a 1<a 2<a 3<a 4,如果满足(a 3﹣a 1)2=(a 4﹣a 3)(a 4﹣a 1),(a 4﹣a 2)2=(a 2﹣a 1)(a 4﹣a 1)则称a 3为a 1,a 4的黄金数,a 2为a 1,a 4的白银数.请根据以上材料,回答下列问题(1)如图,若AB =4,点C 和点D 是线段AB 的黄金分割点,则AC = ,CD = .(2)实数0<a <b <1,且b 为0,1的黄金数,a 为0,1的白银数,求b ﹣a 的值.(3)实数k <n <m <t ,t =2|k |,m ,n 分别为k ,t 的黄金数和白银数,求m n 的值.11.根据以下素材,探索完成任务.题型03平行线分线段成比例定理12.如图,在正方形中,分别以点A 和为圆心,以大于的长为半径作弧,两弧相交于点和ABCD B 12AB E,作直线,再以点A 为圆心,以的长为半径作弧交直线于点(点在正方形内部),连接并延长交于点.若,则正方形的边长为( )AB .CD13.如图是一张矩形纸片,点为AD 中点,点在上,把该纸片沿折叠,点,的对应点分别为,,与相交于点,的延长线过点.若,则.14.如图,、,、分别是和的中点,过的直线依次交、、、于点、、、,求证:.15.如图,,点在上,过点作的平行线,与的平分线交于点,为的中点,点在上,(不与点重合),连接,将线段绕点顺时针旋转,得到线段,连接.F EF AD EFG G ABCD DG BC K 2BK =ABCD 1521ABCD E F BC EF A B A ¢B ¢A E ¢BC G B A ¢¢C 23BF GC =AD AB =AB CD ∥AD CE F G AC FD G AB AD CD CE M N P Q 2PQ PN +=OPQ a Ð=A PQ A PO OPQ ÐB M PB C PM P M ,AC AC A 180a °-AD BD(1)①直接写出线段与之间的数量关系;②用等式表示线段,,之间的数量关系,并证明;(2)连接并延长,分别交,于点,过点作的垂线,交于点.依题意补全图形,用等式表示线段,,之间的数量关系.16.四边形的两条对角线,相交于点O ,.(1)如图1,已知.①求证:;②若,求的值;(2)如图2,若,,,求的值.题型04相似多边形的性质17.如图,已知在矩形 中,,,点 从点 出发,沿 方向以每秒 个单位的速度向点 运动,点 从点 出发,沿射线 以每秒 个单位的速度运动,当点 运动AP AB BD BM MC DC AB PO E F ,M OP DC N CF CN NE ABCD AC BD 90BAD Ð=°AC CD =ACD BAC Ð=Ð225OC OA =OB OD 90BCD Ð=°AB AD =3CD BC =AC BDABCD AB 2=BC 6=E D DA 1A F B AB 3E到点 时,, 两点停止运动.连接 ,过点 作 ,垂足为 ,连接 ,交 于点 ,交 于点 ,连接 .给出下列结论:① ;② ;③ ;④ 的值为定值.上述结论中正确的个数为 ( )个.A.B .C .D .18.已知E、F 、G 、H 各点分别在四边形的、、、边上(如图).(1)当时,求证:(2)当上述条件中比值为3,4,…,n 时(为自然数),那么与之比是多少?19.如图1,矩形ODEF 的一边落在矩形ABCO 的一边上,并且矩形ODEF ∽矩形ABCO ,其相似比为1:4,矩形ABCO 的边AB =4,BC (1)求矩形ODEF 的面积;(2)将图1中的矩形ODEF 绕点O 逆时针旋转一周,连接EC 、EA ,ACE 的面积是否存在最大值或最小A E F BD E EH BD ^H EF BD G BC M CF CDE CBF V V ∽DBC EFC ÐÐ=DE HG AB EH=GH 1234ABCD AB BC CD DA 2AE BF CG DH EB FC GD HA ====59EFGH ABCDS S =四边形四边形n EFGH S 四边形ABCD S 四边形V值?若存在,求出最大值或最小值;若不存在,请说明理由.20,则称这条直线为该矩形的黄金线.例如图所示的矩形中,直线,分别交、于点、,且,显然直线是矩形的黄金线.(1)如图,在矩形中,,.请在图中画出矩形的其中一条黄金线,其中在边上,在边上,并标注出线段的长度;(2)将正方形纸片按图所示的方式折叠.如图所示,按上述方法折叠所得到的折痕是否为正方形的黄金线?请说明理由.ABCD EF BC^AD BC E F AE AB =EF ABCD ABCD 2AB = 3AD =ABCD MN M AD N BC AM GH ABCD(3)在矩形中,,,已知矩形的黄金线恰好将矩形分割成两个黄金矩形,则______(只要求直接写出其中三个答案).21.阅读下列材料,完成任务:自相似图形定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD 中,点E 、F 、G 、H 分别是AB 、BC 、CD 、DA 边的中点,连接EG ,HF 交于点O ,易知分割成的四个四边形AEOH 、EBFO 、OFCG 、HOGD 均为正方形,且与原正方形相似,故正方形是自相似图形.任务:(1)如图1中正方形ABCD 分割成的四个小正方形中,每个正方形与原正方形的相似比为________;(2)如图2,已知△ABC 中,∠ACB=90°,AC=4,BC=3,小明发现△ABC 也是“自相似图形”,他的思路是:过点C 作CD ⊥AB 于点D ,则CD 将△ABC 分割成2个与它自己相似的小直角三角形.已知△ACD ∽△ABC ,则△ACD 与△ABC 的相似比为________;(3)现有一个矩形ABCD 是自相似图形,其中长AD=a ,宽AB=b (a >b ).请从下列A 、B 两题中任选一条作答.A :①如图3﹣1,若将矩形ABCD 纵向分割成两个全等矩形,且与原矩形都相似,则a=________(用含b 的式子表示);ABCD 1AB =AD a =ABCD EF ABCD a=②如图3﹣2若将矩形ABCD 纵向分割成n 个全等矩形,且与原矩形都相似,则a=________(用含n ,b 的式子表示);B :①如图4﹣1,若将矩形ABCD 先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a=________(用含b 的式子表示);②如图4﹣2,若将矩形ABCD 先纵向分割出m 个全等矩形,再将剩余的部分横向分割成n 个全等矩形,且分割得到的矩形与原矩形都相似,则a=________(用含m ,n ,b 的式子表示).题型05相似三角形的性质与判定22.如图,在中,,以为边向三角形外作正方形,作于点,交对角线于点,连接.要求的周长,只需知道( )A .的长B .的长C .的长D .的长23.如图,,,,点E 在边上运动(不与端点重合),边始终过点A ,交于点G 是等腰三角形时,的面积是( ).A .8或B .8C.D .6或 24.由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.将小正方形对角线双向延长,分别交边AB ,和边的延长线于点,.若大正方形与小正方形的面积之比为,,则大正方形的边长为 .Rt ABC △90ACB Ð=°AB ABDE EF BC ^F AD G BG BFG V AC BC BF FG ABC DEF ≌△△5AB AC ==6BC EF ==BC DE EF AC AEG AEG △625108625108625107ABCD EF BC G H 5GH =25.如图,在正方形中,为边上的两个三等分点,点关于的对称点为,的延长线交于点.(1)求证:;(2)求的大小;(3)求证:.26.如图1,四边形是正方形,点E 在边的延长线上,点F 在边上,且,连接交于点P ,连接交于Q ,连接.(1)求证:;(2)连接,如图2,①若的长;②若,则 .27.平移图形是解答几何题目时一种重要的添加辅助线策略.如图①,在正方形中,E 、F 、G 分别是、、上的点,于点Q .求证:.小鹿在分析解题思路时想到了两种平移法:方法一:平移线段使点F 与点B 重合,构造全等三角形;ABCD E F ,AB A DE A ¢AA ¢BC G DE A F ¢∥GA B ¢Ð2A C A B ¢¢=ABCD BC AB AF CE =EF DC AC EF DE DF 、EQ FQ =BQ AQ DP ×=BQ FP FD =PE PQ=ABCD BC AB CD FG AE ^=AE FG FG方法二:平移线段使点B 与F 重合,构造全等三角形;【尝试应用】(1)请按照小鹿的思路,选择其中一种方法进行证明;(2)如图②,点E 、F 、G 、H 分别是矩形边、、、上的点,且,若,,求的值;【拓展探究】(3)如图③,点E 、F 分别是平行四边形边、上的点,连接、交于点G ,若,求证:.28.如图,,,.(1)如图1,不添加辅助线,请写出图中所有相似三角形;(2)如图2,若点E 落在边上,求证:;(3)如图3,若点H ,I ,J 分别为,AB ,AD 中点,判断与的数量关系及夹角度数(锐角).题型06相似三角形的实际应用29.将一本高为(即)的词典放入高(AB )为的收纳盒中(如图1).恰好能盖上盒盖时,测得底部F 离收纳盒最左端B 处,若此时将词典无滑动向右倒,书角的对应点恰为CD 中点.BC ABCD AB CD AD BC EF GH ^3AB =4BC =EF GHABCD AB AD CF DE 180B EGC Ð+Ð=°DE AD CF CD=90BAC AED ÐÐ==°AB AC =EA ED =BC 2222AD EF BF EF =+×BC IJ HE 17cm 17cm EF =16cm 8cm H H ¢(1)收纳盒的长 ;(2)现将若干本同样的词典放入此有盖的收纳盒中,如图2放置,则最多有本书可与边BC 有公共点.30.【问题探究】(1)如图①,在中,,,,将绕点逆时针旋转到的位置,点的对应点落在上,则的长为 ;(2)如图②,在矩形中,,,点是矩形的对称中心,点在边上,且,点是边上的动点,连接与,求的最大值;【问题解决】(3)有一块三角形草地,其示意图如图③所示,,,是一条小道(宽度不计),点是的中点,点在内,、两点之间的距离为,.市政府为丰富市民的业余生活,计划将部分草地改建,在、上分别找点、,在、处栽种梧桐树,,连接、,在.根据规划,现要沿线段修建一段文化长廊(宽度不计),为容纳更多的市民在文化长廊内活动,要求文化长廊的长度尽可能的长,当文化长廊的长最大时,请求出此时点的位置(即的长).31.BC =Rt ABC △90BAC Ð=°4AB=AC =ABC V C DEC V A D BC BD ABCD 2AB =6AD =O ABCD E AD 2AE =F BC EF OF EF OF -ABC 24cm AB BC ==90ABC Ð=°DE D BC E ABC V B E 13cm DE BC ^BC BA M N M N BM BN =EM EN EP EM =PN PN PN NBN32.在光学中,由实际光线会聚成的像,称为实像,而光线能会聚的是因为折射.图中,凸透镜的焦距为f ,主光轴,A ,B ,C ,D 都在l 上,其中O 是光心,,蜡烛(蜡烛可移动,EF l EF ^2OB OD f ==PQ l ^且),光线,其折射光线与另一条经过光心的光线相交于点()即为蜡烛在光屏上所成的实像.图中所有点都在同一平面内.记物高为h ,像高为,物距,像距为v .(1)若,,, .(2)求证.(3)当f 一定时,画出v 与u 之间的函数图象,并结合图象描述v 是怎么随着u 的变化而变化的?33.阅读理解:如图1,在△ABC 中,当DE ∥BC 时可以得到三组成比例线段:① ;② ;③ .反之,当对应线段成比例时也可以推出DE ∥BC .理解运用:三角形的内接四边形是指顶点在三角形各边上的四边形.(1)如图2,已知矩形DEFG 是△ABC 的一个内接矩形,将矩形DEFG 沿CB 方向向左平移得矩形PBQH ,其中顶点D 、E 、F 、G 的对应点分别为P 、B 、Q 、H ,在图2中画出平移后的图形;(2)在(1)所得的图形中,连接CH 并延长交BP 的延长线于点R ,连接AR .求证:AR ∥BC ;(3)如图3,某小区有一块三角形空地,已知△ABC 空地的边AB =400米,BC =600米,∠ABC =45°;准备在△ABC 内建一个内接矩形广场DEFG (点E 、F 在边BC 上,点D 、G 分别在边AB 和AC 上),三角形其余部分进行植被绿化,按要求欲使矩形DEFG 的对角线EG 最短,请在备用图中画出使对角线EG 最短距离(不要求证明).34.阅读理解:如图1,AD 是△ABC 的高,点E 、F 分别在AB 和AC 边上,且EF BC ,可以得到以下结论:.OQ f >PG l ∥GC PP ¢P ¢P Q l ¢¢^()PQ ()P Q ¢¢h ¢()OQ ()OQ ¢10cm f =10cm h =15cm u ==v cm 111u v f+=()u f >AD AE DE AB AC BC ==AD AE BD CE =BD CE AB AC=//AH EF AD BC=拓展应用:(1)如图2,在△ABC中,BC=3,BC边上的高为4,在△ABC内放一个正方形EFGM,使其一边GM在BC 上,点E、F分别在AB、AC上,则正方形EFGM的边长是多少?(2)某葡萄酒庄欲在展厅的一面墙上,布置一个腰长为100cm,底边长为160cm的等腰三角形展台.现需将展台用隔板沿平行于底边,每间隔10cm分隔出一排,再将每一排尽可能多的分隔成若干个无盖正方体格子,要求每个正方体格子内放置一瓶葡萄酒.平面设计图如图3所示,将底边BC的长度看作是0排隔板的长度.①在分隔的过程中发现,当正方体间的隔板厚度忽略不计时,每排的隔板长度(单位:厘米)随着排数(单位:排)的变化而变化.请完成下表:排数/排0123…隔板长度/厘米160__________________…若用n表示排数,y表示每排的隔板长度,试求出y与n的关系式;②在①的条件下,请直接写出该展台最多可以摆放多少瓶葡萄酒?35.阅读以下文字并解答问题:在“测量物体的高度”活动中,某数学兴趣小组的3名同学选择了测量学校里的三棵树的高度,在同一时刻的阳光下,他们分别做了以下工作:小芳:测得一根长为1米的竹竿的影长为0.8米,甲树的影长为4.08米(如1图).小华:发现乙树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如2图),墙壁上的影长为1.2米,落在地面上的影长为2.4米.小明:测得丙树落在地面上的影长为2.4米,落在坡面上影长为3.2米(如3图).身高是1.6米的小明站在坡面上,影子也都落坡面上,小芳测得他的影长为2米.(1)在横线上直接填写甲树的高度为______米,乙树的高度为________米﹔(2)请求出丙树的高度.36.【问题背景】人教版九年级下册教材第58页第11题:如图1,一块材料的形状是锐角三角形,边,高.把它加工成正方形零件,使正方形的一边在上,其余两个顶点分别在上,这个正方形零件的边长是多少?【提出问题】在满足正方形的一边在三角形的一边上,其余两个顶点分别在另外两边上的条件下,能否在上面的材料上,加工一个面积更大的正方形?如何用直角尺(只能画直角)和圆规画出这个正方形?【分析问题】小敏认为,由于正方形的一边在三角形的一边上,这样就存在三种可能.在已知三边长度的情况下,可以通过计算,分别求出三个正方形的边长,然后比较三条边长的大小,进而知道面积最大的正方形;也可以结合当前所学的位似,分别画出满足条件的正方形,再利用圆规比较三个正方形的边长的大小,即可解决问题.【解决问题】为了简化探索过程,小敏取边长分别为的三个等腰三角形(其中为腰)木块进行研究.如图2,正方形的顶点分别在上,边在上.如图3,正方形的顶点分别在上,边在上.请你完成下面两个问题:(1)通过计算,比较这两个正方形的边长的大小;(2)在图4中,用直角尺(只能画直角)和圆规画出面积最大的正方形,使其一边在三角形的一边上,其ABC 120mm BC =80mm AD =BC AB AC,556cm cm cm ,,AB AC ,EFGH E H ,AB AC ,FG BC MNPQ M N ,AB BC ,PQ AC余两个顶点分别在另外两边上(保留画图痕迹).【学以致用】定义:由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.小敏类比上面的研究方法,又提出下面问题:在如图5所示的扇形中,能否用直角尺和圆规画出一个正方形,使其两个顶点在弧上,另外两个顶点在半径上?你认为可以吗?如果可以、在图中画出符合条件的正方形(保留画图痕迹);如果不可以,说明理由.题型07图形的位似37.如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.A ,B ,C 三点是格点,点P 在上,仅用无刻度的直尺在给定网格中完成画图.(1)在图(1)中,将线段沿的方向平移,使点B 与点C 重合,画出平移后的线段;再将绕的中点顺时针旋转,得到,画出线段;(2)在图(2)中,连接,将以C为位似中心缩小为原来的得到,画出;88´BC AB BC CD PC AC 180°GA GA AP APC △12EFC V EFC V(3)在图(3)中,在上画一点M ,在AB 上画一点N ,使得最小.38.(1)在正方形方格纸中,我们把顶点都在“格点”上的三角形称为“格点三角形”,如图,△ABC 是一个格点三角形,点A 的坐标为(-2,2).①△ABC 的面积为______;②在所给的方格纸中,请你以原点O 为位似中心,将△ABC 缩小为原来的一半;(仅用直尺完成作图)③在(2)中,若P (a ,b )为线段AC 上的任一点,则缩小后点P 的对应点P 1的坐标为______.(2)按要求作图,不要求写作法,但要保留作图痕迹:我们知道,三角形具有性质:三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高所在直线相交于一点.请运用上述性质,只用直尺(不带刻度)作图.AC PM PN+①如图1,在平行四边形ABCD 中,E 为CD 的中点,作BC 的中点F .②如图2,在由小正方形组成的4×3的网格中,△ABC 的顶点都在小正方形的顶点上,作△ABC 的高AH .39.如图①,在中,,,点D 是上一点,且.动点F 从点C 出发沿方向以每秒2个单位长度的速度向经点B 运动,以为边构造等腰直角三角形,其中F 为直角顶点,且点E 与点B 位于线段两侧.设点F 的运动时间为t (秒).AI(1)求线段的长度;(2)当点E 落在的中位线上时,求出t 的值:(3)连接,则线段的最小值是______.(4)如图②.以点B 为位似中心,将缩小后得到,且.连接,当与的某条边平行时,直接写出t 的值.题型08旋转背景下的相似三角形的性质与判定40.定义:如果将一个三角形绕着它的一个角的顶点旋转后,使这个角的一边与另一边重叠,再将所旋转后的三角形进行相似缩放,使重叠的两条边相互重合,我们称这样的图形变换为三角形转似,这个三角形的顶点称为转似中心,所得的三角形称为原三角形的转似三角形.如图,在中,,是以点为转似中心的顺时针的一个转似三角形,那么以点A 为转似中心的逆时针的另一个转似三角形 (点分别与对应),其中边的长为Rt ABC △9AB =12BC =AB 2AD BD =CB DF DEFDF AC Rt ABC △CE CE DEF V D E F ¢¢¢△3DF D F ¢¢=E C ¢E C ¢Rt DEF △ABC V 465AB AC BC ===,,AB C ¢¢△ABC V A AB C ¢¢¢¢△B C ¢¢¢¢,B C 、B C ¢¢¢¢41.在矩形中,点是对角线、的交点,直角的顶点与重合,、分别与、边相交于、,连接,(为常数).(1)发现问题:如图1,若,猜想:________;(2)类比探究:如图2,,探究线段,之间的数量关系,并说明理由;(3)拓展运用:如图3,在(2)的条件下,若,的长.42.综合与实践.问题情境:综合与实践课上,同学们开展了以“图形的旋转”为主题的数学活动.实践操作:如图1,将等腰Rt △AEF 绕正方形ABCD 的顶点A 逆时针方向旋转,其中∠AEF =90,EA =EF ,连接CF ,点H 为CF 的中点,连接HD ,HE ,DE ,得到△DHE .应用探究:(1)勤奋组:如图2,当点E 恰好落在正方形ABCD 的对角线AC 上时,判断△DHE 的形状,并说明理由;(2)善思组:如图3,当点E 恰好落在正方形ABCD 的边AB 上时,(1)中的结论还成立吗?请说明理由;深入探究:(3)创新小组:ABCD O AC BD EPF ÐP O OE OF AB BC E F EF BC k AB =×k 1k =OE OF=1k ¹OE OF FO FC =k OD =EF发现若连接BE ,在旋转Rt △AEF 的过程中,为定值,请你直接写出其值 .43.数学课上,有这样一道探究题.如图,已知中,AB =AC =m ,BC =n ,,点P 为平面内不与点A 、C 重合的任意一点,将线段CP 绕点P 顺时针旋转a ,得线段PD ,E 、F 分别是CB 、CD 的中点,设直线AP 与直线EF 相交所成的较小角为β,探究的值和的度数与m 、n 、α的关系,请你参与学习小组的探究过程,并完成以下任务:(1)填空:【问题发现】小明研究了时,如图1,求出了___________,___________;小红研究了时,如图2,求出了___________,___________;【类比探究】他们又共同研究了α=120°时,如图3,也求出了;【归纳总结】最后他们终于共同探究得出规律:__________(用含m 、n 的式子表示);___________ (用含α的式子表示).(2)求出时的值和的度数.BE CFABC V ()0180BAC a a Ð=°<<°EF AP b 60a =°EF PA =b =90a =°EF PA =b =EF PA EF PA =b =120a =°EF PAb44.在学习完《图形的旋转》后,数学小组的同学们展开了新的探究.(1)【问题初探】如图1,在中,点D 在边上,交于点E .绕点A 逆时针旋转得到(点D 的对应点为点,点E 的对应点为点),连接,,得到和,如图2,数学小组的同学们发现.请你帮助他们证明这一发现.(2)【问题应用】如图3,中,,,,M ,N 分别为边与的中点.绕点C 旋转,点M 的对应点为点E ,点N F ,直线与直线交于点G .①如图4,当点E 落在线段AF 上时,求证:;②当点A ,E ,F 三点在同一条直线上时,直接写出的长.(3)【问题拓展】如图5,在(2)条件下,连接,取中点K ,取中点H ,请直接写出的最大值为___________.题型09折叠背景下的相似三角形的性质与判定45.在边长为4的正方形中,E 是边上一动点(不与端点重合),将沿翻折,点A 落在点H 处,直线交于点F ,连接,,分别与AC 交于点P 、Q ,连接,.则以下结论中正确的有________ (写出所有正确结论的序号).①;②;③;④为等腰直角三角形;⑤若连接,则的最小值为.ABC V AB DE BC ∥AC ADE V AD E ¢¢△D ¢E ¢BD ¢CE ¢ABD ¢△ACE ¢V ABD ACE ¢¢△∽△Rt ABC V 90ACB Ð=°6AC =8BC =AC BC CMN V EF BC 90BFE Ð=°BG AF AF EB HK ABCD AD ABE V BE EH CD BF BE BF PD PF =PB PD 2EFD FBC Ð=ÐPQ AP QC =+BPF △DHDH 446.如图,正方形的边长为6,点P 是边上的动点,将沿折叠得到,射线与边和射线的延长线交于F ,E 点.(1)如图①,若四边形是平行四边形,求证:;(2)如图②,当时,求的长;(3)如图③,当时,求的面积.47.如图①,在中,,动点D 从点C 出发沿以每秒5个单位长度的速度向终点A 从点A 出发沿以每秒3个单位长度的速度向终点B 运动.设点D 运动的时间是t 秒.过点D 作于点F ,连结.(1) , ;(用含t 的代数式表示)(2)当四边形是菱形时,t 的值为 ;ABCD BC ABP V AP APB ¢V AB ¢DCBC APED DF EF =DF 2CF =BP FB CF ¢=DFE △Rt ABC △90159ABC AC AB Ð=°==,,CA AB ()03t <<DF BC ^DE EF、AE =AD =AEFD(3)当垂直于的一边时,求t 的值;(4)如图②,将沿翻折,点A 的对应点为点,直接写出点在外部时t 的取值范围.48.在矩形中,点E ,F 分别在边AD ,上,将矩形沿折叠,使点A 的对应点P 落在边CD 上,点B 的对应点为点G ,交于点H .(1)如图1,求证:;(2)如图2,当P 为CD 的中点,,时,求的长;(3)如图3,连接,当P ,H 分别为CD ,的中点时,探究与AB 的数量关系,并说明理由.49.(1)【动手操作】如图1,将正方形沿直线折叠,使点的对应点M 始终落在边上(点M 不与点A ,D 重合),点C 落在点N 处,与交于点P ,折痕分别与边,交于点,,连接.求证:;(2)【问题探究】在图1中,若正方形的边长为,当点运动到的中点时,求的长;(3)【拓展延伸】如图2,若把(1)【动手操作】中的正方形改成矩形,且,其中,其他条件不变,若,直接写出折痕的长度的取值范围是______.(用含m 的式子表示)题型10动点背景下的相似三角形的性质与判定50.如图,在矩形中,厘米,厘米.点沿AB 边从开始向点以厘米/秒的速度移动;同时点沿边从点开始向点以厘米/秒速度移动,用(秒)表示移动的时间().DE ABC V DEA △DE A ¢A ¢ABC V ABCD BC ABCD EF PGBC DEP CPH △∽△2AB =3AD =GH BG BC BG ABCD EF B AD MN CD AB CD E F BM BM EF=ABCD 3P CD MD ABCD ABCD AB mAD =1m ³2AD =EF ABCD 12AB =6BC =P A B 2Q DA D A 1t 06t ££。
专题4.4 相似三角形的性质-重难点题型(举一反三)(北师大版)(解析版)

专题4.4 相似三角形的性质-重难点题型【北师大版】【题型1 相似三角形的性质(对应角相等问题)】【例1】(2020秋•岳阳期末)如图,AE 与BD 相交于点C ,已知AC =5,BC =3,EC =10,DC =6.求证:AB ∥DE .【解题思路】根据已知条件证明△ACB ∽△ECD ,可得∠A =∠E ,进而可得结论.【解答过程】证明:∵AC EC =510=12,BC DC =36=12,∴AC EC =BC DC ,∵∠ACB =∠ECD ,∴△ACB ∽△ECD ,∴∠A =∠E ,∴AB ∥DE .【变式1-1】(2020秋•德江县期末)如图,∠1=∠2,AB AE =AC AD,求证:∠C =∠D .【解题思路】根据∠1=∠2可得∠BAC =∠EAD ,结合AB AE =AC AD,证明△BAC ∽△EAD ,再根据相似三角形的性质即可得到∠C =∠D .【解答过程】证明:∵∠1=∠2,∴∠1+∠CAE =∠2+∠CAE ,∴∠BAC =∠EAD ,∵ABAE=ACAD,∴△BAC∽△EAD,∴∠C=∠D.【变式1-2】(2020秋•遂川县期末)如图,在等腰直角△ABC中,AC=BC,D为平面上一动点,在运动过程上保持AD⊥BD于点D,将△BCD沿BD翻折得到△BED,在直线AD上取点F,作CF∥DE.(1)如图1,若AD与BC相交于点G,求证DGCG=BGAG;(2)猜想△CDF的形状,并说明理由.【解题思路】(1)证明△BDG∽△ACG即可得到结论;(2)先证明△CDG∽△ABG,可得∠ADC=∠ABC=45°,即∠BDC=135°,由翻折得∠BDE=∠BDC =135°,进一步得到∠CDE=90°,由CF∥DE,可得∠DCF=∠CDE=90°,即∠CFD=45°,进而可得△CDF为等腰直角三角形.【解答过程】解:(1)∵△ABC是等腰直角三角形,AC=BC,AD⊥BD,∴∠ADB=∠ACB=90°,又∵∠BGD=∠AGC,∴△BDG∽△ACG,∴DGCG=BGAG;(2)△CDF为等腰直角三角形,理由:由(1)得DGCG=BGAG.又∵∠CGD=∠AGB,∴△CDG∽△ABG,∴∠ADC=∠ABC=45°,即∠BDC=135°,由翻折得∠BDE=∠BDC=135°.∴∠CDE=90°,∵CF∥DE,∴∠DCF=∠CDE=90°,∴∠CFD=45°,∴∠CFD=∠CDF=45°,∴CF=CD,∴△CDF为等腰直角三角形.【变式1-3】(2020秋•中方县期末)在锐角△ABC中,点D,E分别在AC、AB上,AG⊥BC与点G,AF ⊥DE于F,∠EAF=∠GAC.(1)求证:△AEF∽△ACG.(2)求证:∠ADE=∠B.(3)若AD=3,AB=5,求AFAG.【解题思路】(1)利用有两个角对应相等的三角形相似进行判定即可;(2)由(1)的结论可得∠AEF=∠C,∠EAD=∠CAB,可得△EAD∽△CAB,利用相似三角形的对应角相等,结论得证;(3)由△AEF∽△ACG可得AFAG=AEAC;由△EAD∽△CAB可得AEAC=ADAB;则AGAG=ADAB,结论可求.【解答过程】证明:(1)∵AG⊥BC,AF⊥DE于,∴∠AFE=∠AGC=90°.∵∠EAF=∠GAC∴△AEF∽△ACG.(2)由(1)知△AEF∽△ACG,∴∠AEF=∠C∵∠DAE=∠BAC(公共角),∴△EAD∽△CAB.∴∠ADE=∠B.解:(3)由(2)知:△ADE ∽△ABC ,∴AE AC =AD AB.由(1)知△AEF ∽△ACG ,∴AE AC =AF AG .∴AF AG =AD AB.∵AD =3,AB =5,∴AF AG =35.【题型2 相似三角形的性质(对应边成比例问题)】【例2】((2020秋•崇左期末)如图,在矩形ABCD 中,E 是BC 的中点,连接AE ,过点E 作EF ⊥AE 交DC 于点F .若AB =4,BC =6,则DF 的长为( )A .94B .74CD .1【解题思路】结合矩形的性质证明△BAE ∽△CEF 可求得CF 的长,再利用DF =CD ﹣DF 可求解.【解答过程】解:∵四边形ABCD 为矩形,∴∠B =∠C =90°,CD =AB =4,∴∠BAE +∠AEB =90°,∵EF ⊥AE ,∴∠AEF =90°,∴∠AEB +∠CEF =90°,∴∠BAE =∠CEF ,∴△BAE ∽△CEF ,∴AB :CE =BE :CF ,∵E 是BC 的中点,BC =6,∴BE =CE =3,∵AB =4,∴4:3=3:CF ,解得CF =94,∴DF =CD ﹣DF =4―94=74.故选:B .【变式2-1】(2020秋•万荣县期末)如图,在△ABC 中,D 、E 分别在边AB 、AC 上,且DE ∥BC ,若AE EC=23,DE =BC 的长为( )A B C D 【解题思路】由DE ∥BC ,得∠ADE =∠B ,∠AED =∠C ,故△ADE ∽△ABC ,进而推断出AE AC =DE BC.由AEEC =23,DE =BC .【解答过程】解:∵DE ∥BC ,∴∠ADE =∠B ,∠AED =∠C .∴△ADE ∽△ABC .∴AE AC =DE BC.又∵AE EC =23,∴AE =23EC .∴DE BC =23EC AE EC =23EC 23EC EC =25.∴BC =5DE 2=故选:A .【变式2-2】(2021•岳麓区校级二模)如图,在正方形ABCD 中,点G 是对角线上一点,CG 的延长线交AB 于点E ,交DA 的延长线于点F ,连接AG .(1)求证:AG=CG;(2)若GE•GF=9,求CG的长.【解题思路】(1)根据正方形的性质得到∠ADB=∠CDB=45°,AD=CD,从而利用全等三角形的判定定理推出△ADG≌△CDG(SAS),进而利用全等三角形的性质进行证明即可;(2)根据正方形的性质得到AD∥CB,推出∠FCB=∠F,由(1)可知△ADG≌△CDG,利用全等三角形的性质得到∠DAG=∠DCG,结合图形根据角之间的和差关系∠DAB﹣∠DAG=∠DCB﹣∠DCG,推出∠BCF=∠BAG,从而结合图形可利用相似三角形的判定定理得到△AEG∽△FAG,进而根据相似三角形的性质进行求解即可.【解答过程】(1)证明:∵BD是正方形ABCD的对角线,∴∠ADB=∠CDB=45°,又AD=CD,在△ADG和△CDG中,AD=CD∠ADG=∠CDG,DG=DG∴△ADG≌△CDG(SAS),∴AG=CG;(2)解:∵四边形ABCD是正方形,∴AD∥CB,∴∠FCB=∠F,由(1)可知△ADG≌△CDG,∴∠DAG=∠DCG,∴∠DAB﹣∠DAG=∠DCB﹣∠DCG,即∠BCF=∠BAG,∴∠EAG=∠F,又∠EGA=∠AGF,∴△AEG∽△FAG,∴GEGA=GAGF,即GA2=GE•GF,∴GA=3或GA=﹣3(舍去),根据(1)中的结论AG=CG,∴CG=3.【变式2-3】(2021•滕州市一模)在矩形ABCD中,E为DC上的一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F.(1)求证:△ABF∽△FCE;(2)若AB=AD=4,求CE的长.【解题思路】(1)根据矩形的性质得到∠B=∠C=∠D=90°,根据翻折变换的性质得到∠D=∠AFE=90°,结合图形利用角之间的互余关系推出∠BAF=∠EFC,从而根据相似三角形的判定定理证明即可;(2)根据矩形的性质及翻折变换的性质推出BC=AD=AF=4,从而利用勾股定理求得BF=2,进而结合线段之间的和差关系利用相似三角形的性质进行求解即可.【解答过程】(1)证明:∵四边形ABCD是矩形,∴∠B=∠C=∠D=90°,又△ADE沿AE翻折得到△AFE,∴∠D=∠AFE=90°,∵∠BAF+∠AFB=90°,∠EFC+∠AFB=90°,∴∠BAF=∠EFC,∴△ABF∽△FCE;(2)解:∵AB=AD=4,∴BC=AD=AF=4,在Rt△ABF中,BF==2,∴CF=BC﹣BF=4﹣2=2,根据(1)中的结论△ABF∽△FCE,∴ABFC=BFCE,即2CE,解得CE故CE【题型3 相似三角形的性质(周长问题)】【例3】(2020春•罗定市月考)已知△ABC∽△A′B′C′,△ABC的边长分别为3,4,5,△A′B′C′中最小的边长为7,求△A′B′C′的周长.【解题思路】先求出△ABC的周长,再根据相似三角形周长的比等于相似比列出比例式,计算即可求解.【解答过程】解:△ABC的周长为:3+4+5=12,设△A′B′C′的周长为x,∵△ABC∽△A′B′C′,∴12x=37,解得x=28.故答案为:28.【变式3-1】.(2020秋•北碚区校级期中)已知:△ABC∽△A1B1C1,相似比为3:4,AB:BC:CA=2:3:4,△A1B1C1的周长是72cm,求△ABC的各边的长.【解题思路】根据题意,△ABC中,AB:BC:CA=2:3:4,可设AB=2k,BC=3k,AC=4k,则根据△ABC与△A1B1C1的相似比为3:4,可用k表示出A1B1=83k,B1C1=123k,A1C1=163k,然后,根据△A1B1C1的周长是72cm,可得83k+123k+163k=72,解得k=6,代入即可求出△ABC的各边的长;【解答过程】解:∵△ABC中,AB:BC:CA=2:3:4,∴可设AB=2k,BC=3k,AC=4k,∵△ABC与△A1B1C1的相似比为3:4,∴A1B1=43AB=43×2k=83k,B1C1=43BC=43×3k=123k,A1C1=43AC=43×4k=163k,又∵△A1B1C1的周长是72cm,∴83k+123k+163k=72,解得,k=6.【变式3-2】(2020秋•泰兴市期末)如图,分别以△ABC的边AC和BC为腰向外作等腰直角△DAC和等腰直角△EBC,连接DE.(1)求证:△DAC∽△EBC;(2)求△ABC与△DEC的周长比.【解题思路】(1)根据等腰三角形的性质得到∠DAC=∠EBC=90°,∠ACD=∠BCE=45°,从而根据相似三角形的判定定理证明即可;(2)根据相似三角形的性质得到ACDC =BCEC,结合图形由角之间的和差关系推出∠BCA=∠ECD,从而得到△ABC∽△DEC,利用等腰直角三角形的性质推出ACDC【解答过程】证明:(1)∵△DAC和△EBC是等腰直角三角形,∴∠DAC=∠EBC=90°,∠ACD=∠BCE=45°,∴△DAC∽△EBC;(2)根据(1)中的结论△DAC∽△EBC,∴ACDC=BCEC,又∠BCE=∠ACD,∴∠BCE﹣∠ACE=∠ACD﹣∠ACE,即∠BCA=∠ECD,∴△ABC∽△DEC,∴C△ABCC△DEC=ACDC,∵△ADC是等腰直角三角形,∴AC DC∴△ABC 与△DEC 【变式3-3】(2020秋•东莞市校级月考)如图,△OAB ∽△OCD ,OA :OC =3:2.△OAB 与△OCD 的面积分别是S 1与S 2,周长分别是C 1与C 2.则下列说法正确的是( )A .OA OD =32B .OB CD =32C .C 1C 2=32D .S 1S 2=32【解题思路】根据相似三角形的周长比等于相似比,面积比等于相似比的平方,一一判断即可.【解答过程】解:∵△OAB ∽△OCD ,OA :OC =3:2,∴C 1C 2=OA OC =32,S 1S 2=(OA OC )2=94,∴选项C 正确,选项D 错误,∵无法确定OA OD ,OB CD的值,故选项A ,B 错误,故选:C .【题型4 相似三角形的性质(面积问题)】【例4】(2021春•海阳市期末)如图,在△ABC 中,∠C =90°,AD 与BD 分别是△ABC 的内角∠BAC ,∠ABC 的平分线,过点A 作AE ⊥AD 交BD 的延长线于点E ,△ABC ∽△EDA .(1)求∠ABC 的度数;(2)求S△ABC S△EDA 的值.【解题思路】(1)依据三角形内角和定理以及角平分线的定义,即可得到∠1+∠2的度数,根据三角形外角性质即可得出∠3的度数,最后根据相似三角形的对应角相等,即可得出结论;(2)过A 作AF ⊥DE 于点F ,设AF =a ,易得DE =2a ,DF =a ,AD ,BF =+a ,依据勾股定理即可得到AB 2=AF 2+BF 2=(a 2,最后根据相似三角形的面积的比等于相似比的平方,即可得出结论.【解答过程】解:(1)∵AD 与BD 分别是△ABC 的内角∠BAC ,∠ABC 的平分线,∴∠1=12∠ABC ,∠2=12∠BAC ,∵∠C =90°,∴∠1+∠2=12(∠ABC +∠BAC )=12×90°=45°,∴∠3=∠1+∠2=45°,∵△ABC ∽△EDA ,∴∠ABC =∠3=45°;(2)过A 作AF ⊥DE 于点F ,∵∠3=45°,AE ⊥AD ,∴△ADE 是等腰直角三角形,设AF =a ,则DE =2a ,DF =a ,Rt △ADF 中,AD ,∵2∠1=2∠2=45°,∴∠1=∠2,∴AD =BD =,∴BF =+a ,在Rt △ABF 中,AB 2=AF 2+BF 2=a 2++a )2=(a 2,∵△ABC ∽△EDA ,∴S △ABCS △EDA =AB 2ED 2=(2a )【变式4-1】(2020秋•道里区期末)如图,△ABC ∽△ADE ,且BC =2DE ,则S △ADES 四边形BEDC 的值为( )A .12B .13C .23D .14【解题思路】根据相似三角形的性质解答即可.【解答过程】解:∵△ABC ∽△ADE ,且BC =2DE ,∴S △ADE S △ABC =(ED BC )2=14,∴S △ADES 四边形BEDC =141=13,故选:B .【变式4-2】(2020•河北模拟)如图,在等腰三角形△ABC 中,AB =AC ,图中所有三角形均相似,其中最小的三角形面积为1,△ABC 的面积为44,则四边形DBCE 的面积是( )A .22B .24C .26D .28【解题思路】利用△AFH ∽△ADE 得到S △AFH S △ADE =(FH DE )2=916,所以S △AFH =9x ,S △ADE =16x ,则16x ﹣9x =7,解得x =1,从而得到S △ADE =16,然后计算两个三角形的面积差得到四边形DBCE 的面积.【解答过程】解:如图,由题意根据题意得△AFH ∽△ADE ,所有三角形均相似,可得FH :DE =3:4,∴S △AFH S △ADE =(FH DE )2=916,设S △AFH =9x ,则S △ADE =16x ,∴16x ﹣9x =7,解得x =1,∴S △ADE =16,∴四边形DBCE 的面积=44﹣16=28.故选:D .【变式4-3】(2020秋•德江县期末)如图,在▱ABCD 中,E 是AB 的中点,EC 交BD 于点F ,那么S △BEF :S △BCF =( )A .1:2B .1:3C .1:4D .2:3【解题思路】由矩形性质可证明△BEF ∽△DCF ,从而可得BE CD =EF CF =12,由于△BEF 与△BCF 等高,故S △BEF :S △BCF =1:2.【解答过程】解:∵四边形ABCD 为矩形,E 为AB 中点,∴AB ∥CD ,BE =12AB =12CD ,∴△BEF ∽△DCF ,∴BE CD =EF CF =12,∵△BEF 与△BCF 等高,∴S △BEF :S △BCF =EF CF =12.故选:A .【题型5 相似三角形的性质(多结论问题)】【例5】(2021•大埔县模拟)如图,正方形ABCD 的边长是3,BP =CQ ,连接AQ ,DP 交于点O ,并分别与边CD ,BC 交于点F ,E ,连接AE ,下列结论:①AQ ⊥DP ;②OA 2=OE •OP ;③S △AOD =S 四边形OECF ;其中正确结论的个数( )A .1B .3C .2D .0【解题思路】由四边形ABCD 是正方形,得到AD =BC ,∠DAB =∠ABC =90°,根据全等三角形的性质得到∠P =∠Q ,根据余角的性质得到AQ ⊥DP ;故①正确;根据相似三角形的性质得到AO 2=OD •OP ,由OD ≠OE ,得到OA 2≠OE •OP ;故②错误;根据全等三角形的性质得到CF =BE ,DF =CE ,于是得到S △ADF ﹣S △DFO =S △DCE ﹣S △DOF ,即S △AOD =S 四边形OECF ;故③正确.【解答过程】解:∵四边形ABCD 是正方形,∴AD =BC ,∠DAB =∠ABC =90°,∵BP =CQ ,∴AP =BQ ,在△DAP 与△ABQ 中,AD =AB ∠DAP =∠ABQ AP =BQ,∴△DAP ≌△ABQ (SAS ),∴∠P =∠Q ,∵∠Q +∠QAB =90°,∴∠P +∠QAB =90°,∴∠AOP =90°,∴AQ ⊥DP ,故结论①正确;∵∠DOA =∠AOP =90°,∠ADO +∠P =∠ADO +∠DAO =90°,∴∠DAO =∠P ,∴△DAO ∽△APO ,∴AO OD =OP OA,∴AO 2=OD •OP ,∵AE >AB ,∴AE >AD ,∴OD ≠OE ,∴OA 2≠OE •OP ;故结论②错误;在△CQF 与△BPE 中,∠FCQ =∠EBP CQ =BP ∠Q =∠P,∴△CQF ≌△BPE (ASA ),∴CF =BE ,∴DF =CE ,在△ADF 与△DCE 中,AD =CD ∠ADC =∠DCE DF =CE,∴△ADF ≌△DCE (SAS ),∴S △ADF =S △DCE ,∴S △ADF ﹣S △DFO =S △DCE ﹣S △DOF ,即S △AOD =S 四边形OECF ;故结论③正确;故选:C .【变式5-1】(2021春•淮阳区校级期末)如图,平行四边形ABCD 中,AB =2BC .AE 平分∠BAD ,交CD 于点E ,点F 为AB 边的中点,AE 与DF 交于点M ,BD 与EP 交于点N ,连接MN .则下列结论:①四边形ADEF 是菱形;②与△BFN 全等的三角形有5个;③S 四边形BCEN =7S △FMN ;④当FM =FN 时,∠BAD =60°.其中正确的是( )A .①③B .①④C .②③D .②④【解题思路】①根据四边形ABCD 是平行四边形,可得:AD =BC ,AB =CD ,AB ∥CD ,再由AE 平分∠BAD ,可得出∠AED =∠DAE ,进而推出AF =DE ,即可运用菱形的判定方法证得结论;②根据题目条件可证明△BFN ≌△DEN (AAS ),其它三角形均不能证明;③根据题目条件可得出S △FMN =S △DMN =12S △BFN ,再由S 菱形BCEF =4S △BFN ,进而得出S 四边形BCEN =3S △BFN ,即可判断结论③错误;④由FM =FN 可得出DF =AF =AD ,即△ADF 是等边三角形,可判定结论④正确.【解答过程】解:①∵四边形ABCD 是平行四边形,∴AD =BC ,AB =CD ,AB ∥CD ,∵点F 为AB 边的中点,∴AF=12 AB,∵AE平分∠BAD,∴∠BAE=∠DAE,∵AB∥CD,∴∠AED=∠BAE,∴∠AED=∠DAE,∴AD=DE,∴BC=DE,∵AB=2BC.∴BC=12 AB,∴AF=DE,∵AF∥DE,∴四边形ADEF是平行四边形,∵AD=DE,∴四边形ADEF是菱形,故①正确;②∵AB∥CD,∴∠FBN=∠EDN,∵DE=AF=BF,∠BNF=∠DNE,∴△BFN≌△DEN(AAS),能够确定与△BFN全等的三角形只有1个,故②错误;③∵△BFN≌△DEN,∴FN=EN,BN=DN,∵四边形ADEF是菱形,∴DM=FM,∴S△FMN =S△DMN=12S△BFN,同理可证:四边形BCEF是菱形,∴S菱形BCEF =4S△BFN,∴S四边形BCEN =3S△BFN,∵S △BFN =2S △FMN ,∴S 四边形BCEN =6S △FMN ,故③错误;④当FM =FN 时,∵FN =EN ,EF =AF ,∴AF =2FM ,∵DF =2FM ,∴DF =AF =AD ,∴△ADF 是等边三角形,∴∠BAD =60°,故④正确;故选:B .【变式5-2】(2020秋•松桃县期末)如图,点A 在线段BD 上,在BD 的同侧作等腰直角三角形ABC 和等腰直角三角形ADE (∠ABC 和∠AED 是直角),连接BE ,CD 交于点P ,CD 与AE 边交于点M ,对于下列结论:①△BAE ∽△CAD ;②∠BPC =45°;③MP •MD =MA •ME ;④2CB 2=CP •CM ,其中正确的个数为( )A .1个B .2个C .3个D .4个【解题思路】①由等腰Rt △ABC 和等腰Rt △ADE 三边份数关系可证;②根据相似三角形的性质即可得到结论;③通过等积式倒推可知,证明△PME ∽△AMD 即可;④2CB 2转化为AC 2,证明△ACP ∽△MCA 问题可证.【解答过程】解:由已知得:AC =,AD ,∴AC AB =AD AE,∵∠BAC =∠EAD ,∴∠BAE =∠CAD ,∴△BAE ∽△CAD ,∴①正确;如图:设BE 与AC 相交于点O ,则∠AOB=∠POC,∵△BAE∽△CAD,∴∠ABE=∠ACD,∴∠BPC=∠BAC=45°,∴②正确;∵△BAE∽△CAD,∴∠BEA=∠CDA,∵∠PME=∠AMD,∴MPMA=MEMD,∴MP•MD=MA•ME,∴③正确;由③MP•MD=MA•ME,∠PMA=∠DME,∴△PMA∽△EMD,∴∠APD=∠AED=90°,∠CAE=180°﹣∠BAC﹣∠EAD=90°,∠ACP=∠MCA,∴△CAP∽△CMA,∴AC2=CP•CM,∵AC=,∴2CB2=CP•CM,∴④正确,故选:D.【变式5-3】(2021春•龙泉驿区期末)如图,Rt△ABC中,CD⊥AB于D,下列结论中:①∠1=∠A;②∠2+∠B=90°;③CD2=AD•BD;④BC2=BD•AD,一定成立的有( )个.A.1B.2C.3D.4【解题思路】由题意根据直角三角形的判定及相似三角形的判定方法,对各选项﹣﹣分析可得出答案.对于①,根据∠1+∠2=90°,2+∠A=90°,可得结论.对于③,由所给条件,结合夹角相等,易证得△CDA∽△BDC,至此③也就可作出判断了.对于②,由∠B=∠2,但∠2+∠B不一定等于90°.对于④,△CDB∽△ACB,根据形似三角形的性质得CBAB =DBCB,进而得出④不正确.【解答过程】解:∵Rt△ABC中∠ACB=90°,∴∠1+∠2=∠ACB=90°,∵CD⊥AB,∴∠ACB=∠ADC=∠CDB=90°,∴∠2+∠A=90°,∴∠1=∠A,故①正确;∠2=B,但是∠2+∠B不一定等于90°,故②错误;∵∠1=∠A,∠CDB=∠ADC=90°,∴△CDB∽△ADC,则CD:AD=BD:CD,即CD²=AD•BD,故③正确;∵∠1=∠A,∠B=∠B,∴△CDB∽△ACB,则BC:AB=BD:BC,即BC²=BD•AB≠BD•AD,故④错误;所以一定成立的是:①③,故选:B .【题型6 相似三角形的性质(常见辅助线问题)】【例6】(2020秋•开江县期末)如图,△ABC 是等边三角形,点D ,E 分别在边BC ,AC 上,且BD =CE ,AD 与BE 相交于点F .若AF =7,DF =1,则△ABC 的边长等于( )A B C +D +【解题思路】先由△ABC 是等边三角形证明△ABD ≌△BCE ,由此得∠BAD =∠CBE ,再证明△ABD ∽△BFD ,由此得AD BD =BD DF,即BD 2=AD •DF =(AF +DF )•DF =8,BD =D 作DG ⊥AB 于G ,用勾股定理求出AG 、BG 即可.【解答过程】解:∵△ABC 是等边三角形,∴AB =BC ,∠ABD =∠BCE ,在△ABD 与△BCE 中,AB =BC ∠ABC =∠BAC =∠C =60°BD =CE,∴△ABD ≌△BCE (SAS ),∠BAD =∠CBE ,∵∠BDA =∠FDB ,∴△ABD ∽△BFD ,∴AD BD =BD DF,∴BD 2=AD •DF =(AF +DF )•DF =8,∴BD =如图,过点D 作DG ⊥AB 于G ,∵∠DBG =30°,∴BG =12BD∴DG =∴AG∴AB =故选:C .【变式6-1】(2020秋•天长市期末)如图,已知△ABC ,△DCE ,△FEG ,△HGI 是四个全等的等腰三角形,底边BC ,CE ,EG ,GI 在同一直线上,且AB =4,BC =2,连接AI 交FG 于点Q ,则QI 的值为( )A .4B .103C .3D .83【解题思路】过点A 作AM ⊥BC 于点M ,根据题意得到BC =CE =EG =GI =2,BM =MC =12BC =1,AB =AC =4,从而利用勾股定理求得AM =AI =8,再根据同位角相等推出FG ∥AC ,从而得到△IQG ∽△IAC ,进而利用相似三角形的性质进行求解即可.【解答过程】解:如下图所示,过点A 作AM ⊥BC 于点M ,∵△ABC ,△DCE ,△FEG ,△HGI 是四个全等的等腰三角形,AB =4,BC =2,∴BC=CE=EG=GI=2,BM=MC=12BC=1,AB=AC=4,∴AM=又MI=BI﹣BM=7,∴AI=8,∵∠ACB=∠FGE,∴FG∥AC,∴△IQG∽△IAC,∴QIAI=GICI,即QI8=13,解得QI=8 3,故选:D.【变式6-2】(2021•利辛县二模)如图1,在正方形ABCD中,E为BC延长线上一点,且BC=3CE,F 为CD的中点,EF的延长线交AD于点G,连接BG.(1)求AGDG的值;(2)求证:BG=EG;(3)如图2,M为AB的中点,DM交BG于点N,连接CN,求证:CN∥GE.【解题思路】(1)根据已知条件,利用ASA证明△GDF≌△ECF,可得DG=CE,再由BC=3CE,得CE=13BC=DG,AG=23BC,即可得出答案;(2)过点G作GH⊥BC于H,利用SAS证明△ABG≌△HGE,即可证得结论;(3)过点M作MT∥AD交BG于T,利用AAS证明△MNT≌△DNG,进而得出BNBG=BCBE=34,可证△CBN∽△EBG,得出∠BCN=∠BEG,可得CN∥EG.【解答过程】解:(1)∵F为CD的中点,∴DF=CF,∵四边形ABCD为正方形,∴AD∥BC,∴∠GDF=∠ECF=90°.又∵∠DFG=∠CFE.∴△GDF≌△ECF(ASA),∴DG=CE.∵BC=3CE,∴CE=13BC=DG,∴AG=AD﹣DG=BC﹣CE=BC―13BC=23BC,∴AGDG=23BC13BC=2;(2)过点G作GH⊥BC于H,∴CH=DG=CE=13 BC,∴EH=CH+CE=23 BC,在△ABG和△HGE中,AG=EH=23BC∠A=∠GHE=90°AB=GH,∴△ABG≌△HGE(SAS),∴BG=EG;(3)过点M作MT∥AD交BG于T,∵M为AB的中点,∴MT=12AG=DG,∵AD∥MT,∴∠NMT=∠NDG,在△MNT和△DNG中,∠MNT=∠DNG∠NMT=∠NDGMT=DG,∴△MNT≌△DNG(AAS),∴NT=NG,∴BG=4NG,∴BNBG=34,∵BC=3CE,∴BCBE=34,∴BNBG=BCBE,∵∠CBN=∠EBG,∴△CBN∽△EBG,∴∠BCN=∠BEG,∴CN∥EG.【变式6-3】(2020秋•潜山市期末)如图,在△ABC中,∠ACB=90°,BC=2,AC=4,点D在边BC 上,以点D为圆心,BD为半径画弧交边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.(1)求证:△EFG∽△AEG;(2)设FG=x,△EFG的面积为y,求y关于x的函数解析式.【解题思路】(1)由ED=EB得到∠B=∠DEB,再根据等角的余角相等得到∠A=∠FEG,加上公共角∠G,则可判断△EFG∽△AEG;(2)过E点作EH⊥AC于H,如图,先证明△AEF∽△ACB得到EFAE =BCAC=12,再利用△EFG∽△AEG得到FGEG=GEGA=EFAE=12,则EG=2x,GA=4x,AF=3x,在Rt△AEF中利用勾股定理可求出EF=5x,AE,接着利用面积法求出EH=65x,然后根据三角形面积公式得到y关于x的函数解析式.【解答过程】(1)证明:∵ED=EB,∴∠B=∠DEB,∵∠ACB=90°,∴∠A+∠B=90°,∵EF⊥AB,∴∠FBE=90°,∴∠DEB+∠FEG=90°,∴∠A=∠FEG,∵∠EGF=∠AGE,∴△EFG∽△AEG;(2)解:过E点作EH⊥AC于H,如图,∵∠AEF=∠ACB,∠EAF=∠CAB,∴△AEF∽△ACB,∴EFBC=AEAC,∴EFAE=BCAC=24=12,∵△EFG∽△AEG,∴FGEG=GEGA=EFAE=12,∵FG=x,∴EG=2x,GA=4x,∴AF=3x,在Rt△AEF中,∵EF2+AE2=AF2,∴EF2+4EF2=(3x)2,解得EF=5x,∴AE,∵12EH•AF=12EF•AE,∴EH553x =65x,∴△EFG的面积=12•FG•EH=12•65x•x=35x2,即y关于x的函数解析式为y=35x2.。
图形的相似(压轴专练)(十大题型)(原卷版)—2024-2025学年九年级数学上册(北师大版)

图形的相似(压轴专练)(十大题型)题型1:相似三角形解答证明题1.在ABC V 中,AB AC =,点D 在线段CB 的延长线上,连接AD ,过点B 作BE BC ^交线段AD 于点,2120E BED BAC Ð+Ð=°.(1)如图1,求CAD Ð的度数.(2)如图2,若32DE AE =,求BD BC的值.(3)如图3,在(2)的条件下,连接,EC EC 交线段AB 于点F ,若BD =AF 的长.2.如图1,在ABC V 中,90BAC AB AC BD CD Ð=°=^,,于点D ,连接AD ,在CD 上截取CE ,使CE BD =,连接AE .(1)直接判断AE 与AD 的位置关系(2)如图2,延长AD ,CB 交于点F ,过点E 作EG AF ∥交BC 于点G ,试判断FG 与AB 之间的数量关系,并证明;(3)在(2)的条件下,若2AE =,CE =EG 的长.题型2:相似三角形在特殊平行四边形中的应用3.如图1,四边形ABCD 是正方形,点E 在边BC 的延长线上,点F 在边AB 上,且AF CE =,连接EF 交DC 于点P ,连接AC 交EF 于Q ,连接DE DF 、.(1)求证:EQ FQ =;(2)连接BQ ,如图2,①若AQ DP ×=BQ 的长;②若FP FD =,则PE PQ = .4.综合与实践已知:矩形ABCD ,M 是AD 边上一点.【基本图形】(1)如图1,AM MD =,BM 交AC 于F 点,BM 的延长线与CD 的延长线交于点E ,连AE ,求证:MF EM BF EB=;【类比探究】(2)如图2,AM MD =,过点D 任意作直线与BM ,BC 的延长线分别交于点E ,点P ,连AE ,求证:EAD PAD ÐÐ=;【扩展延伸】(3)如图3,E 是CD 延长线上一点,P 是BC 延长线上一点,AP 交CD 于Q 点,BE 交AD 于M 点,延长AD 交EP 于N 点,若M 是AN 的中点,且3AB =,4BC =,求AEP △的面积.题型3:翻折问题5.菱形ABCD 中,5AB =,点F 是AD 边上的点,点Q 是AB 边上的点.(1)如图1,若点F 是AD 的中点,CQ AB ^,连接CF 并延长交BA 的延长线于点P ,连接QF ,①求证:PAF CDF △≌△;②判定FCQ V 的形状,并说明理由;(2)若菱形面积为20,将菱形ABCD 沿CQ 翻折,点B 的对应点为点E .①如图2,当点E 落在BA 边的延长线上时,连接BD ,交CQ 于R ,交EC 于点M ,求DR BM 的值;②如图3,当CE AD ^,垂足为点F ,交AD 于点N ,求四边形CFNQ 的面积.6.如图1,在矩形ABCD 中,3AB =,4=AD ,点E 在BC 上,连接AE ,把ABE V 沿直线AE 翻折得到AFE △,直线EF 与直线CD 交于点G ,连接DF .(1)当DFG GEC Ð=Ð时,求BE 的长.小星看到把ABE V 沿直线AE 翻折得到AFE △,就想到翻折图形的特征特点,对应边相等,对应角相等,对应点连线被对称轴垂直平分,那么他就知道BE FE =,AB AF =,90ABE AFE Ð=Ð=°,根据DFG GEC Ð=Ð,他延长EG 与AD 的延长线相交于点H ,可证AD DF DH ==,AH EH =,再通过勾股定理即可求出BE 的长.请用小星的方法或自己的方法求BE 的长;(2)当G 是CD 的中点时,求BE 的长;(3)如图2,已知等边ABC V 的边长为6,点D 在边BC 上,连接AD ,把ABD △沿直线AD 翻折得到AED △,直线DE 与直线AC 交于点F ,若12CF =,求BD 的长.7.(1)发现:如图1,正方形ABCD 中,点E 在CD 边上,将ADE V 沿AE 对折得到AFE △,延长EF 交BC 边于点G ,连接AG .证明:BG DE EG +=.(2)探究:如图2,矩形ABCD 中AD AB >,O 是对角线的交点,过O 任作一直线分别交BC AD 、于点M 、N ,四边形AMNE 是四边形CMND 沿MN 翻折得到的,连接CN ,若CDN △的面积与CMN V 的面积比为1:3,求MN DN的值.(3)拓展:如图3,在菱形ABCD 中,6AB =,E 为CD 边上的三等分点,60D Ð=°,将ADE V 沿AE 翻折得到AFE △,直线EF 交BC 于点P ,求PC 的长.题型4:旋转问题8.如图,ABC V 和ADE V 是有公共顶点的等腰直角三角形,90BAC DAE Ð=Ð=°.(1)如图1,连接BE 、CD ,BE 的延长线交AC 于F ,交CD 于点P ,求证:①ABE ACD V V ≌;②BP CD ^;(2)如图2,把ADE V 绕点A 顺时针旋转,当点D 落在AB 上时,连接BE 、CD ,CD 的延长线交BE 于点P ,若BC =3AD =.①求证:BDP CDA △∽△,②PDE △的面积是 .9.问题背景:如图(1),在ABC V 和ADE V 中,AB AC AD AE ==,,BAC DAE Ð=Ð,求证:ABD ACE △△≌;尝试应用:如图(2),在ABC V 和ADE V 中,90ABC ADE Ð=Ð=°,30ACB AED Ð=Ð=°,连接CE ,点F 是CE 的中点.判定以B ,D ,F 为顶点的三角形的形状,并证明你的结论;拓展创新:如图(3),在ABC V 中,AC BC =AB 绕点A 逆时针旋转90°得到AD ,连接BD CD ,.若点E 是CD 的中点,连接BE ,直接写出BE 的最大值.10.如图,在V 锐角ABC 中,AB =3BC =,45ACB Ð=°,将ABC V 绕点B 按逆时针方向旋转得到11A BC V .(1)如图①,当点1C 在线段CA 的延长线上时,求11CC A Ð的度数;(2)如图②,连接1AA ,1CC ,若1ABA △的面积为2,求1CBC △的面积;(3)如图③,点E 为线段AB 中点,点P 是线段AC 上的动点,在ABC V 绕点B 按逆时针方向旋转过程中,点P 的对应点是点1P ,求线段1EP 长度的最大值与最小值.题型5:最值问题11.如图,在ABC V 中,90,BAC AB AC Ð=°=,点D 为AC 一点,连接BD .(1)如图1,若CD =,15ABD Ð=°,求AD 的长;(2)如图2,过点A 作AE BD ^于点E ,交BC 于点M ,AG BC ^于点G ,交BD 于点N ,求证:BM CM =;(3)如图3,将ABD △沿BD 翻折至BDE V 处,在AC 上取点F ,连接BF ,过点E 作EH BF ^交AC 于点G ,GE 交BF 于点H ,连接AH ,若:2GE BF =,AB =AH 的最小值.12.如图1和图2,平面上,四边形ABCD 中1582AB BC ==,,252CD =,6DA =,90A Ð=°,点M 在AD边上,且2DM =.点P 从点A 沿折线AB BC -上运动到点C ,将APM △沿MP 翻折,点A 的对应点为点A ¢,设点P 的运动路径长为x (0)x >.(1)如图1,连接BD ,①求CBD Ð的度数;②求证:AB CD ∥.(2)如图2,当点A ¢落到四边形ABCD 内部时,求x 的取值范围.(3)①当点A ¢落在AD 的延长线上时,请直接写出x 的值.②设点A ¢到边BC 所在直线的距离为h ,请直接写出h 的最小值.13.如图,在Rt ABC △中,90ACB Ð=°,AC BC =,点D 在直线AB 上,点E 在直线AC 上,连接BE ,DE ,且BE DE =,直线DE 交BC 于点F .(1)如图①,当点D 在线段AB 上时,AD 4AC =,求BE 的长;(2)如图②,当D 是AB 的中点时,求证:CE CF BF +=;(3)如图③,连接CD ,将ADC △沿着CD 翻折,得到A CD ¢△,M 是AB 上一点,且37BM AB =,当A M ¢最短时,请直接写出DF BE 的值.题型6:比值问题14.如图1,在ABC D 中,AB AC =,点D 、E 分别在边AB 、AC 上,AD AE =,连接DC ,点F 、P 、G分别为DE 、DC 、BC 的中点,连接FP ,PG .(1)图1中,求证:PF PG =;(2)当ADE V 绕点A 旋转到如图2所示的位置时,①PF PG =是否仍然成立?若成立请证明;若不成立,说明理由;②若:1:(1)AD AB n n =>,PDF △和PGC V 的面积分别是1S ,2S ,ABC V 的面积为3S ,求123S S S +的值.15.【特例感知】(1)如图1,在正方形ABCD 中,点P 在边AB 的延长线上,连接PD ,过点D 作DM PD ^,交BC 的延长线于点M .求证:DP DM =.【变式求异】(2)如图2,在Rt ABC △中,90ABC Ð=°,点D 在边AB 上,过点D 作DQ AB ^,交AC 于点Q ,点P 在边AB 的延长线上,连接PQ ,过点Q 作QM PQ ^,交射线BC 于点M .已知8BC =,10AC =,AD =2DB ,求PQ QM的值.【拓展应用】(3)如图3,在Rt ABC △中,90BAC Ð=°,点P 在边AB 的延长线上,点Q 在边AC 上(不与点A ,C 重合),连接PQ ,以Q 为顶点作PQM PBC Ð=Ð,PQM Ð的边QM 交射线BC 于点M .若AC mAB =,CQ nAC =(m ,n 是常数),直接写出PQ QM的值(用含m ,n 的代数式表示).题型7:“手拉手”模型16.在ABC V 中,90ACB Ð=°,AC BC =,点D 是BC 边上一动点,过点C 作CE AD ^交AB 于点E .(1)如图1,若AC AE =,求ADB Ð的度数;(2)如图2,点F 是BD 上一点,连接EF 并延长交AD 的延长线于点G .若点P 为AD 的中点,CP DG =,2G CAD Ð=Ð,求证:2CE EF FG +=;(3)点F 是BC 边上一点,射线EF 与射线AD 交于点G ,BFE ADC Ð=Ð,点H 是AC 上一点,且14CH AC =,连接HF ,H G ,点M 是射线AD 上一动点,连接MH ,MF .在点D 的运动过程中,当GH 取得最小值m 时,在平面内将HFM △沿直线HM 翻折得到HNM V ,连接EN .在点M 的运动过程中,若EN 的最大值为n ,直接写出n m的值.17.如图所示,在ABC V 中,D 、E 分别是AB 、AC 上的点,DE BC ∥,如图1,然后将ADE V 绕A 点顺时针旋转一定角度,得到图2,然后将BD 、CE 分别延长至M 、N ,使DM =12BD ,EN =12CE ,得到图3,请解答下列问题:(1)若AB AC =,请探究下列数量关系:①在图2中,BD 与CE 的数量关系是 ;②在图3中,猜想AM 与AN 的数量关系、MAN Ð与BAC Ð的数量关系,并证明你的猜想;(2)若·1AB k AC k =(>),按上述操作方法,得到图4,请继续探究:AM 与AN 的数量关系、MAN Ð与BAC Ð的数量关系,直接写出你的猜想,不必证明.题型8:定值问题18.如图1,在ABCD Y 中,60A Ð=°,4=AD ,8AB =.Y的面积;(1)请计算ABCD△沿着AC翻折,D点的对应点为D¢,线段CD¢交AB于点M,请计算AM的长度;(2)如图2,将ADC^交AD¢的延(3)如图3,在(2)的条件下,点P为线段CM上一动点,过点P作PN AC^于点N,PG AD¢长线于点G.在点P PG+的长度是否为定值?如果是,请计算出这个定值;如果不是,请说明理由.题型9:情景探究题19.[问题情境](1)王老师给爱好学习的小明和小颖提出这样一个问题:如图①,在ABC V 中,AB AC =,P 为边BC 上的任一点,过点P 作,PD AB PE AC ^^,垂足分别为D ,E ,过点C 作CF AB ^,垂足为F .求证:PD PE CF +=.小明的证明思路是:如图①,连接AP ,由ABP V 与APC △面积之和等于ABC V 的面积可以证得:PD PE CF +=.小颖的证明思路是:如图②,过点P 作PG CF ^,垂足为G ,可以证得:,PD GF PE CG ==,则PD PE CF +=.请你选择小明、小颖两种证明思路中的任意一种,写出详细的证明过程.[变式探究](2)如图③,当点Р在BC 延长线上时,问题情境中,其余条件不变,则PD PE CF 、、之间的数量关系是______.[结论运用](3)如图④,将矩形ABCD 沿EF 折叠,使点D 落在点B 上,点C 落在点C ¢处,点P 为折痕EF 上的任一点,过点Р作,PG BE PH BF ^^,垂足分别为G ,H ,若18,5AD CF ==,求PG PH +的值.[迁移拓展](4)图⑤是一个机器模型的截面示意图,在四边形ABCD 中,E 为AB 边上的一点,,ED AD EC CB ^^,垂足分别为D ,C ,且,3cm,AD CE DE BC AB AD BD ====××,M 、N 分别为AE BE ,的中点,连接DM CN ,,请直接写出DEM △与CEN V 的周长之和___________.题型10:相似三角形在平面直角坐标系的应用20.如图,在平面直角坐标系中;一次函数y kx b =+的图象与x 轴交于点A ,与y 轴交于点B (0,3),与直线OC 交于点8,13C æöç÷èø.(1)求直线AB 的函数表达式;(2)过点C 作CD x ^轴于点D ,将ACD V 沿射线CB 平移得到的三角形记为A C D ¢¢¢△,点A ,C ,D 的对应点分别为A ¢,C ¢,D ¢,若A C D ¢¢¢△与BOC V 重叠部分的面积为S ,平移的距离CC m ¢=,当点A ¢与点B 重合时停止运动,当925S =时,求m 的值.21.综合运用如图1,在平面直角坐标系中,AOB V 是等腰直角三角形,AO BO =,点A 的坐标为()0,6.点C 是边OB 上一点,连接AC ,将线段AC 绕点C 顺时针旋转90°,得到线段CD ,连接AD ,BD .(1)当AB 平分CAD Ð时,OAC Ð=________°;(2)若13CO BO =,求BD 的长;(3)如图2,作点C 关于AD 的对称点E ,连接BE ,CE ,DE .设BDE V 的面积S =,CO m =,求S 关于m 的函数表达式.。
【中考数学】2022-2023学年易错常考专题训练—相似三角形(含解析)

【中考数学】2022-2023学年易错常考专题训练—相似三角形1.如图,抛物线与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴213222y x x =-++交于点C ,连接.BC(1)求点A 、B 、C 的坐标;(2)设x 轴上的一个动点P 的横坐标为t ,过点P 作直线轴,交抛物线于点N ,交直PN x ⊥线于点M .BC ①当点P 在线段上时,设的长度为s ,求s 与t 的函数关系式;AB MN ②当点P 在线段上时,是否存在点P ,使得以O 、P 、N 三点为顶点的三角形与OB 相似?若存在,请求出点P 的坐标;若不存在,请说明理由.COB △2.如图,抛物线经过,,三点.()4,0A ()10B ,()0,2C -(1)求出抛物线的解析式;(2)P 是抛物线在第一象限上的一动点,过P 作PM ⊥x 轴,垂足为M ,是否存在P 点,使得以A ,P ,M 为顶点的三角形与△OAC 相似?若存在,请求出符合条件的点P 的坐标;若不存在,请说明理由;(3)若抛物线上有一点D (点D 位于直线AC 的上方且不与点B 重合)使得,DCA ABCS S=△△直接写出点D 坐标.3.如图,已知,,抛物线经过、两点,交轴于点()2,0A -()4,0B 2y ax bx c =++A B y .点是第一象限内抛物线上的一点,连接,.为上的动点,过点()0,4C P AC BC M OB 作轴,交抛物线于点,交于点.M PM x ⊥P BC Q(1)求抛物线的函数表达式;(2)过点作,垂足为点,设点的坐标为请用含的代数式表示线段P PN BC ⊥N M ()0m ,m 的长,并求出当为何值时有最大值,最大值是多少?PN m PN (3)试探究在运动过程中,是否存在这样的点,使得以,,为顶点的三角形M Q O M Q 与相似.若存在,请求出此时点的坐标;若不存在,请说明理由.AOC Q 4.如图,在平面直角坐标系中,抛物线与两坐标轴分别相交于xOy 213442y x x =-++三点.A B C ,,(1)求证:;90ACB ∠=︒(2)点是第一象限内抛物线上的动点,过点作轴的垂线交于点,交轴于点D D x BCE x .F①②点是的中点,若以点为顶点的三角形与相似,求点的坐标.G AC C D E ,,AOG D 5.如图,在平面直角坐标系中,矩形ABCD 的边BC 与x 轴、y 轴的交点分别为C (8,0),B (0,6),CD =5,抛物线y =ax 2﹣x +c (a ≠0)过B ,C 两点,动点M 从点D 开始以154每秒5个单位长度的速度沿D→A→B→C 的方向运动到达C 点后停止运动.动点N 从点O 以每秒4个单位长度的速度沿方向运动,到达C 点后,立即返回,向CO 方向运动,到达O 点后,又立即返回,依此在线段OC 上反复运动,当点M 停止运动时,点N 也停止运动,设运动时间为t .(1)求抛物线的解析式;(2)求点D 的坐标;(3)当点M ,N 同时开始运动时,若以点M ,D ,C 为顶点的三角形与以点B ,O ,N 为顶点的三角形相似,直接写出t 的值.6.如图.在平面直角坐标系中.抛物线与x 轴交于A 、B 两点,与y 轴交212y x bx c =++于点C .点A 的坐标为,点C 的坐标为.已知点是线段上的动()1,0-()0,2-(),0E m AB 点(点E 不与点A ,B 重合).过点E 作轴交抛物线于点P ,交于点F .PE x ⊥BC(1)求该抛物线的表达式;(2)若,请求出m 的值;:1:2EF PF =(3)是否存在这样的m ,使得与相似?若存在,求出此时m 的值;若不存在,BEP △ABC 请说明理由;(4)当点E 运动到抛物线对称轴上时,点M 是x 轴上一动点,点N 是抛物线上的动点,在运动过程中,是否存在以C 、B 、M 、N 为顶点的四边形是平行四边形?若不存在,请说明理由;若存在,请直接写出点M 的坐标.7.如图,抛物线与y 轴交于点A ,与轴交于点,,P 是26y ax bx =+-x ()3,0B -()1,0C 线段下方抛物线上的一个动点,过点Р作轴的垂线,交轴于点H ,交于点AB x x AB D .设点P 的横坐标为.()30t t -<<(1)求抛物线的解析式.(2)用含t 的式子表示线段的长,并求线段长度的最大值.PD PD (3)连接,当与相似时,求点P 的坐标.AP DPA DHB △8.如图,抛物线与轴交于点,与轴交于点,点234y x bx c =-++x ()4,0A y ()0,3B 为线段上一动点,过点且垂直于轴的直线与直线及抛物线分别交于(),0M m OA M x AB 点,.P N(1)求抛物线的解析式,并写出此抛物线的对称轴和顶点坐标;(2)如果以点P ,N ,B ,O 为顶点的四边形为平行四边形,求的值;m (3)如果以B ,P ,N 为顶点的三角形与相似,求点的坐标.APM △M 9.如图,抛物线经过,两点,与y 轴交于点B ,P 为抛物2y x bx c =-++()4,0A ()1,0C -线上的动点,连接AB ,BC ,PA ,PC ,PC 与AB 相交于点Q .(1)求抛物线的解析式;(2)若P 为第一象限抛物线上的动点,设的面积为,的面积为,当APQ △1S BCQ △2S 时,求点P 的坐标;215S S -=(3)是否存在点P ,使,若存在,直接写出点P 的坐标:若不存在,说45PAB CBO ∠+∠=︒明理由.10.如图,在平面直角坐标系中,抛物线与x 轴的正、负半轴分别交xOy 23y ax bx =++于点B 、A ,与y 轴交于点C ,已知,,.5AB =tan 3CAB ∠=:3:4OC OB =(1)求该抛物线的表达式;(2)设该抛物线的对称轴分别与x 轴、交于点E 、F ,求的长;BC EF (3)在(2)的条件下,联结,如果点P 在该抛物线的对称轴上,当和相似CE CEP △CEB 时,求点P 的坐标11.如图,直线分别交轴、轴于点,过点的抛物线31255y x =-+x y A B ,A 与轴的另一交点为,与轴交于点,抛物线的对称轴交2y x bx c =-++x C y ()04D ,l 于点,连接交于点.AD E OE AB F(1)求抛物线的解析式;(2)求证:;OE AB ⊥(3)为抛物线上的一动点,直线交于点,是否存在这样的点,使以P PO AD M P 为顶点的三角形与相似?若存在,求点的横坐标;若不存在,请说明A O M ,,ACD P 理由.12.如图,以D 为顶点的抛物线交x 轴于A 、B 两点,交y 轴于点C ,直212y x bx c=-++线的表达式为.BC 6y x =-+(1)求抛物线的表达式;(2)在直线上存在一点P ,使的值最小,求此最小值;BC PO PA +(3)在x 轴上是否存在一点Q ,使得以A 、C 、Q 为顶点的三角形与相似?若存在,BCD △请求出点Q 的坐标;若不存在,请说明理由.13.如图,在平面直角坐标系中,抛物线与x 轴交于点A 和点2()0y ax bx c ac =++≠B (点A 在点B 的左侧),与y 轴交于点C .若线段的长满足,OA OB OC 、、2OC OA OB =⋅则这样的抛物线称为“黄金”抛物线.如图,抛物线为“黄金”抛物线,22(0)y ax bx a =++≠其与x 轴交点为A ,B (其中B 在A 的右侧),与y 轴交于点C .且4OA OB=(1)求抛物线的解析式;(2)若P 为上方抛物线上的动点,过点P 作,垂足为D .AC PD AC ⊥①求的最大值;PD ②连接,当与相似时,求点P 的坐标.PC PCD ACO △14.在平面直角坐标系中,O 为坐标原点,直线与x 轴交于点B ,与y 轴交于点3y x =-+C .二次函数的图像过B ,C 两点,且与x 轴交于另一点A ,点M 为线段2y ax 2x c =++OB 上的一个动点(不与端点O ,B 重合).(1)求二次函数的表达式;(2)如图①,过点M 作y 轴的平行线l 交于点F ,交二次函数的图像于BC 2y ax 2x c =++点E ,记的面积为,的面积为,当时,求点E 的坐标;CEF 1S BMF 2S 1212S S =(3)如图②,连接,过点M 作的垂线,过点B 作的垂线,与交于点CM CM 1l BC 2l 1l2l G ,试探究的值是否为定值?若是,请求出的值;若不是,请说明理由.CG CM CGCM 15.如图1,已知抛物线与轴交于两点,与轴交于2y xbx c =-++x ()()2,0,4,0A B -y 点.C (1)求的面积;ABC (2)如图2,点是抛物线上第一象限的一点,且,求点的坐标;P PAB ACO ∠=∠P (3)若点是直线上一点,请在图3中探究:抛物线在轴上方的部分上是否存在点N 2y =x ,使得是以点为直角顶点的等腰直角三角形?若存在,请直接写出所有满足M CMN M 条件的点的坐标;若不存在,请说明理由.M 16.如图,在平面直角坐标系中,已知抛物线经过,xOy 2y ax x c =++()2,0A -两点,直线与轴交于点.()0,4B 3x =x C(1)求,的值;a c (2)经过点的直线分别与线段,直线交于点,,且与的面O AB 3x =D E BDO △OCE △积相等,求直线的解析式;DE (3)是抛物线上位于第一象限的一个动点,在线段和直线上是否分别存在点,P OC 3x =F ,使,,,为顶点的四边形是以为一边的矩形?若存在,求出点的坐G B F G P BF F 标;若不存在,请说明理由.答案:1.(1),,;()10A -,()40B ,()02C ,(2)①;②点P()()221210212042t t t s t t t ⎧--≤<⎪⎪=⎨⎪-+≤≤⎪⎩2.(1)215222y x x =-+-(2)存在,(2,1)(3)点的坐标为(3,1)D 3.(1)2142y x x =-++,当时,有最大值2m =PN (3)存在,或48,33Q ⎛⎫ ⎪⎝⎭84,33Q ⎛⎫ ⎪⎝⎭4.(1)1(2)①;②或.9(4,6)D 25(3,)4D 5.(1)2315684y x x =-+(2)(11,4)或2356.(1);213222y x x =--(2);2m =(3)存在,m 的值为0或3;(4)存在,M 点的坐标为或或()7,0()1,0M 7.(1);2246y x x =+-(2);线段长度的最大值为.226PD t t =--PD 92(3)或()2,6P --755,48P ⎛⎫-- ⎪⎝⎭8.(1),对称轴:,顶点坐标239344y x x =-++32x =375,216⎛⎫ ⎪⎝⎭(2)2(3)或11,09M ⎛⎫ ⎪⎝⎭()3,0M 9.(1)234y x x =-++(2)或16P(,)26P (,)(3)()3,4P 10.(1)239344y x x =-++(2)158EF =(3)P 的坐标为:或.3,52⎛⎫ ⎪⎝⎭39,24⎛⎫ ⎪⎝⎭11.(1)抛物线解析式为234y x x =-++(2)2(3)存在,点的横坐标为P 12.(1)21262y x x =-++(2)10(3)当Q 的坐标为或时,以A 、C 、Q 为顶点的三角形与相似()00,()180,BCD △13.(1)213222y x x =--+(2)①PD ②P 坐标为或(3,2)-325()28,-14.(1);223y x x =-++(2);(1,4)E(3)15.(1)24(2)1523(,)416P (3)存在,或()3,5M 16.(1),12a =-4c =(2)23y x =-(3)存在这样的点,点的坐标为或F F (2,0)。
相似三角形的性质与判定(原卷版)-九年级数学(北师大版)
第22讲相似三角形的性质与判定1、探索相似三角形的性质,能运用性质进行有关计算;2、通过典型实例认识现实生活中物体的相似,能运用图形相似的知识解决一些简单的实际问题(如何把实际问题抽象为数学问题).一、相似三角形的性质1.相似三角形的对应角相等,对应边的比相等.2.相似三角形中的重要线段的比等于相似比.相似三角形对应高,对应中线,对应角平分线的比都等于相似比.要点:要特别注意“对应”两个字,在应用时,要注意找准对应线段.3.相似三角形周长的比等于相似比.∽,则由比例性质可得:4.相似三角形面积的比等于相似比的平方.∽,则分别作出与的高和,则21122=1122ABCA B C BC AD k B C k A D S k S B C A D B C A D '''''''⋅⋅⋅⋅=='''''''''⋅⋅△△要点:相似三角形的性质是通过比例线段的性质推证出来的.二、相似三角形的应用1.测量高度测量不能到达顶部的物体的高度,通常使用“在同一时刻物高与影长的比例相等”的原理解决.要点:测量旗杆的高度的几种方法:平面镜测量法影子测量法手臂测量法标杆测量法2.测量距离测量不能直接到达的两点间的距离,常构造如下两种相似三角形求解。
1.如甲图所示,通常可先测量图中的线段DC、BD、CE的距离(长度),根据相似三角形的性质,求出AB的长.2.如乙图所示,可先测AC、DC及DE的长,再根据相似三角形的性质计算AB的长.要点:1.比例尺:表示图上距离比实地距离缩小的程度,比例尺=图上距离/实际距离;2.太阳离我们非常遥远,因此可以把太阳光近似看成平行光线.在同一时刻,两物体影子之比等于其对应高的比;3.视点:观察事物的着眼点(一般指观察者眼睛的位置);4.仰(俯)角:观察者向上(下)看时,视线与水平方向的夹角.例A.1:C.1:2例例例短边为_________例A .1:2B .1:3C .1:4D .1:16考点2:相似三角形的应用(利用相似三角形测高)例6.如图,身高为1.6m 的小明想测量一下操场边大树的高度,他沿着树影BA 由B 到A 走去,当走到C 点时,他的影子顶端正好与树的影子顶端重合,测得 1.4m BC =,.7m 0CA =,于是得出树的高度为()A .3.2mB .4.8mC .6.4mD .8m例7.如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为20cm 光源,到屏幕的距离为40cm ,且幻灯片中图形的高度为8cm ,则屏幕上图形的高度为()A .8cmB .12cmC .16cmD .24cm例8.中国教育家孔子周游列国14年,其中10年居卫(卫国即现在的濮阳),龙湖论语广场有一尊孔子雕像,数学兴趣小组的同学为了测量雕像的高度(AB 顶端A 到水平地面BE 的距离),在雕像旁边的水平地面上C 处放了一面镜子(平面镜的厚度忽略不计),组长小丽沿直线BC 后退到点E 处,这时恰好在镜子里看到雕像的顶端A ,此时测得7BC =米,2EC =米,小丽的眼睛距地面的高度 1.6DE =米,则雕像的高度AB =______米.考点3:利用相似三角形的性质求解平行问题例9.如图,12l l ∥,AF :BF =2:5,BC :CD =4:1,则AE :EC 的值为()A .5:2B .1:4C .2:1D .3:2例S S:A.3:5B.3:25C.例11.如图,在长线于点D.若ECD的面积等于例12.如图,在=12;③ADAB=OEOB;④ADE A.1个B.2个考点4:网格问题例13.如图,在33⨯的正方形网格中,考点5:分类讨论问题例点的三角形与考点6:最值问题例15.如图,在矩形ABCD 且分别交对角线AC ,直线BC 于点A .25552-B .2552+考点7:相似三角形的性质与判定综合问题例16.ABC 的边上有D 7BE =,4EF =,5FC =,则四边形A .1:3B .1:4C .2:5D .3:8例17.如图,ABC 为等边三角形,相交于点O ,现有如下两个结论:①AP A .①对,②对B .①对,②错例EF 折叠得A .2个B 考点8:相似三角形的性质与判定解答证明题例19.如图,在梯形(1)求证:DE AF=(2)若ABC CDE ∠=∠,求证:2AF BF CE=⋅例20.如图,在ABC 中,AB AC =,(1)求证:BAE CAE ≌;(2)在如图1中,若AE AD =,其它条件不变得到图2,在图点,过点H 作HG AB 交FD 于G ,交DE 于M .求证:①AF MH AM AE ⋅=⋅;②GF GD =.一、单选题1.(2023·重庆·统考中考真题)若两个相似三角形周长的比为1:4,则这两个三角形对应边的比是()A .1:2B .1:4C .1:8D .1:162.(2023·四川巴中·统考中考真题)如图,在Rt ABC △中,6cm 8cm AB BC ==,,D 、E 分别为AC BC 、中点,连接AE BD 、相交于点F ,点G 在CD 上,且12DG GC =::,则四边形DFEG 的面积为()A .22cmB .24cmC .26cmD .28cm 3.(2023·山东东营·统考中考真题)如图,ABC 为等边三角形,点D ,E 分别在边BC ,AB 上,60ADE ∠=︒,若4BD DC =, 2.4DE =,则AD 的长为()A .1.8B .2.4C .3D .3.24.(2023·安徽·统考中考真题)如图,点E 在正方形ABCD 的对角线AC 上,EF AB ⊥于点F ,连接DE 并延长,交边BC 于点M ,交边AB 的延长线于点G .若2AF =,1FB =,则MG =()A .23B .352C .51+D .105.(2023·黑龙江·统考中考真题)如图,在平面直角坐标中,矩形ABCD 的边5,:1:4AD OA OD ==,将矩形ABCD 沿直线OE 折叠到如图所示的位置,线段1OD 恰好经过点B ,点C 落在y 轴的点1C 位置,点E 的坐标是()A .()1,2B .(-二、填空题6.(2022·辽宁阜新·统考中考真题)如图,在矩形ABCD 中,E 是AD 边上一点,且2AE DE =,BD 与CE 相交于点F ,若DEF 的面积是3,则BCF △的面积是______.7.(2022·山东东营·统考中考真题)如图,在ABC 中,点F 、G 在BC 上,点E 、H 分别在AB 、AC 上,四边形EFGH 是矩形,2,EH EF AD =是ABC 的高.8,6BC AD ==,那么EH 的长为____________.三、解答题8.(2018·陕西·统考中考真题)周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A ,在他们所在的岸边选择了点B ,使得AB 与河岸垂直,并在B 点竖起标杆BC ,再在AB 的延长线上选择点D 竖起标杆DE ,使得点E 与点C 、A 共线.已知:CB ⊥AD ,ED ⊥AD ,测得BC =1m ,DE =1.5m ,BD =8.5m .测量示意图如图所示.请根据相关测量信息,求河宽AB .9.(2023·福建·统考中考真题)如图1,在ABC 中,90,,BAC AB AC D ∠=︒=是AB 边上不与,A B 重合的一个定点.AO BC ⊥于点O ,交CD 于点E .DF 是由线段DC 绕点D 顺时针旋转90︒得到的,,FD CA 的延长线相交于点M .(1)求证:ADE FMC △∽△;(2)求ABF ∠的度数;(3)若N 是AF 的中点,如图2.求证:ND NO =.一、单选题A.6B.8 5.如图,已知在ABC中,DE∥①DE AEBC EC=②ADABB CEC=③CECF A.1个6.如图,BD、CE是A.ADEV∽ABCC.BOE△∽COD△7.如图,已知ABC的面积是DEFG1212A.17B.217∠9.如图,直角三角形ABC中,ACB 个.①图中有4个三角形与ACB△相似;②16AE AD二、填空题14.如图,EF分别为矩形ABCD15.如图,点E是平行四边形BF=17.如图,△ABC中,AB=8cm,AC 以A、P、Q为顶点的三角形与△18.如图,边长为6的正方形ABCD三、解答题20.如图,在ABC 和DEF 中,G ,H 分别是边22.如图,为了估计河的宽度,在河的对岸选定一个目标点23.如图,在ABC 中,点D 24.如图,已知cm,cm,2AD a AC b BC ===(1)试证BFG FEG△△∽(2)求:AP PC.27.如图所示,在等腰三角形ABC中,AE²=AQ·AB求证:(1)∠CAE=∠BAF;(2)CF·FQ=AF·BQ,以B为直角顶点向右作等腰直角28.如图1,已知等边ABC(1)若62AC=,求点D到AB边的距离;=+;(2)如图2,过点B作AD的垂线,分别交AD,CD于点E,F,求证:EF CF BE=,连接CM,CN,若AC (3)如图3,点M,N分别为线段AD,BD上一点,AM BN△的面积.取得最小值时,直接写出ACM。
九年级数学中考冲刺---相似三角形复习课件北师大版
G
F
D
B
C
补充练习2:
• 如图,在△ABC中,DE∥BC,且 S△ADE :S
四边形BCED=1:2,BC=2。
• 求DE的长。
A
D B E C
补充练习3:
• 矩形ABCD中,AB=4,BC=6,M是BC的中点, DE⊥AM,E是垂足。①求△ABM的面积;② 求DE的长;③求△ADE的面积。 • A D
应用举例
例1 判断 ①所有的等腰三角形都相似. (×) ②所有的直角三角形都相似. (×)
③所有的等边三角形都相似. (√) ④所有的等腰直角三角形都相似. (√)
小结:相似的形式一
(1)如图1,当
DE∥BC ∠AED=∠B
时,△ABC∽ △ADE 时, △ABC∽ △AED。
(2)如图2,当
(3)如图3,当
C
∴
△
∽ △ DAC
1、 如图1,已知:DE∥BC,EF ∥AB,则图中共 3 有_____对三角形相似.
A D E
B
F
C 如图(1)
2:已知,如图,梯形ABCD中,AD∥BC, ∠A=900,对角线BD⊥CD 求证:(1) △ABD∽△DCB;
证明:(1) ∵AD∥BC, ∴ ∠ADB= ∠DBC ∵ ∠A=∠BDC= 90°, ∴ △ABD∽△DCB (2) ∵ △ABD∽△DCB ∴AD = BD BD BC 即:BD2=AD· BC
y
· P
O
· B
C
·
x
· A
例2 如图,CD是Rt△ABC斜边上的高,E为AC的中点, ED交CB的延长线于F。 这个图形中有几个相似三角形的基本图形 求证:BD· CF=CD· DF
北师大版-相似三角形-测试卷
相似三角形 一、选择题(每小题3分,共30分)1、在相同时刻的物高与影长成比例,如果高为1.5米的测竿的影长为2.5米,那么影长为30米的旗杆的高是( )2、如图,D 、E 分别是AB 、AC 上两点,CD 与BE 相交于点O ,下列条件中不能使ΔABE 和ΔACD 相似的是( )A.∠B=∠CB.∠ADC=∠∶AC=AE ∶AB3、如图所示,D 、E 分别是ΔABC 的边AB 、AC 上的点,DE ∥BC ,并且AD ∶BD=2,那么S ΔADE ∶S 四边形DBCE =( )(A)32 (B)43 (C)54 (D)94 4.在矩形ABCD 中,E 、F 分别是CD 、BC 上的点,若∠AEF=90°,则一定有( )(A)ΔADE ∽ΔAEF (B)ΔECF ∽ΔAEF (C)ΔA DE ∽ΔECF (D)ΔAEF ∽ΔABF(第2题图) (第3题图) (第4题图) (第5题图)5、厨房角柜的台面是三角形(如图所示),如果把各边中点连线所围成的三角形铺成黑色大理石(图中阴影部分),其余部分铺成白色大理石,则黑色大理石面积与白色大理石的面积之比是( ) ∶∶∶∶56、如图,在大小为4×4的正方形网格中,是相似三角形的是( )① ② ③ ④A.①和②B.②和③C.①和③D.②和④7、如图是圆桌正上方的灯泡O 发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.2m ,桌面距离地面1m ,若灯泡O 距离地面3m ,则地面上阴影部分的面积为( ) πm 2πm 2πm 2πm 28、如图,直线l 1∥l 2,AF ∶FB=2∶3,BC ∶CD=2∶1,则AE ∶EC 是( )∶∶∶∶29、如图,三个正六边形全等,其中成位似图形关系的有( )10、平面直角坐标系中,有一条“鱼,它有六个顶点”,则( )A.将各点横坐标乘以2,纵坐标不变,得到的鱼与原来的鱼位似B.将各点纵坐标乘以2,横坐标不变,得到的鱼与原来的鱼位似C.将各点横、纵坐标都乘以2,得到的鱼与原来的鱼位似D.将各点横坐标乘以2,纵坐标乘以21,得到的鱼与原来的鱼位似 二、填空题(每小题4分,共20分)11、两个相似多边形的一组对应边分别为3cm 和4.5cm ,如果它们的面积之和为130cm 2,那么较小的多边形的面积是 cm 2.12、如图,DE 与BC 不平行,当ACAB = 时,ΔABC 与ΔADE 相似.(第12题图) (第13题图) (第14题图) (第15题图)13、如图,AD=DF=FB ,DE ∥FG ∥BC ,则S Ⅰ∶S Ⅱ∶S Ⅲ= .14、如图,正方形ABCD 的边长为2,AE=EB ,MN=1,线段MN 的两端在CB 、CD 上滑动,当CM= 时,ΔAED 与N ,M ,C 为顶点的三角形相似.15、如图,在直角坐标系中有两点A(4,0)、B(0,2),如果点C 在x 轴上(C 与A 不重合),当点C 的坐标为 或 时,使得由点B 、O 、C 组成的三角形与ΔAOB 相似(至少写出两个满足条件的点的坐标).三、解答题(每小题8分,共40分)16、如图,ΔABC 中,BC=a .(1)若AD 1=31AB ,AE 1=31AC ,则D 1E 1= ; (2)若D 1D 2=31D 1B ,E 1E 2=31E 1C ,则D 2E 2= ; (3)若D 2D 3=31D 2B ,E 2E 3=31E 2C ,则D 3E 3= ; ……(4)若D n -1D n =31D n -1B ,E n -1E n =31E n -1C ,则D n E n = . 17、已知:如图,ΔABC 中,∠B=∠C=30°.请你设计三种不同的分法,将ΔABC 分割成四个三角形,使得其中两个是全等三角形,而另外两个是相似三角形但不全等的直角三角形.请画出分割线段,标出能够说明分法的所得三角形的顶点和内角度数或记号,并在各种分法的空格线上填空.(画图工具不限,不要求写出画法,不要求说明理由).分法一 分法二 分法三 分法一:分割后所得的四个三角形中,Δ ≌Δ ,RtΔ ∽RtΔ . 分法二:分割后所得的四个三角形中,Δ ≌Δ ,RtΔ ∽RtΔ . 分法三:分割后所得的四个三角形中,Δ ≌Δ ,RtΔ ∽RtΔ .18、在比例尺为1∶5000的地图上,一块多边形地区的周长是72cm,面积是320cm2,求这个地区的实际周长和面积.19、如图,ΔABC中,BD是角平分线,过D作DE∥AB交BC于点E,AB=5cm,BE=3cm,求EC的长.20、如图,四边形ABCD、CDEF、EFGH都是正方形.(1)⊿ACF与⊿ACG相似吗?说说你的理由.(2)求∠1+∠2的度数.五、(本题10分)21、在ΔABC中,AB=4如图(1)所示,DE∥BC,DE把ΔABC分成面积相等的两部分,即SⅠ=SⅡ,求AD的长.如图(2)所示,DE∥FG∥BC,DE、FG把ΔABC分成面积相等的三部分,即SⅠ=SⅡ=SⅢ,求AD 的长.如图(3)所示,DE∥FG∥HK∥…∥BC,DE、FG、HK、…把ΔABC分成面积相等的n部分,SⅠ=SⅡ=SⅢ=…,请直接写出AD的长.。
中考数学总复习 第一部分 教材考点全解 第四章 三角形 第17讲 相似三角形课件
12/9/2021
第十一页,共四十二页。
5.平行于三角形一边的直线和其他两边相交,所构成的三 角形与原三角形相似. 三角形相似的几种常见基本图形:
12/9/2021
第十二页,共四十二页。
命题点1 平行线分线段成比例(仅2015年考查) 命题点2 与相似三角形性质有关的计算(必考)
12/9/2021
第五页,共四十二页。
考点(kǎo diǎn)一
相似(xiānɡ sì)图形与比例线段
1.相似图形:形状相同的图形称为相似图形.
2.相似多边形:如果两个边数相同的多边形满足对应角 _相__等___,对应边的比_相__等_(_xi_ān,gd那ěng)么这两个多边形相似,相
似多边形对应边的比称为相似比. (1)相似多边形的对应角_相__等___,对应边_成__比__例____. (2) 相 似 多 边 形 的 周 长 比 等 于 _相_似__比____ , 面 积 比 等 于 _相__似__比__的_平__方____.
第四章 三角形
第17讲
相似 三角形 (xiānɡ sì)
(3~13分)
12/9/2021
第一页,共四十二页。
【版本导航】人教:九下第二十七章 P23—P46; 北师:九上第四章 P76—P112; 华师:九上第二十三章 P48—P76.
12/9/2021
第二页,共四十二页。
12/9/2021
第三页,共四十二页。
12/9/2021
第七页,共四十二页。
5.黄金分割:在线段AB上,点C把线段AB分成两条线段AC
和BC(AC>BC),如果
BC AC
=
AC AB
,那么线段AB被点C黄金
分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做 黄金比,黄金比约为__0_.6_1_8___.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
专题17 相似三角形及应用
学校:___________姓名:___________班级:___________
一、选择题:(共4个小题)
1.【2015宜宾】如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,
CO=CD.若B(1,0),则点C
的坐标为( )
A.(1,2) B.(1,1) C.(2,2) D.(2,1)
【答案】B.
【解析】
【考点定位】1.位似变换;2.坐标与图形性质.
2.【2015乐山】如图,1l∥2l∥3l,两条直线与这三条平行线分别交于点A、B、C和D、E、F.已知32ABBC,
则DEDF的值为( )
A.32 B.23 C.25 D.35
【答案】D.
【解析】
试题分析:∵1l∥2l∥3l,32ABBC,∴DEDF=ABAC=332=35,故选D.
【考点定位】平行线分线段成比例.
2
3.【2015绵阳】如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重
合,折痕为EF,点E,F分别在AC和BC上,则CE:CF=( )
A.34 B.45 C.56 D.67
【答案】B.
【解析】
【考点定位】1.翻折变换(折叠问题);2.相似三角形的判定与性质;3.综合题.
4.【2015黔西南州】在数轴上截取从0到3的对应线段AB,实数m对应AB上的点M,如图1;将AB折
成正三角形,使点A、B重合于点P,如图2;建立平面直角坐标系,平移此三角形,使它关于y轴对称,
且点P的坐标为(0,2),PM的延长线与x轴交于点N(n,0),如图3,当m=3时,n的值为( )
A.423 B.432 C.332 D.332
3
【答案】A.
【解析】
【考点定位】1.相似三角形的判定与性质;2.实数与数轴;3.等边三角形的性质;4.平移的性质.
二、填空题:(共4个小题)
5.【2015柳州】如图,矩形EFGH内接于△ABC,且边FG落在BC上.若BC=3,AD=2,EF=23EH,那么
EH
的长为 .
【答案】32.
【解析】
试题分析:∵四边形EFGH是矩形,∴EH∥BC,∴△AEH∽△ABC,∵AM⊥EH,AD⊥BC,∴AMEHADBC,
设EH=3x,则有EF=2x,AM=AD﹣EF=2﹣2x,∴22323xx,解得:x=12,则EH=32.故答案为:32.
【考点定位】1.相似三角形的判定与性质;2.矩形的性质;3.应用题.
4
6.【2015河池】如图,菱形ABCD的边长为1,直线l过点C,交AB的延长线于M,交AD的延长线于N,
则11AMAN= .
【答案】1.
【解析】
【考点定位】1.相似三角形的判定与性质;2.菱形的性质;3.综合题.
7.【2015自贡】将一副三角板按图叠放,则△AOB与△DOC的面积之比等于 .
【答案】1:3.
【解析】
【考点定位】相似三角形的判定与性质.
8.【2015钦州】如图,以O为位似中心,将边长为256的正方形OABC依次作位似变化,经第一次变化后
得正方形OA1B1C1,其边长OA1缩小为OA的12,经第二次变化后得正方形OA2B2C2,其边长OA2缩小为
OA
1
的12,经第三次变化后得正方形OA3B3C3,其边长OA3缩小为OA2的12,......,按此规律,经第n次变化
后,所得正方形OAnBnCn的边长为正方形OABC边长的倒数,则n= .
5
【答案】16.
【解析】
试题分析:由已知有:OA1=12OA;OA2=12OA1=21()2OA,OA3=12OA2=31()2OA,......,∴OAn=1()2nOA,
OAn=1()2nOA=1OA,∴1()2n=1622111()2562OA,∴n
=16.故答案为:16.
【考点定位】1.位似变换;2.坐标与图形性质.
三、解答题:(共2个小题)
9.【2015德阳】如图,四边形ABCD为菱形,M为BC上一点,连接AM交对角线BD于点G,并且∠ABM=2
∠BAM.
(1)求证:AG=BG;
(2)若点M为BC的中点,同时S△BMG=1,求三角形ADG的面积.
【答案】(1)证明见试题解析;(2)4.
【解析】
【考点定位】1.菱形的性质;2.相似三角形的判定与性质.
6
10.【2015南充】如图,矩形纸片ABCD,将△AMP和△BPQ分别沿PM和PQ折叠(AP>AM),点A和点
B
都与点E重合;再将△CQD沿DQ折叠,点C落在线段EQ上点F处.
(1)判断△AMP,△BPQ,△CQD和△FDM中有哪几对相似三角形?(不需说明理由)
(2)如果AM=1,sin∠DMF=53,求AB的长.
【答案】(1)△AMP∽△BPQ∽△CQD;(2)AB=6.
【解析】
试题分析:(1)由矩形的性质得∠A=∠B=∠C=90°,由折叠的性质和等角的余角相等,可得∠BPQ=∠AMP=
∠DQC,所以△AMP∽△BPQ∽△CQD;
(2)先证明MD=MQ,然后根据sin∠DMF=DFMD=53,设DF=3x,MD=5x,表示出AP、BP、BQ,再根据△
AMP
∽△BPQ,列出比例式解方程求解即可.
(2)∵AD∥BC,∴∠DQC=∠MDQ,根据折叠的性质可知:∠DQC=∠DQM,∴∠MDQ=∠DQM,∴MD=MQ,∵AM=ME,
BQ=EQ,∴BQ=MQ﹣ME=MD﹣AM,∵sin∠DMF=DFMD=53,∴设DF=3x,MD=5x,∴BP=PA=PE=32x,BQ=5x
﹣1,
∵△AMP∽△BPQ,∴AMAPBPBQ,∴3123512xxx,解得:29x(舍)或x=2,∴AB=6.
【考点定位】1.翻折变换(折叠问题);2.相似三角形的判定;3.解直角三角形;4.探究型.
7
