北师大版初二数学下册期末测试题及答案(A)
北师大版八年级下册数学期末考试试题附答案

北师大版八年级下册数学期末考试试卷一、单选题1.已知a b <,下列式子不一定成立的是( )A .11a b -<-B .22a b ->-C .111122a b +<+ D .ma mb > 2.已知一个n 边形的内角和等于1800°,则n =( )A .6B .8C .10D .123.等腰三角形的两边长分别为4cm ,8cm ,则该三角形的周长为( ) A .16cm B .20cm C .16cm 或20cm D .以上都不对 4.若分式13x -无意义,则x 的取值范围是( ) A .3x ≠ B .3x = C .3x < D .3x > 5.下列四个图形中,既是轴对称图形,又是中心对称图形的是( )A .B .C .D . 6.在平面直角坐标系中,将点()3,2P -向右平移3个单位得到点P ',则点P '关于x 轴的对称点的坐标为( )A .()0,2-B .()0,2C .()6,2-D .()6,2--7.化简222a b ab a b b a++--的结果是( ) A .a+b B .a ﹣b C .2()a b a b +- D .2()a b a b -+ 8.如图,△ABC 中,△ACB =90°,△ABC =40°.将△ABC 绕点B 逆时针旋转得到△A′BC′,使点C 的对应点C′恰好落在边AB 上,则△CAA′的度数是( )A .50°B .70°C .110°D .120°9.若关于x的分式方程32xx-=2mx-+5的解为正数,则m的取值范围为()A.m<﹣10 B.m≤﹣10C.m≥﹣10且m≠﹣6 D.m>﹣10且m≠﹣610.如图,△ABCD的对角线AC,BD交于点O,DE平分△ADC交BC于点E,△BCD=60°,AD=2AB,连接OE.下列结论:△S△ABCD=AB•BD;△DB平分△ADE;△AB=DE;△S△CDE=S△BOC,其中正确的有()A.1个B.2个C.3个D.4个二、填空题11.因式分解2416x-=__________.12.在ABCD中,如果△A+△C=140°,那么△C等于_____.13.若点P(3a-9,1-a)在第三象限内,且a为整数,则a的值是________.14.如图,函数y=ax和y=bx+c的图象相交于点A(1,2),则不等式ax>bx+c的解集为_____.15.如图,在△ABC中,AC垂直平分线DE分别与BC、AC交于D、E,△ABD的周长是13,AE=5,△ABC的周长是_________.16.已知关于x的方程2-1122kxx x-=--有增根,则k=__________.17.如图,正方形ABCD的边长为2,BE平分△DBC交CD于点E,将△BCE绕点C顺时针旋转90°得到△DCF,延长BE交DF于G,则BF的长为_____.三、解答题18.解不等式组284(2)1xx x<⎧⎨-≤+⎩,并在数轴上表示解集.19.先化简,再求值,(121x x--)÷2212x xx x+-+,其中x=﹣220.如图在边长为1的小正方形组成的网格中,△OAB的顶点都在格点上.(1)请作出△OAB关于直线CD对称的△O1A1B1;(2)请将△OAB绕点B顺时针旋转90°,画出旋转后的△BO2A2.21.某中学为配合开展“垃圾分类进校园”活动,新购买了一批不同型号的垃圾分类垃圾桶,学校先用2700元购买了一批给班级使用的小号垃圾桶,再用3600元购买了一批放在户久使用的大号垃圾桶,已知每个大号垃圾桶的价格是小号垃圾桶的4倍,且购买的数量比小号垃圾桶少40个,求每个小号垃圾桶的价格是多少元?22.如图,在△ABC 中,AD 是边BC 上的中线,△BAD =△CAD ,CE△AD ,CE 交BA 的延长线于点E ,BC =8,AD =3(1)求CE 的长;(2)求证:△ABC 为等腰三角形.23.如图,四边形ABCD 的对角线AC△BD 于点E ,AB =BC ,F 为四边形ABCD 外一点,且△FCA =90°,△CBF =△DCB .(1)求证:四边形DBFC 是平行四边形;(2)如果BC 平分△DBF ,△F =45°,BD =2,求AC 的长.24.某工厂计划生产A ,B 两种产品共10件,其生产成本和利润如下表:(1)若工厂计划获利14万元,问A ,B 两种产品应分别生产多少件?(2)若工厂投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案? (3)在(2)条件下,哪种方案获利最大?并求最大利润.25.如图,在直角坐标系中,已知直线3y kx =+与x 轴相交于点(20)A ,,与y 轴交于点B . (1)求k 的值及AOB ∆的面积;(2)点C 在x 轴上,若ABC ∆是以AB 为腰的等腰三角形,直接写出点C 的坐标;(3)点0(3)M ,在x 轴上,若点P 是直线AB 上的一个动点,当PBM ∆的面积与AOB ∆的面积相等时,求点P 的坐标.参考答案1.D【解析】根据不等式的性质解答.【详解】解:A 、不等式a <b 的两边同时减去1,不等式仍成立,即a−1<b−1,故本选项不符合题意;B 、不等式a <b 的两边同时乘以-2,不等号方向改变,即22a b ->-,故本选项不符合题意;C 、不等式a <b 的两边同时乘以12,不等式仍成立,即:1122a b <,再在两边同时加上1,不等式仍成立,即111122a b +<+,故本选项不符合题意; D 、不等式a <b 的两边同时乘以m ,当m>0,不等式仍成立,即ma mb <;当m<0,不等号方向改变,即ma mb >;当m=0时,ma mb =;故ma mb >不一定成立,故本选项符合题意,故选:D .2.D【解析】根据多边形的内角和公式,计算可得结论.【详解】解:△(n ﹣2)×180=1800,△n =12.故选:D .3.B【解析】根据题意得出两种情况,根据三角形的三边关系定理看看能否组成三角形,再求出周长即可.【详解】解:当等腰三角形的三边长是4cm ,4cm ,8cm 时,4+4=8,不符合三角形的三边关系定理,此时不能组成三角形;当等腰三角形的三边长是4 cm ,8 cm ,8 cm 时,符合三角形的三边关系定理,此时能组成三角形,三角形的周长是4+8+8=20(cm ),所以该三角形的周长是20 cm ,故选:B .4.B【解析】根据分式无意义的条件,即可求解.【详解】△式13x -无意义, △x-3=0,即:3x =,故选B .【点睛】本题主要考查分式无意义的条件,掌握分式的分母不等于0.是解题的关键.5.D【解析】根据把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行解答.【详解】解:A .是轴对称图形,不是中心对称图形,故此选项不合题意;B .是轴对称图形,不是中心对称图形,故此选项不合题意;C .不是轴对称图形,是中心对称图形,故此选项不合题意;D .既是轴对称图形,又是中心对称图形,故此选项符合题意;故选:D .【点睛】此题主要考查了中心对称图形和轴对称图形,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与原图重合. 6.A【解析】【分析】先根据点向右平移3个单位点的坐标特征:横坐标加3,纵坐标不变,得到点P '的坐标,再根据关于x 轴的对称点的坐标特征:横坐标不变,纵坐标变为相反数,得到对称点的坐标即可.【详解】解:△将点()3,2P -向右平移3个单位,△点P '的坐标为:(0,2),△点P '关于x 轴的对称点的坐标为:(0,-2).【点睛】本题考查平移时点的坐标特征及关于x轴的对称点的坐标特征,熟练掌握对应的坐标特征是解题的关键.7.B【解析】【详解】跟据同分母分式相加减的运算法则计算.同分母分式相加减,分母不变,分子相加减.【解答】解:原式====a﹣b.故选:B.【点评】本题主要考查了分式的加减,熟记运算法则是解答本题的关键.8.D【解析】【分析】根据旋转可得△A′BA=△ABC=40°,A′B=AB,得△BAA′=70°,根据△CAA'=△CAB+△BAA′,进而可得△CAA'的度数.【详解】△△ACB=90°,△ABC=40°,△△CAB=90°﹣△ABC=90°﹣40°=50°,△将△ABC绕点B逆时针旋转得到△A′BC′,使点C的对应点C′恰好落在边AB上,△△A′BA=△ABC=40°,A′B=AB,△△BAA′=△BA′A=1(180°﹣40°)=70°,2△△CAA'=△CAB+△BAA′=50°+70°=120°.故选:D.【点睛】本题考查了旋转的性质,等腰三角形的性质,三角形内角和定理,解决本题的关键是掌握旋转的性质.9.D【分析】分式方程去分母化为整式方程,表示出方程的解,由分式方程的解为正数求出m 的范围即可.【详解】解:去分母得35(2)x m x =-+-, 解得102m x +=, 由方程的解为正数,得到100m +>,且2x ≠,104m +≠,则m 的范围为10m >-且6≠-m ,故选:D .【点睛】本题主要考查了分式方程的计算,去分母化为整式方程,根据方程的解求出m 的范围,其中考虑到分式方程的分母不可为零是做对题目的关键.10.D【解析】【分析】求得△ABD =90°,即AB△BD ,即可得到S△ABCD =AB•BD ;依据△ADE =60°,△BDE =30°,可得△ADB =30°=△BDE ,即可得出DB 平分△CDE ;依据AB =CD ,CD =DE ,即可得到AB =DE ;由BE =EC 可得S △CDE =12S △CDB ,由BO =OD 可得S △BOC =12S △CDB ,即可得出S △CDE =S △BOC .【详解】解:△四边形ABCD 为平行四边形,△BCD =60°,△△ADC =120°,△DE 平分△ADC ,△△ADE =△CDE =60°=△BCD ,△△CDE 是等边三角形,△CD =CE =DE ,△AD =2AB ,BC =AD ,CD =AB ,△BC =2CD =2CE =2DE ,△DE =CE =BE ,△△BDE =△DBE =12△CED =30°, △△CDB =90°,△△ABD =90°,即AB△BD ,△S △ABCD =AB•BD ,故△正确;由△知,△ADE =60°,△BDE =30°,△△ADB =30°=△BDE ,△DB 平分△ADE ,故△正确;△AB =CD ,CD =DE ,△AB =DE ,故△正确;△BE =EC ,△S △CDE =12S △CDB ,△BO =OD ,△S △BOC =12S △CDB ,△S △CDE =S △BOC ,故△正确;故选:D .【点睛】本题考查了平行四边形的性质,等边三角形的判定和性质,直角三角形的性质,角平分线定义,熟练掌握各定理是解题的关键.11.()()422x x +-【解析】【分析】所求代数式中含有公因式,可先提取公因式,然后再运用平方差公式继续分解即可.【详解】解:原式=()()()244422x x x -=+- 【点睛】本题主要考查提公因式法,公式法分解因式.关键在于提取公因式后继续利用平方差公式进行二次因式分解,注意要分解彻底.【解析】【分析】由四边形ABCD是平行四边形,根据平行四边形的对角相等,可得: △A=△C,又由△A+△C=140°,即可求得答案.【详解】△四边形ABCD是平行四边形,△△A=△C,△△A+△C=140°,△△C=70°,故答案为:70°.【点睛】本题考查了平行四边形的性质,注意熟记定理是解此题的关键.13.2【解析】【分析】已知点P在第三象限内,可知点P的横坐标小于0,纵坐标小于0,可得到一个关于a的不等式组,由此求解即可.【详解】△点P(3a-9,1-a)在第三象限,△39010aa-<⎧⎨-<⎩,解得:1<a<3,△a为整数,△a=2.故答案为2.【点睛】本题考查了一元一次不等式组的整数解及象限内的点的性质,准确记忆象限内的点的性质是解决问题的关键.14.x>1.【详解】试题分析:观察函数图象,当x >1时,直线y=ax 都在直线y=bx+c 的上方,由此可得不等式ax >bx+c 的解集.解:当x >1时,ax >bx+c ,即不等式ax >bx+c 的解集为x >1.故答案为x >1.15.23【解析】【分析】根据垂直平分线的性质得到AD=CD ,AE=CE ,再由ABD △的周长及AE 的长即可计算出结果.【详解】△DE 垂直平分AC ,△AD=DC ,AE=CE ,△ABD △的周长是13,即AB+BD+AD=13,△AB+BD+DC=13,即AB+BC=13,又△AE=5,△AC=2AE=10,△AB+BC+AC=13+10=23,即ABC 的周长是23.故答案为:23.【点睛】本题考查了垂直平分线的性质,熟练掌握性质是解题的关键.16.0【解析】【分析】增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母20x -=,得到2x =,然后代入化为整式方程即可算出k 的值.【详解】解:方程两边都乘以2x -,得:()()2211x kx ---=-,△原方程有增根,△最简公分母20x -=,解得:2x =,当2x =时,0k =.故答案为:0.【点睛】本题考查了分式方程的增根,解题的关键是掌握增根问题可按如下步骤进行:△让最简公分母为0确定增根;△化分式方程为整式方程;△把增根代入整式方程即可求得相关字母的值.17.【解析】【分析】过点E 作EM△BD 于点M ,则△DEM 为等腰直角三角形,根据角平分线以及等腰直角三角形的性质即可得出ME 的长度,再根据正方形以及旋转的性质即可得出线段BF 的长.【详解】过点E 作EM△BD 于点M ,如图所示.△四边形ABCD 为正方形,△△BDC =45°,△BCD =90°,△△DEM 为等腰直角三角形.△EM ,△BE 平分△DBC ,EM△BD ,△EM =EC ,设EM =EC =x ,△CD =2,△DE =2﹣x ,△x 2﹣x ),解得x =2,△EM =2,由旋转的性质可知:CF=CE=2,△BF=BC+CF=2=.故答案为:【点睛】本题考查了旋转的性质、正方形的性质以及角平分线的性质,解题的关键是求出线段CF 的长度.本题属于基础题,难度不大,解决该题型题目时,结合角平分线以及等腰直角三角形的性质求出线段的长度是关键.18.x≤3;数轴表示见解析.【解析】【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解,确定不等式组的解集.【详解】解:解不等式2x<8,得:x<4,解不等式4(x﹣2)≤x+1,得:x≤3,则不等式组解集为x≤3,将不等式组的解集表示在数轴上如下:【点睛】本题考查解不等式组和用数轴表示不等式组的解集,需要注意用数轴表示解集的时候实心点和空心点的区别.19.﹣21x x -,34【解析】【分析】直接将括号里面通分运算,再利用分式的混合运算法则化简,把x 的值代入即可.【详解】解:原式=[12(1)(1)x x x x x x ----]•2(1)(1)x x x +- =21(1)(1)(1)x x x x x x ---⨯-+ =﹣21x x -, 当x =﹣2时, 原式=﹣221(2)---=34. 【点睛】本题考查了分式的化简求值,熟练掌握因式分解是解题的关键.20.(1)见解析;(2)见解析.【解析】【分析】(1)△OAB 关于直线CD 对称的△O 1A 1B 1在CD 的右侧,对应点到CD 的距离相等; (2)将△OAB 的三个顶点分别绕点B 顺时针旋转90°,再顺次连接所得的三个顶点可得旋转后的△BO 2A 2.【详解】解:(1)如图所示,△O 1A 1B 1即为所求;(2)如图所示,△BO 2A 2即为所求.【点睛】本题主要考查了利用旋转变换和轴对称变换进行作图,旋转作图时,决定图形位置的因素有旋转角度、旋转方向、旋转中心.画一个图形的轴对称图形时,先从一些特殊的对称点开始.21.45【解析】【分析】设每个小号垃圾桶的价格是x元,则每个大号垃圾桶的价格是4x元,由购买大号垃圾桶的数量比小号垃圾桶少40个列出方程解答即可;【详解】设每个小号垃圾桶的价格是x元,则每个大号垃圾桶的价格是4x元依题意得:3600270040 4x x=-解得:45x=经检验,45x=是原方程的解答:每个小号垃圾桶的价格是45元.【点睛】本题考查了分式方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的相等关系,列方程求解.22.(1)6;(2)见解析【解析】【分析】(1)证明AD为△BCE的中位线即可求得CE;(2)通过证明AC=AE得到AB=AC,根据等腰三角形的判定定理即可得到结论.【详解】(1)解:△AD是边BC上的中线,△BD=CD,△CE△AD,△AD为△BCE的中位线,AB AE=∴,△CE=2AD=6;(2)证明:△CE△AD,△△BAD=△E,△CAD=△ACE,而△BAD=△CAD,△△ACE=△E,△AE=AC,又AB=AE,△AB=AC,△△ABC为等腰三角形.【点睛】本题考查了三角形中位线的判定与性质,等腰三角形的判定,是解题的关键.23.(1)见解析(2)【解析】【分析】(1)证BD△CF,CD△BF,即可得出四边形DBFC是平行四边形;(2)由平行四边形的性质得出CF=BD=2,由等腰三角形的性质得出AE=CE,作CM△BF于F,则CE=CM,证出△CFM是等腰直角三角形,由勾股定理得出 ,得出AC的长.【详解】(1)△AC△BD,△FCA=90°,△CBF=△DCB.△BD△CF,CD△BF,△四边形DBFC是平行四边形;(2)△四边形DBFC是平行四边形,△CF=BD=2,△AB=BC,AC△BD,△AE=CE,作CM△BF于F,△BC平分△DBF,△CE=CM,△△F=45°,△△CFM是等腰直角三角形,CM△CM=2=,【点睛】本题考查了平行四边形的判定与性质、等腰三角形的性质、等腰直角三角形的判定与性质、勾股定理;熟练掌握平行四边形的判定与性质是解决问题的关键.24.(1)A生产6件,B生产4件;(2)三种,方案一:A 3件B生产7件.方案二:A 生产4件,B生产6件.方案三:A生产5件,B生产5件;(3)第一种方案获利最大,最大利润是17万元.【解析】【分析】(1)设A种产品x件,B种为(10-x)件,根据共获利14万元,列方程求解.(2)设A种产品x件,B种为(10-x)件,根据若工厂投入资金不多于44万元,且获利多于14万元,列不等式组求解,从利润可看出B越多获利越大.【详解】(1)设生产A种产品x件,则生产B种产品(10-x)件根据题意得:x+2(10-x)=14解之得:x=6答:生产A种产品6件,则生产B种产品4件.(2)设生产A种产品y件,则生产B种产品(10-y)件根据题意得:()() 351044 {21014 y yy y+-≤+->解不等式组得:3≤y <6因为y 为正整数所以y 取3、4、5,则10-y 取7、6、5.因此共有三种生产方案,分别如下:方案一:A 种产品3件,B 种产品7件;方案二:A 种产品4件,B 种产品6件;方案三:A 种产品5件,B 种产品5件.设工厂获得的利润为w 万元,则w=y+2(10-y)=-y+20因为-1<0,所以随的增大而减小,所以当y=3时,的最大值为17万元答:工厂采用方案一即生产A 种产品3件,生产B 种产品7件时获得的利润最大,最大利润为17万元.25.(1)K=- 32,AOB ∆的面积=3;(2)(20)或()或C 3(-2,0);(3)(4,-3)或(-4,9).【解析】【分析】△将()20,代入直线3y kx =+可得K=- 32,AOB ∆的面积=12OB·OA =1232⨯⨯=3. △如详解图,分类讨论c 1,c 2,求坐标.△如详解图,分类讨论p 1,p 2,求坐标.【详解】(1)将()20,代入直线3y kx =+可得K=- 32,点B 坐标为(3,0),AOB ∆的面积=OB·OA·12=2·3·12=3.△已知△ABC为等腰三角形,则AB=AC.可求出AB A为圆心,AB为半径画弧,与x轴交点有2个,易得C点坐标为C1(20)或C2().以B为圆心,BA为半径画弧与x轴交点有一个,坐标为C3(-2,0)△设P点坐标为(x,33 2x-+)△S△BAM=32AOBS∆<,△P点在线段AB外.若P在线段BA延长线上时,S△PBM=S△BAM+S△PAM=113AM OB+(3) 222AM x⎡⎤⋅--+⎢⎥⎣⎦= 3 4 x34x=3,x=4.所以P坐标为(4,-3),若P在线段AB延长线上,S△PBM=S△PAM-S△BAM=﹣3 x 4若﹣3x4=3,x=-4,则P点为(-4,9).【点睛】本题主要考察对称与函数方程的综合运用,能够根据图像求相关数据与方程是解题关键.。
北师大版八年级下册数学期末测试卷及答案【完整版】

1 / 5 北师大版八年级下册数学期末测试卷及答案【完整版】 班级: 姓名:
一、选择题(本大题共10小题,每题3分,共30分) 1.4的算术平方根为( ) A.2 B.2 C.2 D.2 2.已知多项式2x2+bx+c分解因式为2(x-3)(x+1),则b,c的值为( ). A.b=3,c=-1 B.b=-6,c=2 C.b=-6,c=-4 D.b=-4,c=-6 3.函数2yx的图象不经过( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.当22aa有意义时,a的取值范围是( ) A.a≥2 B.a>2 C.a≠2 D.a≠-2 5.中国华为麒麟985处理器是采用7纳米制程工艺的手机芯片,在指甲盖大小的尺寸上塞进了120亿个晶体管,是世界上最先进的具有人工智能的手机处理器,将120亿个用科学记数法表示为( ) A.91.210个 B.91210个 C.101.210个 D.111.210个 6.欧几里得的《原本》记载,形如22xaxb的方程的图解法是:画RtABC,使90ACB,2aBC,ACb,再在斜边AB上截取2aBD.则
该方程的一个正根是( ) A.AC的长 B.AD的长 C.BC的长 D.CD的长 7.若a=7+2、b=2﹣7,则a和b互为( ) A.倒数 B.相反数 C.负倒数 D.有理化因式 2 / 5
8.如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( ) A.90° B.60° C.45° D.30° 9.如图,菱形ABCD的周长为28,对角线AC,BD交于点O,E为AD的中点,
则OE的长等于( ) A.2 B.3.5 C.7 D.14 10.如图,▱ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO
的周长是( ) A.10 B.14 C.20 D.22 二、填空题(本大题共6小题,每小题3分,共18分) 1.若3xx,则x=__________
【新】北师大版初二数学下学期期末试卷(附答案)

度北师大版初二数学下学期期末试卷(附答案)(考试时间:120分钟. 总分数:100分)学校________ 班级________ 姓名________ 分数________一、选择题。
(每小题3分,共24分)1.下列多项式中能用平方差公式分解因式的是( )A 、22)(b a -+B 、mn m 2052-C 、22y x -- D 、92+-x 2. 若a<0,则下列不等式不成立的是 ( ) A . a+5<a+7 B .5a >7a C .5-a <7-a D .75a a > 3.分式x y x y+-有意义,则必须满足条件( ) A 、x =y ≠0 B 、x ≠y C 、x ≠0 D 、y ≠04. -3x<-1的解集是 ( )A 、x<31B 、x<-31C 、x>31D 、x>-31 5、如图,OE 是∠AOB 的平分线,CD ∥OB 交OA 于点C ,交OE 于点D, ∠ ACD=50°,则∠CDE 的度数是 ( )A. 125°B. 130°C.140°D.155°6、如图,在□ABCD 中,E 为BC 的中点,F 为DC 的中点,则△CEF 与□ABCD的面积之比为( )A 、1:2B 、1:4C 、1:8D 、1:167.方程12+=x m x 的解为增根,则增根可能是( ) A .x=2 B .x=0 C .x=-1 D .x=0 或x=-18、不等式组 ⎪⎩⎪⎨⎧≥<212x x 的解集在数轴上应表示为 ( )二、填空题。
(每小题3分,共21分)a =8,ab=15,则a2b+ab2的值为。
9.如果b10.如图,在△中,∠,是△的角平分线,于点,.则∠等于______.11.分解因式:__________.12.若□的周长是30,相交于点,且△的周长比△的周长大,则= .13. 若分式方程的解为正数,则的取值范围是 .14.如图,将一朵小花放置在平面直角坐标系中第三象限内的甲位置,先将它绕原点O旋转180°到乙位置,再将它向下平移2个单位长度到丙位置,则小花顶点A在丙位置中的对应点A′的坐标为________.15.如图(1),平行四边形纸片的面积为,,.沿两条对角线将四边形剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(、重合)形成对称图形戊,如图(2)所示,则图形戊的两条对角线长度之和是 ___ .16.(7分)解方程:23--x x +1=x -2317.(7分)解不等式212-<-x x ,并把解集在数轴上表示出来.18.(7分)解分式方程32121---=-xx x .19.(8分)如图,EF 是Rt ∆ABC 的中位线,D 是BC 延长线上的一点,∠DEC=∠A 求证:四边形EDCF 是平行四边形.20.(8分)甲、乙两地相距,骑自行车从甲地到乙地,出发后,骑摩托车也从甲地去乙地.已知的速度是的速度的3倍,结果两人同时到达乙地.求两人的速度.21.(9分)如图,在ABC ∆中,BC DE //,DE 交AC 于E 点,DE 交AB 于D 点, 若5=AE ,2=CE ,3=DE .求BC 的长.22.(9分)某工艺品厂的手工编织车间有工人20名,每人每天可编织5个座垫或4个挂毯.在这20名工人中,如果派x 人编织座垫,其余的编织挂毯.已知每个座垫可获利16元,每个挂毯可获利24元.(1)写出该车间每天生产这两种工艺品所获得的利润y(元)与x(人)之间的函数关系式;(2)若使车间每天所获利润不小于1800元,最多安排多少人编织座垫?。
【最新】北师大版八年级下册数学《期末考试题》(附答案)

二、填空题(本题共4小题,每小题3分,共12分)
11.不等式2x﹣2≤7的正整数解分别是_____.
【答案】1,2,3,4
【解析】
2x﹣2≤7
2x≤9
x≤4.5
所以不等式的正整数解是1,2,3,4.
故答案是:1,2,3,4.
∴可供选择的地址有4处.
故选:D
【点睛】考查了角平分线的性质.注意掌握角平分线上的点到角两边的距离相等,注意边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于E,则△CDE的周长是( )
A. 6B. 8C. 9D. 10
【答案】B
【解析】
试题分析:根据线段垂直平分线的性质和平行四边形的性质可知,△CDE的周长=CD+DE+CE=CD+DE+AE=CD+AD=AB+BC=3+5=8.
A.2个B.3个C.4个D.5个
【答案】B
【解析】
【分析】
根据分式的定义进行判断;
【详解】 , , , , 中分式有: , , 共计3个.
故选B.
【点睛】考查了分式 定义,解题关键抓住分式中分母含有字母.
2.因式分解正确的是( )
A.m3+m2+m=m(m2+m)B.x3﹣x=x(x2﹣1)
C.(a+b)(a﹣b)=a2﹣b2D.﹣4a2+9b2=(﹣2a+3b)(2a+3b)
∵△ABC和△ADE是等腰直角三角形,
∴∠CAB=45°,
即△ABC绕点A逆时针旋转45°可到△ADE;
如图,
∵△ABC和△ADE是等腰直角三角形,
北师大版八年级数学下册期末试卷及答案【完整版】

北师大版八年级数学下册期末试卷及答案【完整版】班级: 姓名:一、选择题(本大题共10小题,每题3分,共30分)1.已知直角三角形两边的长为3和4,则此三角形的周长为( )A .12B .C .12或D .以上都不对2.(2的平方根是x ,64的立方根是y ,则x+y 的值为( )A .3B .7C .3或7D .1或73.已知点()()121,,2,A y B y 在抛物线2(1)2y x =-++上,则下列结论正确的是( )A .122y y >>B .212y y >>C .122y y >>D .212y y >>4.《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四足五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺.将绳子对折再量长木,长木还剩余1尺,问木长多少尺,现设绳长x 尺,木长y 尺,则可列二元一次方程组为( )A . 4.5112y x y x -=⎧⎪⎨-=⎪⎩B . 4.5112x y y x -=⎧⎪⎨-=⎪⎩C . 4.5112x y x y -=⎧⎪⎨-=⎪⎩D . 4.5112y x x y -=⎧⎪⎨-=⎪⎩ 5.一组数据:1、2、2、3,若添加一个数据2,则发生变化的统计量是( )A .平均数B .中位数C .众数D .方差6.如果a ,那么a 的取值范围是( )A .a 0=B .a 1=C .a 1≤D .a=0a=1或7.若aba 和b 互为( )A .倒数B .相反数C .负倒数D .有理化因式8.关于▱ABCD 的叙述,正确的是( )A .若AB ⊥BC ,则▱ABCD 是菱形 B .若AC ⊥BD ,则▱ABCD 是正方形C .若AC=BD ,则▱ABCD 是矩形 D .若AB=AD ,则▱ABCD 是正方形9.如图,由四个全等的直角三角形拼成的图形,设CE a =,HG b =,则斜边BD 的长是( )A .+a bB .⋅a b C.222a b +D .222a b - 10.如图,已知BD 是ABC 的角平分线,ED 是BC 的垂直平分线,90BAC ∠=︒,3AD =,则CE 的长为( )A .6B .5C .4D .33二、填空题(本大题共6小题,每小题3分,共18分)1.如图,数轴上点A 表示的数为a ,化简:a 244a a +-+=________.2.不等式组34012412x x +≥⎧⎪⎨-≤⎪⎩的所有整数解的积为__________. 3.计算:()()201820195-252+的结果是________.4.如图,把△ABC 绕点C 按顺时针方向旋转35°,得到△A ’B ’C ,A ’B ’交AC 于点D ,若∠A ’DC=90°,则∠A= °.5.如图,△ABC 中,AB=BC ,∠ABC=90°,F 为AB 延长线上一点,点E 在BC上,且AE=CF ,若∠BAE=25°,则∠ACF=__________度.6.如图,在平行四边形ABCD 中,连接BD ,且BD =CD ,过点A 作AM ⊥BD 于点M ,过点D 作DN ⊥AB 于点N ,且DN =32,在DB 的延长线上取一点P ,满足∠ABD =∠MAP +∠PAB ,则AP =________.三、解答题(本大题共6小题,共72分)1.解方程:(1)2(1)30x +-= (2)4(2)3(2)x x x +=+2.先化简,再求值:(x +2)(x -2)+x(4-x),其中x =14.3.已知方程组137x y a x y a-=+⎧⎨+=--⎩中x 为非正数,y 为负数. (1)求a 的取值范围;(2)在a 的取值范围中,当a 为何整数时,不等式221ax x a ++>的解集为1x <?4.如图,在▱ABCD 中,E 是BC 的中点,连接AE 并延长交DC 的延长线于点F .(1)求证:AB=CF;(2)连接DE,若AD=2AB,求证:DE⊥AF.5.如图,将两个全等的直角三角形△ABD、△ACE拼在一起(图1).△ABD不动,(1)若将△ACE绕点A逆时针旋转,连接DE,M是DE的中点,连接MB、MC (图2),证明:MB=MC.(2)若将图1中的CE向上平移,∠CAE不变,连接DE,M是DE的中点,连接MB、MC(图3),判断并直接写出MB、MC的数量关系.(3)在(2)中,若∠CAE的大小改变(图4),其他条件不变,则(2)中的MB、MC的数量关系还成立吗?说明理由.6.某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.(1)该商家购进的第一批衬衫是多少件?(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?参考答案一、选择题(本大题共10小题,每题3分,共30分)1、C2、D3、A4、B5、D6、C7、D8、C9、C10、D二、填空题(本大题共6小题,每小题3分,共18分)1、2.2、0324、55.5、706、6三、解答题(本大题共6小题,共72分)1、(1)11x =,21x =;(2)12x =-,243x =.2、-3.3、(1)a 的取值范围是﹣2<a ≤3;(2)当a 为﹣1时,不等式2ax+x >2a+1的解集为x <1.4、略.5、(1)略;(2)MB =MC .理由略;(3)MB =MC 还成立,略.6、(1)120件;(2)150元.。
北师大版八年级下册数学期末试卷及答案【完美版】
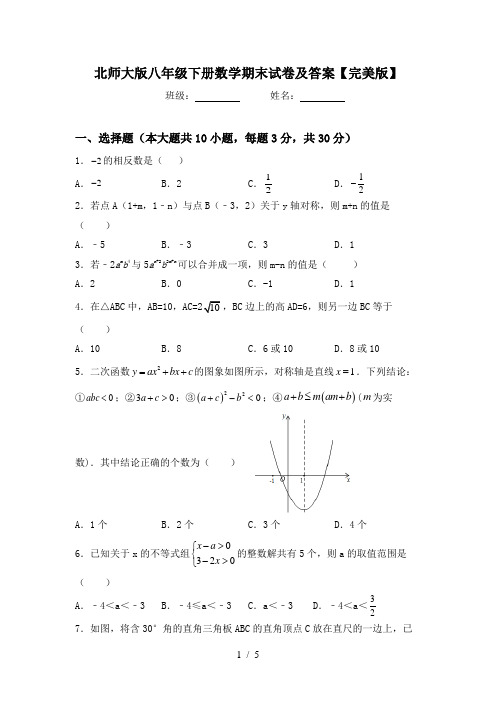
北师大版八年级下册数学期末试卷及答案【完美版】 班级: 姓名:一、选择题(本大题共10小题,每题3分,共30分)1.2-的相反数是( )A .2-B .2C .12D .12- 2.若点A (1+m ,1﹣n )与点B (﹣3,2)关于y 轴对称,则m+n 的值是( )A .﹣5B .﹣3C .3D .13.若﹣2a m b 4与5a n +2b 2m +n 可以合并成一项,则m-n 的值是( )A .2B .0C .-1D .14.在△ABC 中,AB=10,AC=210,BC 边上的高AD=6,则另一边BC 等于( )A .10B .8C .6或10D .8或105.二次函数2y ax bx c =++的图象如图所示,对称轴是直线1x =.下列结论:①0abc <;②30a c +>;③()220a c b +-<;④()a b m am b +≤+(m 为实数).其中结论正确的个数为( )A .1个B .2个C .3个D .4个6.已知关于x 的不等式组0320x a x ->⎧⎨->⎩的整数解共有5个,则a 的取值范围是( )A .﹣4<a <﹣3B .﹣4≤a <﹣3C .a <﹣3D .﹣4<a <327.如图,将含30°角的直角三角板ABC 的直角顶点C 放在直尺的一边上,已知∠A=30°,∠1=40°,则∠2的度数为( )A.55°B.60°C.65°D.70°8.下列图形中,不是轴对称图形的是()A.B.C.D.9.如图,在下列条件中,不能证明△ABD≌△ACD的是().A.BD=DC,AB=AC B.∠ADB=∠ADC,BD=DCC.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC10.如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是()A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD二、填空题(本大题共6小题,每小题3分,共18分)1.若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是______.2x1-x的取值范围是▲.3x2-x的取值范围是________.4.如图,将三个同样的正方形的一个顶点重合放置,那么1∠的度数为__________.5.如图,圆柱形玻璃杯高为14cm ,底面周长为32cm ,在杯内壁离杯底5cm 的点B 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm 与蜂蜜相对的点A 处,则蚂蚁从外壁A 处到内壁B 处的最短距离为___________cm (杯壁厚度不计).6.如图,四边形ABCD 中,∠A=90°,AB=33,AD=3,点M ,N 分别为线段BC ,AB 上的动点(含端点,但点M 不与点B 重合),点E ,F 分别为DM ,MN 的中点,则EF 长度的最大值为 .三、解答题(本大题共6小题,共72分)1.解方程23111x x x -=--.2.先化简,再求值:(x +2)(x -2)+x(4-x),其中x =14.3.已知,a 、b 互为倒数,c 、d 互为相反数,求31ab c d -+的值.4.如图,在四边形ABCD中,AB DC,AB AD=,对角线AC,BD交于点O,AC平分BAD⊥交AB的延长线于点E,连接OE.∠,过点C作CE AB(1)求证:四边形ABCD是菱形;(2)若5BD=,求OE的长.AB=,25.如图,▱ABCD的对角线AC,BD相交于点O,点E、F在AC上,且AF=CE.求证:BE=DF.6.某商场一种商品的进价为每件30元,售价为每件40元.每天可以销售48件,为尽快减少库存,商场决定降价促销.(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;(2)经调查,若该商品每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?参考答案一、选择题(本大题共10小题,每题3分,共30分)1、B2、D3、A4、C5、C6、B7、D8、A9、D10、D二、填空题(本大题共6小题,每小题3分,共18分)1、8≥.2、x1≥3、x24、20°.5、206、3三、解答题(本大题共6小题,共72分)x=1、22、-3.3、0.4、(1)略;(2)2.5、略.6、(1)两次下降的百分率为10%;(2)要使每月销售这种商品的利润达到510元,且更有利于减少库存,则商品应降价2.5元.。
北师大版八年级数学下册期末试卷(附答案)
北师大版八年级数学下册期末试卷(附答案) 班级: 姓名: 一、选择题(本大题共10小题,每题3分,共30分)1.若2n +2n +2n +2n =2,则n=( )A .﹣1B .﹣2C .0D .14 2.若12x y x -=有意义,则x 的取值范围是( ) A .1x 2≤且x 0≠ B .1x 2≠ C .1x 2≤ D .x 0≠3.在实数|﹣3|,﹣2,0,π中,最小的数是( )A .|﹣3|B .﹣2C .0D .π4.已知关于x 的分式方程21m x -+=1的解是负数,则m 的取值范围是( ) A .m ≤3 B .m ≤3且m ≠2C .m <3D .m <3且m ≠2 5.下列说法中,错误的是( )A .不等式x <5的整数解有无数多个B .不等式x >-5的负整数解集有有限个C .不等式-2x <8的解集是x <-4D .-40是不等式2x <-8的一个解6.欧几里得的《原本》记载,形如22x ax b +=的方程的图解法是:画Rt ABC ∆,使90ACB ∠=,2a BC =,AC b =,再在斜边AB 上截取2a BD =.则该方程的一个正根是( )A .AC 的长B .AD 的长C .BC 的长D .CD 的长7.如图,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y 与n 之间的关系是( )A .y=2n+1B .y=2n +nC .y=2n+1+nD .y=2n +n+18.如图是一张直角三角形的纸片,两直角边AC =6 cm 、BC =8 cm ,现将△ABC 折叠,使点B 与点A 重合,折痕为DE ,则BE 的长为( )A .4 cmB .5 cmC .6 cmD .10 cm9.如图,△ABC 中,BD 是 ∠ ABC 的角平分线,DE ∥ BC ,交AB 于 E ,∠A=60º, ∠BDC=95º,则∠BED 的度数是( )A .35°B .70°C .110°D .130°10.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S 1,S 2,则S 1+S 2的值为( )A .16B .17C .18D .19二、填空题(本大题共6小题,每小题3分,共18分)1.因式分解:2()4()a a b a b ---=________.2.如果一个直角三角形的两条直角边的长分别为5、12,则斜边上的高的长度为__________.3.当直线()223y k x k =-+-经过第二、三、四象限时,则k 的取值范围是________.4.如图所示,一次函数y=ax+b 的图象与x 轴相交于点(2,0),与y 轴相交于点(0,4),结合图象可知,关于x 的方程ax+b=0的解是________.5.如图,已知△ABC 是等边三角形,点B 、C 、D 、E 在同一直线上,且CG=CD ,DF=DE ,则∠E=________度.6.如图,在等边三角形ABC 中,BD=CE,AD,BE 交于点F,则AFE ∠=____________;三、解答题(本大题共6小题,共72分)1.解下列方程组:(1)75331x y x y +=⎧⎨+=⎩; (2)()346126x y y x y y ⎧+-=⎪⎨+-=⎪⎩.2.先化简,再求值[(x 2+y 2)-(x-y )2+2y (x-y )]÷2y ,其中x=-2,y=-12.3.解不等式组3(2)2513212x xxx+≥+⎧⎪⎨+-<⎪⎩,并把不等式组的解集在数轴上表示出来.4.如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x 轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标.5.如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A在x轴上,AB=AC,∠BAC=90°,且A(2,0)、B(3,3),BC交y轴于M,(1)求点C的坐标;(2)连接AM,求△AMB的面积;(3)在x轴上有一动点P,当PB+PM的值最小时,求此时P的坐标.6.在我市某一城市美化工程招标时,有甲、乙两个工程队投标,经测算:甲队单独完成这项工程需要60天,若由甲队先做20天,剩下的工程由甲、乙合作24天可完成.(1)乙队单独完成这项工程需要多少天?(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成工程省钱?还是由甲乙两队全程合作完成该工程省钱?参考答案一、选择题(本大题共10小题,每题3分,共30分)1、A2、A3、B4、D5、C6、B7、B8、B9、C10、B二、填空题(本大题共6小题,每小题3分,共18分)1、()()()22a b a a -+-2、60133、13k <<.4、x=25、:略6、60°三、解答题(本大题共6小题,共72分)1、(1) 52x y =⎧⎨=⎩;(2) 20x y =⎧⎨=⎩2、2x-y ;-312.3、–1≤x <34、E (4,8) D (0,5)5、(1)C 的坐标是(﹣1,1);(2)154;(3)点P 的坐标为(1,0).6、(1)乙队单独完成需90天;(2)在不超过计划天数的前提下,由甲、乙合作完成最省钱.。
新北师大版八年级数学下册期末测试卷(附答案)
新北师大版八年级数学下册期末测试卷(附答案) 班级: 姓名: 一、选择题(本大题共10小题,每题3分,共30分)1.4的平方根是( )A .±2B .2C .﹣2D .162.估计7+1的值( )A .在1和2之间B .在2和3之间C .在3和4之间D .在4和5之间3.若x ,y 的值均扩大为原来的3倍,则下列分式的值保持不变的是( )A .2x x y +-B .22y xC .3223y xD .222()y x y - 4.把38a 化为最简二次根式,得 ( )A .22a aB .342aC .322aD .24a a5.方程组33814x y x y -=⎧⎨-=⎩的解为( ) A .12x y =-⎧⎨=⎩ B .12x y =⎧⎨=-⎩ C .21x y =-⎧⎨=⎩ D .21x y =⎧⎨=-⎩6.如图,直线y=ax+b 过点A (0,2)和点B (﹣3,0),则方程ax+b=0的解是( )A .x=2B .x=0C .x=﹣1D .x=﹣37.下面是一位同学做的四道题:①222()a b a b +=+;②224(2)4a a -=-;③532a a a ÷=;④3412a a a ⋅=,其中做对的一道题的序号是( )A .①B .②C .③D .④8.如图,将长方形纸片ABCD 折叠,使边DC 落在对角线AC 上,折痕为CE ,且D 点落在对角线D ′处.若AB=3,AD=4,则ED 的长为( )A .32B .3C .1D .43 9.如图将直尺与含30°角的三角尺摆放在一起,若120∠=︒,则2∠的度数是( )A .30B .40︒C .50︒D .60︒10.下列选项中,不能判定四边形ABCD 是平行四边形的是( )A .AD //BC ,AB //CDB .AB //CD ,AB CD =C .AD //BC ,AB DC = D .AB DC =,AD BC =二、填空题(本大题共6小题,每小题3分,共18分)1.已知a 、b 满足(a ﹣1)22b +,则a+b=________.2.将二次函数245y x x =-+化成2()y a x h k =-+的形式为__________.3.若关于x 的分式方程2222x m m x x+=--有增根,则m 的值为_______. 4.如图,矩形ABCD 中,AB=3,BC=4,点E 是BC 边上一点,连接AE ,把∠B 沿AE 折叠,使点B 落在点B'处,当CEB'△为直角三角形时,BE 的长为______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北师八数学(下)期末测试题(A)
河北饶阳县第二中学 郭杏好 053900
一、选择题(每小题3分,共24分)
1.若47xyx,那么xy的值是( )
A.32 B.43
C.34 D.23
2.如图1,已知△ABC中,DE∥BC,AD=3,DB=2,则DE∶BC的值是( )
图1
A.3∶2 B.3∶5
C.3∶5 D.9∶25
3.已知△ABC中,D是AC上一点,连接BD,∠DBC=∠A,若BC=6,AC=3,
则CD等于( )
A.1 B.32
C.2 D.25
4.一个样本分成5个组,第一、二、三组中共有19个数据,第三、四、五组共有23
个数据,并且第三组的频率是0.2,则第三组的频数是( )
A.5 B.6
C.7 D.8
5.已知数据5、6、7、8、9,则这组数据的标准差为( )
A.4 B.1
C.2 D.2
6.甲、乙两组数据的方差分别是1.12和8.11,下列说法中正确的是( )
A.甲、乙波动大小一样
B.甲的波动比乙的波动大
C.甲的波动比乙的波动小
D.甲、乙的波动大小关系不确定
7.下列命题,真命题是( )
A.若a=0,则ab=0
B.若ab=0,则a=0
C.大于直角的角是钝角
D.直角三角形的两个锐角不相等
8.如果两条平行线被第三条直线所截,那么其中一组同旁内角的平分线( )
A.互相平行 B.互相垂直
C.互相重合 D.关系不确定
二、填空题(每小题3分,共30分)
9.已知点C在AB的延长线上,且AB∶AC=3∶5,则AB∶BC=________.
10.在△ABC中,∠ACB=90°,CD⊥AB于D,若AD=6,BD=2,则BC的长为________.
11.如图2,ABCD的边AD上一点E,DE=n1AD,连接CE,交对角线BD于F,
则DF∶DB=________.
图2
12.已知一组数据-2,-1,0,x,1的平均数是零,则这组数据的方差是________.
13.甲、乙两人比赛飞镖,两人所得平均环数相同,其中甲所得环数的方差为15,乙
所得的环数如下:0,1,5,9,10,那么成绩较为稳定的是________(填“甲”或“乙”).
14.如图3,∠B=∠C,∠ADE=110°,则∠A的度数为________.
图3
15.如图4,在△ABC中,∠A=40°,延长BC到D,作DF⊥AB,垂足为F,若∠D
=43°,则∠ACB的度数为________.
图4
16.如图5,在△ABC中,∠ABC=∠C=2∠A,BD⊥AC,垂足为D,则∠DBC的度
数是________.
图5
18.已知一次函数y=kx+2(k≠0),当K___________,y 随x的增大而减小.
三、解答题(共54分)
19.(10分)如图6,正方形ABCD的边长为1,P是CD边的中点,点Q在边BC上,
问:当BQ为何值时,△ADP∽△QCP.
图6
20.(12分)为了了解某校九年级300名男学生的身体发育情况,从中对20名男学
生的身高进行了测量,结果如下:(单位:厘米)
175 161 171 176 167 181 161 173 171 177 179 172 165 157 173
173 166 177 169 181
下表是根据上述数据填写的频数分布表的一部分:
分 组 频数累计 频 数 频 率
56.5~161.5 3 0.15
161.5~166.5 2 0.10
166.5~171.5 4 0.20
171.5~176.5 正正 0.30
176.5~181.5 正 5
合 计 20 1.00
(1)请填写表中未完成的部分.
(2)样本数据中,男生身高的众数是多少?
(3)该校九年级男学生身高在171.5~176.5(厘米)范围内的人数为多少?
(4)根据频数分布表,绘制频数分布直方图.
21(12分).某农科所为了考察两个品种的棉苗生长高度的情况,从甲、乙两种棉苗中
各抽出10株,测得它们的株高分别如下(单位:厘米):
甲:27 27 44 16 44 36 38 40 42 30
乙:28 46 30 32 44 46 24 18 28 48
(1)分别计算两种棉苗的平均苗高.
(2)哪种棉苗长势比较整齐?
22(10分).已知:如图7,AD平分∠BAC,∠BFE=∠DAC.
图7
求证:∠BFE=∠G.
23(10分).如图8,在△ABC中,AD是高,BE平分∠ABC,∠ABE=20°,∠DAC=
30°,求∠C及∠BEC的度数.
图8
四、综合探索题(12分)
24.(12分)在方格纸中,每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点
三角形,请你在图10×10的方格纸中,画出两个相似但不全等的格点三角形,并加以说明.
要求:所画的三角形是钝角三角形,并标明相应字母.
图9
参考答案
一、1.B 2.B 3.C 4.C 5.C 6.C 7.A 8.B
二、9.3∶2 10.4 11.1∶(n+1) 12.2
13.甲 14.70° 15.93° 16.18° 17. 18.k<0
三、19.(1)0或43新 课标 第一 网
20.(1)6 0.25 (2)173 cm (3)90人 (4)略
21.(1)甲30厘米 乙34.4厘米
(2)甲种棉苗较整齐
22.略
23.60° 100°
24.略
新课标第一网
