苏教版八上数学1.3探索三角形全等的条件(4)教案
苏科版数学八年级上册1.3《探索三角形全等的条件》教学设计7

苏科版数学八年级上册1.3《探索三角形全等的条件》教学设计7一. 教材分析《探索三角形全等的条件》是苏科版数学八年级上册1.3的教学内容。
本节课主要让学生通过探究三角形全等的条件,理解并掌握SAS(边角边)、ASA(角边角)、AAS(角角边)三种全等判定方法,能运用这些方法解决实际问题。
教材通过丰富的图片和实例,引导学生观察、操作、思考,从而发现并证明三角形全等的条件。
二. 学情分析八年级的学生已经学习了相似三角形的性质,对图形的变换有一定的了解。
但全等三角形与相似三角形既有联系又有区别,学生需要通过实例和证明来进一步理解全等三角形的性质。
此外,学生需要具备一定的观察能力、操作能力和逻辑思维能力,才能更好地掌握本节课的内容。
三. 教学目标1.知识与技能目标:让学生掌握三角形全等的条件,能运用SAS、ASA、AAS三种方法判断三角形全等。
2.过程与方法目标:通过观察、操作、思考、交流、证明等过程,培养学生的观察能力、操作能力和逻辑思维能力。
3.情感态度与价值观目标:让学生体验数学与生活的联系,增强对数学的兴趣和信心。
四. 教学重难点1.重点:三角形全等的条件,SAS、ASA、AAS三种全等判定方法。
2.难点:三角形全等条件的证明,全等方法在实际问题中的应用。
五. 教学方法1.情境教学法:通过丰富的图片和实例,激发学生的学习兴趣,引导学生观察、思考。
2.问题驱动法:提出问题,引导学生进行探究、证明,培养学生的逻辑思维能力。
3.合作学习法:分组讨论、操作,让学生在合作中发现问题、解决问题,提高学生的交流能力。
4.实践教学法:让学生动手操作,加深对全等三角形性质的理解。
六. 教学准备1.教学课件:制作课件,展示三角形全等的实例和证明过程。
2.教学素材:准备一些三角形模型和图片,用于引导学生观察和操作。
3.教学设备:多媒体投影仪、白板、黑板等。
七. 教学过程1.导入(5分钟)利用课件展示一些生活中的三角形图片,如:金字塔、自行车架等,引导学生观察并思考:这些三角形有什么共同特点?怎样才能判断两个三角形全等?2.呈现(10分钟)呈现三角形全等的实例,引导学生进行观察和操作。
苏教版八上数学13探索三角形全等的条件教案
注意:利用SSS来证明两个三角形全等时,要找准对应边,同时要找出隐含的等边,如公共边等;
知识点二:三角形的稳定性
自学课本第23页内容,交流一下:什么是三角形的稳定性?什么是四边形的不稳定性?
〖教材解读〗
1、三角形的稳定性:三角形的三边确定后,则这个三角形的形状和大小也随之确定,这就是三角形的稳定性。这是三角形特有的性质,而四边形、五边形以及其他多边形都不具有这样的性质。在日常生活中,人们常利用三角形的稳定性来解决问题,当然,四边形的不稳定性在生活中的应用也很广泛。
八年级上学期数学教案
主备人:
备课
时间
13.9.5
上课
时间
13.9.11
教学
课题
1.3探索三角形全等的条件(6)
教时
计划
6/8
教学
目标
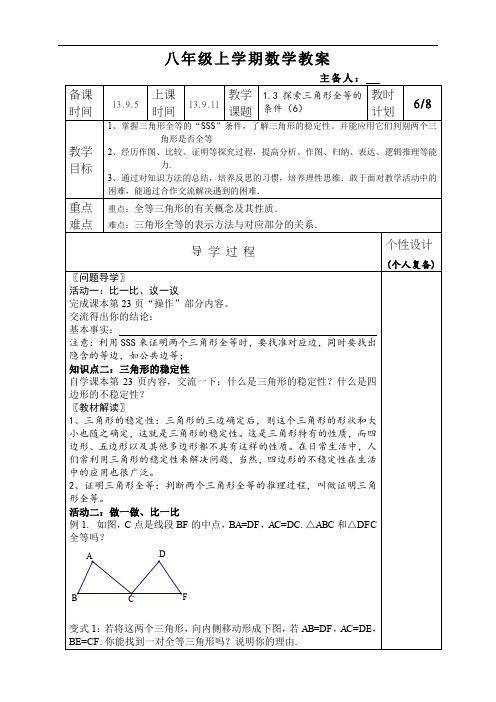
1、掌握三角形全等的“SSS”条件,了解三角形的稳定性。并能应用它们判别两个三角形是否全等
2、经历作图、比较、证明等探究过程,提高分析、作图、归纳、表达、逻辑推理等能力.
小组讨论一下,你对例2的理解,并交流:什么是辅助线?为什么要添加辅助线?
反馈练习:课本第26页练一练的1、2
〖收获体会〗
你在这节课学到了哪些知识?
〖板书设计〗
作业
1、补充习题
2、伴你学
教后
笔记
2、证明三角形全等:判断两个三角形全等的推理过程,叫做证明三角形全等。
活动二:做一做、比一比
例1.如图,C点是线段BF的中点,BA=DF,AC=DC.△ABC和△DFC全等吗?
变式1:若将这两个三角形,向内侧移动形成下图,若AB=DF,AC=DE,BE=CF.你能找到一对全等三角形吗?说明你的理由.
苏科版八年级上册 1.3 探索三角形全等的条件HL 学案(无答案)

1.3探索三角形全等的条件⑸【教学目标】学习目标:⒈理解“HL ”的条件,并运用“HL ”判别两个直角三角形全等; ⒉了解特殊与一般的关系,培养辩证的思维方法;学习重点:理解“HL ”的条件,并运用“HL ”判别两个直角三角形全等 【教学过程】 (一)感情调节(二)自学 (一)、自学导航1.直角三角形是特殊的三角形,可记△Rt,要使两个直角三角形全等,需要有那些边或角相等呢?2.如图1,AD 是△AB C 的边BC 上的高,再加一个条件,就可以根据“HL ”得到△ABD ≌△ACD 。
3.如图2,AC ⊥AB ,DF ⊥DE ,AC=DF ,再加一个条件,就可以根据“HL ”得到△ABC ≌△DEF 。
4.如图3,AB ⊥BC ,AC=BD ,当CD 与BC 互相,就可以根据“HL ”得到△ABC ≌△DCB 。
(二)、小组合作探究:各小组交流,你们所画的直角三角形全等吗?结论:1.如图,AC ⊥BC ,AD ⊥BD ,垂足分别为C 、D ,AC=BD ,Rt △ABC 与Rt △BAD 全等吗?为什么?2.如图,已知∠ACB =∠BDA =90°,若要使△ACB ≌△BDA ,还需要什么条件?把它们分别写出来。
【典型例题】例1 如图,B 、E 、F 、C 在同一直线上,AE ⊥BC ,DF ⊥BC ,AB=DC ,BE=CF ,试判断AB 与CD 的位置关系. 例2 已知 如图,AB ⊥BD ,CD ⊥BD ,AB=DC ,求证:AD ∥BC.例3 公路上A 、B 两站(视为直线上的两点)相距26km ,C 、D 为两村庄(视为两个点),DA ⊥AB 于点A ,CB⊥AB 于点B ,已知DA=16km ,BC=10km ,现要在公路AB 上建一个土特产收购站E ,使CD两村庄到E 站的距离相等,那么E 站应建在距A 站多远才合理?图3 A B C D A B D C 图1 F E B CDA图2 BC例4 如图,AD 是△ABC 的高,E 为AC 上一点,BE 交AD 于F ,具有BF=AC ,FD=CD ,试探究BE 与AC 的位置关系.例5 如图,A 、E 、F 、B 四点共线,AC ⊥CE 、BD ⊥DF 、AE=BF 、AC=BD ,求证:△ACF ≌△BDE.(三)、自我总结,提出质疑(四)、课堂训练:一、请判断满足下列条件的两个直角三角形是否全等,若不全等,在括号内打“×”,若全等,在括号内注明理由。
新苏科版八年级数学上册1.3探索三角形全等的条件(三)教案

复习旧知识,猜想新知识,为本节课做好铺垫。
让学生自己动手验证,通过验证得到初步的猜想。
让学生感受一个三角形有两个角和夹边确定,这个三角形的形状和大小就唯一确定。
教
学
过
程
探(1)你所画的两个三角形是唯一的吗?
(2)你画的两个三角形与其他同学画的能完全重合吗?
掌握三角形全等的条件“ASA”,并能利用它们判定三角形是否全等.
教学难点:
探索三角形全等的条件“ASA”的过程及应用
教学设计:
设计说明及补充:
情
境
导
入
同学们,经过前面内容的学习,我们了解到:
(1)要证明两个三角形全等,需要几个条
件?
(2)上节课我们学习了哪些条件可以构成
全等?你能用几何语言描述吗?
(3)请你们猜想,构成全等还有哪些条件
新苏科版八年级数学上册1.3 探索三角形全等的条件(三)教案
教学目标:
1.掌握三角形全等的条件“ASA”.
2.会利用“ASA”进行有条理的思考和简单的推理.
3.通过多种手段的活动过程,让学生动手操作,激发学生学习的兴趣,并能通过合作交流解决问题,体会数学在现实生活中的应用,增强学生的自信心.
教学重点:
尝试交流
P19练习1、2
巩固练习
P18例4
分析:(1)要证BE=DF,DE=CF,具备了哪些条件?
(2)还缺什么条件?
(3)获得所缺条件的依据是什么?
小结
这节课你学到了什么?哪些三个条件的组合是你还想去探索求证的?
课堂作业
补充练习1.3 探索三角形全等的条件(三)
板书设计:
教学反思:
苏教版八上数学13探索三角形全等的条件(3)教案.doc
八年级上学期数学教案主备人:张东林备课时间13.8.30上课时间13.9.5教学课题1.3探索三角形全等的条件(3 )教时计划3/8教学目标1.探索出三角形全等的“角边角”的条件;在过程中感受知识、总结规律;2.理解ASA的内容,能运用ASA全等识别法来识别三角形全等,进而说明线段或角相等;3.探索出AAS的三角形全等识别方法及其它的应用.重点难点教学重点:公理的发现教学难点:有条理的思考和进行推理:应用“ASA”和“AAS”去判断三角形全等导学过程个性设计(个人复备)I问题导学]活动一:每个学生用硬纸板任意剪一个三角形,如图把三角形纸板撕成两部分。
尝试利用其中的一部分能否再剪一个与原三角形全等的三角形?观察:1.从上面的实践中容易发现利用第II部分可以剪出与原来三角形全等的三角形。
观察、比较第I、II两部分有什么不同?2.第二次剪出来的三角形与原三角形的第II部分,有哪些边和角是重合的?3:从利用第II部分可以剪出与原三角形全等的三角形的事实中,你得到什么启发?活动二:做一做、想一想课本18页中的“做一做”(1)画线段AB=2cm, ZBAP = 45°,ZABQ = 60°,AP 与BQ 相交于点C;(2)剪下所画的AABC,与同学所画的三角形能重合吗?由此可得结论 __________________________________________ 。
活动三:仿写在AABC 和△MNP 中,ZA = ZM,ZB = ZN,BC = NP,AABC ^NP吗?结论:______________通常写成下面的格式:在AABC与ADEF中,ZB = ZE\BC = EFA AABC^ADEF (ASA) 活动四:教学例题例41.如右图,0是4B的中点,ZA=ZB 问题1: AABC和/XADC全等吗?问题2:它们已经有了哪些元素对应相等?问题3 :还缺什么条件?思考:若将第一题中的ZA=ZB改为ZC=ZD,其他条件不变,你还能得到△40C仝△BOD吗?结论:.2.如图,AB=AC, ZB=ZC, 试说明△ ABE^AACD全等思考:如果将上题中的AB=AC改为AD=AE,其他条件不变,你能说明AB=AC吗?反馈练习:课本第19页练一练的1, 20K收获体会H你在这节课学到了哪些知识?K板书设计H1、补充习题作业2、伴你学教后笔记。
苏科版八年级数学上册教案:1.3探索三角形全等的条件1.doc

1.3探索三角形全等的条件(1)总课时数 8第丄课时主备教师 朱玲 参备教师 朱秋阳 教学目标 1. 会利用基本事实:“边角边”判别两个三角形是否全等.2. 在探索三角形全等条件及其基本事实“边角边”运用的过程中能够进行有条理的思 考并进行简单的推理.教学重、难点利用基本事实:“边角边”判别两个三角形是否全等。
教学 设 计 一、 板书课题过渡语:同学们今天我们来学习1.3探索三角形全等的条件(1)(板书)二、 出示目标(一)过渡语:我们要达到什么目标呢?请看: (二) 出示目标 1. 会利用基本事实:“边角边”判别两个三角形是否全等.2. 在探索三角形全等条件及其基本事实“边角边”运用的过程中能够进行有条理的思考并进行简 单的推理.三、 自学指导(一)过渡语:怎样才能达到当堂目标呢?请同学们按照指导认真自学。
(二) 出示自学指导自学指导认真看课本P (13-14)要求:1. 回答“讨论”的几个问题。
2. 回答“交流”的第2小问。
3. 熟记两个三角形全等的一个基本事实;4. 认真看例1,注意解题过程,解题格式;8分钟后看谁能又快又准的回答上面几个问题并仿照例题完成检测题。
.先学(一)学生自学,督促每一位学生认真自学。
(二)检测1.过渡语:能回答上面几个问题的请举手。
教师提问2.过渡语:上面的问题同学们都能答上来了,那能不能正确应用呢?请看检测题。
1.完成练一练第1题。
2.已知:如图,AB=AC,点D、E分别在AB、AC上,且AD=AE.求证:AABE 竺AACD B要求:1.8分钟后独立完成。
c2.注意解题规范,格式正确。
分别请两位同学说出答案,其他同学做到练习本上。
学生练习,教师巡视。
五、后教(一)先交换练习本后更正请同学们认真看堂上板演的内容,能发现错误并能更正的请举手。
(指明尖子生更正)(二)讨论:(先让尖子生“兵教兵”)尖子生讲的不对或不全的,教师更正或补充)2.评:引导学生说出:(三)同桌互改,按满分100分得出相应分数,讨论并纠正座位上同学中存在的不同错误。
苏科版-数学-八年级上册-1.3 探索三角形全等的条件(第一课时)教案
1.3 探索三角形全等的条件(第一课时)一、教学目标:1、让学生懂得三角形全等必须具备三个条件理解“边角边”公理,学会用它来判定两个三角形全等。
2、让学生学会有条理地思考、分析、解决问题的能力,培养学生推理、应用能力和空间想象能力。
3、让学生学会大胆探索、善于归纳、应用、培养学生个性,优化学生数学思维品质。
二、教学重难点:重点:掌握三角形全等的“边角边”条件。
难点:正确运用“边角边”条件判定三角形全等,解决实际问题。
三、教学方法:引导探索法,讲练结合,探索交流。
四、教学过程:(一)创设情境,感悟新知复习:(1)如果两个三角形全等,那么它们的对应边和对应角有什么关系?(2)两个三角形需要具备什么条件,即它们有多少组边或角分别相等时就全等?提问:(1)当两个三角形只有1组边或角相等时,它们全等吗?(2)当两个三角形只有2组边或角相等时,它们全等吗?(3)当两个三角形有3组边或角相等时,它们全等吗?讨论:从三角形的6个元素中任意选出其中的3个元素,共有多少种不同的选法?(二)探索活动,揭示新知活动一 P139做一做(1)任意剪一个直角三角形,同学们得到的三角形全等吗?(2)重新剪一个直角三角形,要使得全班同学剪下的都全等,你能做到吗?说说看C(1)用仿照书本第137页的图12-7给出的几个三角形的图片,请学生先猜想:哪两个三角形全等?(2)验证你的猜想。
活动三 按条件画三角形(1)用书本所说的方法画三角形。
(2)将所得的三角形剪下,并与同学进行比较,你得出什么结论?通过上面几个活动你对三角形全等所需要的条件有什么看法?你能语言将它叙述一下?结论:两边和它们的夹角对应相等的两个三角形全等。
简写成“边角边”或“SAS ”。
(三)例题分析,领悟新知例1 如图, AB=AD ,∠BAC=∠DAC ,请问:△ABC 和△ADC 是否全等?为什么?提问:1、△ABC 和△ADC 全等吗?它们已经有了哪些元素对应相等?还缺什么条件?如何正确的书写证明过程?(示范)2、如果把△ABC 与△ADC 拉开如图形状,若要使得它们全等,还需要什么条件?(四)拓展延伸,运用新知1、分别找出各题中的全等三角形,并说明理由。
苏科初中数学八上《1.3 探索三角形全等的条件》word教案 (27)
(3)归纳、整理.
请你用文字语言归纳你证明的结论?用几何语言表述你的结论.
3.探索活动二.
(1)如图,已知∠ACB=∠BDA=90°,能否判定△ACB≌△BDA?若不能,请增加一个条件使得△ACB≌△BDA,把它们分别写出来,并注明你所用的判定定理.
探索三角形全等的条件
课题:
1.3 探索三角形全等的条件
课时:
1
课型:
新授课
教学目标:
1.利用尺规作图,掌握已知斜边、直角边画直角三角形的画图方法;
2.经历操作、实验、观察、归纳,证明斜边、直角边(HL)定理;
3.运用HL定理及其他三角形全等的判定方法进行证明和计算,发展演绎推理的能力.
教学重点:
“斜边、直角边”定理的证明和应用.
直角三角形是特殊的三角形,判定两个三角形全等,有没有特殊的方法?你有怎样的猜想?
2.探索活动一
P27操作 (1)思考、交流:
①△ABC就是所求作的三角形吗?②你作的直角三角形和其他同学所作的三角形能完全重合吗?③交流之后,你发现了什么?④想一想,在画图时是根据什么条件?它们重合的条件是什么?
(2)P21讨论
板书设计:
教学反思:
主备教师:
使用人:
使用时间:
(3)若AB=DE,BC=EF,则△ABC≌△DEF( ).
上面的每一小题,都只添加了两个条件,就使两个直角三角形全等,你还能添加哪两个不同的条件使这两个直角三角形全等?
问题2为斜边、直角边(HL)定理的证明作好铺垫,提供方法准备.问题3有一定的开放性,为引出斜边、直角边(HL)定理埋下伏笔,让学生感到自然,一切都是那样水到渠成。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
生态课堂教案 沂北中学八年级数学备课组
八年级上学期数学教案
主备人: 张东林
备课 时间 13.9.5 上课 时间 13.9.9 教学 课题 1.3探索三角形全等的条件(4) 教时
计划
4/8
教学
目标
1. 探索出三角形全等的 “角边角”的 条件;在过程中感受知识、总结规
律;
2. 理解ASA的内容,能运用ASA全等识别法来识别三角形全等,进而说明
线段或角相等;
3. 探索出AAS的三角形全等识别方法及其它的应用.
重点
难点
教学重点:公理的发现
教学难点:有条理的思考和进行推理:应用“ASA”和“AAS”去判断三角形全等
导 学 过 程
个性设计
(个人复备)
〖问题导学〗
活动一:比一比、想一想
观察下图中的三角形,先猜一猜,再量一量,哪两个三角形是全等三角
形?
仿做:画一个三角形△ABC,使得∠A=30°,∠B=60°,AC=2cm.
(请你把画出的三角形与同组比较,你有什么发现?)
活动二:想一想、做一做
如图,△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF
△ABC和△DEF全等吗?为什么?
得出基本事实:
两角分别相等且其中一组等角的对边相等的两个三角形全等。
可以简写成:角角边或AAS
仿写:用上节课的方法写出AAS的几何语言。
生态课堂教案 沂北中学八年级数学备课组
1
活动三:例5
例:如图:已知AE交BC于点D,∠1=∠2=∠3,
AB=AD.
求证:DC=BE。
证明:∵∠ADB=∠1+∠C,
∠ADB=∠3+∠E,
又∵∠1=∠3,
∴∠C=∠E。
在△ABE和△ADC中,
∵∠E =∠C,
∠2 =∠1,
AB =AD,
∴ △ABE≌△ADC(AAS)。
∴DC=BE。
解析:要证DC=BE,先观察DC与BE分别在可能全等的两个三角形中.
根据所给条件选择方法
反馈练习:
已知:△ABC≌△ABC,AD、AD分别是△ABC和△ABC的高,你认
为AD 等于AD吗?请说明理由。
A A
B D C B D C
学生独立思考
反馈练习:课本第21页练一练的1,2。
〖收获体会〗
你在这节课学到了哪些知识?
作业
1、补充习题
2、伴你学
教后
A
B
C
E
D
1
2
3
A
生态课堂教案 沂北中学八年级数学备课组
笔记
