矩形菱形正方形四边形练习
矩形菱形正方形(共39题)(解析版)--2023年中考数学真题分项汇编

矩形菱形正方形(39题)一、单选题1(2023·湖南·统考中考真题)如图,菱形ABCD中,连接AC,BD,若∠1=20°,则∠2的度数为()A.20°B.60°C.70°D.80°【答案】C【分析】根据菱形的性质可得BD⊥AC,AB∥CD,则∠1=∠ACD,∠ACD+∠2=90°,进而即可求解.【详解】解:∵四边形ABCD是菱形∴BD⊥AC,AB∥CD,∴∠1=∠ACD,∠ACD+∠2=90°,∵∠1=20°,∴∠2=90°-20°=70°,故选:C.【点睛】本题考查了菱形的性质,熟练掌握是菱形的性质解题的关键.2(2023·湖南常德·统考中考真题)如图1,在正方形ABCD中,对角线AC、BD相交于点O,E,F分别为AO,DO上的一点,且EF∥AD,连接AF,DE.若∠FAC=15°,则∠AED的度数为()A.80°B.90°C.105°D.115°【答案】C【分析】首先根据正方形的性质得到∠OAD=∠ODA=45°,AO=DO,然后结合EF∥AD得到OE= OF,然后证明出△AOF≌△DOE SAS,最后利用三角形内角和定理求解即可.【详解】∵四边形ABCD是正方形∴∠OAD=∠ODA=45°,AO=DO∵EF∥AD∴∠OEF=∠OAD=45°,∠OFE=∠ODA=45°∴∠OEF=∠OFE∴OE=OF又∵∠AOF=∠DOE=90°,AO=DO∴△AOF ≌△DOE SAS∴∠ODE =∠FAC =15°∴∠ADE =∠ODA -∠ODE =30°∴∠AED =180°-∠OAD -∠ADE =105°故选:C .【点睛】此题考查了正方形的性质,全等三角形的性质和判定,等腰直角三角形三角形的性质等知识,解题的关键是熟练掌握以上知识点.3(2023·湖南常德·统考中考真题)下列命题正确的是()A.正方形的对角线相等且互相平分B.对角互补的四边形是平行四边形C.矩形的对角线互相垂直D.一组邻边相等的四边形是菱形【答案】A 【分析】根据正方形、平行四边形、矩形、菱形的各自性质和构成条件进行判断即可.【详解】A 、正方形的对角线相等且互相垂直平分,描述正确;B 、对角互补的四边形不一定是平行四边形,只是内接于圆,描述错误;C 、矩形的对角线不一定垂直,但相等,描述错误;D 、一组邻边相等的平行四边形才构成菱形,描述错误.故选:A .【点睛】本题考查平行四边形、矩形、菱形、正方形的性质和判定,解题的关键是熟悉掌握各类特殊四边形的判定和性质.4(2023·浙江·统考中考真题)如图,在菱形ABCD 中,AB =1,∠DAB =60°,则AC 的长为()A.12B.1C.32D.3【答案】D 【分析】连接BD 与AC 交于O .先证明△ABD 是等边三角形,由AC ⊥BD ,得到∠OAB =12∠BAD =30°,∠AOB =90°,即可得到OB =12AB =12,利用勾股定理求出AO 的长度,即可求得AC 的长度.【详解】解:连接BD 与AC 交于O .∵四边形ABCD是菱形,∴AB∥CD,AB=AD,AC⊥BD,AO=OC=12AC,∵∠DAB=60°,且AB=AD,∴△ABD是等边三角形,∵AC⊥BD,∴∠OAB=12∠BAD=30°,∠AOB=90°,∴OB=12AB=12,∴AO=AB2-OB2=12-12 2=123,∴AC=2AO=3,故选:D.【点睛】此题主要考查了菱形的性质、勾股定理、等边三角形的判定和性质、30°角所对直角边等于斜边的一半,关键是熟练掌握菱形的性质.5(2023·上海·统考中考真题)在四边形ABCD中,AD∥BC,AB=CD.下列说法能使四边形ABCD 为矩形的是()A.AB∥CDB.AD=BCC.∠A=∠BD.∠A=∠D【答案】C【分析】结合平行四边形的判定和性质及矩形的判定逐一分析即可.【详解】A:∵AB∥CD,AD∥BC,AB=CD∴ABCD为平行四边形而非矩形故A不符合题意B:∵AD=BC,AD∥BC,AB=CD∴ABCD为平行四边形而非矩形故B不符合题意C:∵AD∥BC∴∠A+∠B=180°∵∠A=∠B∴∠A=∠B=90°∵AB=CD∴ABCD为矩形故C符合题意D:∵AD∥BC∴∠A+∠B=180°∵∠A=∠D∴∠D+∠B=180°∴ABCD不是平行四边形也不是矩形故D不符合题意故选:C.【点睛】本题主要考查平行线的性质,平行四边形的判定和性质及矩形的判定等知识,熟练掌握以上知识并灵活运用是解题的关键.6(2023·浙江宁波·统考中考真题)如图,以钝角三角形ABC 的最长边BC 为边向外作矩形BCDE ,连结AE ,AD ,设△AED ,△ABE ,△ACD 的面积分别为S ,S 1,S 2,若要求出S -S 1-S 2的值,只需知道()A.△ABE 的面积B.△ACD 的面积C.△ABC 的面积D.矩形BCDE 的面积【答案】C【分析】过点A 作FG ∥BC ,交EB 的延长线于点F ,DC 的延长线于点G ,易得:FG =BC ,AF ⊥BE ,AG⊥CD ,利用矩形的性质和三角形的面积公式,可得S 1+S 2=12S 矩形BCDE ,再根据S =S △ABC +S 矩形BCDE -S 1-S 2=S △ABC +12S 矩形BCDE ,得到S -S 1-S 2=S △ABC ,即可得出结论.【详解】解:过点A 作FG ∥BC ,交EB 的延长线于点F ,DC 的延长线于点G ,∵矩形BCDE ,∴BC ⊥BE ,BC ⊥CD ,BE =CD ,∴FG ⊥BE ,FG ⊥CD ,∴四边形BFGC 为矩形,∴FG =BC ,AF ⊥BE ,AG ⊥CD ,∴S 1=12BE ⋅AF ,S 2=12CD ⋅AG ,∴S 1+S 2=12BE AF +AG =12BE ⋅BC =12S 矩形BCDE ,又S =S △ABC +S 矩形BCDE -S 1-S 2=S △ABC +12S 矩形BCDE ,∴S -S 1-S 2=S △ABC +12S 矩形BCDE -12S 矩形BCDE =S △ABC ,∴只需要知道△ABC 的面积即可求出S -S 1-S 2的值;故选C .【点睛】本题考查矩形的性质,求三角形的面积.解题的关键是得到S 1+S 2=12S 矩形BCDE 7(2023·湖南·统考中考真题)如图所示,在矩形ABCD 中,AB >AD ,AC 与BD 相交于点O ,下列说法正确的是()A.点O 为矩形ABCD 的对称中心B.点O 为线段AB 的对称中心C.直线BD 为矩形ABCD 的对称轴D.直线AC 为线段BD 的对称轴【答案】A【分析】由矩形ABCD是中心对称图形,对称中心是对角线的交点,线段AB的对称中心是线段AB的中点,矩形ABCD是轴对称图形,对称轴是过一组对边中点的直线,从而可得答案.【详解】解:矩形ABCD是中心对称图形,对称中心是对角线的交点,故A符合题意;线段AB的对称中心是线段AB的中点,故B不符合题意;矩形ABCD是轴对称图形,对称轴是过一组对边中点的直线,故C,D不符合题意;故选A【点睛】本题考查的是轴对称图形与中心对称图形的含义,矩形的性质,熟记矩形既是中心对称图形也是轴对称图形是解本题的关键.8(2023·四川宜宾·统考中考真题)如图,边长为6的正方形ABCD中,M为对角线BD上的一点,连接AM并延长交CD于点P.若PM=PC,则AM的长为()A.33-1B.333-2C.63-1D.633-2【答案】C【分析】先根据正方形的性质、三角形全等的判定证出△ADM≅△CDM,根据全等三角形的性质可得∠DAM=∠DCM,再根据等腰三角形的性质可得∠CMP=∠DCM,从而可得∠DAM=30°,然后利用勾股定理、含30度角的直角三角形的性质求解即可得.【详解】解:∵四边形ABCD是边长为6的正方形,∴AD=CD=6,∠ADC=90°,∠ADM=∠CDM=45°,在△ADM和△CDM中,DM=DM∠ADM=∠CDM=45°AD=CD,∴△ADM≅△CDM SAS,∴∠DAM=∠DCM,∵PM=PC,∴∠CMP=∠DCM,∴∠APD=∠CMP+∠DCM=2∠DCM=2∠DAM,又∵∠APD+∠DAM=180°-∠ADC=90°,∴∠DAM=30°,设PD=x,则AP=2PD=2x,PM=PC=CD-PD=6-x,∴AD=AP2-PD2=3x=6,解得x=23,∴PM=6-x=6-23,AP=2x=43,∴AM=AP-PM=43-6-23=63-1,故选:C.【点睛】本题考查了正方形的性质、勾股定理、含30度角的直角三角形的性质、等腰三角形的性质等知识点,熟练掌握正方形的性质是解题关键.9(2023·四川乐山·统考中考真题)如图,菱形ABCD 的对角线AC 与BD 相交于点O ,E 为边BC 的中点,连结OE .若AC =6,BD =8,则OE =()A.2B.52C.3D.4【答案】B【分析】先由菱形的性质得AC ⊥BD ,OC =12AC =12×6=3,OB =12BD =12×8=4,再由勾股定理求出BC =5,然后由直角三角形斜边的中线等于斜边的一半求解.【详解】解:∵菱形ABCD ,∴AC ⊥BD ,OC =12AC =12×6=3,OB =12BD =128=4,∴由勾股定理,得BC =OB 2+OC 2=5,∵E 为边BC 的中点,∴OE =12BC =12×5=52故选:B .【点睛】本考查菱形的性质,勾股定理,直角三角形的性质,熟练掌握菱形的性质,直角三角形的性质是解题的关键.10(2023·甘肃武威·统考中考真题)如图,将矩形ABCD 对折,使边AB 与DC ,BC 与AD 分别重合,展开后得到四边形EFGH .若AB =2,BC =4,则四边形EFGH 的面积为()A.2B.4C.5D.6【答案】B【分析】由题意可得四边形EFGH 是菱形,FH =AB =2,GE =BC =4,由菱形的面积等于对角线乘积的一半即可得到答案.【详解】解:∵将矩形ABCD 对折,使边AB 与DC ,BC 与AD 分别重合,展开后得到四边形EFGH ,∴EF ⊥GH ,EF 与GH 互相平分,∴四边形EFGH 是菱形,∵FH =AB =2,GE =BC =4,∴菱形EFGH的面积为12FH⋅GE=12×2×4=4.故选:B【点睛】此题考查了矩形的折叠、菱形的判定和性质等知识,熟练掌握菱形的面积等于对角线乘积的一半是解题的关键.11(2023·浙江绍兴·统考中考真题)如图,在矩形ABCD中,O为对角线BD的中点,∠ABD=60°.动点E在线段OB上,动点F在线段OD上,点E,F同时从点O出发,分别向终点B,D运动,且始终保持OE =OF.点E关于AD,AB的对称点为E1,E2;点F关于BC,CD的对称点为F1,F2.在整个过程中,四边形E1E2F1F2形状的变化依次是()A.菱形→平行四边形→矩形→平行四边形→菱形B.菱形→正方形→平行四边形→菱形→平行四边形C.平行四边形→矩形→平行四边形→菱形→平行四边形D.平行四边形→菱形→正方形→平行四边形→菱形【答案】A【分析】根据题意,分别证明四边形E1E2F1F2是菱形,平行四边形,矩形,即可求解.【详解】∵四边形ABCD是矩形,∴AB∥CD,∠BAD=∠ABC=90°,∴∠BDC=∠ABD=60°,∠ADB=∠CBD=90°-60°=30°,∵OE=OF、OB=OD,∴DF=EB∵对称,∴DF=DF2,BF=BF1,BE=BE2,DE=DE1∴E1F2=E2F1∵对称,∴∠F2DC=∠CDF=60°,∠EDA=∠E1DA=30°∴∠E1DB=60°,同理∠F1BD=60°,∴DE1∥BF1∴E1F2∥E2F1∴四边形E1E2F1F2是平行四边形,如图所示,当E,F,O三点重合时,DO=BO,∴DE1=DF2=AE1=AE2即E1E2=E1F2∴四边形E1E2F1F2是菱形,如图所示,当E,F分别为OD,OB的中点时,设DB=4,则DF2=DF=1,DE1=DE=3,在Rt△ABD中,AB=2,AD=23,连接AE,AO,∵∠ABO=60°,BO=2=AB,∴△ABO是等边三角形,∵E为OB中点,∴AE⊥OB,BE=1,∴AE=22-12=3,根据对称性可得AE1=AE=3,∴AD2=12,DE21=9,AE21=3,∴AD2=AE21+DE21,∴△DE1A是直角三角形,且∠E1=90°,∴四边形E1E2F1F2是矩形,当F,E分别与D,B重合时,△BE1D,△BDF1都是等边三角形,则四边形E1E2F1F2是菱形∴在整个过程中,四边形E1E2F1F2形状的变化依次是菱形→平行四边形→矩形→平行四边形→菱形,故选:A.【点睛】本题考查了菱形的性质与判定,平行四边形的性质与判定,矩形的性质与判定,勾股定理与勾股定理的逆定理,轴对称的性质,含30度角的直角三角形的性质,熟练掌握以上知识是解题的关键.12(2023·重庆·统考中考真题)如图,在正方形ABCD中,O为对角线AC的中点,E为正方形内一点,连接BE,BE=BA,连接CE并延长,与∠ABE的平分线交于点F,连接OF,若AB=2,则OF的长度为()A.2B.3C.1D.2【答案】D【分析】连接AF ,根据正方形ABCD 得到AB =BC =BE ,∠ABC =90°,根据角平分线的性质和等腰三角形的性质,求得∠BFE =45°,再证明△ABF ≌△EBF ,求得∠AFC =90°,最后根据直角三角形斜边上的中点等于斜边的一半,即可求出OF 的长度.【详解】解:如图,连接AF ,∵四边形ABCD 是正方形,∴AB =BE =BC ,∠ABC =90°,AC =2AB =22,∴∠BEC =∠BCE ,∴∠EBC =180°-2∠BEC ,∴∠ABE =∠ABC -∠EBC =2∠BEC -90°,∵BF 平分∠ABE ,∴∠ABF =∠EBF =12∠ABE =∠BEC -45°,∴∠BFE =∠BEC -∠EBF =45°,在△BAF 与△BEF ,AB =EB∠ABF =∠EBF BF =BF,∴△BAF ≌△BEF SAS ,∴∠BFE =∠BFA =45°,∴∠AFC =∠BAF +∠BFE =90°,∵O 为对角线AC 的中点,∴OF =12AC =2,故选:D .【点睛】本题考查了等腰三角形的判定和性质,三角形内角和定理,正方形的性质,直角三角形特征,作出正确的辅助线,求得∠BFE =45°是解题的关键.二、解答题13(2023·湖南怀化·统考中考真题)如图,矩形ABCD 中,过对角线BD 的中点O 作BD 的垂线EF ,分别交AD ,BC 于点E ,F .(1)证明:△BOF ≌△DOE ;(2)连接BE 、DF ,证明:四边形EBFD 是菱形.【答案】(1)见解析;(2)见解析【分析】(1)根据矩形的性质得出AD ∥BC ,则∠1=∠2,∠3=∠4,根据O 是BD 的中点,可得BO =DO ,即可证明△BOF ≌△DOE AAS ;(2)根据△BOF ≌△DOE 可得ED =BF ,进而可得四边形EBFD 是平行四边形,根据对角线互相垂直的四边形是菱形,即可得证.【详解】(1)证明:如图所示,∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠1=∠2,∠3=∠4,∵O 是BD 的中点,∴BO =DO ,在△BOF 与△DOE 中∠1=∠2∠3=∠4BO =DO,∴△BOF ≌△DOE AAS ;(2)∵△BOF ≌△DOE∴ED =BF ,又∵ED ∥BF∴四边形EBFD 是平行四边形,∵EF ⊥BD∴四边形EBFD 是菱形.【点睛】本题考查了矩形的性质,全等三角形的性质与判定,菱形的判定,熟练掌握特殊四边形的性质与判定是解题的关键.14(2023·湖北随州·统考中考真题)如图,矩形ABCD 的对角线AC ,BD 相交于点O ,DE ∥AC ,CE ∥BD .(1)求证:四边形OCED 是菱形;(2)若BC =3,DC =2,求四边形OCED 的面积.【答案】(1)见解析;(2)3【分析】(1)先根据矩形的性质求得OC =OD ,然后根据有一组邻边相等的平行四边形是菱形分析推理;(2)根据矩形的性质求得△OCD 的面积,然后结合菱形的性质求解.【详解】(1)解:∵ DE ∥AC ,CE ∥BD ,∴四边形OCED 是平行四边形,又∵矩形ABCD 中,OC =OD ,∴平行四边形OCED 是菱形;(2)解:矩形ABCD 的面积为BC ⋅DC =3×2=6,∴△OCD 的面积为14×6=32,∴菱形OCED 的面积为2×32=3.【点睛】本题考查矩形的性质、菱形的判定,属于中考基础题,掌握矩形的性质和菱形的判定方法,正确推理论证是解题关键.15(2023·湖南永州·统考中考真题)如图,已知四边形ABCD 是平行四边形,其对角线相交于点O ,OA =3,BD =8,AB =5.(1)△AOB 是直角三角形吗?请说明理由;(2)求证:四边形ABCD 是菱形.【答案】(1)△AOB 是直角三角形,理由见解析.(2)见解析【分析】(1)根据平行四边形对角线互相平分可得BO =12BD =4,再根据勾股定理的逆定理,即可得出结论;(2)根据对角线互相垂直的平行四边形是菱形,即可求证.【详解】(1)解:△AOB 是直角三角形,理由如下:∵四边形ABCD 是平行四边形,∴BO =12BD =4,∵OA 2+OB 2=32+42=52=AB 2,∴△AOB 是直角三角形.(2)证明:由(1)可得:△AOB 是直角三角形,∴∠AOB =90°,即AC ⊥BD ,∵四边形ABCD 是平行四边形,∴四边形ABCD 是菱形.【点睛】本题主要考查了平行四边形的性质,勾股定理的逆定理,菱形的判定,解题的关键是掌握平行四边形对角线互相平分,对角线互相垂直的平行四边形是菱形.16(2023·新疆·统考中考真题)如图,AD 和BC 相交于点O ,∠ABO =∠DCO =90°,OB =OC .点E 、F 分别是AO 、DO的中点.(1)求证:OE =OF ;(2)当∠A =30°时,求证:四边形BECF 是矩形.【答案】(1)见解析;(2)见解析【分析】(1)直接证明△AOB ≌△DOC ASA ,得出OA =OD ,根据E 、F 分别是AO 、DO 的中点,即可得证;(2)证明四边形BECF 是平行四边形,进而根据∠A =30°,推导出△BOE 是等边三角形,进而可得BC =EF ,即可证明四边形BECF 是矩形.【详解】(1)证明:在△AOB 与△DOC 中,∠ABO =∠DCO =90°OB =OC∠AOB =∠DOC∴△AOB ≌△DOC ASA ,∴OA =OD ,又∵E 、F 分别是AO 、DO 的中点,∴OE =OF ;(2)∵OB =OC ,OF =OE ,∴四边形BECF 是平行四边形,BC =2OB ,EF =2OE ,∵E 为AO 的中点,∠ABO =90°,∴EB =EO =EA ,∵∠A =30°,∴∠BOE =60°,∴△BOE 是等边三角形,∴OB =OE ,∴BC =EF ,∴四边形BECF 是矩形.【点睛】本题考查了全等三角形的性质与判定,等边三角形的性质与判定,矩形判定,熟练掌握以上知识是解题的关键.17(2023·云南·统考中考真题)如图,平行四边形ABCD 中,AE 、CF 分别是∠BAD 、∠BCD 的平分线,且E 、F 分别在边BC 、AD 上,AE =AF .(1)求证:四边形AECF 是菱形;(2)若∠ABC =60°,△ABE 的面积等于43,求平行线AB 与DC 间的距离.【答案】(1)证明见解析;(2)43【分析】(1)先证AD ∥BC ,再证AE ∥FC ,从而四边形AECF 是平行四边形,又AE =AF ,于是四边形AECF 是菱形;(2)连接AC ,先求得∠BAE =∠DAE =∠ABC =60°,再证AC ⊥AB ,∠ACB =90°-∠ABC =30°=∠EAC ,于是有33=AB AC,得AB =33AC ,再证AE =BE =CE ,从而根据面积公式即可求得AC =43.【详解】(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,∠BAD =∠BCD ,∴∠BEA =∠DAE ,∵AE 、CF 分别是∠BAD 、∠BCD 的平分线,∴∠BAE =∠DAE =12∠BAD ,∠BCF =12∠BCD ,∴∠DAE =∠BCF =∠BEA ,∴AE ∥FC ,∴四边形AECF 是平行四边形,∵AE =AF ,∴四边形AECF 是菱形;(2)解:连接AC ,∵AD ∥BC ,∠ABC =60°,∴∠BAD =180°-∠ABC =120°,∴∠BAE =∠DAE =∠ABC =60°,∵四边形AECF 是菱形,∴∠EAC =12∠DAE =30°,∴∠BAC =∠BAE +∠EAC =90°,∴AC ⊥AB ,∠ACB =90°-∠ABC =30°=∠EAC ,∴AE =CE ,tan30°=tan ∠ACB =AB AC 即33=AB AC,∴AB =33AC ,∵∠BAE =∠ABC ,∴AE =BE =CE ,∵△ABE 的面积等于43,∴S △ABC =12AC ⋅AB =12AC ⋅33AC =36AC 2=83,∴平行线AB 与DC 间的距离AC =43.【点睛】本题考查了平行四边形的判定及性质,菱形的判定,角平分线的定义,等腰三角形的判定,三角函数的应用以及平行线间的距离,熟练掌握平行四边形的判定及性质,菱形的判定,角平分线的定义,等腰三角形的判定,三角函数的应用以及平行线间的距离等知识是解题的关键.18(2023·四川遂宁·统考中考真题)如图,四边形ABCD 中,AD ∥BC ,点O 为对角线BD 的中点,过点O 的直线l 分别与AD 、BC 所在的直线相交于点E 、F .(点E 不与点D 重合)(1)求证:△DOE ≌△BOF ;(2)当直线l ⊥BD 时,连接BE 、DF ,试判断四边形EBFD 的形状,并说明理由.【答案】(1)见解析;(2)四边形EBFD 为菱形;理由见解析【分析】(1)根据AAS 证明△DOE ≌△BOF 即可;(2)连接EB 、FD ,根据△DOE ≌△BOF ,得出ED =BF ,根据ED ∥BF ,证明四边形EBFD 为平行四边形,根据EF ⊥BD ,证明四边形EBFD 为菱形即可.【详解】(1)证明:∵点O 为对角线BD 的中点,∴BO =DO ,∵AD ∥BC ,∴∠ODE =∠OBF ,∠OED =∠OFB ,在△DOE 和△BOF 中,∠ODE =∠OBF∠OED =∠OFB BO =DO,∴△DOE ≌△BOF AAS ;(2)解:四边形EBFD 为菱形,理由如下:连接EB 、FD ,如图所示:根据解析(1)可知,△DOE ≌△BOF ,∴ED =BF ,∵ED ∥BF ,∴四边形EBFD 为平行四边形,∵l ⊥BD ,即EF ⊥BD ,∴四边形EBFD 为菱形.【点睛】本题主要考查了三角形全等的判定和性质,菱形的判定,平行线的性质,解题的关键是熟练掌握三角形全等的判定方法和菱形的判定方法.19(2023·浙江嘉兴·统考中考真题)如图,在菱形ABCD 中,AE ⊥BC 于点E ,AF ⊥CD 于点F ,连接EF(1)求证:AE =AF ;(2)若∠B =60°,求∠AEF 的度数.【答案】(1)证明见解析;(2)60°【分析】(1)根据菱形的性质的三角形全等即可证明AE =AF .(2)根据菱形的性质和已知条件可推出∠BAD 度数,再根据第一问的三角形全等和直角三角形的性质可求出∠BAE 和∠DAF 度数,从而求出∠EAF 度数,证明了等边三角形AEF ,即可求出∠AEF 的度数.【详解】(1)证明:∵菱形ABCD ,∴AB =AD ,∠B =∠D ,又∵AE ⊥BC ,AF ⊥CD ,∴∠AEB =∠AFD =90°.在△AEB 和△AFD 中,∠AEB =∠AFD∠B =∠D AB =AD,∴△ABE ≌△ADF (AAS ).∴AE =AF .(2)解:∵菱形ABCD ,∴∠B +∠BAD =180°,∵∠B =60°,∴∠BAD =120°.又∵∠AEB =90°,∠B =60°,∴∠BAE =30°.由(1)知△ABE ≌△ADF ,∴∠BAE =∠DAF =30°.∴∠EAF =120°-30°-30°=60°.∵AE =AF ,∴△AEF 等边三角形.∴∠AEF =60°.【点睛】本题考查了三角形全等、菱形的性质、等边三角形的性质,解题的关键在于熟练掌握全等的方法和菱形的性质.20(2023·湖北鄂州·统考中考真题)如图,点E是矩形ABCD的边BC上的一点,且AE=AD.(1)尺规作图(请用2B铅笔):作∠DAE的平分线AF,交BC的延长线于点F,连接DF.(保留作图痕迹,不写作法);(2)试判断四边形AEFD的形状,并说明理由.【答案】(1)见解析;(2)四边形AEFD是菱形,理由见解析【分析】(1)根据题意结合尺规作角平分线的方法作图即可;(2)根据矩形的性质和平行线的性质得出∠DAF=∠AFE,结合角平分线的定义可得∠EFA=∠EAF,则AE=EF,然后根据平行四边形和菱形的判定定理得出结论.【详解】(1)解:如图所示:(2)四边形AEFD是菱形;理由:∵矩形ABCD中,AD∥BC,∴∠DAF=∠AFE,∵AF平分∠DAE,∴∠DAF=∠EAF,∴∠EFA=∠EAF,∴AE=EF,∵AE=AD,∴AD=EF,∵AD∥EF,∴四边形AEFD是平行四边形,又∵AE=AD,∴平行四边形AEFD是菱形.【点睛】本题主要考查了尺规作角平分线,矩形的性质,平行线的性质,等腰三角形的判定,平行四边形的判定以及菱形的判定等知识,熟练掌握相关判定定理和性质定理是解题的关键.21(2023·吉林长春·统考中考真题)将两个完全相同的含有30°角的直角三角板在同一平面内按如图所示位置摆放.点A,E,B,D依次在同一直线上,连结AF、CD.(1)求证:四边形AFDC是平行四边形;(2)己知BC=6cm,当四边形AFDC是菱形时.AD的长为cm.【答案】(1)见解析;(2)18【分析】(1)由题意可知△ACB≌△DFE易得AC=DF,∠CAB=∠FDE=30°即AC∥DF,依据一组对边平行且相等的四边形是平行四边形可证明;(2)如图,在Rt△ACB中,由30°角所对的直角边等于斜边的一半和直角三角形锐角互余易得AB=2BC= 12cm,∠ABC=60°;由菱形得对角线平分对角得∠CDA=∠FDA=30°,再由三角形外角和易证∠BCD=∠CDA即可得BC=BD=6cm,最后由AD=AB+BD求解即可.【详解】(1)证明:由题意可知△ACB≌△DFE,∴AC=DF,∠CAB=∠FDE=30°,∴AC∥DF,∴四边形AFDC地平行四边形;(2)如图,在Rt△ACB中,∠ACB=90°,∠CAB=30°,BC=6cm,∴AB=2BC=12cm,∠ABC=60°,四边形AFDC是菱形,∴AD平分∠CDF,∴∠CDA=∠FDA=30°,∵∠ABC=∠CDA+∠BCD,∴∠BCD=∠ABC-∠CDA=60°-30°=30°,∴∠BCD=∠CDA,∴BC=BD=6cm,∴AD=AB+BD=18cm,故答案为:18.【点睛】本题考查了全等三角形的性质,平行四边形的判定,菱形的性质,30°角所对的直角边等于斜边的一半和直角三角形锐角互余,三角形外角及等角对等边;解题的关键是熟练掌握相关知识综合求解.22(2023·湖南张家界·统考中考真题)如图,已知点A,D,C,B在同一条直线上,且AD=BC,AE= BF,CE=DF.(1)求证:AE∥BF;(2)若DF=FC时,求证:四边形DECF是菱形.【答案】(1)见解析;(2)见解析【分析】(1)根据题意得出AC=BD,再由全等三角形的判定和性质及平行线的判定证明即可;(2)方法一:利用全等三角形的判定和性质得出DE=CF,又EC=DF,再由菱形的判定证明即可;方法二:利用(1)中结论得出∠ECA=∠FDB,结合菱形的判定证明即可.【详解】(1)证明:∵AD=BC,∴AD+DC=BC+DC,即AC=BD在△AEC和△BFD中,AC=BDAE=BFCE=DF,∴△AEC≌△BFD SSS∴∠A=∠B,∴AE∥BF(2)方法一:在△ADE和△BCF中,AE=BF∠A=∠BAD=BC,∴△ADE≌△BCF SAS∴DE=CF,又EC=DF,∴四边形DECF是平行四边形∵DF=FC,∴▱DECF是菱形;方法二:∵△AEC≌△BFD,∴∠ECA=∠FDB∴EC∥DF,又EC=DF,∴四边形DECF是平行四边形∵DF=FC,∴▱DECF是菱形.【点睛】题目主要考查全等三角形的判定和性质,菱形的判定和性质,理解题意,熟练掌握运用这些知识点是解题关键.23(2023·湖南郴州·统考中考真题)如图,四边形ABCD是平行四边形.(1)尺规作图;作对角线AC的垂直平分线MN(保留作图痕迹);(2)若直线MN分别交AD,BC于E,F两点,求证:四边形AFCE是菱形【答案】(1)见解析;(2)见解析【分析】(1)根据垂直平分线的作图方法进行作图即可;(2)设EF与AC交于点O,证明△AOE≌△COF ASA,得到OE=OF,得到四边形AFCE为平行四边形,根据EF⊥AC,即可得证.【详解】(1)解:如图所示,MN 即为所求;(2)∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴∠CAE =∠ACF ,如图:设EF 与AC 交于点O ,∵EF 是AC 的垂直平分线,∴AO =OC ,EF ⊥AC ,∵∠AOE =∠COF ,∴△AOE ≌△COF ASA ,∴OE =OF ,∴四边形AFCE 为平行四边形,∵EF ⊥AC ,∴四边形AFCE 为菱形.【点睛】本题考查基本作图-作垂线,平行四边形的判定和性质,全等三角形的判定和性质,菱形的判定.熟练掌握菱形的判定定理,是解题的关键.24(2023·湖北十堰·统考中考真题)如图,▱ABCD 的对角线AC ,BD 交于点O ,分别以点B ,C 为圆心,12AC ,12BD 长为半径画弧,两弧交于点P ,连接BP ,CP .(1)试判断四边形BPCO的形状,并说明理由;(2)请说明当▱ABCD的对角线满足什么条件时,四边形BPCO是正方形?【答案】(1)平行四边形,见解析;(2)AC=BD且AC⊥BD【分析】(1)根据平行四边形的性质,得到BP=12AC=OC,CP=12BD=OB,根据两组对边分别相等的四边形是平行四边形判定即可.(2)根据对角线相等、平分且垂直的四边形是正方形判定即可.【详解】(1)四边形BPCO是平行四边形.理由如下:∵▱ABCD的对角线AC,BD交于点O,∴AO=OC,BO=OD,∵以点B,C为圆心,12AC,12BD长为半径画弧,两弧交于点P,∴BP=12AC=OC,CP=12BD=OB∴四边形BPCO是平行四边形.(2)∵对角线相等、平分且垂直的四边形是正方形,∴AC=BD且AC⊥BD时,四边形BPCO是正方形.【点睛】本题考查了平行四边形的判定和性质,正方形的判定和性质,熟练掌握判定和性质是解题的关键.25(2023·四川内江·统考中考真题)如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC交CE的延长线于点F.(1)求证:AF=BD;(2)连接BF,若AB=AC,求证:四边形ADBF是矩形.【答案】(1)见解析;(2)见解析;【分析】(1)根据两直线平行,内错角相等求出∠AFE=∠DCE,然后利用“角角边”证明三角形全等,再由全等三角形的性质容易得出结论;(2)先利用一组对边平行且相等的四边形是平行四边形证明四边形AFBD是平行四边形,再根据一个角是直角的平行四边形是矩形判定即可.【详解】(1)证明:∵AF∥BC,∴∠AFE=∠DCE,∵点E为AD的中点,∴AE=DE,在△AEF和△EDC中,∠AFE=∠DCE∠AEF=∠DECAE=DE,∴△EAF≌△EDC(AAS);∴AF=CD,∵CD=BD,∴AF=BD;(2)证明:∵AF∥BD,AF=BD,∴四边形AFBD是平行四边形,∵AB=AC,BD=CD,∴∠ADB=90°,∴平行四边形AFBD是矩形.【点睛】本题考查了矩形的判定,全等三角形的判定与性质,平行四边形的判定,是基础题,明确有一个角是直角的平行四边形是矩形是解本题的关键.26(2023·湖南岳阳·统考中考真题)如图,点M在▱ABCD的边AD上,BM=CM,请从以下三个选项中①∠1=∠2;②AM=DM;③∠3=∠4,选择一个合适的选项作为已知条件,使▱ABCD为矩形.(1)你添加的条件是(填序号);(2)添加条件后,请证明▱ABCD为矩形.【答案】(1)答案不唯一,①或②;(2)见解析【分析】(1)根据有一个角是直角的平行四边形是矩形进行选取;(2)通过证明△ABM≌△DCM可得∠A=∠D,然后结合平行线的性质求得∠A=90°,从而得出▱ABCD 为矩形.【详解】(1)解:①或②(2)添加条件①,▱ABCD为矩形,理由如下:在▱ABCD中AB=CD,AB∥CD,在△ABM和△DCM中AB=CD∠1=∠2 BM=CM ,∴△ABM≌△DCM ∴∠A=∠D,又∵AB∥CD,∴∠A+∠D=180°,∴∠A =∠D =90°,∴▱ABCD 为矩形;添加条件②,▱ABCD 为矩形,理由如下:在▱ABCD 中AB =CD ,AB ∥CD ,在△ABM 和△DCM 中AB =CDAM =DM BM =CM,∴△ABM ≌△DCM ∴∠A =∠D ,又∵AB ∥CD ,∴∠A +∠D =180°,∴∠A =∠D =90°,∴▱ABCD 为矩形【点睛】本题考查矩形的判定,全等三角形的判定和性质,掌握平行四边形的性质和矩形的判定方法(有一个角是直角的平行四边形是矩形)是解题关键.27(2023·四川乐山·统考中考真题)如图,在Rt △ABC 中,∠C =90°,点D 为AB 边上任意一点(不与点A 、B 重合),过点D 作DE ∥BC ,DF ∥AC ,分别交AC 、BC 于点E 、F ,连接EF.(1)求证:四边形ECFD 是矩形;(2)若CF =2,CE =4,求点C 到EF 的距离.【答案】(1)见解析;(2)455【分析】(1)利用平行线的性质证明∠CED =∠CFD =90°,再利用四边形内角和为360°,证明∠EDF =90°,即可由矩形判定定理得出结论;(2)先由勾股定理求出EF =CF 2+CE 2=25,再根据三角形面积公式求解即可.【详解】(1)证明:∵DE ∥BC ,DF ∥AC ,∴四边形ECFD 为平行四边形,∵∠C =90°,∴四边形ECFD 是矩形.(2)解:∵∠C =90°,CF =2,CE =4,∴EF =CF 2+CE 2=25设点C 到EF 的距离为h ,∵S △CEF =12CE ⋅CF =12EF ⋅h ∴2×4=25h∴h=455答:点C到EF的距离为45 5.【点睛】本题考查矩形的判定,平行线的性质,勾股定理.熟练掌握矩形的判定定理和利用面积法求线段长是解题的关键.28(2023·浙江台州·统考中考真题)如图,四边形ABCD中,AD∥BC,∠A=∠C,BD为对角线.(1)证明:四边形ABCD是平行四边形.(2)已知AD>AB,请用无刻度的直尺和圆规作菱形BEDF,顶点E,F分别在边BC,AD上(保留作图痕迹,不要求写作法).【答案】(1)见解析;(2)见解析【分析】(1)先证明∠ADB=∠CBD,再证明180°-∠ADB+∠A=180°-∠CBD+∠C,即∠ABD=∠CDB,从而可得结论;(2)作对角线BD的垂直平分线交AD于F,交BC于E,从而可得菱形BEDF.【详解】(1)证明:∵AD∥BC,∴∠ADB=∠CBD,∵∠A=∠C,∴180°-∠ADB+∠A=180°-∠CBD+∠C,即∠ABD=∠CDB.∴AB∥CD.∴四边形ABCD是平行四边形.(2)如图,四边形BEDF就是所求作的菱形.【点睛】本题考查的是平行四边形的判定与性质,作线段的垂直平分线,菱形的判定,熟练的利用菱形的判定进行作图是解本题的关键.三、填空题29(2023·黑龙江齐齐哈尔·统考中考真题)如图,在四边形ABCD中,AD=BC,AC⊥BD于点O.请添加一个条件:,使四边形ABCD成为菱形.【答案】AD∥BC(荅案不唯一)【分析】根据题意,先证明四边形ABCD是平行四边形,根据AC⊥BD,可得四边形ABCD成为菱形.【详解】解:添加条件AD∥BC∵AD=BC,AD∥BC∴四边形ABCD是平行四边形,∵AC⊥BD,∴四边形ABCD成为菱形.添加条件AB=CD∵AD=BC,AB=CD∴四边形ABCD是平行四边形,∵AC⊥BD,∴四边形ABCD成为菱形.添加条件OB=OD∵AC⊥BD,∴∠AOD=∠COB=90°∵AD=BC,OB=OD,∴Rt△AOD≌Rt△COB HL∴AD=BC,∴四边形ABCD是平行四边形,∵AC⊥BD,∴四边形ABCD成为菱形.添加条件∠ADB=∠CBD在△AOD与△COB中,∠ADB=∠CBD ∠AOD=∠COB AD=BC∴△AOD≌△COB∴AD=BC,∴四边形ABCD是平行四边形,∵AC⊥BD,∴四边形ABCD成为菱形.故答案为:AD∥BC(AB=CD或OB=OD或∠ADB=∠CBD等).【点睛】本题考查了平行四边形的判定,菱形的判定,熟练掌握菱形的判定定理是解题的关键.30(2023·辽宁大连·统考中考真题)如图,在菱形ABCD中,AC、BD为菱形的对角线,∠DBC=60°, BD=10,点F为BC中点,则EF的长为.。
备战中考数学分点透练真题矩形、菱形、正方形(解析版)

第十九讲矩形、菱形、正方形命题点1 矩形的相关证明与计算1.(2020•怀化)在矩形ABCD中,AC、BD相交于点O,若△AOB的面积为2,则矩形ABCD 的面积为()A.4B.6C.8D.10【答案】C【解答】解:∵四边形ABCD是矩形,对角线AC、BD相交于点O,∴AC=BD,且OA=OB=OC=OD,∴S△ADO=S△BCO=S△CDO=S△ABO=2,∴矩形ABCD的面积为4S△ABO=8,故选:C.2.(2021•遂宁)如图,在矩形ABCD中,AB=5,AD=3,点E为BC上一点,把△CDE 沿DE翻折,点C恰好落在AB边上的F处,则CE的长是()A.1B.C.D.【答案】D【解答】解:设CE=x,则BE=3﹣x.由折叠性质可知,EF=CE=x,DF=CD=AB=5.在Rt△DAF中,AD=3,DF=5.∴AF=4.∴BF=AB﹣AF=1.在Rt△BEF中,BE2+BF2=EF2.即(3﹣x)2+12=x2.解得x=.故选:D.3.(2021•黑龙江)如图,在平行四边形ABCD中,对角线AC、BD相交于点O,在不添加任何辅助线的情况下,请你添加一个条件,使平行四边形ABCD是矩形.【答案】∠ABC=90°(答案不唯一)【解答】解:添加一个条件为:∠ABC=90°,理由如下:∵四边形ABCD是平行四边形,∠ABC=90°,∴平行四边形ABCD是矩形,故答案为:∠ABC=90°(答案不唯一).4.(2021•贵港)如图,在矩形ABCD中,BD是对角线,AE⊥BD,垂足为E,连接CE,若tan∠ADB=,则tan∠DEC的值是.【答案】【解答】解:如图,过点C作CF⊥BD于点F,在△ABE与△CDF中,,∴△ABE≌△CDF(AAS),∴AE=CF,BE=FD,∵AE⊥BD,tan∠ADB==,设AB=a,则AD=2a,∴BD=a,∵S△ABD=BD•AE=AB•AD,∴AE=CF=a,∴BE=FD=a,∴EF=BD﹣2BE=a﹣a=a,∴tan∠DEC==,故答案为:.5.(2021•十堰)如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为.【答案】20【解答】解:∵O是矩形ABCD的对角线AC的中点,M是AD的中点,∴OM=CD=AB=2.5,∵AB=5,AD=12,∴AC==13,∵O是矩形ABCD的对角线AC的中点,∴BO=AC=6.5,∴四边形ABOM的周长为AB+AM+BO+OM=5+6+6.5+2.5=20,故答案为:20.6.(2021•嘉峪关)如图,在矩形ABCD中,E是BC边上一点,∠AED=90°,∠EAD=30°,F是AD边的中点,EF=4cm,则BE=cm.【答案】6【解答】解:∵∠AED=90°,F是AD边的中点,EF=4cm,∴AD=2EF=8cm,∵∠EAD=30°,∴AE=AD•cos30°=8×=4cm,又∵四边形ABCD是矩形,∴AD∥BC,∠B=90°,∴∠BEA=∠EAD=30°,在Rt△ABE中,BE=AE•cos∠BEA=4×cos30°=4×=6(cm),故答案为:6.7.(2021•绍兴)图1是一种矩形时钟,图2是时钟示意图,时钟数字2的刻度在矩形ABCD 的对角线BD上,时钟中心在矩形ABCD对角线的交点O上.若AB=30cm,则BC长为cm(结果保留根号).【答案】【解答】解:过O点作OE⊥CD,OF⊥AD,垂足分别为E,F,由题意知∠FOD=2∠DOE,∵∠FOD+∠DOE=90°,∴∠DOE=30°,∠FOD=60°,在矩形ABCD中,∠C=90°,CD=AB=30cm,∴OE∥BC,∴∠DBC=∠DOE=30°,∴BC=CD=cm,故答案为.8.(2021•内江)如图,矩形ABCD中,AB=6,BC=8,对角线BD的垂直平分线EF交AD 于点E、交BC于点F,则线段EF的长为.【答案】【解答】解:∵四边形ABCD是矩形,∴∠A=90°,又AB=6,AD=BC=8,∴BD==10,∵EF是BD的垂直平分线,∴OB=OD=5,∠BOF=90°,又∠C=90°,∴△BOF∽△BCD,∴=,∴=,解得,OF=,∵四边形ABCD是矩形,∴AD∥BC,∠A=90°,∴∠EDO=∠FBO,∵EF是BD的垂直平分线,∴BO=DO,EF⊥BD,在△DEO和△BFO中,,∴△DEO≌△BFO(ASA),∴OE=OF,∴EF=2OF=.故答案为:.9.(2021•枣庄)如图,∠BOD=45°,BO=DO,点A在OB上,四边形ABCD是矩形,连接AC,BD交于点E,连接OE交AD于点F.下列4个判断:①OE⊥BD;②∠ADB =30°;③DF=AF;④若点G是线段OF的中点,则△AEG为等腰直角三角形,其中,判断正确的是.(填序号)【答案】①③④【解答】解:①∵四边形ABCD是矩形,∴EB=ED,∵BO=DO,∴OE⊥BD故①正确;②∵∠BOD=45°,BO=DO,∴∠ABD=(180°﹣45°)=67.5°,∴∠ADB=90°﹣27.5°=22.5°,故②错误;③∵四边形ABCD是矩形,∴∠OAD=∠BAD=90°,∴∠ABD+∠ADB=90°,∵OB=OD,BE=DE,∴OE⊥BD,∴∠BOE+∠OBE=90°,∴∠BOE=∠BDA,∵∠BOD=45°,∠OAD=90°,∴∠ADO=45°,∴AO=AD,∴△AOF≌△ABD(ASA),∴OF=BD,∴AF=AB,连接BF,如图1,∴BF=AF,∵BE=DE,OE⊥BD,∴DF=BF,∴DF=AF,故③正确;④根据题意作出图形,如图2,∵G是OF的中点,∠OAF=90°,∴AG=OG,∴∠AOG=∠OAG,∵∠AOD=45°,OE平分∠AOD,∴∠AOG=∠OAG=22.5°,∴∠F AG=67.5°,∠ADB=∠AOF=22.5°,∵四边形ABCD是矩形,∴EA=ED,∴∠EAD=∠EDA=22.5°,∴∠EAG=90°,∵∠AGE=∠AOG+∠OAG=45°,∴∠AEG=45°,∴AE=AG,∴△AEG为等腰直角三角形,故④正确;∴判断正确的是①③④.故答案为:①③④.10.(2021•贵阳)如图,在矩形ABCD中,点M在DC上,AM=AB,且BN⊥AM,垂足为N.(1)求证:△ABN≌△MAD;(2)若AD=2,AN=4,求四边形BCMN的面积.【答案】(1)略(2)4﹣8.【解答】(1)证明:在矩形ABCD中,∠D=90°,DC∥AB,∴∠BAN=∠AMD,∵BN⊥AM,∴∠BNA=90°,在△ABN和△MAD中,,∴△ABN≌△MAD(AAS);(2)解:∵△ABN≌△MAD,∴BN=AD,∵AD=2,∴BN=2,又∵AN=4,在Rt△ABN中,AB===2,∴S矩形ABCD=2×2=4,S△ABN=S△MAD=×2×4=4,∴S四边形BCMN=S矩形ABCD﹣S△ABN﹣S△MAD=4﹣8.11.(2021•金华)已知:如图,矩形ABCD的对角线AC,BD相交于点O,∠BOC=120°,AB=2.(1)求矩形对角线的长;(2)过O作OE⊥AD于点E,连结BE.记∠ABE=α,求tanα的值.【答案】(1)4 (2)tanα==【解答】解:(1)∵∠BOC=120°,∴∠AOB=60°,∵四边形ABCD是矩形,∴∠BAD=90°,AC=BD,AO=OC,BO=DO,∴AO=BO,∴△AOB是等边三角形,∴AB=AO=BO,∵AB=2,∴BO=2,∴BD=2BO=4,∴矩形对角线的长为4;(2)由勾股定理得:AD===2,∵OA=OD,OE⊥AD于点E,∴AE=DE=AD=,∴tanα==.命题点2 菱形的相关证明与计算12.(2021•河南)关于菱形的性质,以下说法不正确的是()A.四条边相等B.对角线相等C.对角线互相垂直D.是轴对称图形【答案】B【解答】解:A.菱形的四条边相等,正确,不符合题意,B.菱形的对角线互相垂直且平分,对角线不一定相等,不正确,符合题意,C.菱形的对角线互相垂直且平分,正确,不符合题意,D.菱形是轴对称图形,正确,不符合题意,故选:B.13.(2021•烟台)如图,在直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点B的坐标为(﹣1,0),∠BCD=120°,则点D的坐标为()A.(2,2)B.(,2)C.(3,)D.(2,)【答案】D【解答】解:∵菱形ABCD,∠BCD=120°,∴∠ABC=60°,∵B(﹣1,0),∴OB=1,OA=,AB=2,∴A(0,),∴BC=AD=2,∴OC=BC﹣OB=2﹣1=1,∴C(1,0),D(2,),故选:D.14.(2021•陕西)如图,在菱形ABCD中,∠ABC=60°,连接AC、BD,则的值为()A.B.C.D.【答案】D【解答】解:设AC与BD交于点O,∵四边形ABCD是菱形,∴AO=CO,BO=DO,AC⊥BD,∠ABD=∠ABC=30°,∵tan∠ABD=,∴,故选:D.15.(2021•绍兴)如图,菱形ABCD中,∠B=60°,点P从点B出发,沿折线BC﹣CD 方向移动,移动到点D停止.在△ABP形状的变化过程中,依次出现的特殊三角形是()A.直角三角形→等边三角形→等腰三角形→直角三角形B.直角三角形→等腰三角形→直角三角形→等边三角形C.直角三角形→等边三角形→直角三角形→等腰三角形D.等腰三角形→等边三角形→直角三角形→等腰三角形【答案】C【解答】解:∵∠B=60°,故菱形由两个等边三角形组合而成,当AP⊥BC时,此时△ABP为直角三角形;当点P到达点C处时,此时△ABP为等边三角形;当P为CD中点时,△ABP为直角三角形;当点P与点D重合时,此时△ABP为等腰三角形,故选:C.16.(2021•安徽)如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为()A.3+B.2+2C.2+D.1+2【答案】A【解答】解:如图,连接BD,AC.∵四边形ABCD是菱形,∠BAD=120°,∴AB=BC=CD=AD=2,∠BAO=∠DAO=60°,BD⊥AC,∴∠ABO=∠CBO=30°,∴OA=AB=1,OB=OA=,∵OE⊥AB,OF⊥BC,∴∠BEO=∠BFO=90°,在△BEO和△BFO中,,∴△BEO≌△BFO(AAS),∴OE=OF,BE=BF,∵∠EBF=60°,∴△BEF是等边三角形,∴EF=BE=×=,同法可证,△DGH,△OEH,△OFG都是等边三角形,∴EF=GH=,EH=FG=,∴四边形EFGH的周长=3+,故选:A.17.(2021•朝阳)如图,在菱形ABCD中,点E,F分别在AB,CD上,且BE=2AE,DF =2CF,点G,H分别是AC的三等分点,则的值为()A.B.C.D.【答案】A【解答】解:∵BE=2AE,DF=2FC,∴,∵G、H分别是AC的三等分点,∴,,∴,∴EG∥BC∴,同理可得HF∥AD,,∴,故选:A.18.(2021•南充)如图,在菱形ABCD中,∠A=60°,点E,F分别在边AB,BC上,AE =BF=2,△DEF的周长为3,则AD的长为()A.B.2C.+1D.2﹣1【答案】C【解答】解:如图,连结BD,作DH⊥AB,垂足为H,∵四边形ABCD是菱形,∴AB=AD,AD∥BC,∵∠A=60°,∴△ABD是等边三角形,∠ABC=180°﹣∠A=120°,∴AD=BD,∠ABD=∠A=∠ADB=60°,∴∠DBC=∠ABC﹣∠ABD=120°﹣60°=60°,∵AE=BF,∴△ADE≌△BDF(SAS),∴DE=DF,∠ADE=∠FDB,∴∠EDF=∠EDB+∠FDB=∠EDB+∠ADE=∠ADB=60°,∴△DEF是等边三角形,∵△DEF的周长是3,∴DE=,设AH=x,则HE=2﹣x,∵AD=BD,DH⊥AB,∴∠ADH=∠ADB=30°,∴AD=2x,DH=x,在Rt△DHE中,DH²+HE²=DE²,∴(x)²+(2﹣x)²=()²,解得:x=(负值舍去),∴AD=2x=1+,故选:C.19.(2021•北京)如图,在矩形ABCD中,点E,F分别在BC,AD上,AF=EC.只需添加一个条件即可证明四边形AECF是菱形,这个条件可以是(写出一个即可).【答案】AE=AF【解答】解:这个条件可以是AE=AF,理由:∵四边形ABCD是矩形,∴AD∥BC,即AF∥CE,∵AF=EC,∴四边形AECF是平行四边形,∵AE=AF,∴四边形AECF是菱形,故答案为:AE=AF.20.(2021•山西)如图,在菱形ABCD中,对角线AC,BD相交于点O,BD=8,AC=6,OE∥AB,交BC于点E,则OE的长为.【答案】【解答】解:∵菱形ABCD中,对角线AC,BD相交于点O,∴OA=OC=,OB=,AC⊥BD,∵OE∥AB,∴BE=CE,∴OE为△ABC的中位线,∴,在Rt△ABO中,由勾股定理得:,∴OE=21.(2021•盐城)如图,D、E、F分别是△ABC各边的中点,连接DE、EF、AE.(1)求证:四边形ADEF为平行四边形;(2)加上条件后,能使得四边形ADEF为菱形,请从①∠BAC=90°;②AE平分∠BAC;③AB=AC这三个条件中选择1个条件填空(写序号),并加以证明.【答案】(1)略(2)②【解答】解:(1)证明:已知D、E、F为AB、BC、AC的中点,∴DE为△ABC的中位线,根据三角形中位线定理,∴DE∥AC,且DE==AF.即DE∥AF,DE=AF,∴四边形ADEF为平行四边形.(2)证明:选②AE平分∠BAC,∵AE平分∠BAC,∴∠DAE=∠F AE,又∵ADEF为平行四边形,∴EF∥DA,∴∠DAE=∠AEF,∴∠F AE=∠AEF,∴AF=EF,∴平行四边形ADEF为菱形.选③AB=AC,∵EF∥AB且EF=,DE∥AC且DE=,又∵AB=AC,∴EF=DE,∴平行四边形ADEF为菱形.22.(2021•云南)如图,四边形ABCD是矩形,E、F分别是线段AD、BC上的点,点O是EF与BD的交点.若将△BED沿直线BD折叠,则点E与点F重合.(1)求证:四边形BEDF是菱形;(2)若ED=2AE,AB•AD=3,求EF•BD的值.【答案】(1)略(2)4【解答】解:(1)证明:将△BED沿BD折叠,使E,F重合,∴OE=OF,EF⊥BD,∵四边形ABCD是矩形,∴∠C=90°,AD∥BC,∴∠ODE=∠OBF,在△OBF和△ODE中,,∴△OBF≌△ODE(AAS),∴OB=OD,∵OE=OF,∴四边形BFDE是平行四边形,∵EF⊥BD,∴四边形BFDE是菱形.(2)如图,∵AB•AD=3,∴S△ABD=AB•AD=,∵ED=2AE,∴ED=AD,∴S△BDE:S△ABD=2:3,∴S△BDE=,∴菱形BEDF的面积=EF•BD=2S△BDE=2,∴EF•BD=4.命题点3 正方形的相关证明与计算23.(2021•玉林)一个四边形顺次添加下列条件中的三个条件便得到正方形:a.两组对边分别相等b.一组对边平行且相等c.一组邻边相等d.一个角是直角顺次添加的条件:①a→c→d②b→d→c③a→b→c则正确的是()A.仅①B.仅③C.①②D.②③【答案】C【解答】解:①由a得到两组对边分别相等的四边形是平行四边形,添加c即一组邻边相等的平行四边形是菱形,再添加d即一个角是直角的菱形是正方形,故①正确;②由b得到一组对边平行且相等的四边形是平行四边形,添加d即有一个角是直角的平行四边形是矩形,再添加c即一组邻边相等的矩形是正方形,故②正确;③由a得到两组对边分别相等的四边形是平行四边形,添加b得到一组对边平行且相等的平行四边形仍是平行四边形,再添加c即一组邻边相等的平行四边形是菱形,不能得到四边形是正方形,故③不正确;故选:C.24.(2019•毕节市)如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为()A.B.3C.D.5【答案】B【解答】解:∵四边形ABCD是正方形,∴∠B=90°,∴BC2=EC2﹣EB2=22﹣12=3,∴正方形ABCD的面积=BC2=3.故选:B.25.(2021•重庆)如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为()A.1B.C.2D.2【答案】C【解答】解:∵四边形ABCD是正方形,∴∠MDO=∠NCO=45°,OD=OC,∠DOC=90°,∴∠DON+∠CON=90°,∵ON⊥OM,∴∠MON=90°,∴∠DON+∠DOM=90°,∴∠DOM=∠CON,在△DOM和△CON中,,∴△DOM≌△CON(ASA),∵四边形MOND的面积是1,四边形MOND的面积=△DOM的面积+△DON的面积,∴四边形MOND的面积=△CON的面积+△DON的面积=△DOC的面积,∴△DOC的面积是1,∴正方形ABCD的面积是4,∴AB2=4,∴AB=2,故选:C.26.(2021•湖北)如图,在正方形ABCD中,AB=4,E为对角线AC上与A,C不重合的一个动点,过点E作EF⊥AB于点F,EG⊥BC于点G,连接DE,FG,下列结论:①DE=FG;②DE⊥FG;③∠BFG=∠ADE;④FG的最小值为3.其中正确结论的个数有()A.1个B.2个C.3个D.4个【答案】C【解答】解:①连接BE,交FG于点O,如图,∵EF⊥AB,EG⊥BC,∴∠EFB=∠EGB=90°.∵∠ABC=90°,∴四边形EFBG为矩形.∴FG=BE,OB=OF=OE=OG.∵四边形ABCD为正方形,∴AB=AD,∠BAC=∠DAC=45°.在△ABE和△ADE中,,∴△ABE≌△ADE(SAS).∴BE=DE.∴DE=FG.∴①正确;②延长DE,交FG于M,交FB于点H,∵△ABE≌△ADE,∴∠ABE=∠ADE.由①知:OB=OF,∴∠OFB=∠ABE.∴∠OFB=∠ADE.∵∠BAD=90°,∴∠ADE+∠AHD=90°.∴∠OFB+∠AHD=90°.即:∠FMH=90°,∴DE⊥FG.∴②正确;③由②知:∠OFB=∠ADE.即:∠BFG=∠ADE.∴③正确;④∵点E为AC上一动点,∴根据垂线段最短,当DE⊥AC时,DE最小.∵AD=CD=4,∠ADC=90°,∴AC=.∴DE=AC=2.由①知:FG=DE,∴FG的最小值为2,∴④错误.综上,正确的结论为:①②③.故选:C.27.(2021•黔东南州)如图,在边长为2的正方形ABCD中,若将AB绕点A逆时针旋转60°,使点B落在点B′的位置,连接BB′,过点D作DE⊥BB′,交BB′的延长线于点E,则B′E的长为()A.B.C.D.【答案】A【解答】解:分别延长AD和BE交于点F,由题知,AB=2,∠ABF=60°,∴BF=AB÷cos60°=2÷=4,AF=BF•sin60°=4×=2,∠F=90°﹣∠ABF =30°,∴DF=AF﹣AD=2﹣2,∴EF=DF•cos∠F=(2)×=3﹣,由题知,△ABB'是等边三角形,∴B'E=BF﹣BB'﹣EF=4﹣2﹣(3﹣)=﹣1,故选:A.28.(2021•常德)如图,已知F、E分别是正方形ABCD的边AB与BC的中点,AE与DF 交于P.则下列结论成立的是()A.BE=AE B.PC=PDC.∠EAF+∠AFD=90°D.PE=EC【答案】C【解答】解:∵F、E分别是正方形ABCD的边AB与BC的中点,∴AF=BE,在△AFD和△BEA中,,∴△AFD≌△BEA(SAS),∴∠FDA=∠EAB,又∵∠FDA+∠AFD=90°,∴∠EAB+∠AFD=90°,即∠EAF+∠AFD=90°,故C正确,A、B、D无法证明其成立,故选:C.29.(2021春•新吴区月考)如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为()A.(﹣2,3)B.(﹣3,5)C.(5,﹣2)D.(﹣1,5)【答案】D【解答】解:如图,过点E作ED⊥x轴于点D,过点G和点F分别作y轴和x轴的平行线,交y轴和x轴于点B和A,两线相交于点C,得矩形ACBO,∴AC=OB,AO=CB,∵点E的坐标为(2,3),∴ED=3,OD=2,∵四边形OEFG是正方形,∴∠EOG=∠FGO=90°,∴∠EOD+∠GOB=90°,∵∠GOB+∠OGB=90°,∴∠EOD=∠OGB,在△EOD和△OGB中,,∴△EOD≌△OGB(AAS),∴ED=OB=3,OD=BG=2,同理可证:△EOD≌△FGC(AAS),∴ED=CG=3,OD=CF=2,∴AO=CB=BG+CG=3+2=5,AF=AC﹣CF=OB﹣CF=3﹣2=1,∴F(﹣1,5).故选:D.30.(2020•陕西)如图,在矩形ABCD中,AB=4,BC=8,延长BA至E,使AE=AB,以AE为边向右侧作正方形AEFG,O为正方形AEFG的中心,若过点O的一条直线平分该组合图形的面积,并分别交EF、BC于点M、N,则线段MN的长为.【答案】4【解答】解:如图,连接AC,BD交于点H,过点O和点H的直线MN平分该组合图形的面积,交AD于S,取AE中点P,取AB中点Q,连接OP,HQ,过点O作OT⊥QH 于T,∵四边形ABCD是矩形,∴AH=HC,又∵Q是AB中点,∴QH=BC=4,QH∥BC,AQ=BQ=2,同理可求PO=AG=2,PO∥AG,EP=AP=2,∴PO∥AD∥BC∥EF∥QH,EP=AP=AQ=BQ,∴MO=OS=SH=NH,∠OPQ=∠PQH=90°,∵OT⊥QH,∴四边形POTQ是矩形,∴PO=QT=2,OT=PQ=4,∴TH=2,∴OH===2,∴MN=2OH=4,故答案为:4.31.(2021•湖州)由沈康身教授所著,数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事:如图,三姐妹为了平分一块边长为1的祖传正方形地毯,先将地毯分割成七块,再拼成三个小正方形(阴影部分).则图中AB的长应是.【答案】﹣1【解答】解:∵地毯面积被平均分成了3份,∴每一份的边长为=,∴CD=3×=,在Rt△ACD中,根据勾股定理可得AD==,又根据剪裁可知BD=CK=1,∴AB=AD﹣BD=﹣1.故答案为:﹣1.32.(2021•东营)如图,正方形纸片ABCD的边长为12,点F是AD上一点,将△CDF沿CF折叠,点D落在点G处,连接DG并延长交AB于点E.若AE=5,则GE的长为.【答案】【解答】解:设CF与DE交于点O,∵将△CDF沿CF折叠,点D落在点G处,∴GO=DO,CF⊥DG,∵四边形ABCD是正方形,∴AD=CD,∠A=∠ADC=90°=∠FOD,∴∠CFD+∠FCD=90°=∠CFD+∠ADE,∴∠ADE=∠FCD,在△ADE和△DCF中,,∴△ADE≌△DCF(ASA),∴AE=DF=5,∵AE=5,AD=12,∴DE===13,∵cos∠ADE=,∴,∴DO==GO,∴EG=13﹣2×=,故答案为:.33.(2021•天津)如图,正方形ABCD的边长为4,对角线AC,BD相交于点O,点E,F 分别在BC,CD的延长线上,且CE=2,DF=1,G为EF的中点,连接OE,交CD于点H,连接GH,则GH的长为.【答案】【解答】解:以O为原点,垂直AB的直线为x轴,建立直角坐标系,如图:∵正方形ABCD的边长为4,CE=2,DF=1,∴E(4,﹣2),F(2,3),∵G为EF的中点,∴G(3,),设直线OE解析式为y=kx,将E(4,﹣2)代入得:﹣2=4k,解得k=﹣,∴直线OE解析式为y=﹣x,令x=2得y=﹣1,∴H(2,﹣1),∴GH==,方法二:如下图,连接OF,过点O作OM⊥CD交CD于M,∵O为正方形对角线AC和BD的交点,∴OM=CM=DM=CE=2,易证△OHM≌△EHC,∴点H、点G分别为OE、FE的中点,∴GH为△OEF的中位线,∴GH=OF,在Rt△OMF中,由勾股定理可得OF===,∴GH=OF=,故答案为:.34.(2021•邵阳)如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F是对角线AC上的两点,且AE=CF.连接DE,DF,BE,BF.(1)证明:△ADE≌△CBF.(2)若AB=4,AE=2,求四边形BEDF的周长.【答案】(1)略(2)8【解答】(1)证明:由正方形对角线平分每一组对角可知:∠DAE=∠BCF=45°,在△ADE和△CBF中,,∴△ADE≌△CBF(SAS).(2)解:∵AB=AD=,∴BD===8,由正方形对角线相等且互相垂直平分可得:AC=BD=8,DO=BO=4,OA=OC=4,又AE=CF=2,∴OA﹣AE=OC﹣CF,即OE=OF=4﹣2=2,故四边形BEDF为菱形.∵∠DOE=90°,∴DE===2.∴4DE=,故四边形BEDF的周长为8.。
平行四边形、矩形、菱形、正方形的性质和判定(4) 同步练习

3.3平行四边形、矩形、菱形、正方形的性质和判定⑷ 【新知导读】 讨论: 老师给孩子们一个任务:从一张彩色纸中剪出一个正方形。 小明剪出了一个正方形后,这样检验它:他比较了边的长度,发现4条边是相等的,小明就判定他完成了这个任务。这种检验可信赖吗? 小兵用另一种方法检验:他量的不是边,而是对角线,发现对角线是相等的。小兵就认为他正确地剪出了正方形。这对吗? 小英剪了正方形后,比较了由对角线互相分成的四条线段,发现它们都是相等的。按照小英的意见,这说明了剪出的四边形是正方形。你们的意见怎样? 你们认为应该如何检验,才能又快又准确呢? 【范例点睛】 例1 如图,ABCD是正方形,点G是BC上的任意一点,DE⊥AG于E,BF∥DE,交AG于F,求证:AF—BF=EF. 证明:∵四边形ABCD是正方形, ∴AB=AD,∠BAD=90° ∵DE⊥AG,BF∥DE ∴∠AED=∠BFA=90° ∴∠BAF+∠EAD=90° ∠EAD+∠ADE=90° ∴∠BAF=∠ADE 在△ABF和△DAE中
BAFADEBFAAEDABAD
∴△ABF≌△DAE(AAS) ∴BF=AE∴AF—BF=AF—AE=EF.
例2 如图,正方形ABCD的边CD在正方形ECGF的边CE上,连结BE、DG. ⑴观察猜想BE与DG之间的大小关系,并证明你的结论; ⑵图中是否存在通过旋转能够互相重合的两个三角形?若存在,请说明旋转过程;若不存在,请说明理由. 解:⑴BE=DG. 理由:∵四边形ABCD和四边形ECGF都是正方形, ∴BC=DC,EC=GC, ∴∠BCE=∠DCG=90°, ∴△BCE≌△DCG,
GFEDCBA
EF
GD
CBA
怎么写怎么想要证AF-BF=EF只需证BF=AE只需证△ABF≌△DAE只需找两个三角形全等的条件
思考与表述 ∴BE=DG. ⑵由⑴证明的过程知,存在,是Rt△BCE和Rt△DCG. 将Rt△BCE绕点C顺时针旋转90°,可与Rt△DCG完全重合. (或将Rt△DCG绕点C逆时针旋转90°,可与Rt△BCE完全重合) 【课外链接】
平行四边形、矩形、菱形、正方形提高题
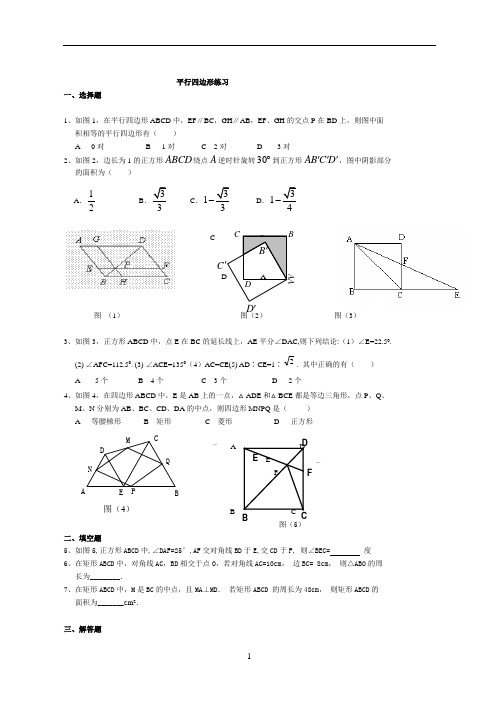
平行四边形练习 一、选择题1、如图1,在平行四边形ABCD 中,EF ∥BC ,GH ∥AB ,EF 、GH 的交点P 在BD 上,则图中面 积相等的平行四边形有( )A 0对B 1对C 2对D 3对 2、如图2,边长为1的正方形ABCD 绕点A 逆时针旋转30︒到正方形AB C D ''',图中阴影部分的面积为( )A .12B .33C .313-D .314-CBD A图 (1) 图(2) 图(3)3、如图3,正方形ABCD 中,点E 在BC 的延长线上,AE 平分∠DAC,则下列结论:(1)∠E=22.50. (2) ∠AFC=112.50. (3) ∠ACE=1350(4)AC=CE(5) AD ∶CE=1∶2. 其中正确的有( ) A 5个 B 4个 C 3个 D 2个4、如图4,在四边形ABCD 中,E 是AB 上的一点,△ADE 和△BCE 都是等边三角形,点P 、Q 、 M 、N 分别为AB 、BC 、CD 、DA 的中点,则四边形MNPQ 是( ) A 等腰梯形 B 矩形 C 菱形 D 正方形A DEFB C图(5)二、填空题5、如图5,正方形ABCD 中,∠DAF=25°,AF 交对角线BD 于E,交CD 于F, 则∠BEC= 度6、在矩形ABCD 中,对角线AC ,BD 相交于点O ,若对角线AC=10cm ,•边BC=•8cm ,•则△ABO 的周 长为________.7、在矩形ABCD 中,M 是BC 的中点,且MA ⊥MD .•若矩形ABCD•的周长为48cm ,•则矩形ABCD 的 面积为_______c m 2.三、解答题C BB '__D C 'D 'DAAQ E PMN DCBA 图(4)_ E _ F_ B_ C8、已知,如图,矩形ABCD 的对角线AC ,BD 相交于点O ,E ,F 分别是OA ,OB 的中点. (1)求证:△ADE ≌△BCF ;(2)若AD=4cm ,AB=8cm ,求OF 的长.10、如图,在正方形ABCD 中,E 是AB 上一点,F 是AD 延长线上一点,且DF =BE . ⑴求证:CE =CF ;⑵在图1中,若G 在AD 上,且∠GCE =45°,则GE =BE +GD 成立吗?为什么? ⑶运用⑴⑵解答中所积累的经验和知识,完成下题:如图2,在直角梯形ABCD 中,AD ∥BC (BC >AD ),∠B =90°,AB =BC =6,E 是AB 上一点, 且∠DCE =45°,BE =2,求DE 的长.6.如图1,在△ABC 中,AB=BC ,P 为AB 边上一点,连接CP ,以PA 、PC 为邻边作□APCD ,AC 与PD 相交于点E ,已知∠ABC=∠AEP=α(0°<α<90°). (1)求证:∠EAP=∠EPA;(2)□APCD 是否为矩形?请说明理由;(3)如图2,F 为BC 中点,连接FP ,将∠AEP 绕点E 顺时针旋转适当的角度,得到∠MEN(点M 、N 分别是∠MEN 的两边与BA 、FP 延长线的交点).猜想线段EM 与EN 之间的数量关系,并证明你的结论.图1ABDCE P 图2ABDCEPM NFB CA G D FEB CA DE图1图2。
平行四边形、矩形、菱形-正方形练习题

平行四边形、矩形、菱形、正方形1.已知:如图,在▱ABCD中,点E、F是对角线AC上的两点,且AE=CF.求证:BF∥DE.2.如图,平行四边形ABCD的对角线AC、BD交于点O,EF过点O且与BC、AD分别交于点E、F.试猜想线段AE、CF的关系,并说明理由.~3.如图,四边形ABCD是平行四边形,E、F分别是BC、AD上的点,∠1=∠2.求证:AF=CE.~4.已知:如图,在平行四边形ABCD中,点M在边AD上,且AM=DM.CM、BA的延长线相交于点E.求证:(1)AE=AB;(2)如果BM平分∠ABC,求证:BM⊥CE.5.如图,在▱ABCD中,点E、F在BD上,且BE=AB,DF=CD.求证:四边形AECF是平行四边形.-6.在▱ABCD中,E,F分别是AB,DC上的点,且AE=CF,连接DE,BF,AF.(1)求证:四边形DEBF是平行四边形;(2)若AF平分∠DAB,AE=3,DE=4,BE=5,求AF的长.)7.如图,在四边形ABCD中,AD∥BC,AC与BD交于点E,点E是BD的中点,延长CD到点F,使DF=CD,连接AF,(1)求证:AE=CE;(2)求证:四边形ABDF是平行四边形;(3)若AB=2,AF=4,∠F=30°,则四边形ABCF 的面积为.!8.如图,在▱ABCD中,E,F分别是AC上两点,BE⊥AC于E,DF⊥AC于F.求证:四边形BEDF为平行四边形.9.已知:如图,点E、F在线段BD上,AB=CD,∠B=∠D,BF=DE.|求证:(1)AE=CF;(2)AF∥CE.10.如图所示,▱ABCD中,E,F分别是AB、CD上的点,AE=CF,M、N分别是DE、BF的中点.(1)求证:四边形ENFM是平行四边形.、(2)若∠ABC=2∠A,求∠A的度数.11.在▱ABCD中,点E,F分别在AD,BC上,AE=CF,连接EF,BD.(1)求证:四边形EBFD是平行四边形;:(2)若∠C+∠ABE=90°,求证:BD=EF.12.如图,在▱ABCD中,AE⊥BD,CF⊥BD,E,F分别为垂足.(1)求证:△ABE≌△CDF.(2)求证:四边形AECF是平行四边形.<13.如图,在△NMB中,BM=6,点A,C,D分别在边MB、BN、MN上,DA∥NB,DC∥MB,∠NDC=∠MDA.求四边形ABCD的周长.;14.在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,0≤t≤5.(1)AE =,EF=|(2)若G,H分别是AB,DC中点,求证:四边形EGFH是平行四边形.(3)在(2)条件下,当t为何值时,四边形EGFH为矩形.15.如图,在▱ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF."(1)求证:四边形BFDE是矩形;(2)已知∠DAB=60°,AF是∠DAB的平分线,若AD=3,求DC的长度.)16.如图,▱ABCD中,O是AB的中点,CO=DO.(1)求证:▱ABCD是矩形.(2)若AD=3,∠COD=60°,求▱ABCD的面积.|17.如图,在△ABC中,AB=AC,D为BC中点,AE∥BD,且AE=BD (1)求证:四边形AEBD是矩形;(2)连接CE交AB于点F,若BE=2,AE=2,求EF的长.,18.如图,在平行四边形ABCD中,对角线AC、BD交于点O,AC⊥BC,AC=2,BC=3.点E是BC 延长线上一点,且CE=3,连结DE.(1)求证:四边形ACED为矩形.(2)连结OE,求OE的长.|19.如图,▱ABCD中,点E在BC延长线上,EC=BC,连接DE,AC,AC⊥AD于点A.(1)求证:四边形ACED是矩形;(2)连接BD,交AC于点F.若AC=2AD,猜想∠E与∠BDE的数量关系,并证明你的猜想.|20.如图,在△ABC中,BD平分∠ABC交AC于D,作DE∥BC交AB于点E,作DF∥AB交BC于点F.(1)求证:四边形BEDF是菱形;(2)若∠BDE=15°,∠C=45°,CD=,求DE的长.|21.如图,在△ABC中,BD平分∠ABC交AC于D,EF垂直平分BD,分别交AB,BC,BD于E,F,G,连接DE,DF.(1)求证:四边形BEDF是菱形;(2)若∠BDE=15°,∠C=45°,DE=2,求CF的长./22.如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE 的延长线于点F.](1)求证:四边形ADCF是菱形;(2)若AC=12,AB=16,求菱形ADCF的面积."23.如图,在四边形ABCD中,对角线AC、BD交于点O,AB∥DC,AB=BC,BD平分∠ABC,过点C 作CE⊥AB交AB的延长线于点E,连接OE.(1)求证:四边形ABCD是菱形;(2)若AB=2,BD=4,求OE的长.24.如图,AC是▱ABCD的对角线,∠BAC=∠DAC.(1)求证:四边形ABCD是菱形;}(2)若AB=2,AC=2,求四边形ABCD的面积.25.同学张丰用一张长18cm、宽12cm矩形纸片折出一个菱形,他沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到四边形AECF(如图).@(1)证明:四边形AECF是菱形;(2)求菱形AECF的面积.!26.如图,EF是平行四边形ABCD的对角线BD的垂直平分线,EF与边AD、BC分别交于点E、F.(1)求证:四边形BFDE是菱形;(2)若ED=5,BD=8,求菱形BFDE的面积.|27.如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.(1)求证:四边形ABCD是菱形;(2)若∠ADB=30°,BD=12,求AD的长.—28.如图,在▱ABCD中,BC=2AB,点E、F分别是BC、AD的中点,AE、BF交于点O,连接EF,OC.(1)求证:四边形ABEF是菱形;(2)若AB=4,∠ABC=60°,求OC的长.<29.已知:如图,菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.#(1)求证:四边形ABCD是正方形.(2)E是OB上一点,DH⊥CE,垂足为H,DH与OC相交于点F,求证:OE=OF.30.已知:如图,在矩形ABCD中,E是BC边一点,DE平分∠ADC,EF∥DC交AD边于点F,连结BD.(1)求证:四边形EFCD是正方形;(2)若BE=1,ED=2,求BD的长.{31.如图,正方形ABCD的对角线AC与BD交于点O,分别过点C、点D作CE∥BD,DE∥AC.求证:四边形OCED是正方形.【32.如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40cm.(1)求证:四边形BFEG是矩形;(2)求四边形EFBG的周长;(3)当AF的长为多少时,四边形BFEG是正方形《33.如图,正方形ABCD的对角线AC、BD相交于点O,BE∥AC,CE∥DB.求证:四边形OBEC是正方形.\34.E、F、M、N分别是正方形ABCD四条边上的点,AE=BF=CM=DN,四边形EFMN是什么图形证明你的结论.35.如图,点E、F分别是矩形ABCD的边AB、CD上的一点,且DF=BE.求证:四边形AECF是平行四边形.;36.如图,矩形ABCD中,对角线AC、BD交于点O,以AD、OD为邻边作平行四边形ADOE,连接BE.求证:四边形AOBE为菱形.>37.如图,在矩形ABCD中,点O为对角线AC的中点,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE,CF.(1)求证:四边形AECF是菱形;(2)连接OB,若AB=8,AF=10,求OB的长.38.如图,已知在菱形ABCD中,∠ABC=60°,对角线AC=8,求菱形ABCD的周长和面积./39.如图,在菱形ABCD中,过点B作BE⊥AD于E,过点B作BF⊥CD于F,求证:AE=CF.>40.如图,菱形ABCD的对角线AC和BD交于点O,AB=10,∠ABC=60°,求AC和BD的长.41.如图,已知菱形ABCD两条对角线BD与AC的长之比为3:4,周长为40cm,求菱形的高及面积.,42.如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,~(1)求证:∠DHO=∠DCO.(2)若OC=4,BD=6,求菱形ABCD的周长和面积.】43.如图,菱形ABCD中,对角线AC、BD相交于点O,点E是AB的中点,已知AC=8cm,BD=6cm,(1)求菱形ABCD的面积.(2)求OE的长度.44.在菱形ABCD中,E是AB边的中点,连接DE,DE⊥AB,对角线AC、BD交于点H.(1)求∠ABC的度数;(2)如果菱形的对角线AC=2,求菱形的面积.<¥45.如图,在正方形ABCD中,点E,F在对角线BD上,AE∥CF,连接AF,CE.(1)求证:△ABE≌△CDF;(2)试判断四边形AECF的形状,并说明理由.46.如图,小方将一个正方形纸片剪去一个宽为4cm的长方形(记作A)后,再将剩下的长方形纸片剪去一个宽为5cm的长方形(记作B).(1)若A与B的面积均为Scm2,求S的值.(2)若A的周长是B的周长的倍,求这个正方形的边长.47.已知:如图,E,F是正方形ABCD的对角线BD上的两点,且BE=DF.求证:四边形AECF是菱形48.如图,正方形ABCD中,点P,Q分别为AD,CD边上的点,且DQ=CP,连接BQ,AP.求证:BQ =AP.49.如图,已知正方形CDEF的面积为169cm2,且AC⊥AF,AB=3cm,BC=4cm,AF=12cm,试判断△ABC的形状,并说明你的理由.50.如图,正方形ABCD中,AB=AD,G为BC边上一点,BE⊥AG,于E,DF⊥AG于F,连接DE.(1)求证:△ABE≌△DAF;(2)若AF=1,EF=4,求四边形ABED的面积.。
九年级数学中考复习课题矩形、菱形、正方形AB组习题专题课后训练分层练习B组提高题含答案解析

九年级数学中考复习课题矩形、菱形、正方形AB组习题专题课后训练分层练习B组提高题含答案解析A组1.下列性质中,菱形具有而平行四边形不具有的性质是()A.对边平行且相等B.对角线互相平分C.对角线互相垂直D.对角互补解:A、平行四边形的对边平行且相等,所以A选项错误;B、平行四边形的对角线互相平分,所以B选项错误;C、菱形的对角线互相垂直,平行四边形的对角线互相平分,所以C选项正确;D、平行四边形的对角相等,所以D选项错误.故选C.2.矩形具有而菱形不一定具有的性质是()A.对边分别相等B.对角分别相等C.对角线互相平分D.对角线相等解:矩形的性质有:①矩形的对边相等且平行,①矩形的对角相等,且都是直角,①矩形的对角线互相平分、相等;菱形的性质有:①菱形的四条边都相等,且对边平行,①菱形的对角相等,①菱形的对角线互相平分、垂直,且每一条对角线平分一组对角;①矩形具有而菱形不一定具有的性质是对角线相等,故选D.3.顺次连接四边形ABCD各边中点所成的四边形为菱形,那么四边形ABCD的对角线AC 和BD只需满足的条件是()A.相等B.互相垂直C.相等且互相垂直D.相等且互相平分解:因为原四边形的对角线与连接各边中点得到的四边形的关系:①原四边形对角线相等,所得的四边形是菱形;①原四边形对角线互相垂直,所得的四边形是矩形;①原四边形对角线既相等又垂直,所得的四边形是正方形;①原四边形对角线既不相等又不垂直,所得的四边形是平行四边形.因为顺次连接四边形ABCD各边中点所成的四边形为菱形,所以四边形ABCD的对角线AC和BD相等.故选A.4.已知菱形的两条对角线长分别是6cm和8cm,则菱形的边长是()A.12cm B.10cm C.7cm D.5cm解:如图:①菱形ABCD中BD=8cm,AC=6cm,①OD=BD=4cm,OA=AC=3cm,在直角三角形AOD中AD===5cm.故选D.5.如图,菱形纸片ABCD,①A=60°,P为AB中点,折叠菱形纸片ABCD,使点C落在DP所在的直线上,得到经过点D的折痕DE,则①DEC等于75度.解:连接BD,①四边形ABCD为菱形,①A=60°,①①ABD为等边三角形,①ADC=120°,①C=60°,①P为AB的中点,①DP为①ADB的平分线,即①ADP=①BDP=30°,①①PDC=90°,①由折叠的性质得到①CDE=①PDE=45°,在①DEC中,①DEC=180°﹣(①CDE+①C)=75°.故答案为:75.6.如图:在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则DE的长是3.解:如图,连接CE,,设DE=x,则AE=8﹣x,①OE①AC,且点O是AC的中点,①OE是AC的垂直平分线,①CE=AE=8﹣x,在Rt①CDE中,x2+42=(8﹣x)2解得x=3,①DE的长是3.故答案为:3.7.如图,矩形ABCD中,对角线AC、BD交于点O,点E是BC上一点,且AB=BE,①1=15°,则①2=30°.解:①四边形ABCD是矩形,①①ABC=①BAD=90°,OB=OD,OA=OC,AC=BD,①OB=OC,OB=OA,①①OCB=①OBC,①AB=BE,①ABE=90°,①①BAE=①AEB=45°,①①1=15°,①①OCB=①AEB﹣①EAC=45°﹣15°=30°,①①OBC=①OCB=30°,①①AOB=30°+30°=60°,①OA=OB,①①AOB是等边三角形,①AB=OB,①①BAE=①AEB=45°,①AB=BE,①OB=BE,①①OEB=①EOB,①①OBE=30°,①OBE+①OEB+①BEO=180°,①①OEB=75°,①①AEB=45°,①①2=①OEB﹣①AEB=30°,故答案为:30°.8.如图,在Rt①ABC中,①ACB=90°,D为AB的中点,AE①CD,CE①AB,连接DE交AC于点O.(1)证明:四边形ADCE为菱形.(2)BC=6,AB=10,求菱形ADCE的面积.证明:(1)①在Rt①ABC中,①ACB=90°,D为AB中点,①CD=AB=AD,又①AE①CD,CE①AB①四边形ADCE是平行四边形,①平行四边形ADCE是菱形;(2)在Rt①ABC中,AC===8.①平行四边形ADCE是菱形,①CO=OA,又①BD=DA,①DO是①ABC的中位线,①BC=2DO.又①DE=2DO,①BC=DE=6,①S菱形ADCE===24.B组9.如图:点P是Rt①ABC斜边AB上的一点,PE①AC于E,PF①BC于F,BC=15,AC=20,则线段EF的最小值为()A.12B.6C.12.5D.25解:如图,连接CP.①①C=90°,AC=3,BC=4,①AB===25,①PE①AC,PF①BC,①C=90°,①四边形CFPE是矩形,①EF=CP,由垂线段最短可得CP①AB时,线段EF的值最小,此时,S①ABC=BC•AC=AB•CP,即×20×15=×25•CP,解得CP=12.故选A.10.如图,在菱形ABCD中,①BAD=80°,AB的垂直平分线交对角线AC于点F,点E为垂足,连接DF,则①CDF为()A.80°B.70°C.65°D.60°解:如图,连接BF,在①BCF和①DCF中,①CD=CB,①DCF=①BCF,CF=CF①①BCF①①DCF①①CBF=①CDF①FE垂直平分AB,①BAF=×80°=40°①①ABF=①BAF=40°①①ABC=180°﹣80°=100°,①CBF=100°﹣40°=60°①①CDF=60°.故选D.11.如图,在菱形ABCD中,①A=110°,E,F分别是边AB和BC的中点,EP①CD于点P,则①FPC的度数为()A.55°B.50°C.45°D.35°解:延长PF交AB的延长线于点G.如图所示:在①BGF与①CPF中,,①①BGF①①CPF(ASA),①GF=PF,①F为PG中点.又①由题可知,①BEP=90°,①EF=PG,①PF=PG,①EF=PF,①①FEP=①EPF,①①BEP=①EPC=90°,①①BEP﹣①FEP=①EPC﹣①EPF,即①BEF=①FPC,①四边形ABCD为菱形,①AB=BC,①ABC=180°﹣①A=70°,①E,F分别为AB,BC的中点,①BE=BF,①BEF=①BFE=(180°﹣70°)=55°,①①FPC=55°;故选:A.12.如图,矩形ABCD中,对角线AC、BD交于点O,点E是BC上一点,且AB=BE,①1=15°,则①2=30°.解:①四边形ABCD是矩形,①①ABC=①BAD=90°,OB=OD,OA=OC,AC=BD,①OB=OC,OB=OA,①①OCB=①OBC,①AB=BE,①ABE=90°,①①BAE=①AEB=45°,①①1=15°,①①OCB=①AEB﹣①EAC=45°﹣15°=30°,①①OBC=①OCB=30°,①①AOB=30°+30°=60°,①OA=OB,①①AOB是等边三角形,①AB=OB,①①BAE=①AEB=45°,①AB=BE,①OB=BE,①①OEB=①EOB,①①OBE=30°,①OBE+①OEB+①BEO=180°,①①OEB=75°,①①AEB=45°,①①2=①OEB﹣①AEB=30°,故答案为:30°.13.(2019•绍兴)如图,在直线AP上方有一个正方形ABCD,①P AD=30°,以点B为圆心,AB长为半径作弧,与AP交于点A,M,分别以点A,M为圆心,AM长为半径作弧,两弧交于点E,连结ED,则①ADE的度数为15°或45°.【分析】分点E与正方形ABCD的直线AP的同侧、点E与正方形ABCD的直线AP的两侧两种情况,根据正方形的性质、等腰三角形的性质解答.解:①四边形ABCD是正方形,①AD=AE,①DAE=90°,①①BAM=180°﹣90°﹣30°=60°,AD=AB,当点E与正方形ABCD的直线AP的同侧时,由题意得,点E与点B重合,①①ADE=45°,当点E与正方形ABCD的直线AP的两侧时,由题意得,E′A=E′M,①①AE′M为等边三角形,①①E′AM=60°,①①DAE′=360°﹣120°﹣90°=150°,①AD=AE′,①①ADE′=15°,故答案为:15°或45°.14.如图:在①ABC中,CE、CF分别平分①ACB与它的邻补角①ACD,AE①CE于E,AF①CF 于F,直线EF分别交AB、AC于M、N.(1)求证:四边形AECF为矩形;(2)试猜想MN与BC的关系,并证明你的猜想;(3)如果四边形AECF是菱形,试判断①ABC的形状,直接写出结果,不用说明理由.(1)证明:①AE①CE于E,AF①CF于F,①①AEC=①AFC=90°,又①CE、CF分别平分①ACB与它的邻补角①ACD,①①BCE=①ACE,①ACF=①DCF,①①ACE+①ACF=(①BCE+①ACE+①ACF+①DCF)=×180°=90°,①三个角为直角的四边形AECF为矩形.(2)结论:MN①BC且MN=BC.证明:①四边形AECF为矩形,①对角线相等且互相平分,①NE=NC,①①NEC=①ACE=①BCE,①MN①BC,又①AN=CN(矩形的对角线相等且互相平分),①N是AC的中点,若M不是AB的中点,则可在AB取中点M1,连接M1N,则M1N是①ABC的中位线,MN①BC,而MN①BC,M1即为点M,所以MN是①ABC的中位线(也可以用平行线等分线段定理,证明AM=BM)①MN=BC;法二:延长MN至K,使NK=MN,因为对角线互相平分,所以AMCK是平行四边形,KC①MA,KC=AM因为MN①BC,所以MBCK是平行四边形,MK=BC,所以MN=BC(3)解:①ABC是直角三角形(①ACB=90°).理由:①四边形AECF是菱形,①AC①EF,①EF①AC,①AC①CB,①①ACB=90°.即①ABC是直角三角形.15.如图,在①ABC中,①ABC=90°,BD为AC的中线,过点C作CE①BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.(1)求证:BD=DF;(2)求证:四边形BDFG为菱形;(3)若AG=13,CF=6,求四边形BDFG的周长.(1)证明:①①ABC=90°,BD为AC的中线,①BD=AC,①AG①BD,BD=FG,①四边形BGFD是平行四边形,①CF①BD,①CF①AG,又①点D是AC中点,①DF=AC,①BD=DF;(2)证明:①BD=DF,①四边形BGFD是菱形,(3)解:设GF=x,则AF=13﹣x,AC=2x,①在Rt①ACF中,①CFA=90°,①AF2+CF2=AC2,即(13﹣x)2+62=(2x)2,解得:x=5,①四边形BDFG的周长=4GF=20.。
16.2 矩形-菱形与正方形的性质同步练习
16.2矩形、菱形与正方形的性质一、课内训练:1.如图,矩形ABCD的两条对角线相交于O,∠AOD=120°,AB=4cm,求对角线AC的长.(1) (2)4.如图,以正方形ABCD的边CD为一边在正方形外作等边△CDE,连接BE,交正方形的对角线AC于点F,连接DF,求∠AFD的度数.5.(1)如图,把一矩形ABCD的纸片,沿EF折叠后,点D、C分别落在D′、C′的位置上,ED′与BC的交点为G,若∠EFG=55°,求∠1、∠2的度数.(2)如图,把一矩形纸片ABCD,沿EF折叠后,点D和点B重合,点C落在C•′位置,若AB=4cm,AD=12cm,求BE的长度.6.已知△ABC,∠A:∠B:∠C=1:2:3,AB=6cm,D为AB边上的中点,求CD的长.7.•已知菱形的边长为10cm,•则菱形对角线的交点到四条边中点的距离之和为_____cm.8.如图所示,在矩形ABCD中,对角线AC分∠BAD为∠1,∠2,且∠1:∠2=1:2,AB=3cm,求AC的长.9.菱形ABCD的两条对角线分别为5cm,12cm,则菱形ABCD的面积为多少?10.对于左栏的案例4,采用“补短法”还可以怎样作辅助线,证明出BE=BG+FC?11.如图,E、F分别在正方形ABCD的边AD、CD上,且∠FBC=∠EBF,• 求证:BE=AE+CF.二、课外演练1.正方形具有而菱形不一定具有的特征是()A.四条边都相等 B.对角线互相垂直平分C.对角线平分一组对角 D.对角线相等2.一个菱形的两条对角线长分别为7cm和8cm,则这个菱形的面积为()A.56cm2 B.28cm2 C.14cm2 D.36cm23.如图,EF为矩形ABCD对角线的交点O,•且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD面积的()A.15B.14C.13D.310(第3题)(第6题)(第8题)4.若矩形的一条对角线与一边的夹角是40°,则两条对角线相交所成的锐角是()A.20° B.40° C.80° D.100°5.菱形的一条对角线与一条边长相等,则这菱形锐角的度数为_______.6.如图,已知矩形ABCD的对角线相交于点O,△AOD的周长比△AOB的周长大8cm,矩形周长是80cm,求矩形ABCD的面积.7.如果矩形的两条对角线所成的角中有一个角为60°,那么()A.它的对角线长是长边长度的2倍 B.它的对角线长是短边长度的2倍C.它的长边是短边长度的2倍 D.上述关系无法确定8.如图,矩形ABCD中,AD=30,AB=20,E、F三等分对角线AC,则S△ABE=()A.60 B.100 C.150 D.2009.能够在图形内找到一点,使该点到四边形的各边距离都相等,则该四边形一定是() A.平行四边形、菱形; B.矩形、正方形; C.矩形、菱形; D.菱形、正方形10.如图16-2-21,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠BAE,则∠EAC为()A.30° B.45° C.60° D.75°(第10题)(第14题)(第15题)11.矩形的一个角的平分线把矩形的一边分成5cm或8cm,此矩形周长为_____cm.12.菱形的面积为24cm2,一条对角线的长为8cm,则另一条对角线的长是_____cm.13.菱形的周长是20cm,那么一边上的中点到两条对角线交点的距离为______cm.14.如图,若点P是正方形ABCD内任意一点,且正方形的边长为1,若S△ABP=0.4,则S△DCP =______.15.如图,正方形ABCD的对角线相交于O点,点O是正方形A′B′C′O的一个顶点,如19.在如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A、B、C、D的面积和是多少?20.阅读以下短文,然后解决下列问题:如果一个三角形和一个矩形满足条件:三角形的一边与矩形的一边重合,且三角形的这边所对的顶点在矩形这边的对边上,•则称这样的矩形为三角形的“友好矩形”,如图①所示,矩形ABEF即为△ABC的“友好矩形”.显然,当△ABC•是钝角三角形时,其“友好矩形”只有一个.(1)仿照以上叙述,说明什么是一个三角形的“友好平行四边形”.(2)如图②,若△ABC为直角三角形,且∠C=90°,在图16-2-28•②中画出△ABC的所有“友好矩形”,并比较这些矩形面积的大小.(3)若△ABC是锐角三角形,且BC>AC>AB.在图③中画出△ABC的所有“友好矩形”,指出其中周长最小的矩形并加以证明.答案:一、课内训练:1.解:∵四边形ABCD是矩形,∴AC=BD,AO=CO=12AC,OB=OD=12BD(矩形对角线相等且互相平分).∴AO=CO=OB=OD.又∵∠AOD=120°,∴∠AOB=60°.∴△AOB是等边三角形.即AO=BO=AB=4(cm).∴AC=2×4=8(cm).点拨:根据矩形的对角线相等且互相平分的特征,矩形的两条对角线把矩形分成了四个等腰三角形,若矩形的两条对角线的夹角中,如果有60°或120°的角,则必有等边三角形.2.解:∵四边形ABCD为菱形,∴AB=AD.又∵∠A=60°,∴△ABD为等边三角形.∴AB=AD=BD=5.∴菱形的周长为4AB=5×4=20.点拨:根据菱形的特征,四条边都相等,所以AB=AD,结合∠A=60°,可得△ABD•为等边三角形,从而求得菱形的边长,进而求得菱形的周长.3.解:(1)因为四边形ABCD是正方形.所以∠BOE=∠AOF=90°,OA=OB.又因为AM⊥EB,所以∠MAE+∠MEA=90°=∠OBE+∠MEA.所以∠MAE=∠OBE.所以△AOF绕O点逆时针方向旋转90°可与△BOE重合.所以OE=OF.(2)OE=OF仍成立,说明如下:因为四边形ABCD是正方形,所以∠BOE=∠AOF=90°,BO=AO.因为AM⊥EB,所以∠OEB+∠OAM=90°=∠OFA+∠OAM.所以∠OEB=∠OFA.所以△AOF绕O点逆时针旋转90°后可与△BOE重合.所以OE=OF.点拨:要使OE=OF,只需证明△AOF和△BOE重合,根据已知条件和正方形的特征易得到,“问题”的基本思路是先假设结论成立,然后用分析法探求其成立条件,•若题设所给条件满足要求,则成立,反之则不成立.4.解:∵四边形ABCD是正方形.∴AB=AD,∠BAF=∠DAF.∴△ABF与△ADF全等.∴∠AFD=∠AFB.∵CB=CE,∴∠CBE=∠CEB.∵∠BCE=∠BCD+∠DCE=90°+60°=150°,∴∠CBE=15°.∵∠ACB=45°,∴∠AFB=∠ACB+∠CBE=60°.∴∠AFD=60°.点拨:易得△ABF与△ADF全等,∠AFD=∠AFB,因此只要求出∠AFB的度数即可.由∠AFB=∠ACB+∠EBC,∠ACB=45°,转化为求∠EBC的度数,在等腰△BCE中可求得.5.(1)解:在矩形ABCD中,AD∥BC,∴∠DEF=∠EFB,∠1+∠2=180°.又∵∠EFG=55°,由对称性可知∠GEF=∠DEF=55°.∴∠1=180°-∠GEF-∠DEF=70°.∴∠2=180°-∠1=110°.10.如图,过点G作BC的平行线交DC的延长线于点H,则得矩形BGHC.∴GH=BC=AB,BG=CH,∵∠HGF+∠AGE=90°,∠BAE+∠AGE=90°,∴∠BAE=∠HGF.解①②得 AD=24,AB=16.∴S矩形ABCD=24×16=384(cm2).点拨:利用矩形的对角线相等且互相平分.7.B 点拨:当矩形两条对角线夹角中有一个为60°时,一定有等边三角形.8.B 点拨:S矩形=20×30=600,S△ABC =12×600=300.9.D 点拨:由于菱形和正方形的对角线平分每一组内角,•而角平分线上的点到角两边的距离相等,因此菱形和正方形对角线的交点即为满足题意的点.10.B 点拨:由∠DAE=3∠BAE,得∠BAE=22.5°,18.如图19.解:由勾股定理得S A+S B+S C+S D=S最大正方形=49.20.解:(1)如果一个三角形和一个平行四边形满足条件:三角形的一边与平行四边形的一边重合,三角形这边所对的顶点在平行四边形这边的对边上,则称这样的平行四边(2)题 (3)题)此时共有3个友好矩形,如图的及ABHK,其中的矩形ABHK证明如下:易知,这三个矩形的面积相等,令其为.∴L1-L2>0,即L1>L2,同理可得L2>L3.∴L3最小,即矩形ABHK的周长最小.点拨:根据矩形的特征、三角形面积的有关知识解决.。
平行四边形、矩形、菱形、正方形综合培优训练
平行四边形、矩形、菱形、正方形综合培优训练1、如图所示,已知□ABCD 中,若AD=2AB ,AB=BF=AE ,则EC 与FD 垂直,试说明理由。
2、如图所示,Rt △ABC 中,∠ACB=90°,CD ⊥AB 于D ,AE 平分∠CAB 交CD 于H ,求证:CE=BH 。
3、如图所示,在□ABCD 中,AB=2BC ,M 为AB 的中点,求证:CM ⊥DM 。
4、如图所示,某市有一个呈四边形的休闲广场,在它的四个角A 、B 、C 、D 处均有一颗古树,为了美化城市决定将广场面积扩大一倍,又必须保留这四颗古树,并要求扩建后的休闲广场呈平行四边形,则该市能否实现这一设想?若能,请设计并画出图形;若不能,请说明理由。
(画图要保留痕迹,不写画法)OD C F B AE BH E D A CC B AM DCDBA5、如图所示,在□ABCD 中,∠A=60°,E 、F 分别为AB 、CD 的重点,AB=2AD ,求证:BD=3EF 。
6、如图所示,AD 为△ABC 的中线,E 为AC 上一点,连接BE ,交AD 于F ,且AE=FE ,试说明:BF=AC 。
7、如图所示,△ABC 为等边三角形,P 是△ABC 内任一点,PD//AB ,PE//BC ,PF//AC ,若△ABC 的周长为12,则PD+PE+PF= 。
8、如图所示,在□ABCD 中,E 、F 、G 、H 分别是四条边上的点,且满足AE=CF ,BG=DH ,连接EF 、GH 。
求证:EF 与GH 互相平行。
9、如图所示,在四边形ABCD 中,AD//BC ,且AD>BC ,BC=6cm ,P 、Q 分别从A 、C 同时出发,P 以1cm/s 的速度由A 向D 运动,Q 以2cm/s 的速度由C 向B 运动,几秒后四边形ABQP 是平行四边形?C BEFDA ACED B F CE DA PB FC GBHDAD CA PBQ10、如图所示,E 为菱形ABCD 边AB 上一点,且AB=AE ,AE 交BD 于O ,且∠DAE=2∠BAE ,求证:EB=OA 。
矩形、菱形与正方形-专题训练(含答案)(可编辑修改word版)
3矩形、菱形与正方形专题训练(含答案)班级姓名成绩一、选择题(每小题3 分,共30 分)1.如图,把矩形ABCD 沿EF 翻折,点B 恰好落在AD 边的B′ 处,若AE=2,DE =6,∠EFB=60°,则矩形ABCD 的面积是( )A.12 B.24 C.12 D.16第1 题图第2 题图第3 题图第4 题图2.如图,菱形ABCD 中,∠B=60°,AB=4,则以AC 为边长的正方形ACEF 的周长为( ) A.14 B.15 C.16 D.173.如图,将矩形ABCD 沿对角线BD 折叠,使点C 与点C′重合.若AB=2,则C′D 的长为( ) A.1 B.2 C.3 D.44.如图,在△ABC 中,AC=BC,点D,E 分别是边AB,AC 的中点.将△ADE 绕点E 旋转180°得△CFE,则四边形ADCF 一定是( )A.矩形B.菱形C.正方形D.梯形5.由菱形的两条对角线的交点向各边引垂线,以各垂足为顶点的四边形是( )A.平行四边形B.矩形C.菱形D.正方形6.如图,▱ABCD 的周长为16 cm,AC,BD 相交于点O,OE⊥AC 交AD 于点E,则△DCE 的周长为( )A.4 cm B.6 cm C.8 cm D.10 cm第6 题图第9 题图第10 题图7.菱形的周长为8 cm,高为1 cm,则菱形两邻角度数比为( )A.3∶1 B.4∶1 C.5∶1 D.6∶138.用两块完全相同的直角三角形拼下列图形:①平行四边形,②矩形,③菱形,④正方形,⑤等腰三角形,⑥等边三角形,一定能拼成的图形是( )A.①④⑤B.②⑤⑥C.①②③D.①②⑤9.如图,边长为6 的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )A.16 B.17 C.18 D.1910.如图,F 为正方形ABCD 的边AD 上一点,CE⊥CF 交AB 的延长线于点E,若正方形ABCD 的面积为64,△CEF 的面积为50,则△CBE 的面积为( )A.20 B.24 C.25 D.26二、填空题(每小题3 分,共24 分)11.如图所示,在菱形ABCD 中,∠ADC=72°,AD 的垂直平分线交对角线BD 于点P,垂足为点E,连结CP,则∠CPB=度.第11 题图第12 题图第14 题图第15 题图12.如图,四边形ABCD 的两条对角线AC,BD 互相垂直,A1,B1,C1,D1分别是四边形ABCD 各边中点,如果AC=8,BD=10,则四边形A1B1C1D1的面积为.13.矩形的对角线相交成的角中,有一个角是60°,这个角所对的边长为20 cm,则其对角线长为-_,矩形的面积为.14.如图,四边形ABCD 是菱形,对角线AC 和BD 相交于点O,AC=4 cm,BD=8 cm,则这个菱形的面积是cm2.15.如图,矩形ABCD 中,点E,F 分别是AB,CD 的中点,连结DE 和BF,分别取DE,BF 的中点M,N,连结AM,CN,MN,若AB=2 2,BC=2 3,则图中阴影部分的面积为.,第16 题图第17 题第18 题图16.如图,▱ABCD 的对角线相交于点O,请你添加一个条件,使▱ABCD 是矩形.17.如图,正方形ABCD 中,对角线AC,BD 交于点O,E 点在BC 上,EG⊥OB,EF⊥OC,垂足分别为点G,F,AC=10,则EG+EF=.18.如图,在平面直角坐标系中,矩形OABC 的顶点A,C 的坐标分别为(10,0),(0,4),点D是OA 的中点,点P 在BC 上运动,当△ODP 是腰长为5 的等腰三角形时,点P 的坐标为.三、解答题(共66 分)19.(6 分)如图,已知矩形ABCD 中,E是AD 上一点,F是AB 上一点,EF⊥EC 且EF=EC,DE=4 cm,矩形ABCD 的周长为32 cm,求AE 的长.20.(8 分)如图,在矩形ABCD 中,对角线BD 的垂直平分线MN 与AD 相交于点M,与BD 相交于点O,与BC 相交于点N,连结BM,DN.(1)求证:四边形BMDN 是菱形;(2)若AB=4,AD=8,求MD 的长.21.(8 分)如图所示,矩形ABCD 中,AE⊥BD 于点E,∠DAE∶∠BAE=3∶1,求∠BAE 和∠EAO的度数.22.(10 分)如图,已知菱形ABCD 中,AB=AC,E,F 分别是BC,AD 的中点,连结AE,CF. (1)证明:四边形AECF 是矩形;(2)若AB=8,求菱形ABCD 的面积.23.(12 分)如图,已知四边形ABCD 是平行四边形,DE⊥AB,DF⊥BC,垂足分别是点E,F,并且DE=DF,求证:(1)△ADE≌△CDF;(2)四边形ABCD 是菱形.24.(10 分)在四边形ABCD 中,AB=CD,M,N,P,Q 分别是AD,BC,BD,AC 的中点,求证:MN 与PQ 互相垂直平分.参考答案一、选择题(每小题3 分,共30 分)1.如图,把矩形ABCD 沿EF 翻折,点B 恰好落在AD 边的B′ 处,若AE=2,DE =6,∠EFB=60°,则矩形ABCD 的面积是( D )A.12 B.24 C.12 D.16第1 题图第2 题图第3 题图第4 题图2.如图,菱形ABCD 中,∠B=60°,AB=4,则以AC 为边长的正方形ACEF 的周长为( C ) A.14 B.15 C.16 D.173.如图,将矩形ABCD 沿对角线BD 折叠,使点C 与点C′重合.若AB=2,则C′D 的长为( B ) A.1 B.2 C.3 D.44.如图,在△ABC 中,AC=BC,点D,E 分别是边AB,AC 的中点.将△ADE 绕点E 旋转180°得△CFE,则四边形ADCF 一定是( A )A.矩形B.菱形C.正方形D.梯形5.由菱形的两条对角线的交点向各边引垂线,以各垂足为顶点的四边形是( B )A.平行四边形B.矩形C.菱形D.正方形6.如图,▱ABCD 的周长为16 cm,AC,BD 相交于点O,OE⊥AC 交AD 于点E,则△DCE 的周长为( C )A.4 cm B.6 cm C.8 cm D.10 cm第6 题图第9 题图第10 题图7.菱形的周长为8 cm,高为1 cm,则菱形两邻角度数比为( C )A.3∶1 B.4∶1 C.5∶1 D.6∶18.用两块完全相同的直角三角形拼下列图形:①平行四边形,②矩形,③菱形,④正方形,⑤等腰三角形,⑥等边三角形,一定能拼成的图形是( D )A.①④⑤B.②⑤⑥C.①②③D.①②⑤9.如图,边长为6 的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( B )A.16 B.17 C.18 D.1910.如图,F 为正方形ABCD 的边AD 上一点,CE⊥CF 交AB 的延长线于点E,若正方形ABCD 的面积为64,△CEF 的面积为50,则△CBE 的面积为( B )A .20B .24C .25D .26二、填空题(每小题 3 分,共 24 分)11. 如图所示,在菱形 ABCD 中,∠ADC =72°,AD 的垂直平分线交对角线 BD 于点 P ,垂足为点E ,连结 CP ,则∠CPB = 72 度.第 11 题图 第 12 题图 第 14 题图 第 15 题图12. 如图,四边形 ABCD 的两条对角线 AC ,BD 互相垂直,A 1,B 1,C 1,D 1 分别是四边形 ABCD各边中点,如果 AC =8,BD =10,则四边形 A 1B 1C 1D 1 的面积为 20 .13. 矩形的对角线相交成的角中,有一个角是 60°,这个角所对的边长为 20 cm ,则其对角线长为40_cm ,矩形的面积为 400_cm 2 .14. 如图,四边形 ABCD 是菱形,对角线 AC 和 BD 相交于点 O ,AC =4 cm ,BD =8 cm ,则这个菱形的面积是 16 cm 2.15. 如图,矩形 ABCD 中,点 E ,F 分别是 AB ,CD 的中点,连结 DE 和 BF ,分别取 DE ,BF 的中点 M ,N ,连结 AM ,CN ,MN ,若 AB =2,BC =2,则图中阴影部分的面积为 2 .,第 16 题图 第 17 题 第 18 题图16. 如图,▱ABCD 的对角线相交于点 O ,请你添加一个条件 AO =BO (答案不唯一),使▱ABCD是矩形.17. 如图,正方形 ABCD 中,对角线 AC ,BD 交于点 O ,E 点在 BC 上,EG ⊥OB ,EF ⊥OC ,垂足分别为点 G ,F ,AC =10,则 EG +EF = 5 .18. 如图,在平面直角坐标系中,矩形 OABC 的顶点 A ,C 的坐标分别为(10,0),(0,4),点 D是O A 三、解答题(共 66 分)19.(6 分)如图,已知矩形 ABCD 中,E 是 AD 上一点,F 是 AB 上一点,EF ⊥EC 且 EF =EC ,DE =4 cm ,矩形 ABCD 的周长为 32 cm ,求 AE 的长.解:∵∠AFE+∠AEF=∠AEF+∠CED=90°,∴∠AFE=∠DEC.又∵∠A=∠D=90°,EF=EC,∴△AEF≌△DCE,∴AE=CD.设AE=x,则CD=x,∴AD+CD=1×32,即x+4+x=16,2∴x=6.即AE=6 cm20.(8 分)如图,在矩形ABCD 中,对角线BD 的垂直平分线MN 与AD 相交于点M,与BD 相交于点O,与BC 相交于点N,连结BM,DN.(1)求证:四边形BMDN 是菱形;(2)若AB=4,AD=8,求MD 的长.解:(1)∵MN 是BD 的垂直平分线,∴BO=DO,∠BON=∠DOM=90°.∵四边形ABCD 是矩形,∴AD∥BC,∴∠BNO=∠DMO,∴△BON≌△DOM(AAS),∴OM=ON.∵OB=OD,∴四边形BMDN 是平行四边形.∵MN⊥BD,∴▱BMDN 是菱形(2)设MD=x,则MB=x,MA=8-x,在Rt△ABM 中,∵BM2=AM2+AB2,∴x2=(8-x)2+42,解得x=5.∴MD 的长为521.(8 分)如图所示,矩形ABCD 中,AE⊥BD 于点E,∠DAE∶∠BAE=3∶1,求∠BAE 和∠EAO 的度数.解:提示:由∠DAE∶∠BAE=3∶1,求出∠BAE=22.5°,而∠ABD=90°-∠BAE=90°-22.5°=67.5°,∵∠BAO=∠ABD=67.5°,∴∠EAO=∠BAO-∠BAE=67.5°-22.5°=45°22.(10 分)如图,已知菱形ABCD 中,AB=AC,E,F 分别是BC,AD 的中点,连结AE,CF.(1)证明:四边形AECF 是矩形;(2)若AB=8,求菱形ABCD 的面积.解:(1)∵四边形ABCD 是菱形,∴AB=BC,又∵AB=AC,∴△ABC 是等边三角形.∵E 是BC 的中点,∴AE⊥BC(等边三角形三线合一),∠AEC=90°.同理,CF⊥AD.∵E,F 分别是BC,AD 的中点,∴AF=1AD,EC=1BC.2 2∵四边形ABCD 是菱形,∴AD 綊BC,∴AF 綊EC,∴四边形AECF 是平行四边形(一组对边平行且相等的四边形是平行四边形).又∵∠AEC=90°,∴四边形AECF 是矩形(有一个角是直角的平行四边形是矩形) (2)在Rt△ABE 中,∵AE==4,∴S 菱形ABCD=8×4=3223.(12 分)如图,已知四边形ABCD 是平行四边形,DE⊥AB,DF⊥BC,垂足分别是点E,F,并且DE=DF,求证:(1)△ADE≌△CDF;(2)四边形ABCD 是菱形.解:证明:(1)∵四边形ABCD 是平行四边形,∴∠A=∠C,又∵DE=DF,DE⊥AB,DF⊥BC,∴∠DEA=∠DFC=90°,∴△ADE≌△CDF(AAS) (2)由(1)知AD=DC,又∵四边形ABCD 是平行四边形,∴四边形ABCD 是菱形24.(10 分)在四边形ABCD 中,AB=CD,M,N,P,Q 分别是AD,BC,BD,AC 的中点,求证:MN 与PQ 互相垂直平分.解:证明:连结MP,NQ,PN,MQ,∵PM 綊1AB,同理NQ 綊1AB,∴PM 綊NQ,∴四边形MPNQ2 2为平行四边形,又∵PN 綊1CD,而CD=AB,∴PN=PM,2∴四边形MPNQ 为菱形,∴MN 与PQ 互相垂直平分。
专题19.1 矩形、菱形与正方形(基础篇)专项练习-2020-2021学年八年级数学下(华东师大版)
专题19.1 矩形、菱形与正方形(基础篇)专项练习一、单选题1.菱形具有而一般平行四边形不具有的性质是( )A .对边相等B .对角相等C .对角线互相平分D .对角线互相垂直 2.下列判断错误的是( )A .两组对边分别相等的四边形是平行四边形B .四个内角都相等的四边形是矩形C .四条边都相等的四边形是菱形D .两条对角线垂直且平分的四边形是正方形3.菱形的周长为8cm ,高为1cm ,则菱形两邻角度数比为( )A .4:1B .5:1C .6:1D .7:1 4.如图,EF 过矩形ABCD 对角线的交点O ,且分别交AB 、CD 于E 、F ,那么阴影部分的面积是矩形ABCD 的面积的( )A .15B .14C .13D .3105.如图,已知菱形的两条对角线分别为6cm 和8cm ,则这个菱形的高DE 为( )A .2.4cmB .4.8cmC .5cmD .9.6cm 6.如图,在平面直角坐标系中,四边形OABC 为菱形,()0,0O ,()4,0A ,60AOC ∠=,则对角线交点E 的坐标为( )A.(B.)2C.)D.(7.如图,矩形ABCD 的对角线AC 与BD 相交于点O,CE∥BD, DE∥AC , AD=, DE =2,则四边形OCED 的面积为()A.B.4C.D.88.如图,在正方形ABCD中,E为DC边上的点,连接BE,将∥BCE绕点C顺时针方向旋转90°得到∥DCF,连接EF,若∥BEC=60°,则∥EFD的度数为()A.10°B.15°C.20°D.25°9.如图,在∥ABC 中,点D 是边BC 上的点(与B、C 两点不重合),过点D作DE∥AC,DF∥AB,分别交AB、AC 于E、F 两点,下列说法正确的是()A.若AD 平分∥BAC,则四边形AEDF 是菱形B.若BD=CD,则四边形AEDF 是菱形C.若AD 垂直平分BC,则四边形AEDF 是矩形D .若 AD ∥BC ,则四边形 AEDF 是矩形10.如图,在菱形ABCD 中,P 是对角线AC 上一动点,过点P 作PE BC ⊥于点E .PF AB ⊥于点F .若菱形ABCD 的周长为20,面积为24,则PE PF +的值为( )A .4B .245C .6D .485二、填空题 11.已知菱形ABCD 的面积是12cm 2,对角线AC =4cm ,则菱形的边长是______cm . 12.如图,在∥ABC 中,AD 是高,E 是AB 的中点,EF∥AD ,交AC 于点F ,若AC=6,则DF 的长为______.13.如图,在长方形ABCD 中,AB =2,BC =3,对角线AC 的垂直平分线分别交AD ,BC 于点E ,F ,连接CE ,则CE 的长为________.14.如图,菱形ABCD 的边长为2,∥DAB=60°,E 为BC 的中点,在对角线AC 上存在一点P ,使∥PBE 的周长最小,则∥PBE 的周长的最小值为________.15.如图:已知:AM MN ⊥,BN MN ⊥,垂足分别为M 、N ,点C 是MN 上使AC BC +的值最小的点.若3AM =,5BN =,15MN =,则AC BC +=________.16.如图,在正方形ABCD 中,E 、F 分别是边BC 、CD 上的点,∥EAF =45°,∥ECF 的周长为4,则正方形ABCD 的边长为_____.17.如图,在Rt∥ABC 中,∥ABC=90°,AC=10cm ,点D 为AC 的中点,则BD=_____cm .18.如图,在菱形ABCD 中,P 是对角线AC 上的一点,PE AB ⊥于点E ,若5PE =,则点P 到AD 的距离为________.19.如图,边长分别为4和8的两个正方形ABCD 和CEFG 并排放在一起,连结BD 并延长交EG 于点T ,交FG 于点P ,则GT 的长为_____.20.如图,在Rt∥BAC 和Rt∥BDC 中,∥BAC =∥BDC =90°,O 是BC 的中点,连接AO 、DO.若AO=3,则DO的长为_____.21.如图,在正方形ABCD,E是对角线BD上一点,AE的延长线交CD于点F,连接∠=︒,则CEFCE.若56BAE∠=______︒.22.如图,边长为1的菱形ABCD中,∥DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∥FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∥HAE=60°…按此规律所作的第n个菱形的边长是___.三、解答题23.如图,∥ABC中,AB=AC,AD是∥ABC的角平分线,点O为AB的中点,连接DO 并延长到点E,使OE=OD,连接AE,BE,(1)求证:四边形AEBD是矩形;(2)当∥ABC满足什么条件时,矩形AEBD是正方形,并说明理由.24.如图,在∥ABC 和∥DCB 中,AB=DC ,AC=DB ,AC 与DB 交于点M .(1)求证:∥ABC∥∥DCB(2)过点C 作CN∥BD ,过点B 作BN∥AC ,CN 与BN 交于点N ,试判断线段BN 与CN 的数量关系,并证明你的结论.25.如图,点E 、F 、G 、H 分别在矩形ABCD 的边AB 、BC 、CD 、DA (不包括端点)上运动,且满足AE CG =,AH CF =.(1)求证:AEH CGF ∆≅∆;(2)试判断四边形EFGH 的形状,并说明理由.(3)请探究四边形EFGH 的周长一半与矩形ABCD 一条对角线长的大小关系,并说明理由.26.在∥ABC 中,M 是AC 边上的一点,连接BM.将∥ABC 沿AC 翻折,使点B 落在点D 处,当DM∥AB 时。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
天际线教育 1 矩形、菱形、正方形辅导练习题(一) 一、 复习矩形、菱形、正方形有关的性质和判定方法。 二、 例题讲解
例1、如图,在平行四边形ABCD中,E是CD的中点,△ABE是等边三角形,求证:四边形ABCD是矩形。
例2、已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AE=2。 求:(1)∠ABC的度数; (2)对角线AC、BD的长; (3)菱形ABCD的面积。
例3、如图①,四边形ABCD是正方形, 点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F.
(1) 求证:DE-BF = EF. (2) 当点G为BC边中点时, 试探究线段EF与GF之间的数量关系, 并说明理由. (3) 若点G为CB延长线上一点,其余条件不变.请你在图②中画出图形,写出此时DE、BF、EF之间的数量关系(不需要证明). 天际线教育
2 三、 巩固提高 (一)选择题 1、矩形具有而一般平行四边形不具有的性质是( ). A、 对角线相等 B、 对边相等 C、 对角相等 D、 对角线互相平分 2、下列对矩形的判定:“(1)对角线相等的四边形是矩形;(2)对角线互相平分且相等的四边形是矩形;(3)有一个角是直角的四边形是矩形;(4)有四个角是直角的四边形是矩形;(5)四个角都相等的四边是矩形;(6)对角线相等,且有一个直角的四边形是矩形;(7)一组邻边垂直,一组对边平行且相等的四边形是矩形;(8)对角线相等且互相垂直的四边形是矩形”中,正确的个数有( ) A、3 个 B、4个 C、5个 D、6个 3、下列性质中,菱形具有而矩形不一定具有的性质是( ) A、对边平行且相等 B、对角线互相平分 C、内角和等于外角和 D、每一条对角线所在直线都是它的对称轴 4、下列条件中,能判定一个四边形为菱形的条件是( ) A、对角线互相平分的四边形 B、对角线互相垂直且平分的四边形 C、对角线相等的四边形 D、对角线相等且互相垂直的四边形 5、已知四边形ABCD是平行四边形,下列结论中不一定正确的是( ) A、AB=CD B、AC=BD C、当AC⊥BD时,它是菱形 D、当∠ABC=90°时,它是矩形 6、正方形具有而矩形不一定具有的性质是( )。
A.四个角都是直角 B.对角线互相平分 C.对角线相等 D.对角线互相垂直 7、正方形具有而菱形不一定具有的性质是( )。 A、对角线相等 B、对角线互相垂直平分 C、四条边相等 D、一条对角线平分一组对角 8、下列条件中不能判定四边形是正方形的条件是( )。 A、对角线互相垂直且相等的四边形 B、一条对角线平分一组对角的矩形 天际线教育 3 BE
DCFA
C、对角线相等的棱形 D、对角线互相垂直的矩形 9、下列命题中,假命题是( )。 A、四个内角都相等的四边形是矩形 B、四条边都相等的平行四边形是正方形 C、既是菱形又是矩形的四边形是正方形 D、对角线互相垂直的平行四边形是菱形 10、在四边形ABCD中,O是对角线的交点,能判定四边形是正方形的条件是( )。
A、BDAC,CDAB// B、BCAD//,CA C、DOCOBOAO,BDAC D、COAO,DOBO,BCAB 11、矩形的两条对角线所成的钝角是120°,若一条对角线的长为2,那么矩形的周长为( )
A、6 B、5.8 C、2(1+3 ) D、5.2 12、如图,菱形ABCD的周长为8,两邻角的比为2∶1,则对角线的长分别为( )
A、4和2 B、1和23 C、2和23 D、2和3 13、如图,矩形ABCD的对角线AC的中垂线与AD、BC分别交于F、E,则四边形AFCE的形状最准确的判断是( ) A、平行四边形 B、菱形 C、矩形 D、正方形
14、如图,设F为正方形ABCD的边AD上一点,CE⊥CF交AB的延长线于E,若S正方形ABCD=64,S△CEF=50,
则S△CBE=( )
ABCD
O
第13题 第14题 第15题 第12 天际线教育
4 A、20 B、24 C、25 D、26 15、如图,在矩形ABCD中,AB=3,AD=4,P是AD上一动点,PF⊥AC于F,PE⊥BD于E,则PE+PF的值为( )
A、125 B、135 C、52 D、2 (二)填空题 16、已知一个菱形的面积为83 ㎝2,且两条对角线的比为1∶3 ,则菱形短的对角线长为_________。 17、直角三角形斜边上的高与中线分别是5cm和6cm,则它的面积为____________________。 18、在Rt△ABC中,斜边AB上的中线长为3,则AC2+BC2+AB2= ______________________。 19、菱形的一边与两条对角线所构成的两角之比为5∶4,则它的各内角度数为___________________。 20、如图,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下列结论①△ODC是等边三角形;
②BC=2AB;③∠AOE=135°;④S△AOE=S△COE,其中正确的结论的序号是 ___________________。 21、如图,矩形内有两个相邻的正方形,面积分别为4和9,则阴影部分的面积为 ______________。
22、点M为矩形ABCD的边AD的中点,P为BC上一点,且PE⊥MC,PF⊥MB,当AB、AD满足条件__________时,四边形PEMF是矩形。 23、如图,E是正方形ABCD内一点,如果△ABE为等边三角形,那么∠DCE= _______________。 (三)解答题 24、已知:如图,在□ABCD中,O为边AB的中点,且∠AOD=∠BOC.求证:□ABCD是矩形.
25、已知菱形ABCD中,AC与BD相交O点,若∠BDC=030,菱形的周长为20厘米,求菱形的面积.
A B C
D O
E 第20题图
第21题图
9 4 A B C D
E
第23题图 第22题
ABCD
O
BACD
O 天际线教育
5 矩形的习题精选 一、性质 1、下列性质中,矩形具有而平行四边形不一定具有的是( ) A、对边相等 B、对角相等 C、对角线相等 D、对边平行 2.在矩形ABCD中,∠AOD=130°,则∠ACB=__ _ 3.已知矩形的一条对角线长是8cm,两条对角线的一个交角为60°,则矩形的周长为______ 4.矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm, 对角线是13cm,那么矩形的周长是____________ 5.如图所示,矩形ABCD中,AE⊥BD于E,∠BAE=30°,BE=1cm,那么DE的长为_____ 6、直角三角形斜边上的高与中线分别是5cm和6cm,则它的面积为___ 7、已知,在Rt△ABC中,BD为斜边AC上的中线,若∠A=35°,那么∠DBC= 。 8、如图,矩形ABCD中,AC与BD交于O点,BE⊥AC于E,CF⊥BD于F. 求证:BE=CF.
9.如图,△ABC中,∠ACB=900,点D、E分别为AC、AB的中点,点F在BC延长线上,且∠CDF=∠A,求证:四边形DECF是平行四边形;
10.已知:如图,在△ABC中,∠BAC≠90° ∠ABC=2∠C,AD⊥AC,交BC或CB的延长线D。试说明:DC=2AB.
11、在△ABC中,∠C=90O,AC=BC,AD=BD,PE⊥AC于点E, PF⊥BC于点F。求证:DE=DF
A B C D E F O 天际线教育
6 二、判定 1、下列检查一个门框是否为矩形的方法中正确的是( ) A.测量两条对角线,是否相等 B.测量两条对角线,是否互相平
分
C.用曲尺测量门框的三个角,是否都是直角 D.用曲尺测量对角线,是否互相
垂直
2、平行四边形ABCD,E是CD的中点,△ABE是等边三角形,求证:四边形ABCD是矩形
3、在平行四边形ABCD中,对角线AC、BD相交于O,EF过点O,且AF⊥BC,求
证:四边形AFCE是矩形
4、平行四边形ABCD中,对角线AC、BD相交于点O,点P是四边形外一点,且PA⊥PC,PB⊥PD,垂足为P。求证:四边形ABCD为矩形
5、已知:如图,平行四边形ABCD的四个内角的平分线分别相交于E、F、G、H,求
证:四边形 EFGH为矩形.
6、如图,△ABC中,点O是AC上一个动点,过点O作直线MN∥BC,设MN交∠
BCA的平分线于点E,交∠BCA的外角平分线于点F, (1)求证:OE=OF; (2)当点O运动到何处时,四边形AECF是
