大学物理(下)公共必做题
大学物理下经典计算题75页PPT

36、如果我们国家的法律中只有某种 神灵, 而不是 殚精竭 虑将神 灵揉进 宪法, 总体上 来说, 法律就 会更好 。—— 马克·吐 温 37、纲纪废弃之日,便是暴政兴起之 时。— —威·皮 物特
38、若是没有公众舆论的支持,法律 是丝毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例,它们 迅速累 聚,进 而变成 法律。 ——朱 尼厄斯
40、人类法律,事物有规律,这是不 容忽视 的。— —爱献 生
谢谢!
51、 52、 生 命 不 等 于是呼 吸,生 命是活 动。——卢 梭
53、 伟 大 的 事 业,需 要决心 ,能力 ,组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
55、 为 中 华 之 崛起而 读书。 ——周 恩来
大学物理(下)习题(学生用)2

大学物理(第10章上)习题1.如图所示,真空中一长为L 的均匀带电细直杆,总电荷为q ,试求在直杆延长线上距杆的一端距离为d 的P 点的电场强度. 解:2. 用绝缘细线弯成的半圆环,半径为R ,其上均匀地带有正电荷Q ,试求圆心O 点的电场强度. 解:3. 若匀强电场的场强为E ,其方向平行于半径为R 的半球面的轴,如图所示.则通过此半球面的电场强度通量Φe 为(A) E R 2π (B) E R 22π(C)E R 221π (D) E R 22π (E) 2/2E R π [ ]4. 有两个电荷都是+q 的点电荷,相距为2a半径作一球形高斯面 . 在球面上取两块相等的小面积S 1和S 2,其位置如图所示. 设通过S 1和S 2的电场强度通量分别为Φ1和Φ2,通 过整个球面的电场强度通量为ΦS ,则L P(A) Φ1>Φ2,ΦS =q /ε0. (B) Φ1<Φ2,ΦS =2q /ε0. (C) Φ1=Φ2,ΦS =q /ε0.(D) Φ1<Φ2,ΦS =q /ε0. [ ]5.如图所示,一个电荷为q 的点电荷位于立方体的A 角上,则通过侧面abcd 的电场强度通量等于:(A) 06εq . (B) 012εq .(C) 024εq .(D) 048εq .[ ]6.根据高斯定理的数学表达式⎰∑⋅=Sq S E 0/d ε可知下述各种说法中,正确的是:(A) 闭合面内的电荷代数和为零时,闭合面上各点场强一定为零.(B) 闭合面内的电荷代数和不为零时,闭合面上各点场强一定处处不为零.(C) 闭合面内的电荷代数和为零时,闭合面上各点场强不一定处处为零.(D) 闭合面上各点场强均为零时,闭合面内一定处处无电荷.[ ]7. 半径为R 的均匀带电球体的静电场中各点的电场强度的大小E 与距球心的距离r 的关系曲线为:[ ]8. 半径为R 的“无限长”均匀带电圆柱面的静电场中各点的电场强度的大小E 与距轴线的距离r 的关系曲线为: 解:[ ]9.(选做)(类似习题8-7)如图,在一电荷体密度为ρ的均匀带电球体中,挖出一个以O 'EO r (A) E ∝1/r为球心的球状小空腔,空腔的球心相对带电球体中心O 的位置矢量用b表示.试证球形空腔内的电场是均匀电场,其场强表达式为b E3ερ=.10. 如图,A 点与B 点间距离为2l ,OCD 是以B 为中心,以l 为半径的半圆路径. A 、B 两处各放有一点电荷,电荷分别为+q 和-q .把另一电荷为Q (Q <0 )的点电荷从D 点沿路径DCO 移到O 点,则电场力所做的功为___________________11. 将电荷均为q 的三个点电荷一个一个地依次从无限远处缓慢搬到x 轴的原点、x = a 和x = 2a 处.求证外界对电荷所作之功为aq A 0285επ=设无限远处电势能为零.12. 真空中一“无限大”均匀带电平面,其电荷面密度为σ (>0).在平面附近有一质量为m 、电荷为q (>0)的粒子.试求当带电粒子在电场力作用下从静止开始垂直于平面方向运动一段距离l 时的速率.设重力的影响可忽略不计.+13. 一半径为R 的均匀带电球面,带有电荷Q .若规定该球面上电势为零,则球面外距球心r 处的P 点的电势U P =___________________________.14. 在边长为a 的正方体中心处放置一点电荷Q ,设无穷远处为电势零点,则在正方体顶角处的电势为: (A)aQ 034επ .(B) a Q032επ.(C) a Q 06επ. (D) aQ 012επ .解:[ ]15. 如图所示,两个同心球壳.内球壳半径为R 1,均匀带有电荷Q ;外球壳半径为R 2,壳的厚度忽略,原先不带电,但与地相连接.设地为电势零点,则在内球壳里面,距离球心为r 处的P 点的场强大小及电势分别为: (A) E =0,U =104R Qεπ.(B) E =0,U =⎪⎪⎭⎫⎝⎛-π210114R R Q ε. (C) E =204r Q επ,U =rQ04επ. (D) E =204r Q επ, U =104R Qεπ.解:[ ]16. 如图所示,一半径为a 的“无限长”圆柱面上均匀带电,其电荷线密度为λ.在它外面同轴地套一半径为b 的薄金属圆筒,圆筒原先不带电,但与地连接.设地的电势为零,则在内圆柱面里面、距离轴线为r 的P 点的场强大小和电势分别为:(A) E =0,U =r aln 20ελπ. (B) E =0,U =abln 20ελπ.(C) E =r 02ελπ,U =rb ln 20ελπ. (D) E =r 02ελπ,U =ab ln 20ελπ. 解:[ ]17.如图所示,两同心带电球面,内球面半径为r 1=5 cm ,带电荷q 1=3×10-8 C ;外球面半径为r 2=20 cm , 带电荷q 2=-6×108C ,设无穷远处电势为零,则空间另一电势为零的球面半径r = __________________. 18. 一半径为R 的均匀带电圆盘,电荷面密度为σ, 设无穷远处为电势零点, 则圆盘中心O 点的电势U =__________________________________.19. 两个带等量异号电荷的均匀带电同心球面,半径分别为R 1=0.03 m 和R 2=0.10 m .已知两者的电势差为450 V ,求内球面上所带的电荷.20. 图示为一个均匀带电的球层,其电荷体密度为ρ,球层内表面半径为R 1,外表面半径为R 2.设无穷远处为电势零点,试用电势迭加法求空腔内任一点的电势.21. 已知某静电场的电势分布为U =8x +12x 2y -20y 2 (SI),则场强分布E= _______________________________________. 22.真空中一均匀带电细直杆,长度为2a ,总电荷为+Q ,沿Ox 轴固定放置(如图).一运动粒子质量为m 、带有电荷+q ,在经过x 轴上的C 点时,速率为v .试求:(1) 粒子在经过C 点时,它与带电杆之间的相互作用电势能(设无穷远处为电势零点);(2) 粒子在电场力作用下运动到无穷远处的速率v ∞ (设v ∞远小于光速).大学物理(第10章下)习题1.一步图示为一半径为a 的、带有正电荷Q 的导体球.球外有一内半径为b 、外半径为c 的不带电的同心导体球壳.设无限远处为电势零点,试求内球和球壳的电势. 解:2. 图示为一半径为a 、不带电的导体球,球外有一内半径为b 、外半径为c 的同心导体球壳,球壳带正电荷+Q .今将内球与地连接,设无限远处为电势零点,大地电势为零,球壳离地很远,试求导体球上的感生电荷.解:3. 一空心导体球壳,其内、外半径分别为R 1和R 2,带电荷q ,如图所示.当球壳中心处再放一电荷为q 的点电荷时,则导体球壳的电势((A)104R qεπ . (B)204R qεπ .(C) 102R q επ . (D) 20R qε2π .解: [ ]4.在一个原来不带电的外表面为球形的空腔导体A 内,放一带有电荷为+Q 的带电导体B ,如图所示.则比较空腔导体A 的电势U A 和导体B 的电势U B 时,可得以下结论: (A) U A = U B . (B) U A > U B .(C) U A < U B . (D) 因空腔形状不是球形,两者无法比较.解: [ ]q5.图示一均匀带电球体,总电荷为+Q ,其外部同心地罩一内、外半径分别为r 1、r 2的金属球壳.设无穷远处为电势零点,则在球壳内半径为r 的P 点处的场强和电势为: (A) 204r Q E επ=,rQU 04επ=.(B) 0=E ,104r QU επ=.(C) 0=E ,r QU 04επ=.(D) 0=E ,204r QU επ=. 解: [ ]6. 半径为R 的金属球与地连接.在与球心O 相距d =2R 处有一电荷为q 的点电荷.如图所示,设地的电势为零,则球上的感生电荷q '为(A) 0. (B) 2q . (C) -2q. (D) -q . 解: [ ]7. 半径为R 的不带电的金属球,在球外离球心O 距离为l 处有一点电荷,电荷为q .如图所示,若取无穷远处为电势零点,则静电平衡后金属球的电势U =______________.8.一“无限大”均匀带电平面A ,其附近放一与它平行的有一定厚度的“无限大”平面导体板B ,如图所示.已知A 上的电荷面密度为+σ ,则在导体板B 的两个表面1和2上的感生电荷面密度为:(A) σ 1 = - σ, σ 2 = + σ.(B) σ 1 = σ21-, σ 2 =σ21+. (C) σ 1 = σ21-, σ 1 = σ21-.(D) σ 1 = - σ, σ 2 = 0.解:[ ]9.A 、B 为两导体大平板,面积均为S ,平行放置,如图所示.A 板带电荷+Q 1,B 板带电荷+Q 2,如果使B 板接地,则AB 间电场强度的大小E 为(A) S Q 012ε . (B) SQ Q 0212ε-.A +σ2(C)S Q 01ε. (D) SQ Q 0212ε+. 解: [ ]10. 三块互相平行的导体板,相互之间的距离d 1和d 2比板面积线度小得多,外面二板用导线连接.中间板上带电,设左右两面上电荷面密度分别为σ1和σ2,如图所示.则比值σ1 / σ2为(A) d 1 / d 2. (B) d 2 / d 1.(C) 1. (D) 2122/d d . 解:[ ]11.如图所示,两块很大的导体平板平行放置,面积都是S ,有一定厚度,带电荷分别为Q 1和Q 2.如不计边缘效应,则A 、B 、C 、D 四个表面上的电荷面密度分别为______________ 、______________、_____________、____________.12.一空气平行板电容器,电容为C ,两极板间距离为d .充电后,两极板间相互作用力为F .则两极板间的电势差为______________,极板上的电荷为______________.13. 半径分别为a 和b 的两个金属球,它们的间距比本身线度大得多.今用一细导线将两者相连接,并给系统带上电荷Q .求:(1) 每个球上分配到的电荷是多少? (2) 按电容定义式,计算此系统的电容.14. 如图,在一带电量为Q 的导体球外,同心地包有一各向同性均匀电介质球壳,相对介电常数为εr ,壳外是真空.则在壳外P 点处(设r OP =)的场强和电位移的大小分别为+Q 2A B(A) E = Q / (4πε0εr r 2),D = Q / (4πε0r 2).(B) E = Q / (4πεr r 2),D = Q / (4πr 2).(C) E = Q / (4πε0r 2),D = Q / (4πr 2).(D) E = Q / (4πε0r 2),D = Q / (4πε0r 2). 解:[ ]15. 一平行板电容器与电源相连,电源端电压为U ,电容器极板间距离为d .电容器中充满二块大小相同、介电常量(电容率)分别为ε1、ε2的均匀介质板,如图所示,则左、右两侧介质中的电位移矢量D的大小分别为:(A) ε0U / d , ε0U / d .(B) ε1U / d , ε2U / d .(C) ε0 ε1U / d , ε0 ε2U / d .(D) U /( ε1 d ), U /( ε2 d ).解:[ ] 16.一个大平行板电容器水平放置,两极板间的一半空间充有各向同性均匀电介质,另一半为空气,如图.当两极板带上恒定的等量异号电荷时,有一个质量为m 、带电荷为+q 的质点,在极板间的空气区域中处于平衡.此后,若把电介质抽去 ,则该质点 (A) 保持不动. (B) 向上运动.(C) 向下运动. (D) 是否运动不能确定.解:[ ]17.一平行板电容器始终与端电压一定的电源相联.当电容器两极板间为真空时,电场强度为0E ,电位移为0D,而当两极板间充满相对介电常量为εr 的各向同性均匀电介质时,电场强度为E ,电位移为D,则(A) r E E ε/0 =,0D D =. (B) 0E E =,0D D rε=.(C) r E E ε/0 =,r D D ε/0 =. (D) 0E E =,0D D=.解:[ ]18. 一平行板电容器,两板间距离为d ,若插入一面积与极板面积相同而厚度为d / 2 的、相对介电常量为εr 的各向同性均匀电介质板(如图所示),则插入介质后的电容值与原来的电容值之比C / C 0为 (A) 11+r ε. (B) 1+r r εε.(C)12+r r εε. (D) 12+r ε. 解:[ ]19.如图所示,一内半径为a 、外半径为b 的金属球壳,带有电荷Q ,在球壳空腔内距离球心r 处有一点电荷q .设无限远处为电势零点,试求: (1) 球壳内外表面上的电荷.p+Q(2) 球心O点处,由球壳内表面上电荷产生的电势.(3) 球心O点处的总电势.解:20.1、2是两个完全相同的空气电容器.将其充电后与电源断开,再将一块各向同性均匀电介质板插入电容器1的两极板间,如图所示, 则电容器2的电压U2,电场能量W2如何变化?(填增大,减小或不变) U2_________,W2_____________.21.在相对介电常量 r = 4的各向同性均匀电介质中,与电能密度w e =2×106 J/cm3相应的电场强度的大小E =_______________________.22. 一空气平板电容器,极板A、B的面积都是S,板电势U B=0.现将一带有电荷q、面积也是S而厚度可忽略的导体片C平行插在两极板的中间位置,如图所示,试求导体片C的电势.大学物理(第11章上)习题1. 边长为2a 的等边三角形线圈,通有电流I ,则线圈中 心处的磁感强度的大小为________________. 2. 边长为l 的正方形线圈,分别用图示两种方式通以电流I (其中ab 、cd 与正方形共面),在这两种情况下,线圈在其中心产生的磁感强度的大小分别为(A) 01=B ,02=B .(B) 01=B,lI B π=0222μ.(C) l IB π=0122μ,02=B .(D) l I B π=0122μ,l IB π=0222μ. 解:[ ]3. 在真空中,电流I 由长直导线1沿垂直bc 边方向经a 点流入一由电阻均匀的导线构成的正三角形线框,再由b 点沿平行ac 边方向流出,经长直导线2返回电源(如图).三角形框每边长为l ,则在该正三角框中心O 点处磁感强度的大小B =_________________________.4. 无限长直导线在P 处弯成半径为R 的圆,当通以电流I 时,则在圆心O 点的磁感强度大小等于 (A) R I π20μ. (B) R I40μ. (C) 0. (D))11(20π-R I μ. (E))11(40π+R Iμ. 解:[ ]5. 如图两个半径为R 的相同的金属环在a 、b 两点接触(ab 连线为环直径),并相互垂直放置.电流I 沿ab 连线方向由a 端流入,b 端流出,则环中心O 点的磁感强度的大小为(A) 0. (B) R I40μ.(C) R I 420μ. (D) RI0μ.解:[ ]6. 如图所示,在宽度为d 的导体薄片上有电流I 沿此导体长度方向流aIIb a2过,电流在导体宽度方向均匀分布.试求导体外在导体中线附近处P 点的磁感强度B7.一弯曲的载流导线在同一平面内,形状如图(O 点是半径为R 1和R 2的两个半圆弧的共同圆心,电流自无穷远来到无穷远 去),则O 点磁感强度的大小是________________________.8. 已知真空中电流分布如图,两个半圆共面,且具有公共圆心,试求O 点处的磁感强度. 解:9. 一半径R = 1.0 cm 的无限长1/4圆柱形金属薄片,沿轴向通有电流I =10.0 A 的电流,设电流在金属片上均匀分布,试求圆柱轴线上任意一点P 的磁感强度. 解:P I俯视图10. 在半径为R 的长直金属圆柱体内部挖去一个半径为r 的长直圆柱体,两柱体轴线平行,其间距为a ,如图.今在此导体上通以电流I ,电流在截面上均匀分布,则空心部分轴线上O ′点的磁感强度的大小为 (A)2202R a a I ⋅πμ (B)22202Rr a a I -⋅πμ(C) 22202r R a a I -⋅πμ (D) )(222220a r R a a I -πμ 解: [ ]11. 如图,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I 从a 端流入而从d 端流出,则磁感强度B沿图中闭合路径L 的积分⎰⋅Ll Bd 等于(A) I 0μ. (B)I 031μ. (C) 4/0I μ. (D) 3/20I μ.解:[ ] 12.半径为 0.5 cm 的无限长直圆柱形导体上,沿轴线方向均匀地流着I = 3 A 的电流.作一个半径r = 5 cm 、长l = 5 cm 且与电流同轴的圆柱形闭合曲面S ,则该曲面上的磁感强度B沿曲面的积分 =⋅⎰⎰S Bd ________________________.13. 均匀磁场的磁感强度B 与半径为r 的圆形平面的法线n的夹角为α ,今以圆周为边界,作一个半球面S ,S 与圆形平面组成 封闭面如图.则通过S 面的磁通量Φ =________________.14.如图,流出纸面的电流为2I ,流进纸面的电流为I ,则下述各式中哪一个是正确的?(A) I l H L 2d 1=⎰⋅. (B)I l H L =⎰⋅2d(C) I l H L -=⎰⋅3d. (D)I l H L -=⎰⋅4d.解:[ ]a R r OO ′I415. 有一同轴电缆,其尺寸如图所示,它的内外两导体中的电流均为I ,且在横截面上均匀分布,但二者电流的流向正相反,则 (1) 在r < R 1处磁感强度大小为________________.(2) 在r > R 3处磁感强度大小为________________..16. 一根很长的圆柱形铜导线均匀载有10 A 电流,在导线内部作一平面S ,S 的一个边是导线的中心轴线,另一边是S 平面与导线表面的交线,如图所示.试计算通过沿导线长度方向长为1m 的一段S 平面的磁通量.(真空的磁导率μ0 =4π×10-7T ·m/A ,铜的相对磁导率μr ≈1) 解:17. 如图,一根载流导线被弯成半径为R 的1/4圆弧,放在磁感强度为B 的均匀磁场中,则载流导线ab 所受磁场的 作用力的大小为____________,方向_________________. 18. 通有电流I的长直导线在一平面内被弯成如图形状,放于垂直进入纸面的均匀磁场B中,求整个导线所受的安培力(R 为已知). 解:BB18.截面积为S ,截面形状为矩形的直的金属条中通有电流I .金属条放在磁感强度为B的匀强磁场中,B的方向垂直于金属条的左、右侧面(如图所示).在图示情况下金属条的侧面将积累____________电荷,载流子所受的洛伦兹力f m =______________.(注:金属中单位体积内载流子数为n )19. 一个通有电流I 的导体,厚度为D ,横截面积为S ,放置在磁感强度为B 的匀强磁场中,磁场方向垂直于导体的侧表面,如图所示.现测得导体上下两面电势差为V ,则此导体的霍尔系数等于 (A) IB VDS . (B) DSIBV .(C) IBD VS . (D) BD IVS.(E) IBVD .解:[ ] 20. 图为四个带电粒子在O 点沿相同方向垂直于磁感线射入均匀磁场后的偏转轨迹的照片.磁场方向垂直纸面向外,轨迹所对应的四个粒子的质量相等,电荷大小也相等,则其中动能最大的带负电的粒子的轨迹是 (A) Oa . (B) Ob .(C) Oc . (D) Od . 解:[ ]21. 如图,均匀磁场中放一均匀带正电荷的圆环,其线电荷密度为λ,圆环可绕通过环心O 与环面垂直的转轴旋转.当圆环以角速度ω 转动时,圆环受到的磁力矩为_________________,其方向__________________________.22. 有一半径为R 的单匝圆线圈,通以电流I ,若将该导线弯成匝数N = 2的平面圆线圈,导线长度不变,并通以同样的电流,则线圈中心的磁感强度和线圈的磁矩分别是原来的 (A) 4倍和1/8. (B) 4倍和1/2. (C) 2倍和1/4. (D) 2倍和1/2. 解:[ ]23. (类似习题11-37)半径为R 的匀质圆盘,表面带有均匀分布的电荷Q .圆盘绕过盘中心与盘面垂直的轴旋转,角速度为ω .(1) 求圆盘产生的圆电流的磁矩p m .(2)若圆盘的质量为m ,求磁矩和动量矩之比p m / L .O解:24.如图,一半径为R 的带电塑料圆盘,其中半径为r 的阴影部分均匀带正电荷,面电荷密度为+σ ,其余部分均匀带负电荷,面电荷密度为-σ 当圆盘以角速度ω 旋转时,测得圆盘中心O 点的磁感强度为零,问R 与r 满足什么关系?解:25. 有两个半径相同的圆环形载流导线A 、B ,它们可以自由转动和移动,把它们放在相互垂直的位置上,如图所示,将发生以下哪一种运动?(A) A 、B 均发生转动和平动,最后两线圈电流同方向并紧靠一起. (B) A 不动,B 在磁力作用下发生转动和平动.(C) A 、B 都在运动,但运动的趋势不能确定. (D) A 和B 都在转动,但不平动,最后两线圈磁矩同方向平行. 解:[ ]大学物理(第11章下)习题1.磁介质有三种,用相对磁导率μr表征它们各自的特性时,(A) 顺磁质μr >0,抗磁质μr <0,铁磁质μr >>1.(B) 顺磁质μr >1,抗磁质μr =1,铁磁质μr >>1.(C) 顺磁质μr >1,抗磁质μr <1,铁磁质μr >>1.(D) 顺磁质μr<0,抗磁质μr<1,铁磁质μr>0.[]2.一个绕有500匝导线的平均周长50 cm的细环,载有0.3 A电流时,铁芯的相对磁导率为600 .(1) 铁芯中的磁感强度B为__________________________.(2) 铁芯中的磁场强度H为____________________________.(μ0 =4π×10-7 T·m·A-1)3.长直电缆由一个圆柱导体和一共轴圆筒状导体组成,两导体中有等值反向均匀电流I通过,其间充满磁导率为μ的均匀磁介质.介质中离中心轴距离为r的某点处的磁场强度的大小H =________________,磁感强度的大小B =__________.4.如图所示的一细螺绕环,它由表面绝缘的导线在铁环上密绕而成,每厘米绕10匝.当导线中的电流I为2.0 A时,测得铁环内的磁感应强度的大小B为1.0 T,则可求得铁环的相对磁导率μr为(真空磁导率μ 0 =4π×10-7 T·m·A-1)(A) 7.96×102(B) 3.98×102(C) 1.99×102 (D) 63.3 解:[]5.一根同轴线由半径为R1的长导线和套在它外面的内半径为R2、外半径为R3的同轴导体圆筒组成.中间充满磁导率为μ的各向同性均匀非铁磁绝缘材料,如图.传导电流I沿导线向上流去,由圆筒向下流回,在它们的截面上电流都是均匀分布的.求同轴线内外的磁感强度大小B 的分布.解:大学物理(第12章)习题1. 载有恒定电流I 的长直导线旁有一半圆环导线cd ,半圆环半径为b ,环面与直导线垂直,且半圆环两端点连线的延长线与直导线相交,如图.当半圆环以速度v沿平行于直导线的方向平移时,半圆环上的感应电动势的大小是____________________.2. 金属杆AB 以匀速v =2 m/s 平行于长直载流导线运动,导线与AB 共面且相互垂直,如图所示.已知导线载有电流I = 40 A ,则此金属杆中的感应电动势i =____________,电势较高端为______.(ln2 = 0.69)3.如图所示,aOc 为一折成∠形的金属导线(aO =Oc =L ),位于xy 平面中;磁感强度为B的匀强磁场垂直于xy 平面.当aOc 以速度v沿x 轴正向运动时,导线上a 、c 两点间电势差U ac =____________;当aOc 以速度v沿y 轴正向运动时,a 、c 两点的电势相比较, 是____________点电势高.4. 如图所示,直角三角形金属框架abc 放在均匀磁场中,磁场B平行于ab 边,bc 的长度为l .当金属框架绕ab 边以匀角速度ω转动时,abc 回路中的感应电动势ε 和a 、c 两点间的电势差U a – U c 为(A) ε =0,U a – U c =221l B ω.(B) ε =0,U a – U c =221l B ω-.(C) ε =2l B ω,U a – U c =221l B ω.(D) ε =2l B ω,U a – U c =221l B ω-.解: [ ]5. 如图所示,一根长为L 的金属细杆ab 绕竖直轴O 1O 2以角速度ω在水平面内旋转.O 1O 2在离细杆a 端L /5处.若已知地磁场在竖直方向的分量为B.求ab 两端间的电势差b a U U -. 解:c a的方向Bx ×××××Bab clωb6. 如图所示,两条平行长直导线和一个矩形导线框共面.且导线框的一个边与长直导线平行,他到两长直导线的距离分别为r 1、r 2.已知两导线中电流都为t I I ωsin 0=,其中I 0和ω为常数,t 为时间.导线框长为a 宽为b ,求导线框中的感应电动势. 解7. 载有电流的I 长直导线附近,放一导体半圆环MeN 与长直导线共面,且端点MN 的连线与长直导线垂直.半圆环的半径为b ,环心O 与导线相距a .设半圆环以速度 v 平行导线平移,求半圆环内感应电动势的大小和方向以及MN 两端的电压U M - U N . 解IIOxr 1r 2 ab8. 在圆柱形空间内有一磁感强度为B 的均匀磁场,如图所示.B的大小以速率d B /d t 变化.在磁场中有A 、B 两点,其间可放直导线AB 和弯曲的导线AB ,则 (A) 电动势只在AB导线中产生.(B) 电动势只在AB 导线中产生. (C) 电动势在AB 和AB 中都产生,且两者大小相等.(D) AB 导线中的电动势小于AB 导线中的电动势. 解:[ ]9. 在半径为R 的圆柱形空间存在着轴向均匀磁场(如图)有一长为2R 的导体棒在垂直磁场的平面内以速度v横扫过磁场,若磁感强度B 以 0d d >tB变化,试求导体棒在如图所示的位置处时,棒上的感应电动势. 解:10.用导线围成的回路(两个以O 点为心半径不同的同心圆,在一处用导线沿半径方向相连),放在轴线通过O 点的圆柱形均匀磁场中,回路平面垂直于柱轴,如图所示.如磁场方向垂直图面向里,其大小随时间减小,则(A)→(D)各图中哪个图上正确表示了感应电流的流向? 解:[ ]11载流长直导线与矩形回路ABCD 共面,导线平行于AB ,如图所示.求下列情况下ABCD 中的感应电动势:(1) 长直导线中电流I = I 0不变,ABCD 以垂直于导线的速度v 从图示初始位置远离导线匀速平移到某一位置时(t 时刻). (2) 长直导线中电流I = I 0 sin ω t ,ABCD 不动.(3) 长直导线中电流I = I 0 sin ω t ,ABCD 以垂直于导线的速度v 远离导线匀速运动,初始位置也如图. 解:Cl12. 两线圈顺接,如图(a),1、4间的总自感为1.0 H .在它们的形状和位置都不变的情况下,如图(b)那样反接后1、3之间的总自感为0.4 H .求两线圈之间的互感系数. 解:13. 如图所示,一半径为r 的很小的金属圆环,在初始时刻与一半径为a (a >>r )的大金属圆环共面且同心.在大圆环中通以恒定的电流I ,方向如图.如果小圆环以匀角速度ω绕其任一方向的直径转动,并设小圆环的电阻为R ,则任一时刻t 通过小圆环的磁通量Φ =______________________.小圆环中的感应电流i =__________________________________________.14.图示为一圆柱体的横截面,圆柱体内有一均匀电场E,其方向垂直纸面向内,E的大小随时间t 线性增加,P 为柱体内与轴线相距为r 的一点则 (1) P 点的位移电流密度的方向为____________. (2) P 点感生磁场的方向为____________. 15.如图,平板电容器(忽略边缘效应)充电时,沿环路L 1的磁场强度H 的环流与沿环路L 2的磁场强度H的环流两者,必有:(A) >'⎰⋅1d L l H ⎰⋅'2d L l H.(B) ='⎰⋅1d L l H ⎰⋅'2d L l H.(C) <'⎰⋅1d L l H⎰⋅'2d L l H.(D) 0d 1='⎰⋅L l H解:[ ]16. 给电容为C 的平行板电容器充电,电流为i = 0.2e -t( SI ),t = 0时电容器极板上无电荷.求:(1) 极板间电压U 随时间t 而变化的关系.123(a)顺接(b) 反接(2) t 时刻极板间总的位移电流I d (忽略边缘效应).17.在感应电场中电磁感应定律可写成t l E LK d d d Φ-=⎰⋅ ,式中K E 为感应电场的电场强度.此式表明:(A) 闭合曲线L 上K E处处相等.(B) 感应电场是保守力场. (C) 感应电场的电场强度线不是闭合曲线.(D) 在感应电场中不能像对静电场那样引入电势的概念. 解: [ ]18.反映电磁场基本性质和规律的积分形式的麦克斯韦方程组为⎰⎰⋅=VSV S D d d ρ , ① ⎰⎰⋅⋅∂∂-=SL S t B l E d d , ②0d =⎰⋅SS B, ③⎰⋅⎰⋅∂∂+=SL S t DJ l Hd )(d . ④试判断下列结论是包含于或等效于哪一个麦克斯韦方程式的.将你确定的方程式用代号填在相应结论后的空白处.(1) 变化的磁场一定伴随有电场;__________________(2) 磁感线是无头无尾的;________________________(3) 电荷总伴随有电场.__________________________ 19.(类似习题13-28)自感系数L =0.3 H 的螺线管中通以I =8 A 的电流时,螺线管存储的磁场能量W =___________________. 20.(类似习题13-28)无限长密绕直螺线管通以电流I ,内部充满均匀、各向同性的磁介质,磁导率为μ.管上单位长度绕有n 匝导线,则管内部的磁感强度为________________,内部的磁能密度为________________.21. 一无限长直导线通有电流tI I 30e -=.一矩形线圈与长直导线共面放置,其长边与导线平行,位置如图所示.求:(1) 矩形线圈中感应电动势的大小及感应电流的方向;(2) 导线与线圈的互感系数.Il大学物理(第5章)习题1.在狭义相对论中,下列说法中哪些是正确的?(1) 一切运动物体相对于观察者的速度都不能大于真空中的光速.(2) 质量、长度、时间的测量结果都是随物体与观察者的相对运动状 态而改变的 (3) 在一惯性系中发生于同一时刻,不同地点的两个事件在其他一切 惯性系中也是同时发生的.(4) 惯性系中的观察者观察一个与他作匀速相对运动的时钟时,会看 到这时钟比与他相对静止的相同的时钟走得慢些. (A)(1),(3),(4) (B)(1),(2),(4) (C)(1),(2),(3) (D)(2),(3),(4)解:[ ]2. 设S'系以速率=v 0.60c 相对于S 系沿xx ’轴运动,且在t=t ’=0时,x =x ’=0.(1) 若有一事件,在S 系中发生于t =7100.2-⨯s ,x =50m 处,则该事件在S ’系中发生时刻为________________________.(2)如有另一事件发生于S 系中t=7100.3-⨯s ,x =10m 处,在S ’系中测得这两个事件的时间间隔为__________________.3. 设有两个参考系S 和S ’,它们的原点在t =0和t ’=0时重合在一起.有一事件,在S ’系中发生在t ’=8100.8-⨯s ,x ’=60m ,y ’=0,z ’=0处,若S ’系相对于S 系以速率v =0.60c 沿xx ’轴运动,问该事件在S 系中的时空坐标x =______________,y=_____________,z =____________,t =_______________4. 在惯性系S 中,某事件A 发生在1x 处,6100.2-⨯s 后,另一事件B 发生在2x 处,已知12x x -=300m .问:(1) 能否找到一个相对S 系作匀速直线运动的参照系S ’,在S ’系中,两事件发生于同一地点?(2) 在S ’系中,上述两事件之间的时间间隔为多少?解:5. 设在正负电子对撞机中,电子和正电子以速度0.90c 相向飞行,它们之间的相对速度为_______________________.6.一固有长度为4.0m 的物体,若以速率0.60c 沿x 轴相对某惯性系运动,试问从该惯性系来测量,此物体的长度为_____________________.7. 半人马星座α星是离太阳系最近的恒星,它距地球10103.4⨯m .设有一宇宙飞船自地球往返于半人马星座α星之间.若宇宙飞船的速率为0.999c ,按地球上时钟计算,飞船往返一次需要的时间为_____________________.如以飞船上时钟计算,往返一次的时间为_______________________.8. 在S 系中有一长为0l 的棒沿x 铀放置,并以速率u 沿xx ’轴运动.若有一S ’系以速率v 相对S 系沿xx ’轴运动,试问在S ’系中测得此棒的长度为多少?9.一火箭的固有长度为L,相对于地面作匀速直线运动的速度为1v ,火 箭上有一个人从火箭的后端向火箭前端上的一个靶子发射一颗相对于火箭的速度为2v 的子弹.在火箭上测得子弹从射出到击中靶的时间间隔是:(A)21v v L + (B)2v L(C)21v v L- (D)211)(1c v v L - (c表示真空中光速)解:[ ]10.某地发生两件事,静止位于该地的甲测得时间间隔为4s,若相对甲作匀速直线运动的。
(完整版)大学物理学上下册习题与答案

习题九一、选择题9.1 关于高斯定理的理解有下面几种说法,其中正确的是:(A) 如果高斯面上E处处为零,则该面内必无电荷.(B) 如果高斯面内无电荷,则高斯面上E处处为零.(C) 如果高斯面上E处处不为零,则高斯面内必有电荷.(D) 如果高斯面内有净电荷,则通过高斯面的电场强度通量必不为零.[A(本章中不涉及导体)、 D ] 9.2有一边长为a 的正方形平面,在其中垂线上距中心O 点a /2处,有一电荷为q 的正点电荷,如图所示,则通过该平面的电场强度通量为(A)03 q . (B) 04 q (C) 03 q . (D) 06 q [D ]q题图9.19.3面积为S 的空气平行板电容器,极板上分别带电量q ,若不考虑边缘效应,则两极板间的相互作用力为(A)S q 02(B)S q 022 (C) 2022S q (D) 202Sq [B ]9.4 如题图9.2所示,直线MN 长为2l ,弧OCD 是以N 点为中心,l 为半径的半圆弧,N 点有正电荷q ,M 点有负电荷q .今将一试验电荷0q 从O 点出发沿路径OCDP 移到无穷远处,设无穷远处电势为零,则电场力作功(A) A <0 , 且为有限常量. (B) A >0 , 且为有限常量.(C) A =∞. (D) A =0. [D ,0O V ]-题图9.29.5静电场中某点电势的数值等于 (A)试验电荷q 0置于该点时具有的电势能.(B)单位试验电荷置于该点时具有的电势能. (C)单位正电荷置于该点时具有的电势能.(D)[C ]9.6已知某电场的电场线分布情况如题图9.3所示.现观察到一负电荷从M 点移到N 点.有人根据这个图作出下列几点结论,其中哪点是正确的?(A) 电场强度M N E E . (B) 电势M N U U .(C) 电势能M N W W . (D) 电场力的功A >0.[C ] 二、计算题9.7 电荷为q 和2q 的两个点电荷分别置于1x m 和1x m 处.一试验电荷置于x 轴上何处,它受到的合力等于零? x2q q 0解:设试验电荷0q 置于x 处所受合力为零,根据电力叠加原理可得022220000(2)(2)ˆˆ0041414141q q q q q q i i x x x x 即:22221(2)0121011x x x x22212210x x x x2610(322)x x x m 。
矿大《大学物理》习题解答(下)
=
σ 2ε 0
1 −
a a2 +
R2
由题意,令 E=σ/(4ε0),得到
From: 理学院
~3~
2018
中国矿业大学(北京)《大学物理》习题
R= 3a
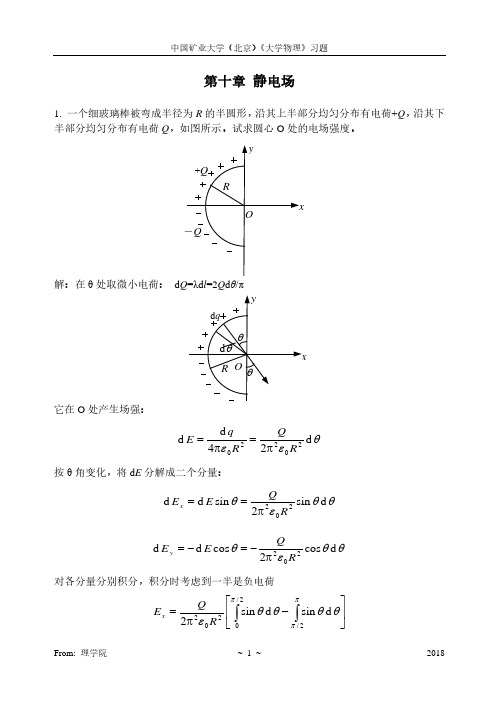
*4. 一半径为 R 的半球面,均匀地带有电荷,电荷面密度为 σ,求球心 O 处的电场强 度。
R dθ
θ
dE
O
x
解:选取坐标轴 Ox 沿半球面的对称轴,如图所示。把半球面分成许多微小宽度的环带, 每一环带之面积:
O 点处的总场强:
∫ σ
E= 2ε 0
π /2
sinθ
0
d(sinθ )
=
σ 2ε 0
sin 2 θ 2
|π0 / 2 =
σ 4ε 0
E = σ i 4ε 0
其中 i 为沿 x 轴正方向的单位矢量。
5. 半径为 R 的均匀带电球体内的电荷体密度为 ρ ,若在球内挖去一块半径为 r < R 的 小球体,如图所示.试求:两球心 O 与 O′ 点的场强,并证明小球空腔内的电场是均匀
E1
=
λ 4πε 0 R
(− i
−
j )
半无限长直线 B∞在 O 点产生的场强 E2 :
E2
=
λ 4πε 0 R
(− i
+
j学(北京)《大学物理》习题
半圆弧线段在 O 点产生的场强 E3 :
E3
=
λ 2πε 0 R
i
由场强叠加原理,O 点合场强为:
E = E1 + E2 + E3 = 0
From: 理学院
~4~
2018
的.
中国矿业大学(北京)《大学物理》习题
大学物理作业答案(下)

65. 如图所示,几种载流导线在平面内分布,电流均为I ,求:它们在O 点的磁感应强度。
1 RIB 80μ=方向 垂直纸面向外2 R I R I B πμμ2200-= 方向 垂直纸面向里 3 RI R I B 4200μπμ+= 方向 垂直纸面向外 66. 一半径为R 的均匀带电无限长直圆筒,电荷面密度为σ,该筒以角速度ω绕其轴线匀速旋转。
试求圆筒内部的磁感应强度。
解:如图所示,圆筒旋转时相当于圆筒上具有同向的面电流密度i , σωσωR R i =ππ=)2/(2作矩形有向闭合环路如图中所示.从电流分布的对称性分析可知,在ab 上各点B的大小和方向均相同,而且B 的方向平行于ab ,在bc 和fa 上各点B的方向与线元垂直,在de , cd fe ,上各点0=B.应用安培环路定理∑⎰⋅=I l B 0d μ 可得 ab i ab B 0μ= σωμμR i B 00==圆筒内部为均匀磁场,磁感强度的大小为σωμR B 0=,方向平行于轴线朝右.i ω σc deab f67.在半径为R 的长直金属圆柱体内部挖去一个半径为r 的长直圆柱体,两柱体轴线平行,其间距为a (如图)。
今在此导体内通以电流I ,电流在截面上均匀分布,求:空心部分轴线上O ' 点的磁感应强度的大小。
解:)(22r R IJ -=π10121r k J B ⨯=μ 20221r k J B ⨯-=μj Ja O O k J r r k J B B B 021********21)(21μμμ=⨯=-⨯=+=j r R IaB )(2220-=πμ68.一无限长圆柱形铜导体,半径为R ,通以均匀分布的I 今取一矩形平面S (长为L ,宽为2R ),位置如图,求:通过该矩形平面的磁通量。
解:在圆柱体内部与导体中心轴线相距为r 处的磁感强度的大小,由安培环路定律可得:)(220R r r R IB ≤π=μ因而,穿过导体内画斜线部分平面的磁通Φ1为⎰⎰⋅==S B S B d d 1 Φr rL R I Rd 2020⎰π=μπ=40LIμ在圆形导体外,与导体中心轴线相距r 处的磁感强度大小为 )(20R r rIB >π=μ因而,穿过导体外画斜线部分平面的磁通Φ2为⎰⋅=S B d 2Φr r IL R Rd 220⎰π=μ2ln 20π=ILμ穿过整个矩形平面的磁通量 21ΦΦΦ+=π=40LIμ2ln 20π+ILμ69.如图所示,载有电流I 1和I 2的无限长直导线相互平行,相距3r ,今有载有电流I 3的导线MN = r 水平放置,其两端M 、N 分别与I 1、I 2距离均为r ,三导线共面,求:导线MN 所受的磁场力的大小与方向。
大学物理(下) No.6作业解析

《大学物理》作业 No.6 光的偏振一、选择题1. 在双缝干涉试验中,用单色自然光,在屏上形成干涉条纹。
若在两缝后放一个偏振片,则[ B ] (A) 干涉条纹的间距不变,但明纹的亮度加强。
(B) 干涉条纹的间距不变,但明纹的亮度减弱。
(C) 干涉条纹的间距变窄,但明纹的亮度减弱。
(D) 无干涉条纹。
解:双缝后放置的偏振片使光强减弱,但不影响其它干涉因素,所以干涉条纹位置间距不变,只是明纹亮度减弱。
2. 使一光强为0I 的平面偏振光先后通过两个偏振片1P 和2P 。
1P 和2P 的偏振化方向与原入射光光矢量振动方向的夹角分别是α和 90,则通过这两个偏振片后的光强I 是 [ C ] (A)α20cos 21I (B) 0 (C) ()α2sin 4120I (D)α20sin 41I (E) α40cos I 解:由马吕斯定律,光强为0I 的偏振光通过第一个偏振片后,光强为α201cos I I =, 再通过第二个偏振片,光强变为()ααααπα2sin 41sin cos 2cos cos 202202202I I I I ==⎪⎭⎫⎝⎛-=3. 一束光强为0I 的自然光,相继通过三个偏振片1P 、2P 、3P 后,出射光的光强为8/0I I =。
已知1P 和3P 的偏振化方向相互垂直,若以入射光线为轴,旋转2P,要使出射光的光强为零,2P 最少要转过的角度是[ B ] (A)30 (B)45 (C)60 (D)90解:设1P 和2P 偏振化方向之间夹角为α,光强为0I 的自然光通过三个偏振片后,光强 ()ααπα2sin 812cos cos 2120220I I I =⎪⎭⎫ ⎝⎛-⋅⋅=由题意, 80I I =,所以()4,12sin 2παα==要使出射光强为零,2P 的偏振化方向应与1P 或3P 的偏振化方向平行,即最少要转过4π。
4. 自然光以60°的入射角照射到不知其折射率的某一透明介质表面时,反射光为线偏振光,则知[ B ] (A) 折射光为线偏振光,折射角为30°。
大学普通物理B(下)复习资料。
x − x0 y( x, t ) = Acos ω (t m ) +ϕ u
说明: 说明: 1) “±”反映波的传播方向; 反映波的传播方向; ± 反映波的传播方向 2) x0 是波源坐标; 是波源坐标; 是波源的振动初相位。 3) ϕ 是波源的振动初相位。
波函数物理意义: 波函数物理意义:
时的波形曲线, 例:如图为一平面简谐波在t=0时的波形曲线,波 如图为一平面简谐波在 时的波形曲线 线上x=1m处P点的振动曲线如图所示,求波函数。 点的振动曲线如图所示, 线上 处 点的振动曲线如图所示 求波函数。 y(m) u y(m) 0.2 0.2 P o 1 2 x(m) o 0.1 0.2 t(s) 解:由波形曲线 由P点振动曲线 点振动曲线
x 若 y = Acosωt − u
λ
∆x
x
∂y x v= = −Aωsin ωt − ∂t u ∂2 y x 2 a = 2 = −Aω cosωt − ∂t u
一般计算类型: 一般计算类型 1、比较标准波动表达式得到: A, ω, 、比较标准波动表达式得到:
C
5m
B A
x0 = 5
9m
D
x
yA振 = 3cos 4πt
(2) 以 B 为原点 )
波函数: 波函数:
x − x0 y = Acosωt − +ϕ u
x x −5 y = 3cos 4π t − = 3cos4π t − +π 20 20
Ek = Ep = 0
平衡位置处 y = 0, Ek = Ep
⇒ Emax
波的能量密度和能流密度 能量密度: 能量密度:单位体积中的波动能量
大学物理习题下(完整版)
物理(下)作业专业班级:姓名:学号:第十章真空中的静电场(1)一、选择题1、根据电场强度定义式0/q F E(0q 为正的实验点电荷),下列说法中哪个是正确的?(A)、若场中某点不放实验电荷0q ,则F =0,从而E=0;(B)、电场中某点场强的大小与实验点电荷q 0的大小成反比;(C)、电场中某点场强的方向,就是正电荷在该点所受电场力的方向;(D)、以上说法都不正确。
[]2、如图所示,在坐标(a ,0)处放置一点电荷+q ,在坐标(-a ,0)处放置另一点电荷-q .P点是x 轴上的一点,坐标为(x ,0).当x >>a 时,该点场强的大小为:(A)xq04 ;(B)30xqa;(C)302xqa;(D)204xq 。
[]3、(2010年北京科技大学)两个带有等量同号电荷,形状相同的金属小球1和2,相互作用力为F ,它们之间的距离远大于小球本身直径.现在用一个带有绝缘柄的原来不带电的相同金属小球3去和小球1接触,再和小球2接触,然后移去.这样小球1和2之间的作用力变为:(A)F/2;(B)F/4;(C)3F/8;(D)F/10.[]二、填空题1、一电量为–5×10―9C 的试验电荷放在电场中某点时,受到20×10―9N 向下的力,则该点的电场强度大小为___________________,方向__________________。
2、(2011年电子科技大学)由一根绝缘细线围成的边长为l 的正方形线框,今使它均匀带电,其电荷线密度为λ,则在正方形中心处的电场强度大小E=__________________。
3、铁原子核里两质子间相距4.0×10-15米,每个质子的电荷都是1.6×10-19库仑,则它们之间的库仑力应为______________牛顿。
三、计算题1、(2012年深圳大学)如图,在O x 轴上有长为a 的细杆OM ,其电荷线密度为Cx ,其中C为大于零的常量,求:(1)在OM 延长线上距M点为b的P点的电场强度的大小;(2)如果在P点放置一个带电量为+q 的点电荷,该点电荷所受库仑力大小为多少?2、有一半径为R的半圆细环上均匀地分布电荷Q,若在其环心处放置一电荷量为q的点电荷,求该点电荷q所受到的电场力的大小及方向。
大学物理(下) No.8作业解析
《大学物理》作业 No.8 量子力学基础一、选择题1. 如果两种不同质量的粒子,其德布罗意波长相同,则这两种粒子的 [ A ] (A) 动量相同。
(B) 能量相同。
(C) 速度相同。
(D) 动能相同。
解: 由德布罗意关系λhp =可知,粒子波长相同,动量必然相同。
由于粒子质量不同,所以,粒子速度、动能和能量将不同。
2. 若α 粒子在磁感应强度为B 的均匀磁场中沿半径为R 的圆形轨道运动,则粒子的德布罗意波长是[ A ] (A)eRB h 2 (B) eRB h(C) eRB 21 (D) eRBh 1 解:半径eB mv qB mv R 2==,所以德布罗意波长eBRhmv h 2==λ。
3. 设粒子运动的波函数图线分别如图(A)、(B)、(C)、(D)所示,那么其中确定粒子动量的精确度最高的波函数是哪个图?[ A ]解:由不确定关系 ≥∆⋅∆x p x 可知,x ∆大,x p ∆小,图(A)x ∆最大,所以x p ∆最小,确定粒子动量的精确度最高。
4. 关于不确定关系⎪⎭⎫ ⎝⎛=≥∆⋅∆π2h p x x有以下几种理解:(1) 粒子的动量不可能确定。
(2) 粒子的坐标不可能确定。
(3) 粒子的动量和坐标不可能同时确定。
(4) 不确定关系不仅适用于电子和光子,也适用于其它粒子。
其中正确的是:[ C ] (A) (1)、(2) (B) (2)、(4) (C) (3)、(4) (D) (4)、(1)()D xx x ()A()B ()C5. 已知粒子在一维矩形无限深势阱中运动,其波函数为:()()a x a a x ax ≤≤-⋅=23cos1πψ那么粒子在65ax =处出现的概率密度为 [ A ] (A)a 21 (B) a 1(C) a 21 (D) a1 解:概率密度()a x a x 23cos 122πψ=,将6/5a x =代入,得()aa a a x 216523cos 122=⋅=πψ二、填空题1. 若中子的德布罗意波长为2Å,则它的动能为J 1029.321-⨯。
《大学物理学》第二版下册习题解答
第九章 静电场中的导体9.1 选无穷远处为电势零点,半径为R 的导体球带电后,其电势为U 0,则球外离球心距离为r 处的电场强度的大小为(A) 302rU R . (B) R U 0. (C) 20rRU . (D) r U 0. [ C ] 9.2如图所示,一厚度为d 的“无限大”均匀带电导体板,电荷面密度为σ ,则板的两侧离板面距离均为h 的两点a 、b 之间的电势差为:(A) 0. (B)2εσ. (C) 0εσh . (D) 02εσh. [ A ]9.3 一个未带电的空腔导体球壳,内半径为R .在腔内离球心的距离为d 处( d < R ),固定一点电荷+q ,如图所示. 用导线把球壳接地后,再把地线撤去.选无穷远处为电势零点,则球心O 处的电势为 (A) 0 . (B)dq04επ.(C)R q 04επ-. (D) )11(4Rd q -πε. [ D ]9.4 在一不带电荷的导体球壳的球心处放一点电荷,并测量球壳内外的场强分布.如果将此点电荷从球心移到球壳内其它位置,重新测量球壳内外的场强分布,则将发现: (A) 球壳内、外场强分布均无变化. (B) 球壳内场强分布改变,球壳外不变. (C) 球壳外场强分布改变,球壳内不变.(D) 球壳内、外场强分布均改变. [ B ]9.5在一个孤立的导体球壳内,若在偏离球中心处放一个点电荷,则在球壳内、外表面上将出现感应电荷,其分布将是:(A) 内表面均匀,外表面也均匀. (B) 内表面不均匀,外表面均匀. (C) 内表面均匀,外表面不均匀.(D) 内表面不均匀,外表面也不均匀. [ B ]9.6当一个带电导体达到静电平衡时: (A) 表面上电荷密度较大处电势较高. (B) 表面曲率较大处电势较高. (C) 导体内部的电势比导体表面的电势高.(D) 导体内任一点与其表面上任一点的电势差等于零. [ D ]9.7如图所示,一内半径为a 、外半径为b 的金属球壳,带有电荷Q ,在球壳空腔内距离球心r 处有一点电荷q .设无限远处为电势零点,试求: (1) 球壳内外表面上的电荷. (2) 球心O 点处,由球壳内表面上电荷产生的电势. (3) 球心O 点处的总电势.解:(1) 由静电感应,金属球壳的内表面上有感生电荷-q ,外表面上带电荷q +Q .(2) 不论球壳内表面上的感生电荷是如何分布的,因为任一电荷元离O 点的 距离都是a ,所以由这些电荷在O 点产生的电势为adqU q 04επ=⎰-aq04επ-=(3) 球心O 点处的总电势为分布在球壳内外表面上的电荷和点电荷q 在O 点产生的电势的代数和q Q q q O U U U U +-++=r q 04επ=a q 04επ-b q Q 04επ++ )111(40b a r q +-π=εbQ04επ+9.8有一"无限大"的接地导体板 ,在距离板面b 处有一电荷为q 的点电荷.如图所示,试求: (1) 导体板面上各点的感生电荷面密度分布.(2) 面上感生电荷的总电荷.解:(1) 选点电荷所在点到平面的垂足O 为原点,取平面上任意点P ,P 点距离原点为r ,设P 点的感生电荷面密度为σ.在P 点左边邻近处(导体内)场强为零,其法向分量也是零,按场强叠加原理,()024cos 0220=++=⊥εσεθb r q E P π 2分 ∴ ()2/3222/b r qb +-=πσ 1分(2) 以O 点为圆心,r 为半径,d r 为宽度取一小圆环面,其上电荷为 ()2/322/d d b r qbrdr S Q +-==σ总电荷为 ()q brrdrqb dS Q S-=+-==⎰⎰∞2/322σ 2分O9.9 如图所示,中性金属球A ,半径为R ,它离地球很远.在与球心O 相距分别为a 与b 的B 、C 两点,分别放上电荷为q A 和q B 的点电荷,达到静电平衡后,问: (1) 金属球A 内及其表面有电荷分布吗?(2) 金属球A 中的P 点处电势为多大?(选无穷远处为电势零点)B解:(1) 静电平衡后,金属球A 内无电荷,其表面有正、负电荷分布,净带电荷为零. (2) 金属球为等势体,设金属球表面电荷面密度为σ. ()()0004///4/d εεσπ++π⋅==⎰⎰a q a q R S U U B A S P A∵0d =⋅⎰⎰AS S σ∴ ()()04///επ+=a q a q U B A P9.10三个电容器如图联接,其中C 1 = 10×10-6 F ,C 2 = 5×10-6 F ,C 3 = 4×10-6 F ,当A 、B 间电压U =100 V 时,试求:(1) A 、B 之间的电容;(2) 当C 3被击穿时,在电容C 1上的电荷和电压各变为多少?解:(1) =+++=321321)(C C C C C C C 3.16×10-6 F(2) C 1上电压升到U = 100 V ,电荷增加到==U C Q 111×10-3 C第十章 静电场中的电介质10.1 关于D的高斯定理,下列说法中哪一个是正确的? (A) 高斯面内不包围自由电荷,则面上各点电位移矢量D为零.(B) 高斯面上处处D为零,则面内必不存在自由电荷.(C) 高斯面的D通量仅与面内自由电荷有关.(D) 以上说法都不正确. [ C ]10.2一导体球外充满相对介电常量为εr 的均匀电介质,若测得导体表面附近场强为E ,则导体球面上的自由电荷面密度σ为(A) ε 0 E . (B) ε 0 ε r E .(C) ε r E . (D) (ε 0 ε r - ε 0)E . [ B ]10.3 一平行板电容器中充满相对介电常量为εr 的各向同性均匀电介质.已知介质表面极化电荷面密度为±σ′,则极化电荷在电容器中产生的电场强度的大小为:(A) 0εσ'. (B) r εεσ0'. (C) 02εσ'. (D)rεσ'. [ A ]10.4一平行板电容器始终与端电压一定的电源相联.当电容器两极板间为真空时,电场强度为0E ,电位移为0D,而当两极板间充满相对介电常量为εr 的各向同性均匀电介质时,电场强度为E ,电位移为D,则(A) r E E ε/0 =,0D D =. (B) 0E E =,0D D rε=.(C) r E E ε/0 =,r D D ε/0 =. (D) 0E E =,0D D=. [ B ]10.5如图所示, 一球形导体,带有电荷q ,置于一任意形状的空腔导体中.当用导线将两者连接后,则与未连接前相比系统静电场能量将 (A) 增大. (B) 减小.(C) 不变. (D) 如何变化无法确定. [ B ]q10.6将一空气平行板电容器接到电源上充电到一定电压后,断开电源.再将一块与极板面积相同的各向同性均匀电介质板平行地插入两极板之间,如图所示. 则由于介质板的插入及其所放位置的不同,对电容器储能的影响为:(A) 储能减少,但与介质板相对极板的位置无关. (B) 储能减少,且与介质板相对极板的位置有关. (C) 储能增加,但与介质板相对极板的位置无关.(D) 储能增加,且与介质板相对极板的位置有关. [ A ]介质板10.7静电场中,关系式 P E D+=0ε(A) 只适用于各向同性线性电介质. (B) 只适用于均匀电介质. (C) 适用于线性电介质.(D) 适用于任何电介质. [ D ]10.8一半径为R 的带电介质球体,相对介电常量为εr ,电荷体密度分布ρ = k / r 。
