河北省衡水市冀州中学2015-2016学年高一政治上学期第一次月考试题B卷
河北省衡水市冀州中学2015-2016学年高一上学期第一次月考物理试卷B卷Word版含答案

试卷类型:B卷冀州市中学2015 -- 2016学年度高一月考高一年级物理试题考试时间:90分钟总分100分一、单项选择题(本题共15小题,每小题2分,共30分。
)1、以下的计时数据指时间间隔的是()A.天津开往德州的625次硬座普快列车于13时35分从天津西站发车B.中央电视台新闻联播节目19时开播C.某人用15s跑完100mD.早上6时起床2、下列各组物理量中,都是矢量的是()A.位移、时间、速度B.速度、速率、加速度C.加速度、速度的变化、速度D.速度、路程、位移3、关于位移和路程,下列说法中错误的是()A.物体沿直线向某一方向运动,通过的路程就是位移B.物体沿直线向某一方向运动,通过的路程等于位移的大小C.物体通过一段路程,其位移可能为0D.物体通过的路程不等,但位移可能相同4、在研究物体的运动时,下列物体中可以当做质点处理的是()A、研究一端固定并可绕该端转动的木杆的运动时B、研究乒乓球的旋转时,可以将乒乓球看作质点C、研究一体操运动员在平衡木上的运动时D、研究月球绕地球运动时5.南北朝时期的傅翕曾写下这样一首诗:“空手把锄头,步行骑水牛。
人在桥上走,桥流水不流。
”其中“桥流水不流”一句应理解成其选择的参考系是A.水 B.桥 C.人 D.地面6.2010年广州亚运会上中国运动员刘翔以13秒09的好成绩获得男子110米栏金牌,刘翔之所以能够取得冠军是因为( )A .冲刺时的末速度大B .平均速度大C .起跑时的初速度大D .起跑时的加速度大7.关于速度、速度的变化量、速度变化率(加速度)的关系,下列说法中正确的是( ) A .速度越大,速度变化量一定越大 B .速度变化越快,加速度越大C .加速度方向保持不变,速度方向也一定保持不变D .速度变化量越大,加速度越大8.下面关于加速度的描述中正确的是 ( ) A.加速度描述了物体速度变化的多少B.加速度在数值上等于单位时间里速度的变化C.当加速度与位移方向相反时,物体做减速运动D.当加速度与速度方向相同且又减小时,物体做减速运动9、一列车队从同一地点先后开出n 辆汽车在平直的公路上排成直线行驶,各车均由静止出发先做加速度为a 的匀加速直线运动,达到同一速度v 后改做匀速直线运动,欲使n 辆车都匀速行驶时彼此距离约为x ,则各辆车依次启动的时间间隔为(不计汽车的大小) ( )A 、a v 2 B 、a v 2 C 、v x 2 D 、vx10、两个做直线运动的物体,甲的加速度为,乙的加速度为,下列说法中正确的是 ( )A.甲的加速度比乙的加速度大B.甲做加速运动,乙做减速运动C.乙的加速度比甲的加速度大,甲、乙的加速度方向一定相反D.乙的加速度比甲的加速度大,甲、乙的加速度方向可能相同,也可能相反11、一物体做直线运动的图象如图所示,则该物体 ( ) A 、先做加速运动,后做减速运动,速度方向相反B 、先做加速运动,后做减速运动,速度方向相同C 、先做减速运动,后做加速运动,速度方向相同D 、先做减速运动,后做加速运动,速度方向相反12、某物体做直线运动的速度图像如图,下列有关物体运动情况判断正确的是( )A 、s 8末物体距出发点最远B 、s 4末物体回到出发点C 、s 6末物体距出发点最远D 、前两秒加速度为2/5s m13、甲乙两辆汽车在平直的公路上沿同一方向做直线运动,0=t 时刻同时经过公路旁的同一个路标。
河北省衡水市冀州中学高一上学期第一次月考语文试卷B卷 Word版含答案.pdf

试卷类型:B卷 河北冀州中学 2015—2016学年度上学期第一次月考 高一年级 语文试题 考试时间150分钟 试题分数120分 第Ⅰ卷 阅读题(共50分) 一、现代文阅读(6分,每题2分) 阅读下面的文字, 完成1—3题。
“常回家看看”入法折射中国养老困局 ①近日,民政部有关官员表示,依据新修订的《老年法》,“以后子女不经常回家看望老人,老人可以诉诸法律”。
看望父母本是做人的基本伦理,从这个意义上说,“常回家看看”入法着实有些多余。
但揣测立法者的动机,就会发现这条规定基于“空巢老人”愈来愈多而子女看望老人愈来愈少的现实。
从这个意义上说,“常回家看看”入法,折射出了传统养老模式遭受的严峻挑战。
②中国60岁以上的人口已达1.67亿,我国事实上已经进入老龄社会。
而在市场经济体制改革纵深推进的背景下,一方面社会成员的流动性增大,异地就业的青年人增多;另一方面,年青一代的生活压力和工作压力增大,购房置业、子女教育和人际应酬令人疲惫不堪。
受此影响,传统意义上三世同堂甚至四世同堂的家庭逐渐瓦解,子女与父母分居甚至相隔甚远的分居情况十分普遍,常回家看看自然变得奢侈。
诚然,孝顺作为重要的家庭美德,子女应该尽最大可能履行赡养义务。
但现实情况是,面对社会成员流动频繁、父母与子女分居成为常态、人口老龄化高峰日益临近的现实,政府部门却依然将希望寄托在养儿防老的传统模式上。
各级政府针对老年人的统一、规范、完善的养老保险体系长期未能建立,对相当一部分老年人而言,老有所养、老有所医、老有所教、老有所学、老有所为、老有所乐还只是一个梦想。
解决人口老龄化问题,需要政府、社会和家庭共同努力。
在传统中国,老人赡养在很大程度上属于子女义务,而不是政府责任。
这种观念不仅会增加年青一代的负担,也会影响人力资源的最佳配置,同时有悖于以人为本的价值取向。
将养老问题纳入社会统筹和政府责任范围,不仅会使老龄人口受益,也会减轻年青一代的负担。
2016届河北省衡水市冀州中学高三上学期第一次月考政治试题A卷及答案

试卷类型:A卷河北冀州中学2015---2016学年上学期第一次月考高三年级政治试题考试时间:90分钟试题分数:100分第Ⅰ卷(单选,共50小题,每题1分,共50分)1、商品是用于交换的劳动产品。
下列对商品的表述,正确的一项是A、大陆向台湾赠送的用来救助“苏迪罗”强台风灾害的棉衣、板房是商品B、为纪念反法西斯战争胜利70周年发行的纪念币是商品C、有使用价值的东西一定是商品D、小明读书时所用的政治教科书是商品2、在其它条件不变的前提下,某企业依靠技术进步,率先提高了劳动生产率。
结果该企业①生产成本降低,单位商品价值减少,利润增加②生产商品的社会必要劳动时间减少③在社会劳动生产率不变的条件下,同一时间创造的商品价值总量增加④同一时间内生产的商品数量增多A.①②B.③④C.②③ D.①④3、2014年1件A 商品可以兑换7件B商品,1件B商品可以兑换4件C商品。
假如2015生产A商品的社会劳动生产率提高了40%,1件B商品可以兑换5件C商品,若生产B 商品的条件不变,不考虑其他因素,则下列判断正确的有①2015年1件A商品可以兑换25件C商品 xx.k.②2015年1件A商品可以兑换20件C商品③生产C商品的社会劳动生产率提高了20% [Zx④生产C 商品的社会劳动生产率提高了25%A.①③ B.①④ C.②③D.②④4①表明外汇汇率降低,美元贬值②表示外汇汇率升高,人民币贬值③有利于我国产品的出口,但不利于进口④有利于产品进口,但不利于我国产品出口A.①③ B.②④ C.①④ D.②③5、2015年春茶开始上市了,较往年今年的上市时间更早。
今年的采茶成本、管理成本、加工成本都有所上涨,同时茶叶的质量安全水平也有所提高。
致使春茶上市之初,呈现“抢货”情形,价格有所上涨,对春茶价格上涨的现象认识正确的是A.春茶的需求弹性比较大B.春茶供不应求决定其价格上涨C.春茶的使用价值变大D.春茶的价值量变大6、W商品价格与需求之间的关系如图所示。
河北省衡水市冀州中学2015-2016学年高二上学期第一次月考文综(理)政治试题A卷

试卷类型:A卷河北冀州中学2015-2016学年上学期第一次月考高二年级理科文综试题Ⅰ卷(90*1=90分)1.下列关于文化的理解,正确的是①文化就是指人们受教育的程度②文化是相对于经济、政治而言的人类全部精神活动及其产品③纯粹“自然”的东西不能称为文化④文化不具有意识形态性质A.①② B.①③ C.②③ D.②④2.乡土中国不仅是地理意义上的农村,也是整个中国社会文化的基本特性。
据统计,中国每天消失的村落有80至100个。
在急速的城市化进程中,城市毫无节制地膨胀,农村被一步步地蚕食。
割裂的城市与村庄之间,充斥的不仅仅是“乡韵”的遗失,还有被毁的精神家园。
由此可见( )A.文化是人类社会特有的现象 B.传统村落是民族情感的集中表达C.人们的精神活动离不开物质载体 D.文化是一种重要的精神力量3.下列属于文化现象的是( )①中共十八大于2012年下半年在北京召开②第二十二届冬季奥林匹克运动会于当地时间2014年2月在俄罗斯索契市开幕③2014年2月,台北举办动漫节④2013年2月20日即期市场上,人民币对美元走出了有史以来的首次1%跌停A.①② B.③④ C.②③ D.①④4.黄山作为世界自然与文化双重遗产,集中国各大名山的美景于一身,尤其以奇松、怪石、云海、温泉“四绝”著称,其源远流长的宗教文化和精品荟萃的黄山艺术,对各方游客有着无限的吸引力。
这表明( )A.文化只能存在于自然之中B.自然中不存在文化C.文化由人所创造,为人所特有D.人们参与文化活动就是为了享用文化5.追溯中国结的渊源应从远古年代的结绳记事开始。
东汉郑玄在《周易注》中道:“结绳为记,事大,大结其绳;事小,小结其绳。
”“结”与“吉”谐音,在漫长的演变过程中,小小绳结被人们赋予了各种情感愿望,“同心结”、“平安结”、“团圆结”,一个个美丽的中国结蕴含着人们对美好生活的向往。
对上述材料中文化现象的正确解读是( )①文化是人类社会实践的产物②追求真善美是中华民族精神的核心③从绳结之中可以透视人们的精神世界和精神生活④结绳使人类文明得以传承,标志人类进入文明时代A.①③ B.②④ C.①② D.①④6.“重男轻女”本来是中国封建社会的思想意识,是生产资料私有制财产继承关系的反映,但直到今天,这种思想依然残留在一些人的头脑里。
河北省衡水市冀州中学2015-2016学年高一上学期第三次月考政治试题A卷
试卷类型:A卷河北冀州中学2015 年-----2016学年月三考试高一年级政治试题考试时间90分钟试题分数100分第Ⅰ卷(选择题共70分)本卷共50小题,每小题1.4分,共70分1. 黄金自古以来被视为五金之首,有“金属之王”的称号,享有其它金属无法比拟的盛誉,其显赫的地位几乎永恒。
正因如此,黄金成为财富和华贵的象征,具有金融储备、货币、首饰等功能。
到目前为止黄金在上述领域中的应用仍然占主要地位。
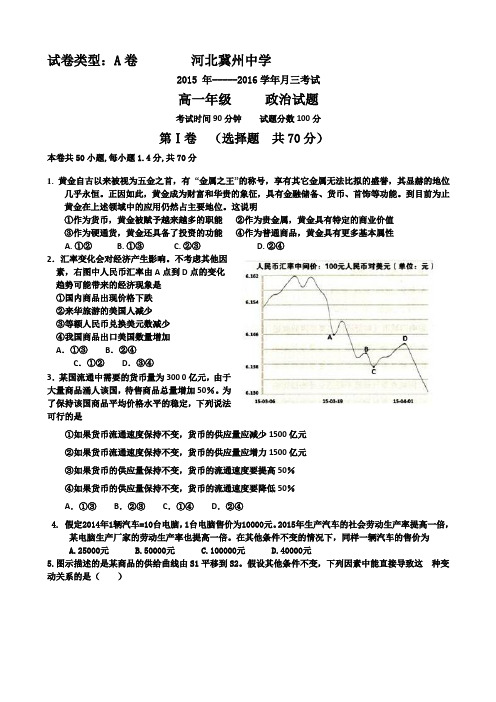
这说明①作为货币,黄金被赋予越来越多的职能②作为贵金属,黄金具有特定的商业价值③作为硬通货,黄金还具备了投资的功能④作为普通商品,黄金具有更多基本属性A. ①②B. ①③C. ②③D. ②④2.汇率变化会对经济产生影响。
不考虑其他因素,右图中人民币汇率由A点到D点的变化趋势可能带来的经济现象是①国内商品出现价格下跌②来华旅游的美国人减少③等额人民币兑换美元数减少④我国商品出口美国数量增加A.①③B.②④C.①②D.③④3.某国流通中需要的货币量为300 0亿元,由于大量商品涌人该国,待售商品总量增加50%。
为了保持该国商品平均价格水平的稳定,下列说法可行的是①如果货币流通速度保持不变,货币的供应量应减少1500亿元②如果货币流通速度保持不变,货币的供应量应增力1500亿元③如果货币的供应量保持不变,货币的流通速度要提高50%④如果货币的供应量保持不变,货币的流通速度要降低50%A.①③B.②③C.①④D.②④4. 假定2014年1辆汽车=10台电脑,1台电脑售价为10000元。
2015年生产汽车的社会劳动生产率提高一倍,某电脑生产厂家的劳动生产率也提高一倍。
在其他条件不变的情况下,同样一辆汽车的售价为A.25000元B.50000元C.100000元D.40000元5.图示描述的是某商品的供给曲线由S1平移到S2。
假设其他条件不变,下列因素中能直接导致这种变动关系的是()①该商品的生产成本大幅度增加②部分生产者率先提高生产效率③城乡居民收入水平大幅度提高④政府对该商品生产者给予补贴A. ①④B. ②③C. ②④D.③④6.2014年某市出台政策鼓励单位和个人购买使用新能源汽车,市民购置一辆可获得最高12万元、最低7万元的补贴,补贴直接从车价中扣除,D1表示补贴前,D2表示补贴后。
河北省衡水市冀州中学2015-2016学年高一上学期第五次月考语文试卷B卷 Word版含答案

资料概述与简介 试卷类型:B卷河北冀州中学 2015—2016学年度上学期第五次月考 高一年级语文试题 考试时间150分钟试题分数150分 第Ⅰ卷阅读题甲必考题 一、现代文阅读(6分,每小题2分) 阅读下面的文字,完成1-3题。
唐朝的反腐败 唐太宗亲眼目睹了隋炀帝“驱天下以纵欲,罄万物而自奉”,终致“率土分崩”,深刻指出:“为主贪,必丧其国。
”他即位伊始便把后宫美女释放3000人,任其择偶出嫁。
贞观十二年(638年)出巡山西,浦州刺史赵元楷大肆铺张接迎,太宗斥责他此举纯属“亡隋弊俗”,吓得赵元楷“数日不食而卒”。
唐朝制定的反腐败专项法律法规是唐律中的《职律》。
唐律规定对监临主司受财“二十五匹绞”,收受钱财而枉法者“加役流”。
形象点说,在唐宋明清四朝,正七品官(相当于现在的县委书记、县长和处长们)贪污受贿相当于其一个多月甚至低于一个月的俸禄,就要被绞杀。
唐太宗曾告诫群臣“陷其身者,皆为贪冒财利,与夫鱼鸟何以异哉?”,谕劝百官不要因贪图钱财而毁了身家性命。
《唐律·诈伪》设有谎报、虚报政绩罪,即自报、指使下属或授意他人谎报、虚报均属此列。
《唐律·职制》设有请托说情罪,明确规定没有使用财物而仅靠人情向主管人员求办某事,也要禁止。
非主管人员替别人请托,只要开口,就要杖一百;如果枉法,和主管人员同等处罚。
《唐律》还规定,主管官员受财枉法,受贿相当于一尺绢的,要判处杖刑一百,并且一匹加一等,十五匹判处绞刑。
官员在其管辖范围内收受百姓财物、牛羊瓜果等供馈,或向百姓借贷财物,役使人力等,均以贪污罪论处,以防止官吏对下属及百姓吃拿卡要、敲诈勒索。
而普通百姓盗窃,即使五十匹,只是流放服役而已。
唐代开始,监察官“二周年一替”,且以较快的速度升迁,既鼓励了他们的工作积极性,又防止了在位长久带来的弊病,因为“久则情亲而弊生,望轻而法玩。
”唐代对官吏的考核主要是“德”、“行”两个方面。
“德”包括官吏的品质、道德修养、对君主的忠、信、笃、卫等;“行’包括官吏的能力大小,守职的勤惰、政绩的好坏等。
河北省衡水市冀州中学2015-2016学年高一上学期第四次月考(B卷)语文试题(原卷版)
考试时间150分钟试题分数150分第Ⅰ卷阅读题甲必考题一、现代文阅读(6分,每小题2分)阅读下面的文字,完成后面小题。
社会主义核心价值观念体系中的每个概念都具有丰富的内涵。
这些概念需要凝结成一个整体,以应对无限丰富的现实问题。
反思当代的审美文化现象,有助于我们梳理核心价值观的内涵。
以两个概念为例。
一个是“富强”。
民众求富,国家求强。
日常生活中,总有人以珠光宝气、香车美人“炫富”。
“炫富”表面上是在展示美,但在观者的眼中却是丑,或者“臭美”。
人们对这种美丑区分的一般解释是:“炫富”是物质追求,审美是精神追求。
以物质和精神区分“炫富”与审美其实是一个误解。
且看“炫富”的内容,集中于名牌服饰、名酒、名表、名车、名度假地。
奢侈品林林总总,共同点却只有一个,就是观念性的符号(“名”)。
在审美活动中,自然美、艺术美都属于精神世界的内心意象,却也离不开物质的载体(比如有一定的质地、色彩、声响等)。
因此,奢靡炫富虽然基于物质,实质却是精神性的。
奢靡与审美都属于精神的追求,意义的深度却有天壤之别。
对追逐符号的人而言,大量珍贵的人力物力被降低为一纸商标的陪衬。
追逐奢华揭示着意义的贫瘠和精神的无力。
审美的意象则以意义的充盈见长。
人心的意象,既可以让金银珠玉装点堂皇的宫殿庙宇,也能令日常的景色转换成大师的杰作,使普通的词语凝结成千古不朽的诗句。
审美和艺术创造体现着人的精神世界的富足。
例如在戏曲艺术中,舞台角色的气象全系于演员的一举一动、一颦一笑。
正是为了突出人的因素,戏里的一切饰物皆为假扮,道具也被精简到了“以鞭代马”“一桌二椅”。
在物质较为充裕的今天,“富”的体现应该是一种由内而外的富贵气。
富贵气是一种自然流露的美,这种美得自个人长期的、自觉的涵养,也得自社会的普遍氛围。
富贵之美是花钱买不到的。
另一个是“和谐”。
孔子说“君子和而不同”,意思是不同的利益、意见、信念在一个统一体中既保持着各自的特点,又彼此相容、互补,进而造就一个共生多赢的局面。
河北省衡水市冀州中学2015-2016学年高一上学期第五次月考数学(文)试卷B卷 Word版含答案
试卷类型:B卷河北冀州中学 2015—2016学年上学期月五考试 高一年级文科数学试题 考试时间120分钟试题分数150分 一、选择题:(共12小题。
每小题5分,共60分。
在每个小题给出的四个选项中,只有一项是符合要求的。
) 1.设,,则=( ). A.|0<≤1} B.|0≤<1} C.|<0} D.|>1} 2.() A. 0 B. 1 C. 2 D. 4 3.设,则=() A.1 B.2 C. 4 D.8 的倾斜角为,则等于() A. B. C. D.不存在 5.在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的侧(左)视图可以为() .已知是三条不同的直线,是三个不同的平面,下列命题 正确的是() A.若,则 B.若,则 C.若,则 D.若,则 ,>1,则( ). A.>1,>0 B.>1,<0 C.0<<1,<0 D. 0<<1,>0 8.函数的值域为() A. B. C. D. .三棱锥三条侧棱两两垂直,三条侧棱长分别为,则该三棱锥的外接球体积为() A.B. C. D. 中,满足“对任意,当时,都有的是( ). A.= B.= C .= D.= 11.已知直线:在轴和轴上的截距相等,则的值是( ) A.1 B.-1C.-2或-1 D.-2或1 是定义在实数集上的函数,满足条件是偶函数,且当时,,则,,的大小关系是() A. B. C. D. 二.填空题:(共4小题,每小题5分,共20分。
) 13.已知集合则AB=____. 14.在三棱锥中,分别是的中点,若与所成的角是,那么为 . 15.已知函数在上是增函数,函数在上是减函数,则实数的取值范围是__________________. .若函数有一个零点是2,那么函数的零点是________. 6个小题,共70分。
解答时应写出必要的文字说明、证明过程或演算步骤.) 17.(本小题满分10分) 函数的定义域为A,的定义域为B. (1)求集合A;(2)若,求实数的取值范围. 18.12分) 当m为何值时,直线(2m2+m-3)x+(m2-m)y=4m-1. (1)倾斜角为45°;(2)在x轴上的截距为1. 1 若二次函数满足,且. 1)求的解析式; 2)若在区间上,不等式恒成立,求实数的取值范围. 20. (本小题满分12分) 如图,在四棱锥中,底面是正方形,底面,分别为的中点,且. (Ⅰ)求证:平面; (2)求三棱锥的体积. 21.(本小题满分12分) 函数对于x>0有意义,且满足条件减函数。
河北省衡水市冀州中学2015-2016学年高二上学期第一次月考数学试卷(理科)(b卷)Word版含解析
2015-2016学年河北省衡水市冀州中学高二(上)第一次月考数学试卷(理科)(B卷)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设集合P={x∈R|x2+2x<0},Q={x∈R|>0},则P∩Q=()A.(﹣2,1)B.(﹣1,0)C.∅D.(﹣2,0)2.已知菱形ABCD的边长为a,∠ABC=60°,则=()A.﹣a2B.﹣a2C.a2D.a23.若则下列不等式:(1)a+b<a•b;(2)|a|>|b|(3)a<b中,正确的不等式有()A.1个B.2个C.3个D.0个4.已知数列{a n}满足3a n+a n=0,a2=﹣,则{a n}的前10项和等于()+1A.﹣6(1﹣3﹣10)B.C.3(1﹣3﹣10)D.3(1+3﹣10)5.函数f(x)=2cosx(sinx+cosx)的最大值和最小正周期分别是()A.2,π B. +1,πC.2,2πD. +1,2π6.若按如图的算法流程图运行后,输出的结果是,则输入的N的值为()A.5 B.6 C.7 D.87.一个四棱锥的三视图如图所示,其侧视图是等边三角形.则该四棱锥的体积等于()A. B.C.D.8.函数f(x)=﹣cosx•lg|x|的部分图象是()A.B.C.D.9.在锐角△ABC中,a=2,b=2,B=45°,则A等于()A.30°B.60°C.60°或120°D.30°或150°10.把y=ln(x+1)的图象的纵坐标不变,横坐标伸长为原来的三倍,再向右移动一个单位,得到的函数解析式是()A.y=ln3x B.y=ln C.y=ln D.y=ln(3x﹣2)11.△ABC是边长为2的等边三角形,已知向量,满足=2,=2+,则下列结论正确的是()A.||=1 B.⊥C.•=1 D.(4+)⊥12.若tanα=2tan,则=()A.1 B.2 C.3 D.4二、填空题(本大题共4小题,每小题5分,共20分.)13.若x,y满足则z=x+2y的最大值为.14.已知三棱锥S﹣ABC,所有顶点都在球O的球面上,侧棱SA⊥平面ABC,SA=AC=2,BC=2,∠A=90°,则球O的表面积为.15.在△ABC中,a=4,b=5,c=6,则=.16.如果函数f(x)=(m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[]上单调递减,则mn的最大值为.三、解答题(本大题共6小题,共70分.解答须写出文字说明、证明过程和演算步骤.)17.△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,已知3acosC=2ccosA ,tanA=,求B . 18.设数列{a n }(n=1,2,3,…)的前n 项和S n 满足S n =2a n ﹣a 1,且a 1,a 2+1,a 3成等差数列.(Ⅰ)求数列{a n }的通项公式;(Ⅱ)记数列{}的前n 项和为T n ,求使得|T n ﹣1|成立的n 的最小值. 19.如图,在四棱锥P ﹣ABCD 中,底面ABCD 为菱形,∠BAD=60°,Q 为AD 的中点. (1)若PA=PD ,求证:平面PQB ⊥平面PAD ;(2)若平面PAD ⊥平面ABCD ,且PA=PD=AD=2,点M 在线段PC 上,且PM=3MC ,求三棱锥P ﹣QBM 的体积.20.已知函数f (x )=sin cos +﹣(1)求f (x )的最小正周期及其对称中心;(2)如果三角形ABC 的三边 a .b .c 满足b 2=ac ,且边b 所对角为 x ,试求x 的范围及此时函数f (3x )的值域.21.已知首项是1的两个数列{a n },{b n }(b n ≠0,n ∈N *)满足a n b n +1﹣a n +1b n +2b n +1b n =0.(1)令c n =,求数列{c n }的通项公式;(2)若b n =3n ﹣1,求数列{a n }的前n 项和S n .22.已知函数f (x )=log 9(9x +1)+kx (k ∈R )为偶函数.(1)求k 的值;(2)解关于x 的不等式f (x )﹣log 9(a +)>0(a >0).2015-2016学年河北省衡水市冀州中学高二(上)第一次月考数学试卷(理科)(B卷)参考答案与试题解析一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设集合P={x∈R|x2+2x<0},Q={x∈R|>0},则P∩Q=()A.(﹣2,1)B.(﹣1,0)C.∅D.(﹣2,0)【考点】交集及其运算.【分析】分别求出P与Q中不等式的解集确定出P与Q,找出两集合的交集即可.【解答】解:由P中不等式变形得:x(x+2)<0,解得:﹣2<x<0,即P=(﹣2,0),由Q中不等式,得到x+1>0,解得:x>﹣1,即Q=(﹣1,+∞),则P∩Q=(﹣1,0).故选:B.2.已知菱形ABCD的边长为a,∠ABC=60°,则=()A.﹣a2B.﹣a2C.a2D.a2【考点】平面向量数量积的运算.【分析】由已知可求,,根据=()•=代入可求【解答】解:∵菱形ABCD的边长为a,∠ABC=60°,∴=a2,=a×a×cos60°=,则=()•==故选:D3.若则下列不等式:(1)a+b<a•b;(2)|a|>|b|(3)a<b中,正确的不等式有()A.1个B.2个C.3个D.0个【考点】不等式的基本性质.【分析】由,可得b<a<0.利用不等式的性质即可得出.【解答】解:∵,∴b<a<0.则下列不等式:(1)a+b<0<a•b,正确;(2)|a|>|b|,不正确;(3)a<b不正确.故正确的不等式只有1个.故选:A.4.已知数列{a n}满足3a n+1+a n=0,a2=﹣,则{a n}的前10项和等于()A.﹣6(1﹣3﹣10)B.C.3(1﹣3﹣10)D.3(1+3﹣10)【考点】等比数列的前n项和.【分析】由已知可知,数列{a n}是以﹣为公比的等比数列,结合已知可求a1,然后代入等比数列的求和公式可求【解答】解:∵3a n+1+a n=0∴∴数列{a n}是以﹣为公比的等比数列∵∴a1=4由等比数列的求和公式可得,S10==3(1﹣3﹣10)故选C5.函数f(x)=2cosx(sinx+cosx)的最大值和最小正周期分别是()A.2,π B. +1,πC.2,2πD. +1,2π【考点】二倍角的余弦;两角和与差的正弦函数;二倍角的正弦;三角函数的周期性及其求法.【分析】利用两角和的正弦公式,二倍角公式,把函数y化为y=sin(2x+)+1,即可求出函数f(x)=2cosx(sinx+cosx)的最大值和最小正周期.【解答】解:函数y=2cosx(sinx+cosx)=2sinxcosx+2cos2x=sin2x+cos2x+1=sin(2x+)+1,故它的最大值为+1,最小正周期等于=π,.故选:B.6.若按如图的算法流程图运行后,输出的结果是,则输入的N的值为()A.5 B.6 C.7 D.8【考点】程序框图.【分析】由已知中的程序框图可知:程序的功能是利用循环计算并输出变量S的值,模拟程序的运行过程,根据输出的结果是,可分析出判断框中的条件.【解答】解:进行循环前k=1,S=0,进行循环后S=,不满足退出循环的条件;k=2,S=,不满足退出循环的条件;k=3,S=,不满足退出循环的条件;k=4,S=,不满足退出循环的条件;k=5,S=,不满足退出循环的条件;k=6,S=,满足退出循环的条件;故满足条件的N值为6,故选B7.一个四棱锥的三视图如图所示,其侧视图是等边三角形.则该四棱锥的体积等于()A. B.C.D.【考点】由三视图求面积、体积.【分析】由已知中的三视图可得,该几何体是一个以俯视图为底面的四棱锥,代入棱锥体积公式,可得答案.【解答】解:由已知中的三视图可得,该几何体是一个以俯视图为底面的四棱锥,其底面为上底2,下底四,高为4的梯形,锥体的高为=2,故锥体的体积V==×[×(2+4)×4]×2=8,故选:A8.函数f(x)=﹣cosx•lg|x|的部分图象是()A.B.C.D.【考点】函数的图象.【分析】根据函数的奇偶性排除BD,再根据x的变化趋势排除C.【解答】解:由于f(x)=﹣cosx•lg|x|,∴f(﹣x)=﹣cos(﹣x)•lg|﹣x|=﹣cosx•lg|x|=f(x),故函数f(x)是偶函数,排除B,D;又当x→0时,lg|x|→﹣∞,cosx→1,∴f(x)→+∞,故排除C,故选:A.9.在锐角△ABC中,a=2,b=2,B=45°,则A等于()A.30°B.60°C.60°或120°D.30°或150°【考点】正弦定理.【分析】由正弦定理可得sinA=,再由大边对大角可得A>B=45°,从而求得A的值.【解答】解:由正弦定理可得=,∴sinA=.∵B=45°,a>b,再由大边对大角可得A>B,故B=60°或120°,故选,C.10.把y=ln(x+1)的图象的纵坐标不变,横坐标伸长为原来的三倍,再向右移动一个单位,得到的函数解析式是()A.y=ln3x B.y=ln C.y=ln D.y=ln(3x﹣2)【考点】函数的图象与图象变化.【分析】根据函数图象之间的变化关系即可得到结论.【解答】解:把y=ln(x+1)的图象的纵坐标不变,横坐标伸长为原来的三倍,得到函数y=ln(),再向右移动一个单位,得到y=ln()=ln,故选:C11.△ABC是边长为2的等边三角形,已知向量,满足=2,=2+,则下列结论正确的是()A.||=1 B.⊥C.•=1 D.(4+)⊥【考点】平面向量数量积的运算.【分析】由题意,知道,,根据已知三角形为等边三角形解之.【解答】解:因为已知三角形ABC的等边三角形,,满足=2,=2+,又,∴的方向应该为的方向.所以,,所以=2,=1×2×cos120°=﹣1,4=4×1×2×cos120°=﹣4,=4,所以=0,即(4)=0,即=0,所以;故选D.12.若tanα=2tan,则=()A.1 B.2 C.3 D.4【考点】三角函数的积化和差公式;三角函数的化简求值.【分析】直接利用两角和与差的三角函数化简所求表达式,利用同角三角函数的基本关系式结合已知条件以及积化和差个数化简求解即可.【解答】解:tanα=2tan,则=============3.故答案为:3.二、填空题(本大题共4小题,每小题5分,共20分.)13.若x,y满足则z=x+2y的最大值为2.【考点】简单线性规划.【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,由直线方程可知,要使z最大,则直线在y轴上的截距最大,结合可行域可知当直线z=x+2y过点B时z最大,求出B的坐标,代入z=x+2y得答案.【解答】解:由足约束条件作出可行域如图,由z=x+2y,得y=﹣+.要使z最大,则直线y=﹣+的截距最大,由图可知,当直线y=﹣+.过点A时截距最大.联立,解得,∴A(0,1),∴z=x+2y的最大值为0+2×1=2.故答案为:2.14.已知三棱锥S﹣ABC,所有顶点都在球O的球面上,侧棱SA⊥平面ABC,SA=AC=2,BC=2,∠A=90°,则球O的表面积为16π.【考点】球的体积和表面积.【分析】根据题意,三棱锥的外接球扩展为长方体的外接球,外接球的直径就是长方体的对角线的长度,求出长方体的对角线的长度,即可求解球的半径,从而可求三棱锥S﹣ABC的外接球的表面积.【解答】解:三棱锥S﹣ABC的所有顶点都在球O的表面上,侧棱SA⊥平面ABC,SA=AC=2,BC=2,∠A=90°,故三棱锥的外接球扩展为长方体的外接球,外接球的直径就是长方体的对角线的长度.∴球的半径R==2.球的表面积为:4πR2=4π×22=16π.故答案为:16π.15.在△ABC中,a=4,b=5,c=6,则=1.【考点】余弦定理;二倍角的正弦;正弦定理.【分析】利用余弦定理求出cosC,cosA,即可得出结论.【解答】解:∵△ABC中,a=4,b=5,c=6,∴cosC==,cosA==∴sinC=,sinA=,∴==1.故答案为:1.16.如果函数f(x)=(m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[]上单调递减,则mn的最大值为18.【考点】二次函数的性质.【分析】函数f(x)=(m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[,2]上单调递减,则f′(x)≤0,即(m﹣2)x+n﹣8≤0在[,2]上恒成立.而y=(m﹣2)x+n﹣8是一次函数,在[,2]上的图象是一条线段.故只须在两个端点处f′()≤0,f′(2)≤0即可.结合基本不等式求出mn的最大值.【解答】解:∵函数f(x)=(m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[,2]上单调递减,∴f′(x)≤0,即(m﹣2)x+n﹣8≤0在[,2]上恒成立.而y=(m﹣2)x+n﹣8是一次函数,在[,2]上的图象是一条线段.故只须在两个端点处f′()≤0,f′(2)≤0即可.即,由②得m≤(12﹣n),∴mn≤n(12﹣n)≤=18,当且仅当m=3,n=6时取得最大值,经检验m=3,n=6满足①和②.∴mn的最大值为18.故答案为:18.三、解答题(本大题共6小题,共70分.解答须写出文字说明、证明过程和演算步骤.)17.△ABC的内角A、B、C的对边分别为a、b、c,已知3acosC=2ccosA,tanA=,求B.【考点】正弦定理的应用;三角函数中的恒等变换应用.【分析】由3acosC=2ccosA,利用正弦定理可得3sinAcosC=2sinCcosA,再利用同角的三角函数基本关系式可得tanC,利用tanB=tan[π﹣(A+B)]=﹣tan(A+B)即可得出.【解答】解:∵3acosC=2ccosA,由正弦定理可得3sinAcosC=2sinCcosA,∴3tanA=2tanC,∵tanA=,∴2tanC=3×=1,解得tanC=.∴tanB=tan[π﹣(A+C)]=﹣tan(A+C)=﹣=﹣=﹣1,∵B∈(0,π),∴B=18.设数列{a n}(n=1,2,3,…)的前n项和S n满足S n=2a n﹣a1,且a1,a2+1,a3成等差数列.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)记数列{}的前n项和为T n,求使得|T n﹣1|成立的n的最小值.【考点】数列的求和.【分析】(Ⅰ)由已知数列递推式得到a n=2a n﹣1(n≥2),再由已知a1,a2+1,a3成等差数列求出数列首项,可得数列{a n}是首项为2,公比为2的等比数列,则其通项公式可求;(Ⅱ)由(Ⅰ)求出数列{}的通项公式,再由等比数列的前n项和求得T n,结合求解指数不等式得n的最小值.【解答】解:(Ⅰ)由已知S n=2a n﹣a1,有a n=S n﹣S n﹣1=2a n﹣2a n﹣1(n≥2),即a n=2a n﹣1(n≥2),从而a2=2a1,a3=2a2=4a1,又∵a1,a2+1,a3成等差数列,∴a1+4a1=2(2a1+1),解得:a1=2.∴数列{a n}是首项为2,公比为2的等比数列.故;(Ⅱ)由(Ⅰ)得:,∴.由,得,即2n>1000.∵29=512<1000<1024=210,∴n≥10.于是,使|T n﹣1|成立的n的最小值为10.19.如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.(1)若PA=PD,求证:平面PQB⊥平面PAD;(2)若平面PAD ⊥平面ABCD ,且PA=PD=AD=2,点M 在线段PC 上,且PM=3MC ,求三棱锥P ﹣QBM 的体积.【考点】平面与平面垂直的判定;棱柱、棱锥、棱台的体积.【分析】(1)由PA=PD ,得到PQ ⊥AD ,又底面ABCD 为菱形,∠BAD=60°,得BQ ⊥AD ,利用线面垂直的判定定理得到AD ⊥平面PQB 利用面面垂直的判定定理得到平面PQB ⊥平面PAD ;2)由平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD=AD ,PQ ⊥AD ,得PQ ⊥平面ABCD ,BC ⊂平面ABCD ,得PQ ⊥BC ,得BC ⊥平面PQB ,即得到高,利用椎体体积公式求出;【解答】解:(1)∵PA=PD ,∴PQ ⊥AD ,又∵底面ABCD 为菱形,∠BAD=60°,∴BQ ⊥AD ,PQ ∩BQ=Q ,∴AD ⊥平面PQB又AD ⊂平面PAD ,∴平面PQB ⊥平面PAD ;(2)∵平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD=AD ,PQ ⊥AD ,∴PQ ⊥平面ABCD ,BC ⊂平面ABCD ,∴PQ ⊥BC ,又BC ⊥BQ ,QB ∩QP=Q ,∴BC ⊥平面PQB ,又PM=3MC ,∴V P ﹣QBM =V M ﹣PQB =20.已知函数f (x )=sin cos +﹣ (1)求f (x )的最小正周期及其对称中心;(2)如果三角形ABC 的三边 a .b .c 满足b 2=ac ,且边b 所对角为 x ,试求x 的范围及此时函数f (3x )的值域.【考点】三角函数中的恒等变换应用;三角函数的周期性及其求法;正弦函数的对称性;余弦定理的应用.【分析】(1)先利用辅助角公式以及降幂公式把函数f (x )化简为sin (),再利用周期和对称中心的求法代入即可求得结论.(2)先利用余弦定理以及基本不等式得到cosx===,求出x∈(0,];再代入f(3x)利用正弦函数的单调性即可求出函数f(3x)的值域.【解答】解:(1)f(x)=sin cos+﹣=sin+=sin cos+cos sin=sin().∴f(x)的最小正周期T==3πf(x)的对称中心为(,0)(k∈Z).(2)∵b2=ac,∴cosx===.又x∈(0,π),∴x∈(0,],而f(3x)=sin(2x+),由2x+∈(,π]∴f(3x)=sin(2x+)∈[0,1]21.已知首项是1的两个数列{a n},{b n}(b n≠0,n∈N*)满足a n b n+1﹣a n+1b n+2b n+1b n=0.(1)令c n=,求数列{c n}的通项公式;(2)若b n=3n﹣1,求数列{a n}的前n项和S n.【考点】数列递推式;数列的求和.【分析】(1)由a n b n+1﹣a n+1b n+2b n+1b n=0,c n=,可得数列{c n}是以1为首项,2为公差的等差数列,即可求数列{c n}的通项公式;(2)用错位相减法来求和.【解答】解:(1)∵a n b n+1﹣a n+1b n+2b n+1b n=0,c n=,∴c n﹣c n+1+2=0,∴c n+1﹣c n=2,∵首项是1的两个数列{a n },{b n },∴数列{c n }是以1为首项,2为公差的等差数列, ∴c n =2n ﹣1;(2)∵b n =3n ﹣1,c n =,∴a n =(2n ﹣1)•3n ﹣1,∴S n =1×30+3×31+…+(2n ﹣1)×3n ﹣1,∴3S n =1×3+3×32+…+(2n ﹣1)×3n ,∴﹣2S n =1+2•(31+…+3n ﹣1)﹣(2n ﹣1)•3n , ∴S n =(n ﹣1)3n +1.22.已知函数f (x )=log 9(9x +1)+kx (k ∈R )为偶函数. (1)求k 的值;(2)解关于x 的不等式f (x )﹣log 9(a +)>0(a >0).【考点】函数奇偶性的性质;指、对数不等式的解法.【分析】(1)转化为log 9﹣log 9(9x +1)=2kx 恒成立求解.(2)利用(3x ﹣a )(3x ﹣)>0,分类讨论求解.【解答】解:(1)∵f (x )为偶函数,∴f (﹣x )=f (x ),即log 9(9﹣x +1)﹣kx=log 9(49+1)+kx ,∴log 9﹣log 9(9x +1)=2kx ,∴(2k +1)x=0,∴k=﹣,(2),( I )①a >1时⇒3x >a 或⇒{x |x >log 3a 或,②0<a <1时或3x <a ,{x |x >log 或x <log 3a }, ③a=1时⇒3x ≠1,{x |x ≠0}.2016年11月4日。
河北省衡水市冀州中学2015-2016学年高二上学期第一次月考数学试卷(文科)(b卷)Word版含解析
2015-2016学年河北省衡水市冀州中学高二(上)第一次月考数学试卷(文科)(B卷)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合A={x|﹣3≤x≤0},B={x|﹣1≤x≤3},则A∩B=()A.[﹣1,0] B.[﹣3,3] C.[0,3]D.[﹣3,﹣1]2.下列图象表示函数图象的是()A.B.C.D.3.在△ABC中,若tanAtanB>1,则△ABC是()A.锐角三角形B.直角三角形C.钝角三角形D.无法确定4.在△ABC中,若a=2,,B=60°,则角A的大小为()A.30°或150°B.60°或120°C.30°D.60°5.将函数y=sin(x﹣)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图象向左平移个单位,则所得函数图象对应的解析式为()A.y=sin(x﹣) B.y=sin(2x﹣)C.y=sin x D.y=sin(x﹣)6.已知函数f(x)=,则f[f()]的值是()A.B.C.4 D.97.已知点A(1,2),B(3,1),则线段AB的垂直平分线的方程是()A.4x+2y=5 B.4x﹣2y=5 C.x+2y=5 D.x﹣2y=58.若a,b,c∈R,且a>b,则下列不等式一定成立的是()A.a+c≥b﹣c B.(a﹣b)c2≥0 C.ac>bc D.9.下列条件中,能判断两个平面平行的是()A.一个平面内的一条直线平行于另一个平面B.一个平面内的两条直线平行于另一个平面C.一个平面内有无数条直线平行于另一个平面D.一个平面内的任何一条直线都平行于另一个平面10.如图所示的程序框图,若输出的S=41,则判断框内应填入的条件是()A.k>3?B.k>4?C.k>5?D.k>6?11.已知平面向量=(1,2),=(﹣2,m),且∥,则实数m的值为()A.1 B.﹣4 C.﹣1 D.412.已知数列{a n},如果a1,a2﹣a1,a3﹣a2,…,a n﹣a n,是首项为1,公比为2的等比﹣1数列,那么a n=()A.2n+1﹣1 B.2n﹣1 C.2n﹣1D.2n+1二、填空题(本大题共4小题,每小题5分,满分20分.)13.已知||=2,||=4,⊥(+),则与夹角的度数为.14.如果一个几何体的三视图如图所示,则此几何体的表面积是.15.如果实数x,y满足条件那么2x﹣y的最大值为.16.函数的最小值是.三、解答题:(本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤.)17.已知函数f(x)=sin2x﹣cos2x的图象过点(,0).(Ⅰ)求实数a的值;(Ⅱ)求函数f(x)的最小正周期及最大值.18.已知数列{a n}满足a1=3,a n﹣3a n=3n(n∈N*),数列{b n}满足b n=.+1(Ⅰ)求证:数列{b n}是等差数列,并求数列{a n}的通项公式;(Ⅱ)求数列{a n}的前n项和S n.19.如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.(1)若PA=PD,求证:平面PQB⊥平面PAD;(2)若平面PAD⊥平面ABCD,且PA=PD=AD=2,点M在线段PC上,且PM=3MC,求三棱锥P﹣QBM的体积.20.在△ABC中,角A,B,C的对应边分别是a,b,c满足b2+c2=bc+a2.(Ⅰ)求角A的大小;(Ⅱ)已知等差数列{a n}的公差不为零,若a1cosA=1,且a2,a4,a8成等比数列,求{}的前n项和S n.21.已知向量=(cosωx,1),=(2sin(ωx+),﹣1)(其中≤ω≤),函数f(x)=•,且f(x)图象的一条对称轴为x=.(1)求f(π)的值;(2)若f()=,f(﹣)=,且,求cos (α﹣β)的值.22.某人上午7:00乘汽车以v1千米/小时(30≤v1≤100)匀速从A地出发到距300公里的B地,在B地不作停留,然后骑摩托车以v2千米/小时(4≤v2≤20)匀速从B地出发到距50公里的C地,计划在当天16:00至21:00到达C地.设乘汽车、骑摩托车的时间分别是x,y小时,如果已知所需的经费p=100+3(5﹣x)+2(8﹣y)元,那么v1,v2分别是多少时走的最经济,此时花费多少元?2015-2016学年河北省衡水市冀州中学高二(上)第一次月考数学试卷(文科)(B卷)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合A={x|﹣3≤x≤0},B={x|﹣1≤x≤3},则A∩B=()A.[﹣1,0] B.[﹣3,3] C.[0,3]D.[﹣3,﹣1]【考点】交集及其运算.【分析】根据A与B,求出两集合的交集即可.【解答】解:∵A=[﹣3,0],B=[﹣1,3],∴A∩B=[﹣1,0].故选:A.2.下列图象表示函数图象的是()A.B.C.D.【考点】函数的概念及其构成要素;函数的图象.【分析】根据函数的定义可知:对于x的任何值y都有唯一的值与之相对应.紧扣概念,分析图象.【解答】解:根据函数的定义,对任意的一个x都存在唯一的y与之对应而A、B、D都是一对多,只有C是多对一.故选C3.在△ABC中,若tanAtanB>1,则△ABC是()A.锐角三角形B.直角三角形C.钝角三角形D.无法确定【考点】三角形的形状判断.【分析】利用两角和的正切函数公式表示出tan(A+B),根据A与B的范围以及tanAtanB >1,得到tanA和tanB都大于0,即可得到A与B都为锐角,然后判断出tan(A+B)小于0,得到A+B为钝角即C为锐角,所以得到此三角形为锐角三角形.【解答】解:因为A和B都为三角形中的内角,由tanAtanB>1,得到1﹣tanAtanB<0,且得到tanA>0,tanB>0,即A,B为锐角,所以tan(A+B)=<0,则A+B∈(,π),即C都为锐角,所以△ABC是锐角三角形.故答案为:锐角三角形4.在△ABC中,若a=2,,B=60°,则角A的大小为()A.30°或150°B.60°或120°C.30°D.60°【考点】正弦定理.【分析】由B的度数求出sinB的值,再由a与b的值,利用正弦定理求出sinA的值,由a 小于b,根据大边对大角得到A小于B,利用特殊角的三角函数值即可求出A的度数.【解答】解:∵a=2,b=2,B=60°,∴由正弦定理=得:sinA==,又a<b,∴A<B,则A=30°.故选C5.将函数y=sin(x﹣)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图象向左平移个单位,则所得函数图象对应的解析式为()A.y=sin(x﹣) B.y=sin(2x﹣)C.y=sin x D.y=sin(x﹣)【考点】函数y=Asin(ωx+φ)的图象变换.【分析】根据函数y=Asin(ωx+φ)的图象变换规律即可得解,注意三角函数的平移原则为左加右减上加下减.【解答】解:将函数y=sin(x﹣)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的图象对应的解析式为y=sin(x﹣),再将所得图象向左平移个单位,则所得函数图象对应的解析式为y=sin[(x+)﹣]=sin(x﹣),故选:D.6.已知函数f(x)=,则f[f()]的值是()A.B.C.4 D.9【考点】函数的值.【分析】利用分段函数,先求f()的值,然后求f[f()]的值即可.【解答】解:由分段函数可知f()=,所以f[f()]=f(﹣2)=.故选A.7.已知点A(1,2),B(3,1),则线段AB的垂直平分线的方程是()A.4x+2y=5 B.4x﹣2y=5 C.x+2y=5 D.x﹣2y=5【考点】直线的点斜式方程;两条直线垂直与倾斜角、斜率的关系;中点坐标公式.【分析】先求出中点的坐标,再求出垂直平分线的斜率,点斜式写出线段AB的垂直平分线的方程,再化为一般式.【解答】解:线段AB的中点为,k AB==﹣,∴垂直平分线的斜率k==2,∴线段AB的垂直平分线的方程是y﹣=2(x﹣2)⇒4x﹣2y﹣5=0,故选B.8.若a,b,c∈R,且a>b,则下列不等式一定成立的是()A.a+c≥b﹣c B.(a﹣b)c2≥0 C.ac>bc D.【考点】不等式比较大小.【分析】A.当c≤0时,a+c≥b﹣c不一定成立;B.由于a>b,可得a﹣b>0,又c2≥0,可得(a﹣b)c2≥0.C.c≤0时,ac>bc不成立;D.当c=0时,,即可判断出.【解答】解:A.当c≤0时,a+c≥b﹣c不一定成立;B.∵a>b,∴a﹣b>0,又c2≥0,∴(a﹣b)c2≥0.故B一定成立.C.c≤0时,ac>bc不成立;D.当c=0时,,故D不成立.综上可知:只有B成立.故选B.9.下列条件中,能判断两个平面平行的是()A.一个平面内的一条直线平行于另一个平面B.一个平面内的两条直线平行于另一个平面C.一个平面内有无数条直线平行于另一个平面D.一个平面内的任何一条直线都平行于另一个平面【考点】平面与平面平行的判定.【分析】利用两个平面平行的判定定理判断即可.【解答】解:对于A,一个平面内的一条直线平行于另一个平面,这两个平面可能相交.对于B,一个平面内的两条直线平行于另一个平面,如果这两条直线平行,则这两个平面可能相交.对于C,一个平面内有无数条直线平行于另一个平面,如果这无数条直线平行,则这两个平面可能相交.对于D,一个平面内的任何一条直线都平行于另一个平面,满足平面与平面平行的判定定理,所以正确.故选:D.10.如图所示的程序框图,若输出的S=41,则判断框内应填入的条件是()A.k>3?B.k>4?C.k>5?D.k>6?【考点】程序框图.【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输入S的值,条件框内的语句是决定是否结束循环,模拟执行程序即可得到答案.【解答】解:程序在运行过程中各变量值变化如下表:K S 是否继续循环循环前1 0第一圈2 2 是第二圈3 7 是第三圈4 18 是第四圈5 41 否故退出循环的条件应为k>4?故答案选:B.11.已知平面向量=(1,2),=(﹣2,m),且∥,则实数m的值为()A.1 B.﹣4 C.﹣1 D.4【考点】平面向量共线(平行)的坐标表示.【分析】利用向量共线的充要条件,列出方程求解即可.【解答】解:平面向量=(1,2),=(﹣2,m),且∥,可得:1×m=﹣2×2.解得m=﹣4.故选:B.12.已知数列{a n},如果a1,a2﹣a1,a3﹣a2,…,a n﹣a n,是首项为1,公比为2的等比﹣1数列,那么a n=()A.2n+1﹣1 B.2n﹣1 C.2n﹣1D.2n+1【考点】等比数列的前n项和;等比数列的通项公式.【分析】由题意可得,,然后利用累加法,结合等比数列的求和公式即可求解【解答】解:由题意可得,∴a2﹣a1=2a3﹣a2=22…以上n﹣1个式子相加可得,a n﹣a1=2+22+…+2n﹣1==2n﹣2∴a n=2n﹣1故选B二、填空题(本大题共4小题,每小题5分,满分20分.)13.已知||=2,||=4,⊥(+),则与夹角的度数为120°.【考点】平面向量数量积的运算.【分析】根据已知求出•=﹣4,代入夹角公式,求出夹角的余弦值,进而可得答案.【解答】解:∵||=2,||=4,⊥(+),∴•(+)=2+•=||2+•=0,∴•=﹣4,∴cos<,>=,∴<,>=120°,故答案为:120°14.如果一个几何体的三视图如图所示,则此几何体的表面积是.【考点】由三视图求面积、体积.【分析】先判断三视图复原的结合体的形状,上部是正四棱锥,下部是正方体,确定棱长,可求结合体的表面积.【解答】解:三视图复原的结合体,上部是正四棱锥,底面棱长为4,高为2,下部是正方体,底面棱长为4,所以结合体的表面积是:5×42+=80+16故答案为:80+1615.如果实数x,y满足条件那么2x﹣y的最大值为1.【考点】简单线性规划.【分析】先根据约束条件画出可行域,再利用几何意义求最值,z=2x﹣y表示直线在y轴上的截距,只需求出可行域直线在y轴上的截距最大值即可.【解答】解:先根据约束条件画出可行域,当直线2x﹣y=t过点A(0,﹣1)时,t最大是1,故答案为:1.16.函数的最小值是﹣3.【考点】基本不等式在最值问题中的应用.【分析】=,再利用基本不等式可得结论.【解答】解:=≥2﹣3=﹣3,当且仅当时取等号,∴函数的最小值是﹣3.故答案为:﹣3.三、解答题:(本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤.)17.已知函数f(x)=sin2x﹣cos2x的图象过点(,0).(Ⅰ)求实数a的值;(Ⅱ)求函数f(x)的最小正周期及最大值.【考点】三角函数的周期性及其求法;同角三角函数基本关系的运用.【分析】(Ⅰ)由已知函数f(x)=sin2x﹣cos2x的图象过点(,0),可得sin﹣cos=0,由此解得a的值.(Ⅱ)由(Ⅰ)得函数函数f(x)=sin(2x﹣),由此求得函数的最小正周期和最大值.【解答】解:(Ⅰ)由已知函数f(x)=sin2x﹣cos2x的图象过点(,0),∴sin﹣cos=0,解得a=2.(Ⅱ)由(Ⅰ)得函数函数f(x)=sin2x﹣cos2x=sin(2x﹣),∴最小正周期T==π,最大值为.18.已知数列{a n}满足a1=3,a n﹣3a n=3n(n∈N*),数列{b n}满足b n=.+1(Ⅰ)求证:数列{b n}是等差数列,并求数列{a n}的通项公式;(Ⅱ)求数列{a n}的前n项和S n.【考点】数列递推式.【分析】(Ⅰ)利用条件,结合等差数列的定义,即可证明数列{b n}是等差数列,从而求数列{a n}的通项公式;(Ⅱ)利用错位相减法求数列{a n}的前n项和S n.【解答】(I)证明:∵,,,∴b n﹣b n=,…+1∴数列{b n}是等差数列,…∵,∴,∴数列{a n}的通项公式;…(II)解:∵,∴,当n≥2时,相减得:∴,…整理得,当n=1时,,…综上,数列{a n}的前n项和.…19.如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.(1)若PA=PD,求证:平面PQB⊥平面PAD;(2)若平面PAD⊥平面ABCD,且PA=PD=AD=2,点M在线段PC上,且PM=3MC,求三棱锥P﹣QBM的体积.【考点】平面与平面垂直的判定;棱柱、棱锥、棱台的体积.【分析】(1)由PA=PD,得到PQ⊥AD,又底面ABCD为菱形,∠BAD=60°,得BQ⊥AD,利用线面垂直的判定定理得到AD⊥平面PQB利用面面垂直的判定定理得到平面PQB⊥平面PAD;2)由平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PQ⊥AD,得PQ⊥平面ABCD,BC⊂平面ABCD,得PQ⊥BC,得BC⊥平面PQB,即得到高,利用椎体体积公式求出;【解答】解:(1)∵PA=PD,∴PQ⊥AD,又∵底面ABCD 为菱形,∠BAD=60°,∴BQ ⊥AD ,PQ ∩BQ=Q ,∴AD ⊥平面PQB又AD ⊂平面PAD ,∴平面PQB ⊥平面PAD ;(2)∵平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD=AD ,PQ ⊥AD ,∴PQ ⊥平面ABCD ,BC ⊂平面ABCD ,∴PQ ⊥BC ,又BC ⊥BQ ,QB ∩QP=Q ,∴BC ⊥平面PQB ,又PM=3MC ,∴V P ﹣QBM =V M ﹣PQB =20.在△ABC 中,角A ,B ,C 的对应边分别是a ,b ,c 满足b 2+c 2=bc +a 2.(Ⅰ)求角A 的大小;(Ⅱ)已知等差数列{a n }的公差不为零,若a 1cosA=1,且a 2,a 4,a 8成等比数列,求{}的前n 项和S n .【考点】数列的求和;等比数列的性质;余弦定理.【分析】(Ⅰ)由已知条件推导出=,所以cosA=,由此能求出A=. (Ⅱ)由已知条件推导出(a 1+3d )2=(a 1+d )(a 1+7d ),且d ≠0,由此能求出a n =2n ,从而得以==,进而能求出{}的前n 项和S n .【解答】解:(Ⅰ)∵b 2+c 2﹣a 2=bc ,∴=,∴cosA=,∵A ∈(0,π),∴A=.(Ⅱ)设{a n }的公差为d ,∵a 1cosA=1,且a 2,a 4,a 8成等比数列,∴a 1==2,且=a 2•a 8,∴(a 1+3d )2=(a 1+d )(a 1+7d ),且d ≠0,解得d=2,∴a n =2n ,∴==,∴S n =(1﹣)+()+()+…+()=1﹣=.21.已知向量=(cosωx,1),=(2sin(ωx+),﹣1)(其中≤ω≤),函数f(x)=•,且f(x)图象的一条对称轴为x=.(1)求f(π)的值;(2)若f()=,f(﹣)=,且,求cos(α﹣β)的值.【考点】三角函数中的恒等变换应用;平面向量数量积的运算.【分析】(1)根据向量的数量积公式,倍角公式,辅助角公式,化简函数的解析式,结合f(x)图象的一条对称轴为x=,求出ω=1,代入可得f(π)的值;(2)若f()=,f(﹣)=,且,可得α,β的余弦值,代入差角的余弦公式,可得答案.【解答】解:(1)∵向量=(cosωx,1),=(2sin(ωx+),﹣1)=((sinωx+cosωx),﹣1)∴函数f(x)=•=2cosωx(sinωx+cosωx)﹣1=2sinωxcosωx+2cos2ωx﹣1=sin2ωx+cos2ωx=sin(2ωx+),∵f(x)图象的一条对称轴为x=.∴2ω×+=+kπ,(k∈Z).又由≤ω≤,∴ω=1,∴f(x)=sin(2x+),∴f(π)=sin(2×π+)=﹣cos=﹣1,(2)∵f()=,f(﹣)=,∴sinα=,sinβ=,∵,∴cosα=,cosβ=,∴cos(α﹣β)=cosαcosβ+sinαsinβ=.22.某人上午7:00乘汽车以v1千米/小时(30≤v1≤100)匀速从A地出发到距300公里的B地,在B地不作停留,然后骑摩托车以v2千米/小时(4≤v2≤20)匀速从B地出发到距50公里的C地,计划在当天16:00至21:00到达C地.设乘汽车、骑摩托车的时间分别是x,y小时,如果已知所需的经费p=100+3(5﹣x)+2(8﹣y)元,那么v1,v2分别是多少时走的最经济,此时花费多少元?【考点】简单线性规划的应用.【分析】先建立满足题意的约束条件及目标函数,作出满足条件的x,y的区域,利用几何意义可求目标函数的最小值【解答】解:由题意得,,∵30≤v1≤100,4≤v2≤20∴由题设中的限制条件得9≤x+y≤14于是得约束条件目标函数p=100+3(5﹣x)+2(8﹣y)=131﹣3x﹣2y做出可行域(如图),当平行移动到过(10,4)点时纵截距最大,此时p最小.所以当x=10,y=4,即v1=30,v2=12.5时,p min=93元(没有图扣2分)2016年11月27日。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河北冀州中学2015---2016年高一月考
高一年级政治试题
考试时间:60分钟试题分数:100分
第Ⅰ卷(单选,共35小题,每题2分,共70分)
1、为了提高原奶中蛋白质的含量,不法分子往奶中添加三聚氰氨;为了让猪长得更快瘦肉更
多,无良养殖户给猪喂食了瘦肉精;为了让米面更白更好看,黑心商家使用了吊白块??凡此
种种,均令老百姓的生命安全遭受了严重威胁。这些被加入了三聚氰氨、瘦肉精和吊白块的
商品
A.是商品,因为它凝结着无差别的人类劳动 B.是商品,因为它用于消费
C.不是商品,因为它不用于交换 D.不应成为商品,因为它不具备应有的使用价值
2、一句经典的广告往往能贴切地反映出产品的特色,给人留下深刻的印象。如“雀巢咖啡:
味道好极了”“麦氏咖啡:滴滴香浓,意犹未尽”。这里的“味道”“香浓”是商品的
A.价值 B.价格 C.使用价值 D.交换价值
3、人们把货币看得很神秘,把货币看成是财富的象征,这是因为
A、货币是商品交换发展的产物 B、货币是商品,有价值
C、倾向是由贵重金属制造的 D、货币的本质是一般等价物
4、小李采用银行按揭贷款的方式买了价格80万元的新房,首付现金30万元,然后在15年
内付清银行贷款50万元及利息18万元。其中18万元利息、80万元房价、30万元首付金分
别体现了货币的职能是
A.贮藏手段、流通手段、价值尺度 B. 支付手段、价值尺度、流通手段
C.支付手段、流通手段、贮藏手段 D. 价值尺度、流通手段、支付手段 5、2014
年9月19日,美国苹果公司新推出的iphone6手机在香港上市。港币标价折合人民币约为
6271-6814元。因为本次首批发售国家中没有中国大陆,导致大批“黄牛”在香港苹果零售
店门前加价收货在内地倒卖,倒卖的最高价格竟然爆炒到2.8万人民币。下列选项中货币执
行的职能与这里的“6271-6814元”和“2.8万元”所执行的职能一致的是
A.开学前,小王花了1200元在学校附近租了一间住房
B.小张去香港旅游时花费6800元买了一台iPhone 6手机 C.月初,公司发给小李4500元
工资
D.第17届亚洲运动会于2014年9月19日至10月4日在韩国仁川举行,其开、闭幕式入场
券价格折合人民币分别约在588-5880元、588-3532元
6、某商品的进价是60元,售价是80元。赵某用100元人民币购买该商品,店主找回赵某
20元。事后店主发现赵某的100元是假钞。在此次交易中店主实际损失了
A. 80元 B.60元 C. 20元 D.120元
7、比特币是虚拟的数字货币,如今已可套现,其币值大幅上涨。2013年12月5日,中国人
民银行发布《关于防范比特币风险的通知》,规定金融机构和支付机构不得开展与比特币相关
的业务,这是因为比特币
A.不是由国家(或地区)发行并强制使用的 B.发行量以流通中所需要的货币量为限度
C.本质是固定充当一般等价物的虚拟商品 D.可以按其潜在的价值参与市场流通 8、2014
年,中国人民银行和其他金融机构因收购外汇资产而相应投放的人民币新增2.76 1
