实验1用MATLAB进行信号频谱分析
离散信号的产生和频谱分析(matlab)-西工大

离散信号的产生和频谱分析实验目的:仿真掌握采样定理学会用FFT 进行数字谱分析掌握FFT 进行数字谱分析的计算机编程实现方法培养学生综合分析、解决问题的能力、加深对课堂内容的理解 实验要求:掌握采样定理和数字谱分析方法、编制FFT 程序;完成正弦信号、线性条调频信号等模拟水声信号的数字谱分析; 实验内容:单频脉冲(CWP )为)2ex p()()(0t f j Ttrect t s π=。
式中,)(Tt rect 是矩形包络,T 是脉冲持续时间,0f 是中心频率。
矩形包络线性调频脉冲信号(LFM )为)]21(2ex p[)()(20Mt t f j Ttrect t s +=π。
式中,M 是线性调频指数。
瞬时频率Mtf +0是时间的线性函数,频率调制宽度为MT B =。
设参数为kHz f 200=,ms T 50=,kHz B 10=,采样频率kHz f s100=。
1.编程产生单频脉冲、矩形包络线性调频脉冲。
2.编程实现这些信号的谱分析。
3.编程实现快速傅立叶变换的逆变换。
实验步骤:1.编程产生单频脉冲、矩形包络线性调频脉冲。
2.应用快速傅立叶变换(FFT )求这两种信号的频谱,分析离散谱位置、归一化频率、实际频率的关系。
调用函数Y=fft(x) or Y=fft(x,N) or Y=fft(x,N,dim)。
3.对于步骤2的结果,应用快速傅立叶变换的逆变换(IFFT )求两种信号的时域波形,并与已给的单频脉冲、矩形包络线性调频脉冲和伪随机脉冲信号波形进行对照。
调用函数x=ifft(Y) or x=ifft(Y,N) or x=ifft(Y ,N,dim)。
4.对于步骤2的结果,进行频谱移位调整。
将FFT 变换的结果Y (频谱数据)进行移位调整,使其符合频谱常观表示方法,调整后,频谱的直流成分(即频率为0处的值)移到频谱的中间位置。
分析离散谱位置、归一化频率、实际频率的关系。
移位调整调用函数Z=fftshift(Y)。
matlab软件仿真实验(信号与系统)(1)
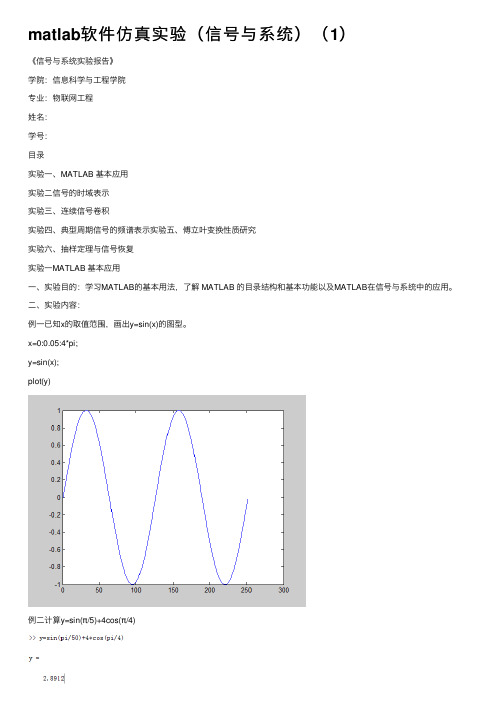
matlab软件仿真实验(信号与系统)(1)《信号与系统实验报告》学院:信息科学与⼯程学院专业:物联⽹⼯程姓名:学号:⽬录实验⼀、MATLAB 基本应⽤实验⼆信号的时域表⽰实验三、连续信号卷积实验四、典型周期信号的频谱表⽰实验五、傅⽴叶变换性质研究实验六、抽样定理与信号恢复实验⼀MATLAB 基本应⽤⼀、实验⽬的:学习MATLAB的基本⽤法,了解 MATLAB 的⽬录结构和基本功能以及MATLAB在信号与系统中的应⽤。
⼆、实验内容:例⼀已知x的取值范围,画出y=sin(x)的图型。
x=0:0.05:4*pi;y=sin(x);plot(y)例⼆计算y=sin(π/5)+4cos(π/4)例三已知z 取值范围,x=sin(z);y=cos(z);画三维图形。
z=0:pi/50:10*pi;x=sin(z);y=cos(z);plot3(x,y,z)xlabel('x')ylabel('y')zlabel('z')例四已知x的取值范围,⽤subplot函数绘图。
参考程序:x=0:0.05:7;y1=sin(x);y2=1.5*cos(x);y3=sin(2*x);y4=5*cos(2*x);subplot(2,2,1),plot(x,y1),title('sin(x)')subplot(2,2,2),plot(x,y2),title('1.5*cos(x)')subplot(2,2,3),plot(x,y3),title('sin(2*x)')subplot(2,2,4),plot(x,y4),title('5*cos(2*x)')连续信号的MATLAB表⽰1、指数信号:指数信号Ae at在MATLAB中可⽤exp函数表⽰,其调⽤形式为:y=A*exp(a*t) (例取 A=1,a=-0.4)参考程序:A=1;a=-0.4;t=0:0.01:10;ft=A*exp(a*t);plot(t,ft);grid on;2、正弦信号:正弦信号Acos(w0t+?)和Asin(w0t+?)分别由函数cos和sin表⽰,其调⽤形式为:A*cos(w0t+phi) ;A*sin(w0t+phi) (例取A=1,w0=2π,?=π/6) 参考程序:A=1;w0=2*pi; phi=pi/6; t=0:0.001:8;ft=A*sin(w0*t+phi);plot(t,ft);grid on ;3、抽样函数:抽样函数Sa(t)在MATLAB中⽤sinc函数表⽰,其定义为:sinc(t)=sin(πt)/( πt)其调⽤形式为:y=sinc(t)参考程序:t=-3*pi:pi/100:3*pi;ft=sinc(t/pi);plot(t,ft);grid on;4、矩形脉冲信号:在MATLAB中⽤rectpuls函数来表⽰,其调⽤形式为:y=rectpuls(t,width),⽤以产⽣⼀个幅值为1,宽度为width,相对于t=0点左右对称的矩形波信号,该函数的横坐标范围由向量t决定,是以t=0为中⼼向左右各展开width/2的范围,width的默认值为1。
应用Matlab对图像信号进行频谱分析及滤波

应用Matlab对图像信号进行频谱分析及滤波选取一张彩色图片,建议把像素设置成200*200,提取图像的灰度值,并显示出灰度图像;在图像中增加正弦噪声信号(自己设置几个频率的正弦信号),画出加入噪声信号后的灰度图像;给定滤波器的性能指标,采用窗函数法或者双线性变换设计数字低通滤波器,并画出滤波器的频率响应;然后用自己设计的滤波器对含噪声图像信号进行滤波,画出滤波后图像信号的灰度图像。
利用频谱分析对原始灰度图像、加入噪声信号的灰度图像、和滤波后的灰度图像进行频谱分析和对比,分析信号的变化。
x=imread('D:\1.jpg');x1=rgb2gray(x);[M,N]=size(x1);x2=im2double(x1);figure(1);subplot(1,3,1)imshow(x2);x3=zeros(1,M*N);for i=1:Mfor j=1:N;x3(M*(i-1)+j)= x2(i,j);endendL=M*N;fs=40000;dt=1/fs;n=0:L-1;x7=(sin(2*pi*15000*n*dt)/10+sin(2*pi*18000*n*dt)/6)x4=x3+x7;for i=1:Mfor j=1:N;x5(i,j) = x4(M*(i-1)+j);endendfigure(1)subplot(132);imshow(x5)wp=0.5*pi;ws=0.75*pi;rp=3;rs=50;[n,wn]=buttord(wp/pi,ws/pi,rp,rs,'s'); [Bz,Az]=butter(n,wp/pi);%[z,p,k]=buttap(n);%[Bap,Aap]=zp2tf(z,p,k);%[B,A]=lp2lp(Bap,Aap,wn);%[Bz,Az]=bilinear(B,A,F);[h,w]=freqz(Bz,Az,L,fs);figure(3)subplot(121);plot(w,abs(h));x6=zeros(1,L);for i=1:Mfor j=1:N;x6(M*(i-1)+j)= x5(i,j);endendx8=zeros(1,L);x8=filter(Bz,Az,x6);x3k=fft(x3,L)figure(2)subplot(131)plot(w*2,abs(x3k))x4k=fft(x4,L)figure(2)subplot(132)plot(w*2,abs(x4k))x7k=fft(x7,L)figure(3)subplot(122)plot(w*2,abs(x7k))x8k=fft(x8,L)figure(2)subplot(133)plot(w*2,abs(x8k))for i=1:Mfor j=1:N;x9(i,j) = x8(M*(i-1)+j);endendfigure(1)subplot(133);imshow(x9);。
Matlab中的脑电图信号处理与频谱分析方法

Matlab中的脑电图信号处理与频谱分析方法一、引言脑电图(Electroencephalogram,简称EEG)是记录大脑电生理活动的一种非侵入性方法。
在临床和研究中,脑电图被广泛应用于诊断神经系统疾病、研究认知过程等领域。
而Matlab作为一种功能强大的科学计算软件,提供了丰富的工具箱和函数,可以有效地处理和分析脑电图数据。
本文将介绍Matlab中常用的脑电图信号处理方法和频谱分析技术。
二、脑电图信号处理方法1. 清除噪声在进行脑电图信号分析之前,首先需要对原始信号进行预处理,以去除噪声和伪迹。
Matlab提供了多种滤波器函数,如低通滤波器和带通滤波器,可以有效地去除不需要的高频噪声和低频噪声。
2. 分段处理脑电图信号常常是一个连续的时间序列,在某些情况下,可以将信号分成较短的时间段。
这样做有助于分析信号在不同时间段的特性。
Matlab中可以使用窗函数对信号进行分段处理,并通过遍历每个窗口进行连续的分析。
3. 时域分析时域分析是对信号在时间上的变化进行定量描述的方法。
常用的时域分析方法包括计算信号的平均值、方差、峰值和时域波形图等。
在Matlab中,可以使用相应的函数和工具箱进行时域特征提取和可视化,从而实现对脑电图信号的时域分析。
4. 频域分析频域分析是对信号在频率上的变化进行研究和描述的方法。
脑电图信号通常包含不同频率的成分,因此频域分析对于理解信号的特征和性质非常重要。
Matlab提供了多种频谱分析方法,如快速傅里叶变换(FFT)、小波变换(Wavelet Transform)和自相关函数等。
这些函数可以帮助我们从频域的角度来研究脑电图信号,并提取出频率成分的信息。
三、频谱分析方法1. 快速傅里叶变换(FFT)FFT是一种常见的频谱分析方法,可以将信号从时域转换为频域。
通过计算信号的幅度谱和相位谱,我们可以获得信号在不同频率下的能量分布。
Matlab 中的fft函数可以高效地计算快速傅里叶变换,并绘制出脑电图信号的频谱图。
用MATLAB模拟实现数字信号的调制与频谱分析

维普资讯 28 0 耳8月 0 2S A K调 制是正 弦载波 的幅 度随基 带信 号的变化 而变 化 的数字调制 , 是最早出现 的也是最简单 的。 抗噪声 能力较
差 , 际 应 用 并 不广 泛 , 可 以作 为 其 他 调 制 方 式 的研 究基 实 但
础 。2 S A K信号 的时域表达 式为:. - A o (o e ̄- * cs-t b ) 。式中 b
Sr:A p n E ti FlL ct n"e1 . ” rc y ^e [ t = p d xFl i oai A a 1x ,< nw1I l e e( e o t ml e 】 t p "e [ a r = nw2I I‘’ h m= ^e 3I" ] u "nw [ ̄ ] 、
电 脑 学 习
第4 期
用 MA L B模拟 实现数 字信号 的调制 与频 谱分 析 TA
杨
摘
峰’
苏 玉萍
余冬 菊
要 :运用 MA L B语言模拟实现 了数 字信号的 A K F K I K调制与频谱分析。 TA S 、S 、3 X 双极性非归零 电平码 幅度键控 频移键控 相移键控 频谱分析
为二进 制数 序列 , 当基 带 信 号 a 为 正 电平 时 b 取 “ ” 当 1,
基带 信 号 a 为负 电平 时 b 取 “ ”, a 转 化 为 b 的硬件 0 由 实现 只需 一个单 向导通 的二极 管 电路; A为调制 信 号 的幅
度; 。 为调制信 号的频率 。显 然, 当基带信 号为 正电平 ( + 1 时 ,A K时域信号为一正弦波 ; ) 2S 当基带信 号为负 电平 ( 一 1 时 ,A K时域信号对应 为 “ ” ) 2S 0 。正弦 载波 频率要 比基带
在Matlab中如何进行时间频率分析

在Matlab中如何进行时间频率分析在Matlab中进行时间频率分析随着数字信号处理和数据分析的不断发展,时间频率分析成为了信号处理领域中重要的技术之一。
在Matlab中,我们可以利用强大的信号处理工具箱来进行时间频率分析,以深入探究信号的频率特性和变化模式。
本文将介绍Matlab中几种常用的时间频率分析方法,并对其应用进行讨论。
一、傅里叶变换傅里叶变换是一种将时域信号转换为频域信号的方法,可以得到信号的频谱信息。
在Matlab中,我们可以使用fft函数来进行傅里叶变换,代码如下:```x = [1 2 3 4]; % 输入信号N = length(x); % 信号长度X = fft(x); % 傅里叶变换f = (0:N-1)/N; % 频率坐标plot(f, abs(X)) % 绘制频谱图```通过傅里叶变换,我们可以得到信号的频谱图,从而分析信号的频域特性。
在时域上,我们可以观察到信号随时间的变化模式,而在频域上,可以观察到信号的频率分布情况。
二、小波变换小波变换是一种将信号分解为不同频率分量的方法,可以得到信号的时频域特性。
在Matlab中,我们可以利用cwt函数进行连续小波变换,使用wavedec函数进行离散小波变换,代码如下:```x = [1 2 3 4]; % 输入信号wname = 'db4'; % 小波名称level = 3; % 分解层数[C, L] = wavedec(x, level, wname); % 离散小波变换plot(1:length(x), x, 'r'); hold on; % 绘制原始信号for i = 1:level % 绘制各层小波分量D = detcoef(C, L, i);plot(1:length(D), D); hold on;end```通过小波变换,我们可以得到信号的时频图,即可以观察信号在时域和频域上的变化情况。
探究Matlab中的频谱分析技巧

探究Matlab中的频谱分析技巧引言频谱分析是信号处理中的重要技术,用于分析信号的频谱特征和频率分量。
在实际应用中,频谱分析被广泛应用于音频、图像、通信系统等领域。
Matlab作为一种强大的数学计算和数据可视化工具,提供了丰富的频谱分析工具和函数。
本文将探究Matlab中的频谱分析技巧,介绍常用的频谱分析方法和相应的Matlab函数。
一、时域信号和频域信号在开始讨论频谱分析之前,需要了解时域信号和频域信号的概念。
时域信号是指随时间变化而变化的信号,可以通过波形图表示。
频域信号是指信号在频率域上的表示,即将信号分解为不同频率的分量。
频谱分析的目的就是将时域信号转化为频域信号,以便更好地理解和处理信号。
二、傅里叶变换傅里叶变换是频谱分析中最基本和重要的数学工具之一。
它可以将时域信号转换为频域信号,提取信号中的频率、幅度和相位信息。
在Matlab中,可以使用fft函数进行傅里叶变换。
例如,我们有一个包含多个正弦波分量的信号,现在我们想要对其进行频谱分析。
首先,我们可以生成一个包含多个正弦波的信号:```matlabFs = 1000; % 采样率T = 1/Fs; % 采样间隔L = 1000; % 信号长度t = (0:L-1)*T; % 时间向量S = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t) + 2*sin(2*pi*300*t);```然后,我们使用fft函数对信号进行傅里叶变换,并计算频率和幅度:```matlabY = fft(S);P2 = abs(Y/L);P1 = P2(1:L/2+1);P1(2:end-1) = 2*P1(2:end-1);f = Fs*(0:(L/2))/L;```最后,我们可以绘制频谱图:```matlabplot(f,P1);title('单边幅度谱');xlabel('频率(Hz)');ylabel('幅度');```通过绘制的频谱图,我们可以清晰地看到信号中各个频率的成分。
实验一 FFT频谱分析及应用

实验一 FFT频谱分析及应用实验学时:2学时实验类型:验证实验要求:必修一、实验目的:1、学习MATLAB语言的编程和调试技巧;、2、通过实验加深对FFT的理解;3、熟悉应用FFT对典型信号进行频谱分析的方法。
二、实验内容使用MATLAB程序实现信号频域特性的分析。
涉及到离散傅立叶变换(DFT)、快速傅立叶变换(FFT)及信号频率分辨率等知识点。
三、实验原理与方法和手段在各种信号序列中,有限长序列占重要地位。
对有限长序列可以利用离散傅立叶变换(DFT)进行分析。
DFT不但可以很好的反映序列的频谱特性,而且易于用快速算法(FFT)在计算机上进行分析。
有限长序列的DFT是其z变换在单位圆上的等距离采样,或者说是序列傅立叶的等距离采样,因此可以用于序列的谱分析。
FFT是DFT的一种快速算法,它是对变换式进行一次次分解,使其成为若干小数据点的组合,从而减少运算量。
在MATLAB信号处理工具箱中的函数fft(x,n),可以用来实现序列的N点快速傅立叶变换。
经函数fft求得的序列一般是复序列,通常要求出其幅值和相位。
MATLAB 中提供了求复数的幅值和相位的函数:abs、angle,这些函数一般和fft同时使用。
四、实验组织运行要求1、学生在进行实验前必须进行充分的预习,熟悉实验内容;2、学生根据实验要求,读懂并理解相应的程序;3、学生严格遵守实验室的各项规章制度,注意人身和设备安全,配合和服从实验室人员管理;4、教师在学生实验过程中予以必要的辅导,独立完成实验;5、采用集中授课形式。
五、实验条件1、具有WINDOWS 98/2000/NT/XP 操作系统的计算机一台;2.、MATLAB 编程软件。
六、实验步骤在“开始--程序”菜单中,找到MATLAB 程序,运行启动;进入MATLAB 后 ,在Command Window 中输入实验程序,并执行;记录运行结果图形,作分析。
具体步骤如下:1、模拟信号)8cos(5)4sin(2)(t t t x ππ+=,以)1:0(01.0-==N n n t 进行采样,求:(1)N =40点FFT 的幅度频谱,从图中能否观察出信号的2个频谱分量?(2)提高采样点数,如N =128,再求该信号的幅度频谱,此时幅度频谱发生了什么变化?信号的2个模拟频率和数字频率各为多少?FFT 频谱分析结果与理论上是否一致?2、一个连续信号含三个频谱分量,经采样得以下序列:))215.0(2cos())15.0(2cos()15.02sin()(n df n df n n x +⨯++⨯+⨯=πππ(1)N =64,df 分别为161、1/64,观察其频谱;(2)N =64、128,df 为1/64,做128点得FFT ,其结果有何不同?3、被噪声污染得信号,比较难看出所包含得频率分量,如一个由50Hz 和120Hz 正弦信号构成的信号,受零均值随机噪声的干扰,数据采样率为1000Hz ,试用FFT 函数来分析其信号频率成分,要求:(1)画出时域波形;(2)分析信号功率谱密度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验1用MATLAB进行信号频谱分析
提供一个实验步骤,帮助您用MATLAB进行信号频谱分析。
以下是一
个详细步骤,您可以按照提示进行操作。
1.准备信号数据
选择一个信号数据,可以是一个音频文件或一个由数字数据表示的信号。
确保该文件位于MATLAB当前工作目录下,或者提供文件的完整路径。
2.导入信号数据
在MATLAB命令窗口中键入以下命令,将信号数据导入到MATLAB中:`data = audioread('filename.wav');`
或者,如果信号数据是数字数据矩阵,可以直接将其赋值给变量:
`data = your_signal_data;`
3.绘制时域波形图
使用以下命令可以绘制信号的时域波形图:
`plot(data);`
这将绘制出信号的波形图。
可以使用音频播放器在MATLAB环境中播
放信号,以便更好地了解信号特征:
`sound(data, Fs);`
这里的Fs是信号的采样率,通常以赫兹(Hz)为单位。
4.计算信号的频谱
频谱可以通过对信号进行傅里叶变换来获得。
在MATLAB中,可以使用fft函数执行傅里叶变换。
使用以下命令来计算信号的频谱:`N = length(data); %获取信号数据的长度`
`Y = fft(data); %执行傅里叶变换`
`P = abs(Y/N); %计算信号的频谱(单侧幅度谱)`
5.绘制频谱图
使用以下命令可以绘制信号的频谱图:
`f=(0:N-1)*(Fs/N);%计算频率轴`
`plot(f, P); %绘制频谱图`
`xlabel('频率(Hz)');`
`ylabel('幅度');`
6.可选步骤:去除直流分量
信号的频谱通常包含一个直流分量(频率为0Hz),可以通过以下步骤将其去除:
`P(1)=0;%设置直流分量的幅度为0`
`plot(f, P); %绘制修正后的频谱图`
到此为止,我们已经使用MATLAB完成了信号频谱分析的基本步骤。
使用这些步骤,您可以分析音频信号、传感器数据或其它数字信号的频谱特征。
此外,MATLAB还提供一系列可用于分析频谱的函数和工具箱,可帮助您更深入地了解信号的频谱特性。
希望这个实验步骤能对您有所帮助!。
