图论最大流问题
第六章 图论方法

第八章图论方法§1 图论中图的概念在人们从事的各种活动中,为了反映事物之间的关系,常在纸上用点和线画出各种各样的示意图。
例如,为了反映某地区的铁路交通、公路网分布情况,画出铁路、公路交通图。
在这些图中以点表示城镇,用点与点之间的连线表示城镇之间的铁路或公路的沟通情况。
诸如此类的图还有电缆线分布图、供水道及下水道分布图、航空线图等等。
再如,在一场有5支球队参加的球类比赛中,比赛情况也可以用图表示出来,如图6-1,我们用点代表各个球队,某两个队比赛过一次,就在两个点之间画一条箭线。
从图中可以看出A队与其他各队都比赛过,只有一场败给C 队。
而B队和E队各比赛过两场,成绩都是一胜一负,等等。
图6-1从上述例子中可以看出,图的最基本要素是:点、以及点与点之间的一些连线。
通常用点表示我们所要研究的对象(如城市、运动队、状态等等),用线表示研究对象间的某种特定关系(如两个城市之间有铁路,两个运动队之间已经比赛过等)。
因此可以说,图是反映对象之间关系的一种工具。
如果两个对象之间有某种特定关系,那么就用一条线连接这两个点。
必须指出:上述图中点的相对位置如何,点与点之间连线的长短曲直,对于反映研究对象之间的关系并不很重要,因此,图论中的图与几何图、工程图本质上是不同的。
另外在许多情况下,我们要研究的“关系”只用一条线反映还是不够完全。
比如说比赛,我们关心的如果不只是两个队是否比赛过,还要了解比赛的胜负情况,我们可以用一条箭线(有向线)来表示,如果A队胜了B队,就表示为A→B。
如图6-1所示,从图中可以看出A队三胜一负,D队三场全负等。
类似的情况在生产和生活中也是常见的,例如交通运输中的“单行线”、部门之间的领导与被领导关系、一项生产活动中各工序之间的先后次序关系等等。
图论中把不带箭头的连线叫做边,把带箭头的连线叫做弧。
如果一个图是由点和边所构成的,则称之为无向图,记作G=(V,E),其中V表示图G中的所有点组成的点集合,E表示图G中所有边组成的边集合。
数学建模中的图论方法

数学建模中的图论方法一、引言我们知道,数学建模竞赛中有问题A和问题B。
一般而言,问题A是连续系统中的问题,问题B是离散系统中的问题。
由于我们在大学数学教育内容中,连续系统方面的知识的比例较大,而离散数学比例较小。
因此很多人有这样的感觉,A题入手快,而B题不好下手。
另外,在有限元素的离散系统中,相应的数学模型又可以划分为两类,一类是存在有效算法的所谓P类问题,即多项式时间内可以解决的问题。
但是这类问题在MCM中非常少见,事实上,由于竞赛是开卷的,参考相关文献,使用现成的算法解决一个P类问题,不能显示参赛者的建模及解决实际问题能力之大小;还有一类所谓的NP问题,这种问题每一个都尚未建立有效的算法,也许真的就不可能有有效算法来解决。
命题往往以这种NPC问题为数学背景,找一个具体的实际模型来考验参赛者。
这样增加了建立数学模型的难度。
但是这也并不是说无法求解。
一般来说,由于问题是具体的实例,我们可以找到特殊的解法,或者可以给出一个近似解。
图论作为离散数学的一个重要分支,在工程技术、自然科学和经济管理中的许多方面都能提供有力的数学模型来解决实际问题,所以吸引了很多研究人员去研究图论中的方法和算法。
应该说,我们对图论中的经典例子或多或少还是有一些了解的,比如,哥尼斯堡七桥问题、中国邮递员问题、四色定理等等。
图论方法已经成为数学模型中的重要方法。
许多难题由于归结为图论问题被巧妙地解决。
而且,从历年的数学建模竞赛看,出现图论模型的频率极大,比如:AMCM90B-扫雪问题;AMCM91B-寻找最优Steiner树;AMCM92B-紧急修复系统的研制(最小生成树)AMCM94B-计算机传输数据的最小时间(边染色问题)CMCM93B-足球队排名(特征向量法)CMCM94B-锁具装箱问题(最大独立顶点集、最小覆盖等用来证明最优性)CMCM98B-灾情巡视路线(最优回路)等等。
这里面都直接或是间接用到图论方面的知识。
要说明的是,这里图论只是解决问题的一种方法,而不是唯一的方法。
数学建模图论模型

任意两点均有通路的图称为连通图。
连通而无圈的图称为树,常用T=<V,E>表示树。
若图G’是图 G 的生成子图,且G’又是一棵树, 则称G’是图G 的生成树。
例 Ramsey问题
图1
图2
并且常记: V = v1, v2, … , vn, |V | = n ; E = {e1, e2, … , em}ek=vivj , |E | = m
称点vi , vj为边vivj的端点 在有向图中, 称点vi , vj分别为边vivj的 始点和终点. 该图称为n,m图
8
对于一个图G = V, E , 人们常用图形来表示它, 称其 为图解 凡是有向边, 在图解上都用箭头标明其方向.
4、P'代替P,T'代替T,重复步骤2,3
定理2 设 T为V的子集,P=V-T,设 (1)对P中的任一点p,存在一条从a到p的最短路径,这条路径仅有P中的
点构成, (2)对于每一点t,它关于P的指标为l(t),令x为最小指标所在的点, 即:
l(x)mli(tn )} t{ ,T
(3)令P’=P Ux,T’=T-{x},l’(t)表示T'中结点t关于P'的指标,则
解:用四维01向量表示人,狼,羊,菜例在过河西河岸问的题状态(在
岸则分量取1;否则取0),共有24 =16 种状态; 在河东岸 态类似记作。
由题设,状态(0,1,1,0),(0,0,1,1),(0,1,1,1)是不允许的
其对应状态:(1,0,0,1), (1,1,0,0),(1,0,0,0)也是不允许
运筹学第6章 图与网络

也就是说| V1 |必为偶数。
定理6.2有学者也称作定理6.1的推论。根据定理6.2,握手定理也可以 表述为,在任何集体聚会中,握过奇次手的人数一定是偶数个。
12 该课件的所有权属于熊义杰
另外,现实中不存在面数为奇数且每个面的边数也是奇数的多面 体,如表面为正三角形的多面体有4个面,表面为正五边形的多面体有 12个面等等,也可以用这一定理予以证明。因为在任意的一个多面体 中, 当且仅当两个面有公共边时,相应的两顶点间才会有一条边,即 任意多面体中的一个边总关联着两个面。所以,以多面体的面数为顶
v j V2
(m为G中的边数)
因式中 2m 是偶数, d (v j ) 是偶数,所以 d (vi ) 也必为偶数
v j V2
vi V1
( 两个同奇同偶数的和差必为偶数 ), 同时,由于 d (vi ) 中的每个加数 d (vi )
均为奇数,因而 d (vi ) 为偶数就表明, d (vi ) 必然是偶数个加数的和 ,
图论、算法图论、极值图论、网络图论、代数图论、随机图论、 模糊图论、超图论等等。由于现代科技尤其是大型计算机的迅 猛发展,使图论的用武之地大大拓展,无论是数学、物理、化 学、天文、地理、生物等基础科学,还是信息、交通、战争、 经济乃至社会科学的众多问题.都可以应用图论方法子以解决。
1976年,世界上发生了不少大事,其中一件是美国数学家 Appel和Haken在Koch的协作之下,用计算机证明了图论难题— —四色猜想(4CC):任何地图,用四种颜色,可以把每国领土染 上一种颜色,并使相邻国家异色。4CC的提法和内容十分简朴, 以至于可以随便向一个人(哪怕他目不识丁)在几分钟之内讲清 楚。1852年英国的一个大学生格思里(Guthrie)向他的老师德·摩 根(De Morgan)请教这个问题,德·摩根是当时十分有名的数学家, 他不能判断这个猜想是否成立,于是这个问题很快有数学界流 传开来。1879年伦敦数学会会员Kemple声称,证明了4CC成立, 且发表了论文。10年后,Heawood指出了Kemple的证明中
运筹学上机试题5-图论
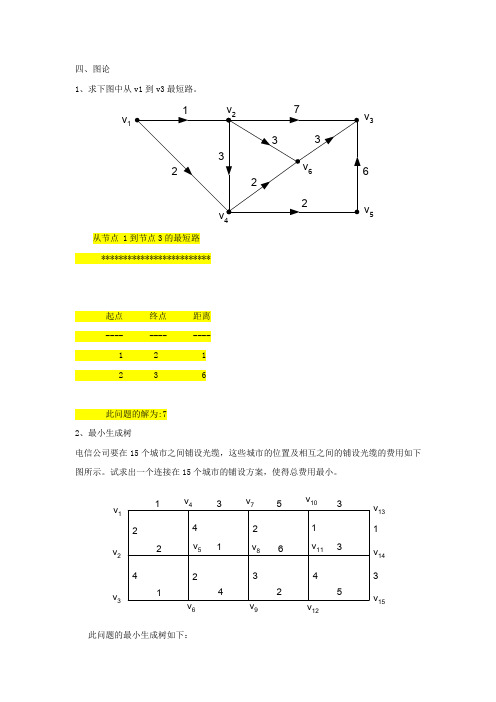
四、图论1、求下图中从v1到v3最短路。
v 1v 3v 546从节点 1到节点3的最短路 *************************起点 终点 距离 ---- ---- ---- 1 2 1 2 3 6此问题的解为:7 2、最小生成树电信公司要在15个城市之间铺设光缆,这些城市的位置及相互之间的铺设光缆的费用如下图所示。
试求出一个连接在15个城市的铺设方案,使得总费用最小。
v 1v 2v 3v 4v 5v 6v 7v 8v 9v 10v 11v 12v 13v 14v 152241131456422323135134此问题的最小生成树如下:*************************起点终点距离---- ---- ----1 4 11 2 22 5 25 8 15 6 26 3 18 7 28 9 39 12 212 11 411 10 110 13 313 14 114 15 3此问题的解为:283、最短路问题例. 求下图中从v1到各点的最短路,并指出有哪些点是不可达到的。
vv7v8v4从节点 1到节点2的最短路*************************起点终点距离---- ---- ---- 1 2 4此问题的解为:41到3没有路1到4没有路从节点 1到节点5的最短路*************************起点终点距离 ---- ---- ---- 1 5 1此问题的解为:1从节点 1到节点6的最短路*************************起点终点距离 ---- ---- ---- 1 5 1 5 6 6此问题的解为:7从节点 1到节点7的最短路*************************起点终点距离 ---- ---- ---- 1 7 3此问题的解为:3从节点 1到节点8的最短路*************************起点终点距离 ---- ---- ---- 1 5 1 5 6 66 8 3此问题的解为:104、最短路问题有6个村庄,各村庄的距离如下图所示。
图论和网络优化

v4
2
4 5
v7
3
v6
2
v5
最小树,权为13
17
v3
v1 v2 v3
v1 v2
v5
v3
v3
v3
v5
v6v1 v4
v5 v6
v4
v1
v1
v2
v2
v3
v1 v2
v5 v6
(2)破圈法:
① 在图中寻找一种圈。
若不存在圈,则已经 得到最短树或网络不 存在最短树;
② 去掉该圈中权数最 大旳边; ③ 反复反复 ① ② 两
权数,记为:
w Tk w e e Ek
若 T T ,使
w T min Tk T
w Tk
则称 T * 为图G旳一棵最小支撑树。
14
b4
2 a
2
4
3
f5
c 5
2d 6
e
最小 树
例如,城市间交 通线旳建造等,能够 归结为这一类问题。
再如前面例3,在已知旳几种城市之间联结电话 线网,要求总长度最短和总建设费用至少,此类问 题旳处理都能够归结为最小树问题。
24
如下图所示旳单行线交通网,每个弧旁边旳
数字表达这条单行线旳长度。目前有一种人要从v1 出发,经过这个交通网到达v6,要谋求总旅程最短
旳线路。
v2
6
v4
3
v1
14
5
1 v3
3
2
v6
6
v5
25
v2
6
v4
3
3
v1
14
5
2 6
v6
1
v3
从v1到v6旳路线是诸多旳。例如:
计算机科学典型问题示例
计算机科学典型问题示例计算机科学是研究计算机及其周围各种现象和规律的科学,亦即研究计算机系统结构、程序系统、以及计算本身的性质和问题的学科。
下面,我们将通过几个典型问题来深入理解计算机科学的基本原理和挑战。
1、排序算法在计算机科学中,排序算法是一种经典的问题,它涉及到对一组数据进行有序排列。
常见的排序算法包括冒泡排序、选择排序、插入排序、快速排序、归并排序等。
每种算法都有其独特的原理和优缺点,适用的场景也不同。
例如,冒泡排序适合于小规模数据的排序,而快速排序则适合于大规模数据的排序。
2、图论图论是计算机科学中的一个重要分支,它研究的是图的性质和结构。
图论中的经典问题包括:欧拉路径问题、哈密尔顿回路问题、最大流问题、最小割问题等。
这些问题在理论和应用方面都有广泛的研究。
例如,哈密尔顿回路问题在解决旅行商问题中具有重要应用,而最大流问题则在解决网络流量问题中具有重要应用。
3、人工智能人工智能是计算机科学中的一个热门领域,它研究的是如何让计算机模拟人类的智能行为。
人工智能中的经典问题包括:图像识别、语音识别、自然语言处理、机器学习等。
这些问题需要计算机具备类似于人类的感知、认知和学习能力,是计算机科学中的前沿问题。
4、数据库系统数据库系统是计算机科学中的一个重要应用领域,它研究的是如何有效地管理和存储数据。
数据库系统中的经典问题包括:查询优化、事务处理、并发控制、数据恢复等。
这些问题需要计算机具备高效的数据存储和检索能力,同时也需要保证数据的安全性和完整性。
5、计算机网络计算机网络是计算机科学中的一个重要领域,它研究的是如何实现计算机之间的通信和资源共享。
计算机网络中的经典问题包括:路由选择、拥塞控制、数据传输、网络安全等。
这些问题需要计算机具备高效的通信能力和资源共享能力,同时也需要保证网络的安全性和稳定性。
以上这些问题是计算机科学中的典型代表,它们不仅仅是学术研究的重要课题,也在实际应用中具有重要的应用价值。
动点问题知识点大全
动点问题知识点大全动点问题是图论中的一个重要概念,涉及到图中节点的移动和路径规划等问题。
本文将介绍动点问题的基本知识点,并逐步展开。
一、基本概念 1. 图的定义:图是由节点(顶点)和边组成的一种数据结构,用于表示节点之间的关系。
2. 路径:路径是指图中连接两个节点的边的序列。
3. 简单路径:不经过重复节点的路径称为简单路径。
4. 环:路径的起点和终点相同的路径称为环。
5. 有向图和无向图:有向图中的边具有方向性,表示节点之间的单向关系;无向图中的边没有方向性,表示节点之间的双向关系。
二、动点问题分类 1. 最短路径问题:给定图中两个节点,求出连接它们的最短路径。
2. 最小生成树问题:在连通图中找到一棵包含所有节点的树,使得树的边权值之和最小。
3. 路径规划问题:给定起点和终点,找到一条满足特定条件的路径,如最短路径、最少转弯等。
4. 最大流问题:在有向图中找到从源节点到汇节点的最大流量。
5. 赛车问题:给定赛道地形和车辆速度等信息,求解车辆在赛道上的最佳路径。
三、解决动点问题的算法 1. 深度优先搜索(DFS):从起点开始,沿着一条路径一直向前,直到无法继续为止,然后回溯到上一个节点,继续搜索其他路径。
2. 广度优先搜索(BFS):从起点开始,依次将与当前节点相邻且未访问过的节点加入队列,然后将当前节点标记为已访问,继续处理队列中的下一个节点。
3. Dijkstra算法:用于求解最短路径问题,通过不断更新起点到各个节点的最短距离来逐步确定最短路径。
4. Bellman-Ford算法:用于求解含有负权边的最短路径问题,通过多次迭代更新起点到各个节点的最短距离。
5. Prim算法:用于求解最小生成树问题,从一个起始节点开始,逐步将与当前生成树相连且权值最小的节点加入生成树中。
6. Kruskal算法:用于求解最小生成树问题,通过不断选择权值最小的边加入生成树,直至生成树包含所有节点。
运筹学-13图论概念及最小树
第一节 图的基本概念与模型
起点与终点相重合的链,称做圈。 起点与终点相重合的路,称做回路。 若在一个图中,每一对顶点之间至少存 在一条链,称这样的图为连通图。 否则,称该图不是连通的。
第一节 图的基本概念与模型
• 一个简单图中任意两点之间有边相连,称这样的图为完全图。
• 其边数有
Cn2
1 2
nn
树,称为该图的最小部分树(也称最小支撑树) (minimum spanning tree) • 定理1:图中任一点i,若 j是相邻点中距离最近的,则 边[i,j]一定必含在该图的最小树内。
• 推论:把图的所有点分成V和 V 两个集合,则两个集
合之间连线的最短的边一定包含在最小部分树内。
2-3 避圈法求最小部分树
图G1={V1,E1}和G2={V2,E2},如果有V1 V2 和E1 E2 ,称 G1是G2的一个子图。 若有V1= V2 , E1 E2 ,则称G1是G2的一个部分图。
第一节 图的基本概念与模型
• 要对研究的问题确定具体对象及这些对象间的性质联系,并 用图形式表示出来,这就是对研究的问题建立图的模型,用
例:e1为环 如果两个点之间的边多于一条,则 称为具有多重边;(平行边) 例:e4和e5为多重边。 对无环,无多重边的图称为简单图;
有平行边,不是简单图
有环边,不是简单图
简单图
第一节 图的基本概念与模型
与某一个点vi相关联的边的数目称为点 的次,(也叫度或线数)记为d(vi)。 例: d(v1) = 4 d(v3) = 5 d(v5) = 1
树图。
• 说明1:树图上只要任意再加上一条边,必定 会出现圈;
• 说明2:由于树图是无圈的连通图,即树图上 任意两点之间有一条且仅有一条惟一通路。是 最脆弱的连通图。
图论中的最长路径问题与最短路径问题
图论中的最长路径问题与最短路径问题图论是数学中研究图的理论,其中最长路径问题和最短路径问题是图论中的经典问题。
本文将介绍这两个问题的定义、求解方法以及应用领域。
一、最长路径问题最长路径问题是指在给定的图中寻找一条路径,使得该路径的长度在所有路径中最长。
路径的长度可以根据边或顶点的数量来计算。
解决最长路径问题的方法有多种,其中最常用的是动态规划算法。
动态规划是一种将问题分解为子问题并逐步解决的算法。
在最长路径问题中,动态规划算法通常通过求解顶点的最长路径长度来得到整个图的最长路径。
在应用中,最长路径问题可以用来解决实际生活中的许多问题,例如交通规划、物流路径优化等。
通过找到最长路径,可以使得交通系统更加高效,减少行程时间和成本。
二、最短路径问题最短路径问题是指在给定的图中寻找一条路径,使得该路径的长度在所有路径中最短。
路径的长度可以根据边或顶点的权重来计算。
解决最短路径问题的方法同样有多种,其中最著名的是Dijkstra算法和Floyd-Warshall算法。
Dijkstra算法是一种贪婪算法,用于解决单源最短路径问题;Floyd-Warshall算法是一种动态规划算法,用于解决所有顶点对之间的最短路径问题。
最短路径问题在现实生活中有广泛应用,例如导航系统、网络路由等。
通过找到最短路径,可以计算出最佳的行进方向,使得路程更加迅捷和经济。
三、最长路径问题与最短路径问题的联系与区别最长路径问题和最短路径问题都是求解图中不同路径的问题,但两者在定义和目标上有所不同。
最长路径问题试图找到一条路径,使得其长度最大化,而最短路径问题试图找到一条路径,使得其长度最小化。
最长路径问题通常通过动态规划算法求解,而最短路径问题则可以通过Dijkstra算法和Floyd-Warshall算法等多种方法解决。
最长路径问题和最短路径问题在应用中也有差异。
最长路径问题主要应用于交通规划、物流路径优化等领域,而最短路径问题则广泛应用于导航系统、网络路由等领域。
