2017高考新课标数学理二轮复习配套检测:知识专题大突破 专题四 数列2-4-1 含解析 精品
2017高考新课标数学理二轮复习配套检测:知识专题大突

专题训练(五) 导数的简单应用及定积分一、选择题1.(2016·东北师大附中月考)曲线f (x )=ax n (a ,n ∈R )在点(1,2)处的切线方程是y =4x -2,则下列说法正确的是( )A .函数f (x )是偶函数且有最大值B .函数f (x )是奇函数且有最大值C .函数f (x )是偶函数且有最小值D .函数f (x )是奇函数且有最小值答案:C 解析:由题知f ′(x )=nax n -1,k =f ′(1)=na =4,f (1)=a =2,∴n =2.所以f (x )=2x 2.显然函数f (x )是偶函数且有最小值.2.设函数f (x )=2x +ln x ,则( ) A .x =12为f (x )的极大值点 B .x =12为f (x )的极小值点 C .x =2为f (x )的极大值点 D .x =2为f (x )的极小值点答案:D 解析:∵f (x )=2x +ln x (x >0), ∴f ′(x )=-2x 2+1x . 由f ′(x )=0,解得x =2.当x ∈(0,2)时,f ′(x )<0,f (x )为减函数; 当x ∈(2,+∞)时,f ′(x )>0,f (x )为增函数. ∴x =2为f (x )的极小值点.3.若曲线f (x )=ln x +ke x 在点(1,f (1))处的切线方程为y =f (1),则k =( )A .eB .1eC .-1D .1答案:D 解析:∵f ′(x )=e x x -(ln x +k )e x(e x )2=1x -ln x -ke x ,由曲线在点(1,f (1))处的切线方程为y =f (1)得f ′(1)=1-ke =0,则k =1,故选D.4.当a >0时,函数f (x )=(x 2+2ax )e x 的图象大致是()答案:B 解析:∵f ′(x )=e x (x 2+2ax )+(2x +2a )e x =e x x 2+2x (a +1)+2a ],令f ′(x )=0得x =±a 2+1-(a +1)<0, ∴f (x )的两个极值点均小于0.结合函数的图象,选项B 为f (x )的大致图象.5.(2016·安徽毫州一中月考)已知函数f (x )=sin(x -φ),且⎠⎜⎜⎛02π3f (x )d x =0,则函数f (x )的图象的一条对称轴是( )A .x =5π6 B .x =7π12 C .x =π3D .x =π6答案:A 解析:∵函数f (x )=sin(x -φ), ∴⎠⎜⎜⎛02π3f (x )d x =-cos(x -φ) ⎪⎪⎪2π3=-cos ⎝ ⎛⎭⎪⎫2π3-φ--cos(-φ)] =32cos φ-32sin φ=3cos ⎝ ⎛⎭⎪⎫φ+π6=0,∴φ+π6=k π+π2,k ∈Z ,即φ=k π+π3,k ∈Z ,故可取φ=π3, ∴f (x )=sin ⎝ ⎛⎭⎪⎫x -π3.令x -π3=k π+π2,求得x =k π+5π6,k ∈Z , 则函数f (x )的图象的一条对称轴为x =5π6.6.定义在⎝ ⎛⎭⎪⎫0,π2上的函数f (x ),f ′(x )是它的导函数,且恒有f (x )<f ′(x )·tan x 成立,则( )A.3f ⎝ ⎛⎭⎪⎫π4>2f ⎝ ⎛⎭⎪⎫π3 B .f (1)<2f ⎝ ⎛⎭⎪⎫π6sin 1C.2f ⎝ ⎛⎭⎪⎫π6>f ⎝ ⎛⎭⎪⎫π4D.3f ⎝ ⎛⎭⎪⎫π6<f ⎝ ⎛⎭⎪⎫π3答案:D 解析:因为0<x <π2,f (x )<f ′(x )tan x , 所以f ′(x )sin x -f (x )cos x >0.因为⎝ ⎛⎭⎪⎫f (x )sin x ′=f ′(x )sin x -f (x )cos xsin 2x >0, 所以y =f (x )sin x 在⎝ ⎛⎭⎪⎫0,π2上单调递增,所以f ⎝ ⎛⎭⎪⎫π612<f ⎝ ⎛⎭⎪⎫π332,即3f ⎝ ⎛⎭⎪⎫π6<f ⎝ ⎛⎭⎪⎫π3,故选D.二、填空题7.(2016·云南师大附中月考)设函数f (x )=e x (ln x +1)在⎣⎢⎡⎦⎥⎤1e 2,1上的最小值为m ,则ln|m |的值是________.答案:1e 2 解析:∵f ′(x )=e x ⎝ ⎛⎭⎪⎫ln x +1x +1,令g (x )=ln x +1x +1,∴g ′(x )=1x -1x 2=x -1x 2,∴g (x )在(0,1)上递减,在(1,+∞)上递增,∴g (x )≥g (1)=2>0,∴f ′(x )>0,∴f (x )在⎣⎢⎡⎦⎥⎤1e 2,1上为增函数,∴m =f ⎝ ⎛⎭⎪⎫1e 2=-e 1e 2, ∴ln|m |=1e 2.8.若曲线C 1:y =ax 3-6x 2+12x 与曲线C 2:y =e x 在x =1处的两条切线互相垂直,则实数a 的值为________.答案:-13e 解析:因为(ax 3-6x 2+12x )′=3ax 2-12x +12,所以曲线C 1在x =1处的切线的斜率为3a .又曲线C 2在x =1处的切线的斜率为e ,故由题意得3a e =-1,解得a =-13e .9.(2016·陕西安康三模)若函数f (x )=ax 2-1x 在(2,3)上为增函数,则实数a 的取值范围是________.答案:⎣⎢⎡⎭⎪⎫-19,+∞ 解析:由题意得f ′(x )=⎝ ⎛⎭⎪⎫ax -1x ′= a +1x 2,又f (x )在(2,3)上为增函数,故a +1x 2≥0对x ∈(2,3)恒成立,即a ≥-1x 2,x ∈(2,3).当x =3时,⎝ ⎛⎭⎪⎫-1x 2max =-19. ∴a ≥-19.10.曲线C :y =x 22在点B ⎝ ⎛⎭⎪⎫1,12处的切线为l ,则曲线C 、直线l 与x 轴所围成的几何图形的面积是________.答案:124 解析:由导数的几何意义,l 的斜率k =y ′|x =1=1. ∴直线l 的方程为y =x -12,作曲线C 与直线l (如图所示),阴影部分的面积为所求几何图形的面积,且点A ⎝ ⎛⎭⎪⎫12,0,则S 阴=S 曲边三角形OCB -S △ABC .又S 曲边三角形OCB =⎠⎛01x 22d x =x 3610=16,S △ABC =12×12×12=18.因此所求几何图形的面积S 阴=16-18=124. 三、解答题11.设函数f (x )=1-a2x 2+ax -ln x (a ∈R ). (1)当a =3时,求函数f (x )的极值; (2)当a >1时,讨论函数f (x )的单调性. 解:(1)函数的定义域为(0,+∞). 当a =3时,f (x )=-x 2+3x -ln x , f ′(x )=-2x 2+3x -1x =-(2x -1)(x -1)x . 当12<x <1时,f ′(x )>0,f (x )单调递增; 当0<x <12或x >1时,f ′(x )<0,f (x )单调递减. 所以f (x )极大值=f (1)=2,f (x )极小值=f ⎝ ⎛⎭⎪⎫12=54+ln 2.(2)∵f ′(x )=(1-a )x +a -1x =(1-a )x 2+ax -1x=(1-a )⎝ ⎛⎭⎪⎫x -1a -1(x -1)x.当1a -1=1,即a =2时, f ′(x )=-(1-x )2x ≤0,f (x )在定义域上是减函数. 当0<1a -1<1,即a >2时,令f ′(x )<0得0<x <1a -1或x >1;令f ′(x )>0得1a -1<x <1.当1a -1>1,即1<a <2时,由f ′(x )>0得1<x <1a -1;由f ′(x )<0得0<x <1或x >1a -1.综上,当a =2时,f (x )在(0,+∞)上是减函数;当a >2时,f (x )在⎝ ⎛⎭⎪⎫0,1a -1上和(1,+∞)上单调递减,在⎝ ⎛⎭⎪⎫1a -1,1上单调递增;当1<a <2时,f (x )在(0,1)上和⎝ ⎛⎭⎪⎫1a -1,+∞上单调递减,在⎝ ⎛⎭⎪⎫1,1a -1上单调递增.12.(2016·华中师大附中模拟)已知函数f (x )=x +a ln x ,在x =1处的切线与直线x +2y =0垂直,函数g (x )=f (x )+12x 2-bx .(1)求实数a 的值;(2)设x 1,x 2(x 1<x 2)是函数g (x )的两个极值点,记t =x 1x 2,若b ≥133:①求t 的取值范围; ②求g (x 1)-g (x 2)的最小值. 解:(1)由题可得f ′(x )=1+ax . 由题意知f ′(1)=1+a =2,即a =1. (2)由g (x )=ln x +12x 2-(b -1)x , g ′(x )=x 2-(b -1)x +1x, 令g ′(x )=0,x 2-(b -1)x +1=0, 即x 1+x 2=b -1,x 1x 2=1,而(x 1+x 2)2x 1x 2=x 1x 2+2+x 2x 1=t +2+1t =(b -1)2≥1009⎝⎛⎭⎪⎫b ≥133.由x 1<x 2,即0<t <1,解上不等式可得0<t ≤19.而g (x 1)-g (x 2)=ln x 1x 2-12⎝ ⎛⎭⎪⎫x 1x 2-x 2x 1=ln t -12⎝ ⎛⎭⎪⎫t -1t (利用根与系数的关系化简整理得),构造函数h (t )=ln t -12⎝ ⎛⎭⎪⎫t -1t ,t ∈⎝ ⎛⎦⎥⎤0,19,由t ∈⎝⎛⎦⎥⎤0,19,h ′(t )=-(t -1)22t 2<0, 故h (t )在定义域内单调递减,h (t )min =h ⎝ ⎛⎭⎪⎫19=409-2ln 3,所以g (x 1)-g (x 2)的最小值为409-2ln 3.。
2017高考新课标数学理二轮复习配套检测:知识专题大突
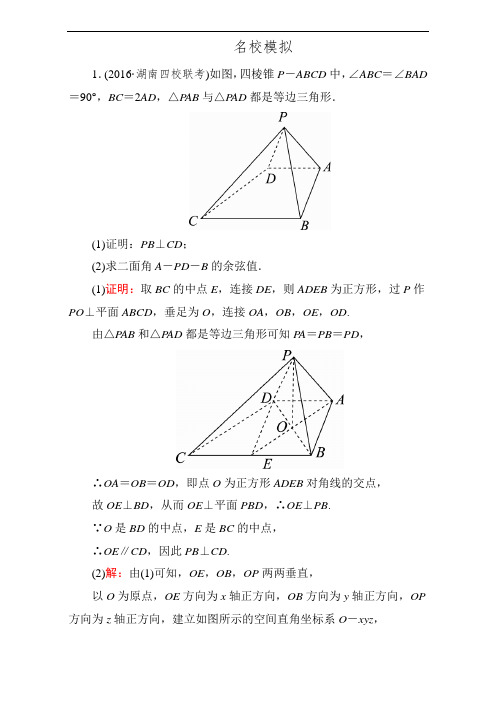
名校模拟1.(2016·湖南四校联考)如图,四棱锥P-ABCD中,∠ABC=∠BAD =90°,BC=2AD,△P AB与△P AD都是等边三角形.(1)证明:PB⊥CD;(2)求二面角A-PD-B的余弦值.(1)证明:取BC的中点E,连接DE,则ADEB为正方形,过P作PO⊥平面ABCD,垂足为O,连接OA,OB,OE,OD.由△P AB和△P AD都是等边三角形可知P A=PB=PD,∴OA=OB=OD,即点O为正方形ADEB对角线的交点,故OE⊥BD,从而OE⊥平面PBD,∴OE⊥PB.∵O是BD的中点,E是BC的中点,∴OE∥CD,因此PB⊥CD.(2)解:由(1)可知,OE,OB,OP两两垂直,以O为原点,OE方向为x轴正方向,OB方向为y轴正方向,OP 方向为z轴正方向,建立如图所示的空间直角坐标系O-xyz,设|AB |=2,则A (-2,0,0),D (0,-2,0),P (0,0,2), AD →=(2,-2,0),AP →=(2,0,2),设平面P AD 的法向量为n =(x ,y ,z ),则⎩⎨⎧n ·AD →=2x -2y =0,n ·AP →=2x +2z =0,取x =1,得y =1,z =-1,即n =(1,1,-1).∵OE ⊥平面PBD ,设平面PBD 的法向量为m ,取m =(1,0,0), 由图象可知二面角A -PD -B 的大小为锐角, ∴二面角A -PD -B 的余弦值为cos θ=|n ·m ||n ||m |=13=33. 2.(2016·湖南师大附中模拟)如图,在平行四边形ABCD 中,AB =2AD ,∠BAD =60°,E 为AB 的中点,将△ADE 沿直线DE 折起到△PDE的位置,使平面PDE ⊥平面BCDE .(1)证明:CE ⊥PD ;(2)设F ,M 分别为PC ,DE 的中点,求直线MF 与平面PDE 所成的角.(1)证明:因为AB =2AD ,E 为AB 的中点,则AE =AD . 又∠BAD =60°,则△ADE 为正三角形,所以∠AED =60°. 因为BE =BC ,∠CBE =120°,则∠CEB =30°. 从而∠CED =180°-∠AED -∠CEB =90°, 即CE ⊥DE .因为平面PDE ⊥平面BCDE ,平面PDE ∩平面BCDE =DE ,CE ⊂平面BCDE .则CE ⊥平面PDE ,所以CE ⊥PD .(2)解:如图,以E 为原点,建立如图所示的空间直角坐标系. 由已知,△PDE 为正三角形,则PM ⊥ED . 又平面PDE ⊥平面BCDE ,则PM ⊥平面BCDE . 设AD =2,则EM =1,PM =3, CE =4+4-2×2×2cos 120°=2 3. 所以点M (0,1,0),P (0,1,3),C (23,0,0).因为F 为PC 的中点,所以点F ⎝⎛⎭⎪⎫3,12,32,所以MF →=⎝⎛⎭⎪⎫3,-12,32.由(1)知,CE ⊥平面PDE ,则n =(1,0,0)为平面PDE 的一个法向量. 设直线MF 与平面PDE 所成的角为θ,则sin θ=cos 〈MF →,n 〉=MF →·n |MF →||n |=32,得θ=60°.故直线MF 与平面PDE 所成的角为60°.3.(2016·江西南昌二中模拟)如图,在直角梯形ABCD 中,AD ∥BC ,∠ADC =90°,AE ⊥平面ABCD ,EF ∥CD ,BC =CD =AE =EF =12AD =1.(1)求证:CE ∥平面ABF ;(2)在直线BC 上是否存在点M ,使二面角E -MD -A 的大小为π6?若存在,求出CM 的长;若不存在,请说明理由.(1)证明:如图,作FG ∥EA ,AG ∥EF ,连接EG 交AF于H ,连接BH ,∵EF ∥CD 且EF =CD ,∴AG ∥CD ,即点G 在平面ABCD 内,由AE ⊥平面ABCD ,知AE ⊥AG , 又∠ADC =90°,∴四边形AEFG 为正方形,四边形CDAG 为矩形, ∴H 为EG 的中点,B 为CG 的中点,∴BH ∥CE .∵BH ⊂平面ABF ,CE ⊄平面ABF , ∴CE ∥平面ABF .(2)解:如图,以A 为原点,AG 为x 轴,AD 为y 轴,AE 为z 轴,建立空间直角坐标系A -xyz.则A (0,0,0),E (0,0,1),D (0,2,0), 设M (1,y 0,0),∴ED →=(0,2,-1),DM →=(1,y 0-2,0). 设平面EMD 的一个法向量为n =(x ,y ,z ),则⎩⎨⎧n ·ED →=2y -z =0,n ·DM →=x +(y 0-2)y =0,令y =1,得z =2,x =2-y 0, ∴n =(2-y 0,1,2). 又∵AE ⊥平面AMD ,∴AE →=(0,0,1)为平面AMD 的一个法向量, ∴|cos 〈n ,AE →〉|=|2|1×(2-y 0)2+1+4=cos π6=32,解得y 0=2±33,∴在直线BC 上存在点M ,且|CM |=⎪⎪⎪⎪⎪⎪2-⎝⎛⎭⎪⎫2±33=33,使二面角E-MD -A 的大小为π6.。
《高考调研》2017届高考数学(理)(新课标)二轮专题复习作业20数列2Word版含解析

数列专练(二)·作业(二十)1.(2016·长沙模拟)已知数列{a n }满足a 1+a 22+…+a n n =2n +1,(1)求{a n }的通项公式;(2)求{a n }的前n 项和.解析 (1)当n =1时,由题设知a 1=4;当n ≥2时,由题设a 1+a 22+…+a n n =2n +1知a 1+a 22+…+a n -1n -1=2n , 两式相减得a n n =2n +1-2n ,即a n =n ×2n (n ≥2),故{a n }的通项公式为a n =⎩⎨⎧4,n =1,n ×2n (n ≥2,n ∈N *).(2)设{a n }的前n 项和为S n ,则S n =1×22+2×22+…+n ×2n ,2S n =1×23+2×23+…+(n -1)×2n +n ×2n +1,两式相减得S n =n ×2n +1-(22+23+…+2n ) =n ×2n +1-4×(2n -1-1)=(n -1)×2n +1+4.2.(2016·四川达州调研)已知等比数列{a n }的首项a 1=13,前n 项和S n 满足S 1,2S 2,3S 3成等差数列.(1)求{a n }的通项公式;(2)设b n =2-(11+a n +11-a n +1),数列{b n }的前n 项和为T n ,求证:T n <13. 解析 (1)因为S 1,2S 2,3S 3成等差数列,所以4S 2=S 1+3S 3,当q =1时,不符合;当q ≠1时,得4a 1(1-q 2)1-q =a 1+3a 1(1-q 3)1-q,故q =13或q =0(舍去). 综上可知,a n =(13)n .(2)由(1)知a n =(13)n ,所以b n =2-[11+(13)n +11-(13)n +1]=2-11+(13)n -11-(13)n +1=1-11+(13)n +1-11-(13)n +1=(1-3n3n +1)+(1-3n +13n +1-1)=13n+1-13n +1-1, 由13n +1<13n ,13n +1-1>13n +1得13n +1-13n +1-1<13n -13n +1,所以b n <13n -13n +1, 从而T n =b 1+b 2+…+b n <(13-132)+(132-133)+…+(13n -13n +1)=13-13n +1<13,因此T n <13.3.(2016·湖南东部六校联考)已知△ABC 的角A ,B ,C 的对边分别为a ,b ,c ,其面积S =43,B =60°,且a 2+c 2=2b 2;等差数列{a n }中,a 1=a ,公差d =b.数列{b n }的前n 项和为T n ,且T n -2b n +3=0,n ∈N *.(1)求数列{a n }、{b n }的通项公式;(2)设c n =⎩⎪⎨⎪⎧a n ,n 为奇数,b n ,n 为偶数,求数列{c n }的前2n +1项和P 2n +1. 解析 (1)∵S =12acsinB =43,∴ac =16,又a 2+c 2=2b 2,b 2=a 2+c 2-2accosB ,∴b 2=ac =16,∴b =4,从而(a +c)2=a 2+c 2+2ac =64,a +c =8,∴a =c =4.故可得⎩⎨⎧a 1=4,d =4,∴a n =4n. ∵T n -2b n +3=0,∴当n =1时,b 1=3,当n ≥2时,T n -1-2b n -1+3=0,两式相减,得b n =2b n -1(n ≥2),∴数列{b n }为等比数列,∴b n =3·2n -1.(2)依题意,c n =⎩⎨⎧4n ,n 为奇数,3·2n -1,n 为偶数. P 2n +1=(a 1+a 3+…+a 2n +1)+(b 2+b 4+…+b 2n )=[4+4(2n +1)]·(n +1)2+6(1-4n )1-4=22n +1+4n 2+8n +2.4.(2016·保定调研)已知数列{a n }中,a 1=1,a 2=3,其前n 项和为S n ,且当n ≥2时,a n +1S n -1-a n S n =0.(1)求证:数列{S n }是等比数列,并求数列{a n }的通项公式;(2)令b n =9a n (a n +3)(a n +1+3),记数列{b n }的前n 项和为T n ,求T n . 解析 (1)当n ≥2时,a n +1S n -1-a n S n =(S n +1-S n )S n -1-(S n -S n -1)S n =S n +1S n -1-S n 2=0,∴S n 2=S n -1S n +1(n ≥2),又由S 1=1≠0,S 2=4≠0,可推知对一切正整数n 均有S n ≠0,则数列{S n }是等比数列,S n =4n -1.当n ≥2时,a n =S n -S n -1=3×4n -2,又a 1=S 1=1,∴a n =⎩⎨⎧1,(n =1),3×4n -2,(n ≥2). (2)当n ≥2时,b n =9a n (a n +3)(a n +1+3)=9×3×4n -2(3×4n -2+3)(3×4n -1+3)=3×4n -2(4n -2+1)(4n -1+1),又b 1=38, ∴b n =⎩⎪⎨⎪⎧38,(n =1),3×4n -2(4n -2+1)(4n -1+1),(n ≥2),则T 1=b 1=38当n ≥2时,b n =3×4n -2(4n -2+1)(4n -1+1)=14n -2+1-14n -1+1, 则T n =38+(142-2+1-142-1+1)+…+(14n -2+1-14n -1+1)=78-14n -1+1. 综上:T n =78-14n -1+1.5.(2016·河南联考)已知数列{a n }满足前n 项和S n =n 2+1,数列{b n }满足b n =2a n +1,且前n 项和为T n ,设c n =T 2n +1-T n . (1)求数列{b n }的通项公式;(2)判断数列{c n }的单调性;(3)当n ≥2时,T 2n +1-T n <15-712log a (a -1)恒成立,求a 的取值范围.解析 (1)当n =1时,a 1=S 1=2,当n ≥2时,a n =S n -S n -1=2n -1.∴数列{b n }的通项公式为b n =⎩⎪⎨⎪⎧23,n =1,1n ,n ≥2.(2)∵c n =T 2n +1-T n ,∴c n =b n +1+b n +2+…+b 2n +1=1n +1+1n +2+…+12n +1. ∴c n +1-c n =12n +2+12n +3-1n +1=12n +3-12n +2=-1(2n +3)(2n +2)<0. ∴数列{c n }是递减数列.(3)由(2)知,当n ≥2时,c 2=13+14+15为最大,∴13+14+15<15-712log a (a -1)恒成立,即log a (a -1)<-1.由真数a -1>0,得a>1,∴a -1<1a .整理为a 2-a -1<0,解得1<a<5+12. ∴a 的取值范围是(1,5+12).。
2017高考新课标数学(理)二轮复习配套检测:知识专题大突破专题一集合与常用逻辑2-1-2含解析

名校模拟1.(2016·天津一中模拟)设a>0,b〉0。
若3是3a与3b的等比中项,则错误!+错误!的最小值为()A.8 B.4C.1 D.错误!答案:B 解析:因为3a·3b=3,所以a+b=1,错误!+错误!=(a+b)错误!=2+错误!+错误!≥2+2错误!=4,当且仅当错误!=错误!,即a=b=错误!时,等号成立.2.(2016·河北衡水中学模拟)设变量x,y满足|x|+|y|≤1,则x+2y的最大值和最小值分别为()A.1,-1 B.2,-2C.1,-2 D.2,-1答案:B 解析:由约束条件|x|+|y|≤1,作出可行域如图中阴影部分所示.设z =2x +y ,则y =-2x +z ,平移直线y =-2x ,当经过点A (1,0)时,z 取得最大值2,当经过点B (-1,0)时,z 取得最小值-2。
3.(2016·江西宜春中学与新学一中联考)设x ,y 满足约束条件错误!则错误!的取值范围是( )A .1,5]B .2,6]C .2,10]D .3,11]答案:D 解析:设z =x +2y +3x +1=错误!=1+2·错误!,设z ′=错误!,则z ′的几何意义为动点P (x ,y )到定点D (-1,-1)的斜率.画出可行域,如图阴影部分所示,则易得z ′∈k DA ,k DB ],易得z ′∈1,5],∴z =1+2·z ′∈3,11].4.(2016·济宁微山一中模拟)若log (a +1)m =log 错误!n 〉0(0<a 〈1),则关于x 的不等式错误!≥0的解集为________.答案:(-∞,m ]∪(n ,+∞) 解析:若log a +1m =log 错误!n >0 (0<a <1),则m 〉1,n >1,又a +1-错误!=错误!=错误!〈0,即有1<a +1<错误!,即有m 〈n 。
2017高考新课标数学理二轮复习配套检测:知识专题大突破 专题二 函数与导数 2-2-2 含解析 精品

名校模拟1.(2016·四川新津中学月考)设函数f (x )=⎩⎪⎨⎪⎧x 2+bx +c ,x ≤0,3,x >0. 若f (-4)=f (0),f (-2)=-2,则关于x 的方程f (x )=x 的解的个数为( )A .4B .3C .2D .1答案:B 解析:先由f (-4)=f (0)可得,16-4b +c =c ,解得b =4.再由f (-2)=-2可得,4-2b +c =-2,解得c =2.故f (x )=⎩⎪⎨⎪⎧ x 2+4x +2,x ≤0,3,x >0. 令f (x )=x 可得⎩⎪⎨⎪⎧ x 2+4x +2=x ,x ≤0或⎩⎪⎨⎪⎧3=x ,x >0, 解得x =3或x =-1或x =-2.2.(2016·江西南昌二中模拟)f (x )是定义在R 上的奇函数,且当x ∈(0,+∞)时,f (x )=2 016x +log 2 016x ,函数f (x )的零点的个数是( )A .1B .2C .3D .4答案:C 解析:作出函数y =2 016x ,y =-log 2 016x 的图象,可知函数f (x )=2 016x +log 2 016x 在x ∈(0,+∞)上存在一个零点,又因为f (x )是定义在R 上的奇函数,所以f (x )在x ∈(-∞,0)上只有一个零点.又f (0)=0,所以函数f (x )的零点的个数是3,故选C.3.(2016·湖南四校联考)已知函数f (x )=|x 2-2ax +b |(x ∈R ),给出下列命题:①∃a 0∈R ,使f (x )为偶函数;②若f (0)=f (2),则f (x )的图象关于x =1对称;③若a 2-b ≤0,则f (x )在区间a ,+∞)上是增函数;④若a 2-b -2>0,则函数h (x )=f (x )-2有2个零点.其中正确命题的序号为________.答案:①③ 解析:①当a =0时,f (x )=|x 2+b |显然是偶函数,故①正确;②由f (0)=f (2),则|b |=|4-4a +b |,而f (x +1)=|(x +1)2-2a (x +1)+b |=|x 2+(2-2a )x +1-2a +b |, f (1-x )=|(1-x )2-2a (1-x )+b |=|1-2x +x 2-2a +2ax +b |=|x 2+(2a -2)x +1-2a +b |.∴f (x +1)≠f (1-x ),∴f (x )的图象不关于x =1对称,故②错误; ③f (x )=|(x -a )2+b -a 2|=(x -a )2+b -a 2在区间a ,+∞)上是增函数,故③正确;④h (x )=|(x -a )2+b -a 2|-2有4个零点,故④错误.4.(2016·天津一中月考)已知函数f (x )=⎩⎪⎨⎪⎧2-|x |,x ≤2,(x -2)2,x >2,函数g (x )=3-f (2-x ),则函数y =f (x )-g (x )的零点有________个.答案:2 解析:∵g (x )=3-f (2-x ),∴y =f (x )-g (x )=f (x )-3+f (2-x ),由f (x )-3+f (2-x )=0得f (x )+f (2-x )=3.设h (x )=f (x )+f (2-x ).若x ≤0,则-x ≥0,2-x ≥2,则h (x )=f (x )+f (2-x )=2+x +x 2;若0≤x ≤2,则-2≤-x ≤0,0≤2-x ≤2,则h (x )=f (x )+f (2-x )=2-x +2-|2-x |=2-x +2-2+x =2; 若x >2,-x <0,2-x <0,则h (x )=f (x )+f (2-x )=(x -2)2+2-|2-x |=x 2-5x +8.即h (x )=⎩⎪⎨⎪⎧ x 2+x +2,x ≤0,2,0<x ≤2,x 2-5x +8,x >2,作出函数h (x )的图象,如图所示.当y =3时,两个函数有2个交点,故函数y =f (x )-g (x )的零点有2个.。
2017高考新课标数学(理)二轮复习配套检测:知识专题大突破专题二 函数与导数2-2-2含解析

名校模拟1.(2016·四川新津中学月考)设函数f(x)=错误!若f(-4)=f(0),f(-2)=-2,则关于x的方程f(x)=x的解的个数为()A.4 B.3 C.2 D.1答案:B 解析:先由f(-4)=f(0)可得,16-4b+c=c,解得b =4。
再由f(-2)=-2可得,4-2b+c=-2,解得c=2。
故f(x)=错误!令f(x)=x可得错误!或错误!解得x=3或x=-1或x=-2。
2.(2016·江西南昌二中模拟)f(x)是定义在R上的奇函数,且当x∈(0,+∞)时,f(x)=2 016x+log2 016x,函数f(x)的零点的个数是()A.1 B.2 C.3 D.4答案:C 解析:作出函数y=2 016x,y=-log2 016x的图象,可知函数f(x)=2 016x+log2 016x在x∈(0,+∞)上存在一个零点,又因为f(x)是定义在R上的奇函数,所以f(x)在x∈(-∞,0)上只有一个零点.又f(0)=0,所以函数f(x)的零点的个数是3,故选C.3.(2016·湖南四校联考)已知函数f(x)=|x2-2ax+b|(x∈R),给出下列命题:①∃a0∈R,使f(x)为偶函数;②若f(0)=f(2),则f(x)的图象关于x=1对称;③若a2-b≤0,则f(x)在区间a,+∞)上是增函数;④若a2-b-2>0,则函数h(x)=f(x)-2有2个零点.其中正确命题的序号为________.答案:①③解析:①当a=0时,f(x)=|x2+b|显然是偶函数,故①正确;②由f(0)=f(2),则|b|=|4-4a+b|,而f(x+1)=|(x+1)2-2a(x+1)+b|=|x2+(2-2a)x+1-2a +b|,f(1-x)=|(1-x)2-2a(1-x)+b|=|1-2x+x2-2a+2ax +b|=|x2+(2a-2)x+1-2a+b|。
∴f(x+1)≠f(1-x),∴f(x)的图象不关于x=1对称,故②错误;③f(x)=|(x-a)2+b-a2|=(x-a)2+b-a2在区间a,+∞)上是增函数,故③正确;④h(x)=|(x-a)2+b-a2|-2有4个零点,故④错误.4.(2016·天津一中月考)已知函数f(x)=错误!函数g(x)=3-f(2-x),则函数y=f(x)-g(x)的零点有________个.答案:2 解析:∵g(x)=3-f(2-x),∴y=f(x)-g(x)=f(x)-3+f(2-x),由f(x)-3+f(2-x)=0得f(x)+f(2-x)=3.设h(x)=f(x)+f(2-x).若x≤0,则-x≥0,2-x≥2,则h(x)=f(x)+f(2-x)=2+x+x2;若0≤x≤2,则-2≤-x≤0,0≤2-x≤2,则h(x)=f(x)+f(2-x)=2-x+2-|2-x|=2-x+2-2+x=2;若x〉2,-x<0,2-x<0,则h(x)=f(x)+f(2-x)=(x-2)2+2-|2-x|=x2-5x+8.即h(x)=错误!作出函数h(x)的图象,如图所示.当y=3时,两个函数有2个交点,故函数y=f(x)-g(x)的零点有2个.。
2017年高考数学二轮专题复习与策略第1部分专题2数列突破点4等差数列、等比数列专题限时集训理
专题限时集训(四) 等差数列、等比数列[建议A 、B 组各用时:45分钟][A 组 高考达标]一、选择题1.(2016·青岛模拟)在等比数列{a n }中,a 2a 3a 4=8,a 7=8,则a 1=( ) A .1 B .±1 C .2D .±2A [a 2a 3a 4=a 33=8,所以a 3=2,所以a 7=a 3q 4=8, 从而q 2=2,所以a 1=a 3q2=1,故选A.]2.(2016·福州模拟)已知数列{a n }是等差数列,且a 7-2a 4=6,a 3=2,则公差d =( ) A .2 2 B .4 C .8D .16B [法一:由题意得a 3=2,a 7-2a 4=a 3+4d -2(a 3+d )=6,解得d =4,故选B. 法二:在公差为d 的等差数列{a n }中,a m =a n +(m -n )d (m ,n ∈N *). 由题意得⎩⎪⎨⎪⎧a 7-2a 4=a 1+6d -a 1+3d =6,a 3=a 1+2d =2,解得⎩⎪⎨⎪⎧a 1=-6,d =4.]3.已知等比数列{a n }的公比为q ,其前n 项和为S n ,若S 3,S 9,S 6成等差数列,则q 3等于( ) 【导学号:67722021】A .-12B .1C .-12或1D .-1或12A [若q =1,则3a 1+6a 1=2×9a 1, 得a 1=0,矛盾,故q ≠1.所以a 1-q 31-q +a 1-q 61-q=2a 1-q 91-q,解得q 3=-12或1(舍),故选A.]4.已知数列{a n },{b n }满足a 1=b 1=3,a n +1-a n =b n +1b n=3,n ∈N *.若数列{c n }满足c n =ba n ,则c 2 016=( )A .92 015B .272 015C .92 016D .272 016D [由已知条件知{a n }是首项为3,公差为3的等差数列.数列{b n }是首项为3,公比为3的等比数列,∴a n =3n ,b n =3n.又c n =ba n =33n,∴c 2 016=33×2 016=272 016,故选D.]5.设S n ,T n 分别是等差数列{a n },{b n }的前n 项和,若S n T n =n 2n +1(n ∈N *),则a 5b 6=( )A.513 B.919 C.1123D.923D [根据等差数列的前n 项和公式及S n T n =n2n +1(n ∈N *),可设S n =kn 2,T n =kn (2n +1),又当n ≥2时,a n =S n -S n -1=k (2n -1),b n =T n -T n -1=k (4n -1),所以a 5b 6=923,故选D.] 二、填空题6.(2016·长沙模拟)设等差数列{a n }的前n 项和为S n ,若S 3=2a 3,S 5=15,则a 2 016=__________.2 016 [在等差数列{a n }中,由S 3=2a 3知,3a 2=2a 3,而S 5=15,则a 3=3,于是a 2=2,从而其公差为1,首项为1,因此a n =n ,故a 2 016=2 016.]7.已知{a n }为等差数列,a 1+a 3+a 5=105,a 2+a 4+a 6=99,以S n 表示{a n }的前n 项和,则使得S n 达到最大值的n 是________.20 [由等差数列的性质可得a 3=35,a 4=33,故d =-2,a n =35+(n -3)×(-2)=41-2n ,易知数列前20项大于0,从第21项起为负项,故使得S n 达到最大值的n 是20.]8. 设等比数列{a n }中,S n 是前n 项和,若27a 3-a 6=0,则S 6S 3=__________.28 [由题意可知,公比q 3=a 6a 3=27,∴S 6S 3=1-q 61-q3=1+q 3=1+27=28.]三、解答题9.设数列{a n }的前n 项和为S n ,满足(1-q )S n +qa n =1,且q (q -1)≠0. (1)求{a n }的通项公式;(2)若S 3,S 9,S 6成等差数列,求证:a 2,a 8,a 5成等差数列. [解] (1)当n =1时,由(1-q )S 1+qa 1=1,得a 1=1.1分当n ≥2时,由(1-q )S n +qa n =1,得(1-q )S n -1+qa n -1=1,两式相减得a n =qa n -1.5分 又q (q -1)≠0,所以{a n }是以1为首项,q 为公比的等比数列,故a n =q n -1.6分(2)证明:由(1)可知S n =1-a n q1-q ,7分又S 3+S 6=2S 9,得1-a 3q 1-q +1-a 6q1-q=-a 9q1-q,9分化简得a 3+a 6=2a 9,两边同除以q 得a 2+a 5=2a 8.11分 故a 2,a 8,a 5成等差数列.12分10.(2016·广州五校联考)已知等差数列{a n }的前n 项和为S n ,且a 3+a 6=4,S 5=-5. (1)求数列{a n }的通项公式;(2)若T n =|a 1|+|a 2|+|a 3|+…+|a n |,求T 5的值和T n 的表达式. [解] (1)由题知⎩⎪⎨⎪⎧2a 1+7d =4,5a 1+5×42d =-5,解得⎩⎪⎨⎪⎧a 1=-5,d =2,故a n =2n -7(n ∈N *).5分(2)由a n =2n -7<0,得n <72,即n ≤3,所以当n ≤3时,a n =2n -7<0,当n ≥4时,a n =2n -7>0.6分 易知S n =n 2-6n ,S 3=-9,S 5=-5,所以T 5=-(a 1+a 2+a 3)+a 4+a 5=-S 3+(S 5-S 3)=S 5-2S 3=13.8分 当n ≤3时,T n =-S n =6n -n 2;当n ≥4时,T n =-S 3+(S n -S 3)=S n -2S 3=n 2-6n +18.故T n =⎩⎪⎨⎪⎧6n -n 2,n ≤3,n 2-6n +18,n ≥4.12分[B 组 名校冲刺]一、选择题1.(2016·河北五个一联盟)已知等差数列{a n }的前n 项和为S n ,且S 2=10,S 5=55,则过点P (n ,a n )和Q (n +2,a n +2)(n ∈N *)的直线的斜率是( )【导学号:67722022】A .4B .3C .2D .1A [设等差数列{a n }的公差为d ,因为S 2=2a 1+d =10,S 5=52(a 1+a 5)=5(a 1+2d )=55,所以d =4,所以k PQ =a n +2-a n n +2-n =2d2=d =4,故选A.]2.已知数列{a n }满足log 3a n +1=log 3a n +1(n ∈N *),且a 2+a 4+a 6=9,则log 13(a 5+a 7+a 9)的值是( )A .-5B .-15C .5D.15A [根据已知得3a n =a n +1,∴数列{a n }是等比数列且其公比为3, ∴a 5+a 7+a 9=(a 2+a 4+a 6)×33=9×33=35, ∴log 13(a 5+a 7+a 9)=log 1335=-5.]3.(2016·东北三省四市联考)如图41所示的数阵中,每行、每列的三个数均成等差数列,如果数阵中所有数之和等于63,那么a 52=( )⎝ ⎛⎭⎪⎫a41 a 42 a 43a 51 a 52 a 53a61a 62 a 63 图41 A .2 B .8 C .7D .4C [第一行三数成等差数列,由等差中项的性质有a 41+a 42+a 43=3a 42,同理第二行也有a 51+a 52+a 53=3a 52,第三行也有a 61+a 62+a 63=3a 62,又每列也成等差数列,所以对于第二列,有a 42+a 52+a 62=3a 52,所以a 41+a 42+a 43+a 51+a 52+a 53+a 61+a 62+a 63=3a 42+3a 52+3a 62=3×3a 52=63,所以a 52=7,故选C.]4.(2016·郑州二模)设数列{a n }满足:a 1=1,a 2=3,且2na n =(n -1)a n -1+(n +1)a n +1,则a 20的值是( )A.215B.225C.235D.245D [由2na n =(n -1)a n -1+(n +1)a n +1得na n -(n -1)a n -1=(n +1)a n +1-na n ,又因为1×a 1=1,2×a 2-1×a 1=5,所以数列{na n }为首项为1,公差为5的等差数列,则20a 20=1+19×5,解得a 20=245,故选D.]二、填空题5.(2016·湖北七校2月联考)已知数列{a n }为等差数列,其前n 项和为S n ,若S k -2=-4(k >2),S k =0,S k +2=8,则k =__________.6 [由题意,得S k +2-S k =a k +1+a k +2=8,S k -S k -2=a k -1+a k =4(k >2),两式相减,得4d =4,即d =1.由S k =ka 1+k k -2=0,得a 1=-k -12,将a 1=-k -12代入a k -1+a k =4,得-(k -1)+(2k -3)=k -2=4,解得k =6.]6.(2016·河北第二次大联考)数列{log k a n }是首项为4,公差为2的等差数列,其中k >0,且k ≠1.设c n =a n lg a n ,若{c n }中的每一项恒小于它后面的项,则实数k 的取值范围为__________. 【导学号:67722023】⎝⎛⎭⎪⎫0,63∪(1,+∞) [由题意得log k a n =2n +2,则a n =k 2n +2,∴a n +1a n =k n ++2k 2n +2=k 2,即数列{a n }是以k 4为首项,k 2为公比的等比数列,c n =a n lg a n =(2n +2)·k 2n +2lg k ,要使c n <c n +1对一切n ∈N *恒成立,即(n +1)lg k <(n +2)·k 2·lg k 对一切n ∈N *恒成立.当k >1时,lg k >0,n +1<(n +2)k 2对一切n ∈N *恒成立;当0<k <1时,lg k <0,n +1>(n +2)k 2对一切n ∈N *恒成立,只需k 2<⎝ ⎛⎭⎪⎫n +1n +2min .∵n +1n +2=1-1n +2单调递增,∴当n =1时,n +1n +2取得最小值,即⎝ ⎛⎭⎪⎫n +1n +2min =23,∴k 2<23,且0<k <1,∴0<k <63.综上,k ∈⎝⎛⎭⎪⎫0,63∪(1,+∞).]三、解答题7.已知数列{a n }的前n 项和为S n ,且S n =2n 2+2n . (1)求数列{a n }的通项公式;(2)若点(b n ,a n )在函数y =log 2x 的图象上,求数列{b n }的前n 项和T n . [解] (1)当n ≥2时,a n =S n -S n -1=2n 2+2n -[2(n -1)2+2(n -1)]=4n ,3分当n =1时,a 1=S 1=4=4×1,4分 所以数列{a n }的通项公式为a n =4n .6分(2)由点(b n ,a n )在函数y =log 2 x 的图象上得a n =log 2b n ,且a n =4n ,8分 所以b n =2a n =24n=16n,故数列{b n }是以16为首项,公比为16的等比数列,10分 所以T n =-16n1-16=16n +1-1615.12分 8.已知等差数列{a n }的公差为2,其前n 项和为S n =pn 2+2n ,n ∈N *. (1)求p 的值及a n ;(2)在等比数列{b n }中,b 3=a 1,b 4=a 2+4,若等比数列{b n }的前n 项和为T n ,求证:数列⎩⎨⎧⎭⎬⎫T n +16为等比数列.[解] (1)由已知可得a 1=S 1=p +2,S 2=4p +4,即a 1+a 2=4p +4,∴a 2=3p +2.2分 由已知得a 2-a 1=2p =2,∴p =1,∴a 1=3,∴a n =2n +1,n ∈N *.4分(2)证明:在等比数列{b n }中,b 3=a 1=3,b 4=a 2+4=9,则公比为b 4b 3=3.由b 3=b 1·32,得b 1=13,∴数列{b n }是以13为首项,以3为公比的等比数列,7分∴T n =13-3n1-3=16·(3n-1),8分 即T n +16=16×3n =12×3n -1.9分又∵T 1+16=12,T n +16T n -1+16=3,n ≥2,n ∈N *,10分∴数列⎩⎨⎧⎭⎬⎫T n +16是以12为首项,以3为公比的等比数列.12分。
2017届高三数学二轮复习高考小题专攻练4数列理
高考小题专攻练 4.数列小题强化练,练就速度和技能,掌握高考得分点!一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知{a n}为等差数列,a1+a3+a5=105,a2+a4+a6=99,则a20=( )A.-1B.1C.3D.7【解析】选B.因为a1+a3+a5=105,即3a3=105,所以a3=35.同理可得a4=33,所以公差d=a4-a3=-2,所以a20=a4+(20-4)×d=1.2.等比数列{a n}的前n项和为S n,已知S3=a2+10a1,a5=9,则a1等于( )A. B.- C. D.-【解析】选C.设等比数列{a n}的公比为q,由S3=a2+10a1得a1+a2+a3=a2+10a1,即a3=9a1,所以q2=9,又a5=a1q4=9,所以a1=.3.在等比数列{a n}中,若a4,a8是方程x2-4x+3=0的两根,则a6的值是( )A. B.- C.± D.±3【解析】选A.依题意得,a4+a8=4,a4a8=3,故a4>0,a8>0,因此a6>0(注:在一个实数等比数列中,奇数项的符号相同,偶数项的符号相同),a6==.4.等差数列{a n}中,a1>0,公差d<0,S n为其前n项和,对任意自然数n,若点(n,S n)在以下4条曲线中的某一条上,则这条曲线应是( )【解析】选C.因为S n=na1+d,所以S n=n2+n,又a1>0,公差d<0,所以点(n,S n)所在抛物线开口向下,对称轴在y轴右侧.5.设等差数列{a n}的前n项和为S n,S m-1=-2,S m=0,S m+1=3,则m等于( )A.3B.4C.5D.6【解析】选C.由S m-1=-2,S m=0,S m+1=3,得a m=2,a m+1=3,所以d=1,因为S m=0,故ma1+d=0,故a1=-,因为a m+a m+1=5,故a m+a m+1=2a1+(2m-1)d=-(m-1)+2m-1=5,即m=5.6.已知数列{a n}的通项公式是a n=,其前n项和S n=,则项数n等于( )A.13B.10C.9D.6【解析】选D.因为a n=1-,所以S n=+++…+=n-=n-=n-1+.因为S n=,所以n-1+==5+,所以n=6.7.下面是关于公差d>0的等差数列{a n}的四个命题:p1:数列{a n}是递增数列;p2:数列{na n}是递增数列;p3:数列是递增数列;p4:数列{a n+3nd}是递增数列.其中的真命题为( )A.p1,p2B.p3,p4C.p2,p3D.p1,p4【解析】选D.设a n=a1+(n-1)d=dn+a1-d,它是递增数列,所以p1为真命题;若a n=3n-12,则满足已知,但na n=3n2-12n并非递增数列,所以p2为假命题;若a n=n+1,则满足已知,但=1+是递减数列,所以p3为假命题;a n+3nd=4dn+a1-d,它是递增数列,所以p4为真命题.8.在等差数列{a n}中,满足3a4=7a7,且a1>0,S n是数列{a n}前n项的和,若S n取得最大值,则n= ( )A.7B.8C.9D.10【解析】选 C.设公差为d,由题设3(a1+3d)=7(a1+6d),所以d=-a1<0.解不等式a n>0,即a1+(n-1)>0,所以n<,则n≤9,当n≤9时,a n>0,同理可得n≥10时,a n<0.故当n=9时,S n取得最大值.9.已知函数f(x)是定义在R上的单调增函数且为奇函数,数列{a n}是等差数列,a1009>0,则f(a1)+f(a2)+f(a3)+…+f(a2016)+f(a2017)的值( )A.恒为正数B.恒为负数C.恒为0D.可正可负【解析】选A.因为{a n}是等差数列,所以a1+a2017=a2+a2016=…=2a1009>0,得a1>-a2017,a2>-a2016,…,又f(x)是定义在R上的单调增函数,且f(-x)=-f(x),所以f(a1)>-f(a2017),即f(a1)+f(a2017)>0,同理,f(a2)+f(a2016)>0,…,所以f(a1)+f(a2)+…+f(a2016)+f(a2017)的值恒为正数.10.已知数列{a n}的通项公式为a n=(-1)n(2n-1)·cos+1(n∈N*),其前n项和为S n,则S60= ( )A.-30B.-60C.90D.120【解析】选D.由题意可得,当n=4k-3(k∈N*)时,a n=a4k-3=1;当n=4k-2(k∈N*)时,a n=a4k-2=6-8k;当n=4k-1(k∈N*)时,a n=a4k-1=1;当n=4k(k∈N*)时,a n==8k.所以a4k-3+a4k-2+a4k-1+=8,所以S60=8×15=120.11.已知f(x)=x+1,g(x)=2x+1,数列{a n}满足a1=1,a n+1=则a2016= ( )A.22016-2016B.21007-2016C.22016-2D.21009-2【解析】选D.a 2n+2=a2n+1+1=(2+1)+1=2+2.即a2n+2+2=2(+2),所以{+2}是以2为公比,a 2+2=4为首项的等比数列.所以+2=4×2n-1=2n+1.所以=2n+1-2.所以a2016=21009-2.12.设函数f1(x)=x,f2(x)=log2016x,a i=(i=1,2,…,2016),记I k=|f k(a2)-f k(a1)|+|f k(a3)-f k(a2)|+…+|f k(a2016)-f k(a2015)|,k=1,2,则( )A.I1<I2B.I1=I2C.I1>I2D.I1与I2的大小关系无法确定【解析】选A.依题意知,f1(a i+1)-f1(a i)=a i+1-a i=-=,因此I1=|f1(a2)-f1(a1)|+|f1(a3)-f1(a2)|+…+|f1(a2016)-f1(a2015)|=.因为f2(a i+1)-f2(a i)=log2016a i+1-log2016a i=log2016-log2016>0,所以I2=|f2(a2)-f2(a1)|+|f2(a3)-f2(a2)|+…+|f2(a2016)-f2(a2015)|=+(log2016-log2016)+…+=log2016-log2016=1,因此I1<I2.二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.在等差数列{a n}中,已知log2(a5+a9)=3,则等差数列{a n}的前13项的和S13=________. 【解析】因为log2(a5+a9)=3,所以a5+a9=23=8.所以S13====52.答案:5214.已知等差数列{a n}中,a1,a99是函数f(x)=x2-10x+16的两个零点,则a50+a20+a80=________. 【解析】依题意a1+a99=10,所以a50=5.所以a50+a20+a80=a50+2a50=.答案:15.数列{a n}的通项公式a n=,若{a n}的前n项和为24,则n=________.【解析】a n==-.所以(-1)+(-)+…+(-)=24,所以=25,所以n=624.答案:62416.对正整数n,设曲线y=x n(1-x)在x=2处的切线与y轴交点的纵坐标为a n,则的前n项和是________.【解析】曲线y=x n(1-x)=x n-x n+1,曲线导数为y′=nx n-1-(n+1)x n,所以切线斜率为k=n2n-1-(n+1)2n=-(n+2)2n-1,切点为(2,-2n),所以切线方程为y+2n=-(n+2)2n-1(x-2),令x=0得,y+2n=(n+2)2n,即y=(n+1)2n,所以a n=(n+1)2n,所以=2n,所以数列是以2为首项,q=2为公比的等比数列,所以S n==2n+1-2.答案:2n+1-2。
2017高考数学文科二轮复习对点练:第一部分 专题四 数
第一部分 专题四 第1讲1.在等差数列{a n }中,若a 2=4,a 4=2,则a 6=( B ) A .-1 B .0 C .1D .6解析:设数列{a n }的公差为d ,由a 4=a 2+2d ,a 2=4, a 4=2,得2=4+2d ,d =-1,∴a 6=a 4+2d =0.故选B.2.已知等比数列{a n }满足a 1=3,a 1+a 3+a 5=21,则a 3+a 5+a 7=( B ) A .21 B .42 C .63D .84解析:设{a n }的公比为q ,由a 1=3,a 1+a 3+a 5=21得1+q 2+q 4=7,解得q 2=2(负值舍去).∴a 3+a 5+a 7=a 1q 2+a 3q 2+a 5q 2=(a 1+a 3+a 5)q 2=21×2=42.3.已知{a n }是等差数列,公差d 不为零,前n 项和是S n .若a 3,a 4,a 8成等比数列,则( B )A .a 1d >0,dS 4>0B .a 1d <0,dS 4<0C .a 1d >0,dS 4<0D .a 1d <0,dS 4>0解析:由a 24=a 3a 8,得(a 1+2d )(a 1+7d )=(a 1+3d )2,整理得d (5d +3a 1)=0,又d ≠0,∴a 1=-53d ,则a 1d =-53d 2<0, 又∵S 4=4a 1+6d =-23d , ∴dS 4=-23d 2<0,故选B.4.在等差数列{a n }中,若a 3+a 4+a 5+a 6+a 7=25,则a 2+a 8=__10__. 解析:利用等差数列的性质可得a 3+a 7=a 4+a 6=2a 5, 从而a 3+a 4+a 5+a 6+a 7=5a 5=25, 故a 5=5,所以a 2+a 8=2a 5=10.5.已知数列{a n }是递增的等比数列,a 1+a 4=9,a 2a 3=8,则数列{a n }的前n 项和等于2n -1.解析:由已知得,a 1a 4=a 2a 3=8,又a 1+a 4=9,解得⎩⎨⎧ a 1=1,a 4=8或⎩⎨⎧a 1=8,a 4=1.而数列{a n }是递增的等比数列,∴a 1<a 4,∴a 1=1,a 4=8,从而q 3=a 4a 1=8,即q =2,则前n 项和S n =a 1(1-q n )1-q=2n-1.6.设S n 是数列{a n }的前n 项和,且a 1=-1,a n +1=S n S n +1,则S n =-1n . 解析:∵a n +1=S n +1-S n ,∴S n +1-S n =S n +1S n , 又由a 1=-1,知S n ≠0, ∴S n +1S n +1S n -S nS n +1S n =1, 即1S n +1-1S n =-1, ∴⎩⎨⎧⎭⎬⎫1S n 是等差数列,且公差为-1, 而1S 1=1a 1=-1,∴1S n=-1+(n -1)×(-1)=-n ,∴S n =-1n .7.(2016·辽宁协作体一模)已知数列{a n }满足(a n +1-1)·(a n -1)=3(a n -a n +1),a 1=2,令b n =1a n -1.(1)证明:数列{b n }是等差数列; (2)求数列{a n }的通项公式.解析:(1)∵1a n +1-1-1a n -1=a n -a n +1(a n +1-1)(a n -1)=13,∴b n +1-b n =13, ∴{b n }是等差数列. (2)由(1)及b 1=1a 1-1=12-1=1,知b n =13n +23,∴a n -1=3n +2,∴a n =n +5n +2.8.已知数列{a n }满足a n +2=qa n (q 为实数,且q ≠1),n ∈N *,a 1=1,a 2=2,且a 2+a 3,a 3+a 4,a 4+a 5成等差数列.(1)求q 的值和{a n }的通项公式; (2)设b n =log 2a 2na 2n -1,n ∈N *,求数列{b n }的前n 项和.解析:(1)由已知,有(a 3+a 4)-(a 2+a 3)=(a 4+a 5)-(a 3+a 4),即a 4-a 2=a 5-a 3, 所以a 2(q -1)=a 3(q -1). 又因为q ≠1,故a 3=a 2=2, 由a 3=a 1·q ,得q =2. 当n =2k -1(k ∈N *)时,a n =a 2k -1=2k -1=2n -12 ;当n =2k (k ∈N *)时,a n =a 2k =2k =2n 2.所以{a n }的通项公式为a n =⎩⎨⎧2n -12,n 为奇数,2n2 ,n 为偶数.(2)由(1)得b n =log 2a 2n a 2n -1=n 2n -1.设{b n }的前n 项和为S n ,则S n =1×120+2×121+3×122+…+(n -1)×12n -2+n ×12n -1,12S n =1×121+2×122+3×123+…+(n -1)×12n -1+n ×12n , 上述两式相减,得12S n =1+12+122+…+12n -1-n 2n =1-12n1-12-n 2n =2-22n -n 2n , 整理得,S n =4-n +22n -1.所以,数列{b n }的前n 项和为4-n +22n -1,n ∈N *. 9.数列{a n }满足:a 1+2a 2+…+na n =4-n +22n -1,n ∈N *.(1)求a 3的值.(2)求数列{a n }的前n 项和T n ;(3)令b 1=a 1,b n =T n -1n +⎝ ⎛⎭⎪⎫1+12+13+…+1n a n (n ≥2),证明:数列{b n }的前n 项和S n 满足S n <2+2ln n .解析:(1)令n =3,a 1+2a 2+3a 3=114,令n =2,a 1+2a 2=2,解得a 3=14. (2)当n =1,a 1=1,当n ≥2,na n =⎝⎛⎭⎪⎫4-n +22n -1-⎝ ⎛⎭⎪⎫4-n +12n -2=n2n -1,∴a n =12n -1(n ≥2),当n =1时代入a 1也满足,故a n =12n -1.所以数列{a n }为等比数列, 所以T n =1-12n1-12=2-12n -1. (3)当n =1时,显然命题成立. 当n ≥2时,∵b n =T n -1n +⎝ ⎛⎭⎪⎫1+12+13+…+1n a n=T n -1n +⎝ ⎛⎭⎪⎫1+12+13+…+1n (T n -T n -1)=⎝ ⎛⎭⎪⎫1+12+13+…+1n T n -⎝ ⎛⎭⎪⎫1+12+13+…+1n -1T n -1, ∴S n =b 1+b 2+b 3+…+b n =1+⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1+12T 2-T 1+⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1+12+13T 3-⎝ ⎛⎭⎪⎫1+12T 2+…+ ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1+12+…+1n T n -⎝ ⎛⎭⎪⎫1+12+…+ 1n -1T n -1=⎝ ⎛⎭⎪⎫1+12+13+…+1n T n =⎝ ⎛⎭⎪⎫1+12+13+…+1n ⎝ ⎛⎭⎪⎫2-12n -1 <2+2⎝ ⎛⎭⎪⎫12+13+…+1n .∵f (x )=1-1x -ln x ,在(1,+∞)为减函数,(可用导数证明) ∴f (x )<f (1)=0,∴1-1x <ln x ,∴1-n -1n <ln nn -1=ln n -ln(n -1),故两边叠加得12+13+…+1n <ln n ,所以S n <2+2⎝ ⎛⎭⎪⎫12+13+…+1n <2+2ln n . 10.(2016·四川成都诊断)已知数列{a n },如果数列{b n }满足b 1=a 1,b n =a n +a n-1,n ≥2,n ∈N *,则称数列{b n }是数列{a n }的“生成数列”.(1)若数列{a n }的通项为a n =n ,写出数列{a n }的“生成数列”{b n }的通项公式; (2)若数列{c n }的通项为c n =2n +b (其中b 是常数),试问数列{c n }的“生成数列”{q n }是否是等差数列,请说明理由;(3)已知数列{d n }的通项为d n =2n +n ,求数列{d n }的“生成数列”{p n }的前n 项和T n .解析:(1)当n ≥2时,b n =a n +a n -1=2n -1, 当n =1时,b 1=a 1=1适合上式, ∴b n =2n -1(n ∈N *). (2)q n =⎩⎨⎧2+b ,n =1,4n +2b -2,n ≥2,当b =0时,q n =4n -2,由于q n +1-q n =4, 所以此时数列{c n }的“生成数列”{q n }是等差数列. 当b ≠0时,由于q 1=c 1=2+b ,q 2=6+2b ,q 3=10+2b , 此时q 2-q 1≠q 3-q 2,所以数列{c n }的“生成数列”{q n }不是等差数列.综上,当b =0时,{q n }是等差数列;当b ≠0时,{q n }不是等差数列. (3)p n =⎩⎨⎧3,n =1,3·2n -1+2n -1,n ≥2,当n >1时,T n =3+(3·2+3)+(3·22+5)+…+(3·2n -1+2n -1), ∴T n =3+3(2+22+23+…+2n -1)+(3+5+7+…+2n -1)=3·2n +n 2-4. 又n =1时,T 1=3,适合上式,∴T n =3·2n +n 2-4.。
2017高考新课标数学理二轮复习配套检测:知识专题大突
名校模拟1.(2016·天津六校联考)设全集U =R ,集合A ={x |x 2-1<0},B ={x |x (x -2)≥0},则A ∩(∁U B )=( )A .{x |0<x <2}B .{x |0<x <1}C .{x |0≤x <1}D .{x |-1<x <0}答案:B 解析:∵A ={x |-1<x <1},B ={x |x ≥2或x ≤0}, ∁U B ={x |0<x <2}, ∴A ∩∁U B ={x |0<x <1}.2.(2016·四川新津中学模拟)已知p :|x +1|≤4,q :x 2<5x -6,则p 是q 成立的( )A .必要不充分条件B .充分不必要条件C .充要条件D .既不充分也不必要条件答案:A 解析:由|x +1|≤4得-5≤x ≤3,由x 2<5x -6得2<x <3,故p :-5,3],q :(2,3),又-5,3](2,3),故选A.3.(2016·湖南师大附中模拟)已知集合P =⎣⎢⎡⎦⎥⎤12,1,Q ={x |(x -a )(x -a -1)<0},则使得P ∩Q ≠∅的一个充分不必要条件是( )A .-1<a <1B .-1<a <0C .-12<a <1D .0<a <1答案:D 解析:由已知得Q =(a ,a +1),又p =⎣⎢⎡⎦⎥⎤12,1, 则P ∩Q ≠∅⇔⎩⎨⎧a <1,a +1>12,即-12<a <1,所以当0<a <1时,P ∩Q ≠∅,反之不然,故选D.4.(2016·云南昆明一中模拟)设命题p :∀x ∈R,3x >2x ,则綈p 为( ) A .∃x 0∈R,3 x 0<2 x 0 B .∃x 0∈R,3 x 0≤2 x 0 C .∃x 0∈R,3 x 0=2 x 0D .∀x ∈R,3x ≤2x答案:B 解析:綈p :∃x 0∈R,3x 0≤2x 0,故选B.5.(2016·东北师大附中模拟)若命题“∀x ∈R ,ax 2-ax -2<0”是真命题,则实数a 的取值范围是________.答案:(-8,0] 解析:当a =0时,原不等式变形为-2<0,恒成立,符合题意;当a ≠0时,要使不等式恒成立,需满足⎩⎪⎨⎪⎧a <0,Δ=(-a )2-4a ×(-2)<0,解得-8<a <0. 综上,a 的取值范围为(-8,0].。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
名校模拟
1.(2016·江西南昌十所省重点中学二模)已知数列{a n }满足:当p +q =11(p ,q ∈N *,p <q )时,a p +a q =2p ,则数列{a n }的前10项和S 10=( )
A .31
B .62
C .170
D .1 023
答案:B 解析:∵数列{a n }满足:当p +q =11(p ,q ∈N *,p <q )时,a p +a q =2p ,
∴a 1+a 10=2,a 2+a 9=22,a 3+a 8=23,a 4+a 7=24,a 5+a 6=25, ∴数列{a n }的前10项的和S 10=a 1+a 2+…+a 10=2+22+23+24+
25=2×(25-1)2-1
=26-2=62. ∴数列{a n }的前10项和S 10=62.
2.(2016·安徽亳州一中模拟)已知数列{a n },{b n }满足b n =log 2a n ,n
∈N *,其中{b n }是等差数列,且a 8·a 2 008=14,则b 1+b 2+b 3+…+b 2 015
=( )
A .log 22 015
B .2 015
C .-2 015
D .1 008
答案:C 解析:∵数列{a n },{b n }满足b n =log 2a n ,n ∈N *,其中{b n }是等差数列,
∴数列{a n }是等比数列,
由a 8a 2 008=14可得a 21 008=14,即a 1 008=12,
∴a 1a 2 015=a 2a 2 014=…=a 1 007a 1 009=a 21 008=14,
∴b 1+b 2+b 3+…+b 2 015=log 2(a 1a 2…a 2 015)=log 2⎝ ⎛⎭
⎪⎫122 015=-2 015. 3.(2016·河南中原名校联考)已知等比数列{a n }为递增数列,a 1=-2,且3(a n +a n +2)=10a n +1,则公比q =________.
答案:13 解析:因为等比数列{a n }为递增数列且a 1=-2<0,所以
公比0<q <1.又因为3(a n +a n +2)=10a n +1,两边同除以a n ,得3(1+q 2)=
10q ,即3q 2
-10q +3=0,解得q =3或q =13,而0<q <1,所以q =13. 4.(2016·湖南四校联考)已知数列{a n }与{b n }满足a n +1-a n =2(b n +1-b n )(n ∈N *).
(1)若a 1=1,b n =3n +5,求数列{a n }的通项公式;
(2)若a 1=6,b n =2n (n ∈N *)且λa n >2n +n +2λ对一切n ∈N *恒成立,求实数λ的取值范围.
解:(1)∵b n =3n +5,
∴a n +1-a n =2(b n +1-b n )=2(3n +8-3n -5)=6, ∴{a n }是等差数列,首项为a 1=1,公差为6,即a n =6n -5.
(2)∵b n =2n ,∴a n +1-a n =2(2n +1-2n )=2n +1, 当n ≥2时,a n =(a n -a n -1)+(a n -1-a n -2)+…+(a 2-a 1)+a 1=2n +2n -1+…+22+6=2n +1+2,
当n =1时,a 1=6,符合上式,∴a n =2n +1+2,由λa n >2n +n +2λ得λ>2n +n 2n +1=12+n 2n +1,当n ≥2时,n 2n +1-n -12n =2-n 2
n +1≤0, ∴当n =1,2时,2n +n 2
+取最大值34,故λ的取值范围为⎝ ⎛⎭⎪⎫34,+∞.。
