基于二、四阶累积量的双模式盲均衡算法
适用于高阶QAM系统的多模盲均衡新算法

adl e e ys t Me q a r r E a e cne ec mpr i e ocr n MAa d D n w rta - ae a S ur E r ( ) f r ovr ne o ae wt t nur t o sd t n e o MS t g c d hhc e C D n S
维普资讯
第 3 卷 第 2期 0 2 0 年 2月 08
电 子
与
信
息
学
报
V_ .0 . 0 3 No 2 1 F b 2 0 e l .0 8
J u n l f e t o is& I f r to e h o o y o r a cr n c o El n o ma i n T c n l g
Ti ha 【等人分别独立提出的常数模算法( MA 由于计 r i 。 c e r】 C 1
算量小及 良好的收敛性能 已广泛 用于高阶 Q AM 系统中 。
本文的 内容安排如下:文章 的第 2节介绍 了文献 『提 出 4 1 的 CMA+S D 算法 ,第 3节介绍 了本文提 出的两种含软判 D
适用 于高阶 Q AM 系统 的多模盲均衡新算法
窦高奇 高 俊
( 海军工程 大学通信 工程 系 武汉 403 ) 303
摘 要 :利 用 QA 信 号星 座 图特 点 ,该 文 提 出 了两种 含 软 判 决 的多 模盲 均 衡算 法 :MMA+ DD 算 法 和 M S
适用于高阶QAM信号的双模式分数间隔盲均衡

适用于高阶QAM信号的双模式分数间隔盲均衡王乐平【摘要】为了克服常数模算法收敛速度慢稳态误差大的缺点,利用高阶QAM信号分布在多个不同模值上的特点,提出了一种适用于高阶QAM信号的双模式分数间隔盲均衡算法.该算法采用T/2分数间隔结构,并以常数模算法为基础模式,而在第二模式中采用一种多模算法,且通过判决条件对均衡器的输出信号进行判决,使均衡器能在多个模值中自动切换.计算机仿真实验结果表明新方法具有快收敛速度和低稳态误差.【期刊名称】《江西科学》【年(卷),期】2011(029)003【总页数】4页(P399-402)【关键词】常数模算法;双模式;盲均衡【作者】王乐平【作者单位】南昌大学共青学院,江西共青城332020【正文语种】中文【中图分类】TP391.90 前言在带宽受限的传输信道中进行高速数字通信时,多径传播会导致严重的码间干扰(Inter-symbol interference,ISI)使传输信号发生畸变,并在接收端产生误码。
为克服ISI需采用自适应均衡技术。
不同于传统的自适应均衡,盲均衡不需要预先知道信道的特性,也无需周期地给出训练序列,对信道的先验知识要求低,对信道的利用率更高,因而更适合高速通信。
在盲均衡技术中,常数模算法(Constant modulus algorithm,CMA)应用最为广泛,且非常适用于如BPSK和QPSK等模值为常数的信号。
然而当需要较高通信速率时,需要采用信道利用率较高的信号形式,如正交幅度调制信号(QAM)[1]。
QAM信号分布在多个模值所对应的圆上,即其信号模值不为常数,所以将该类信号称之为非常模信号。
CMA不但适用于常模信号,而且还适用于上述非常模信号。
在一些理想环境中,对于常模信号CMA 可以实现理想(迫零)均衡,但是对于非常模信号CMA稳态均方误差(Mean square error,MSE) 无法至零[2,3]。
因此CMA虽可对其稳定收敛,但是收敛速度慢,稳态误差大。
【CN109672462A】基于四阶累积量的二维天线阵列空域滤波方法【专利】

( 12 )发明专利申请
(21)申请号 201910036644 .9
(22)申请日 2019 .01 .15
()申请人 西安电子科技大学 地址 710071 陕西省西安市太白南路2号
(72)发明人 相征 李桥 任鹏 常子豪
(74)专利代理机构 西安嘉思特知识产权代理事 务所(普通合伙) 61230
3
CN 109672462 A
说 明 书
1/6 页
基于四阶累积量的二维天线阵列空域滤波方法
技术领域 [0001] 本发明属于信号处理技术领域,具体涉及一种基于四阶累积量的二维天线阵列空 域滤波方法。
背景技术 [0002] 空域滤波,亦称自适应波束成形,是阵列信号处理的一个主要部分,其实质是通过 对各阵元加权进行空域滤波 ,以达到增强期望信号、抑制干扰信号的目的 ,而且可以根据信 号环境的变化自适应地改变各阵元的加权因子。 [0003] 一维天线阵列可以在空域滤波中解决信源方向为一维波达方向的情况,一维波达 方向为θk,其中k=1 ,2 ,… ,K表示第k个信源,其中θk表示第k个信源的来波方向。二维天线阵 列是所有阵元分布在x-y平面上的阵列,可以在空域滤波中解决信源方向为二维波达方向 的情况,二维波达方向为(θk ,φk) ,其中k=1 ,2 ,… ,K表示第k个信源,其中θk和φk分别表示 第k个信源的俯仰角与方位角。四阶累积量是高阶统计量的一种,描述了随机过程的数字特 征,其应用在阵列天线中可以扩展出虚拟阵元,增加阵列天线的有效数量,提升天线阵列自 由度,从而可以利用新产生的阵元去产生更多的零陷,即抗更多的干扰。 [0004] 二维天线阵列在工作过程中,会接收来自空间中的窄带远场信号,包括期望信号 和干扰信号。期望信号是希望接收的 信号 ,干扰信号则是需要在空域滤波过程中滤除的 信 号。零陷指使 用算法在干扰信号处将干扰信号的幅值增益降 到一个很低的水平 ,与此同时 , 期望信号方向处的幅值增益不会受到影响 ,从而达到抑制干扰信号的目的。 [0005] 目前,都是针对于一维天线阵列使用四阶累积量进行扩展,之后再进行空域滤波, 若直接对二维天线阵列进行空域滤波处理,则当干扰信号与期望信号数量之和大于二维天 线阵列的阵元数目时,空域滤波会完全失效。
【计算机仿真】_盲均衡_期刊发文热词逐年推荐_20140723
推荐指数 3 1 1 1 1 1 1 1 1
2012年 序号 1 2 3 4 5 6 7 8
2012年 科研热词 盲均衡 水声信道 遗传算法 神经网络 码间干扰 水声通信 常数模 分数间隔 推荐指数 3 2 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
推荐指数 6 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3
2009年 科研热词 过采样 盲辨识 盲均衡 推荐指数 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9
科研热词 盲均衡 遗传算法 神经网络 收敛速度 后验概率 同相关状态 双模常模算法 卡尔曼滤波 代价函数
科研热词 盲均衡 水声信道 遗传算法 蚁群优化 自适应软约束常模算法 码间干扰 水声通信 正交幅度调制信号 正交小波变换 果蝇算法 常模盲均衡算法 双模式 动量粒子群优化 代价函数
推荐指数 4 2 1 1 1 1 1 1 1 1 1 1 1 1
2014年 序号 1 2 3 4
科研热词 遗传算法 水声信道 时变 多途环境
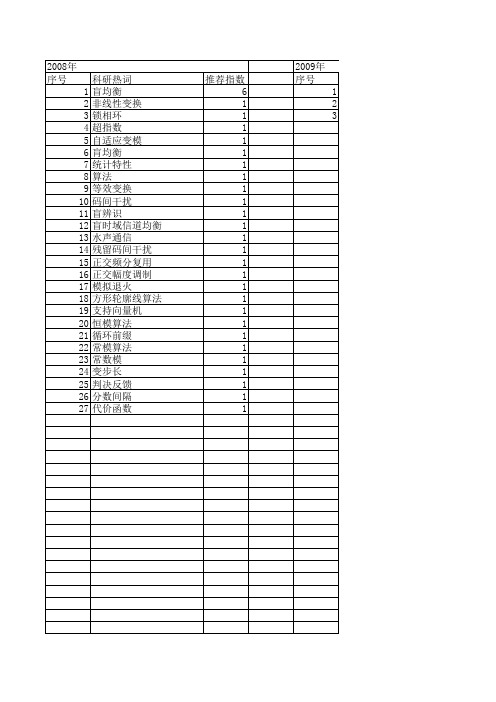
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
科研热词 盲均衡 非线性变换 锁相环 超指数 自适应变模 肓均衡 统计特性 算法 等效变换 码间干扰 盲辨识 盲时域信道均衡 水声通信 残留码间干扰 正交频分复用 正交幅度调制 模拟退火 方形轮廓线算法 支持向量机 恒模算法 循环前缀 常模算法 常数模 变步长 判决反馈 分数间隔 代价函数
利用子空间算法实现一类盲均衡的方法

单输入单输出 ( <TUV) 系统盲均衡十分典型的算法, 笔者将子空间算法从 <TUV 系统推广到信道长度相同的 UTUV 系统, 从 <TUV 子空间算法可知盲辨识就是消除 ST9 效应, 因此在 UTUV 系统中可先消除 ST9 效应, 使
!"#
&
(1)
% 利用输出 $ ( $)的 二 阶 统 计 信 息, 估 计 出 传 输 矩 阵 %3 或 者 包 含 所 有 因 数 的 矩 阵 % # [% (&) , …, # # % % % ( () ], 然后通过式 ( ) )的逆过程均衡出输入 4 ( $) ) 为了进行算法推导, 在此进行如下假设:
8 5 (# ( $)# ( $) ) , "( 6 * )
( 29 )输出数目大于输入数目, 即 * 7 +)
!" #$#% 系统的盲均衡
传输矩阵 % 3 为一个 *+,-"./"0 矩阵, 所以在利用子空间方法估计信道时可以考虑应用 *+,-"./"0 矩阵的性 质7 有理子空间是与 *+,-"./"0 矩阵的性质相关的一个重要的理论, 它可以很好地解释 *:;< 系统的子空间方 法, 同时也为 ;:;< 系统的子空间方法提供了重要的理论基础7 !" #$ 最小多项式基及其性质
!"#
())
( ! $) ( " $) # ( $) !"# !"# , , ( $)# & ( $ ) ’ ( $ ) 这里 $ # # # # # # # # 分别为输出、 ( ! $ / 3 0 $) ( " $ / 3 / ( 0 $) # ( $ / 3 0 $) 输入及噪声) 传输矩阵 % 3 是一个 3* 2( 3 0() + 的 *+,-"./"0 矩阵: (&) . ($) . & . (&) !"# %3 # # # & & & & … … … … . ( () & … . ( ( / $) . ( () … . (&) & . ($) … . (&) … ’ ) & . ( () &
基于余弦代价函数的双模盲均衡算法

基于仿射投影的CMA盲均衡算法
基于仿射投影的CMA盲均衡算法王琨;刘大茂【摘要】经典 CMA 算法计算复杂度低,性能稳健,但收敛速度慢。
传统的仿射投影算法能够加快算法的收敛速度,但算法复杂度较高点。
针对以上问题,该文将仿射投影思想引入到 CMA 算法,克服了两种算法的缺点,加快了算法的收敛速度,降低了算法的复杂度。
通过实验仿真表明,该算法适用于短波信号的盲均衡,且复杂度较低,收敛速度更快。
%Blind equalization is one of the hot technologies in digital shortwave communication. The Classic Constant Modulus Algorithm is with low complexity and steady performance,but with low convergence speed. Tra-ditional affine projection algorithm can accelerate the convergence rate,but with the higher complexity of thealgo-rithm. To solve the problem,this paper introduces the idea of affine projection to the Constant Modulus Algo-rithm,which overcomes the shortcomings of the first two algorithms,speeds up the convergencerate,reduces the complexity of the algorithm. The simulation results show that the algorithm is suitable for blind equalization of shortwave signals,with less complex and faster convergence.【期刊名称】《绵阳师范学院学报》【年(卷),期】2016(035)002【总页数】3页(P24-26)【关键词】盲均衡算法;仿射投影;CMA 算法;复杂度;收敛速度【作者】王琨;刘大茂【作者单位】阳光学院电子信息工程系,福建福州 350015;福州大学物理与信息工程学院,福建福州 350108【正文语种】中文【中图分类】TN911.5盲均衡技术在现代短波通信中发挥着极其重要的作用,该技术可以在未知训练序列的情况下,只根据接收信号的统计特性,来完成对信号的自适应均衡,是近年来数字通信领域中的研究热点之一.在各种盲均衡算法中,经典CMA算法[1]由于计算复杂度低、均衡能力强,算法稳健,受到广泛的应用,但收敛速度慢,为克服该缺点,经过多年的研究,提出了诸如MCMA、CMA-DD[2]、NCMA-LMS[3]、变步长常数模盲均衡算法[4]等多种改进型算法,这些算法在一定程度上可以加快算法的收敛速度,然而所需要的数据量较多,同时又不能充分的利用信号间的有效信息.而仿射投影算法[5],则通过引入输入信号方向向量的概念,可以重复使用输入信号以提高算法收敛速度,从而达到加快整体收敛速度的目的.本文将仿射投影算法引入到CMA盲均衡算法,加快了收敛速度,并通过实验仿真,取得了不错的效果.定义输入信号为[x(1),x(2),…,x(N)],设仿射投影维数为M,那么输入向量可以表示为:X(k)=[x(k),x(k-1),…,x(k-M+1)] M≤k≤N通过上述,可以看出,传统仿射投影算法的核心是将L+M个数据通过重用成为M 个向量完成一次迭代.但是涉及到矩阵的逆运算,算法比较复杂,不利于实际应用.而经典CMA算法计算复杂度低、方法简单,易于实现,因此,本文将仿射投影算法思想引入到经典CMA中,推导出一种基于仿射投影的CMA盲均衡算法.假设输入数据矩阵为XH(k)=[X(k),X(k-1),…,X(k-L+1)],其中X(k)=[x(k),x(k-1),…,x(k-M+1)] M≤k≤N为输入信号,均衡器系数为W(k)=[w(k),w(k-1),…,w(k-M+1)],则每一次迭代结果为:Y(k)=X(k)W(k)CMA算法中,通过建立代价函数,使代价函数最小代,从而得到最优化的均衡器迭代方法.本文算法中,定义代价函数为每次迭代后每个向量的模值和固定模值R 间的距离,该代价函数为一M×1维向量,可表示为:对每一个向量都经过“最速梯度下降法”进行迭代,即为:(|X(k-i)*W(k)| =(|X(k-i)*W(k)|-R)×(X(k-i)*W(k))X(k-i)T i=1,…,M定义误差向量e(k)为:e(k)=|X(k-i)*W(k)|-R i=1,…,M结合式(8),则可以得到均衡滤波器抽头系数的迭代式为:W(k+1)=W(k)-μXH(k)Y(k)e(k)其中μ为学习步长.该算法提高了信号中的对有效信息的利用率,使其能够在较短的时间内就可以达到收敛,同时通过对比式(12)和式(7)可以发现,经典仿射投影数算法需要每次求矩阵的逆运算,需要很大的计算量,特别是仿射投影维数越多,则矩阵的逆运算的计算量也就越大,严重影响了在实际当中的运用,而本文的算法则是以每次的迭代结果Y(k)替代了经典仿射投影算法的逆运算,大大降低了该算法的计算复杂度.为了验证本文算法在盲均衡中的收敛性能,对基于仿射投影的CMA盲均衡算法和经典CMA算法的收敛速度、收敛精度进行仿真分析.实验条件如下:(1)均衡器抽头系数为11阶,采用中心抽头初始化;(2)信道采用冲激响应为:[0.26,0.93,0.26];(3)采用剩余码间干扰作为度量指标;(4)仿真结果均采用100次蒙特卡罗实验.实验1:采用8PSK信号,仿射投影维数为5阶,信噪比SNR=25 dB,两种算法的仿真曲线分别如图1所示.由图1可以看出,当对8PSK信号进行均衡时,本文算法的收敛速度要快于经典CMA算法的,符合前面的推理.实验2:采用8PSK信号,信噪比SNR=25 dB,仿射投影维数分别为5阶、11阶、17阶,本文算法的仿真图如图2所示.由图2中可以看出,当对8PSK信号进行均衡时,仿射维数不同,则算法的收敛速度和收敛精度也不一样,仿射维数越高,利用数据中的有效信息就越多,收敛速度就越快,但是也存在着收敛精度降低,计算量增加等缺点,在实际应用中,可以选择合适的仿射投影维数,该实验也符合前面的理论分析.本文针对传统仿射投影算法复杂度高、实用性差的问题,以及经典CMA算法收敛速度慢的问题,将仿射投影算法思想引入到经典CMA算法中来,推导出一种基于仿射投影的CMA盲均衡算法.实验仿真表明,该算法明显地加快了收敛速度,提高了实用性.下一步工作是如何将此算法进一步引入到无线体域网中的超宽带接收机中,以期进一步提高其性能.。
适用于高阶QAM信号的双模式分数间隔盲均衡
常数模算 法为基 础模 式 , 第二 模式 中采 用一种 多模 算法 , 而在 且通过 判决条件对均衡 器的输 出信号进行判 决 , 使均衡 器能在 多个模值 中 自 动切 换 。计 算机 仿真 实验结果表 明新方 法具有快收敛速度和低稳 态误差 。
关键词 : 常数模 算法 ; 双模 式; 盲均衡
W ANG L — i g epn
( o gigC l g f aca gU i ri , agi o gighn 30 0P C G nqn o eeo nhn n esy J nx G n qnce g 2 2 R ) l N v t i 3
Ab ta t I r e v ro h lw c n eg n ert n e lrese d ・tt a q aee- sr c :nod rt o ec mete s o v re c aea dt ag ta y・ e me n s u r r o o h s a ・
r ( S ) f ecnt t ouu a o t ( M ) a e / r tnl pcdbn ula o M E o t s n m d l l r m C A , nwT 2Fa i a sae l de az— r o a h s gi h co — i q i
tnsibefrhg — drQ M i asi pooe. hsa o tm Ue eC stebsl i ut l o i o e A s n l s r sd T i l r SSt MA a h aa o a hr g p gi h h
王 乐 平
( 昌大学共青学院 , 南 江西 共青城 322 ) 300
摘要 : 了克服 常数模算 法收敛速 度慢稳 态误 差大 的缺点 , 用 高阶 Q M信 号 分布在 多个不 同模 值上 的特 为 利 A 点 , 出了一种 适用 于高阶 Q M 信号 的双模 式分数 间隔盲均衡 算 法。该算 法采 用 T 2分数 间隔结构 , 以 提 A / 并
面向毫米波应用的一种改进的常数模盲均衡算法
面向毫米波应用的一种改进的常数模盲均衡算法王瑜【摘要】本文面向毫米波零中频架构,针对毫米波系统信道时变性、环境敏感性,以及零中频载波同步性能等问题,对现有的盲均衡算法进行了理论分析,并对CMA、MCMA两种具备工程化意义的算法进行了仿真实验分析.结合毫米波大容量数据高速处理需求,给出了可硬件实现的并行处理方法.最后,针对CMA算法收敛后剩余误差较大的问题进行了改进,结合泄漏算法和高阶累积量思想提出了一种修正的CMA 算法,在与传统CMA算法收敛速度相当的条件下降低了系统的码间干扰.【期刊名称】《现代导航》【年(卷),期】2019(010)002【总页数】6页(P107-112)【关键词】盲均衡;常数模算法;高阶累积量;毫米波【作者】王瑜【作者单位】中国电子科技集团公司数据链技术重点实验室,西安 710068【正文语种】中文【中图分类】TN9110 概述在实际系统中,由于滤波器的有限长度截断和定时采样时刻的偏差,都会造成码间前后拖尾的叠加,从而引起码间串扰。
宽带射频器件和数模转换器件的带内幅相不一致,宽带信道的幅度、相位非线性衰落及多径信道等也会引起码间串扰,这就需要利用均衡技术来消除或减少这些码间串扰并恢复原始信号。
由于实际信道及器件的非线性影响往往是未知的,且信道也是时变的,因此往往需要采用自适应均衡算法来实时更新均衡器系数以消除时变影响。
传统的自适应均衡技术,可以在一定程度上克服码间串扰,但它需要不断发送已知的训练序列,对均衡器进行周期性的训练,从而增加了传输开销,降低了信道利用率。
采用盲均衡信道估计算法,则不需要对均衡器参数进行周期训练,能够大大提高信道利用率。
此外,由于盲均衡算法仅与信号的幅值有关,因此对载波同步的要求有所降低,更利于工程系统实现。
考虑毫米波的信道时变性以及对气候的敏感性,以及低功耗低成本的零中频方案中载波同步较高的实现难度,盲均衡算法是一种理想的选择。
1 自适应均衡器研究现状与算法分类图1 自适应线性均衡器结构均衡器一般可分为三类:第一种是基于最大似然(ML)序列检测准则,从错误概率看是最佳均衡器,但复杂度过高难以实现。
高阶统计量及在阵列信号处理中的应用
高阶统计量及在阵列信号处理中的应用作者:姚泽昊贾瑛卓来源:《电子技术与软件工程》2018年第02期摘要在阵列信号处理方面,通常采用传统MUSIC方法进行信号波达方向估计。
但是在处理非高斯信号时,信号中含有高斯色噪声,采用传统方法难以进行波达方向准确估计。
结合这一问题,本文对高阶统计量及在阵列信号处理中的应用问题展开了分析,发现采用高阶统计量可以有效解决非高斯信号处理问题。
【关键词】高阶统计量阵列信号处理高斯色噪声1 高阶统计量的概念分析对于概率密度f(x)来讲,随机变量x拥有两个特征函数,同时拥有k阶矩、k阶累量。
在随机过程中{x(n)}中,随机变量则拥有r阶矩、r阶累量。
所谓的高阶谱,则是将随机过程k阶累量(k-1)维傅里叶变换当成是随机过程的k阶谱。
在k阶谱定义上,之所以采用k阶累量,主要是由于其能避免高斯有色噪声印象,采用高阶矩容易受到高斯噪声影响。
其次,在独立统计的随机过程之和计算中,总累量为两个随机过程累量之和。
采用该种方法进行加性信号处理,可以轻松完成累量计算。
2 高阶统计量及在阵列信号处理中的应用2.1 阵列信号波达方向估计问题在阵列信号处理方面,需要完成远场信号波达方向估计,以完成信号空间谱估计。
在对波达方向进行估计时,可以采用两大类方法,即参数化方法和基于空间谱方法。
采用参数化方法,需搜索感兴趣参数。
比如采用极大似然法,就能进行参数搜索,以至于导致计算量不断增加。
采用空间谱分析方法,需完成由空间方位构成的谱函数构造,然后通过搜索谱峰完成信号波动方向检测。
2.2 基于四阶累积量的MUSIC方法在阵列信号处理上,过去通常假设噪声或信号服从高斯分布,所以只需要利用二阶统计量就能完成信号处理。
但在实际生活中,多数信号为非高斯分布,比如存在色噪声的非理想均匀线性阵列信号。
针对该类信号,还要采用基于四阶累积量的MUSIC方法,以达到抑制色噪声的目的。
采用该方法,可以借助四阶累积量实现阵列扩展,采用的方法与传统协方差MUSIC 方法相似,但是需要利用四阶累积量噪声子空间完成空间谱函数构造。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
c t ro o r a ie u lntmac i g p e e t d A e HOS a g rt m s t e rv d, a n i i r e n f rno m lz d c mu a t h n r s n e . n w o h i h n de e l i i nd a
仿真结果表明, 双模 式 盲 均 衡算 法 比 由准 则 直接 导 出的 盲 均衡 算 法 误 差 小 , 着 更 优 越 的性 能 。 有
关 键 词 :归一 化 累 积量 : O H S算 法 ; 双模 式 盲 均 衡 算 法 中 图分 类 号 : N 9 1 T 1. 5 文 献 标 识 码 : A 文章 编 号 :0 0 3 3 ( 0 6 .30 2 -4 1 0 . 6 0 2 0 ) .2 20 0
n r l ie u ln o ssi g o e o d a d f u t u ln si r p s d, a d a b i d e u l a in o ma z d c mu a tc n it fs c n n o rh c mu a t s p o o e n n l q ai t n z o
维普资讯
Байду номын сангаас
第 2 5卷第 3期
20 0 6年 0 6月
声
学
技
术
Vo . 5, No3 12 .
Te h c Ac usis c nia l o t c
J n,2 0 u. 06
基 于二 、 四阶累积量 的双模 式盲均衡算法
王华荣 ,王英 民
D ualm ode al - gor t i hm or blnd f i equalz i i at on bas d e on e ond s c and our h de um ul f t or r c ant s
W ANG a r n Hu —o g,W ANG n — n Yi g mi
S 1 W[准则 和 一种 有 约束 条件 的 S 准 则 _ 出盲 均 3 W 2 ] 导
衡算 法 不直接 性 的弊 端 。本文 介绍 了一 种归 一化 累
积量 的盲均衡 准 则 。同 时介绍 了基 于此 准则 导 出 的 通 过线 性 时 不变 系 统 的盲 均 衡算 法 ( O H S算 法 ) 并 ; 将 此 算 法 结 合 传 统 的直 接 判 决 算 法 ( 称 D 简 D算 法 )形 成 了一种 基 于二 阶和 四 阶累积 量 的双模 式盲 ,
( ol eo r eE gneigN r w s r oy c n a U i r t, z 10 2 C i ) C l g e fMai n i r ot et nPlt h i l nv sy Xil7 0 7 , hn n e n h e e c ei o a
Abs r c t a t: Th s p p rc n i e s t e e a ln q lz to r b e o o — ni m y tms A i a e o sd r he g n r lb i d e uaia in p o l m fn n mi mu s se .
均衡 算 法 (u l o eH S算 法 ) d a m d O — 。
练序列 , 获得信道特征 , 以 这将 占用 大 量 并 不 富裕 的水 下 信道 带宽 。而 目前 发展起 来 的盲均 衡技 术可 以不需 要 训 练序 列 .即可 自动跟 踪 通 道 的变 化 , 大
大 减少 对水 下信 道 的带 宽 的 占用 。
i rvd a o tm mpo e l rh gi
(u — o eagrh d a m d o tm) po oe . C m ue i lt n rsl r n ld d t l l i rp sd o p trs ai eut aeicu e o mu o s
c mp r h e f r a eo h r po e g rt m. o a e t e p ro m nc ft e p o s d a o h l i Ke r s:n r a ie u l n ; y wo d o m l d c mu a t HOS a g rt ; a— d z lo hm du lmo e HOS a g rt m i o h l i
信号 盲 均衡 技术 。基 于平 稳信 号盲 均衡 技术 ,针 对
1 引 言
水 声 信道 的 带宽 非 常有 限 , 且存 在 着 严 重 的 多
途 干扰 。这 在很 大 程度 上 限 制 了水 下 通讯 的速 率 。 传 统 的 自适 应 均 衡 技 术 ( MS . 要 发 送 大量 的训 L )需
( 北 工 业 大 学 航 海 学 院 ,西 安 西 707 ) 10 2
摘 要 : 对 S a i i e (W ) 则 和 一种 有 约 束 条 件 的 S 准 则 而 导 出 盲 均 衡 算 法 有 不 直 接 性 的 弊端 , 绍 了一 针 hl. s i S 准 v We t n W 介 种 归 一 化 累 积 量 的 盲均 衡 准 则 。 时介 绍 了基 于 此 准 则 导 出 的 通 过 线 性 时 不 变 系统 的 盲均 衡 算 法 ( O 同 H S算 法 ) 并 将 ; 此 算 法结 合 传 统 的 直接 判 决 算 法 。 成 了一 种 基 于 二 阶 和 四 阶 累积 量 的 双模 式 盲 均 衡 (u 1 d O ) 法 。计算 机 形 d a mo eH S 算 .
