2010年陆丰市八年级数学竞赛
2010年数学竞赛获奖名单

张藩藉 兰彧 唐利彬 唐媛艺 万奇挧
荣县中学 荣县中学 荣县中学 荣 王县 大中 山学 中 学
李劲松 李劲松 李劲松 李劲松 万永利
赵逸飞 钟豪 钟远志 周婧珂 邹俊志
田家炳中学 田家炳中学 江姐中学 自贡28中 解放路中学
第 1 页,共 8 页
周浪 周浪 宋生贵
田华
夏青 谢津宝 徐敏 周慎博 程瑞静 范皓然 高华礼 胡体彬 姜文浩 刘一霖 郑剑 雷茂林 涂小波 晏粮清 余涵知 曾真 郑月 罗钞予 邓青清 邓志聪 龚雅琼 桂源
杨倩
王大山学校: 陈 勇 自贡34中: 邵丹银 回龙中学: 王 浩
邱彦 李杭雨 曹 罗
旭川中学: 范婷婷 自贡11中: 张 杰
熊智临 何 浩
陈雨佳
自贡18中: 李 雪
仙市中学:
王杨嵌 宇
赖弈昆 钟慧 聂檄晨
陈静 邹胜 李祥林
管其舜 邱柏森 何 倩
江 雪 付程晗 李志超 富顺二职中: 舒 俊 童寺中心校: 郭 桃 长滩乡中: 伍晋衡
指导教师 田华 周浪 周勇 李劲松 周浪 范其金 王小惠 李劲松 魏明全 李劲松 李劲松
代高声
全国二等奖(74人)
姓名
刘书言 倪雪珂 涂珊珊 李昕 邓棼木 郝祎婷 梁茂 胡采曦 王银季 赵梓涵
学校
荣县中学 自贡28中 自 解贡 放1路9中中 学 解放路中 学 荣县中学 板 解桥 放中 路学 中 学 蜀光中学 荣县中学
杰 张光雨 刘雨杰
周锋
古文强 周夕寒
钟春燕 徐娜
金珂 杜丽双 黄蓉
曾彦俊 刘庆宇 高逸雯 赵梦寒 刘郑健 喻晨峰
王俊杰 项瑞麟 车怡 朱寒迪 刘钰婷 罗凌杰
朱寒迪 蒋沁吟 陈衍瑜 余唯唯 刘洋铭 邹森
中山市2010年初中数学竞赛试卷及答案
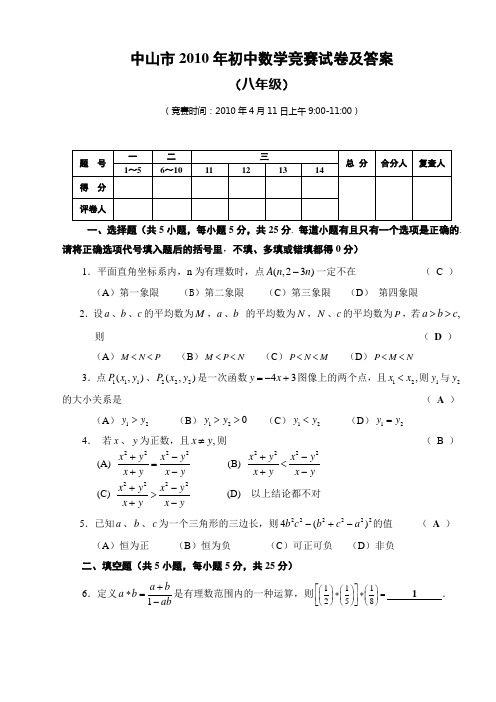
中山市2010年初中数学竞赛试卷及答案(八年级)(竞赛时间:2010年4月11日上午9:00-11:00)一、选择题(共5小题,每小题5分,共25分. 每道小题有且只有一个选项是正确的. 请将正确选项代号填入题后的括号里,不填、多填或错填都得0分)1.平面直角坐标系内,n 为有理数时,点(,23)A n n -一定不在 ( C ) (A )第一象限 (B )第二象限 (C )第三象限 (D ) 第四象限2.设a 、b 、c 的平均数为M ,a 、b 的平均数为N ,N 、c 的平均数为P ,若,a b c >> 则 ( D ) (A )M N P << (B )M P N << (C )P N M << (D )P M N << 3.点111(,)P x y 、222(,)P x y 是一次函数43y x =-+图像上的两个点,且12,x x <则1y 与2y 的大小关系是 ( A )(A )12y y > (B )120y y >> (C )12y y < (D )12y y =4. 若x 、y 为正数,且,x y ≠则 ( B )(A) 2222x y x y x y x y +-=+- (B) 2222x y x y x y x y+-<+- (C) 2222x y x y x y x y+->+- (D) 以上结论都不对 5.已知a 、b 、c 为一个三角形的三边长,则2222224()b c b c a -+-的值 ( A ) (A )恒为正 (B )恒为负 (C )可正可负 (D )非负 二、填空题(共5小题,每小题5分,共25分) 6.定义1a b a b ab +*=-是有理数范围内的一种运算,则111258⎡⎤⎛⎫⎛⎫⎛⎫**= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦ 1 .7321,a b ==试用a 、b 0.28=5b a. 8.如图,一个六边形的6个内角都是120,其连续四边的长依次是1、9、9、5()cm ,那么这个六边形的周长是 42 cm .9.由n 个相同的小正方体搭成的几何体的视图如图所示,则n = 5 .10.若4360,270(0),x y z x y z xyz --=+-=≠则代数式222222522310x y z x y z +---的值等于 -13 .三、解答题(共4小题,共70分)11.(本题满分15分)设abcde 是一个五位数,其中a 、b 、c 、d 、e 是阿拉伯数字,且<<<a b c d ,试求y a b b c c d d e =-+-+-+-的最大值.解:(1)当d e ≤时,(),(),a b a b b c b c -=---=--(),().c d c d d e d e -=---=--……………(4分)所以()()()()y a b b c c d d e e a =--------=-.……………(6分)因为a e 、只能取0-9这10个数字,且0a ≠,当9,1e a ==时,y 取得最大值为8. ……………(8分)(2)当>d e 时,()()()()2.y a b b c c d d e d a e =------+-=--……………(10分)当9,1,0d a e ===时, y 取得最大值为17. ……………(13分)综上可知, y 的最大值为17. ……………(15分)12.(本题满分15分)已知一次函数y Ax B =+与反比例函数ky x=的图像相交于点(2,3)M 、(4,)N m -.(1)求一次函数y Ax B =+与反比例函数ky x=的解析式; (2)求MON ∆的面积(其中O 为坐标原点).解:(1)因为点(2,3)M 、(4,)N m -在反比例函数k y x =的图像上,所以32k =,4km =-,解得6k =,32m =-……………(2分)于是有3(4,)2N --,……………(3分)又点M 、N 在一次函数y Ax B =+的图像上,所以32342A B A B =+⎧⎪⎨-=-+⎪⎩,………(5分)解得:A =34,B =32,……………(7分)故所求函数解析式为:3342y x =+,6y x=.……………(8分)(2)设直线与x 轴、y 轴相交于P 、Q 两点,易得(2,0)P -,3(0,)2Q …(10分)故MON MOQ QOP PON s s s s =++……(12分)=13222⨯⨯+13222⨯-⨯+13222⨯-⨯-=92……(15分) 13.(本题满分20分)在直角坐标系中,有四个点(8,3),(4,5),(0,),(,)A B C n D m o --,当四边形ABCD 的周长最短时,求mn的值.解:如图,作83A -(,)点关于x 轴的对称点8345A B '---(,),(,)点关于y 轴的对称点(45)B ',,……………(4分)连接''A B ,交y 轴于C 点,交x 轴于D 点,则四边形ABCD 的周长最短. ……………(5分) 事实上,设P 是y 轴上任意一点,Q 是x 轴上任意一点,则'''',,,.PB PB QA QA BC B C AD A D ====''''(),AB BP PQ QA AB PB PQ QA AB A B ∴+++=+++>+即''.AB BP PQ QA AB B C CD DA AB BC CD DA +++>+++=+++ 由于P 、Q 的任意性,所以四边形ABCD 的周长最短. ……………(10分) 为了求出C 、D 两点的坐标,要先求出直线''A B 的解析式.设直线''A B 的解析式为y kx b =+,则5438k b k b=+⎧⎨-=-+⎩解得 27,33k b == ∴ 直线''A B 的解析式为2733y x =+……………(15分)令0x =得777,(0,),333y C n =∴= 令0,y =得777,(,0),222x D m =--=-故 3.2m n =-……………(20分)14.(本题满分20分)如图,在四边形ABCD 中,30,60,.ABC ADC AD CD ∠=∠==求证:2()().BD BC BD BC AB +-=DCBA解:过B 作,BE AB ⊥且使,BE BC =连AE 、CE 、AC ,……………(3分) 则22222AE AB BE AB BC =+=+ ①……………(6分)30,ABC ∠=∴ 903060,CBE ∠=-=BCE Δ为等边三角形,……………(8分) ∴ ,60,BC CE BCE =∠=……………(10分)又 60,,ADC AD CD ∠==∴ ADC 为等边三角形,……………(12分) ∴ ,60,DC AC ACD =∠=……………(15分)在BDC 与EAC 中,,,60.DC AC BC CE BCD ACB ECA ==∠=+∠=∠ ∴ .BDC EAC ≅……………(18分)于是.BD AE =结合①式,得222.BD AB BC =+即2()().BD BC BD BC AB +-=……………(20分)。
2010年浙江省温州四中“摇篮杯”八年级数学竞赛初赛试卷(解析版)

2010年浙江省温州四中“摇篮杯”八年级数学竞赛初赛试卷一、选择题1.(3分)把足够大的一张厚度为0.1mm的纸连续对折,要使对折后的整叠纸总厚度超过20mm,至少要对折()A.6次 B.7次 C.8次 D.9次2.(3分)小明同学从运动场的A点出发,向东走8米到达B点,再向北走10米到达C点,再向西走4米到达D点,再向南走7米到达E点.则E、A两点相距()米.A.3 B.4 C.5 D.63.(3分)初二(2)班有42名同学,其中有男同学n名,将他们编成1号、2号、…,n号.在寒假期间,1号给3名同学打过电话,2号给4名同学打过电话,3号给5名同学打过电话,…,n号同学给一半同学打过电话,由此可知该班女同学的人数是()A.22 B.23 C.24 D.254.(3分)初二(1)班有37名学生,其中参加数学竞赛的有30人,参加物理竞赛的有20人,有4人没有参加任何一项竞赛,则同时参加这两项竞赛的学生共有()人.A.16 B.17 C.18 D.195.(3分)A、B、C三种服装的进价分别是20元、30元、40元,售价分别是24元、m元、52元,经核算,三种服装的总利润相同,且A、B两种服装的销售量之和C服装销售量的4倍,则m=()A.35 B.40 C.42 D.446.(3分)如果时钟上的时针、分针和秒针都是匀速地转动,那么从1时整(1:00)开始,在1分钟的时间内,3根针中,出现一根针与另外两根针所成的角相等的情况有()A.1次 B.2次 C.3次 D.4次7.(3分)某工厂今年计划产值为a万元,比去年增长11%.如果今年实际产值可超过计划1%,那么实际产值将比去年增长()A.11% B.11.1% C.12% D.12.11%8.(3分)某学校有小学六个年级,每个年级6个班;初中三个年级,每个年级8个班;高中三个年级,每个年级12个班.现要从中抽取36个班做调查研究,使得各种类型的班级抽取的比例相同,那么初中每个年级抽取()个班.A.1 B.2 C.3 D.49.(3分)钟面上有十二个数1,2,3,…,12.将其中某些数的前面添上一个负号,使钟面上所有数之代数和等于零,则至少要添n个负号,这个数n是()A.4 B.5 C.6 D.710.(3分)A,B,C,D四人参加某一期的体育彩票兑奖活动,现已知:如果A 中奖,那么B也中奖:如果B中奖,那么C中奖或A不中奖:如果D不中奖,那么A中奖,C不中奖:如果D中奖,那么A也中奖则这四个人中,中奖的人数是()A.1 B.2 C.3 D.411.(3分)如果有2002名学生排成一列,按1,2,3,4,5,4,3,2,1,2,3,4,5,…的规律报数,那么第2002名学生所报的数是()A.1 B.2 C.3 D.412.(3分)跳格游戏如图:人从格外进入格中,每次可向前跳1格或2格,那么人从格外跳到第6格可以有()种方法.A.6 B.8 C.13 D.1513.(3分)A、B、C、D四个盒子中分别入有6,4,5,3个球,第一个小朋友找到放球最少的盒子,从其他盒子中各取1个球放入这个盒子中,然后第二个小朋友又找到放球最少的盒子,从其他盒子中各取1个球放入这个盒子…如此进行下去,当第2010个小朋友放完后,A、B、C、D四个盒子中的球数依次是()A.3,5,6,4 B.4,6,3,5 C.5,3,4,6 D.6,4,5,314.(3分)在体育活动中,初二(1)班的n个学生围成一圈做游戏,与每个学生左右相邻的两个学生的性别不同.则n的取值可能是()A.43 B.44 C.45 D.4615.(3分)古人用天干和地支记序,其中天干有10个;甲乙丙丁戊己庚辛壬癸,地支有12个;子丑寅卯辰巳午未申酉戌亥,将天干的10个汉字和地支的12个汉字对应排列成如下两行;甲乙丙丁戊己庚辛壬癸甲乙丙丁戊己庚辛壬癸甲乙丙丁…子丑寅卯辰巳午未申酉戌亥子丑寅卯辰巳午未申酉戌亥…从左向右数,第1列是甲子,第2列是乙丑,第3列是丙寅…,我国的农历纪年就是按这个顺序得来的,如公历2007年是农历丁亥年,那么从今年往后,农历纪年为甲亥年的那一年在公历中()A.是2019年B.是2031年C.是2043年D.没有对应的年号16.(3分)初二某班有33位同学,他们之间的年龄最多相差3岁,若按生肖分组,那么人数最多的一组中至少有同学()位.A.5 B.8 C.9 D.1017.(3分)小杨在商店购买了a件甲种商品,b件乙种商品,共用213元,已知甲种商品每件5元,乙种商品每件19元,那么a+b的最大值是()A.37 B.27 C.23 D.2018.(3分)10个人围成一圈做游戏.游戏的规则是:每个人心里都想一个数,并把目己想的数告许与他相邻的两个人,然后每个人将与他相邻的两个人告诉他的数的平均数报出来,若报出来的数如图所示,则报出来的数是3的人心里想的数是()A.2 B.﹣2 C.4 D.﹣419.(3分)甲、乙、丙、丁4人打靶,每人打4枪,每人各自中靶的环数之积都是72(中靶环数最高为10),且4人中靶的总环数恰为4个连续整数,那么,其中打中过4环的人数为()A.0 B.1 C.2 D.320.(3分)某靶场有红、绿靶标共100个,其中红靶标的数量不到绿靶标数量的三分之一,若打中一个红靶标得10分,打中一个绿靶标得8.5分,小明打中了全部绿靶标和部分红靶标,在计算他所得的总分时,发现总分与红靶标的总数无关(包括打中的和没有打中的),则靶场有红靶标()个.A.22 B.20 C.18 D.162010年浙江省温州四中“摇篮杯”八年级数学竞赛初赛试卷参考答案与试题解析一、选择题1.(3分)把足够大的一张厚度为0.1mm的纸连续对折,要使对折后的整叠纸总厚度超过20mm,至少要对折()A.6次 B.7次 C.8次 D.9次【解答】解:∵第一次对折后厚度为2×0.1mm,第二次对折后厚度为2×2×0.1mm,第三次对折后的厚度为2×2×2×0.1,mm,…,∴第n次对折后的厚度为2n×0.1mm,∵2n×0.1mm>20mm,∴当n=8时,2n×0.1mm=25.6mm,∴至少要对折8次.故选:C.2.(3分)小明同学从运动场的A点出发,向东走8米到达B点,再向北走10米到达C点,再向西走4米到达D点,再向南走7米到达E点.则E、A两点相距()米.A.3 B.4 C.5 D.6【解答】解:由题意可得图形:延长DE交AB于F点,∵AB=8米,DC=4米,∴AF=8﹣4=4(米),∵BC=10米,DE=7米,∴EF=3米,在Rt△AEF中,AE==5米,故选:C.3.(3分)初二(2)班有42名同学,其中有男同学n名,将他们编成1号、2号、…,n号.在寒假期间,1号给3名同学打过电话,2号给4名同学打过电话,3号给5名同学打过电话,…,n号同学给一半同学打过电话,由此可知该班女同学的人数是()A.22 B.23 C.24 D.25【解答】解:由题意得,一半同学有42÷2=21人,1号给3=2+1名打电话,2号给4=2+2名打电话,3号给5=2+3名打电话,…n号给2+n=21名打电话,所以n=19,即男生有19名,故女生有:42﹣19=23,即该班有女生23名,故选:B.4.(3分)初二(1)班有37名学生,其中参加数学竞赛的有30人,参加物理竞赛的有20人,有4人没有参加任何一项竞赛,则同时参加这两项竞赛的学生共有()人.A.16 B.17 C.18 D.19【解答】解:设同时参加两项竞赛的学生有x人,根据题意可列出方程:37=30+20+4﹣x,解得x=17(人);故选:B.5.(3分)A、B、C三种服装的进价分别是20元、30元、40元,售价分别是24元、m元、52元,经核算,三种服装的总利润相同,且A、B两种服装的销售量之和C服装销售量的4倍,则m=()A.35 B.40 C.42 D.44【解答】解:设A服装销售了x件,B服装销售了y件,则C服装销售了(x+y)件三种服装每件的利润分别是4元、(m﹣30)元、12元,根据题意知:4x=(m﹣30)y=3(x+y),由4x=3(x+y),解得x=3y,代入4x=(m﹣30)y中,解得m=42.故选:C.6.(3分)如果时钟上的时针、分针和秒针都是匀速地转动,那么从1时整(1:00)开始,在1分钟的时间内,3根针中,出现一根针与另外两根针所成的角相等的情况有()A.1次 B.2次 C.3次 D.4次【解答】解:从3时整(3:00)开始,在1分钟的时间内,3根针中,出现一根针与另外两根针所成的角相等的情况有:①当秒针转到大约15°的位置时,以及大约195°的位置时秒针平分时针与分针.②当秒针转到大约60°的位置时,时针平分秒针与分针.③当秒针转到大约330°的位置时,分针平分秒针与时针.综上,共4次.故选:D.7.(3分)某工厂今年计划产值为a万元,比去年增长11%.如果今年实际产值可超过计划1%,那么实际产值将比去年增长()A.11% B.11.1% C.12% D.12.11%【解答】解:∵今年计划产值为a万元,比去年增长11%,∴去年的产值为:a÷(1+11%),∵今年实际产值可超过计划1%,∴今年实际产值为:a×(1+1%)=1.01a,∴所求的增长率=[1.01a﹣a÷(1+11%)]÷[a÷(1+11%)]×100%=12.11%.故选:D.8.(3分)某学校有小学六个年级,每个年级6个班;初中三个年级,每个年级8个班;高中三个年级,每个年级12个班.现要从中抽取36个班做调查研究,使得各种类型的班级抽取的比例相同,那么初中每个年级抽取()个班.A.1 B.2 C.3 D.4【解答】解:∵小学六个年级,每个年级6个班;初中三个年级,每个年级8个班;高中三个年级,每个年级12个班,∴先算出这个学校总班数一共是6×6+3×8+3×12=96个,∴算出抽到初中一个班的概率为:=,∴初中每个年级抽取×8=2个班.故选:B.9.(3分)钟面上有十二个数1,2,3,…,12.将其中某些数的前面添上一个负号,使钟面上所有数之代数和等于零,则至少要添n个负号,这个数n是()A.4 B.5 C.6 D.7【解答】解:因为1+2+3+…+11+12=78,所以78÷2=39,也就是添上负号的数的和为﹣39,其余数的和为39使代数和等于零,要填负号最少,首先从大数前面加负号,因此﹣10﹣11﹣12=﹣33,﹣33﹣6=﹣39,由此得到至少要添4个负号.故选:A.10.(3分)A,B,C,D四人参加某一期的体育彩票兑奖活动,现已知:如果A 中奖,那么B也中奖:如果B中奖,那么C中奖或A不中奖:如果D不中奖,那么A中奖,C不中奖:如果D中奖,那么A也中奖则这四个人中,中奖的人数是()A.1 B.2 C.3 D.4【解答】解:根据题意,可将已知条件大致分为三类:(为叙述方便,将中奖简写为“中”)①如果A中,则B中;②如果B中,则C中或A不中;③如果D不中,则A中且C不中;已知了A中且D中,当A中时,由①知:B也中;当B中时,由②知C也中(由于A已中奖,因此A不中的条件可以舍去);因此A、B、C、D四人都中奖了,由此可得出中奖的人数为4人,故选D.11.(3分)如果有2002名学生排成一列,按1,2,3,4,5,4,3,2,1,2,3,4,5,…的规律报数,那么第2002名学生所报的数是()A.1 B.2 C.3 D.4【解答】解:∵根据题意可知,每8个同学为一个循环,2002÷8=250…2.∴第2002名学生所报的数是2,故选:B.12.(3分)跳格游戏如图:人从格外进入格中,每次可向前跳1格或2格,那么人从格外跳到第6格可以有()种方法.A.6 B.8 C.13 D.15【解答】解:每次只跳一格的,只有1种;仅有一次跳2格,有5种:跳1,2;跳2,3;跳3,4;跳4,5;跳5,6;仅有两次跳2格的,其余每次跳一格的,有6种:跳1,2和跳3,4;跳1,2和跳4,5;跳1,2和跳5,6;跳2,3和跳4,5;跳2,3和跳5,6;跳3,4和跳5,6;每次跳2格的,只有1种;所以:1+5+6+1=13种.故选:C.13.(3分)A、B、C、D四个盒子中分别入有6,4,5,3个球,第一个小朋友找到放球最少的盒子,从其他盒子中各取1个球放入这个盒子中,然后第二个小朋友又找到放球最少的盒子,从其他盒子中各取1个球放入这个盒子…如此进行下去,当第2010个小朋友放完后,A、B、C、D四个盒子中的球数依次是()A.3,5,6,4 B.4,6,3,5 C.5,3,4,6 D.6,4,5,3【解答】解:A B C D原来的球 6 4 5 3第一次 5 3 4 6第二次 4 6 3 5第三次 3 5 6 4第四次 6 4 5 3由此可以看出经过四次,盒子中的球和原来每一个盒子对应球的数相同,又因2010=502×4+2,所以当第2010个小朋友放完后,A,B,C,D四个盒子中的球数和第二个小朋友放完后每一个盒子对应球的数相同为:4,6,3,5.故选:B.14.(3分)在体育活动中,初二(1)班的n个学生围成一圈做游戏,与每个学生左右相邻的两个学生的性别不同.则n的取值可能是()A.43 B.44 C.45 D.46【解答】解:假设有一个学生为男,那么他左边为男,则右边一定为女,这个女生的左边为男生,右边一定是女生,那么排列的可能为男,男,女,女,男,男,女,女,…∵每4个数为一组循环,∴这组学生数应为4的倍数,故选:B.15.(3分)古人用天干和地支记序,其中天干有10个;甲乙丙丁戊己庚辛壬癸,地支有12个;子丑寅卯辰巳午未申酉戌亥,将天干的10个汉字和地支的12个汉字对应排列成如下两行;甲乙丙丁戊己庚辛壬癸甲乙丙丁戊己庚辛壬癸甲乙丙丁…子丑寅卯辰巳午未申酉戌亥子丑寅卯辰巳午未申酉戌亥…从左向右数,第1列是甲子,第2列是乙丑,第3列是丙寅…,我国的农历纪年就是按这个顺序得来的,如公历2007年是农历丁亥年,那么从今年往后,农历纪年为甲亥年的那一年在公历中()A.是2019年B.是2031年C.是2043年D.没有对应的年号【解答】解:∵10与12的最小公倍数为60,∴按照天干与地支组合循环60次后又开始循环.故只要检测这60年即可.可知没有甲亥年.故选:D.16.(3分)初二某班有33位同学,他们之间的年龄最多相差3岁,若按生肖分组,那么人数最多的一组中至少有同学()位.A.5 B.8 C.9 D.10【解答】解:由题意知,33位同学分四个年龄段,构造4个抽屉,33=8×4+1,所以人数最多的一组中至少有同学8+1=9位.故选:C.17.(3分)小杨在商店购买了a件甲种商品,b件乙种商品,共用213元,已知甲种商品每件5元,乙种商品每件19元,那么a+b的最大值是()A.37 B.27 C.23 D.20【解答】解:由题意得,5a+19b=213,∴a=,∴a+b=+b=,∵a+b是关于b的一次函数且a+b随b的增大而减小,∴当b最小时,a+b取最大值,又∵a,b是正整数,∴当b=2时,a+b的最大值=37.故选:A.18.(3分)10个人围成一圈做游戏.游戏的规则是:每个人心里都想一个数,并把目己想的数告许与他相邻的两个人,然后每个人将与他相邻的两个人告诉他的数的平均数报出来,若报出来的数如图所示,则报出来的数是3的人心里想的数是()A.2 B.﹣2 C.4 D.﹣4【解答】解:设报3的人心里想的数是x,则报5的人心里想的数应是8﹣x,于是报7的人心里想的数是12﹣(8﹣x)=4+x,报9的人心里想的数是16﹣(4+x)=12﹣x,报1的人心里想的数是20﹣(12﹣x)=8+x,报3的人心里想的数是4﹣(8+x)=﹣4﹣x,所以得x=﹣4﹣x,解得x=﹣2.故选:B.19.(3分)甲、乙、丙、丁4人打靶,每人打4枪,每人各自中靶的环数之积都是72(中靶环数最高为10),且4人中靶的总环数恰为4个连续整数,那么,其中打中过4环的人数为()A.0 B.1 C.2 D.3【解答】解:∵72=9×4×2×1=8×3×3×1=6×6×2×1=6×3×4×1=6×2×3×2=3×2×3×4=9×8×1×1,共6种情况在这6种情况中,总环数分别为16,15,15,14,13,12因为4人中靶的总环数恰为4个连续整数,所以其中必然包括15,14,13,这三个总环数中只有1个4环;第4个总环数为16或12,其中都会有1个4环.所以总共有2个4环,故选:C.20.(3分)某靶场有红、绿靶标共100个,其中红靶标的数量不到绿靶标数量的三分之一,若打中一个红靶标得10分,打中一个绿靶标得8.5分,小明打中了全部绿靶标和部分红靶标,在计算他所得的总分时,发现总分与红靶标的总数无关(包括打中的和没有打中的),则靶场有红靶标()个.A.22 B.20 C.18 D.16【解答】解:设红靶x个,则绿靶(100﹣x)个,打中红的数目为k,打中了全部绿靶标得分:S=8.5(100﹣x)=850﹣8.5x,又总分=S+10x=85+10k﹣8.5x为一常数,所以10k=8.5x,又由“靶标的数量不到绿靶标数量的三分之一“知:x<即x<25,又x,k为自然数,所以x=20,k=17,即靶场有红靶标20个.故选:B.。
2010年第6届“锐丰杯”初中数学邀请赛试卷(解析版)

2010年第6届“锐丰杯”初中数学邀请赛试卷一、选择题(共6小题,每小题6分,满分36分)1.(6分)水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如图是一个正方体的表面展开图,若图中的“仲”在正方体的后面,则此正方体的前面是()A.仲B.元C.中D.学2.(6分)若ab≠1,且有a2+2010a+6=0及6b2+2010b+1=0,则的值是()A.6 B.C.2010 D.3.(6分)以正方形ABCD的BC边为直径作半圆O,过点D作直线切半圆于点F,交AB边于点E.则三角形ADE和直角梯形EBCD周长之比为()A.3:4 B.4:5 C.5:6 D.6:74.(6分)现有一列数a1,a2,a3,…,a2008,a2009,a2010,其中a2=﹣1,a31=﹣7,a2010=9,且满足任意相邻三个数的和为相等的常数,则a1+a2+a3+…+a98+a99+a100的值为()A.0 B.40 C.32 D.265.(6分)方程(x2+x﹣1)x+3=1的所有整数解的个数是()A.5个 B.4个 C.3个 D.2个6.(6分)如图,直线DE与BC不平行,已知A为线段DE上一点且满足,设△DBC、△ABC、△EBC的面积分别为S1、S2、S3,则满足S1、S2、S3之间的关系式的点A为()A.只能是线段DE的中点B.线段DE的中点和三等分点C.线段DE上除两端点外任意一点都满足D.线段DE上满足n为整数的点二、填空题(共6小题,每小题9分,满分54分)7.(9分)观察下面表格中数字的规律,如果4018在表中排在第m行第n列,则m×n=8.(9分)若函数中自变量的取值范围是一切实数,则实数k的取值范围是.9.(9分)规定一种运算“*”:对于任意实数对(x,y)恒有(x,y)*(x,y)=(x+y+1,x2﹣y﹣1).若实数a,b满足(a,b)*(a,b)=(b,a),则a=,b=.10.(9分)如图,点A、C在反比例函数的图象上,B、D在x轴上,△OAB,△BCD均为正三角形,则点C的坐标是.11.(9分)已知t是实数,若a,b是关于x的一元二次方程x2﹣x+t﹣4=0的两个非负实根,则(a2﹣4)(b2﹣4)的最大值与最小值的差为.12.(9分)如图,一个半径为1的圆纸片,第一次剪去半径为的圆,得到的图形P1的面积为S1,第二次剪去半径为的圆,得到的图形P2的面积为S2,第三次剪去半径为的圆,得到的图形P3的面积为S3,…,依此,第n次剪完后得到的图形P n的面积为S n则S2009﹣S2010=.三、解答题(共3小题,满分60分)13.(20分)学生节活动有一个抽奖节目,给每个游戏者一个均匀色子(正方体,六个面分别是1到6这六个数字),分别丢两次,则朝上一面的两个数字和如果大于或等于10,或者两数字和小于或等于3都算中奖.问:(1)丢两次的数字之和共有多少种不同的和?分别是什么?(2)中奖的概率为多少?14.(20分)△ABC的内切圆分别切BC、CA、AB三边于D、E、F,G是EF上的一点,且DG⊥EF.(1)连接DF、DE,设N、K分别是DF、DE的中点,连接BN、CK.是否存在三个三角形,使得它们彼此都相似,若有写出来;(2)求证:DG平分∠BGC.15.(20分)金秋仲元,绿荫有情,湖水弄波,盛装以待,宾朋汇聚,相约一个共同的庆典﹣﹣2009年广东仲元中学七十五周年华诞.近年来仲元中学共有14位同学荣获理科综合省状元.各学科竞赛国家级、省级奖数不胜数…闪光的奖牌,凝聚着智慧与汗水;诸多的殊荣,彰显厚重与气度.而数字2009在数学上也有着它特别的性质.就如有些自然数可以分成两个自然数的平方和,如:5=12+22,13=22+32,41=42+52,65=42+72,…,请你探究:2009能分成两个自然数的平方和吗?若能,请写出来;若不能,请说明理由.2010年第6届“锐丰杯”初中数学邀请赛试卷参考答案与试题解析一、选择题(共6小题,每小题6分,满分36分)1.(6分)水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如图是一个正方体的表面展开图,若图中的“仲”在正方体的后面,则此正方体的前面是()A.仲B.元C.中D.学【解答】解:∵正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,∴在此正方体上与“仲”相对的面上的汉字是“学”,故“仲”在正方体的后面,则这个正方体的前面是“学”.故选:D.2.(6分)若ab≠1,且有a2+2010a+6=0及6b2+2010b+1=0,则的值是()A.6 B.C.2010 D.【解答】解:由6b2+2010b+1=0得:+2010×+6=0,又a2+2010a+6=0,所以得到a与都为x2+2010x+6=0的两根,根据根与系数的关系得到:a•=6即=6.故选:A.3.(6分)以正方形ABCD的BC边为直径作半圆O,过点D作直线切半圆于点F,交AB边于点E.则三角形ADE和直角梯形EBCD周长之比为()A.3:4 B.4:5 C.5:6 D.6:7【解答】解:根据切线长定理得,BE=EF,DF=DC=AD=AB=BC.设EF=x,DF=y,则在直角△AED中,AE=y﹣x,AD=CD=y,DE=x+y.根据勾股定理可得:(y﹣x)2+y2=(x+y)2,∴y=4x,∴三角形ADE的周长为12x,直角梯形EBCD周长为14x,∴两者周长之比为12x:14x=6:7.故选:D.4.(6分)现有一列数a1,a2,a3,…,a2008,a2009,a2010,其中a2=﹣1,a31=﹣7,a2010=9,且满足任意相邻三个数的和为相等的常数,则a1+a2+a3+…+a98+a99+a100的值为()A.0 B.40 C.32 D.26【解答】解:∵a1+a2+a3=a2+a3+a4,∴a1=a4,同理可得a1=a4=a7=…=a100=a31=﹣7,a2=a5=a8=…=a98=﹣1,a3=a6=a9=…=a99=a2010=9,由各数出现的规律可知,从a1开始到a100的数列中,﹣7出现了34次,﹣1出现了33次,9出现了33次,则a1+a2+a3+…+a98+a99+a100=(﹣7)×34+(﹣1)×33+9×33=26.故选:D.5.(6分)方程(x2+x﹣1)x+3=1的所有整数解的个数是()A.5个 B.4个 C.3个 D.2个【解答】解:(1)当x+3=0,x2+x﹣1≠0时,解得x=﹣3;(2)当x2+x﹣1=1时,解得x=﹣2或1.(3)当x2+x﹣1=﹣1,x+3为偶数时,解得x=﹣1因而原方程所有整数解是﹣3,﹣2,1,﹣1共4个.故选:B.6.(6分)如图,直线DE与BC不平行,已知A为线段DE上一点且满足,设△DBC、△ABC、△EBC的面积分别为S1、S2、S3,则满足S1、S2、S3之间的关系式的点A为()A.只能是线段DE的中点B.线段DE的中点和三等分点C.线段DE上除两端点外任意一点都满足D.线段DE上满足n为整数的点【解答】解:①分别过点D,A,E作DM⊥BC于M,AN⊥BC于N,EF⊥BC于F,∴DM∥AN∥EF,若A是线段DE的中点,∴DA=AE,∴MN=FN,∴AN=(DM+EF),=BC•AN=BC•(DM+EF)=BC•(DM+EF),S△DBC+S△∴S△ABC=BC•DM+BC•EF=BC•(DM+EF),EBC=(S△DBC+S△EBC).∴S△ABC∵DA:AE=1:n,∴n=1.∴S2=(S1+S3).故A是线段DE的中点时成立.②若A是线段DE的三等分点,(如图:E、F是梯形的腰AB、CD的三等分点,则可得:EF=(BC+AD),)同①,可证得:AN=(DM+EF).=BC•AN=BC•(DM+EF),S△DBC+S△EBC=BC•DM+BC•EF=BC•∵S△ABC(DM+EF),∴此时不成立.故A正确,B,C,D错误.故选:A.二、填空题(共6小题,每小题9分,满分54分)7.(9分)观察下面表格中数字的规律,如果4018在表中排在第m 行第n 列,则m ×n= 2010【解答】解:由题意可知,①表中第1行第n 列的数字是2n ﹣1; ②表中第m 行第n 列的数字是2m ﹣1(2n ﹣1);③因为4018=2×2009,又2009=2×1005﹣1,故4018的位置是第2行,第1005列.则m=2,n=1005, m ×n=2×1005=2010. 故答案为:2010.8.(9分)若函数中自变量的取值范围是一切实数,则实数k 的取值范围是.【解答】解:(1)若k=0,y=是常量函数,与x 无关,故k=0符合已知条件. (2)若k ≠0.①当k >0时,由kx 2+4kx +3=k (x +2)2+3﹣4k , ∵k (x +2)2≥0,∴需要3﹣4k >0,即k <. 故0<k <.②当k<0时,有k(x+2)2≤0,需要3﹣4k<0,即k>.与k<0矛盾,说明此种情况不可能成立.故实数k的取值范围是.故答案为:.9.(9分)规定一种运算“*”:对于任意实数对(x,y)恒有(x,y)*(x,y)=(x+y+1,x2﹣y﹣1).若实数a,b满足(a,b)*(a,b)=(b,a),则a=﹣1,b=1.【解答】解:由题意得:,解得,故答案两空分别填﹣1,1.10.(9分)如图,点A、C在反比例函数的图象上,B、D在x轴上,△OAB,△BCD均为正三角形,则点C的坐标是(1+,).【解答】解:如图,过A作AM⊥OB于M,设点A(a,b),则a•b=①,OB=2a,OM=a,AM=b,又△OAB为正三角形,∴AM=OM,∴b=a②,联立①②即可求出a=∴OB=,设点C(m,n),则n=(m﹣),∴m•(m﹣)=,∴m=1+,n=.故答案为:(1+,).11.(9分)已知t是实数,若a,b是关于x的一元二次方程x2﹣x+t﹣4=0的两个非负实根,则(a2﹣4)(b2﹣4)的最大值与最小值的差为.【解答】解:∵a,b是关于x的一元二次方程x2﹣x+t﹣4=0的两个非负实根,∴可得a+b=1,ab=t﹣4≥0,∴t≥4,又△=1﹣4(t﹣4)≥0,可得t≤,∴≥t≥4,又(a2﹣4)(b2﹣4)=(ab)2﹣4(a2+b2)+16=(ab)2﹣4(a+b)2+8ab+16,∴(a2﹣4)(b2﹣4),=(t﹣4)2﹣4+8(t﹣4)+16,=t2﹣4,又∵≥t≥4,∴()2﹣4﹣(42﹣4)=,故答案为:.12.(9分)如图,一个半径为1的圆纸片,第一次剪去半径为的圆,得到的图形P1的面积为S1,第二次剪去半径为的圆,得到的图形P2的面积为S2,第三次剪去半径为的圆,得到的图形P3的面积为S3,…,依此,第n次剪完后得到的图形P n的面积为S n则S2009﹣S2010=.【解答】解:根据题意第n次减去的圆的半径是()n.则S2009﹣S2010=π[()2010]2=.故答案是:.三、解答题(共3小题,满分60分)13.(20分)学生节活动有一个抽奖节目,给每个游戏者一个均匀色子(正方体,六个面分别是1到6这六个数字),分别丢两次,则朝上一面的两个数字和如果大于或等于10,或者两数字和小于或等于3都算中奖.问:(1)丢两次的数字之和共有多少种不同的和?分别是什么?(2)中奖的概率为多少?【解答】解:以第一次丢出的数字为列,第二次丢出的数学为行,则两次丢出数学之和可表示为下面表格(1)由表可知数字之和有:2,3,4,5,6,7,8,9,10,11,12共11种.(2)中奖的情况:小于等于3的有三种,大于等于10的有6种共有9种中奖情况,总共有36种抽奖的结果,所以中奖的概率为.14.(20分)△ABC的内切圆分别切BC、CA、AB三边于D、E、F,G是EF上的一点,且DG⊥EF.(1)连接DF、DE,设N、K分别是DF、DE的中点,连接BN、CK.是否存在三个三角形,使得它们彼此都相似,若有写出来;(2)求证:DG平分∠BGC.【解答】(1)连接DF、DE,设N、K分别是DF、DE的中点,连接BN、CK.则有:Rt△BFN∽Rt△BDN∽Rt△DEG,或Rt△CEK∽Rt△CDK∽Rt△DFG.(2)证明:Rt△BFN∽Rt△DEG,Rt△CEK∽Rt△DFG,∴B F•GE=DF•DE=CE•FG∴,而∠BFG=∠CEG∴△BFG∽△CEG,于是∠BGF=∠CGE.∵DG⊥EF,∴∠BGD=∠CGD.即DG平分∠BGC.15.(20分)金秋仲元,绿荫有情,湖水弄波,盛装以待,宾朋汇聚,相约一个共同的庆典﹣﹣2009年广东仲元中学七十五周年华诞.近年来仲元中学共有14位同学荣获理科综合省状元.各学科竞赛国家级、省级奖数不胜数…闪光的奖牌,凝聚着智慧与汗水;诸多的殊荣,彰显厚重与气度.而数字2009在数学上也有着它特别的性质.就如有些自然数可以分成两个自然数的平方和,如:5=12+22,13=22+32,41=42+52,65=42+72,…,请你探究:2009能分成两个自然数的平方和吗?若能,请写出来;若不能,请说明理由.【解答】解:若能,这两个自然数必然一奇数一偶数.不妨设2009=(2n+1)2+(2m)2(※),∵其中m,n为自然数.化简方程(※)得:m2+n2+n=502①,对方程①进行变形,得如下两个等式:m2=502﹣n(n+1)②与n(n+1)=502﹣m2③,首先,由②式可知,m必然是偶数.∵n和n+1是连续自然数,∴n(n+1)必是偶数,∴502﹣n(n+1)必是偶数.即m2必是偶数,于是m必是偶数.再由③得,502﹣m2≥0,∴0≤m<23.综上可知,m的可取值是2,4,6,8,10,12,14,16,18,20,22.∵n是自然数,∴计算这些方程的根的判别式:△=1+4(502﹣m2),只要找到m取哪些值能使△的值为完全平方数即可.列表如上图:从表可以看出,当m=14时,△是完全平方数.此时自然数n=17,2n+1=35,2m=28.∴2009=352+282.。
2010年全国初中数学联赛南昌市八年级竞赛试卷

2010年全国初中数学联赛南昌市八年级竞赛试卷一、选择题(每题7分,共42分)1.(7分)若a﹣b=m,b﹣c=n,则a2+b2+c2﹣ab﹣bc﹣ca的值是()A.m2+n2+mn B.n2n+n3C.m2n+mn2D.m2n﹣mn22.(7分)已知c<﹣1,a=|c+1|﹣|c|,b=|c|﹣|c﹣1|,那么,a与b的关系是()A.a>b B.a=b C.a≤b D.a<b3.(7分)若n是正整数,下列代数式中,哪一个代数式的值一定不是某个自然数的平方()A.3n2﹣3n+3 B.4n2+4n+4 C.5n2﹣5n﹣5 D.7n2﹣7n+74.(7分)用下列方式表达的各对函数图象相同的是()A.y=与y=()2B.xy=1与y=C.y=︳x︳与y=D.y=x与=15.(7分)若P是边长为2的等边三角形内任一点,则P到这个三角形三边的距离之和是()A.1 B.C.2 D.6.(7分)周长相同的圆、正方形、等边三角形的面积分别为s1、s2、s3,则s1、s2、s3的大小关系是()A.s1>s2>s3B.s1>s3>s2C.s2>s1>s3D.s2>s3>s1二、填空题(每小题7分,共28分)7.(7分)已知直角三角形有一边是11,另两边的长度均为自然数,那么这个三角形的周长是.8.(7分)已知实数a、b满足条件a>0,b>0,且a+b=4,则代数式+的最小值是.9.(7分)如图,已知△ABC,△BCD,△ACD,△ABD的面积分别等于:5,9,10,6;则△AOB的面积=.10.(7分)已知实数p、q满足条件:,则代数式﹣的值为.三、解答题(第11题20分,第12、13题各25分,共70分)11.(20分)(1)分解因式:x7+x5+1(2)对任何正数t,证明:t4﹣t+>0.12.(25分)在平面直角坐标系中,点A坐标为(1,0),在直线y=x上取点P,使△OPA是等腰三角形,求所有满足条件的点P坐标.13.(25分)在n×n的正方形棋盘上,按以下法则放置棋子:如果某小格子上没有棋子,则在过这格的水平线与竖直线上的棋子总数不小于n.求证:在棋盘上的棋子数不少于个.2010年全国初中数学联赛南昌市八年级竞赛试卷参考答案一、选择题(每题7分,共42分)1.A;2.B;3.B;4.B;5.B;6.A;二、填空题(每小题7分,共28分)7.132;8.5;9.2;10.1;三、解答题(第11题20分,第12、13题各25分,共70分)11.;12.;13.;。
青铜峡市五中2010年八年级数学竞赛试题

青铜峡市五中2010年八年级数学竞赛试题一、选择题:(每小题5分,共35分) 1、以下哪个数在2-和1之间 [ D ]A 、3-B 、3C 、2D 、0 2、下列变形中,一定正确的是 [ D ]A 、33x x y y -=-B 、x mx y my =C 、2x x y xy= D 、2x xy y y =3、已知一次函数()22m -1-+=m x y ,函数y 随着x 的增大而减小,且其图象不经过第一象限,则m 的取值范围是 [ C ] A 、21>m B 、2≤m C 、221<<m D 、221≤<m 4、已知分式(8)(1)1x x x -+-的值为零,则x 的值为 [ C ].A 、1±B 、1-C 、8D 、1-或85、某文化商场同时卖出两台电子琴,每台均卖960元,以成本计算其中一台盈利20%,另一台亏本20%,则本次出售中商场 [ D ].A 、不赔不赚B 、赚160元C 、赚80元D 、赔80元6、直角三角形的周长是62+ 斜边上的中线长为1,则它的面积是[ B ]A 、 ;B 、 ;C 、1 ;D 、27、设有一凸多边形,除去一个内角外,其他内角和是2570°,则该内角的度数是 [ D ] (A )40°(B )90° (C )120 (D )130 ° 二、填空题:(每小题5分,共35分)8、已知关于x的负整数解只有-1,-2,则m ∵ mx-2≤O 的负整数解只有-1,-2,∴当m >0时,有 当m <0时,有而只有当取x ≥-2时,才只有-1,-2两个负整数解, ∴ 则 m=-19、设a ★b=a 2-2b ,则(-2) ★(3★4)的值为 。
解:(-2) ★(3★4) =2 ∵ a ★b=a 2-2b ,则(-2) ★(3★4) ∴ 3★4=32-2×4=1∴ (-2) ★(3★4)=(-2)★1=(-2)2-2×1=210、如图1⊥FG ,∠AEM=50°,∠NHC=55°. 则∠FGH 解:延长FG 交AB 于点Q ,延长HG 交AB 于点P ,∵ AB ∥CD , ∴ ∠EPG=∠DHG∵ ∠DHG=∠NHC=55° ∴ ∠EPG=55°班级____________________________ 姓名____________________ 考场号_______ 考号_____----------------------------------------------------密---------------------------------封--------------------------------线------------------------------------------------4121 2m x 2≥mx 2≥22-=m∵ MF ⊥FG , ∴ EFG=90°∵ ∠FEP=∠AEM=50°,∴ ∠PQG=90°-∠FEP=90°-50°=40° ∵ ∠EPG=∠PQG+∠PGQ∴ ∠PGQ=∠EPG-∠PQG=55°-40°=15° ∵ ∠FGH=∠PGQ ∴ ∠FGH=15°11、如图2,把一个长26cm ,宽14cm 的长方形分成五块,其中两个大正方形和两个长方形分别全等.那么中间小正方形的面积是 cm 。
2010四川省初中数学竞赛(初二组)决赛试卷
2010年四川初中数学联赛(初二组)决赛试卷(4月11日上午9:00—11:30)1、三角形的边长为整数,且周长为9的不全等的三角形个数为( ). (A )1 (B ) 2 (C )3 (D ) 42、已知321+=a ,则122+-a a 的值为( ).(A ) 13- (B ) 31- (C )311+ (D )311-3、已知12-=a , 223-=b ,23-=c ,则c b a ,,的大小关系是( ).(A ) c b a >> (B )a b c >> (C ) b a c >> (D ) b c a >>4、若实数z y x ,,满足:11,11=+=+zy y x ,则xyz 的值为( ). (A ) 1 (B )2 (C )-1 (D )-25、如图,在△ABC 中,AB =AC ,040=∠B ,BD 是B ∠的平BD 至E ,使DE=AD ,则ECA ∠的度数为( ).(A )30 (B )40 (C )50 (D )606、如图,在矩形ABCD 中,对角线长2,且4321∠=∠=∠=∠, 则四边形EFGH 的周长为( ). (A )22 (B ) 4 (C )24 (D )6二、填空题(本题满分28分,每小题7分)1、已知正整数b a ,,满足0||,02|2|=-+-=-+-b a b a b b 且b a ≠, 则ab 的值为 .2、若11=-xx ,则132+-x x 的值为 .3、已知梯形的边长分别为3、4、5、6,则此梯形面积等于 .4、如图,在ABC ∆中,D 是BC 上一点,满足AC AD =,E 是AD 的中点,且满足ACE BAD ∠=∠.若1=∆BDE S ,则ABC S ∆为 .三、(本大题满分20分)某项工程,甲队单独做需12天完成,乙队单独做需9天完成,若按整日安排两队工作,有几种方案可以使这项工程完工的天数不超过8天?四、(本大题满分25分)如图,在直角坐标系中,A 、B 是某个一次函数图像上的两点,满足AOB ∠是直角,且2==BO AO ,若AO 与y 轴的夹角是60. 求这个一次函数.y x五、(本大题满分25分)如图,在ABC Rt ∆中,90=∠C ,AM 、AN 分别为BC 边上的中线和BAC ∠的平分线.过C 作AN CD ⊥于D .(I )求证:)(21AC AB DM -= (II )求证:2)(41AC AB MC MN -=⋅.地(市) 县(区) 学校 年级 班 姓 名 性 别 考 号 指导教师 ………………………………………………… 密……………………… 封 …………………… 线 ……………………………………………………………2010年四川初中数学联赛(初二组)决赛试卷答案一、1、C2、A3、A4、C5、C6、B二、7、解:∵|b-2|+b-2=0, ∴|b-2|=2-b , ∴2-b≥0, 解得b≤2,∵|a-b|+a-b=0, ∴|a-b|=b-a , ∵a≠b , ∴b >a , ∴a <2, ∴ab <4. 故答案为:<49、解:过点D 作DE ∥AB 交BC 于E , ∵AD ∥BC ,∴四边形ABED 是平行四边形, ∴DE=AB ,BE=AD ,若AD=3,AB=4,BC=5,CD=6,则DE=4,EC=BC-BE=BC-AD=5-3=2, ∵DE+EC=4+2=6=CD ,∴此时不能组成三角形,即不能组成梯形, 同理可判定:AD=3,AB=4,BC=6,CD=5, ∵EC=BC-BE=6-3=3,CD=5,DE=4, ∴△DCE 为直角三角形, ∴梯形ABCD 为直角梯形,∴S 梯形ABCD = 12(AD+BC )•DE= 12×(3+6)×4=18. 故答案为:18.10、解:∵E 是AD 的中点,∴S △ABD =2S △BDE =2(等高,底边AD=2DE ),取CD 中点F ,连接EF ,很容易证明△ABD ∽△CEF , ∴ AD/EF = 1/2,∴S △CEF = 1/4,S △ABD = 1/2,又∵△CEF 与△ACE 等高,底边AC=2EF , ∴S △ACE =2S △CEF =1, ∴S △ADC =2S △ACE =2,故S △ABC =S △ABD +S △ACD =4. 故答案为:4.三、11、解:①设甲乙合作x天,然后甲单独做y天,由题意得,{(11/2+1/9)x+1/12y=1①x+y≤8②,此时解得y≤5,又∵整日安排两队工作,∴满足题意的只有:x=3,y=5;②设甲乙合作x天,然后乙单独做y天,{(1/12+1/9)x+1/9y=1①x+y≤8②,此时解得:y≤4,又∵整日安排两队工作,∴满足题意的只有:x=4,y=2;综上可得共有两种方案可以使这项工程完工的天数不超过8天.四、12、解:如图,作AC⊥CE,BE⊥CE,∵AO与y轴的夹角是60°,即∠AOF=60°,∴∠AOC=30°,∵∠AOB是直角,∠FOE是直角,∴∠BOE=60°,∴∠OBE=30°,又∵AO=BO=2,∴AC=1,OE=1,∴C0= √3,BE= √3,∴点A(- √3,1),点B(1,√3),设一次函数的解析式为y=kx+b,∴一次函数关系式是y=﹙2-√3)x+ 2√3-2.五、13、(1)证明:延长CD交AB于E,∵AN平分∠BAC,∴∠BAN=∠CAN,∵∠ACB=90°,CD⊥AN,∴∠ADC=∠ADE=∠ACB=90°,∴∠CAN+∠ACD=∠ACD+∠ECB=90°,∴∠ECB=∠CAD=∠BAD,在△AED和△ACD中{∠EAD=∠CADAD=AD∠ADE=∠ADC,∴△AED≌△ACD,∴AE=AC,ED=DC,∵AM是边BC上的中线,∴DM∥BE,DM= 1/2BE= 1/2(AB-AE),即DM= 1/2(AB-AC).。
2010年全国初中数学联赛
2010年全国初中数学联赛
徐胜林
【期刊名称】《中等数学》
【年(卷),期】2010(000)010
【摘要】@@ 第一试\r\n一、选择题(每小题7分,共42分)\r\n1.已知a、b、c 均为整数,且满足\r\n(a-b)10+(a-c)10=1.\r\n则|a-b|+|b-c|+|c-a|=( ).
【总页数】4页(P23-26)
【作者】徐胜林
【作者单位】
【正文语种】中文
【中图分类】G424.79
【相关文献】
1.2010年全国初中数学联赛模拟卷 [J],
2.2010年全国初中数学联赛江西省初赛 [J], 陶平生
3.2010年全国初中数学联赛武汉赛区预赛 [J], 罗锦海
4.2010年四川省初中数学联赛决赛(初二) [J], 李昌勇
5.2002年全国初中数学联赛预赛暨2001年山东省初中数学竞赛 [J], 李耀文因版权原因,仅展示原文概要,查看原文内容请购买。
2010年株洲市初中数学竞赛初二试卷和答案
2010年株洲市初中数学竞赛试卷(初二年级)时量:120分钟 总分:100分 注意事项:1、用黑色、蓝色钢笔或圆珠笔作答;2、在密封线内答题,答题内容不要超过密封线;3、不准使用计算器。
1.下列各式运算中,正确的是A .|3|3--=B .222()a b a b +=+C .3412a a a ⋅= D 3=2、甲种蔬菜保鲜适宜的温度是1℃~5℃,乙种蔬菜保鲜适宜的温度是3℃~8℃,将这两种蔬菜放在一起同时保鲜,适宜的温度是A .1℃~3℃B .3℃~5℃C .5℃~8℃D .1℃~8℃ 3.若x 的绝对值小于1,则化简 |1||1|x x -++ 得A .0B .2C .2xD .- 2x4.某商店出售某种商品每件可获利m 元,利润率为20%.若这种商品的进价提高25%,而商店将这种商品的售价提高到每件仍可获利m 元,则提价后的利润率为A .25%B .20%C .16%D .12.5%5.如图为一个棱长为1的正方体的展开图, A 、B 、C 是展开后小正方形的顶点,则∠ABC 的度数为A .30°B .45°C . 50°D . 60°6.某校初二运动队为了备战校运动会需要购置一批运动鞋.已知该队伍有20名同学,统计表如下表.由于不小心弄脏了表格,有两个数据看不到.下列说法中正确的是A .这组数据的中位数一定是40,众数是39B .这组数据的中位数与众数一定相等C .这组数据的平均数比39大,比40小D .以上说法都不对7.某个游泳池有2个进水口和一个出水口,每个进水口的进水量与时间的关系如图1所示,出水口的出水量与时间的关系如图2所示,某天早上5点到10点,该游泳池的蓄水量与时间的关系如图3所示.(第5题图)在下面的论断中: ①5点到6点,打开全部进水口,关闭出水口;②6点到8点,同时关闭两个进水口和一个出水口;③8点到9点,关闭两个进水口,打开出水口;④10点到11点,同时打开两个进水口和一个出水口. 正确的是A.①③ B .①④ C .②③ D .②④8.如图,将边长为1的正方形OAPB 沿x 轴正方向连续翻转2012次,点P 依次落在点12342012P P P P P ,,,,,的位置,则20122012P x =的横坐标A .2012B .2011C .2010D .2009 二、填空题(每题 5分,共30分,请将答案填在表格内) 9. 1,2,___________________ab a b =--=22则a +b = 。
2010年全国初中数学竞赛(海南赛区)
第1页(共4页)2010年全国初中数学竞赛(海南赛区)初 赛 试 卷一、选择题(本大题满分50分,每小题5分)在下列各题的四个备选答案中,只有一个是正确的,请把你认为正确的答案的字母1. 若x 为实数,则代数式|x|-x 的值一定是 A. 正数B. 非正数C. 非负数D. 负数2.已知(a+b)2=8,(a-b)2=12,则ab 的值为 A .1B .-1C .4D .-43.若bk <0,则直线y=kx+b 一定通过 A .第一、二象限 B .第二、三象限 C .第三、四象限D .第一、四象限4.甲、乙两人下棋,甲获胜的概率为30%,和棋的概率为50%,那么乙不输的概率为 A .20% B .50%C .70%D .80%5.已知20102011-20102009=2010x×2009×2011,那么x 的值是A .2008B .2009C .2010D .20116. 一项工程,甲建筑队单独承包需要a 天完成,乙建筑队单独承包需要b 天完成. 现两队联合承包,那么完成这项工程需要A. b a +1天B.(b a 11+)天 C. b a ab+天 D. ab 1天第2页(共4页)7.在平面上,如果点A 和点B 到点C 的距离分别为3和4,那么A 、B 两点的距离d 应该是 A. d=1B. d=5C. d=7D. 1≤d ≤78.如图1,在直角梯形ABCD 中, AB ∥CD ,∠ABC=90°,动点P 从点B 出发,沿B →C →D 的线路匀速运动至点D 停止.设点P 运动的路程为x ,△ABP 的面积为y ,如果y 关于x 的函数图象如图2所示,则△BCD 的面积是 A .3B .4C .5D .69.如图3,C 是⊙O 外一点,CA 、CB 分别与⊙O 相切于点A 、B ,P 是上一点,若∠C=x °,则∠APB 的度数是A .x °B .(90-2x)°C .(90-x)°D .(180-x)°10.如图4,在等腰直角三角形ABC 中,∠C=90°,D 为BC 的中点,将△ABC 折叠,使 点A 与点D 重合,EF 为折痕,则sin ∠BED 的值是A .53B .43C .32D .75二、填空题(本大题满分40分,每小题5分)11.已知点P 在直角坐标系中的坐标为(0,1),O 为坐标原点,∠QPO=150°,且P 到Q 的距离为2,则Q 的坐标为 .12.点A ,B 是在数轴上不同的两个点,它们所对应的数分别是-4,5322-+x x ,且点A 、B 到原点的距离相等,则x 的值为 .13.50名学生中,会讲英语的有36人,会讲日语的有20人,既不会讲英语也不会讲日语的有8B AOC图3Px ° m BAC 图4FED图2 yxO 25图1 ABC DP第3页(共4页)人,则既会讲英语又会讲日语的人数为 人.14.已知3122=+x x ,且x <0,则x x 1+的值是 . 15.设c <b <0<a ,a+b+c=1,a cb M +=,b ca N +=,c b a P +=,则M,N,P 之间 的关系是 .16.如图5,已知矩形ABCD ,AB=2,BC=3,MB=MC ,则点D 到AM 的距离为 .17.如图6,在梯形ABCD 中,AD ∥BC ,AB=CD=AD=1,∠B:∠A=1:2,M 、N 分别是AD 、BC 的中点,P 是直线MN 上的一点,则PC+PD 的最小值为 .18.如图7,在平行四边形ABCD 中,P 为BC 上任一点,连结DP 并延长交AB 延长线于Q ,则BQ ABBP BC -= .三、解答题(本大题满分30分,每小题15分)19.如图8,△ABC 是边长为1的等边三角形,P 是AB 边上的一个动点(P 与B 不重合),以线段CP 为边作等边△CPD (D 、A 在BC 的同侧),连结AD . (1)判断四边形ABCD 的形状,并给予证明;(2)设BP=x ,△PAD 的面积为y ,求出y 关于x 的函数关系式,并求出△PAD 面积的最大值及取得最大值时x 的值.CBDA图8PCBDA图5M图6CBDA图7PQ第4页(共4页)20.某单位欲购买A 、B 两种电器.根据预算,共需资金15750元.购买一件A 种电器和两件B种电器共需资金2300元;购买两件A 种电器和一件B 种电器共需资金2050元. (1)购买一件A 种电器和一件B 种电器所需的资金分别是多少元? (2)若该单位购买A 种电器不超过5件,则可购买B 种电器至少有多少件?(3)为节省开支,该单位只购买A 、B 两种电器共6件,并知道获政府补贴资金不少于700元;自己出资金不超过4000元;其中政府对A 、B 两种电器补贴资金分别为每件100元和150元.请你通过计算求出有几种购买方案?2010年全国初中数学竞赛(海南赛区)初赛试卷参考答案一、选择题1. 若x ≥0,则|x|-x=x-x=0;若x <0,则|x|-x=-x-x=-2x >0,故选C.2.由题意有a 2+2ab+b 2=8,a 2-2ab+b 2=12,两式相减得4ab=-4,得ab=-1,故选B .3.由bk <0,知b >0,k <0或b <0,k >0,前者直线经过第一、二、四象限,后者直线经过第一、三、四象限,因而必经过第一、四象限,选D .4.由已知条件知乙胜的概率为20%,又和棋概率为50%,故乙不输的概率为70%,选C .5.由20102011-20102009=2010x×2009×2011,20102009(2010-1)(2010+1)= 2010x×2009×2011,则有20102009×2009×2011= 2010x×2009×2011,则有x=2009,选B .6. 两队联合承包每天完成工程的b a 11+,完成这项工程需要的时间为1÷(b a 11+)=b a ab + 天.选C.7.根据题意可知符合条件的点A 和点B 分别在以点C 为圆心的两个同心圆上. 故选D. 8.由图象可知,直角梯形的高BC=2,上底CD=3,所以33221=⨯⨯=∆BCD S ,选A .9.分别连结OA 、OB ,则OA ⊥CA ,OB ⊥CB ,即可求得,选B .10.由已知条件知∠EDF=45°,由三角形外角性质得∠CDF+45°=∠BED+45°,∴∠BED=∠CDF ,设CD=1,CF=x ,则CA=CB=2,所以DF=FA=2-x ,在Rt △CDF 中,有x 2+1=(2-x)2,解第5页(共4页)得x=43,所以sin ∠BED=sin ∠CDF=53=DF CF ,选A .二、填空题11.(1,1+3)或(-1,1+3);在直角坐标系中,以P(0,1)为顶点,作出∠QPO=150°可求得.12.由45322=-+x x 解得511=x . 13.英语、日语至少会一门的人数为50-8=42人,设既会英语又会日语的为x 人,则只会英语的为(36-x)人;只会日语的为(20-x)人,于是得(36-x)+x +(20-x)=42,解得x=14.14.由3122=+x x ,得5122=++x x ,所以5)1(2=+x x ,又x <0,所以51-=+x x .15.由a+b+c=1可得a a cb 11=++,则M=11-=+a a c b ,同理11-=+=b b c a N ,P=11-=+c c b a ,由c <b <0<a ,得b c a 111>>,111111->->-b c a,∴M >P >N . 16.过D 作DG ⊥AM ,则有2×3=2221⨯⋅+⋅BMAB DG AM ,DG=2.4;17.3;当P 在对角线AC 与MN 的交点处时PC+PD 最小.18.1;∵ BQ AQ BP AD BP BC ==,∴ 1==-=-=-BQ BQBQ AB AQ BQ AB BQ AQ BQ AB BP BC .三、解答题 19.(1)四边形ABCD 是梯形或菱形,证明如下:① 当点P 不与点A 重合时,∵ △ABC 与△CPD 都是等边三角形, ∴ ∠ACB=∠DCP=60°,∴ ∠1=∠2,又AC=BC ,DC=PC ,∴△ADC ≌△BPC ,∴∠DAC=∠B=∠BCA=60°,∴ AD ∥BC.又∠1=∠2<60°,∴ ∠DCB <120°,即 ∠B +∠DCB <180°,∴ DC 与AB 不平行, ∴ 四边形ABCD 是梯形.② 当点P 与点A 重合时,PC 与AC 重合,此时AB=BC=CA=AD=DC ,四边形ABCD 是菱形,综上所述,四边形ABCD 是梯形或菱形.C BD A P1 2M第6页(共4页)(2)由(1)知∠BAD=120°,AD=BP=x ,过P 作DA 延长线的垂线PM ,M 为垂足,则∠PAM=60°,∠APM=30°,又BP=x ,AB =1,∴ AP=1-x ,∴ AM=)1(21x -,PM=)1(23x -∴163)21(43)(43)1(23212122+--=--=-⋅=⋅=x x x x x PM AD y (0<x <1). 当21=x 时,y 取最大值为163,即当21=x 时△PAD 面积取得最大面积为163. 20.(1)设购买一件A 种电器和一件B 种电器所需的资金分别为a 元和b 元.依题意得: ⎩⎨⎧=+=+2050223002b a b a 解之得⎩⎨⎧==850600b a (答略) (2)设该单位购买A 、B 两种电器分别为m 件和n 件.则600m+850n=15750 ,153151217+-=n m .∵ A 种电器不超过5件,∴ 153151217+-n ≤5. ∴ n ≥15,即可购买B 种电器至少有15件. (3)设购买A 种电器x 件,则购买B 种电器为(6-x)件,依题意得:⎩⎨⎧≥-+≤-+700)6(1501004000)6(700500x x x x , 解之得1≤x ≤4 .∵ x 取整数,∴ x=1,2,3,4. 即共有4种购买方案.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年陆丰市八年级数学竞赛
决 赛 试 题
时间:2010年6月6日9:30-11:30
一、选择题(每小题5分,共25分)
1.按下面的程序计算,若开始输入的值x为正数,最后输出的结果为656,则满足条件的x的不
同值最多有( )
A.2个 B.3个 C.4个 D.5个
2.如图,三个天平的托盘中形状相同的物体质量相等.图(1)、图(2)所示的两个天平处于平
衡状态,要使第三个天平也保持平衡,则需在它的右盘中放置( )
A.3个球 B.4个球 C.5个球 D.6个球
3.当x分别取值12010,12009,12008,…,12,1,2 ,…,2008,2009,2010时,计算代
数式2211xx的值,将所得的结果相加,其和等于( )
A.-1 B.1 C.0 D.2010
4.在△ABC中,∠ACB=90°,AC=12,BC=5,AN=AC,BM=BC,
则MN的长为( )
A.4 B.5 C.6 D.7
5.一次函数232yaxa的图象,在—2≤x≤1的一段都在x轴
上方,则a的取值范围是( )
A.13a B.1833a C.263a D.23a
二、填空题(每小题5分,共25分)
6.有一等腰钝角三角形纸片,若能从一个顶点出发,将其剪成两个等腰三角形纸片,则等腰三
角形纸片的顶角为 度.
7.已知下面等式对任意实数x都成立(n为正整数):
输入x 计算5x+1的值
>
500
输出结果
是
否
C
B
N
M
A
第4题图
(1) (2) (3)
23111xxx…
1nx
2012aaxax…n
n
ax
,
且123aaa…na=57,则满足条件的n的一个可能值是 .
8.如图,第(1)个多边形由正三角形“扩展”而来,边数记为3a,第(2)个多边形由正方形“扩
展”而来,边数记为4a,…,依次类推,由正n边形“扩展”而来的多边形的边数记为na(n≥3).当
345111aaa…+1n
a
的结果是197600时,n的值是 .
9.在有理数范围内分解因式:123aaaa+1= .
10.甲、乙、丙三人进行智力抢答活动,规定:第一个问题由乙提出,由甲、丙抢答.以后在抢
答过程中若甲答对1题,就可提6个问题,乙答对1题就可提5个问题,丙答对1题就可提
4个问题,供另两人抢答.抢答结束后,总共有16个问题没有任何人答对,则甲、乙、丙答
对的题数分别是 .
三、解答题(每小题14分,共70分)
11.小王沿街匀速行走,发现每隔6分钟从背后驶过一辆18路公交车,每隔3分钟从迎面驶来
一辆18路公交车.假设每辆18路公交车行驶速度相同,而且18路公交车总站每隔固定时
间发一辆车,那么发车间隔的时间是多少分钟?
12.如图,要在河边修建一个水泵站,分别向张村A和李庄B送水.已知张村A、李庄B到河边
的距离分别是2km和7km,且张、李两村庄相距13km. 问:
(1)水泵应建在什么地方,可使所用的水管最短? 请在图中设计出水泵站的位置;并
说明理由.
(2)如果铺设水管的工程费用为每千米3000元,为使铺设水管程费用最节省,请求出最节
省的铺设水管的费用为多少元?
A
B
l
河边
·
·
(1)
(2)
(3)
(4)
…
…
13.四边形ABCD中,∠A=∠C=90°,AB=AD,BC+CD=10.
(1)求四边形ABCD的面积;
(2)若∠ADC=60°,求四边形ABCD的周长.
14.如图所示,△ABC中,E,D是BC边上的两个三等分点,AF=2CF,BF=12厘米.
求:FM,MN,BN的长.
A
B
C
D
A
B
E
D C
F
M
N
15.在直角坐标系 xOy中,一次函数 y = kx + b ( k≠0)的图象与 x轴、y轴的正半轴分别交于A,
B 两点,且使得△OAB的面积值等于|OA| + |OB| + 3.
(1) 用 b 表示 k;
(2) 求△OAB面积的最小值.
