动网格生成技术及非定常计算方法进展综述
2级涡轮内部流动定常与非定常计算差异研究

2级涡轮内部流动定常与非定常计算差异研究杨杰;周颖;潘尚能;卢聪明【摘要】为获取进而认识涡轮内部流动状态,以某2级约化形式的动力涡轮为研究对象,分别对其进行定常和非定常数值计算和分析.研究表明:定常计算与非定常计算对涡轮内部流动的模拟结果,如叶片表面的压力分布、叶排进出口的气流角、叶片通道中的二次流流向涡、展向涡、叶片通道中的损失等,均存在差异;流动的非定常性越强,定常与非定常计算结果的差异越大,且该差异大小对于静叶与动叶呈相反的展向分布规律.【期刊名称】《航空发动机》【年(卷),期】2016(042)003【总页数】7页(P21-27)【关键词】涡轮;内部流动;定常;非定常;数值模拟;涡;航空发动机【作者】杨杰;周颖;潘尚能;卢聪明【作者单位】中航工业航空动力机械研究所,湖南株洲412002;中航工业航空动力机械研究所,湖南株洲412002;中航工业航空动力机械研究所,湖南株洲412002;中航工业航空动力机械研究所,湖南株洲412002【正文语种】中文【中图分类】V231.3引用格式:杨杰,周颖,潘尚能,等.2级涡轮内部流动定常与非定常计算差异研究[J].航空发动机,2016,42(3):21-27.YANG Jie,ZHOU Ying,PANShangneng,et al.Study of differences between steady and unsteady computation for two-stage turbines internalflow[J].Aeroengine,2016,42(3):21-27.对涡轮内部流动的数值模拟是获取进而认识涡轮内部流动状态的重要手段,有定常计算和非定常计算2种方法。
定常计算方法所需的计算机硬件资源少、花费的机时少,能快速获取模拟结果。
涡轮内部的流动本质上是非定常的,定常的数值计算必然会丢失相关的非定常信息,无法获取非定常流动特征。
掌握定常计算结果与非定常计算结果之间的差异是衡量选用何种计算方式的重要依据,更是工程计算中用定常计算代替非定常计算的必要前提。
Fluent学习总结

FLUENT学习总结1 概述:FLUENT是目前处于世界领先地位的商业CFD软件包之一,最初由FLUENT Inc.公司发行。
2006年2月ANSYS Inc.公司收购FLUENT Inc.公司后成为全球最大的CAE软件公司。
FLUENT是一个用于模拟和分析复杂几何区域内的流体流动与传热现象的专用软件。
FLUENT提供了灵活的网格特性,可以支持多种网格。
用户可以自由选择使用结构化或者非结构化网格来划分复杂的几何区域,例如针对二维问题支持三角形网格或四边形网格;针对三维问题支持四面体、六面体、棱锥、楔形、多面体网格;同时也支持混合网格。
用户可以利用FLUENT提供的网格自适应特性在求解过程中根据所获得的计算结果来优化网格。
FLUENT是使用C语言开发的,支持并行计算,支持UNIX和Windows等多种平台,采用用户/服务器的结构,能够在安装不同操作系统的工作站和服务器之间协同完成同一个任务。
FLUENT通过菜单界面与用户进行交互,用户可以通过多窗口的方式随时观察计算的进程和计算结果。
计算结果可以采用云图、等值线图、矢量图、剖面图、XY散点图、动画等多种方式显示、存贮和打印,也可以将计算结果保存为其他CFD软件、FEM软件或后处理软件所支持的格式。
FLUENT还提供了用户编程接口,用户可以在FLUENT的基础上定制、控制相关的输入输出,并进行二次开发。
1.1 FLUENT软件包的组成针对不同的计算对象,CFD软件都包含有3个主要功能部分:前处理、求解器、后处理。
其中前处理是指完成计算对象的建模、网格生成的程序;求解器是指求解控制方程的程序;后处理是指对计算结果进行显示、输出的程序。
FLUENT软件是基于CFD软件的思想设计的。
FLUENT软件包主要由GAMBIT、Tgrid、Filters、FLUENT几部分组成。
(1)前处理器。
包括GAMBIT、Tgrid和Fliters。
其中GAMBIT是由FLUENT Inc.公司自主开发的专用CFD前置处理器,用于模拟对象的几何建模以及网格生成。
Particle-in-cell

Particle-in-cell(PIC方法,质点网格法)计算二维非定常可压缩理想流动问题的欧拉-拉格朗日混合方法,简称PIC法,它特别适用于计算具有多种介质和大变形流动的问题。
在流体动力学中,通常可用欧拉和拉格朗日两种不同坐标系来求解流体动力学问题,即所谓欧拉法和拉格朗日法。
欧拉法可用于求解流体大畸变问题,但精度不高,而且在各个区域进行物质输运时会产生严重的物质扩散,使界面和自由面的位置不能精确确定。
拉格朗日法正好相反,计算精度较高,能精确确定界面和自由面,但不能处理流体大畸变和在各种介质之间有剪切间断的滑移现象。
针对这种情况,美国F.H.哈洛等人于1955年成功地把欧拉法和拉格朗日法结合起来,提出了质点网格法。
基本要点:PIC法的基本要点是,把含有多种介质的流动所通过的区域用欧拉法分成有限个网格,每个网格中的每种流体,用一组特定的离散化拉格朗日质点表示。
只包含一种流体质点的格子称为纯单元,两种流体质点同时存在的格子称为混合单元,不存在任何流体质点的格子称为空单元。
每个质点具有一定的质量,每个网格单元内的质点数目和质点分布都以流体流动的初始状态为依据,而且这些质点具有一定的速度和能量。
计算开始后,质点在欧拉网格之间迁移,表示流体在运动。
在每个时间步长内,计算分两步:第一步用欧拉法计算,即忽略偏微分方程中的输运效应,用差分方法计算由压力分布所引起的欧拉网格上速度(或动量)和能量的变化。
若一个网格内含有多种流体,就应按一定的规则把能量的改变量适当分配给不同的质点。
第二步是质点迁移计算,它是在第一步的基础上,按一定的加权平均方法计算出每个质点的速度和在时间步长结束时的新位置。
一个质点从一个网格迁移到另一个网格,就把所携带的质量以及相应的动量和能量从原来的网格输送到新的网格中去。
这一步实质上是对第一步计算中忽略的输运效应计算的补偿。
在具有激波间断的流动中,处理激波间断是一个难题(见激波数值处理)。
PIC法由于有非线性的耗散效应,不仅可以减少差分格式所引起的起伏现象,而且起着类似于人工粘性的作用。
【国家自然科学基金】_非定常计算_基金支持热词逐年推荐_【万方软件创新助手】_20140801
非定常的热传导-对流问题 非定常流场 非定常流动计算方法 非定常流动数值计算 非定常气动载荷 非定常气动力 非定常数值模拟 非darcy流 隔舌间隙 降阶模型 阻力特性 逆压梯度 远场噪声 进展 运动模型 迎风格式 边坡稳定分析 轴流转桨式水轮机 轴流式通风机 轴流式水轮机 跨声压气机 超声速底部绕流 贯流风机 试验 计算流体力学 解析解 蠕变参数反演 虚拟质量力 自然超空泡 脱落涡 脉动风压 能量法 胸鳍 网格局部重构 结构振动 细长体 线抽样技术 线性波理论 精度 粒子图像测速 空间结构 空穴漏气 空化流动 空化模型 空化 离散速度坐标法 离心风机 瞬态过程 瞬态启动 直升机 盐析特性 独立膨胀原理 特低渗透 热声
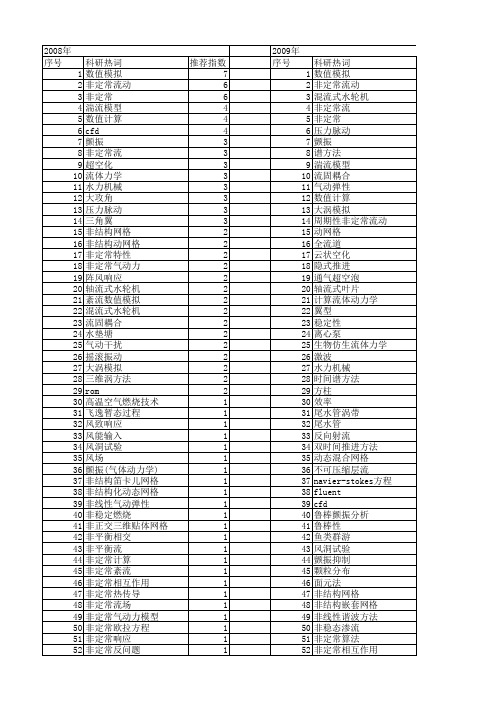
科研热词 数值模拟 非定常流动 非定常 湍流模型 数值计算 cfd 颤振 非定常流 超空化 流体力学 水力机械 大攻角 压力脉动 三角翼 非结构网格 非结构动网格 非定常特性 非定常气动力 阵风响应 轴流式水轮机 紊流数值模拟 混流式水轮机 流固耦合 水垫塘 气动干扰 摇滚振动 大涡模拟 三维涡方法 rom 高温空气燃烧技术 飞逸暂态过程 风致响应 风能输入 风洞试验 风场 颤振(气体动力学) 非结构笛卡儿网格 非结构化动态网格 非线性气动弹性 非稳定燃烧 非正交三维贴体网格 非平衡相交 非平衡流 非定常计算 非定常紊流 非定常相互作用 非定常热传导 非定常流场 非定常气动力模型 非定常欧拉方程 非定常响应 非定常反问题
非定常分析 非定常n-s方程 雷达散射截面 阵风响应因子 阀门 锥形流方程 采样时间 通道涡 退移速率+ 进水流道 进气道 返流量 近似最优内迭代次数 轴流泵 轴流压气机 跨音速流动 跨音速动导数 跨声压气机 超空泡 超空化流动 超声速冲压喷气发动机 贯流风扇 计算研究 计算机仿真 解耦方法 解析解 补气 血液流动 血液动力学 虚拟压缩方法 薄膜 蓄热式加热炉 航空、航天推进系统 自激振荡 脱落频率 脉动流 能量输入 耦合 翼型结冰模拟 细长体理论 线性方程组 系统辨识 精度 管口效应 突然起动翼型 空化器 稳态流动 稳定性 积分方程方法 离心泵 离心压缩机 瞬态流动 生物仿生流体力学 热源模型
利用嵌套网格数值求解某型通用飞机的动导数

关键词:CFD;动导数;嵌套网格;强迫 化会使得部件网格和背景网格超出对方计算域
振动法
的部分(例如图中 wall 边界以外的区域)被判
动导数是飞行器气动力系数和ቤተ መጻሕፍቲ ባይዱ动力矩系 数对姿态参数变化率的导数,对飞行器的气动 性能和操纵性能有重要影响。动导数通常通过
定为“死单元”(dead cell) 不参与计算,而网 格重叠的区域会通过插值进行数据传递,如图 1 下图所示。
CHINA FLIGHTS
图4 部件网格和背景网格
图3 某型通用飞机计算模型
(5) 如图 2 所示,则飞机在升沉振动中的实际 迎角为:
在升沉振动中有
(6) 均为 0,且
(7)
代入 (1) 式,有
(8)
得到 ,也就得到了 3 动导数计算 3.1 模型和网格
的值。
本文计算采用的模型是某型在研通用飞
机,如图 3 所示,其特征长度取平均气动弦弦
结果表明利用强迫俯仰振动得到的俯仰组合动 于计算部件周围的近壁面流动;部件网格的外
导数,以及利用强迫升沉振动分离得到的俯仰 侧边界则称为嵌套边界 (overset BC)。在计算过
力矩系数对迎角变化率和俯仰角速度的动导 程中,部件网格会随着部件一起运动,每过一
数,与实际结果均具有较好的符合性。
个时间步,网格会进行一次初始化,网格初始
长,有
。
计算用的网格分为背景网格和部件网格两
部分,如图 4 所示。机翼的前后缘、翼梢、前
缘下垂截面等大曲率或外形复杂的物面均作了
加密处理;飞机物面设置了附面层网格,保证 第一层网格 y+ < 1,附面层网格充分膨胀,与 外层网格平滑过渡;整个部件网格内部网格尺 寸设置得足够密,以捕捉流动分离区和尾迹区 的流场结构。全套网格总量为 2550 万,其中 部件网格 2300 万,背景网格 250 万。
风力机翼型挥舞摆振非定常气动特性分析

风力机翼型挥舞摆振非定常气动特性分析吕坤;谢永慧;张荻【摘要】参考实际运行状态下的风力机翼型,应用动网格并采用k-ωSST湍流模型对NREL S809翼型在Re=1×106情况下的翼型振荡进行了数值模拟,同时分析了挥舞、摆振及二者耦合振动对风力机翼型气动性能的影响.结果表明:相同振幅和频率下,翼型挥舞比摆振引起的气动力波动大得多;翼型未达到失速时,翼型吸力面的流动分离可以使翼型获得额外的升力;挥舞的振幅或频率较大时,翼型会发生失速,且来流攻角越大,挥舞使得翼型更易发生失速;在挥舞-摆振耦合引起的翼型气动力变化中,挥舞起主导作用.%The moving mesh and the k-w SST model were adopted to simulate the aerodynamic performance of the NREL S809 airfoil at the Reynolds number of 1X106. The effects of flapwise, edgewise and combined flap/lead-lag oscillations on the aerodynamic performance of the airfoil were analyzed- The results show that the aerodynamic fluctuation caused by flapwise oscillation is much larger than that caused by edgewise oscillation with the same amplitude and frequency. The lift is greater due to flow separation on the suction surface of the airfoil when the airfoil is not in stall status. Larger amplitude and higher frequency of the oscillation will lead to dynamic stall of the airfoil, and the dynamic stall of the airfoil occurs more easily with the increase in the attack angle. In addition, flapwise oscillation plays a dominant role in the aerodynamic fluctuation caused by combined flap/lead-lag oscillation.【期刊名称】《西安交通大学学报》【年(卷),期】2011(045)009【总页数】8页(P47-53,100)【关键词】挥舞;摆振;风力机翼;湍流模型;数值模拟【作者】吕坤;谢永慧;张荻【作者单位】西安交通大学能源与动力工程学院,710049,西安;西安交通大学能源与动力工程学院,710049,西安;西安交通大学能源与动力工程学院,710049,西安【正文语种】中文【中图分类】TK83在气动力、惯性力和弹性力的耦合作用下,风力机叶片旋转时容易发生振动,通常振动有3种形式:①挥舞,即叶片在垂直于旋转平面上的弯曲振动;②摆振,即叶片在旋转平面内的弯曲振动;③扭转,即绕叶片变距轴的扭转振动[1].这3种形式的振动在一起还会引发耦合,由此产生气动弹性不稳定.风力机叶片的振动及气弹耦合对风力机的气动性能及安全性有重要影响,所以深入研究翼型振荡状态下的气动特性,对改进翼型设计、提高风力机的气动效率和安全性具有重要的意义.许多学者对翼型振动的气动性能进行了深入研究,如:Ekaterinaris等[2]采用 Baldw in-Barth湍流模型对NACA 0012翼型的俯仰、平振及耦合运动下的动态失速性能进行了计算,指出振动状态下翼型的气动性能有别于静止状态;Walker等[3]对翼型等速上仰问题进行了大量的实验研究,指出当攻角大于静态失速攻角时,动态失速涡的存在对翼型上表面的速度和压力分布有重大影响,随着翼型上仰速度的增加,动态失速涡附着在翼型上的时间更长,由此可以显著增加翼型大攻角条件下的时均气动力;Ramsay等[4]通过风洞实验系统地研究了不同的雷诺数、平均迎角、迎角振幅和减缩频率下NREL S809翼型俯仰振荡的动态失速性能,分析了各因素对动态失速性能的影响;Guerri等[5-6]应用计算流体动力学方法深入研究了风力机叶型的流固耦合效应,得到了翼型的不同振型和气动力变化,同时着重研究了叶型的挥舞-扭转耦合振动.但是,迄今为止的大多研究是针对翼型俯仰振荡运动的动态失速进行的,而针对翼型挥舞、摆振及二者耦合振动时的气动性能却不多见.本文应用动网格技术,采用k-ω SST湍流模型,在实验[3]和Re=l×l06下对二维NREL S809翼型振荡进行了数值模拟.1 数值模型1.1 数值方法求解雷诺平均N-S方程利用商业软件CFX,计算模型采用k-ωSST湍流模型[5,7-8],瞬态项离散采用二阶迎风后插隐式时间步方法,空间离散采用二阶迎风格式.k-ωSST湍流模型[9]的计算方程如下湍流黏性系数湍动能方程湍流频率方程式中 :F1和 F2是混合函数;β、γ、σk、σω为模型参数.k-ωSST湍流模型利用函数F1将 k-ε和k-ω方程结合起来,然后利用函数F2来改进涡团黏性系数μt在壁面逆压流动区域的结果,充分发挥k-ε模型处理自由流、k-ω模型处理壁面约束流动的特长,同时还借鉴了 Johnson-King模型[10]不平衡作用的思想,以增强对复杂流的适应性.1.2 计算模型风力机翼选用S809翼型[4](主要应用于两叶片NREL PhaseⅥ风力机),额定功率为19.8 kW,叶片展长为5.03m.参照实际建立了风力机模型,如图1所示,图中:V为来流风入口的相对速度;α为攻角;β1为桨距角;F为作用在桨叶上的气动合力.F可以分解为F x、F y,Fx与来流风向垂直,称为驱动力,使桨叶旋转做功,Fy与来流风向平行,称为轴向推力,通过塔架作用在地面上.摆振沿x轴方向进行,挥舞沿y轴方向进行. 图1 风力机翼型受力模型参考文献[7]中的风力机模型,其叶片产生的最大功率区域在0.75倍展长附近,该区域桨距角β1=0°,因此取β1=0°建立计算域.计算网格用C 型结构化网格,翼型表面分布了300个节点,翼型前缘和尾缘网格采用加密处理,总网格数为12万.计算域及翼型周围网格如图 2所示,图中翼型弦长c=600 mm,计算域外边界距离翼型边界面至少为15倍弦长.计算域分内、外2个区,内区是直径为2倍于翼型弦长的圆,通过动网格来控制内区网格的移动可模拟翼型振动.图2 翼型计算区域及其周围网格分布图为了验证计算模型的正确性,对不同来流攻角下翼型的升力、阻力系数进行了计算,结果如图3所示.由图3可见,来流攻角在0°~18°内 ,计算与实验的阻力系数基本吻合.来流攻角小于10°,计算获得的升力系数与实验的偏差很小;来流攻角大于10°,计算获得的升力系数与实验之间出现了偏差,但在工程上该偏差是可以容忍的.所以,来流攻角在6°~12°之间时,可以采用本文模型进行数值分析.图3 不同来流攻角下翼型升力、阻力系数为了便于研究翼型振荡对风力机输出功率的影响,在参考文献[8]中定义式中:Cx为驱动力系数;Cy为轴向推力系数.2 数值模拟及分析2.1 翼型挥舞翼型挥舞在y方向上的位移[5-6]为式中:A为翼型挥舞的振幅;f为振动频率;φ为相位差,φ=0.直径为45 m左右的叶轮,其自激振动频率在1~3 Hz之间,且随着叶片展长的减小,自激振动频率增加[11-12].该叶轮的叶片振型以一阶挥舞和一阶摆振为主,在极限挥舞载荷作用下通过叶片有限元模型计算和实验得到的叶尖挠度可以达到8m以上.文献[13]在Re=1×105、缩减频率 k=0.8、无量纲挥舞振幅h=A/c=0.4~0.7下数值模拟了NACA 0012翼型的气动性能.参考文献[5-6,13-14]、结合实际风力机振动情况确定A=0.05~0.5 m,f=1~3 Hz,其中 3 Hz对应于最大的k=0.44.每个振动周期的时间步长数n对计算精度有显著影响.图4为 A=0.3m 、f=3 H z、α=10°时,n分别取15、30、60的 Cx计算结果.图4 不同n下的Cx计算结果由图4可见:n取30、60时,对应二者的驱动力系数曲线几乎完全重合;n取15时,对应曲线与前二者有明显区别.n不同时,对应驱动力系数峰值间存在最大误差.经分析知:n=15时,Cx峰值偏差ΔCx=6.9%;n=60 时,ΔCx=2.3%,该值与 n=30时相差无几,所以计算时本文的n=30.图5为 f=3 H z、α=10°且在不同挥舞振幅下Cx、Cy随时间的变化,该结果与文献[6,14]相似.图 5 f=3 Hz、α=10°且在不同挥舞振幅下Cx、Cy随时间的变化由图5可见,Cx和Cy随着翼型的振动产生了周期性的变化.结合翼型的运动规律可以发现:当翼型在平衡位置沿y轴正向运动时,Cx和Cy达到最小值;当翼型在平衡位置沿y轴负向运动时,Cx和Cy达到最大值.翼型振动时,对应来流速度的大小和方向均发生了变化:翼型沿 y轴正向运动时,对应来流速度和攻角最小,翼型产生的升力最小,Cx和Cy达到最小值;翼型沿y轴负向运动时,翼型仍未失速,其产生的结果恰好与正向运动时相反,所以Cx和Cy均达到最大值.翼型的挥舞不仅导致来流速度和攻角发生变化,还会引发流动分离和旋涡.图6为 A=0.2 m、f=3 H z、α=10°且翼型在平衡位置沿y轴正向和负向运动时的流场.当翼型沿y轴正向运动时,对应来流攻角较小,翼型表面不会发生流动分离.当翼型从最大位移处沿y轴负向运动时,对应来流攻角逐渐增大,翼型表面逐渐出现流动分离;当翼型负向运动至平衡位置时,对应来流攻角达到最大值,流动分离更为严重;当翼型继续负向运动时,对应来流攻角逐渐减小,流动分离现象逐渐减弱,直至消失.1.17 s时,对应来流的速度和攻角达到最大值,流动分离最为严重,这2种因素均有可能导致Cx 和Cy达到最大值.考虑翼型振动前后Cx和Cy的变化如图7所示.图6 翼型在平衡位置沿y轴正向和负向运动时的流场正向运动负向运动图7 考虑翼型振动前后Cx和Cy的变化曲线1、2对应于翼型静止状态;曲线3、4分别对应A=0.2m、f=3 Hz、α=10°的曲线由图7可以发现:翼型沿y轴负向运动时,正常振动状态下的Cx和Cy均大于仅考虑来流速度及攻角的情况,振动下的Cx和Cy表现出增大的特性;翼型负向运动至平衡位置时,压力面附近气流压力增大,其大于吸力面,由此产生压力梯度,此时气流绕过翼型尾缘由压力面流向吸力面,并带动下游流体回流,使得边界层内的流体质点离开壁面挤向主流,从而加剧了边界层分离.下游回流的流体受到主流的冲击折返向下游流动,并在分离点的下游产生剪切涡和尾流区,造成能量损失,促使吸力面产生低压区,因而翼型获得额外的升力,使得Cx和Cy增大.所以,来流速度和攻角增大和翼型振动引起的流动分离都会加剧Cx和Cy增大.以上研究中挥舞振幅比较小,翼型未达到失速.当挥舞振幅较大时,叶片会发生失速颤振.研究发现 ,在 f=3 Hz、α=10°下 ,当 A 大于或等于 0.4m时,翼型失速.图8为 A=0.5 m时不同频率下Cx的变化规律.图8 A=0.5m时不同频率下Cx的变化由图8可见,在f=3 H z下,A=0.5 m与A=0.05~0.3 m时 Cx情况有很大区别,其中:A=0.05~0.3 m时驱动力一直为正值;A=0.5 m且翼型沿y轴负向运动至平衡位置附近时,驱动力会急剧降至负值,Cx甚至达到-0.4.由图8还可见:在相同的挥舞振幅下,振动频率越大,翼型受到的气动力波动越剧烈,当频率达到一定程度时,翼型失速;随着振动频率的增加,翼型沿y轴负向运动且在相同位移处的速度增大,来流速度和攻角随之增大,流动分离和旋涡产生的可能性就越大.频率增大到了一定程度时,流动分离会导致翼型失速,如图8中f=3 H z的情况.图9为翼型在一个振动周期内的流场演化.在1~1.17 s之间,翼型从最大位移处沿y轴负向振动,但仅在翼型吸力面尾缘附近发生了流动分离.1.17 s时,翼型在平衡位置达到最大速度,此时来流速度和攻角最大,翼型前缘附近流动在逆压梯度的作用下开始发生流动分离,并在1.18 s时形成前缘分离涡.前缘分离涡在向后扩展的运动中,翼型升力迅速增加,从而导致Cx迅速增加,这与文献[15]的实验结论吻合,说明前缘涡和翼型表面剪切涡的存在,有助于在翼型上表面产生低压区,进而获得额外的升力. 图9 不同时刻的流场演化情况前缘涡继续向后运动,在1.23 s时翼型尾缘上部诱导出反向旋转的二次涡结构,翼型进入失速状态.尽管此时前缘涡和剪切涡进一步增强,但后缘出现的反向旋转的后缘涡抵消了一部分前缘涡和剪切涡,从而造成升力迅速下降,阻力迅速增加,Cx迅速降低,甚至达到 Cx=-0.4的情况.在 1.27 s时后缘涡脱离翼面向后运动,翼型脱离失速区.此后,翼型继续沿y轴负向振动,对应的来流速度和攻角逐渐减小,翼型重新摆脱了失速状态.2.2 翼型摆振翼型摆振沿 x方向的振荡形式[6,16]为式中:B为翼型摆振振幅;φ为相位差,φ=0.叶片振型是以一阶挥舞和一阶摆振为主的,尽管不同振型时参振的惯性矩不同,但一般情况下,机翼的一阶挥舞和一阶摆振的固有频率比较接近.图10 为且在不同摆振振幅下Cx、Cy随时间的变化.对比图10和图5发现,在相同的振幅和频率下,翼型摆振比挥舞引起的气动力波动小得多.摆振时,翼型沿x轴方向振动,远处来流在 x轴方向的速度分量比y轴的大得多,所以摆振引起的来流速度和来流攻角的变化比挥舞小得多,同时摆振引起的流动分离也远不及挥舞的严重,因此在相同的振幅和频率下,翼型摆振比挥舞引起的气动力波动要小得多.图11为时挥舞和摆振下Cx随X、Y变化的曲线.由图10 不同摆振振幅下Cx、Cy随时间变化的曲线图11 不同频率下 Cx随X、Y变化的曲线图11可以看出,相同振幅和频率下,翼型摆振比挥舞引起的气动力波动要小得多.2.3 翼型挥舞-摆振耦合振动挥舞-摆振不稳定性是风力机单个叶片在挥舞与摆振耦合下产生的.研究表明:当风力机叶片在载荷作用下或者挥舞和摆振频率接近时,挥舞-摆振不稳定性显现出来.本文将挥舞和摆振的频率均设为2 Hz,在参考文献[5-6,17]的基础上,得到耦合振动下叶型受力的运动方程下面研究A分别为 0.05、0.1、0.2、0.3 m 时的情况.图12为耦合振动时不同挥舞振幅下Cx、Cy随时间变化的曲线.图12 耦合振动时不同挥舞振幅下 Cx、Cy随时间变化的曲线(B=0.2m)对比图12和图5发现,耦合振动时翼型受到的气动力的规律与挥舞时很相似,即Cx 和Cy均随着翼型的振动产生周期性的变化.另外还发现,在相同的挥舞振幅下,耦合振动时气动力波动比挥舞时略小,这与采用的耦合振动方程有关.由于2种振型的相位差为π,所以翼型在以最大速度沿y轴负向振动的同时,又以最大速度沿 x轴正向振动,此刻受翼型沿x轴方向运动的影响,对应的来流速度和攻角有所减小.为了研究耦合振动时摆振对翼型气动力的影响,本文取 A=0.2 m,B 分别为 0.05、0.10、0.20、0.30 m,攻角α=10°.图13为耦合振动时不同摆振振幅下Cx、Cy随时间变化的曲线.图 13 耦合振动时不同摆振振幅下Cx、Cy随时间变化的曲线(A=0.2m)由图13可见,B 分别为0.05、0.10、0.20、0.30 m时,对应的Cx变化曲线几乎完全重合.对比图13与图12发现,在耦合振动中,摆振对翼型气动力的影响比挥舞小得多,这个结果与非耦合振动下的结果是一致的.由此可以推断,在耦合振动引起的翼型气动力变化中,挥舞起主导作用.来流攻角的变化对风力机翼型气动性能的影响很大.采用耦合振型研究不同来流攻角对翼型气动性能的影响时,取A=0.2 m,B=0.2 m,攻角α分别为6°、8°、10°、12°.图 14 为不同来流攻角下 Cx、Cy随时间变化的曲线.由图14可见,来流攻角对翼型气动性能的影响很显著.相同振型下,同一时刻来流攻角越大,Cx和Cy越大.这是因为,翼型未失速,对应来流攻角越大,翼型的升力越大.同时还发现,相同振型下,来流攻角越大,Cx的波动越大,而Cy的波动越小.来流攻角在逐渐增大直至接近失速攻角的过程中(见图3),翼型升力的增加逐渐减缓,因而攻角较大时翼型振动引起的升力变化较小.轴向推力主要是翼型升力沿y轴的正向分力,因此Cy的波动较小.但是,由 f=3 Hz时的情况(见图8)知,来流攻角在逐渐增大直至接近失速攻角的过程中,翼型驱动力仍可以快速增大,因而Cx的波动较大.图14 不同来流攻角下Cx、Cy随时间变化的曲线对不同来流攻角的翼型挥舞失速颤振研究发现:在 f=3 H z下,当α=8°、A ≥0.5 m 时 ,翼型接近失速;当α=10°、A=0.4 m 时,翼型会失速;当α=12°、A=0.33 m 时,翼型失速.当来流攻角接近于翼型失速攻角区域时,较小的挥舞振幅会使翼型进入失速状态,这说明来流攻角越大,挥舞更易导致翼型失速.3 结论本文参考实际状态下的风力机模型,应用动网格技术,采用 k-ωSST湍流模型,对NREL S809翼型在Re=1×106时的翼型振动进行了数值模拟,分析了挥舞、摆振及二者耦合振动对风力机翼型气动性能的影响,由此得出如下结论.(1)翼型在挥舞和摆振中,Cx和Cy产生周期性的变化.与摆振相比,挥舞更易引起气动力的大幅波动.(2)翼型在未失速时,其吸力面的流动分离可以使翼型获得额外的升力,翼型振动引起的流动分离会促进Cx和Cy增大.(3)当挥舞的振幅、频率较大时,翼型会发生失速.挥舞时 ,f=3 Hz、α=10°、A≥0.4 m,或者 A=0.4 m 、α=10°、f ≥3 Hz,翼型会达到失速 .来流攻角越大,挥舞更易导致翼型失速.(4)在耦合振动引起的翼型气动力变化中,挥舞起主导作用,摆振是次要的.参考文献:[1] 李本立,宋宪耕,贺德馨,等.风力机结构动力学[M].北京:北京航空航天大学出版社,1999:4-5.[2] EKATERINARIS JA,SORENSEN N N.Numerical investigation of airfoil dynam ic stall in simultaneous harmonic oscillatory and translatory motion[J].Journal of So lar Energy Engineering,1998,120(1):75-83.[3] WALKER JM,HELIN H E,STRICKLAND J H.An experimental investigation of an airfoil undergoing large-amp litude pitching motions[J].A IAA Journal,1985,23(8):1141-1142.[4] RAMSAY R R,HOFFMAN M J.Effects of grid roughness and pitch oscillations on the S809 airfoil,NREL/TP-442-7817[R].W ashingtonDC,USA:National Renewab le Energy Lab.,1995:1-166.[5] GUERRIO,HAMDOUNI A,SAKOUT A.Fluid structure interaction of wind turbineairfoils[J].Wind Engineering,2008,32(6):539-557.[6] GUERRIO,HAMDOUNI A,SAKOUT A.Numerical simu lation of the flow around oscillating w ind turbine airfoils:part 2 free vibrating airfoil[J].Multi-Science Publishing,2008,2(4):387-405.[7] G IGUERE P,SELIG M S.Design of a tapered and twisted blade for the NREL combined experiment rotor,NREL/SR-500-26173[R].Washington DC,USA:National Renew able Energy Lab.,1999:1-32.[8] MARTIN.Aerodynamics of wind turbines[M].London,UK:James and James Ltd.:Science Pub lishers,2008:7-13.[9] MENTER F R.Zonal tw o equation k-ωturbulence models for aero dynam ic flows,A IAA 93-2906[R].Reston,VA,USA:A IAA,1993.[10]JOHNSON D,KING L.A mathematically simp le turbu lence closure mode l for attached and separated turbulence boundary layers[J].AIAA Journal,1985,23(11):1684-1692.[11]周梅,朱志坚,乔印虎,等.风力发电机振动保护仪的研制[J].机械研究与应用,2006,19(3):103-104.ZHOU M ei,ZHU Zhijian,QIAO Yinhu,et al.Research for wind turbineo f vibration guard module[J].M echanicalResearch&Application,2006,19(3):103-104.[6]商炳章,白清源.基于特征项权重改进的关联文本分类[J].计算机研究与发展,2008,45(S0):252-256.SHANG Bingzhang,BAIQingyuan.Improved association text classification based on feature weight [J].Journal of Computer Research and Development,2008,45(S0):252-256.[7]蔡金凤,白清源.挖掘重要项集的关联文本分类[J].南京大学学报,2011,47(5):544-550.CAI Jinfeng,BAI Qingyuan.Association text classification of mining ItemSet significance [J].Journal of Nanjing University,2011,47(5):544-550.[8] BARALIS E,GARZA P.I-prune:item selection for associative classification [J].International Journal of Intelligent Systems,2012,27(3):279-299.[9] YANG Yiming,PEDERSON J O.A comparative study on feature selection in text categorization[C]∥Proceedings of the 14th International Conference on Machine Learning.San Francisco,CA,USA:Morgan Kaufmann,1997:412-420.[10]AGRAWAL R,SRIKANT R.Fast algorithms for mining association rules[C]∥Proceedings of the 20th VLDB Conference.San Francisco,CA,USA:Morgan Kaufmann,1994:487-499.[11]HAN Jiawei,PEI Jian,YIN Yiwen,et al.Mining frequent patterns without candidate generation:a frequent-pattern tree approach[J].Data Mining and Knowledge Discovery,2004,8(1):53-87. [12]SEBASTIANI F.Machine learning in automated text categorization [J].ACM Computing Surveys,2002,34(1):1-47.。
基于大涡模拟方法的多层动网格技术识别平板气动参数

基于大涡模拟方法的多层动网格技术识别平板气动参数刘祖军;葛耀君;杨泳昕【摘要】Based on Fluent software redevelopment, the motion of a structure was described with UDF and moving grids were also used to realize fluid-solid coupling from view of a loosely coupled model. A new method of multi-moving grid technique was proposed to resolve problems of structure movement restricted by fluid mesh size and calculation failure caused by large deformation of grids under the condition that the velocity of dynamic meshes was in conformity with the space conservation law . In hydrodynamic calculations, the method of large eddy simulation was used to solve N-S equation in order to consider the impact of turbulence. Numerical simulation of flow field around a single degree of freedom forced vibration plate was given. Its aerodynamic parameteis were acquired by fitting aerodynamic time-history curves with the least-square method. The results were in better agreement with Thodorsen theoretic solutions.%从弱耦合的角度出发,对流体计算软件fluent进行二次开发,利用其用户自定义函数(UDF)描述结构的运动状态并结合动网格技术实现流固耦合.在保证动网格运动速度符合空间守恒法则的条件下,针对固体模型在流场中运动受网格尺寸限制且易造成网格变形过大导致计算失败的问题提出了多层动网格的解决方法.流体动力计算时考虑湍流的作用,采用大涡模拟方法求解N-S方程.数值模拟了平板做单自由度强迫振动的断面绕流流场,通过最小二乘法拟合气动力时程曲线获得气动导数.仿真结果与通过Theodorsen理论导出的平板气动导数具有良好的一致性.【期刊名称】《振动与冲击》【年(卷),期】2011(030)004【总页数】5页(P156-160)【关键词】多层动网格;大涡模拟;气动参数;UDF;流固耦合;空间守恒法则【作者】刘祖军;葛耀君;杨泳昕【作者单位】同济大学,桥梁工程系,上海200092;同济大学,桥梁工程系,上海200092;同济大学,桥梁工程系,上海200092【正文语种】中文【中图分类】U441目前桥梁风工程中的气动导数一般通过风洞节段模型试验来获得,采用的方法主要有自由振动法和强迫振动法。
cfl3d宣传

其中,Q为方程的解向量,J为网格转换的雅克比矩阵。 方程右边的第二项为网格体积变化导致的几何守恒律。
气动/结构耦合方法
全耦合方法通过将流体方程和结构方程整合成统一的方 程来构建系统的控制方程。该方法能保证时间同步,精度较 高,但系统的高度非线性会导致方程求解困难,故应用不广。 松耦合方法是在两个模型各自收敛后进行信息交换,所 以整个系统仅有一阶时间精度。但该方法形式简单,计算效 率高。 紧耦合方法通过特定的数据交换界面将问题耦合成一个 整体进行计算,能在减少时间积分不同步带来的误差,提高 了时间精度。但该方法计算效率低。
对应的频率分别为:
9.60Hz,38.2Hz, 48.35Hz和91.54Hz
演示算例二
从其一阶模态所
对应的曲线可以
看出,该状态已 经越过颤振边界,
是动不稳定状态
马赫数0.9,动压89.3psi下广义位移曲线
演示算例二 从图中可以看出, 此动压为该马赫数 下的颤振动压。其 对应的颤振频率为 14.8Hz 。一阶模态 所对应的曲线表征 了该状态下气弹系 统的临界稳定性。
动网格算法结合无限插值的有限宏单元变形法初始网格30舵偏最终网格60舵偏初始宏单元最终宏单元动网格算法几何守恒律11jjjjtqhhggfftqjttt????????????????????对于流体力学方程的求解总的方程形式如下
软件理论说明及功能介绍
浙江大学航空航天学院
二〇一一年十二月
目录
软件主要功能介绍 软件理论基础说明 软件演示算例 项目组后续开发工作
软件主要功能 包含多种湍流模型的,基于NS方程/Euler方程的常规气动力/ 气动热数值模拟。 结合嵌套网格技术的非定常气动力/气动热数值模拟,可处理 多体分离等非定常问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动网格生成技术及非定常计算方法进展综述
张来平;邓小刚;张涵信
【期刊名称】《力学进展》
【年(卷),期】2010(040)004
【摘 要】对应用于飞行器非定常运动的数值计算方法(包括动态网格技术和相应的
数值离散格式)进行了综述.根据网格拓扑结构的不同,重点论述了基于结构网格的非
定常计算方法和基于非结构/混合网格的非定常计算方法,比较了各种方法的优缺点.
在基于结构网格的非定常计算方法中,重点介绍了刚性运动网格技术、超限插值动
态网格技术、重叠动网格技术、滑移动网格技术等动态结构网格生成方法,同时介
绍了惯性系和非惯性系下的控制方程,讨论了非定常时间离散方法、动网格计算的
几何守恒律等问题.在基于非结构/混合网格的非定常计算方法中,重点介绍了重叠非
结构动网格技术、重构非结构动网格技术、变形非结构动网格技术以及变形/重构
耦合动态混合网格技术等方法,以及相应的计算格式,包括非定常时间离散、几何守
恒律计算方法、可压缩和不可压缩非定常流动的计算方法、各种加速收敛技术等.
在介绍国内外进展的同时,介绍了作者在动态混合网格生成技术和相应的非定常方
法方面的研究与应用工作.
【总页数】24页(P424-447)
【作 者】张来平;邓小刚;张涵信
【作者单位】空气动力学国家重点实验室,绵阳,621000;中国空气动力研究与发展
中心,绵阳,621000;空气动力学国家重点实验室,绵阳,621000;中国空气动力研究与
发展中心,绵阳,621000;中国空气动力研究与发展中心,绵阳,621000
【正文语种】中 文
【相关文献】
1.定常多相位与非定常计算方法在双吸离心泵数值模拟中的应用 [J], 胡乐;张淑佳;
毛鹏展;徐铖
2.用改进非结构动网格方法模拟跨音速非定常绕流 [J], 王军利;周洲
3.基于非结构动网格的非定常激波装配法 [J], 刘君;邹东阳;徐春光
4.预处理法求解定常/非定常混合网格的全速流场 [J], 肖天航;昂海松;余少志;王旭
刚;段文博
5.动态混合网格生成及隐式非定常计算方法 [J], 张来平;王志坚;张涵信
因版权原因,仅展示原文概要,查看原文内容请购买
