沪科版2018-2019学年九年级数学上册《第22章相似形》单元测试卷(含答案)
沪科版九年级上册数学第22章 相似形 含答案

沪科版九年级上册数学第22章相似形含答案一、单选题(共15题,共计45分)1、已知两个相似三角形的相似比为1:4,则它们的周长比为()A.1:4B.4:1C.1:2D.1:162、如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,下面四个结论:①CF=2AF;②tan∠CAD=;③DF=DC;④△AEF∽△CAB;⑤ S四边形CDEF =S△ABF,其中正确的结论有()A.2个B.3个C.4个D.5个3、如图,将△ABC沿DE翻折,折痕DE∥BC,若,BC=9 ,则DE的长等于()A.2B.3C.4D.4.54、如图,AB为半圆O的直径,AD、BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD :S△BOC=AD2:AO2,④OD:OC=DE:OE,⑤OD2=DE•CD,正确的有()A.2个B.3个C.4个D.5个5、如图,⊙O的直径为6,在⊙O上位于直径AB的异侧有定点C和动点P.已知BC:CA=4:3,P在半圆上运动,CP⊥CD交PB的延长线于D点.当点P运动到什么位置时,△PCD的面积最大为()A.36B.24C.18D.126、直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3,把一块含有45°角的直角三角形如图放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为()A. B. C. D.7、如图,在中,,若,则与的面积之比为()A. B. C. D.8、在△ABC中,DE∥BC,若AD=1,DB=2,则的值为()A. B. C. D.9、已知a:b:c=4:3:2,且a+3b-3c=14,则4a-3b+c的值是( )A.8B.10C.16D.1810、已知∠PAQ=36°,点B为射线AQ上一固定点,按以下步骤作图:①分别以A,B为圆心,大于AB的长为半径画弧,相交于两点M,N;②作直线MN交射线AP 于点D,连接 BD;③以B为圆心,BA长为半径画弧,交射线AP 于点C;根据以上作图过程及所作图形,下列结论中错误的是()A.∠CDB=72°B.△ADB∽△ABCC.CD:AD=2:1D.∠ABC=3∠ACB11、下列各组线段中,能成比例的是()A.1cm,3cm,4cm,6cmB.30cm,12cm,0.8cm,0.2cmC.11cm,22cm,33cm,44cmD.12cm,16cm,45cm,60cm12、下列命题中,假命题的是( )A.两条弧的长度相等,它们是等弧B.等弧所对的圆周角相等C.所有的等边三角形都相似D.位似图形一定有位似中心13、如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:①△AED≌△AEF;②△ABE∽△ACD;③BE+DC>DE;④BE2+DC2=DE2,其中正确的有()个.A.1B.2C.3D.414、如图,在△ABC中,∠B=70°,AB=4,BC=6,将△ABC沿图示中的虚线DE 剪开,剪下的三角形与原三角形相似的有()A.1个B.2个C.3个D.4个15、如图,己知四边形ABCD中,E、F分别为AB、CD 上的两点,且AD∥BC∥EF,AB=4BE,则DF与FC的关系是()A.DF=4FCB.DF=3FCC.DF= FCD.DF=2FC二、填空题(共10题,共计30分)16、已知线段AB = 4厘米,点P是线段AB的黄金分割点(AP > BP),那么线段AP =________厘米.(结果保留根号)17、如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB :S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,其中正确结论的个数是________.18、如图,在四边形ABCD中,以AB为直径的半圆O经过点C,D.AC与BD相交于点E,CD2=CE·CA,分别延长AB,DC相交于点P,PB=BO,CD=2 .则BO的长是________.19、已知△ABC∽△DEF,且BC=5cm,EF=3cm,若S△ABC =25cm2,则S△DEF=________。
(B卷)沪科版九年级上册数学第22章 相似形含答案

沪科版九年级上册数学第22章相似形含答案一、单选题(共15题,共计45分)1、如图,菱形ABCD中,点M,N在AC上,ME⊥AD, NF⊥AB. 若NF = NM = 2,ME = 3,则AN =()A.3B.4C.5D.62、如图,已知M,N分别为AB,AC上的两点,且MN∥BC,AN=4CN,若AB=10,则BM的长为()A.1B.2C.3D.43、如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB :S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,其中正确结论的个数是()A.1B.2C.3D.44、如图,E是矩形ABCD中AD边的中点,BE交AC于点的面积为2,则四边形CDEF的面积为()A.4B.5C.6D.75、如图,AB与CD相交于点E,AD∥BC,,CD=16,则DE的长为()A.3B.6C.D.106、如图,□ABCD中,EF∥AB,DE∶EA = 2∶3,EF = 4,则CD的长为()A. B.8 C.10 D.167、如图,△ABC中,DE∥BC,= ,则OE:OB=()A. B. C. D.8、如图,四边形ABCD∽四边形A1B1C1D1, AB=12,CD=15,A1B1=9,则边C1D1的长是()A.10B.12C.D.9、如图,在中,,将绕点顺时针旋转,使点旋转至边上的点处,点的对应点为点,的延长线恰好经过点,则的长为()A. B. C. D.10、如图,△ABC中,∠BAC=45°,∠ACB=30°,将△ABC绕点A顺时针旋转得到△AB1C1,当点C1、B1、C三点共线时,旋转角为α,连接BB1,交AC于点D.下列结论:①△AC1C为等腰三角形;②△AB1D∽△BCD;③α=75°;④CA=CB1,其中正确的是()A.①③④B.①②④C.②③④D.①②③④11、如图,在△ABC中,D为AB上的一点,过点D作DE∥BC交AC于点E,过点D作DF∥AC交BC 于点F,则下列结论错误的是()A. B. C. D.12、把ab= cd写成比例式,下列写法错误的是()A. B. C. D.13、如图,在Rt△ABC中,∠C=90°,P是斜边上一定点,过点P作直线与一直角边交于点Q使图中出现两个相似三角形,这样的点Q有 ( )A.1个B.2个C.3个D.4个14、若2a=3b,则的值为( )A. B. C. D.15、如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )A. B. C. D.二、填空题(共10题,共计30分)16、如图,在面积为80 cm²的矩形ABCD中作等边△BEF,点E,F分别落在AD,BC上,将△BEF向右平移得到△B1E1F1(点B1在F的左侧),再将△B1E1F1向右平移,使得F1与C重合,得到△B2E2C(点B2在F1的左侧),且第二次平移的距离是第一次平移距离的1.4倍.若FB2= BE,则阴影部分面积为________cm²。
沪科版九年级数学上册第22章:相似形 达标测试卷(含答案)

的面积之比为( )
A.1:2
B.1:3
C.3:4
D.1:4
3.如图,AD 是直角三角形 ABC 斜边上的中线,AE⊥AD 交 CB 的延长线于 E,
则图中一定相似的三角形是( )
A.△AED 与△ACB
B.△AEB 与△ACD
C.△BAE 与△ACE
D.△AEC 与△DAC
4.如图,在平面直角坐标系中,有点 A(6,3),B(6,0),以原点 O 为位似中心,
14.如图,正△ABC 的边长为 2,以 BC 边上的高 AB1 为边作正△AB1C1,△ABC 与△AB1C1 公共部分的面积记为 S1,再以正△AB1C1 的边 B1C1 上的高 AB2 为 边作正△AB2C2,△AB1C1 与△AB2C2 公共部分的面积记为 S2,…,以此类推, 则 Sn=________.(用含 n 的式子表示)
知识像烛光,能照亮一个人,也能照亮无数的人。--培根 20.如图,在边长为 1 个单位长度的小正方形网格中:
(1)画出△ABC 向上平移 6 个单位长度,再向右平移 5 个单位长度后的 △A1B1C1;
(2)以点 B 为位似中心,将△ABC 放大为原来的 2 倍,得到△A2BC2,请在网 格中画出△A2BC2;
11 / 17
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
2018年秋沪科版九年级数学上《第22章相似形》复习试题含答案

第22章 相似形类型之一 比例线段与比例性质1.如果x ∶(x +y)=3∶5,那么x ∶y 等于( )A .B .C .D . 853823322.如图22-X -1,直线l 1∥l 2∥l 3,直线AC 分别交直线l 1,l 2,l 3于点A ,B ,C ,直线DF 分别交直线l 1,l 2,l 3于点D ,E ,F.若DE =3,EF =6,AB =4,则AC 的长是( )A .6B .8C .9D .12图22-X -13.如图22-X -2,在▱ABCD 中,AC 与BD 相交于点O ,E 是OD 的中点,连接AE 并延长交CD 于点F ,则DF ∶FC 等于( )A .1∶4B .1∶3C .1∶2D .1∶1图22-X -24.如图22-X -3,在△ABC 中,AM ∶MD =4∶1,BD ∶DC =2∶3,求AE ∶EC 的值.图22-X -3类型之二 相似三角形的判定与性质5.如图22-X -4,( )图22-X -4A .①和②B .②和③C .①和③D .②和④6.如果两个相似三角形的面积比是1∶2,那么它们的周长比是( )A .1∶2B .1∶4C .1∶D .2∶127.在△ABC 与△A′B′C′中,有下列条件:(1)=;(2)=;(3)∠A =AB A ′B ′BC B ′C ′BC B ′C ′AC A ′C ′∠A′;(4)∠C =∠C′.如果从中任取两个条件组成一组,那么能判断△ABC ∽△A′B′C′的共有( )A .1组B .2组C .3组D .4组8.如图22-X -5,在直角梯形ABCD 中,AB =7,AD =2,BC =3,若在线段AB 上取一点P ,使得以P ,A ,D 为顶点的三角形和以P ,B ,C 为顶点的三角形相似,则这样的P 点有( )A .1个B .2个C .3个D .4个图22-X -59.[2016·泰安]如图22-X -6,△ABC 是边长为4的等边三角形,P 为BC 边上的任意一点(不与点B ,C 重合),且∠APD =60°,PD 交AB 于点D ,设BP =x ,BD =y ,则y 关于x 的函数图象大致是( )图22-X -6图22-X -710.[2016·宿州二模]在▱ABCD 中,M ,N 是AD 边上的三等分点,连接BD ,MC 相交于点O ,则S △MOD ∶S △COB =________.11.如图22-X -8,在矩形ABCD 中,AB =10 cm ,AD =20 cm ,两只小虫P 和Q 分别从点A ,B 同时出发沿AB ,BC 向终点B ,C 方向前进,小虫P 的速度为1 cm /s ,小虫Q 的速度为2 cm /s .它们同时出发多少秒时,以P ,B ,Q 为顶点的三角形与以A ,C ,D 为顶点的三角形相似?12.如图22-X-9所示,先把一张矩形纸片ABCD对折,设折痕为MN,再把点B叠在折痕线上,得到△ABE,过点B折纸片使点A叠在直线AD上,得折痕PQ.(1)求证:△PBE∽△QAB.(2)你认为△PBE和△BAE相似吗?如果相似,给出证明;如果不相似,请说明理由.图22-X-9类型之三 相似三角形的实际应用13.如图22-X-10,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去.当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3米,CA=1米,则树的高度为( )A.3米B.4米C.4.5米D.6米图22-X-1014.如图22-X-11,为了估计河的宽度,在河的对岸选定一个目标点P,在近岸取点Q 和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60 m,ST=120 m,QR=80 m,则河的宽度PQ为( )A.40 m B.60 mC.120 m D.180 m图22-X-1115.如图22-X-12,小军在地面上合适的位置平放了一块平面镜(平面镜的高度忽略不计),刚好在平面镜中的点C处看到旗杆顶部E,此时小军的站立点B与点C的水平距离为2m ,旗杆底部D 与点C 的水平距离为12 m .若小军的眼睛距离地面的高度为1.5 m (即AB =1.5 m ),则旗杆的高度为________m .图22-X -1216.如图22-X -13所示的示意图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF 来测量操场旗杆AB 的高度,他们通过调整测量位置,使斜边DF 与地面保持平行并使直角边DE 与旗杆顶点A 在同一直线上,已知DE =0.5米,EF =0.25米,且测点D 到地面的距离DG =1.5米,到旗杆的水平距离DC =25米,求旗杆AB 的高度.图22-X -13类型之四 位似图形的性质及作法17.如图22-X -14,在平面直角坐标系中,矩形OABC 的顶点O 在坐标原点,边OA 在x 轴上,OC 在y 轴上,如果矩形OA′B′C′与矩形OABC 关于点O 位似,且矩形OA′B′C′的面积等于矩形OABC 面积的,那么点B′的坐标是( )14A .(-2,3)B .(2,-3)C .(3,-2)或(-2,3)D .(-2,3)或(2,-3)图22-X -1418.如图22-X -15所示,正方形OEFG 和正方形ABCD 是位似图形,若点F 的坐标为(-1,1),点C 的坐标为(-4,2),则这两个正方形的位似中心的坐标是____________.图22-X -1519.[2017·包河区二模]如图22-X -16,在边长为1个单位的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网格线的交点)和直线l ,按要求画图.(1)作出四边形ABCD 关于直线l 成轴对称的四边形A′B′C′D′;(2)以B为位似中心,在点B的下方将四边形ABCD放大2倍得到四边形A1B1C1D1,画出四边形A1B1C1D1.类型之五 阅读理解型的相似问题20.如图22-X-17(a),P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫做△ABC的费马点.(1)如果△ABC是锐角三角形,点P为△ABC的费马点,且∠ABC=60°.①求证:△ABP∽△BCP;②若PA=3,PC=4,则PB=________.(2)如图(b),已知△ABC是锐角三角形,分别以AB,AC为边向外作△ABE和△ACD,△ABE和△ACD均为等边三角形,且CE和BD相交于点P.①求∠CPD的度数;②求证:点P为△ABC的费马点.图22-X-1721.[2016·宁波]从三角形(不是等腰三角形的)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.(1)如图22-X -18①,在△ABC 中,CD 为∠ACB 的平分线,∠A =40°,∠B =60°,求证:CD 为△ABC 的完美分割线;(2)在△ABC 中,若∠A =48°,CD 是△ABC 的完美分割线,且△ACD 为等腰三角形,求∠ACB 的度数;(3)如图22-X -18②,△ABC 中,AC =2,BC =,CD 是△ABC 的完美分割线,且2△ACD 是以CD 为底边的等腰三角形,求完美分割线CD 的长.图22-X -18类型之六 数学活动22.类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.原题:如图22-X -19①,在▱ABCD 中,E 是BC 边的中点,F 是线段AE 上一点,BF 的延长线交射线CD 于点G.若=3,求的值.AF EF CD CG(1)尝试探究在图22-X -19①中,过点E 作EH ∥AB ,交BG 于点H ,则AB 和EH 的数量关系是________,CG 和EH 的数量关系是________,的值是________.CD CG(2)类比延伸如图22-X -19②,在原题的条件下,若=m(m >0),则的值是____________(用含AF EF CD CGm 的代数式表示),试写出解答过程.(3)拓展迁移如图22-X -19③,四边形ABCD 中,DC ∥AB ,E 是BC 延长线上的一点,AE 和BD 相交于点F.若=a ,=b(a >0,b >0),则的值是________(用含a ,b 的代数式表示).AB CD BC BE AF EF图22-X -191.D [解析] ∵x ∶(x +y)=3∶5,∴5x =3x +3y ,整理,得2x =3y ,∴x ∶y =3∶2.2.D [解析] ∵l 1∥l 2∥l 3,∴=,即=.AB BC DE EF 4BC 36∴BC =8,∴AC =AB +BC =12.故选D .3.C [解析] 在▱ABCD 中,AB ∥CD ,则△DFE ∽△BAE ,∴=.DE BE DF AB ∵O 为对角线的交点,∴DO =BO.又∵E 为OD 的中点,∴DE =BD ,14则DE ∶BE =1∶3,∴DF ∶AB =1∶3.∵CD =AB ,∴DF ∶CD =1∶3,∴DF ∶FC =1∶2.4.解:如图,过点D 作DF ∥BE 交AC 于点F ,则EF ∶FC =BD ∶DC ,AM ∶MD =AE ∶EF.∵BD ∶DC =2∶3,∴EF ∶FC =2∶3.设EF =2a ,则CF =3a.∵AM ∶MD =4∶1,∴AE ∶EF =4∶1,∴AE =8a ,∴AE ∶EC =8a ∶5a =8∶5.5.C6.C [解析] ∵两个相似三角形的面积比是1∶2,∴这两个相似三角形的相似比是1∶,2∴它们的周长比是1∶.2故选C .7.C [解析] 共有3组,其组合分别是(1)和(2),根据是三边成比例的两个三角形相似;(2)和(4),根据是两边成比例且夹角相等的两个三角形相似;(3)和(4),根据是两角分别相等的两个三角形相似.8.C [解析] ①当△DAP ∽△CBP 时,AD ∶AP =BC ∶BP ,即=,解得AP =2AP 7-AP 3145;②当△DAP ∽△PBC 时,AD ∶AP =BP ∶BC ,即=,解得AP =1或AP =6.2AP 7-AP 3综上可得,这样的点P 有3个.9.C [解析] ∵△ABC 是等边三角形,∴∠B =∠C =60°.又∵∠BPD +∠APD =∠C +∠CAP ,∠APD =60°,∴∠BPD =∠CAP ,∴△BPD ∽△CAP ,∴BP ∶AC =BD ∶PC.∵△ABC 的边长为4,BP =x ,BD =y ,∴x ∶4=y ∶(4-x),∴y =-x 2+x.14故选C .10.4∶9或1∶9 [解析] 已知M ,N 是AD 边上的三等分点.(1)当=时,如图①所示.DM BC 23∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴△MOD ∽△COB ,∴S △MOD ∶S △COB =()2=4∶9.DM BC(2)当=时,如图②所示.DM BC 13∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴△MOD ∽△COB ,∴S △MOD ∶S △COB =()2=1∶9.DM BC故答案为4∶9或1∶9.11.解:设它们同时出发t s 时,以P ,B ,Q 为顶点的三角形与以A ,C ,D 为顶点的三角形相似,则AP =t cm ,BQ =2t cm ,PB =(10-t)cm .(1)当△PBQ ∽△ADC 时,有=,PB AD BQ DC即=,解得t =2;10-t 202t 10(2)当△PBQ ∽△CDA 时,有=,PB CD BQ DA即=,解得t =5.10-t 102t 20综上可得,当它们同时出发2 s 或5 s 时,以P ,B ,Q 为顶点的三角形与以A ,C ,D 为顶点的三角形相似.12.解:(1)证明:∵∠PBE +∠ABQ =180°-90°=90°,∠PBE +∠PEB =90°,∴∠ABQ =∠PEB.又∵∠BPE =∠AQB =90°,∴△PBE ∽△QAB.(2)相似.证明:∵△PBE ∽△QAB ,∴=.BE AB PE BQ 由折叠可知BQ =PB ,∴=,即=.BE AB PE PB BE PE AB PB又∵∠ABE =∠BPE =90°,∴△PBE ∽△BAE.13.D14.C [解析] ∵RQ ⊥PS ,TS ⊥PS ,∴RQ ∥TS ,∴△PQR ∽△PST ,∴=,即=,PQ PS QR ST PQ PQ +6080120∴PQ =120(m ).故选C .15.9 [解析] 由题意可得AB =1.5 m ,BC =2 m ,DC =12 m .易得△ABC ∽△EDC ,则=,即=,解得ED =9.AB ED BC DC 1.5ED 212故答案为9.16.解:∵∠ADC =∠FDE ,∠ACD =∠FED =90°,∴△ACD ∽△FED ,∴=,即=,AC EF CD DE AC 0.25250.5解得AC =12.5.∵AB ⊥BG ,DG ⊥BG ,DC ⊥AB ,∴∠ABG =∠BGD =∠DCB =90°,∴四边形BGDC 是矩形,∴BC =DG =1.5,∴AB =AC +BC =12.5+1.5=14(米).答:旗杆AB 的高度是14米.17.D [解析] ∵矩形OA′B′C′与矩形OABC 关于点O 位似,∴矩形OA′B′C′∽矩形OABC.∵矩形OA′B′C′的面积等于矩形OABC 面积的,14∴矩形OA′B′C′与矩形OABC 的相似比为1∶2.∵点B 的坐标为(-4,6),∴点B′的坐标是(-2,3)或(2,-3).故选D .18.(2,0)或(-,) [解析] ①当两个位似图形在位似中心同旁时,位似中心就是CF 与4323x 轴的交点.设直线CF 所对应的函数表达式为y =kx +b ,将C(-4,2),F(-1,1)代入,得解得{-4k +b =2,-k +b =1,){k =-13,b =23,)即y =-x +.令y =0,得x =2,1323∴点O′的坐标是(2,0).②当位似中心点O′在两个正方形之间时,可求得直线OC 所对应的函数表达式为y =-12x ,直线DE 所对应的函数表达式为y =x +1.联立得解得即点O′的坐14{y =-12x ,y =14x +1,){x =-43,y =23,)标是(-,).4323综上可知,点O ′的坐标为(2,0)或(-,).432319.解:(1)如图,四边形A′B′C′D′即为所求.(2)如图,四边形A 1B 1C 1D 120.解:(1)①证明:∵∠PAB 60°,∠PBC +∠PBA =∠ABC =60°,∴∠PAB =∠PBC.又∵∠APB =∠BPC =120°,∴△ABP ∽△BCP.②∵△ABP ∽△BCP ,∴=,PA PB PB PC∴PB 2=PA·PC =12,∴PB =2 .3(2)①如图,∵△ABE 与△ACD 都为等边三角形,∴BAE =∠CAD =60°,AE =AB ,AC =AD ,∴∠BAE +∠BAC =∠CAD +∠BAC ,即∠EAC =∠BAD.在△ACE 与△ADB 中,∵{AC =AD ,∠EAC =∠BAD ,AE =AB ,)∴△ACE ≌△ADB ,∴∠1=∠2.∵∠3=∠4,∴∠CPD =∠5=60°.②证明:如图,连接AP ,设AC 与BD 交于点F.易证△ADF ∽△PCF ,∴=.AF PF DF CF又∵∠AFP =∠CFD ,∴△AFP ∽△DFC ,∴∠APF =∠DCF =60°.∴∠APC =∠CPD +∠APF =60°+60°=120°.同理可得∠BPA =120°,∴∠BPC =360°-∠BPA -∠APC =120°,∴点P 为△ABC 的费马点.21.解:(1)证明:如图①.∵∠A =40°,∠B =60°,∴∠ACB =80°,∴△ABC 不是等腰三角形.∵CD 平分∠ACB ,∴∠ACD =∠BCD =∠ACB =40°,12从而∠ACD =∠A =40°,∴△ACD 为等腰三角形.∵∠BCD =∠A =40°,∠CBD =∠ABC ,∴△BCD ∽△BAC ,∴CD 是△ABC的完美分割线.(2)(i )当AD =CD 时,如图①,∠ACD =∠A =48°.∵△BDC ∽△BCA ,∴∠BCD =∠A =48°,∴∠ACB =∠ACD +∠BCD =48°+48°=96°.(ii )当AD =AC 时,如图②,∠ACD =∠ADC ==66°.180°-48°2∵△BDC ∽△BCA ,∴∠BCD =∠A =48°,∴∠ACB =∠ACD +∠BCD =66°+48°=114°.(iii )当AC =CD 时,如图③,∠ADC =∠A =48°.∵△BDC ∽△BCA ,∴∠BCD =∠A =48°.∵∠ADC 应大于∠BCD ,∴此种情况不存在.综上可知∠ACB 的度数为96°或114°.(3)由已知得AC =AD =2.∵△BCD ∽△BAC ,∴=.设BD =x ,从而=,BC BA BD BC 2x +2x 2即()2=x(x +2).2∵x>0,∴x =-1,即BD =-1.33∵△BCD ∽△BAC ,∴=,CD AC BD BC即=,CD 23-12∴CD =×2=-.3-126222.[解析] (1)体现了“特殊”的情形,=3是一个确定的数值.如图a ,过点E 作AB EF的平行线,构造相似三角形,利用相似三角形和中位线的性质,分别将各相关线段统一用EH 来表示,即可求得比值.(2)体现了“一般”的情形,=m 不再是一个确定的数值,但(1)问中的方法仍适用,如AF EF 图b 所示.(3)体现了“类比”与“转化”的情形,将(1)(2)问中的方法推广转化到梯形中,如图c 所示.解:(1)AB =3EH CG =2EH 32(2) 过点E 作EH ∥AB ,交BG 于点H ,则△ABF ∽EHF ,∴==m ,则AB =m 2AB EH AF EFm·EH ,CD =m·EH.易得EH 为△BCG 的中位线,则CG =2EH.∴==.CD CG m·EH 2EH m 2(3)ab。
第22章 相似形数学九年级上册-单元测试卷-沪科版(含答案)

第22章相似形数学九年级上册-单元测试卷-沪科版(含答案)一、单选题(共15题,共计45分)1、如图,在四边形ABCD中,对角线AC与BD相交于点O,AC平分∠DAB,且∠DAC=∠DBC,那么下列结论不一定正确的是()A.△AOD∽△BOCB.△AOB∽△DOCC.CD=BCD.BC•CD=AC•OA2、如果点D、E,F分别在△ABC的边AB、BC,AC上,联结DE、EF,且DE∥AC,那么下列说法错误的是()A.如果EF∥AB,那么AF:AC=BD:ABB.如果AD:AB=CF:AC,那么EF∥ABC.如果△EFC∽△ABC,那么EF∥ABD.如果EF∥AB,那么△EFC∽△BDE3、如图,∠APD=90°,AP=PB=BC=CD,则下列结论成立的是()A.△PAB∽△PCAB.△PAB∽△PDAC.△ABC∽△DBAD.△ABC∽△DCA4、如图,在菱形ABCD中,∠A=60°,AB=2,点M为边AD的中点,连接BD交CM于点N,则BN的长是()A.1B.C.D.5、如图所示,△ABC∽△ACD,且AB=10cm,AC=8cm,则AD的长是()A.6.4cmB.6cmC.2cmD.4cm6、如图,线段CD两个端点的坐标分别为C(4,4)、D(6,2),以原点O为位似中心,在第一象限内将线段CD缩小为线段AB,若点B的坐标为(3,1),则点A的坐标为()A.(0,3)B.(1,2)C.(2,2)D.(2,1)7、已知= ,则下列结论一定正确的是()A.x=2,y=3B.2x=3yC.D.8、已知,下列变形错误的是()A. B. C. D.9、若△ABC∽△DEF,且对应中线比为2:3,则△ABC与△DEF的面积比为()A.3:2B.2:3C.4:9D.9:1610、若,则的值为( )A. B. C. D.11、如图,在四边形ABCD中,∠ABC=90°,AB=BC= ,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为 ( )A.2B.C.D.312、如图,过菱形ABCD的顶点C的直线与AB的延长线交于点E,与AD的延长线交于点F,若菱形的边长为x,BE=a,DF=b,则a,b,x满足的关系是()A.2x=a+bB.x 2=a•bC.x(a+b)=a•bD.2x 2=a 2+b 213、把△ABC的各边分别扩大为原来的3倍,得到△A′B′C′,下列结论不能成立的是()A.△ABC∽△A′B′C′B.△ABC与△A′B′C′的各对应角相等C.△ABC与△A′B′C′的相似比为D.△ABC与△A′B′C′的相似比为14、如图,等边三角形ABC的边长为3,点P为BC边上一点,且BP=1,点D为AC边上一点,若∠APD=60°,则CD的长为( )A. B. C. D.115、下列命题中,①有一组邻边互相垂直的菱形是正方形②若2x=3y,则=③若(﹣1,a)、(2,b)是双曲线y= 上的两点,则a>b正确的有()个.A.1B.2C.3D.0二、填空题(共10题,共计30分)16、如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP=________.17、如图,在Rt△ABC中,∠C=90°,点D在边AB上,线段DC绕点D逆时针旋转,端点C恰巧落在边AC上的点E处.如果=m,=n.那么m与n满足的关系式是:m=________(用含n的代数式表示m).18、小明身高是1.6m,影长为2m,同时刻教学楼的影长为24m,则楼的高是________.19、在△ABC中,AB=5,AC=4,BC=3,D是边AB上的一点,E是边AC上的一点(D,E均与端点不重合),如果△CDE与△ABC相似,那么CE=________20、如图,小明在A时测得某树的影长为3米,B时又测得该树的影长为12米,若两次日照的光线互相垂直,则树的高度为________米.21、已知线段AB=1,点C是线段AB的黄金分割点(AC>BC),则AC=________(精确到0.01)22、如图,在Rt△BEG中,∠BEG=90°,ED平分∠BEG,点H、F在EG上,∠CFG=2∠EDH,∠EBG=∠DEB+∠EDH,BD=CD=CG=2,则CF的长为________。
沪科版九年级上册数学第22章 相似形 含答案
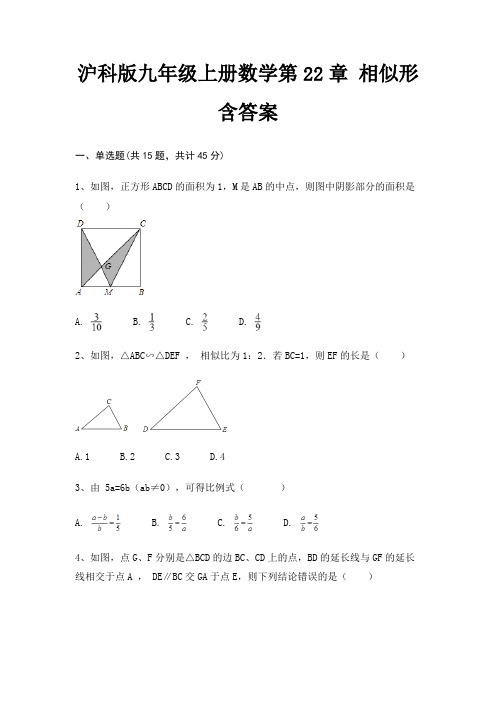
沪科版九年级上册数学第22章相似形含答案一、单选题(共15题,共计45分)1、如图,正方形ABCD的面积为1,M是AB的中点,则图中阴影部分的面积是()A. B. C. D.2、如图,△ABC∽△DEF ,相似比为1:2.若BC=1,则EF的长是()A.1B.2C.3D.43、由 5a=6b(ab≠0),可得比例式()A. B. C. D.4、如图,点G、F分别是△BCD的边BC、CD上的点,BD的延长线与GF的延长线相交于点A , DE∥BC交GA于点E,则下列结论错误的是()A. B. C. D.5、如图,□ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC 等于()A.3:2B.3:1C.1:1D.1:26、已知=,那么下列等式中,不一定正确的是()A.2a=5bB. =C.a+b=7D. =7、如图,△ABC内接于⊙O,AD⊥BC于点D,AD=2cm,AB=4cm,AC=3cm,则⊙O 的直径是( )A.2cmB.4cmC.6cmD.8cm8、如图,在中,于点,若,则的值为()A. B. C. D.9、如图,直线l1∥l2∥l3,直线AC分别交l1, l2, l3于点A , B ,C;直线DF分别交l1, l2, l3于点D , E , F . AC与DF相交于点H ,且AH=2,HB=1,BC=5,则的值为().A. B.2 C. D.10、已知x:y=3:2,则下列各式中不正确的是()A. B. C. D.11、下列各组图形中一定相似的有()A.两个矩形B.两个等腰梯形C.两个等腰三角形D.两个等边三角形12、如图,△ABC中,D是边AC上的一点,且∠DBC=∠A,BC=, AC=3,则CD的长是 ( )A.1B.C.2D.13、雨后初晴,一学生在运动场上玩耍,从他前面2米远一块小积水处,他看到旗杆顶端的倒影,如果旗杆底端到积水处的距离为40米,该生的眼部高度是1.5米,那么旗杆的高度是()A.30米B.40米C.25米D.35米14、已知,那么的值为()A. B. C. D.15、如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥AB,若AB=3BD。
第一学期沪科版九年级上册数学第22章《相似形》单元测试卷(有答案)
第一学期沪科版九年级上册数学第22章《相似形》单元测试卷(有答案)一、填空题〔共10 小题,每题 3 分,共30 分〕1.Rt△ABC的三边长AB=5,BC=4,AC=3,Rt△A′B′C′的三边长A′B′=10,B′C′=8,A′C′=6,那么Rt△ABC________Rt△A′B′C′.2.如图,在△ABC中,DE // BC,AEEC =23,那么△ADE与△ABC的面积比为________.3.如图,P是Rt△ABC的形内一点,过点P作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线最多有________.4.如图,点P是△ABC的边AB上的一点,过点P作不时线,把三角形分红两局部,使截得的三角形与原三角形相似,这种直线最多可作________条.5.早晨,小亮走在大街上.他发现:当他站在大街两边的两盏路灯之间,并且自己被两边路灯照在地上的两个影子成不时线时,自己左边的影子长为3米,左边的影子长为1.5米.又知自己身高1.80米,两盏路灯的高相反,两盏路灯之间的距离为12米.那么路灯的高为________米.6.如图,在△ABC中,D、E两点区分在边BC、AC上,AE:EC=CD:BD=1:2,AD与BE相交于点F,假定△ABC的面积为21,那么△ABF的面积为________.7.假定△ABC的三条边长的比为3:5:6,与其相似的另一个△A′B′C′的最小边长为12cm,那么△A′B′C′的最大边长是________.8.小明的身高是1.6米,它的影长是2米,同一时辰学校旗杆的影长是13米,那么学校旗杆的高是________.9.△ABC中,D、E区分是边AB与AC的中点,BC=4,下面四个结论:①DE=2;②△ADE∽△ABC;③△ADE的面积与△ABC的面积之比为1:4;④△ADE的周长与△ABC的周长之比为1:4;其中正确的有________.〔只填序号〕10.如图,在△ABC中,己知AB=AC=5 cm,BC=8 cm,点P在边BC上沿B到C的方向以每秒1 cm的速度运动〔不与点B,C重合〕,点Q在AC上,且满足∠APQ=∠B,设点P运动时间为t秒,当△APQ是等腰三角形时,t=________.二、选择题〔共10 小题,每题 3 分,共30 分〕11.以下各组线段〔单位:cm〕中,成比例线段的是〔〕A.1、2、3、4B.1、2、2、4C.3、5、9、13D.1、2、2、312.如图,身高为1.5米的某先生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=4米,CA=2米,那么树的高度为〔〕A.6米B.4.5米C.4米D.3米13.在三条线段a,b,c中,a的一半等于b的四分之一长,也等于c的六分之一长,那么这三条线段的和与b的比等于〔〕A.1:6B.6:1C.1:3D.3:114.点C是线段AB的黄金联系点,且AB=6cm,那么BC的长为〔〕A.(3√5−3)cmB.(9−3√5)cmC.(3√5−3)cm或(9−3√5)cmD.(9−3√5)cm或(6√5−6)cm15.以下说法不正确的选项是〔〕A.含30∘角的直角三角形与含60∘角的直角三角形是相似的B.一切的矩形是相似的C.一切边数相等的正多边形是相似的D.一切的等边三角形都是相似的16.:如图△ABC中,AF:FC=1:2,且BD=DF,那么BE:EC等于〔〕A.1:4B.1:3C.2:5D.2:317.如图,AD // BE // CF,直线l1、l2与这三条平行线区分交于点A、B、C和点D、E、F,假定AB=2,AC=6,DE=1.5,那么DF的长为〔〕A.7.5B.6C.4.5D.318.如图,在△ABC中,∠ACB=90∘,CD是斜边AB上的高,那么图中相似三角形有〔〕A.1对B.2对C.3对D.4对19.以下说法正确的选项是〔〕A.四条边对应成比例的两个四边形相似B.相似三角形的面积的比等于相似比C.对应角相等的多边形相似D.三边对应成比例的两个三角形相似20.假定△ABC∽△A′B′C′,那么相似比k等于〔〕A.A′B′:ABB.∠A:∠A′C.S△ABC:S△A′B′C′D.△ABC周长:△A′B′C′周长三、解答题〔共6 小题,每题10 分,共60 分〕21.如图,在Rt△ABC中,∠BAC=90∘,AD⊥BC于点D,求证:AD2=CD⋅BD.22.如图,MN // PQ // BC,且AN3=NQ2=QC.(1)梯形MNQP与梯形PBCQ能否位似?假设位似,求出它们的相似比,假设不位似,说明理由;(2)假定S△ABC=30cm2.求梯形MNQP的面积.23.△ABC中,D为BC上的一点,BDDC =2,E是AD上一点,AEED=14,求BEEF,AFFC的值.24.如图,在△ABC中,AD平分∠BAC,AD的垂直平分线交AD于E,交BC的延伸线于F,求证:FD2=FB×FC.25.如下图,∠C=90∘,BC=8cm,AC=6cm,点P从点B动身,沿BC向点C以2cm/s的速度移动,点Q从点C动身沿CA向点A以1cm/s的速度移动,假设P、Q区分从B、C同时动身,过多少时,以C、P、Q为顶点的三角形恰与△ABC相似?26.如图,有一块塑料矩形模板ABCD,长为10cm,宽为4cm,将你手中足够大的直角三角板PHF的直角顶点P落在AD边上〔不与A、D重合〕,在AD上适当移动三角板顶点P.(1)能否使你的三角板两直角边区分经过点B与点C?假定能,请你求出这时AP的长;假定不能,请说明理由;(2)再次移动三角板位置,使三角板顶点P在AD上移动,直角边PH一直经过点B,另不时角边PF与DC延伸线交于点Q,与BC交于点E,能否使CE=2 cm?假定能,请你求出这时AP 的长;假定不能,请你说明理由.答案1.∽2.4:253.34.45.6.66.67.24cm8.10.4米9.①②③10.3秒或398秒11-20:BBDCB BCCDD21.证明:∵AD⊥BC于点D,∵∠ADB=∠ADC=90∘,∵∠B+∠BAD=90∘,而∠BAD=∠DAC=90∘,∵∠B=∠DAC,∵Rt△ADB∽Rt△CDA,∵AD:CD=BD:AD,∵AD2=CD⋅BD.22.解:(1)梯形MNQP与梯形PBCQ不位似,∵AN 3=NQ2=QC,∵AN:NQ:QC=3:2:1,∵MN // PQ // BC,∵NQ QC =MPPB=2,MNPQ=ANAQ=35,∵梯形MNQP与梯形PBCQ不位似;(2)∵MN // BC,∵S△AMN:S△ABC=(ANAC )2=14,又S△ABC=30,∵S△AMN=152,∵MN // PQ,∵S△AMN:S△APQ=(ANAQ )2=925,又S△AMN=152,∵S△APQ=1256,∵梯形MNQP的面积=S△APQ−S△AMN=403.23.解:作DG // AC交BF于G,如图,∵BDDC=2,∵BD BC =23,∵DG // CF,∵BG BF =DGCF=BDBC=23,∵FC=32DG,GF=13BF,∵DG // AF ,∵EF GE =AF DG =AE ED =14,∵AF =14DG ,EF =14EG ,∵AF:FC =16,BE EF =14:1.24.解:如图:衔接AF ,∵EF 垂直平分AD ,∵FA =FD .∠FAD =∠FDA ,∵AD 平分∠BAC ,∵∠BAD =∠CAD .在△FAC 和△FBA 中,∠AFC =∠BFA ,∠ACF =∠B +2∠BAD =∠FDA +∠BAD =∠FAD +∠BAD =∠BAF . ∵△ACF ∽△BAF ,∵CF AF =AF BF .∵AF 2=BF ⋅FC .又∵FA =FD∵FD 2=FB ⋅FC .25.解:设经过y 秒后,△CPQ ∽△CBA ,此时BP =2y ,CQ =y . ∵CP =BC −BP =8−2y ,CB =8,CQ =y ,CA =6.∵△CPQ ∽△CBA ,∵CP CB =CQ CA ,∵8−2y 8=y 6 ∵y =2.4设经过y 秒后,△CPQ ∽△CAB ,此时BP =2y ,CQ =y .∵CP =BC −BP =8−2y .∵△CPQ ∽△CAB ,∵CP CA =CQ CB∵8−2y 6=y 8∵y =3211所以,经过2.4秒或许经事先3211两个三角形都相似26.解:(1)设AP =xcm ,那么PD =(10−x)cm ,由于∠A =∠D =90∘,∠BPC =90∘,所以∠DPC =∠ABP ,所以△ABP ∽△DPC ,那么ABPD =APDC,即AB⋅DC=PD⋅AP,所以4×4=x(10−x),即x2−10x+16=0,解得x1=2,x2=8,所以可以使三角板两直角边区分经过点B与点C,AP=2cm或8cm;(2)能.设AP=xcm,CQ=ycm.∵ABCD是矩形,∠HPF=90∘,∵△BAP∽△ECQ,△BAP∽△PDQ,∵AP CQ =ABCE,APDQ=ABPD,∵AP⋅CE=AB⋅CQ,AP⋅PD=AB⋅DQ,∵2x=4y,即y=x2,∵x(10−x)=4(4+y),∵y=x2,即x2−8x+16=0,解得x1=x2=4,∵AP=4cm,即在AP=4cm时,CE=2 cm.。
沪科版九年级上册数学第22章 相似形含答案
沪科版九年级上册数学第22章相似形含答案一、单选题(共15题,共计45分)1、如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,则GH长为()A.1B.1.2C.2D.2.52、如图,已知直线l∥m∥n,直线a分别与l,m,n交于点A,B,C,过点B 作直线b交直线l,n于点D,E,若AB=2,BC=1,BD=3,则BE的长为()A.4B.2C.D.3、下列命题中不成立的是()A.矩形的对角线相等B.三边对应相等的两个三角形全等C.两个相似三角形面积的比等于其相似比的平方D.一组对边平行,另一组对边相等的四边形一定是平行四边形4、如图,△ABC中,D、E分别为边AB、AC上的点,且DE∥BC,下列判断错误的是()A. =B. =C. =D. =5、如图,△ABC, AB=12,AC=15,D为AB上一点,且AD= AB ,在AC上取一点E,使以A,D,E为顶点的三角形与ABC相似,则AE等于()A. B.10 C. 或10 D.以上答案都不对6、如图,已知,,那么下列结论中,正确的是()A. B. C. D.7、如图;在△ABC中,∠CAB=Rt∠,以△ABC的各边为边作三个正方形,点E 落在FH上,点J落在ED的延长线上,若图中两块阴影部分面积的差是30,则AB的长是()A. B. C.8 D.8、如图,在△ABC中,已知∠ADE=∠B,则下列等式成立的是()A. =B. =C. =D. =9、如果两个相似三角形的面积比是1:4,那么它们的周长比是()A.1:16B.1:4C.1:6D.1:210、在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2012个正方形的面积为()A.5×2010B.5×2010C.5×2012D.5×402211、两相似三角形对应高长的比为3:4,则对应中线长的比为()A.3:4B.9:16C. :2D.4:312、如图,在ABC中,AD平分∠BAC,AE:AC=AF:AB=1:3,那么AG:GD的值为()A.1:2B.1:3C.2:5D.3:513、如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射到桌面后在地面上形成(圆形)的示意图. 已知桌面直径为1.2米,桌面离地面1米. 若灯泡离地面3米,则地面上阴影部分的面积()A.0.36π米2B.0.81π米2C.2π米2D.3.24π米214、某一时刻,身高1.6m 的小明在阳光下的影长是0.4m.同一时刻同一地点,测得某旗杆的影长是5m,则该旗杆的高度是()A.1.25mB.10mC.20mD.8m15、如图所示,长为8cm,宽为6cm的矩形中,截去一个矩形(图中阴影部分),如果剩下矩形与原矩形相似,那么剩下矩形的面积是()A.28cm 2B.27cm 2C.21cm 2D.20cm 2二、填空题(共10题,共计30分)16、如图,点A,点B分别在y轴x轴上,OA=OB,点E为AB的中点,连接并延长OE交反比例函数(x>0)的图象于点C,过点C作CD⊥x轴于点D,点D关于直线AB的对称点恰好在反比例函数图象上,则=________.17、如图,在正方形ABCD中,点E为AD的中点,连接EC,过点E作EF⊥EC,交AB于点F,则tan∠ECF=________.18、在上午的某一时刻身高1.7米的小刚在地面上的影长为3.4米,同时一棵树在地面上的影子长12米,则树的高度为________米.19、将一副三角板按图叠放,则△AOB与△DOC的面积之比等于________20、如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=,则线段CE的最大值为________ .21、如图,在△ABC中,DE∥BC,AH⊥BC于点H,与DE交于点G.若,则=________.22、已知,则=________23、若,则=________.24、如图,在矩形ABCD中,AB=4,BC=,M为BC边中点,E为AD边上的一动点,过点A作BE的垂线,垂足为F,连接FM,则FM的最小值为________.在线段FM上取点G,使GM=FM,将线段GM绕点M顺时针旋转60°得到NM,连接GN,CN,则CN的最小值为________.25、在△ABC中,D,E分别在边AB,AC上,且DE∥BC,过点A作平行于BC的直线分别交CD和BE的延长线于点M,N,若DE=2,BC=6,则MN=________.三、解答题(共5题,共计25分)26、已知x:y:z=2:3:4,求的值.27、已知:如图,四边形ABCD是平行四边形,F是AB上一点,连接DF并延长交CB的延长线于E.求证:AD:AF=CE:AB28、在△ABC中,M是AB上一点,若过M的直线所截得的三角形与原三角形相似,试说明满足条件的直线有几条,画出相应的图形加以说明.29、网格中每个小正方形的边长都是1.(1)将图1中画一个格点三角形DEF,使得△DEF≌△ABC(2)将图2中画一个格点三角形MNL,使得△MNL∽△ABC,且相似比为2:1(3)将图3中画一个格点三角形OPQ,使得△OPQ∽△ABC,且相似比为:130、如图,要测量河岸相对的两点A、B的距离,先从点B出发与AB成90°角方向,向前走50m到C处立一根标杆,然后方向不变继续朝前走10m到D处,在D处转90°沿DE方向再走17m,这时A、C、E在同一直线上.问A、B间的距离约为多少?参考答案一、单选题(共15题,共计45分)1、B2、D3、D4、B5、C6、A7、A8、B9、D10、D11、A12、A13、B14、C15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、23、24、25、三、解答题(共5题,共计25分)26、27、29、30、。
沪科版九年级上册数学第22章 相似形 含答案
沪科版九年级上册数学第22章相似形含答案一、单选题(共15题,共计45分)1、如图,AD是的一条角平分线,点E在AD上.若,,则与的面积比为()A.1:5B.5:1C.3:20D.20:32、如图,Rt△ABC中,AB⊥AC,AB=3,AC=4,P是BC边上一点,作PE⊥AB于E,PD⊥AC于D,设BP=x,则PD+PE=()A. B. C. D.3、下列两个图形一定相似的是)A.任意两个矩形B.任意两个等腰三角形C.任意两个正方形D.任意两个菱形4、如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是()A. B. C. D.5、如图,△ABC 与△A′B′C′是位似图形,点O 是位似中心,若OA=2AA′,S △ABC =8,则S △A′B′C′=( )A.18B.12C.32D.166、如图,Rt△ABC 中,∠BAC=90°,AD⊥BC 于点D ,若BD :CD=3:2,则= ( )A. B. C. D.7、如图,中,,则下列等式中不成立的是( )A.B.C.D.8、已知△ABC∽△DEF,且相似比为2:3,则△ABC 与△DEF 的对应高之比为( )A.2:3B.3:2C.4:9D.9:4 9、如图所示,不能判定△ABC∽△DAC 的条件是( )A.∠B=∠DACB.∠BAC=∠ADCC.AD 2=BD•BCD.AC 2=DC•BC10、如图,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=,则△ABC的边长是()A.3B.4C.5D.611、已知:,下列式子中错误的是()A. B. C. D.12、如图△ABC∽△ACD,则下列式子中不成立的是()A. =B. =C.AC 2=AD•ABD. =13、按100分制60分及格来算,满分是150分的及格分是()A.60分B.72分C.90分D.105分14、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有()A.1个B.2个C.3个D.4个15、如图所示,E为□ABCD的边AD上的一点,且AE∶ED=3∶2,CE交BD于F,则BF∶FD ()A.3∶5B.5∶3C.2∶5D.5∶2二、填空题(共10题,共计30分)16、如图是的中线,是上一点,且,的延长线交于点,若,则________.17、在同一时刻,太阳光下身高1.6m的小强的影长是1.2m,学校旗杆的影长是15m,则旗杆高为________ m18、如图,已知顶点,以原点为位似中心,把缩小到原来的,则与点对应的点的坐标是________.19、如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为________时,△ADP和△ABC相似.20、如图,在方格纸中,以每个小方格的边长为单位1,△ABC和△EPD的顶点均在格点上,请你提供一个符合条件的点P,使△ABC与以E,P,D为顶点的三角形相似,则点P所在的格点坐标可以是________21、如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②;③△PMN为等边三角形;④当∠ABC=45°时,BN=PC.其中正确的是________ .22、如图,内接于,于点D,,若的半径,则的长为________.23、如图,某风景区在建设规划过程中,需要测量两岸码头A、B之间的距离.设计人员在O点设桩,取OA、OB的三等分点C、D,测得CD=25m,则AB=________ .24、如图,A的坐标是(0,2),点C是x轴上的一个动点,点B与点O在直线AC两侧,∠BAC=∠OAC,BC⊥AC,点B的坐标为(x,y),y与x的函数关系式为________.25、如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD,AB=2,OD=3,则BC的长为________.三、解答题(共5题,共计25分)26、已知a、b、c满足,且,分别求出a、b、c 的值.27、如图:已知等边三角形ABC,D为AC边上的一动点,CD=nDA,连线段BD,M为线段BD上一点,∠AMD=60°,AM交BC于E.(1)若n=1,则= .= ;(2)若n=2,求证:BM=6DM;(3)当n= 时,M为BD中点.(直接写结果,不要求证明)28、已知:如图,Rt△ABC中,∠ACB=90°,P是边AB上一点,AD⊥CP,BE⊥CP,垂足分别为D、E,已知AB=3, BC=3, BE=5.求DE的长.29、如图,小明在地面上放置一个平面镜来测量铁塔的高度,镜子与铁塔的距离米,镜子与小明的距离米时,小明刚好从镜子中看到铁塔顶端.已知小华的眼睛距地面的高度CD=1.6米,求铁塔的高度.(根据光的反射原理,)30、如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E。
沪科版九年级数学上册《第22章相似形》单元检测试题(有答案)
第一学期沪科版九年级数学上册第22章_相似形单元检测试题考试总分: 120 分考试时间: 120 分钟学校:__________ 班级:__________ 姓名:__________ 考号:__________一、选择题(共 10 小题,每小题 3 分,共 30 分)1.下列各组线段(单位:)中,成比例线段的是()A.、、、B.、、、C.、、、D.、、、2.如图,身高为米的某学生想测量一棵大树的高度,她沿着树影由向走去,当走到点时,她的影子顶端正好与树的影子顶端重合,测得米,米,则树的高度为()A.米B.米C.米D.米3.在三条线段,,中,的一半等于的四分之一长,也等于的六分之一长,那么这三条线段的和与的比等于()A. B. C. D.4.点是线段的黄金分割点,且,则的长为()A. B.C.或D.或5.下列说法不正确的是()A.含角的直角三角形与含角的直角三角形是相似的B.所有的矩形是相似的C.所有边数相等的正多边形是相似的D.所有的等边三角形都是相似的6.已知:如图中,,且,那么等于()A. B. C. D.7.如图,,直线、与这三条平行线分别交于点、、和点、、,若,,,则的长为()A. B. C. D.8.如图,在中,,是斜边上的高,则图中相似三角形有()A.对B.对C.对D.对9.下列说法正确的是()A.四条边对应成比例的两个四边形相似B.相似三角形的面积的比等于相似比C.对应角相等的多边形相似D.三边对应成比例的两个三角形相似10.若,则相似比等于()A. B.C. D.周长:周长二、填空题(共 10 小题,每小题 3 分,共 30 分)11.的三边长,,,的三边长,,,则________.12.如图,在中,已知,,则与的面积比为________.13.如图,是的形内一点,过点作直线截,使截得的三角形与相似,满足这样条件的直线最多有________.14.如图,点是的边上的一点,过点作一直线,把三角形分成两部分,使截得的三角形与原三角形相似,这种直线最多可作________条.15.晚上,小亮走在大街上.他发现:当他站在大街两边的两盏路灯之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子长为米,左边的影子长为米.又知自己身高米,两盏路灯的高相同,两盏路灯之间的距离为米.则路灯的高为________米.16.如图,在中,、两点分别在边、上,,与相交于点,若的面积为,则的面积为________.17.若的三条边长的比为,与其相似的另一个的最小边长为,那么的最大边长是________.18.小明的身高是米,它的影长是米,同一时刻学校旗杆的影长是米,则学校旗杆的高是________.19.中,、分别是边与的中点,,下面四个结论:① ;② ;③ 的面积与的面积之比为;④ 的周长与的周长之比为;其中正确的有________.(只填序号) 20.如图,在中,己知,,点在边上沿到的方向以每秒的速度运动(不与点,重合),点在上,且满足,设点运动时间为秒,当是等腰三角形时,________.三、解答题(共 6 小题,每小题 10 分,共 60 分)21.如图,在中,,于点,求证:.22.如图,,且.梯形与梯形是否位似?如果位似,求出它们的相似比,如果不位似,说明理由;若.求梯形的面积.23.中,为上的一点,,是上一点,,求,的值.24.如图,在中,平分,的垂直平分线交于,交的延长线于,求证:.25.如图所示,,,,点从点出发,沿向点以的速度移动,点从点出发沿向点以的速度移动,如果、分别从、同时出发,过多少时,以、、为顶点的三角形恰与相似?26.如图,有一块塑料矩形模板,长为,宽为,将你手中足够大的直角三角板的直角顶点落在边上(不与、重合),在上适当移动三角板顶点.能否使你的三角板两直角边分别通过点与点?若能,请你求出这时的长;若不能,请说明理由;再次移动三角板位置,使三角板顶点在上移动,直角边始终通过点,另一直角边与延长线交于点,与交于点,能否使?若能,请你求出这时的长;若不能,请你说明理由.答案1.B2.B3.D4.C5.B6.B7.C8.C9.D10.D11.12.13.14.15.16.17.18.米①②③20.秒或秒21.证明:∵ 于点,∴ ,∴ ,而,∴ ,∴ ,∴ ,∴ .22.解:梯形与梯形不位似,∵,∴ ,∵ ,∴,,∴梯形与梯形不位似; ∵ ,∴,又,∴,∵ ,∴,又,∴,∴梯形的面积.23.解:作交于,如图,∵,∴,∵ ,∴,∴,,∵ ,∴,∴,,∴,.24.解:如图:连接,∵ 垂直平分,∴ .,∵ 平分,∴ .在和中,,.∴ ,∴.∴ .又∵∴ .25.解:设经过秒后,,此时,.∵ ,,,.∵ ,∴,∴∴设经过秒后,,此时,.∴ .∵ ,∴∴∴所以,经过秒或者经过后两个三角形都相似26.解:设,则,因为,,所以,所以,则,即,所以,即,解得,,所以可以使三角板两直角边分别通过点与点,或;能.设,.∵ 是矩形,,∴ ,,∴,,∴ ,,∴ ,即,∴ ,∵,即,解得,∴ ,即在时,.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018-2019学年度第一学期沪科版九年级数学上册
第22章_相似形单元检测试题
考试总分: 120 分考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题,每小题 3 分,共 30 分)
1.下列各组线段(单位: )中,成比例线段的是()
A. 、 、 、 B. 、 、 、
C. 、 、 、 D. 、 、 、
2.
如图,身高为 米的某学生想测量一棵大树的高度,她沿着树影 由 向
走去,当走到 点时,她的影子顶端正好与树的影子顶端重合,测得 米,
米,则树的高度为()
A. 米 B. 米 C. 米 D. 米
3.
在三条线段 , , 中, 的一半等于 的四分之一长,也等于 的六分之一长,
那么这三条线段的和与 的比等于()
A. B. C. D.
4.点 是线段 的黄金分割点,且 ,则 的长为()
A. B.
C. 或 D. 或
5.下列说法不正确的是()
A.
含
角的直角三角形与含 角的直角三角形是相似的
B.所有的矩形是相似的
C.所有边数相等的正多边形是相似的
D.所有的等边三角形都是相似的
6.已知:如图 中, ,且 ,那么 等于()
A. B. C. D.
7.
如图, ,直线
、 与这三条平行线分别交于点 、 、 和点
、 、 ,若 , , ,则 的长为()
A. B. C. D.
8.
如图,在 中,
, 是斜边 上的高,则图中相似三角形
有()
A. 对 B. 对 C. 对 D. 对
9.下列说法正确的是()
A.四条边对应成比例的两个四边形相似B.相似三角形的面积的比等于相似比
C.对应角相等的多边形相似D.三边对应成比例的两个三角形相似
10.若 ,则相似比 等于()
A. B.
C. D. 周长: 周长
二、填空题(共 10 小题,每小题 3 分,共 30 分)
11.
的三边长 , , , 的三边长
, , ,则 ________ .
12.
如图,在 中,已知 ,
,则 与 的面积比为
________.
13.
如图, 是 的形内一点,过点 作直线截 ,使截得的三角形
与 相似,满足这样条件的直线最多有________.
14.
如图,点 是 的边 上的一点,过点 作一直线,把三角形分成两部
分,使截得的三角形与原三角形相似,这种直线最多可作________条.
15.
晚上,小亮走在大街上.他发现:当他站在大街两边的两盏路灯之间,并且
自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子长为 米,左
边的影子长为 米.又知自己身高 米,两盏路灯的高相同,两盏路灯之间
的距离为 米.则路灯的高为________米.
16.
如图,在 中, 、 两点分别在边 、 上,
, 与 相交于点 ,若 的面积为 ,则 的面积为________.
17.
若 的三条边长的比为 ,与其相似的另一个 的最小边长为
,那么 的最大边长是________.
18.
小明的身高是 米,它的影长是 米,同一时刻学校旗杆的影长是 米,则
学校旗杆的高是________.
19.
中, 、 分别是边 与 的中点, ,下面四个结论:
① ;② ;③ 的面积与 的面积之比为
;
④ 的周长与 的周长之比为 ;其中正确的有________
.(只填序
号) 20.如图,在 中,己知 , ,点 在边 上
沿 到 的方向以每秒 的速度运动(不与点 , 重合),点 在 上,且满
足 ,设点 运动时间为 秒,当 是等腰三角形时, ________.
三、解答题(共 6 小题,每小题 10 分,共 60 分)
21.如图,在 中, , 于点 ,求证:
.
22.如图, ,且 .
梯形 与梯形 是否位似?如果位似,求出它们的相似比,如果不
位似,说明理由;
若
.求梯形 的面积.
23.
中, 为 上的一点, , 是 上一点,
,求 , 的
值.
24.
如图,在 中, 平分 , 的垂直平分线交 于 ,交 的延
长线于 ,求证:
.
25.
如图所示,
, , ,点 从点 出发,沿 向点
以 的速度移动,点 从点 出发沿 向点 以 的速度移动,如果 、
分别从 、 同时出发,过多少时,以 、 、 为顶点的三角形恰与 相
似?
26.
如图,有一块塑料矩形模板 ,长为 ,宽为 ,将你手中足够大
的直角三角板 的直角顶点 落在 边上(不与 、 重合),在 上适当移
动三角板顶点 .
能否使你的三角板两直角边分别通过点 与点 ?若能,请你求出这时 的
长;若不能,请说明理由;
再次移动三角板位置,使三角板顶点 在 上移动,直角边 始终通过点 ,
另一直
角边 与 延长线交于点 ,与 交于点 ,能否使 ?若能,请你
求出这时 的长;若不能,请你说明理由.
答案
1.B
2.B
3.D
4.C
5.B
6.B
7.C
8.C
9.D
10.D
11.
12.
13.
14.
15.
16.
17.
18. 米
①②③
20.
秒或
秒
21.证明:∵ 于点 ,
∴
,
∴
,
而 ,
∴ ,
∴ ,
∴ ,
∴ .
22.解: 梯形 与梯形 不位似,
∵ ,
∴ ,
∵ ,
∴
,
,
∴梯形 与梯形 不位似; ∵ ,
∴ ,又 ,
∴
,
∵ ,
∴
,又 ,
∴
,
∴
梯形 的面积
.
23.解:作 交 于 ,如图,
∵ ,
∴
,
∵ ,
∴
,
∴ , ,
∵ ,
∴
,
∴ , ,
∴ , .
24.解:如图:
连接 ,∵ 垂直平分 ,
∴ . ,
∵ 平分 ,
∴ .
在 和 中,
,
.
∴ ,
∴
.
∴ .
又∵
∴ .
25.解:设经过 秒后, ,此时 , .
∵ , , , .
∵ ,
∴
,
∴
∴
设经过 秒后, ,此时 , .
∴ .
∵ ,
∴
∴
∴
所以,经过 秒或者经过 后两个三角形都相似
26.解: 设 ,则 ,
因为 , ,
所以 ,
所以 ,
则 ,即 ,
所以 ,即
,
解得
, ,
所以可以使三角板两直角边分别通过点 与点 , 或 ; 能.
设 , .
∵
是矩形,
,
∴ , ,
∴
,
,
∴ , ,
∴
,即
,
∴ ,
∵
,
即
,
解得
,
∴ ,
即在 时, .
