2020佛山二模(扫描版)
2020年广东省佛山市高考数学二模试卷(一)(有答案解析)

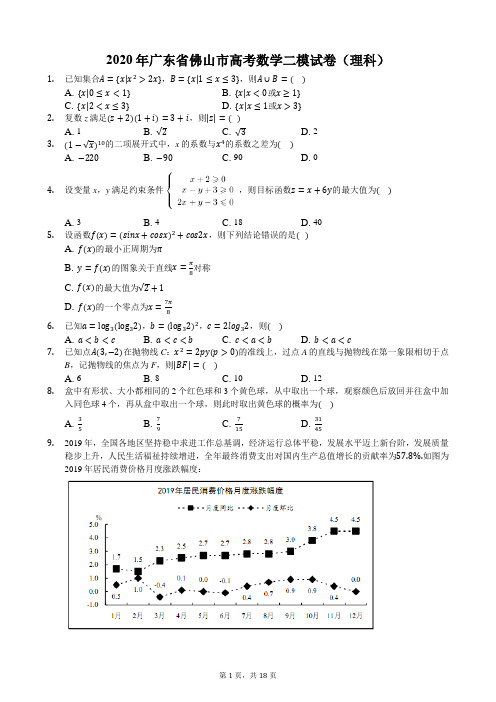
2020年广东省佛山市高考数学二模试卷(一)一、选择题(本大题共12小题,共60.0分)1.若集合A={x|−5<x<2},B={x||x|<3},则A∩B=()A. {x|−3<x<2}B. {x|−5<x<2}C. {x|−3<x<3}D. {x|−5<x<3}2.复数z=(2+i)(1−i),其中i为虚数单位,则z的实部是()A. −1B. 1C. 2D. 33.若向量m⃗⃗⃗ =(0,−2),n⃗=(√3,1),则与2m⃗⃗⃗ +n⃗共线的向量可以是()A. (√3,−1)B. (−1,√3)C. (−√3,−1)D. (−1,−√3)4.设变量x,y满足约束条件{3x+y−6≥0x−y−2≤0y−3≤0,则目标函数z=y−2x的最大值为()A. −7B. −4C. 1D. 25.将函数的图象向右平移π12单位后,所得图象对应的函数解析式为()A. B.C. D.6.已知等差数列{a n},a4=9,a8=−a9,则a1=()A. 21B. 19C. 17D. 157.已知cosα=√210,α∈(−π,0),则cos(α−π4)=()A. −35B. −45C. 35D. 458.若函数f(x)={x2+x,x≥0x2−ax,x<0(a∈R)为偶函数,则下列结论正确的是()A. f(a)>f(2a)>f(0)B. f(a)>f(0)>f(2a)C. f(2a)>f(a)>f(0)D. f(2a)>f(0)>f(a)9.如图是1990年−2017年我国劳动年龄(15−64岁)人口数量及其占总人口比重情况:根据图表信息,下列统计结论不正确的是()A. 2000年我国劳动年龄人口数量及其占总人口比重的年增幅均为最大B. 2010年后我国人口数量开始呈现负增长态势C. 2013年我国劳动年龄人口数量达到峰值D. 我国劳动年龄人口占总人口比重极差超过6%10.已知正四面体P−ABC的棱长为2,D为PA的中点,E,F分别是线段AB,PC(含端点)边上的动点,则DE+DF的最小值为()A. √2B. √3C. 2D. 2√211.已知a>0,b>0,则“a>b”是“e a+2a=e b+3b”的()A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件12.已知F为双曲线C:x2a2−y2b2=1(a>b>0)的右焦点,AB是双曲线C的一条渐近线上关于原点对称的两点,AF⊥BF,且AF的中点在双曲线C上,则C的离心率为()A. √5−1B. 2√2−1C. √3+1D. √5+1二、填空题(本大题共4小题,共20.0分)13.直线y=ax是曲线的切线,则实数a=________.14.设数列{a n}的前n项和为S n,且满足a1+2a2+⋯+2n−1a n=n,则S5=______.15.已知抛物线x2=2py(p>0)的焦点为F,准线为l,点P(4,y0)在抛物线上,K为l与y轴的交点,且|PK|=√2|PF|,则y0=______.16.已知矩形ABCD,AB=1,BC=√3,将△ADC沿对角线AC进行翻折,得到四棱锥D−ABC,则在翻折的过程中有下列结论:①四棱锥D−ABC的体积最大值为14;②四棱锥D−ABC的外接球体积不变;③异面直线AB与CD所成角的最大值为90°.其中正确的是______(填写所有正确结论的编号)三、解答题(本大题共7小题,共82.0分)17.已知a,b,c分别为△ABC内角A,B,C的对边,cosC=c+2b2a.(Ⅰ)求A;(Ⅱ)已知点D在BC边上,DC=2BD=2,AC=√3,求AD.18.如图,四棱锥E−ABCD中,四边形ABCD是边长为2的菱形,∠DAE=∠BAE=45°,∠DAB=60°.(Ⅰ)证明:平面ADE⊥平面ABE:(Ⅱ)若DE=√10,求四棱锥E−ABCD的体积.19.移动支付极大地方便了我们的生活,也为整个杜会节约了大量的资源与时间成本.2018年国家高速公路网力推移动支付车辆高速通行费.推广移动支付之前,只有两种支付方式:现金支付或ETC支付,其中使用现金支付车辆比例的为60%,使用ETC支付车辆比例约为40%,推广移动支付之后,越来越多的车主选择非现金支付,如表是推广移动支付后,随机抽取的某时间段内所有经由某高速公路收费站驶出高速的车辆的通行费支付方式分布及其他相关数据:并以此作为样本来估计所有在此高速路上行驶的车辆行费支付方式的分布.已知需要取卡的车辆进入高速平均每车耗时为10秒,不需要取卡的车辆进入高速平均每车耗时为4秒.(Ⅰ)若此高速公路的日均车流量为9080辆,估计推广移动支付后比推广移动支付前日均可少发卡多少张?(Ⅱ)在此高速公路上,推广移动支付后平均每辆车进出高速收费站总耗时能否比推广移动支付前大约减少一半?说明理由.20.已知F为椭圆C:x2a2+y2b2=1(a>b>0)的左焦点,过原点O的动直线l与C交于A、B两点.当A的坐标为(1,2√55)时,|OB|=|BF|.(Ⅰ)求椭圆C的标准方程;(Ⅱ)延长BF交椭圆C于Q,求△QAB的面积的最大值.21.已知函数f(x)=a−sinxx,0<x<π.(1)若x=x0时,f(x)取得极小值f(x0),求实数a及f(x0)的取值范围;(2)当a=π,0<m<π时,证明:f(x)+mlnx>0.22.在平面直角坐标系xOy中,曲线C的参数方程为{x=1+costy=√3+sint(t为参数).(Ⅰ)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求曲线C的极坐标方程;(Ⅱ)若射线θ=α与C有两个不同的交点M、N,求证|OM|+|ON|的取值范围.23.设函数f(x)=|2x+a|+|x−1|,其中a∈R.(Ⅰ)当a=3时,求不等式f(x)<6的解集;(Ⅱ)若f(x)+f(−x)≥5,求a的取值范围.-------- 答案与解析 --------1.答案:A解析:解:B ={x||x|<3}={x|−3<x <3}, 则A ∩B ={x|−3<x <2}, 故选:A .求出集合的等价条件,结合集合交集的定义进行求解即可.本题主要考查集合的基本运算,结合集合交集的定义是解决本题的关键. 2.答案:D解析:解:∴z =(2+i)(1−i)=2−2i +i +1=3−i , ∴z 的实部是3. 故选:D .直接利用复数代数形式的乘除运算化简得答案.本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题. 3.答案:B解析:【分析】可求出2m ⃗⃗⃗ +n ⃗ =−√3(−1,√3),从而得出向量2m⃗⃗⃗ +n ⃗ 与(−1,√3)共线. 考查向量坐标的加法和数乘运算,共线向量基本定理. 【解答】 解:2m ⃗⃗⃗ +n ⃗ =(√3,−3)=−√3(−1,√3); ∴2m ⃗⃗⃗ +n ⃗ 与(−1,√3)共线. 故选:B . 4.答案:C解析:【分析】本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案. 【解答】解:由变量x ,y 满足约束条件{3x +y −6≥0x −y −2≤0y −3≤0作出可行域如图,联立{y =33x +y −6=0,解得B(1,3),化目标函数z =y −2x 为直线方程的斜截式:y =2x +z .当直线y =2x +z 过B 时,直线在y 轴上的截距最大,z 有最大值为3−2×1=1. 故选:C . 5.答案:D解析:【分析】本题主要考查函数y =Asin(ωx +φ)的图象变换规律,属于基础题. 由题意利用函数y =Asin(ωx +φ)的图象变换规律,得出结论. 【解答】解:将函数y =√2sin(2x +π4)的图象向右平移π12单位后,所得图象对应的函数解析式y =√2sin(2x −π6+π4)=√2sin(2x +π12),故选:D . 6.答案:D解析:【分析】本题考查等差数列的首项的求法,考查等差数列的性质等基础知识,考查运算求解能力,是基础题.利用等差数列通项公式列出方程组,能求出首项a 1. 【解答】解:∵等差数列{a n },a 4=9,a 8=−a 9,∴{a 1+3d =9a 1+7d =−a 1−8d, 解得a 1=15,d =−2. 故选:D . 7.答案:A解析:解:∵cosα=√210,α∈(−π,0),∴sinα=−√1−cos 2α=−7√210, ∴cos(α−π4)=cosαcos π4+sinαsin π4=√210×√22+(−7√210)×√22=−35.故选:A .由已知求得sinα,然后展开两角差的余弦求cos(α−π4).本题考查三角函数的化简求值,考查同角三角函数基本关系式与两角差的余弦,是基础题.8.答案:C解析:【分析】本题考查分段函数的奇偶性与单调性,属于基础题.先根据偶函数的定义求出a 的值,然后根据单调性比较大小. 【解答】解:因为f(x)是偶函数,所以f(−1)=f(1), 即1+a =2,所以a =1,易知当x ≥0时,f(x)是增函数, 又知2a >a >0,所以f(2a)>f(a)>f(0),故选C.9.答案:B解析:【分析】本题考查了读图识图的能力,属于基础题.【解答】A选项,2000年我国劳动年龄人口数量增幅约为6000万,是图中最大的,2000年我国劳动年龄人口数量占总人口比重的增幅约为3%,也是最多的.故A对.B选项,2010年到2011年我国劳动年龄人口数量有所增加,故B错.C选项,从图上看,2013年的长方形是最高的,即2013年我国劳动年龄人口数量达到峰值,C对,D选项,我国劳动年龄人口占总人口比重最大为2011年,约为74%,最小为1992年,约为67%,故极差超过6%.D对.故选:B.10.答案:B解析:【分析】本题考查空间中的距离的计算,属中档题.过D作DG⊥AB垂足为G,过D作DH⊥PC,垂足为H,根据DE≥DG,DF≥DH可得.【解答】解:过D作DG⊥AB垂足为G,过D作DH⊥PC,垂足为H,∴DE≥DG=12×√32AB=12×√32×2=√32,DF≥DH=12×√32PC=12×√32×2=√32,故DE+DF≥√32+√32=√3.故选:B.11.答案:B解析:解:若e a+2a=e b+3b,则e a+2a−(e b+2b)=b>0,∴e a+2a>e b+2b,由f(x)=e x+2x在x>0时单调递增,∴a>b.反之不一定成立:“a>b”不一定得出“e a+2a=e b+3b”,例如取a=100,b=1.则“e a+2a=e100+200>e+3=e b+3b”.∴a>b”是“e a+2a=e b+3b”的必要不充分条件.故选:B.若e a+2a=e b+3b,则e a+2a−(e b+2b)=b>0,可得a>b.反之不一定成立:例如取a=100,b=1.即可得出.本题考查了函数的单调性、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.12.答案:A解析:解:双曲线的渐近线方程bx+ay=0,AF⊥BF,AB是双曲线C的一条渐近线上关于原点对称的两点,∴F(c,0),AO=OB=c,∴A(−a,b),∴AF的中点坐标(c−a2,b2 ),∴(c−a)24a2−b24b2=1,∴(c−a)2a2=5,∴e+1=±√5,∴e=√5−1,e=−√5−1(舍去),故选:A.求出双曲线的渐近线方程,推出A的坐标,然后求解AF的中点,代入双曲线方程求解即可.本题考查双曲线的简单性质的应用,考查计算能力.13.答案:1解析:【分析】本小题主要考查直线的方程、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.属于基础题.欲求a的值,只须求出切线的斜率的值即可,故先利用导数求出在切点处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.【解答】解:∵y=1+lnx,,设切点为(m,1+lnm),得切线的斜率为1m,所以曲线在点(m,1+lnm)处的切线方程为:y−lnm−1=1m(x−m),它过原点,∴−lnm=0,∴m=1,∴a=1m=1.故答案为:1.14.答案:3116解析:解:a1+2a2+⋯+2n−1a n=n,可得n=1时,a1=1,n≥2时,a1+2a2+⋯+2n−2a n−1=n−1,又a1+2a2+⋯+2n−1a n=n,相减可得2n−1a n=1,即a n=(12)n−1,上式对n=1也成立,可得数列{a n}首项为1,公比为12的等比数列,可得S5=1−1251−12=3116.故答案为:3116.由题意可得数列的首项,将n换为n−1,相减可得数列的通项公式,再由求和公式计算可得所求和.本题考查数列的通项公式的求法,考查等比数列的定义和求和公式的运用,考查化简运算能力,属于基础题.15.答案:2解析:解:过P作准线l的垂线,垂足为M,则|PM|=|PF|,在Rt△PKM中,∵|PK|=√2|PF|=√2|PM|,∴PM=KM=4,∴y0=4−p2,把P(4,4−p2)代入抛物线方程x2=2py,解得p=4.∴y0=4−2=2.故答案为:2.过P作准线l的垂线,垂足为M,则PK|=√2|PM|,于是y0=4−p2,代入抛物线方程计算p的值即可求出y0.本题考查了抛物线的简单性质,属于基础题.16.答案:①②③解析:解:矩形ABCD,AB=1,BC=√3,可得AC=2,在翻折的过程中,当面ACD⊥面ACB时,D到底面的距离最大,且为直角三角形ACD斜边AC边上的高为√32,可得四棱锥D−ABC的体积最大值为13⋅12⋅1⋅√3⋅√32=14,故①正确;取AC的中点O,连接OB,OD,可得OA=OB=OC=OD,即O为四棱锥D−ABC的外接球的球心,且半径为1,体积为43π,故②正确;若AB⊥CD,又AB⊥BC,可得AB⊥平面BCD,即有AB⊥BD,由AB=1,AD=√3,BD=√2成立,故③正确.故答案为:①②③.考虑在翻折的过程中,当面ACD⊥面ACB时,D到底面的距离最大,进而得到棱锥体积最大,可判断①;取AC的中点O,可得O为棱锥的外接球的球心,计算可判断②;假设AB⊥CD,由线面垂直的判断和性质,可判断③.本题考查空间线面和线线的位置关系的判断,以及棱锥的体积计算,考查运算能力和推理能力,属于基础题.17.答案:解:(Ⅰ)∵cosC=c+2b2a =a2+b2−c22ab,∴整理可得:b2+c2−a2=−bc,∴cosA=b2+c2−a22bc =−bc2bc=−12,∵A∈(0,π),∴A=2π3,(Ⅱ)∵A=2π3,DC=2BD=2,b=AC=√3,可得:a=BC=3,∴由余弦定理a2=b2+c2−2bccosA,可得:9=3+c2−2×√3×c×(−12),可得:c2+√3c−6=0,∴解得:c=√3(负值舍去),∴cosC=a2+b2−c22ab =9+3−32×3×√3=√32,∴△ADC中,由余弦定理可得:AD=√AC2+CD2−2AC⋅CD⋅cosC=√3+4−2×√3×2×√32=1.解析:(Ⅰ)由余弦定理化简已知可得b2+c2−a2=−bc,可求cosA=−12,结合范围A∈(0,π),可求A的值.(Ⅱ)由已知可求BC=3,由余弦定理解得c的值,可求cos C的值,△ADC中,由余弦定理可得AD的值.本题主要考查了余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于基础题.18.答案:(I)证明:过D做DO⊥AE,垂足为O,连接OB,∵AD=2,∠DAE=45°,∴OD=OA=√2,在△AOB中,由余弦定理可得OB2=OA2+AB2−2OA⋅AB⋅cos∠OAB=2+4−2×√2×√22=2,∴OB=√2,∵AB=AD=2,∠DAB=60°,∴△ABD是等边三角形,∴BD=2.∴OD2+OB2=BD2,∴OB⊥OD,又OD⊥AE,AE∩OB=O,∴OD⊥平面ABE,又OD⊂ADE,∴平面ADE⊥平面ABE.(II)∵DE=√10,∴OE=√DE2−OD2=2√2,∴AE=3√2.∴V E−ABCD=2V E−ABD=2V D−ABE=2×13×12×3√2×√2×√2=2√2.解析:(I)过D做DO⊥AE,垂足为O,连接OB,利用勾股定理证明OB⊥OD,结合OD⊥AE得出OD⊥平面ABE,故而平面ADE⊥平面ABE;(II)先计算EO ,再根据V E−ABCD =2V E−ABD =2V D−ABE 计算体积.本题考查了面面垂直的判定,棱锥的体积计算,属于中档题.19.答案:解:(I)移动支付推出前,需在入口处停车取卡的车辆大约为9080×60%=5448辆,移动支付后,需在入口处停车取卡的车辆大约为9080×135+240135+240+750+375=2270辆, 估计推广移动支付后比推广移动支付前日均可少发卡5448−2270=3178张. (II)移动支付推出前,平均每辆车进出高速收费站大约耗时(10+30)×60%+(4+4)×40%=27.2秒, 移动支付推出后,平均每辆车进出高速收费站大约耗时(10+30)×1351500+(10+15)×2401500+(4+4)×750+3751500=3.6+4+6=13.6秒,所以推广移动支付后平均每辆车进出高速收费站总耗时比推广移动支付前大约减少一半.解析:(I)分别计算移动支付推广前后的发卡量即可得出结论;(II)分别计算移动支付推广前后的车辆总耗时的平均数得出结论.本题考查了数据统计与整理,考查加权平均数的计算与样本估计总体的统计思想,属于基础题.20.答案:解:(Ⅰ)由A(1,2√55),得B(−1,−2√55), 而|OB|=|BF|,∴F(−2,0),即c =2.由{1a 2+45b 2=1a 2=b 2+4,解得a 2=5,b 2=1. ∴椭圆C 的标准方程为x 25+y 2=1;(Ⅱ)当直线BF 斜率不存在时,BF :x =−2,此时B(−2,−√55),|BQ|=2√55,A(2,√55), S QAB =12×2√55×2=2√55; 当BF 所在直线斜率存在时,设BF :y =k(x +2)(k ≠0).联立{y =k(x +2)x 25+y 2=1,得(1+5k 2)x 2+20k 2x +20k 2−5=0. 设B(x 1,y 1),Q(x 2,y 2),则x 1+x 2=−20k 21+5k 2,x 1x 2=20k 2−51+5k 2. 则|BQ|=√1+k 2√(x 1+x 2)2−4x 1x 2 =√1+k 2⋅√(−20k 21+5k 2)2−80k 2−201+5k 2=√1+k 2⋅4√5√1+k 21+5k 2. O 到BQ 的距离d =|2k|√1+k 2,则A 到BQ 的距离为4|k|√1+k 2. ∴S △QAB =12⋅√1+k 2⋅4√5√1+k 21+5k 2⋅√1+k 2=8√5√k 4+k 21+5k 2.令1+5k 2=t(t >1),则S △QAB =8√5⋅√−425(1t )2+325t +125. 当1t =38时,(S △QAB )max =2√5.综上,△QAB 的面积的最大值为2√5.解析:(Ⅰ)由已知求得c =2,再由{1a 2+45b 2=1a 2=b 2+4,解得a 2=5,b 2=1.则椭圆C 的标准方程可求;(Ⅱ)当直线BF 斜率不存在时,BF :x =−2,求出三角形QAB 的面积;当BF 所在直线斜率存在时,设BF :y =k(x +2)(k ≠0).联立直线方程与椭圆方程,利用弦长公式求|BQ|,再由点到直线距离公式求O 到BQ 的距离,得到A 到BQ 的距离,代入三角形面积公式,换元后利用配方法求最值.本题考查椭圆标准方程的求法,考查数学转化思想方法,考查直线与椭圆位置关系的应用,考查计算能力,是中档题.21.答案:解:(1)由函数f(x)=a−sinx x ,0<x <π, 得,∵当x =x 0时,f(x)取得极小值f(x 0),,∴a =sinx 0−x 0cosx 0,∴f(x 0)=−x 0cosx 0x 0=−cosx 0,∵0<x <π,∴cosx 0∈(−1,1),∴f(x 0)∈(−1,1),即f(x 0)的取值范围为(−1,1);(2)挡a =π时,f(x)=π−sinx x (0<x <π), 要证f(x)+mlnx =π−sinxx +mlnx >0成立,即证mlnx >sinx −π成立,令g(x)=mlnx ,ℎ(x)=sinx −π,则,ℎ(x)=sinx −π∈(−π,1−π], 令,则x =1e ,∴当0<x <1e 时,,此时g(x)递减, 当1e <x <π时,0'/>,此时g(x)递增, ∴g(x)min =g(1e )=−m e ,显然∀m ∈(0,π),−me >1−π,∴0<m <π,g(x)>ℎ(x),即当a =π,0<m <π时,f(x)+mlnx >0.解析:本题考查了利用导致研究函数的极值,考查了运算求解能力和化归与转化思想,属较难题.(1)根据x =x 0时,f(x)取得极小值f(x 0),可得,解方程得a =sinx 0−x 0cosx 0,将a 代入f(x)进一步求出f(x 0)的范围;(2)证明f(x)+mlnx >0成立,即证明mlnx >sinx −π成立,构造函数g(x)=mlnx ,ℎ(x)=sinx −π,根据g(x)和ℎ(x)的图象和最值可证该不等式成立.22.答案:解:(Ⅰ)曲线C 的直角坐标方程为(x −1)2+(y −√3)2=1,即x 2+y 2−2x −2√3y +3=0,又x 2+y 2=ρ2,x =ρcosθ,y =ρ=sinθ,所以曲线C 的极坐标方程为ρ2−2(cosθ+√3sinθ)ρ+3=0.(Ⅱ)联立射线θ=α与曲线C ,得ρ2−2(cosα+√3sinα)ρ+3=0,设M(ρ1,α),N(ρ2,α), |OM|+|ON|=ρ1+ρ2=2(cosα+√3sinα)=4sin(α+π6), 又圆心C(1,√3)的极坐标为(2,π3),所以α的取值范围是π6<α<π2,所以π3<α+π6<2π3,√32<sin(α+π6)≤1,2√3<4sin(α+π6)≤4, 所以|OM|+|ON|的取值范围为(2√3,4].解析:(Ⅰ)先消去参数得曲线C 的直角坐标方程再利用互化公式可得曲线C 的极坐标方程;(Ⅱ)利用极径的几何意义以及三角函数的性质可得.本题考查了简单曲线的极坐标方程,属中档题.23.答案:解:(Ⅰ)当a =3时,f(x)=|2x +3|+|x −1|<6即{x ≥13x +2<6或{−32≤x <1x +4<6或{x <−32−3x −2<6, 解得−83<x <43,综上所述,不等式f(x)<6的解集为(−83,43).(Ⅱ)f(x)+f(−x)=|2x +a|+|x −1|+|−2x +a|+|−x −1|=(|2x +a|+|2x −a|)+(|x −1|+|x +1|)≥|2a|+2,所以|2a|+2≥5解得a ≤−32或a ≥32,即a 的取值范围是(−∞,−32]∪[32,+∞).解析:(Ⅰ)分段去绝对值解不等式,最后可得解;(Ⅱ)利用绝对值不等式的性质求出左边的最小值,再解关于a 的不等式可得. 本题考查了绝对值不等式的解法,属中档题.。
广东省佛山市2020届高三教学质量检测(二模)英语

2020 年佛山市普通高中高三教学质量检测(二)英语本试卷共8 页,满分120 分,考试用时120 分钟。
注意事项:1. 本试卷分选择题和非选择题两部分。
答卷前,考生务必将自己的姓名和考生号、考场号、座位号填写在答题卡上,用2B 铅笔在答题卡的相应位置填涂考生号及试卷类型(A),并将条形码贴在答题卡上的“条形码粘贴处”。
因听力另考,试卷从第二部分的“阅读理解”开始,试题序号从“21”开始。
2.回答选择题时,选出每小题答案后,用2B 铅笔在答题卡上将对应题目的答案信息点涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案。
写在本试卷上无效。
3.答非选择题时,必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
写在本试卷上无效。
4.考试结束后,将试卷和答题卡一并交回。
第二部分阅读理解(共两节,满分40 分)第一节(共15 小题;每小题2 分,满分30 分)阅读下列短文,从每题所给的四个选项(A、B、C 和D)中,选出最佳选项,并在答题卡上将该项涂黑。
AWhich country can you travel to in 2020 that will allow you to go for longer, enjoy a higher standard, and save more money? The following destinations offer accommodation, transportation, and food for less.Kyrgyzstan, $25/dayKyrgyzstan is the choice for most travelers interested in trying out Central Asia, and most well-suited to travelers of all budgets. Food is cheap, so is getting around using the minibuses. You can find hostels and local home stays for less than $10. Meals cost $4 – $8 per day.Romania, $33/dayIf you are planning a European trip that’s affordable and a little bit off the beaten path, Romania is perfect for you. Unlike other popular places, many charming towns here remain unknown to most foreigners. You can also take free walking tours in the numerous historical sites. Hostels run $10 – $15 per night, food is hearty and delicious, and the public transportation is reliable and affordable. Meals cost$10 – $15 per day.Arizona & Utah, $55/dayFor an American Southwest road trip, you’ll spend an average of $110/day when you are solo. If you have just one other person, you’d be able to split the costs almost perfectly in half. If you have two other people along, take it down to one third and so on. The more the merrier.South Africa, $40/dayAny hostels in South Africa are in beautiful settings and each has a unique personality, and affordable too. Food can get expensive. To save money, cook your own food. Grocery stores are plentiful and have reasonable prices. By at least cooking your own breakfast, you can save a lot of money. The best (and possibly cheapest) way to get around the country is to rent a car and share with 3 other people. Meals cost$12 – $15 per day.21.What makes Romania different from the other places?A.Nice hostels.B.Delicious food.C.Less-visited towns.D.Cheap transportation.22.What may the author recommend for travelling in South Africa?A.Drive your own cars.B.Cook your own lunches.C.Stay in excellent hotels.D.Find unique travel partners.23.What feature do the four destinations share?A.They’re famous for historical places.B.They’re the best places for travelling.C.They have convenient public transportation.D.They’re good travel choices for saving money.BHot dogs, peanuts, an orderly green field: Sal Miyake loves everything about her first baseball game– a love shared by author Scott Simon as a kid at Wrigley Field in Chicago, Illinois.Sal is the main character in Simon’s first kids novel, Sunnyside Plaza. To create her world, Simon made use of his job at a halfway house when he was 19 years old. He cared for adults with mental disabilities. Working the evening shift, he made sure they brushed their teeth and took their medicine before bedtime.“All my life I’ve wanted to write about that experience,” said Simon, a journalist who hosts Weekend Edition Saturday for a radio station. He said the job changed his life.Like Simon’s long-ago clients, Sal lives in a home for adults with mental challenges. It’s called Sunnyside Plaza. Sal is kind and hard-working, and she helps the cook in the kitchen every day. She is also very observant. Sal may not be able to read, but she notices details that others often miss. When some of her Sunnyside friends begin to die, Sal tries to figure out why. Because of her disability, people don’t always take her seriously, but others help, sometimes in surprising ways.At the halfway house, “I enjoyed getting to know people who at first sight seemed a world away from me,” said Simon. “Then I realized how much we had in common. We talke d and joked. I liked spending time with them.” One of Simon’s favorite memories: taking 12 of the residents to a Chicago Cubs baseball game, where their amazement mirrors Sal’s in the book.Simon based Sal on several people he knew, and he did additional research to make sure her voice and viewpoint are believable. “I wanted to get all this right,” said Simon. “The books you read when you’re young really stay with you.” For him, this meant the classics his mother guided him to, including his favorites Black Beauty by Anna Sewell and A Tale of Two Cities by Charles Dickens.24.What do we know about Sal Miyake from the text?A.She resembles Simon in personality.B.She is an imaginary person in a fiction.C.She loves playing baseball with Simon.D.She works in Sunnyside Plaza as Simon did.25.What does Simon think of his job at the halfway house?A.A means of earning his living.B.A chance to make foreign friends.C.A platform to improve his baseball skills.D.An experience influencing his life greatly.26.What can be learned about the novel Sunnyside Plaza?A.It reflects Simon’s working experience.B.Its main character was based on Simon.C.It was written in memory of Simon’s mother.D.It has encouraged thousands of disabled men.27.Which can be a suitable title for the text?A.Classics Reading Makes a Great WriterB.Working Experiences Change Your ViewC.Life-changing Job Inspires First Kids NovelD.Helping the Disabled Brings You HappinessCLife expectancy in the United States has been in decline for the first time in decades, and public health officials have identified a series of potential causes, including inaccessible health care, rising drug addiction and rates of mental health disorders, and socio-economic factors. Now, a study led by the Yale School of Medicine has attempted to find out the relative impact of two factors most often linked to life expectancy – race and education – by looking at data about 5,114 black and white participants in four U.S. cities.The lives and deaths among this group of people – who took part in the study approximately 30 years ago when they were in their early 20s – show that the level of education, and not race, is the best predictor of who will live the longest.Among the 5,114 people followed in the study, 395 had died. These deaths were occurring in working-age people, often with children, before the age of 60. The rates of death among participants in this group did clearly show racial differences, with approximately 9% of blacks dying at an early age compared to 6% of whites. There were also differences in causes of death by race. For instance, black men were significantly more likely to die of murder and white men from AIDS. The most common causes of death across all groups over time were cardiovascular disease and cancer.But there were also obvious differences in rates of death by education level. Approximately 13% of participants with a high school degree or less education died compared with only approximately 5% of college graduates.Strikingly, when looking at race and education at the same time, the researchers found that differences related to race almost disappeared: 13.5% of black subjects and 13.2% of white subjects with a high school degree or less died during the course of the study. By contrast, 5.9% of black subjects and 4.3% of whites with college degrees had died.Therefore, improving overall quality of education is something tangible that can help reverse (扭转)this troubling trend in reduction of life expectancy among middle-aged adults.28.What can we learn about the participants in the study?A.The whites are more aggressive.B.The whites got higher education.C.More blacks than whites died young.D.More whites than blacks died of cancer.pared with education, the influence of race on death rates is .A. significantB. unnoticeableC. growingD. long-lasting30.What does the underlined word “tangible” probably mean?A. Realistic.B. Creative.C. Challenging.D. Temporary.31.What can be inferred from the research findings?A.People can get smart through learning.B.One should not discriminate other races.C.People don’t enjoy equal rights for education.D.One can live longer by getting more education.DAs the coronavirus spreads, remote work arrangements preserve continuity and allow people to stay busy doing something familiar during a time of crisis. At first glance, telecommuting (远程办公) might not seem so bad.While it works well for some, it doesn’t for everyone. Working remotely has widespread negative consequences, including people spending time working that they might otherwise have spent with family or friends – because they can easily cross their work-life boundaries, they end up working longer hours.People who telecommute may also have trouble freeing themselves from work and from the technology that enables it, which contributes to the harmful consequences of reducing face-to-face time and personal interactions. When humans rely on technology, we may forget how essential these interactions are to human happiness.As a university professor, my days consist of social interactions with students and colleagues. I generally find those conversations and the resulting relationships inspiring and rewarding. The coronavirus situation means that countless teachers like me face the possibility of standing in front of a camera instead of a classroom. I’d prefer doing that to canceling class, but I can’t help wondering whether my job, along with so many others, is about to experience a great and potentially permanent change.I wonder how many faculty members might be laid off if the university decides teaching remotely is good enough, or how many people will be let go when their bosses realize they don’t need to show up every day, or even at all. Finally, here’s the most important question: whether people believe their firsthand, lived experiences can be replaced – and not just during a pandemic (大流行病).The coronavirus will accelerate our rush into the arms of technology. Ironically, our faith in technology may end up speeding up our own obsolescence (过时).32.According to the text, what may telecommuting result in?A.Shortened working hours.B.Loss of personal freedom.C.Increased family happiness.D.Fewer personal interactions.33. Which is true about the author?A.She loves teaching in front of a camera.B.She enjoys popularity among her students.C.She considers social interactions to be beneficial.D.She’s concerned about the spread of coronavirus.34. What does the author intend to express in Paragraph 5?A.Anxiety over the future.B.Expectation of education.C.Views on unemployment.D.Love for lived experience.35. Which section of a website is the passage probably from?A. Fashion.B. Opinion.C. Health.D. Events.第二节(共 5 小题,每小题2 分,满分10 分)根据短文内容,从短文后的选项中选出能填入空白处的最佳选项。
【KS5U解析】广东省佛山市2020届高三教学质量检测(二模考试)数学(文)试题 Word版含解析

又点 在抛物线 的准线上,
所以 ,解得 ,
所以抛物线 的方程为 ,
由题意知直线 的斜率存在,可设直线 的方程为 ,即 ,
由 ,得 ,(*)
因为直线 与抛物线相切,所以 ,
解得 或 (舍去),将 代入(*)解得 ,
当 时, ,所以点 的坐标为 ,
根据抛物线 定义可得 .
在D中,不妨设1月份消费价格为 ,故可得2月份价格为 ;
同理可得 月份价格为 ;
4月份价格为 ;
月份价格和4月份价格相同;6月份价格为 ,
【详解】由折线图知:从2019年每月的环比增长率看,2019年第三季度的居民消费价格一直都在增长,故A正确;
在B中,从2019年每月的同比增长率看,2018年7月份的居民消费价格比同年8月份要低一些,故B正确;
在C中,从2019年每月的同比增长率看,从4月份以后每月同比增长率都在 以上,进而估计出2019年全年居民消费价格比2018年涨了2.5%以上,故C正确;
2019~2020学年佛山市普通高中高三教学质量检测(二)
数学(文科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
注意事项:
1. 答卷前,考生要务必填写答题卷上的有关项目.
2. 选择题每小题选出答案后,用2B铅笔把答案涂在答题卷相应的位置上.
3. 非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液,不按以上要求作答的答案无效.
下列结论中不正确的是( )
A. 2019年第三季度的居民消费价格一直都在增长
B. 2018年7月份的居民消费价格比同年8月份要低一些
2024年广东佛山市高三二模地理高考试卷试题(含答案)

2023~2024学年佛山市普通高中教学质量检测(二)高三地理2024.4本试卷共6页,19小题,满分100分。
考试用时75分钟。
注意事项:1.答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2.作答选择题时,选出每小题答案后,用2B铅笔在答题卡上对应题目后面的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保持答题卡的整洁。
考试结束后,请将答题卡交回。
第Ⅰ卷一、选择题(本卷共16个小题,每小题3分,共48分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)城市区域空间的演进始终伴随着集聚与扩散的过程。
基于大城市地域圈层聚散规律,可将城市圈的发展演化分为四个阶段(图1)。
武汉城市圈以武汉市主城区为核心,并包括周边的8个地级市。
研究表明:目前武汉城市圈正从阶段Ⅰ向阶段Ⅱ过渡。
据此回答1~2题。
1.城市圈四个阶段的发展特征主要表现为A.阶段Ⅰ城市圈内部差距缩小B.阶段Ⅱ核心圈层辐射功能减弱C.阶段Ⅲ外围圈层吸引力最强D.阶段Ⅳ生产要素城际流动活跃2.为提升武汉城市圈整体竞争力,其核心圈层当前应该①发展现代金融贸易业②培育城市圈次级增长极③加快建设特色化新城④向区外疏散低端制造业A.①②B.①④C.②③D.③④青稞喜光,生长周期短。
甘孜州位于青藏高原东南缘,平均海拔3500m以上,这里是四川最大的青稞生产区,建有国家青稞良种繁育基地。
2019年,该州建立格萨尔青稞文化产业园,以青稞产业为核心,结合川藏特色文化,形成“订单式种植+收购+加工+休闲观光”一体化发展模式,提高了青稞产业附加值,带动更多农户增收致富。
据此回答3~4题。
广东省佛山市2020届高三二模(数学理)(WORD版)

2020届广东省佛山市高三教学质量检测(二模)数学(理)试题学校:___________姓名:___________班级:___________考号:___________1.已知集合{}2|2A x x x =>,{}|13B x x =≤≤,则AB =( )A .{}|01x x ≤<B .{0x x <或}1x ≥ C .{}|23x x <≤D .{1x x ≤或}3x >2.复数z 满足()()21i 3i z ++=+,则z =( ) A .1 BCD .23.(101的二项展开式中,x 的系数与4x 的系数之差为( )A .220-B .90-C .90D .04.设变量,x y 满足约束条件2030230x x y x y +≥⎧⎪-+≥⎨⎪+-≤⎩,则目标函数6z x y =+的最大值为( )A .3B .4C .18D .405.设函数()()2sin cos cos 2f x x x x =++,则下列结论错误的是( ) A .()f x 的最小正周期为π B .()y f x =的图像关于直线8x π=对称C .()f x1D .()f x 的一个零点为78x π=6.已知()33log log 2a =,()23log 2b =,32log 2c =,则( ) A .a b c <<B .a c b <<C .c a b <<D .b a c <<7.已知点()3,2A -在抛物线C :22x py =(0p >)的准线上,过点A 的直线与抛物线在第一象限相切于点B ,记抛物线的焦点为F ,则BF =( ) A .6B .8C .10D .128.盒中有形状、大小都相同的2个红色球和3个黄色球,从中取出一个球,观察颜色后放回并往盒中加入同色球4个,再从盒中取出一个球,则此时取出黄色球的概率为( ) 377319.2019年,全国各地区坚持稳中求进工作总基调,经济运行总体平稳,发展水平迈上新台阶,发展质量稳步上升,人民生活福祉持续增进,全年最终消费支出对国内生产总值增长的贡献率为57.8%.下图为2019年居民消费价格月度涨跌幅度:(同比=(本期数-去年同期数)/去年同期数100%⨯,环比=(本期数-上期数)/上期数100%⨯下列结论中不正确的是( )A .2019年第三季度的居民消费价格一直都在增长B .2018年7月份的居民消费价格比同年8月份要低一些C .2019年全年居民消费价格比2018年涨了2.5%以上D .2019年3月份的居民消费价格全年最低10.已知P 为双曲线C :22221x y a b-=(0a >,0b >)上一点,O 为坐标原点,1F ,2F 为曲线C 左右焦点.若2OP OF =,且满足21tan 3PF F ∠=,则双曲线的离心率为( )AB C D 11.已知A ,B ,C 是球O 的球面上的三点,60AOB AOC ∠=∠=︒,若三棱锥O ABC -体积的最大值为1,则球O 的表面积为( ) A .4πB .9πC .16πD .20π12.双纽线最早于1694年被瑞士数学家雅各布·伯努利用来描述他所发现的曲线.在平面直角坐标系xOy 中,把到定点()1,0F a -,()2,0F a 距离之积等于2a (0a >)的点的轨迹称为双纽线C .已知点()00,P x y 是双纽线C 上一点,下列说法中正确的有( ) ①双纽线C 关于原点O 中心对称; ②022a ay -≤≤;③双纽线C 上满足12PF PF =的点P 有两个; ④PO .13.设命题p :()0,x ∀∈+∞,21e 12xx >+,则p ⌝为___________. 14.已知函数()()21sin 12x x x f x x+++=,若()3f a =-,则()f a -=___________.15.在面积为1的平行四边形ABCD 中,6DAB π∠=,则AB BC ⋅=___________;点P 是直线AD 上的动点,则22PB PC PB PC +-⋅的最小值为___________.16.数学兴趣小组为了测量校园外一座“不可到达”建筑物的高度,采用“两次测角法”,并自制了测量工具:将一个量角器放在复印机上放大4倍复印,在中心处绑上一个铅锤,用于测量楼顶仰角(如图);推动自行车来测距(轮子滚动一周为1.753米).该小组在操场上选定A 点,此时测量视线和铅锤线之间的夹角在量角器上度数为37°;推动自行车直线后退,轮子滚动了10卷达到B 点,此时测量视线和铅锤线之间的夹角在量角器上度数为53°.测量者站立时的“眼高”为1.55m ,根据以上数据可计算得该建筑物的高度约为___________米.(精确到0.1) 参考数据:3sin 375︒≈,sin 5345︒≈17.已知等比数列{}n a 的前n 项和为n S (0n S ≠),满足1S ,2S ,3S -成等差数列,且123a a a =.(1)求数列{}n a 的通项公式; (2)设()()1311nn n n a b a a +-=++,求数列{}n b 的前n 项和n T .18.如图,在四棱锥P ABCD -中,底面ABCD是矩形,PA PD ==,PB PC =90APB CPD ∠=∠=︒,点M ,N 分别是棱BC ,PD 的中点.(1)求证://MN 平面PAB ;(2)若平面PAB ⊥平面PCD ,求直线MN 与平面PCD 所成角的正弦值.19.已知椭圆C :22221x y a b +=(0a b >>)的离心率为2,且过点()2,1.(1)求椭圆C 的方程;(2)过坐标原点的直线与椭圆交于M ,N 两点,过点M 作圆222x y +=的一条切线,交椭圆于另一点P ,连接PN ,证明:|PM PN =.20.2020年是我国全面建成小康社会和“十三五”规划收官之年,也是佛山在经济总量超万亿元新起点上开启发展新征程的重要历史节点.作为制造业城市,佛山一直坚持把创新摆在制造业发展全局的前置位置和核心位置,聚焦打造成为面向全球的国家制造业创新中心,走“世界科技+佛山智造+全球市场”的创新发展之路.在推动制造业高质量发展的大环境下,佛山市某工厂统筹各类资源,进行了积极的改革探索.下表是该工厂每月生产的一种核心产品的产量x (520x ≤≤)(件)与相应的生产总成本y (万元)的四组对照数据.工厂研究人员建立了y 与x 的两种回归模型,利用计算机算得近似结果如下:模型①:31733x y =+模型②:68160y x =-.其中模型①的残差(实际值-预报值)图如图所示:(1)根据残差分析,判断哪一个模型更适宜作为y 关于x 的回归方程?并说明理由; (2)市场前景风云变幻,研究人员统计历年的销售数据得到每件产品的销售价格q (万元)是一个与产量x 相关的随机变量,分布列为:结合你对(1)的判断,当产量x 为何值时,月利润的预报期望值最大?最大值是多少(精确到0.1)? 21.已知函数()sin f x x =(x a ≥).(1)若()0f x ≥恒成立,求a 的取值范围;(2)若14a <-,证明:()f x 在0,2π⎛⎫ ⎪⎝⎭有唯一的极值点x ,且()00012f x x x π>--. 22.在平面直角坐标系xOy 中,曲线1C 的参数方程为2cos 22sin x ty t=⎧⎨=+⎩(t 为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为4cos ρθ=.(1)说明1C 是哪种曲线,并将1C 的方程化为极坐标方程; (2)设点M 的极坐标为()4,0,射线θα=(02πα<<)与1C 的异于极点的交点为A ,与2C 的异于极点的交点为B ,若4AMB π∠=,求tan α的值.23.已知函数()2cos 15f x x a a =+-+-,a ∈R .(1)若()08f >,求实数a 的取值范围; (2)证明:对x ∀∈R ,()151f x a a≥--+恒成立.参考答案1.B 【解析】 【分析】解一元二次不等式得到集合A ,根据并集的概念即可得出结果. 【详解】 ∵{}{222A x x x x x ==>或}0x <,{}|13B x x =≤≤,∴AB ={0x x <或}1x ≥,故选:B . 【点睛】本题主要考查了一元二次不等式的解法,集合间并集的运算,属于基础题. 2.A 【解析】 【分析】把已知等式变形,然后利用复数代数形式的乘除运算化简,再由复数求模公式计算得答案. 【详解】因为复数z 满足()()213z i i ++=+, ∴()()()()313422221112i i ii z i i i i +-+-=-=-=-=-++-, 则1z =, 故选:A . 【点睛】本题主要考查了复数代数形式的乘除运算,考查了复数模的求法,属于基础题. 3.D 【解析】 【分析】由题意利用二项展开式的通项公式,求出x 的系数与4x 的系数,再求其差即可. 【详解】∵(101的二项展开式中,通项公式为()21101r rr r TC x +=⋅-,故x 的系数与4x 的系数之差为2810100C C -=, 故选:D . 【点睛】本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题. 4.C 【解析】不等式20{30230x x y x y +≥-+≥+-≤所表示的平面区域如下图所示,当6z x y =+所表示直线经过点(0,3)B 时,z 有最大值18.考点:线性规划. 5.D 【解析】 【分析】先利用二倍角公式和辅助角公式化简函数,即可根据()sin y A ωx φ=+的图象与性质判断出各选项的真假. 【详解】因为()()2sin cos cos 21sin 2cos 2124f x x x x x x x π⎛⎫=++=++=++⎪⎝⎭,所以()f x 的最小正周期为π,()f x 1,A 、C 正确; 当8x π=时,sin 2184ππ⎛⎫⨯+= ⎪⎝⎭,所以()y f x =的图象关于直线8x π=对称,B 正确; 因为718f π⎛⎫=⎪⎝⎭,所以78x π=不是函数()f x 的零点,D 错误. 故选:D . 【点睛】本题主要考查利用二倍角公式,辅助角公式进行三角变换,以及函数()sin y A ωx φ=+的图象与性质的应用,属于中档题. 6.A 【解析】 【分析】首先得出30log 21<<,然后利用对数函数和指数函数的性质求解即可. 【详解】∵30log 21<<,∴()33log log 20<,即0a <, ∴()230log 21<<,即01b <<, ∵332log 2log 41c ==>,∴a b c <<, 故选:A . 【点睛】本题考查三个数的大小的比较,是基础题,解题时要认真审题,注意对数函数和指数函数的性质的合理运用. 7.C 【解析】 【分析】由点()3,2A -在准线上可知p 的值,从而确定抛物线的方程,设点B 的坐标为2,8m m ⎛⎫⎪⎝⎭,0m >,通过对抛物线方程求导,可得点直线AB 的斜率,再通过A 、B 两点的坐标也可求得AB k ,于是建立关于m 的方程,解之可得m 的值,最后利用抛物线的定义即可得解. 【详解】抛物线()2:20C x py p =>的准线方程为2py =-, ∵点()3,2A -在准线上,∴22p-=-即4p =, 抛物线的方程为28x y =,即218y x =,设点B 的坐标为2,8m m ⎛⎫⎪⎝⎭,0m >,对218y x =求导可得,14y x '=,∴直线AB 的斜率为14m ,由()3,2A -、2,8m B m ⎛⎫ ⎪⎝⎭,可知221843AB m k m m =+-=,解之得,8m =或2-(舍负), ∴点()88B ,,由抛物线的定义可知,48102BF =+=, 故选:C . 【点睛】本题考查抛物线的定义、准线方程等,还涉及利用导数求抛物线上某点处切线的斜率,考查学生的分析能力和运算能力,属于中档题. 8.A 【解析】 【分析】若取出的是红色球,再从盒中取出一个球,则此时取出黄色球的概率为:13925P =⨯,若取出的是黄色球,再从盒中取出一个球,则此时取出黄色球的概率为:23759P =⨯,由此能求出再从盒中取出一个球,则此时取出黄色球的概率. 【详解】盒中有形状、大小都相同的2个红色球和3个黄色球, 从中取出一个球,观察颜色后放回并往盒中加入同色球4个,若取出的是红色球,再从盒中取出一个球, 则此时取出黄色球的概率为:13295152P =⨯=, 若取出的是黄色球,再从盒中取出一个球, 则此时取出黄色球的概率为:23775915P =⨯=, ∴再从盒中取出一个球,则此时取出黄色球的概率为:1221573155P P P =+=+=, 故选:A . 【点睛】本题考查概率的求法,考查相互独立事件概率乘法公式、互斥事件概率计算公式等基础知识,考查运算求解能力,属于中档题. 9.D 【解析】 【分析】根据已知中的图表,结合同比增长率和环比增长率的定义,逐一分析给定四个命题的真假,可得答案. 【详解】由折线图知:从2019年每月的环比增长率看,2019年第三季度的居民消费价格一直都在增长,故A 正确;在B 中,从2019年每月的同比增长率看,2018年7月份的居民消费价格比同年8月份要低一些,故B 正确;在C 中,从2019年每月的同比增长率看,从4月份以后每月同比增长率都在2.5%以上,进而估计出2019年全年居民消费价格比2018年涨了2.5%以上,故C 正确; 在D 中,不妨设1月份消费价格为a ,故可得2月份价格为()11% 1.01a a +=; 同理可得3月份价格为()1.0110.4% 1.00596a a -=; 4月份价格为()1.0059610.1% 1.00696596a a +=;5月份价格和4月份价格相同;6月份价格为()1.0069659610.1% 1.00595899404a a -=,而后面每个月都是增长的.故1月份的价格是最低的,故D 错误.故选:D . 【点睛】本题考查命题真假的判断,考查折线图等基础知识,考查运算求解能力、数据处理能力,考查函数与方程思想,属于基础题. 10.C 【解析】 【分析】点P 在双曲线C 的右支上,且满足2OP OF =,即有O 为12PF F △外接圆的圆心,即有1290F PF ∠=︒,运用勾股定理和双曲线的定义,化简整理,结合离心率公式计算即可得到.【详解】点P 在双曲线C 的右支上,且满足2OP OF =,即有O 为12PF F △外接圆的圆心, 即有1290F PF ∠=︒,由双曲线的定义可得122PF PF a -=, ∵21tan 3PF F ∠=,所以213PF PF =, 则13PF a =,2PF a =,由2221212PF PF F F +=,即()22234a a c +=,即有2252c a =,e =,故选:C . 【点睛】本题主要考查双曲线的定义和性质,考查勾股定理的运用,运用平面几何中直径所对的圆周角为直角是解题的关键,属于中档题. 11.C 【解析】 【分析】作出草图,易得AOB 和AOC △均为等边三角形,当面AOC ⊥面AOB 时,三棱锥O ABC -的体积最大可求出球的半径R ,进而可得球的表面积.【详解】设球的半径为R ,如图所示,∵60AOB AOC ∠=∠=︒,∴AOB 和AOC △均为等边三角形,边长为R , 由图可得当面AOC ⊥面AOB 时,三棱锥O ABC -的体积最大,此时3111132228V R R R R =⨯⨯⨯⨯==,解得2R =, 则球O 的表面积为24216S ππ=⨯=, 故选:C . 【点睛】本题考查球的表面积的求法,球的内含体与三棱锥的关系,考查空间想象能力以及计算能力,属于中档题. 12.B 【解析】 【分析】对①,设动点(,)C x y ,把(,)x y 关于原点对称的点(,)x y --代入轨迹方程,显然成立; 对②,根据12PF F △的面积范围证明即可.对③,易得若12PF PF =则P 在y 轴上,再根据()00,P x y 的轨迹方程求解即可.对④,根据题中所给的定点()1,0F a -,()2,0F a 距离之积等于2a ,再画图利用余弦定理分析12PF F △中的边长关系,进而利用三角形三边的关系证明即可.【详解】对①,设动点(,)C x y ,由题可得C 22222)][()]x a y x a y a ,把(,)x y 关于原点对称的点(,)x y --代入轨迹方程显然成立.故①正确;对②,因为()00,P x y ,故12121212011||||sin ||22PF F SPF PF F PF F F y =⋅⋅∠=⋅. 又212||||PF PF a ⋅=,所以2120sin 2a FPFa y ∠=⋅, 即012sin 22a ay F PF =∠≤,故022a a y -≤≤.故②正确; 对③, 若12PF PF =则()00,P x y 在12FF 的中垂线即y 轴上. 故此时00x =,22222)][()]x a y x a y a ,可得00y =,即()0,0P ,仅有一个.故③错误;对④,因为12POF POF π∠+∠=,故12cos cos 0POFPOF ∠+∠=, 即222222112212||||||||||||02||||2||||OP OF PF OP OF PF OP OF OP OF +-+-+=⋅⋅, 因为12||||OF OF a ==,212||||PF PF a ⋅= 故2222122||2||||OP a PF PF +=+.即()22212122||2||||2||||OP a PF PF PF PF +=-+⋅, 所以()22122||||||OP PF PF =-.又1212||||||2PF PF F F a -≤=,当且仅当12,,P F F 共线时取等号.故()()222122||||||2OP PF PF a =-≤,即22||2OP a ≤,解得||OP ≤.故④正确.故①②④正确. 故选:B 【点睛】本题主要考查了动点轨迹方程的性质判定,因为该方程较复杂,故在作不出图像时,需要根据题意求出动点的方程进行对称性的分析,同时需要结合解三角形的方法对所给信息进行辨析.属于难题.13.()00,x ∃∈+∞,0201e 12x x ≤+【解析】 【分析】根据全称命题的否定是特称命题求解. 【详解】因为命题p :()0,x ∀∈+∞,21e 12xx >+,是全称命题, 所以其否定是特称命题,即:()00,x ∃∈+∞,0201e12x x ≤+. 故答案为:()00,x ∃∈+∞,0201e 12x x ≤+. 【点睛】本题主要考查命题的否定,还考查了理解辨析的能力,所以基础题. 14.4 【解析】 【分析】化简()f x 成奇函数加一个常数的结构,再求解()()f x f x +-的值即可. 【详解】由题, ()()221sin 1sin 11222x x x x x x f x x x +++++==+,设()2sin 12x x x g x x ++=,则()()()()()()22sin 1sin 122x x x x x x g x g x x x-+--+++-===---为奇函数.故()()()()11122f x f xg x g x +-=++-+=.故()()14f a f a -=-=. 故答案为:4 【点睛】本题主要考查了奇函数的性质运用,需要将所给的函数分离出奇函数加常数的结构,再利用奇函数的性质求解.属于中档题.15【解析】 【分析】由平行四边形的面积为1可得2AB AD ⋅=,根据向量数量积的定义即可得出AB BC ⋅的值;由于222PB PC PB PC BC PB PC +-⋅=+⋅,取BC 的中点Q ,连接PQ ,则2PB PC PQ +=,()()2214PB PC PB PC PB PC ⎡⎤⋅=+--⎢⎥⎣⎦,再利用基本不等式的性质即可得出结果. 【详解】∵平行四边形ABCD 的面积为1,即sin 1AB AD DAB ⋅∠=, ∴2AB AD ⋅=,故cos 2AB BC AB BC DAB ⋅=⋅∠==()2222PB PC PB PC PC PB PB PC BC PB PC +-⋅=-+⋅=+⋅,取BC 的中点Q ,连接PQ ,则2PB PC PQ +=,()()2214PB PC PB PC PB PC ⎡⎤⋅=+--⎢⎥⎣⎦, ∴()()2222221344PB PC P BC PB PC BC BC P P Q B C ⎡⎤+--=⎢⎥⎣+⋅++⎦= 223334ABCD S BC PQ BC PQ ≥=⋅≥=⋅四边形,此时PQ BC ⊥,32PQ BC =,【点睛】本题考查了向量的平行四边形法则、数量积运算性质、基本不等式的性质,考查了变形能力与计算能力,属于中档题. 16.31.6 【解析】 【分析】由题意画出简图,设CD h =,即可得43h BC ≈、34h AC ≈,利用17.53AB BC AC ==-即可得解. 【详解】由题意画出简图,如图:由题意可得53CAD ∠=,37CBD ∠=,10 1.75317.53AB =⨯=,所以sin 37tan tan 37cos3734CBD ∠≈==,sin 53cos37tan tan 53cos5433sin 37CAD ∠===≈,设CD h =,则在Rt BCD 中,4tan 3CD hBC CBD =∠≈,在Rt ACD 中,3tan 4CD hAC CAD =∠≈, 所以717.5312AB BC AC h -≈==,解得30.05h ≈, 所以该建筑的高度约为30.05 1.5531.6+=米. 故答案为:31.6. 【点睛】本题考查了三角函数的实际应用,关键是把实际问题转化为数学模型,属于基础题.17.(1)()2nn a =-.(2)()()112221n n n T ++-+=--+ 【解析】 【分析】(1)设数列{}n a 的公比为q ,由题意结合等差数列、等比数列的性质转化条件可得()()21121a q q a q -+=+、2211a q a q =,即可得解;(2)由题意()()1112121n nn b +=--+-+,利用裂项相消法即可得解.【详解】(1)设数列{}n a 的公比为q ,依题意得()1322S S S +-=, 所以()()23122a a a a -+=+即()()21121a q qa q -+=+,因为10a ≠,所以2320q q ++=,解得1q =-或2q =-, 因为0n S ≠,所以2q =-,又因为123a a a =,所以2211a q a q =即12a q ==-,所以()2nn a =-;(2)题意可得()()()()()()()111322*********n n nn n n n n b +++-----==⎡⎤⎡⎤⎡⎤⎡⎤-+-+-+-+⎣⎦⎣⎦⎣⎦⎣⎦()()1112121nn +=--+-+,则()()()()()()12231111111212121212121n n n T +⎡⎤⎡⎤⎡⎤=-+-++-⎢⎥⎢⎥⎢⎥-+-+-+-+-+-+⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦()()()11122112121n n n +++-+=--=--+-+. 【点睛】本题考查了等差数列与等比数列的综合应用,考查了利用裂项相消法求数列前n 项和的应用,属于中档题. 18.(1)见解析(2)9【解析】 【分析】(1)取PA 的中点为Q ,连接NQ ,BQ ,由平面几何知识可得//NQ BM 且NQ BM =,进而可得//MN BQ ,由线面平行的判定即可得证;(2)过点P 作PE AB ⊥交AB 于点E ,作PF CD ⊥交CD 于点F ,连接EF ,取EF 的中点为O ,连接OP ,建立空间直角坐标系后,求出平面PCD 的一个法向量为n 、直线MN 的方向向量MN ,利用sin cos n MN n MN n MNθ⋅=⋅=⋅即可得解.【详解】(1)证明:取PA 的中点为Q ,连接NQ ,BQ ,如图:又点N 是PD 的中点,则//NQ AD 且12NQ AD =, 又点M 是BC 的中点,底面ABCD 是矩形, 则12BM AD =且//BM AD , ∴//NQ BM 且NQ BM =,∴四边形MNQB 是平行四边形,∴//MN BQ , 又MN ⊄平面PAB ,BQ ⊂平面PAB ,∴//MN 平面PAB ;(2)过点P 作PE AB ⊥交AB 于点E ,作PF CD ⊥交CD 于点F ,连接EF , 则PF AB ⊥,PE PF P =,∴AB ⊥平面 PEF ,又AB平面ABCD ,∴平面 PEF ⊥平面ABCD ,∵PA PD ==,PB PC =90APB CPD ∠=∠=︒,∴3AB CD ==,PE PF ==2BE CF ==,1AE DF ==. 设平面PAB ⋂平面PCD l =,可知////l CD AB , ∵平面PAB ⊥平面PCD ,∴90EPF ∠=︒,∴2EF =,取EF 的中点为O ,连接OP 、OM ,则OP ⊥平面ABCD ,1OP =, ∴OM 、OF 、OP 两两垂直,以O 为坐标原点,分别以OM ,OF ,OP 所在直线为x ,y ,z 轴建立空间直角坐标系,O xyz -,如图所示,则()0,0,1P ,()2,1,0C ,()1,1,0D -,()2,0,0M ,111,,222N ⎛⎫-⎪⎝⎭, ∴()2,1,1PC =-,()1,1,1PD =--,511,,222MN ⎛⎫=- ⎪⎝⎭, 设平面PCD 的一个法向量为(),,n x y z =,则由020n PD x y z n PC x y z ⎧⋅=-+-=⎨⋅=+-=⎩,令1y =可得()0,1,1n =.设直线MN 与平面PCD 所成角为θ,则sin cos 2n MN n MN n MNθ⋅=⋅===⋅ ∴直线MN 与平面PCD 所成角的正弦值为9【点睛】本题考查了线面平行的判定及利用空间向量求线面角,考查了空间思维能力与运算求解能力,属于中档题.19.(1)22163x y +=(2)见解析【解析】 【分析】(1)根据椭圆的离心率为2,且过点()2,1,由2c a =,22411a b +=,结合222a b c =+求解.(2)当直线PM 的斜率不存在时,可得直线PM的方程为x =x =验证即可. 当直线PM 斜率存在时,设直线PM 的方程为y kx m =+,根据直线PM 与圆相切,得到||m =,设()11,M x y ,()22,P x y ,则()11 ,N x y --,联立22163y kx mx y =+⎧⎪⎨+=⎪⎩,由弦长公式求得 PM ,然后由两点间的距离公式,将韦达定理代入求得PN 即可. 【详解】(1)设椭圆的半焦距为c ,且过点()2,1. 所以2c a =,22411a b +=,又222a b c =+, 解得26a =,23b =,所以椭圆C 的方程为:22163x y +=.(2)①当直线PM 的斜率不存在时,依题意,可得直线PM 的方程为x =或x =若直线PM :x =直线MN :y x =,可得M,(N,P,则PM =,PN =PM PN =; 其他情况,由对称性,同理可得PM PN =.②当直线PM 斜率存在时,设直线PM 的方程为y kx m =+, ∵直线PM 与圆222x y +=相切, ∴圆心O 到直线PM=||m =,设()11,M x y ,()22,P x y ,则()11 ,N x y --,联立22163y kx m x y =+⎧⎪⎨+=⎪⎩,消元y ,整理得()222124260k x kmx m +++-=,则122412km x x k +=-+,21222612m x x k-=+.∴12PM x =-==,∵PN =()12122242221212km m y y k x x m k m k k -⎛⎫+=++=+= ⎪++⎝⎭,∴PN ==.∵m =∴212PN PM k==+. 综上可知PM PN =成立. 【点睛】本题主要考查椭圆方程的求法,直线与椭圆,直线与圆的位置关系以及弦长问题,还考查了运算求解的能力,属于难题.20.(1)模型①更适宜作为y 关于x 的回归方程,见解析(2)产量为11件时,月利润的预报期望值最大,最大值是774.8万元. 【解析】 【分析】(1)作出模型②的残点图,再对比①的残点图分析即可.(2)根据题意作出Y 的分布列,进而得出其数学期望()3213217332x x E Y x =--+-,再求导分析其单调性求出最大值即可. 【详解】(1)模型②的残差数据如下表:模型②的残点图如图所示.模型①更适宜作为y 关于x 的回归方程,因为:理由1:模型①这个4个样本点的残差的绝对值都比模型②的小.理由2:模型①这4个样本的残差点落在的带状区域比模型②的带状区域更窄. 理由3:模型①这4个样本的残差点比模型②的残差点更贴近x 轴. (2)设月利润为Y ,由题意知Y qx y =-,则Y 的分布列为:()2323231211401731301731001732322352310x x x x x x E Y x x x ⎛⎫⎛⎫⎛⎫=---⋅+---⋅+---⋅⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭3213217332x x x =--+-.设函数()3213217332x x f x x =--+-,()0,x ∈+∞,()2132f x x x '=--+,令()0f x '=,解得11x =或12x =-(舍),当()0,11x ∈时,()0f x >′,则()f x 单调递增;当()11,x ∈+∞时,()0f x <′,则()f x 单调递减.则函数()f x 的最大值()4649116f =,即产量为11件时,月利润的预报期望值最大,最大值是774.8万元. 【点睛】本题主要考查了根据题意作出分布列求解数学期望最值的问题.同时也考查了求导分析函数单调性与最值的问题,属于中档题.21.(1){}|22,a k a k k Z πππ-≤≤∈.(2)见解析 【解析】 【分析】(1)计算()0f a ≥得到22k a k πππ-≤≤,再证明当22k a k πππ-≤≤(k Z ∈)时,()0f x ≥sin x ≥(0x ≥),讨论22k a k πππ-≤≤和2x k π≥两种情况,计算得到证明.(2)求导得到()cos f x x '=-,()()321sin 4g x x x a '=-+-,得到存在唯一实数00,2t π⎛⎫∈ ⎪⎝⎭,使()00g t '=,存在唯一实数0,32x ππ⎛⎫∈ ⎪⎝⎭,使()00g x =,得到()()00000011sin 2cos 2cos f x x x x x x +=+->,得到证明.【详解】(1)由()0f a ≥,得sin 0a -≥,即sin 0a ≤,解得22k a k πππ-≤≤,k Z ∈, 以下证明,当22k a k πππ-≤≤(k Z ∈)时,()0f x ≥.sin x (0x ≥). 若1x >1sin x >≥; 若01x ≤<x ≥.令()sin g x x x =-(0x ≥),可知()1cos 0g x x '=-≥,函数单调递增, 故()()00g x g ≥=,即sin x x ≥(0x ≥),sin x (0x ≥).若22k a k πππ-≤≤(k Z ∈),则当2a x k π≤≤时,sin 0x ≤,0sin x ≥≥,即()0f x ≥;当2x k π≥sin x ≥(0x ≥),()sin 2sin x k x π-=.故当22k a k πππ-≤≤(k Z ∈)时,()0f x ≥.综上,所求a 的取值范围是{}|22,a k a k k Z πππ-≤≤∈. (2)()cos f x x '=-,令()cos g x x =-,()()321sin 4g x x x a '=-+-,∵14a <-,∴()g x '是0,2π⎛⎫ ⎪⎝⎭上的增函数,又()00g '<,32110242g a ππ⎛⎫'=-> ⎪⎝⎭⎛⎫- ⎪⎝⎭, 故存在唯一实数00,2t π⎛⎫∈ ⎪⎝⎭,使()00g t '=,当()0 0,x t ∈时,()0g x '<,()g x 递减;当0,2x t π⎛⎫∈ ⎪⎝⎭时,()0g x '>,()g x 递增.又14a <-,则14a ->12>,1>, ∴()010g =-<,1110322g π⎛⎫⎪⎛⎫⎪=-=< ⎪⎪⎝⎭⎪⎭,2gπ⎛⎫=>⎪⎝⎭.故存在唯一实数,32xππ⎛⎫∈ ⎪⎝⎭,使()00cos0g x x=-=.当()00,x x∈时,()()0f xg x'=<,()f x递减;当,2x tπ⎛⎫∈ ⎪⎝⎭时,()()0f xg x'=>,()f x递增.所以()f x在区间0,2π⎛⎫⎪⎝⎭有唯一极小值点x,且极小值为()00sinf x x=.又由()00cos0g x x=-=12cos x=,∴()001sin2cosf x xx=-.又()()00000011sin2cos2cosf x x x xx x+=+->.以下只需证明,即证00112cos2x xπ>-,0002cos2x xπ<<-.∵0,2xπ⎛⎫∈ ⎪⎝⎭,∴00002cos2sin2222x x x xπππ⎛⎫⎛⎫=-<-=-⎪ ⎪⎝⎭⎝⎭.则()()0000000111sin2cos2cos2f x x x xx x xπ+=+->>-,所以()0012f x xxπ>--. 【点睛】本题考查了不等式恒成立问题,极值点问题,证明不等式,先算后证是解题的关键.22.(1)1C是圆心为()0,2,半径为2的圆.4sinρθ=;(2)1tan2α=.【解析】【分析】(1)由曲线1C的参数方程消去参数t,得到曲线1C的直角坐标方程,再由222,sinx y yρρθ=+=,得到曲线1C的极坐标方程;(2)设()1,A ρθ,()2,B ρθ,θα=.可得4cos 4sin AB OB OA αα=-=-,4sin BM α=.由4AMB π∠=,得AB BM =,即求tan α的值.【详解】(1)1C 是圆心为()0,2,半径为2的圆.1C ∴的直角坐标方程为()2224x y +-=,即2240x y y +-=.222x y ρ=+,sin y ρθ=,得24sin 0,4sin ρρθρθ-=∴=.1C ∴的极坐标方程为4sin ρθ=.(2)设()1,A ρθ,()2,B ρθ,∵θα=,∴4sin OA α=,4cos OB α=,4cos 4sin AB OB OA αα=-=-,4OM =,∴4sin BM α=,∵4AMB π∠=,∴AB BM =,则4cos 4sin 4sin ααα-=,即cos 2sin αα=,所以1tan 2α=. 【点睛】本题考查参数方程、直角坐标方程、极坐标方程的互化,考查极坐标系下求极角,属于中档题.23.(1){}|06x a x <>或.(2)见解析 【解析】 【分析】(1)将0x =代入函数,列出不等式,再根据零点分段法即可求出实数a 的取值范围; (2)根据不等式恒成立问题的解法可知,只要()min 1112cos a x a---+≤即可, 亦即1112a a-++≥,再根据绝对值三角不等式以及基本不等式即可证出. 【详解】(1)∵()02158f a a =+-+->,即156a a -+->.当5a ≥时,不等式化为1565a a a -+->⎧⎨≥⎩,解得6a >;当15a <<时,不等式化为15615a a a -+->⎧⎨<<⎩,此时a 无解;当1a ≤时,不等式化为1561a a a -+->⎧⎨≤⎩,解得0a <.综上,原不等式的解集为{}|06x a x <>或. (2)要证明对x ∀∈R ,()151f x a a≥--+恒成立.只需证明 对x ∀∈R ,12cos 11x a a ≥---+恒成立.即证明()min 1112cos a x a ---+≤, ∵()min 2cos 2x =-,1112a a---+≤-,即1112a a -++≥.∵111111112a a a a a a aa -++≥-++=+=+≥,所以原命题得证. 【点睛】本题主要考查利用零点分段法求解含有两个绝对值的不等式,基本不等式,绝对值三角不等式的应用,以及不等式恒成立问题的解法应用,意在考查学生的转化能力,分类讨论意思的应用能力,属于中档题.。
2020年广东省佛山市高考数学二模试卷(理科)
2020年广东省佛山市高考数学二模试卷(理科)1.已知集合A={x|x2>2x},B={x|1≤x≤3},则A∪B=()A. {x|0≤x<1}B. {x|x<0或x≥1}C. {x|2<x≤3}D. {x|x≤1或x>3}2.复数z满足(z+2)(1+i)=3+i,则|z|=()A. 1B. √2C. √3D. 23.(1−√x)10的二项展开式中,x的系数与x4的系数之差为()A. −220B. −90C. 90D. 04.设变量x,y满足约束条件,则目标函数z=x+6y的最大值为()A. 3B. 4C. 18D. 405.设函数f(x)=(sinx+cosx)2+cos2x,则下列结论错误的是()A. f(x)的最小正周期为πB. y=f(x)的图象关于直线x=π8对称C. f(x)的最大值为√2+1D. f(x)的一个零点为x=7π86.已知a=log3(log32),b=(log32)2,c=2log32,则()A. a<b<cB. a<c<bC. c<a<bD. b<a<c7.已知点A(3,−2)在抛物线C:x2=2py(p>0)的准线上,过点A的直线与抛物线在第一象限相切于点B,记抛物线的焦点为F,则|BF|=()A. 6B. 8C. 10D. 128.盒中有形状、大小都相同的2个红色球和3个黄色球,从中取出一个球,观察颜色后放回并往盒中加入同色球4个,再从盒中取出一个球,则此时取出黄色球的概率为()A. 35B. 79C. 715D. 31459.2019年,全国各地区坚持稳中求进工作总基调,经济运行总体平稳,发展水平迈上新台阶,发展质量稳步上升,人民生活福祉持续增进,全年最终消费支出对国内生产总值增长的贡献率为57.8%.如图为2019年居民消费价格月度涨跌幅度:(同比=本期数−去年同期数去年同期数×100%,环比=本期数−上期数上期数×100%)下列结论中不正确的是( )A. 2019年第三季度的居民消费价格一直都在增长B. 2018年7月份的居民消费价格比同年8月份要低一些C. 2019年全年居民消费价格比2018年涨了2.5%以上D. 2019年3月份的居民消费价格全年最低 10. 已知P 为双曲线C :x 2a 2−y 2b 2=1(a >0,b >0)上一点,O 为坐标原点,F 1,F 2为曲线C 左、右焦点.若|OP|=|OF 2|,且满足tan∠PF 2F 1=3,则双曲线的离心率为( )A. √52B. √2C. √102D. √311. 已知A ,B ,C 是球O 的球面上的三点,∠AOB =∠AOC =60°,若三棱锥O −ABC 体积的最大值为1,则球O 的表面积为( )A. 4πB. 9πC. 16πD. 20π12. 双纽线最早于1694年被瑞士数学家雅各布⋅伯努利用来描述他所发现的曲线.在平面直角坐标系xOy中,把到定点F 1(−a,0),F 2(a,0)距离之积等于a 2(a >0)的点的轨迹称为双纽线C.已知点P(x 0,y 0)是双纽线C 上一点,下列说法中正确的有( )①双纽线C 关于原点O 中心对称;②−a2≤y 0≤a2;③双纽线C 上满足|PF 1|=|PF 2|的点P 有两个;④|PO|的最大值为√2a. A. ①② B. ①②④ C. ②③④ D. ①③ 13. 设命题p :∀x ∈(0,+∞),e x >1+12x 2,则¬p 为______. 14. 已知函数f(x)=x 2+x(1+sinx)+12x,若f(a)=−3,则f(−a)=______.15. 在面积为1的平行四边形ABCD 中,∠DAB =π6,则AB⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ = (1) ;点P 是直线AD 上的动点,则PB ⃗⃗⃗⃗⃗ 2+PC ⃗⃗⃗⃗⃗ 2−PB ⃗⃗⃗⃗⃗ ⋅PC⃗⃗⃗⃗⃗ 的最小值为 (2) . 16. 数学兴趣小组为了测量校园外一座“不可到达”建筑物的高度,采用“两次测角法”,并自制了测量工具:将一个量角器放在复印机上放大4倍复印,在中心处绑上一个铅锤,用于测量楼顶仰角(如图);推动自行车来测距(轮子滚动一周为1.753米).该小组在操场上选定A 点,此时测量视线和铅锤线之间的夹角在量角器上度数为37°;推动自行车直线后退,轮子滚动了10圈达到B 点,此时测量视线和铅锤线之间的夹角在量角器上度数为53°.测量者站立时的“眼高”为1.55m ,根据以上数据可计算得该建筑物的高度约为______米.(精确到0.1)17.已知等比数列{a n}的前n项和为S n(S n≠0),满足S1,S2,−S3成等差数列,且a1a2=a3.(1)求数列{a n}的通项公式;(2)设b n=−3a n(a n+1)(a n+1+1),求数列{b n}的前n项和T n.18.如图,在四棱锥P−ABCD中,底面ABCD是矩形,PA=PD=√3,PB=PC=√6,∠APB=∠CPD=90°,点M,N分别是棱BC,PD的中点.(1)求证:MN//平面PAB;(2)若平面PAB⊥平面PCD,求直线MN与平面PCD所成角的正弦值.19.已知椭圆C:x2a2+y2b2=1(a>b>0)的离心率为√22,且过点(2,1).(1)求椭圆C的方程;(2)过坐标原点的直线与椭圆交于M,N两点,过点M作圆x2+y2=2的一条切线,交椭圆于另一点P,连接PN,证明:|PM|=|PN|.20.2020年是我国全面建成小康社会和“十三五”规划收官之年,也是佛山在经济总量超万亿元新起点上开启发展新征程的重要历史节点.作为制造业城市,佛山一直坚持把创新摆在制造业发展全局的前置场”的创新发展之路.在推动制造业高质量发展的大环境下,佛山市某工厂统筹各类资源,进行了积极的改革探索.如表是该工厂每月生产的一种核心产品的产量x(5≤x ≤20)(件)与相应的生产总成本x 5 7 9 11 y200298431609工厂研究人员建立了与的两种回归模型,利用计算机算得近似结果如下: 模型①:y ̂=x 33+173;模型②:ŷ=68x −160. 其中模型①的残差(实际值−预报值)图如图所示:(1)根据残差分析,判断哪一个更适宜作为y 关于x 的回归方程?并说明理由;(2)市场前景风云变幻,研究人员统计历年的销售数据得到每件产品的销售价格q(万元)是一个与产量q 140−x 2130−x 2100−x 2p0.50.40.1(精确到0.1)?21. 已知函数f(x)=√x −a −sin x(x ≥a).(1)若f(x)≥0恒成立,求a 的取值范围;(2)若a <−14,证明:f(x)在(0,π2)有唯一的极值点x 0,且f(x 0)>1π−2x 0−x 0.22. 在平面直角坐标系xOy 中,曲线C 1的参数方程为{x =2costy =2+2sint(t 为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρ=4cosθ. (1)说明C 1是哪种曲线,并将C 1的方程化为极坐标方程;(2)设点M 的极坐标为(4,0),射线θ=α(0<α<π2)与C 1的异于极点的交点为A ,与C 2的异于极点的交点为B ,若∠AMB =π4,求tanα的值.23. 已知函数f(x)=2cosx +|a −1|+|a −5|,a ∈R .(1)若f(0)>8,求实数a 的取值范围;(2)证明:对∀x ∈R ,f(x)≥|a −5|−|1a +1|恒成立.答案和解析1.【答案】B【解析】解:∵集合A={x|x2>2x}={x|x<0或x>2},B={x|1≤x≤3},∴A∪B={x|x<0或x≥1}.故选:B.求出集合A,B,由此能求出A∪B.本题考查并集的求法,考查并集定义等基础知识,考查运算求解能力,是基础题.2.【答案】A【解析】【分析】本题考查了复数代数形式的乘除运算,考查了复数模的求法,属于基础题.把已知等式变形,然后利用复数代数形式的乘除运算化简,再由复数求模公式计算得答案.【解答】解:因为复数z满足(z+2)(1+i)=3+i,所以z=3+i1+i −2=(3+i)(1−i)(1+i)(1−i)−2=4−2i2−2=−i,则|z|=1,故选:A.3.【答案】D【解析】【分析】由题意利用二项展开式的通项公式,求出x的系数与x4的系数之差的值.本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.【解答】解:∵(1−√x)10的二项展开式中,通项公式为T r+1=C10r⋅(−1)r⋅x r2.故x的系数与x4的系数之差为C102−C108=0,故选:D.4.【答案】C【解析】【分析】本题考查简单的线性规划,考查了数形结合的解题思想方法,属于中档题.由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合的得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.【解答】解:由变量x,y满足约束条件作出可行域如图,A(0,3),化目标函数z=x+6y为y=−x6+z6,由图可知,当直线y=−x6+z6过A时,直线在y轴上的截距最大,z有最大值为18.故选:C.5.【答案】D【解析】【分析】本题主要考查利用二倍角公式,辅助角公式进行三角变换,以及函数y=Asin(ωx+φ)的图象与性质的应用,属于中档题.先利用二倍角公式和辅助角公式化简函数,即可根据y=Asin(ωx+φ)的图象与性质判断出各选项的真假.【解答】解:因为f(x)=(sinx+cosx)2+cos2x=1+sin2x+cos2x=1+√2sin(2x+π4),所以f(x)的最小正周期为π,f(x)的最大值为√2+1,A、C正确;当x=π8时,sin(2×π8+π4)=1,所以y=f(x)的图象关于直线x=π8对称,B正确;因为f(7π8)=1,所以x=7π8不是函数f(x)的零点,错误.故选:D.6.【答案】A【解析】解:∵0<log32<1,∴log3(log32)<0,即a<0,∴0<(log32)2<1,即0<b<1,∵c=2log32=log34>1,∴a<b<c,故选:A.利用对数函数和指数函数的性质求解.本题考查三个数的大小的求法,是基础题,解题时要认真审题,注意对数函数和指数函数的性质的合理运【解析】解:抛物线C:x2=2py(p>0)的准线方程为y=−p2,∵点A(3,−2)在准线上,∴−p2=−2即p=4,抛物线的方程为x2=8y即y=18x2.设点B的坐标为(m,m28),m>0,对y=18x2求导可得,y′=14x,∴直线AB的斜率为14m,由A(3,−2)、B(m,m28)可知,kAB=m28+2m−3=14m,解之得,m=8或−2(舍负),∴点B(8,8),由抛物线的定义可知,|BF|=8+42=10.故选:C.由点A(3,−2)在准线上可知p的值,从而确定抛物线的方程,设点B的坐标为(m,m28),m>0,通过对抛物线方程求导,可得点B处切线的斜率,也就是直线AB的斜率,再通过A、B两点的坐标也可求得k AB,于是建立关于m的方程,解之可得m的值,最后利用抛物线的定义即可得解.本题考查抛物线的定义、准线方程等,还涉及利用导数求抛物线上某点处切线的斜率,考查学生的分析能力和运算能力,属于中档题.8.【答案】A【解析】【分析】若取出的是红色球,再从盒中取出一个球,则此时取出黄色球的概率为:P1=25×39=215,若取出的是黄色球,再从盒中取出一个球,则此时取出黄色球的概率为:P1=35×79=715,由此能求出再从盒中取出一个球,则此时取出黄色球的概率.本题考查概率的求法,考查相互独立事件概率乘法公式、互斥事件概率计算公式等基础知识,考查运算求解能力,是基础题.【解答】解:盒中有形状、大小都相同的2个红色球和3个黄色球,从中取出一个球,观察颜色后放回并往盒中加入同色球4个,若取出的是红色球,再从盒中取出一个球,则此时取出黄色球的概率为:P1=25×39=215,若取出的是黄色球,再从盒中取出一个球,则此时取出黄色球的概率为:P1=35×79=715,∴再从盒中取出一个球,则此时取出黄色球的概率为:P=P1+P2=215+715=35.【解析】解:由折线图知:从2019年每月的环比增长率看,2019年第三季度的居民消费价格一直都在增长,故A正确;在B中,从2019年每月的同比增长率看,2018年7月份的居民消费价格比同年8月份要低一些,故B正确;在C中,从2019年每月的同比增长率看,2019年全年居民消费价格比2018年涨了4.5%−1.7%=2.8%,故C正确;在D中,从2019年每月的同比增长率看,2019年2月份的居民消费价格全年最低,故D错误.故选:D.根据已知中的图表,结合;同比增长率和环比增长率的定义,逐一分析给定四个命题的真假,可得答案.本题考查命题真假的判断,考查折线图等基础知识,考查运算求解能力、数据处理能力,考查函数与方程思想,是基础题.10.【答案】C【解析】【分析】本题主要考查双曲线的定义和性质,考查勾股定理的运用,运用平面几何中直径所对的圆周角为直角是解题的关键,属于中档题.点P在双曲线C的右支上,且满足|OP|=|OF2|,即有O为△PF1F2外接圆的圆心,即有∠F1PF2=90°,运用勾股定理和双曲线的定义,化简整理,结合离心率公式计算即可得到.【解答】解:点P在双曲线C的右支上,且满足|OP|=|OF2|,即有O为△PF1F2外接圆的圆心,即有∠F1PF2=90°,由双曲线的定义可得|PF1|−|PF2|=2a,∵tan∠PF2F1=3,∴|PF1|=3|PF2|,则|PF1|=3a,|PF2|=a,由|PF1|2+|PF2|2=|F1F2|2,即(3a)2+a2=4c2,a2,即有c2=52,则=√102故选:C.11.【答案】C【解析】【分析】本题考查多面体外接球表面积的求法,考查数形结合的解题思想方法,考查空间想象能力与思维能力,是中档题.由题意画出图形,把△AOB的面积用求的半径表示,再写出C到平面AOB的距离,代入三棱锥体积公式,求得体积取得最大值时的外接球的半径,则球的表面积可求.【解答】设求O 的半径为r ,点B ,C 在圆M 上,由∠AOB =∠AOC =60°,可得圆M 的半径为√32r ,OA ⊥平面MBC ,V O−ABC =V C−AOB =13×(12r 2×√32)×√32r ×sin∠BMC =18r 3×sin∠BMC .则当且仅当∠BMC =π2时,V O−ABC 取得最大值18r 3=1.∴r =2.则球O 的表面积为4πr 2=4π×4=16π. 故选:C . 12.【答案】B【解析】解:根据双纽线C 的定义可得,√(x 2+y 2√(x −a)2+y 2=a 2,用(−x,−y)替换方程中的(x,y),原方程不变,所以双纽线C 关于原点O 中心对称,①正确; 根据三角形的等面积法可知,12|PF 1||PF 2|sin∠F 1PF 2=12×2a ×|y 0|,即|y 0|=a2sin∠F 1PF 2≤a2, 亦即−a2≤y 0≤a2,②正确;若双纽线C 上点P 满足|PF 1|=|PF 2|,则点P 在y 轴上,即x =0,代入方程, 解得y =0,所以这样的点P 只有一个,③错误;因为PO ⃗⃗⃗⃗⃗ =12(PF 1⃗⃗⃗⃗⃗⃗⃗ +PF 2⃗⃗⃗⃗⃗⃗⃗ ),所以|PO ⃗⃗⃗⃗⃗ |2=14[|PF 1⃗⃗⃗⃗⃗⃗⃗ |2+2|PF 1⃗⃗⃗⃗⃗⃗⃗ ||PF 2⃗⃗⃗⃗⃗⃗⃗ |cos∠F 1PF 2+|PF 2⃗⃗⃗⃗⃗⃗⃗ |2]由余弦定理可得,4a 2=|PF 1⃗⃗⃗⃗⃗⃗⃗ |2−2|PF 1⃗⃗⃗⃗⃗⃗⃗ ||PF 2⃗⃗⃗⃗⃗⃗⃗ |cos∠F 1PF 2+|PF 2⃗⃗⃗⃗⃗⃗⃗ |2|PO ⃗⃗⃗⃗⃗ |2=a 2+|PF 1⃗⃗⃗⃗⃗⃗⃗ ||PF 2⃗⃗⃗⃗⃗⃗⃗ |cos∠F 1PF 2=a 2+a 2cos∠F 1PF 2≤2a 2,所以PO|的最大值为√2a ,④正确.故选:B .根据双纽线C 的定义求出其曲线方程,即可判断各命题的真假.本题主要考查新定义的应用,以及利用曲线方程研究其简单几何性质,属于中档题.13.【答案】∃x 0∈(0,+∞),e x 0≤1+12x 02【解析】解:因为全称命题的否定是特称命题, 所以命题p :∀x ∈(0,+∞),e x >1+1x 2,则¬p 为::∃x 0∈(0,+∞),e x 0≤1+12x 02; 故答案为:∃x 0∈(0,+∞),e x 0≤1+12x 02.直接利用全称命题的否定是特称命题写出结果即可.本题考查全称命题与特称命题的否定关系,考查推理能力,属于基础题. 14.【答案】4【解析】 【分析】本题考查函数的奇偶性,属于基础题.根据题意,对函数的解析式变形可得f(x)=x2+12x +sinx 2+12,据此可得f(−x)=−(x 2+12x +sinx 2)+12,分析可得f(x)+f(−x)=1,即可求解. 【解答】解:根据题意,f(x)=x 2+x(1+sinx)+12x=x 2+12x +sinx 2+12,则f(−x)=−(x2+12x +sinx 2)+12,则有f(x)+f(−x)=1, 则有f(a)+f(−a)=1,又由f(a)=−3,则f(−a)=4; 故答案为:4. 15.【答案】√3√3【解析】解:∵S ABCD =2S △ABC =2×12|AB||AD|sin∠DAB =|AB|⋅|BC|⋅sin π6=1, ∴|AB|⋅|AD|=2,∴AB ⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ ⋅AD⃗⃗⃗⃗⃗⃗ =|AB||AD|cos∠DAB =2×√32=√3, 取BC 的中点Q ,连接PQ ,则PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ =2PQ ⃗⃗⃗⃗⃗ ,PB ⃗⃗⃗⃗⃗ ⋅PC ⃗⃗⃗⃗⃗ =14[(PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ )2−(PB ⃗⃗⃗⃗⃗ −PC ⃗⃗⃗⃗⃗ )2]=14(4PQ ⃗⃗⃗⃗⃗ 2−CB ⃗⃗⃗⃗⃗ 2), ∴PB ⃗⃗⃗⃗⃗ 2+PC ⃗⃗⃗⃗⃗ 2−PB ⃗⃗⃗⃗⃗ ⋅PC ⃗⃗⃗⃗⃗ =(PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ )2−3PB ⃗⃗⃗⃗⃗ ⋅PC ⃗⃗⃗⃗⃗ =4PQ ⃗⃗⃗⃗⃗ 2−34(4PQ ⃗⃗⃗⃗⃗ 2−CB ⃗⃗⃗⃗⃗ 2)=PQ ⃗⃗⃗⃗⃗ 2+34BC ⃗⃗⃗⃗⃗ 2≥2|PQ|⋅√32|BC|=√3|PQ|⋅|BC|≥√3S 四边形ABCD =√3,当且仅当|PQ|=√32|BC|且PQ ⊥BC 时取等号,故答案为:√3,√3.根据四边形的面积计算|AB||AD|的值,再计算AB ⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ ;取BC 的中点Q ,连接PQ ,则PB ⃗⃗⃗⃗⃗ 2+PC ⃗⃗⃗⃗⃗ 2−PB ⃗⃗⃗⃗⃗ ⋅PC ⃗⃗⃗⃗⃗ =(PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ )2−3PB ⃗⃗⃗⃗⃗ ⋅PC ⃗⃗⃗⃗⃗ =PQ ⃗⃗⃗⃗⃗ 2+34BC ⃗⃗⃗⃗⃗ 2,再利用基本不等式和四边形的面积求出最小值.本题考查了向量的平行四边形法则、数量积运算性质、基本不等式的性质,考查了变形能力与计算能力,属于中档题. 16.【答案】31.6【解析】 【分析】本题考查了解三角形的应用问题,也考查了运算求解能力,属于中档题.根据题意画出图形,结合图形利用三角形的边角关系列方程求出建筑物的高度. 【解答】解:如图所示,设C′D =x ,A′C′=y ;在Rt △A′C′D 中,∠DA′C′=90°−37°=53°, 所以tan53°=xy ,即xy =sin53°cos53∘=4535=43; 所以y =3x 4;在Rt △B′C′D 中,∠DB′C′=90°−53°=37°, 所以tan37°=xy+17.53,x y+17.53=sin37°cos37∘=3545=34,所以x 34x+17.53=34,x ≈30.05,CD =CC′+C′D =1.55+30.05=31.60≈31.6(米); 根据以上数据可计算该建筑物的高度约为31.6米. 故答案为:31.6.17.【答案】解:(1)等比数列{a n }的前n 项和为S n (S n ≠0),满足S 1,S 2,−S 3成等差数列,且a 1a 2=a 3,设公比为q ,则{2S 2=S 1−S 3a 1a 2=a 3,整理得q 2+3q +2=0, 解得q =−1或−2,当q =−1时,a 1=−1,所以a 2=1,故S 2=0,与S n ≠0相矛盾, 当q =−2时,a 1=−2, 所以a n =(−2)n .(2)由于a n =(−2)n ,所以b n =−3a n(an +1)(a n+1+1)=−3(−2)n[(−2)n +1][(−2)n+1+1]=1(−2)n +1−1(−2)n+1+1,所以T n =1(−2)+1−1(−2)2+1+1(−2)2+1−1(−2)3+1+⋯+1(−2)n +1−1(−2)n+1+1=−1−1(−2)n+1+1.【解析】本题考查数列的通项公式的求法及应用,裂项相消法在数列求和中的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题.(1)直接利用题意,建立方程组求出首项和公比,进一步求出数列的通项公式; (2)利用(1)的结论,进一步利用裂项相消法在数列求和中的应用求出数列的和. 18.【答案】(1)证明:取PA 的中点为Q ,连结NQ ,BQ , 又点N 是PD 的中点,则NQ//AD ,且NQ =12AD , 又点M 是BC 的中点,底面ABCD 是矩形, 则BM =12AD ,且BM//AD ,∴NQ//BM ,且NQ =BM , ∴四边形MNQB 是平行四边形, ∴MN//BQ ,又MN ⊄平面PAB ,BQ ⊂平面PAB , ∴MN//平面PAB .(2)解:过点P 作PE ⊥AB ,交AB 于点E ,作PF ⊥CD ,交CD 于点F ,连结EF ,因为AB//CD ,则PF ⊥AB , 又PE ∩PF =P ,, ∴AB ⊥平面PEF ,又AB ⊂平面ABCD ,∴平面PEF ⊥平面ABCD ,∴AB =CD =3,PE =PF =√2,BE =CF =2,AE =DF =1, ∵平面PAB ⊥平面PCD , ∴∠EPF =90°,∴EF =2,取EF 的中点为O ,连结OP ,则OP ⊥EF ,OP =1,以O 为原点,OM ,OF ,OP 所在直线分别为x ,y ,z 轴,建立空间直角坐标系, 则P(0,0,1),C(2,1,0),D(−1,1,0),M(2,0,0),N(−12,12,12), ∴PC ⃗⃗⃗⃗⃗ =(2,1,−1),PD ⃗⃗⃗⃗⃗ =(−1,1,−1),MN ⃗⃗⃗⃗⃗⃗⃗ =(−52,12,12), 设平面PCD 的一个法向量n⃗ =(x,y ,z), 则{n ⃗ ⋅PC⃗⃗⃗⃗⃗ =2x +y −z =0n ⃗ ⋅PD ⃗⃗⃗⃗⃗ =−x +y −z =0, 取z =1,得n⃗ =(0,1,1), 设直线MN 与平面PCD 所成角为θ,则sinθ=|n⃗⃗ ⋅MN⃗⃗⃗⃗⃗⃗⃗ ||n⃗⃗ |⋅|MN⃗⃗⃗⃗⃗⃗⃗ |=1√2⋅3√32=√69,∴直线MN与平面PCD所成角的正弦值为√69.【解析】本题考查线面平行的证明,考查线面角的正弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.(1)取PA的中点为Q,连结NQ,BQ,推导出四边形MNQB是平行四边形,MN//BQ,由此能证明MN//平面PAB.(2)过点P作PE⊥AB,交AB于点E,作PF⊥CD,交CD于点F,连结EF,推导出AB⊥平面PEF,平面PEF⊥平面ABCD,取EF的中点为O,连结OP,则OP⊥EF,OP=1,以O为原点,OM,OF,OP所在直线分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出直线MN与平面PCD所成角的正弦值.19.【答案】解:(1)设椭圆的半焦距为c,由题设可得{ca =√224 a2+1b2=1,结合a2=b2+c2,解得a2=6,b2=3,所以椭圆出的方程为:x26+y23=1;(2)证明:①当直线PM的斜率不存在时,可得直线PM的方程为x=√2或x=−√2,若直线PM:x=√2,直线MN:y=x,可得M(√2,√2),N(−√2,−√2),P(√2,−√2),则|PM|=2√2,|PN|=2√2,所以|PM|=|PN|;②当直线PM的斜率存在时,设直线PM的方程为:y=kx+m,设M(x1,y1),P(x2,y2),由题设知N(−x1,−y1),联立{y=kx+m x26+y23=1,可得:(1+2k2)x2+4kmx+2m2−6=0,则x1+x2=−4km1+2k2,x1⋅x2=2m2−61+2k2,∵直线PM与x2+y2=2相切,∴原点O到直线PM的距离d=√1+k2=√2,即|m|=√2⋅2.∴|PM|=√1+k2√(x1+x2)2−4x1x2=2√2√1+k2⋅√1+4k21+2k2,又∵|PN|=√(x1+x2)2+(y1+y2)2,y1+y2=k(x1+x2)+2m=2m1+2k2,∴|PN|=√(−4km1+2k2)2+(2m1+2k2)2=2|m|√1+4k21+2k2=2√2√1+k2⋅√1+4k21+2k2,∴|PM|=|PN|.综合①②知:|PM|=|PN|.【解析】本题主要考查椭圆标准方程的求法及圆锥曲线中的综合问题,属于中档题.(1)由题设列出含a与b的方程组,解出即可得椭圆C的方程;(2)根据直线PM的斜率是否存在进行讨论,联立直线PM与椭圆的方程,得到坐标之间的关系式,求出|PM|与|PN|,即可证明结论.x 5 7 9 11y 200 298 431 609ê 20−18−21 21模型②的残差图如图所示,模型①更适宜作为y关于x的回归方程.理由如下:理由①:模型①这4个样本点的残差的绝对值都比模型②的小.理由②:模型①这4个样本的残差点落在的带状区域比模型②的带状区域更窄.理由③:模型①这4个样本的残差点比模型②的残差点更贴近x轴.(2)设月利润为Y,由题意得Y=qx−y,YY140x−x22−(x33+173)130x−x22−(x33+170)100x−x22−(x33+173)P0.50.40.1E(Y)=(140x −x 2−x 3−173)×1+(130x −x 2−x 3−173)×2+(100x −x 2−x 3−173)×1=−x 33−x 22+132x −173,设函数f(x)=−x 33−x 22+132x −173,x ∈(0,+∞),f′(x)=−x 2−x +132,令f′(x)=0,解得x =11或x =−12(舍), 当x ∈(0,11)时,f′(x)>0,则f(x)单调递增, 当x ∈(11,+∞)时,f′(x)<0,则f(x)单调递减, ∴f(x)的最大值为f(11)=46496≈774.8,即产量为11件时,月利润的预报期望值最大,最大值是774.8万元.【解析】本题考查回归直线方程的判断与应用,考查离散型随机变量的分布列、概率的求法,考查导数性质等基础知识,考查推理论证能力与运算求解能力,属于中档题.(1)求出模型②的残差数据,作出模型②的残差图,得到模型①更适宜作为y 关于x 的回归方程. (2)设月利润为Y ,由题意得Y =qx −y ,求出Y 的分布列,从而E(Y)=(140x −x 22−x 33−173)×12+(130x −x 22−x 33−173)×25+(100x −x 22−x 33−173)×110=−x 33−x 22+132x −173,设函数f(x)=−x 33−x 22+132x −173,x ∈(0,+∞),利用导数研究函数的单调性即可得到答案.21.【答案】解:(1)由f(a)≥0,得−sina ≥0,即sina ≤0,解得2kπ−π≤a ≤2kπ,k ∈Z , 以下证明,当2kπ−π≤a ≤2kπ(k ∈Z)时,f(x)≥0. 为此先证:√x ≥sinx(x ≥0).若x >1,则√x >1≥sinx ;若0≤x <1,则√x ≥x .令g(x)=x −sinx(x ≥0),可知g′(x)=1−cosx ≥0,故g(x)≥g(0)=0, 即x ≥sinx(x ≥0),故√x ≥sinx(x ≥0).若2kπ−π≤a ≤2kπ(k ∈Z),则当a ≤x ≤2kπ时,sinx ≤0, 故√x −a ≥0≥sinx ,即f(x)≥0; 当x ≥2kπ时,√x −a ≥√x −2kπ,由√x ≥sinx(x ≥0),得√x −2kπ≥sin(x −2kπ)=sinx . 故当2kπ−π≤a ≤2kπ(k ∈Z)时,f(x)≥0.综上,a 的取值范围是{a|2kπ−π≤a ≤2kπ,k ∈Z}. (2)f′(x)=2√x−a cosx ,令g(x)=2√x−a cosx ,g′(x)=−14(x−a)32+sinx ,∵a <−14,∴g′(x)是(0,π2)上的增函数, 又g′(0)<0,g′(π2)=1−14(π2−a)32>0, 故存在唯一实数t 0∈(0,π2),使g′(t 0)=0, 当x ∈(0,t 0)时,g′(x)<0,g(x)递减; 当x ∈(t 0,π2)时,g′(x)>0,g(x)递增, 又a <−14,则−a >14,√−a >12,2√−a >1,∴g(0)=2−a1<0,g(π3)=2√π3−a −12=12(√π3−a 1)<0,g(π2)=2√π2−a >0. 故存在唯一实数x 0∈(π3,π2),使g(x 0)=2x −a −cosx 0=0. 当x ∈(0,x 0)时,f′(x)=g(x)<0,f(x)递减; 当x ∈(t 0,π2)时,f′(x)=g(x)>0,f(x)递增.∴f(x)在区间有唯一极小值点x 0,且极小值为f(x 0)=√x 0−a −sinx 0. 又由g(x 0)=2√x −a cosx 0=0,得√x 0−a =12cosx 0,∴f(x 0)=12cosx 0−sinx 0,又f(x 0)+x 0=12cosx 0+(x 0−sinx 0)>12cosx 0.以下只需证明12cosx 0>1π−2x 0,0<2cosx 0<π−2x 0.∵x 0∈(0,π2),∴2cosx 0=2sin(π2−x 0)<2(π2−x 0)=π−2x 0.则f(x 0)+x 0=12cosx 0+(x 0−sinx 0)>12cosx 0>1π−2x 0,∴f(x 0)>1π−2x 0−x 0.【解析】(1)先根据f(a)≥0,求出a 的一个范围,然后证明√x ≥sinx(x ≥0),再进一步证明当2kπ−π≤a ≤2kπ时,f(x)≥0恒成立,即可确定a 的范围;(2)对f(x)求导,然后构造函数g(x)=2√x−a cosx ,求出g(x)零点,再判断f(x)的单调情况,进一步证明f(x)在(0,π2)有唯一的极值点x 0,且f(x 0)>1π−2x 0−x 0.本题考查了利用导数研究函数的极值和最值,不等式恒成立问题和利用综合法证明不等式,考查了函数思想和分类讨论思想,属难题.22.【答案】解:(1)曲线C 1的参数方程为{x =2costy =2+2sint (t 为参数),所以该曲线为以(0,2)为圆心,2为半径的圆. 转换为直角坐标法方程为x 2+y 2−4y =0. 转换为极坐标方程为ρ=4sinθ. (2)设A(ρ1,θ),B(ρ2,θ),射线θ=α(0<α<π2)与C 1的异于极点的交点为A ,与C 2的异于极点的交点为B , 所以|OA|=4sinα,|OB|=4cosα, 由于∠AMB =π4, 所以|AB|=|BM|,则4cosα−4sinα=4sinα,整理得tanα=12.【解析】本题考查的知识要点:参数方程极坐标方程和直角坐标方程之间的转换,同角三角函数基本关系,主要考查学生的运算能力和转换能力及思维能力,属于中档题.(1)直接利用转换关系,把参数方程极坐标方程和直角坐标方程之间进行转换.(2)设A(ρ1,θ),B(ρ2,θ),可得|OA|=4sinα,|OB|=4cosα,因为∠AMB =π4,所以|AB|=|BM|,4cosα−4sinα=4sinα,即可得到答案.23.【答案】(1)解:由f(0)=2+|a −1|+|a −5|>8,得|a −1|+|a −5|>6. 当a ≥5时,不等式化为{a −1+a −5>6a ≥5,解得a >6;当1<a <5时,不等式化为{a −1+5−a >61<a <5,此不等式无解;当a ≤1时,不等式化为{1−a +5−a >6a ≤1,解得a <0.综上,原不等式的解集为{a|a <0或a >6};(2)证明:要证明对∀x ∈R ,f(x)≥|a −5|−|1a +1|恒成立,需证明对∀x ∈R ,2cosx ≥−|a −1|−|1a +1|恒成立,即−|a −1|−|1a +1|≤(2cosx)min . ∵(2cosx)min =−2,∴证−|a −1|−|1a +1|≤−2,即|a −1|+|1a +1|≥2. ∵|a −1|+|1a+1|≥|a −1+1a+1|=|a +1a|=|a|+|1a|≥2,当且仅当a =±1时,等号成立. ∴原命题成立.【解析】本题考查绝对值不等式的解法,考查数学转化思想方法,利用基本不等式求最值,属于中档题. (1)由f(0)=2+|a −1|+|a −5|>8,得|a −1|+|a −5|>6,然后分a ≥5,1<a <5,a ≤1三类转化为关于a 的不等式组求解;(2)要证明对∀x ∈R ,f(x)≥|a −5|−|1a +1|恒成立,即−|a −1|−|1a +1|≤(2cosx)min ,也就是|a −1|+|1a +1|≥2,利用绝对值的不等式变形后再由基本不等式证明.。
2020佛山二模生物试题及答案
2019~2020学年佛山市普通高中教学质量检测(二)高三理综生物试题2020.5一、选择题1.细胞自噬是指细胞内衰老、损伤的细胞器,过量储存的糖原等,可被内质网膜包裹形成自噬体;当自噬体与溶酶体融合后,形成自噬溶酶体,将包裹的内容物降解。
关于该过程的说法正确的是A.细胞自噬的结果就是细胞凋亡B.吞噬并杀死侵入细胞的病毒或病菌属于细胞自噬C.降解后的产物均排放至细胞外,避免对细胞造成损伤D.自噬溶酶体的形成反映出生物膜的组成成分和结构具有相似性2.研究人员将某植物的绿色果肉薄片与NaHCO3溶液混合置于密闭反应室,提供一定的光照,水浴加热保持恒温,测定反应室中O2浓度,结果如下图所示。
下列相关叙述错误的是A.NaHCO3溶液的作用是提供光合作用的原料CO2B.15~20 min O2浓度不变,表明光合作用已经停止C.若在15 min 时停止光照,则短时间内叶绿体中C3化合物含量增多D.若在20 min 后停止光照,推测20~25 min范围内曲线斜率为负值3.下列关于DNA和RNA的叙述,正确的是A.原核细胞拟核中的DNA不能与蛋白质结合B.噬菌体侵染实验证明了DNA是主要的遗传物质C.真核细胞内DNA和RNA的合成都在细胞核内完成D.基因表达过程与mRNA、tRNA、rRNA都有一定的关系4.肾上腺素和迷走神经都参与兔血压的调节,下列有关叙述错误的是A.兔血压的调节方式为神经—体液调节B.肾上腺素在心脏代谢中起传递信息的作用C.剪断迷走神经后刺激其靠近心脏的一端,心脏活动减弱、血压降低,该过程属于反射D.肾上腺素和迷走神经末梢释放的乙酰胆碱都需要与细胞膜上的受体结合才能发挥作用5.下列有关生物学实验的叙述中,错误的是A.煮熟的豆浆也能与双缩脲试剂发生紫色反应B.探究不同浓度生长素对插条生根的影响,插条上芽的数量应相等C.研究酵母菌的种群数量变化时,应振荡均匀后再吸取培养液进行计数D.低温诱导染色体数目加倍实验中,将洋葱根尖制成装片后再进行低温处理6.某小组调查人群中的某种遗传病,获得如下家系图,下列相关分析正确的是A.图中2号为纯合子或杂合子B.由5号、6号与9号,可推知该致病基因在X染色体上C.由1号、2号、4号和5号,可推知该此病为显性遗传病D.要得出该遗传病的发病率,需要在大量的患者家系中进行随机调查二、非选择题(一)必考题29.(10分)目前农业用地的盐碱化程度在不断加重,农作物在高盐分土壤中生长发育缓慢、产量下降。
2020佛山二模文数试题(含答案)
2
D. 5π 6
A. π 3
C. π 6
B. π 6
D. π 3
O
π
3
13π x 12
x y 0 7.变量 x, y 满足约束条件 x 2 y 2 0 ,若 z 2x y 的最大值为 2 ,则实数 m 等于( )
mx y 0
A. 2
B. 1
C.1
高三教学质量检测(二)文科数学试题 第 1 页 共 4 页
2ab
10b
7
解得 b 7 ,所以 c 8 .
……………………………………………………………3 分
由余弦定理可得 cos B a2 c2 b2 25 64 49 1 ,
2ac
258 2
且△ ABC 中, B (0, π) ,所以 B π . 3
……………………………………………………………5 分
二、填空题:本大题共 4 小题,每小题 5 分,满分 20 分.
13.六名男同学参加校运会的“百米飞人”决赛,其中有两名同学来自高三(1)班,则高三(1)班包揽
冠亚军的概率为
.
14.数列 an 满足 anan1 1 0 ,若 a9 2 ,则 a1
.
15.已知 P 为双曲线 C :
x2 a2
圆大小相同,若正四棱锥 P ABCD 的高为 2 ,则球 O 的表面积为( )
A. 8π
B. 9π
C.12π
D.16π
第Ⅱ卷(非选择题 共 90 分)
本卷包括必考题和选考题两部分.第 13~21 题为必考题,每个试题考生都必须作答.第 22~23 为选 考题,考生根据要求作答.
高三教学质量检测(二)文科数学试题 第 2 页 共 4 页
广东省佛山市2020届高三教学质量检测(二模)文科数学试题(附答案解析)
请考生在第 22,23 题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清楚题号.
22.(本小题满分 10 分)[选修 4 4 :坐标系与参数方程选讲]
在平面直角坐标系
xOy
中,曲线
C1
的参数方程为
x y
2 2
cos 2
t sin
t
(t
为参数
)
,以坐标原点
O
为极点,
x 轴的正半轴为极轴建立极坐标系,曲线 C2 的极坐标方程为 4 cos .
高三教学质量检测(二)文科数学试题 第 4 页 共 4 页
2019~2020 年佛山市普通高中高三教学质量检测(二)
数 学(文科)参考答案与评分标准
一、选择题:本大题共 12 小题,每小题 5 分,满分 60 分.
题号 1
2
3
4
5
6
7
8
9
10
11
12
答案 B
A
D
C
C
B
C
D
D
C
B
A
二、填空题:本大共 4 小题,每小题 5 分,满分 20 分.
圆大小相同,若正四棱锥 P ABCD 的高为 2 ,则球 O 的表面积为( )
A. 8π
B. 9π
C.12π
D.16π
第Ⅱ卷(非选择题 共 90 分)
本卷包括必考题和选考题两部分.第 13~21 题为必考题,每个试题考生都必须作答.第 22~23 为选 考题,考生根据要求作答.
高三教学质量检测(二)文科数学试题 第 2 页 共 4 页
13. 1 15
14. 2
15. 10 2
16. 2,[ 2 4
2020年佛山外国语学校高三英语二模试卷及参考答案
2020年佛山外国语学校高三英语二模试卷及参考答案第一部分阅读(共两节,满分40分)第一节(共15小题;每小题2分,满分30分)阅读下列短文,从每题所给的A、B、C、D四个选项中选出最佳选项ALocated inLos Angeles,UniversityofSouthern Californiais in the heart of a leading city. Although LA ranks highly in The Economist’s Safe Cities Index, navigating and city calls for certain safety precautions (预防措施) along with practicing common sense.♦Mobile Safety App Powered by LiveSafeThe Mobile Safety App powered by LiveSafe, manage by the USC Department of Public Safety and the USC Department of Emergency Planning, is a free downloadable app that mobile users can use to initiate contact with emergency responders around the campus. Features include: immediate “push button” calls to DPS, easy reporting for suspicious activity or crimes in progress, and location services to notify friends of your route through campus.♦Blue Light Phone LocationsTheUniversity Parkhas multiple blue light phones that are strategically placed throughout campus. Take note of where the closest ones are on your route. They come in handy in case you lose your phone or in an emergency. These phones are directly connected to USC’s Department of Public Safety’s 24-hour communications center. Besides emergency needs, it can also be used to report suspicious activity, request for an escort (护送) if you feel unsafe and to report a crime.♦Trojans AlertTrojans Alert is an emergency notification system that allows university officials to contact you during an emergency by sending messages via text message or email. When an emergency occurs, authorized USC senders will instantly notify you with real-time updates, instructions on where to go, what to do (or what not to do), whom to contact and other important information. All members of the USC community, as well as parents and regular visitors to campus, are strongly encouraged to sign up for Trojans Alert.1. What do blue light phones do for students?A. Guide students through campus.B. Alert students to crime activities.C. Light up the way if students feel unsafe.D. Connect them with the safety department.2. How does USC send out instructions during an emergency?A. With blue light phones.B. Via text message or email.C. Through mobile safe app.D. By calling all USC members.3. What is the purpose of the text?A. To encourage students to fight crime.B. To introduce USC’s safety department.C. To provide safety services for USC students.D. To inform parents of safety risks on campus.BGuangzhououtbreak linked to strains inIndiaThe gene sequencing of the COVID-19 outbreak inGuangzhou.Guangdongprovince, indicates it is very similar in structure to the mutatedstrains detected inIndia, a senior health official from the city said on Sunday.“And it has the characteristic of quick spread.” Chen Bin, deputy director of the city's health commission, said at a news conference inGuangzhouon Sunday.She urged relevant departments and medical staff to act quickly to block the chain of infection and control the spread of the coronavirus in the southern metropolis.Zhang Zhoubin, deputy director of theGuangzhoucenter for disease control and prevention, said the strain of coronavirus spreads easily.“The virus can be spread through a meal or through a short period of indirect contact,” he said.The city reported five confirmed eases and 21 asymptomatic carriers as of 2 pm Sunday after the first con finned case was detected in the city's Liwan district on May 21, Chen said.To prevent the virus from spreading, the city government tightened its disease control and prevention measures over the weekend. Six communities and housing estates previously designated as low-risk areas were raised to medium-risk ones, Chen said.In addition to asking local residents to get vaccinated, the city has organized nucleic acid testing in Haizhu and Yuexiu districts starting from Sunday. Residents in specific areas of Tianhe, Baiyun and Panyu districts have also been required to take nucleic acid tests to expand the screening of suspected patients and asymptomatic carriers.Liwan previously required all its residents to take nucleic acid tests.As of Saturday, more than 2-25 million residents of the city have had samples collected for nucleic acid tests, Chen said. More than 10,000 medical workers from the entire city have been sent to Liwan to help vaccinate locals against COVID-19 and collect samples for nucleic acid testing.Deng Wenjun, director of circulation section with Guangzhou Supply and Marketing Cooperative, said there are sufficient supplies of food and daily necessities in the medium-risk areas.4. What is the characteristic of the COVID-19 which broke out inGuangzhou?A. It disappears quickly.B. It spreads fast.C. It has a lot to do with temperature.D. It has the same nature as the seasonal flu.5. Which district have residents who have not been required to take nucleic acid tests?A. Tianhe.B. Haizhu.C. Panyu.D. Zengcheng.6. Which of the following statements is TRUE?A. The virus can hardly be spread through a short period of indirect contact.B. There are 21 symptomatic carriers in the Liwan district as of 2 pm Sunday.C. All the people living in Liwan district arc previously asked to take nucleic acid tests.D. Supplies of food and daily necessities in the medium-risk areas arc still not enough.7. Where can you probably find this article?A. On a news website.B. In a fashion magazine.C. In a history book.D. In a travel journal.CHave you ever done something for someone else—knowing that your actions would solely benefit THEM and not YOU? Maybe you opened a door or donated blood or volunteered in a hospital’s ER during the pandemic. This is called a prosocial behavior. Humans engage in these types of behaviors all the time.But a question remains in science: Are we the only species who do this? As one of out closest s, chimpanzees have long been studied for signs of this. So far, research has provided mixed results on the question.Some studies show that chimps cooperatively hunt, share food and comfort each other. But one study came to a very different conclusion. The study used a controlled lab experiment where chimpanzees in enclosures were given two options: push a button to give food to themselves or push the button to give food to themselves AND a partner chimp. If they chose the latter, it was seen as a prosocial behavior. But the result is that chimps showed no special preferences for feeding themselves and a friend over feeding just themselves. Another study conducted byDeTroy, however, discovered a totally different result.Compared to previous controlled lab-based experiments, the setup for DeTroy’s research was very naturalistic. “We installed a button and a fountain into the chimpanzees’ outer enclosures. When an individual pushes the button, it releases juice from the fountain. However, since the button and fountain are approximately five meters apart, the individual pushing cannot directly drink from the fountain. And if any other chimpanzees are at the fountain when the button is pushed, they, and not the pusher, will be able to drink the juice.In this experiment, chimpanzees showed a willingness to act in the interest of others, with individual chimpanzees prepared to push the button without benefiting themselves.“It is really fascinating to see that many of the chimpanzees were willing to prosocially provide valuable resources to the group members even if they couldn’t benefit themselves from their behavior.” said DeTroy.Further research may reveal what lies behind their prosocial motivation. But for now, it’s safe to assume that chimpanzees are not simply aping human behavior.8. Which of the following belongs to prosocial behaviors?A. Jack participated in voluntary work in the library just to earn credits.B. Mark turned to his classmate for help when feeling stressful in study.C. Tim guided a lost child back home on his way to an important job interview.D. Rose often interrupted the teacher to ask questions actively in the math’s class.9. What is the task of the chimpanzees in the lab-based study?A. Sharing food.B. Making a choice.C. Comforting others.D. Showing sympathy.10. How is DeTroy’s study different from the previous ones?A. It was based on controlled lab experiment.B. It gave juice to the chimpanzees as a reward.C. It offered the tested chimpanzees a natural surrounding.D. It provided a chance for chimpanzees to help their partners.11. What can we learn from DeTroy’s quotes?A. Chimpanzees can develop abilities to help others.B. Chimpanzees have acquired many human behaviors.C. Chimpanzees in the wild is cleverer than those in the lab.D. Chimpanzees displayed prosocial behaviors for certain rewards.D"Long time no see." is a very interesting sentence. When I first read this sentence from an American friend's e-mail, I laughed. I thought it was a perfect example of Chinglish.Obviously, it is a word-by-word literal translation of the Chinese greeting with wrong English grammar and structure! Later on, my friend told me that it is a standard American greeting. I was too surprised to believe her. Her words were unbelievable at all. So I did research onGoogle. com. To my surprise, there are over 60 thousand web pages containing "Long time no see." Though it is sort of informal, it is part of the language that Americans use daily. Interestingly, if you type this phrase in Microsoft Word, the software will tell you that the grammar needs to be corrected.Nobody knows the origin of this Chinglish sentence. Some people believe that it came from Charlie Chan's movies. In the 1930s, Hollywood moviemakers successfully created a worldwide famous Chinese detective named "Charlie Chan" on wide screens. Detective Chan liked to teach Americans some Chinese wisdom by quoting Confucius. "Long time no see." was his symbol. Soon after Charlie Chan, "Long time no see." became a popular expression in America thanks to the popularity of these movies.Some scholars compare America to a hugemelting pot. All kinds of cultures are mixed in the pot together, and they change the colour and taste of each other. Language is usually the first thing to be influenced in the mixed pot.You can have some examples from other countries such as pizza from Italian, sushi from Japanese, and déjà vu from French etc. There is a long list! Since Americans admire Chinese culture more and more nowadays, I believe more Chinese words will become American English in the future. In this way, the American's melting pot keeps adding richness and flavour.12. What did the writer himself feel surprised at?A. The Chinglish expression "Long time no see."B. So many literal translations of the expressions used in America.C. "Long time no see." is used as a standard American English greeting.D. Finding out Americans use the expression every day.13. What do the underlined words "melting pot" in Paragraph 4 probably mean?A. Confucius's words.B. Culture mixture.C. A kind of cooked dish.D. American changing cultures.14. According to the passage, what can be inferred?A. Detectives translated the phrase "Long time no see."B. Cultures cannot be changed in the huge melting pot.C. The huge melting pot greatly affects all kinds of languages.D. Hollywood made "Long time no see." popular.15. What is the main idea of the passage?A. Some Chinese expressions are introduced into English.B. You'll not be surprised at a tofu and peanut butter hamburger in a restaurant in America.C. Some American expressions can be used in China.D. American English keeps being enriched by different cultures.第二节(共5小题;每小题2分,满分10分)阅读下面短文,从短文后的选项中选出可以填入空白处的最佳选项。
