phi-fourth model on a circle

合集下载

Synphilin-1寡核苷酸对帕金森病caspase-8表达影响的实验研究

Ab stra ct:Objective: To investigate the re lation between Synphilin 2 1 and ca spase2 8 of Pa rkinson disease. Me thods: Fifty hea lthy m ale Sprague2 Dawley ra ts were divided into five groups. The first group of ten ra ts were p repa red to be he m ipa rkinsonian mode ls induced by unila tera l stereotaxic infusion of 6 2 hydroxydop a m ine ( 6 2 OHDA ) in right substantia nigra of m idbrain. Eve ry week afte r operation, The c ircles the ra ts run we re observed in 30 m inute afte r injec ting apomo r2 phine by peritonea l cavity. If the ra t ran more than 6 circle s eve rym inute a t the fourth week afte r operation, theywere suc2 cessful PD rat models . The groups from the second to the fourth we re given antisen se, sense and m issense oligonuc leotides respective ly, then they were induced to be hem ipa rkinsonian models in the sam e way as the first group. The fifth group we re jnjec ted with natrium sa line and se rved as the control group. F inally, we compared the exp re ssion of synphilin 2 1 p rote in through imm unohistochem istry, and compared the exp ression of caspa se2 8 pr ote in and mRNA through immunohistoche m istry in situ hybridiza tion . R esults: Compared to the normal group, the exp re ssion of Synphilin2 1 in PD significantly inc rea sed; Compared to no r ma l group, the expression of caspa se2 8 p rotein and mRNA in PD significantly increa sed; compa red to PD gr oup, the exp re ssion of ca spase2 8 in antisense group significantly increased. Conc lusion: The role of abnor ma l expression of Synphilin 2 1 in the mechanis m of P D m ay be connec ted with the effec t on the expre ssion of ca spase2 8. Key wor d s: Synphilin2 1; caspa se2 8; pa rkinson disease; rats

曲面曲线 curves and surfaces for CAGD

dimensional transformations (rotation, translation, scaling, reﬂection, and shearing) and
how they are described mathematically by a 4×4 transformation matrix. This mate-
A more general example is a rectangular surface patch constructed as a sweep surface by translating an arbitrary proﬁle along another curve, the trajectory. Given the two cubic B´ezier curves
Figure 9.1: Two Sweep Surfaces.
Exercise 9.1: Calculate the sweep surface obtained when line C(u) = (3u, 0, 0, 1) is translated along the z axis and at the same time translated in the y direction along a sine curve.
C(t) = (1 − t)3(0, 1, 1) + 3t(1 − t)2(1, 1, 0) + 3t2(1 − t)(4, 2, 0) + t3(6, 1, 1) = (−3t3 + 6t2 + 3t, −3t3 + 3t2 + 1, 3t2 − 3t + 1) and
Q(t) = (1 − t)3(0, 0, 0) + 3t(1 − t)2(1, 2, 1) + 3t2(1 − t)(3, 2, 2) + t3(2, 0, 1) = (−4t3 + 3t2 + 3t, −6t2 + 6t, −2t3 + 3t)

2005年高考英语试题及答案(全国卷2)

2005年普通高等学校招生全国统一考试英语YCYYCY本试卷分为第一卷（选择题）和第二卷（非选择题）两部分.第一卷1至13页。

第二卷14至17页.考试结束，将本试卷和答题卡一并交回.第一卷注意事项：1．答第一卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

不能答在试卷上。

第一部分：听力（共两节，满分30分）做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节（共5小题；每小题 1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

例：How much is the shirt ?A．￡19.15. B．￡9.15. C．￡9.18.答案是 B.1．How much will the woman pay if she buys two skirts ?A．$18. B．$19. C．$20.2．What will the speakers discuss ?A．A report . B．A computer . C．A report on computer . 3．What are the speakers talking about ?A．A child . B．A room . C．A present .4．What can we learn from this conversation ?A．The woman does not get along well with the man .B．The woman does not get along well with here roommate .C．T he man will talk with the woman’s roommate .5．Where are the two speakers now ?A．On the first floor . B．On the fourth floor . C．On the fifth floor.第二节（共15小题；每题 1.5分，满分22.5分）听下面5段对话或独白。

力学中的数学方法期末大作业(试题)2017

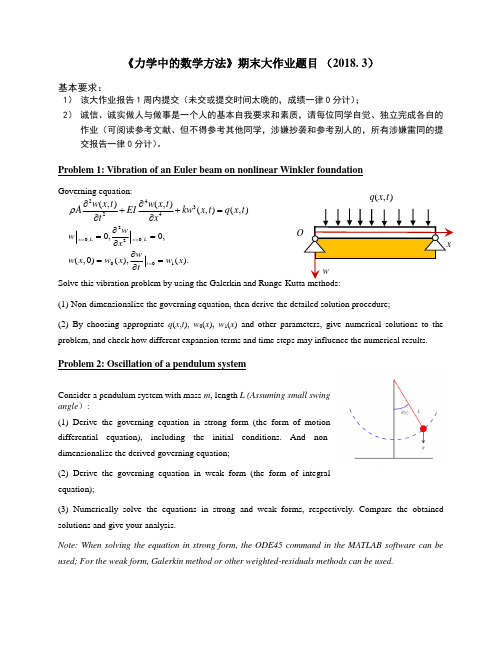
《力学中的数学方法》期末大作业题目（2018. 3）基本要求：1）该大作业报告1周内提交（未交或提交时间太晚的，成绩一律0分计）；2）诚信、诚实做人与做事是一个人的基本自我要求和素质，请每位同学自觉、独立完成各自的作业（可阅读参考文献、但不得参考其他同学，涉嫌抄袭和参考别人的，所有涉嫌雷同的提交报告一律0分计）。

Problem 1: Vibration of an Euler beam on nonlinear Winkler foundation Governing equation: 24324(,)(,)(,)(,)w x t w x t A EI kw x t q x t t xρ∂∂++=∂∂ 20,0,20010,0,(,0)(),().x L x L t w w x ww x w x w x t ===∂==∂∂==∂ Solve this vibration problem by using the Galerkin and Runge-Kutta methods:(1) Non-dimensionalize the governing equation, then derive the detailed solution procedure;(2) By choosing appropriate q (x ,t ), w 0(x ), w 1(x ) and other parameters, give numerical solutions to the problem, and check how different expansion terms and time steps may influence the numerical results.Problem 2: Oscillation of a pendulum systemConsider a pendulum system with mass m , length L (Assuming small swingangle ）:(1) Derive the governing equation in strong form (the form of motiondifferential equation), including the initial conditions. And non-dimensionalize the derived governing equation;(2) Derive the governing equation in weak form (the form of integralequation);(3) Numerically solve the equations in strong and weak forms, respectively. Compare the obtained solutions and give your analysis.Note: When solving the equation in strong form, the ODE45 command in the MATLAB software can be used; For the weak form, Galerkin method or other weighted-residuals methods can be used. O xw (,)q x t。

希腊字符及数学符号读法

特殊符号的英文读法＜ is less than ＞ is more than≤ is not less than≥ is not more than≢ is less than or equal to 小于或等于号- hyphen 连字符≣ is more than or equal to 大于或等于号' apostrophe 省略号,英文中省略字符用的撇号;所有格符号％ percent－ dash 破折号‰ per mille∞ infinity 无限大号∝ varies as 与…成比例( ) parentheses 圆括号√ (square) root 平方根[ ] square brackets 方括号∵ since; because 因为《》 French quotes 法文引号;书名号∴ hence 所以… ellipsis 省略号∷ equals, as (proportion) 等于，成比例¨ tandem colon 双点号∟ angle 角∶ ditto 双点号≨ semicircle 半圆‖ parallel 双线号≦ circle圆／ virgule 斜线号○ circumference 圆周～ swung dash 代字号△ triangle 三角形§ section; division 分节号≧ perpendicular to 垂直于→ arrow 箭号；参见号∪ union of 并，合集∩ intersection of 交，通集∫ the integral of …的积分ª plus or minus 正负号∑ summation of 总和× is multipli ed by 乘号© degree 度÷ is divided by 除号′ minute 分″ second 秒≠ is not equal to 不等于号≡ is equivalent to 全等于号℃ Celsius degree 摄氏度≌ is equal to or approximately equal to 等于或约等于号计算机编成常用符号英语读音` backquote 反引号~ tilde! exclam@ at# numbersign,英语国家是hash，美语是pound,音乐里作sharp,如C# $ dollar% percent^ caret& ampersand* asterisk,star(美语),数学公式中作multiply( parenleft,opening parentheses) parenright,closing paretheses- minus;hyphen连字符,不读_ underscore+ plus= equal[ bracketleft,opening bracket] bracketright,closing bracket{ braceleft} braceright; semicolon: colon' quote" doublequote/ slash\ backslash 反斜杠| bar, comma< less> greater. period? questionspace 空格: plus(positive正的)－：minus（negative负的）*：multiplied by÷：divided by＝: be equal to≈ : be approximately equal to() : round brackets(parenthess)[] : square brackets{} : braces∵ : because∴ : therefore≢ : less than or equal to≣ ：greater than or equal to∞：infinity: logx to the base n: the nth power of xf(x) : the function of xdx : diffrencial of xx+y : x plus y(a+b) : bracket a plus b bracket closed a=b : a equals ba≠b：a isn't equal to ba>b : a is greater than ba>>b : a is much greater than ba≣b : a is greater than or equal to bx→∞ ：x approches infinity: x square: x cube: the square root of x数学公式的英文读法&数学英文词汇1. Logic∃there exist∀for allp⇒q p implies q / if p, then qp⇔q p if and only if q /p is equivalent to q / p and q are equivalent 2.Sets x∈A x belongs to A / x is an element (or a member) of Ax∉A x does not belong to A / x is not an element (or a member) ofA⊂B A is contained in B / A is a subset of BA⊃B A contains B / B is a subset of AA∩B A cap B / A meet B / A intersection BA∪B A cup B / A join B / A union BA\B A minus B / the diference between A and BA×B A cross B / the cartesian product of A and B3. Real numbersx+1 x plus onex-1 x minus onex±1 x plus or minus onexy xy / x multiplied by y(x - y)(x + y) x minus y, x plus yx y x over y= the equals signx = 5 x equals 5 / x is equal to 5x≠5 x (is) not equal to 5x≡y x is equivalent to (or identical with) yx ≡ y x is not equivalent to (or identical with) yx > y x is greater than yx≥y x is greater than or equal to yx < y x is less than yx≤y x is less than or equal to y0 < x < 1 zero is less than x is less than 10≤x≤1 zero is less than or equal to x is less than or equal to 1| x | mod x / modulus xx 2 x squared / x (raised) to the power 2x 3 x cubedx 4 x to the fourth / x to the power fourx n x to the nth / x to the power nx −n x to the (power) minus nx (square) root x / the square root of xx 3 cube root (of) xx 4 fourth root (of) xx n nth root (of) x( x+y ) 2 x plus y all squared( x y ) 2 x over y all squaredn! n factorial《现代英汉综合大辞典》4的阶乘读作the factorial of 4;《美国传统词典》，4 factorial, usually written 4!, is equal to 24 (1 ×2 ×3 ×4 = 24).x ^ x hatx ¯x barx ˜ x tildex i xi / x subscript i / x suffix i / x sub i∑ i=1 n a i the sum from i equals one to n a i / the sum as i runs from 1 to n of the a i4. Linear algebra‖x ‖the norm (or modulus) of xOA → OA / vector OAOA ¯OA / the length of the segment OAA T A transpose / the transpose of AA −1 A inverse / the inverse of A5. Functionsf( x ) fx / f of x / the function f of xf:S→T a function f fro m S to Tx→y x maps to y / x is sent (or mapped) to yf'( x ) f prime x / f dash x / the (first) derivative of f with respect to xf''( x ) f double-prime x / f double-dash x / the second derivative of f with respect to xf'''( x ) triple-prime x / f triple-dash x / the third derivative of f with respect to xf (4) ( x ) f four x / the fourth derivative of f with respect to x∂f ∂ x 1 the partial (derivative) of f with respect to x1∂ 2 f ∂ x 1 2 the second partial (derivative) of f with respect to x1∫ 0 ∞ the integral from zero to infinitylim⁡x→0 the limit as x approaches zerolim⁡x→ 0 + the limit as x approaches zero from abovelim⁡x→ 0 − the limit as x approaches zero from belowlog e y log y to the base e / log to the base e of y / natural log (of) y ln⁡y log y to the base e / log to the base e of y / natural log (of) y数学mathematics, maths(BrE), math(AmE)公理axiom定理theorem计算calculation运算operation证明prove假设hypothesis, hypotheses(pl.)命题proposition算术arithmetic加plus(prep.), add(v.), addition(n.)被加数augend, summand加数addend和sum减minus(prep.), subtract(v.), subtraction(n.)被减数minuend减数subtrahend差remainder乘times(prep.), multiply(v.), multiplication(n.)被乘数multiplicand, faciend乘数multiplicator积product除divided by(prep.), divide(v.), division(n.)被除数dividend除数divisor商quotient等于equals, is equal to, is equivalent to大于is greater than小于is lesser than大于等于is equal or greater than小于等于is equal or lesser than运算符operator数字digit数number自然数natural number整数integer小数decimal小数点decimal point分数fraction分子numerator分母denominator比ratio正positive负negative零null, zero, nought, nil十进制decimal system二进制binary system十六进制hexadecimal system权weight, significance进位carry截尾truncation四舍五入round下舍入round down上舍入round up有效数字significant digit无效数字insignificant digit代数algebra公式formula, formulae(pl.)单项式monomial多项式polynomial, multinomial系数coefficient未知数unknown, x-factor, y-factor, z-factor 等式，方程式equation一次方程simple equation二次方程quadratic equation三次方程cubic equation四次方程quartic equation不等式inequation阶乘factorial对数logarithm指数，幂exponent乘方power二次方，平方square三次方，立方cube四次方the power of four, the fourth power n次方the power of n, the nth power开方evolution, extraction二次方根，平方根square root三次方根，立方根cube root四次方根the root of four, the fourth root n次方根the root of n, the nth root集合aggregate元素element空集void子集subset交集intersection并集union补集complement映射mapping函数function定义域domain, field of definition值域range常量constant变量variable单调性monotonicity奇偶性parity周期性periodicity图象image数列，级数series微积分calculus微分differential导数derivative极限limit无穷大infinite(a.) infinity(n.)无穷小infinitesimal积分integral定积分definite integral不定积分indefinite integral有理数rational number无理数irrational number实数real number虚数imaginary number复数complex number矩阵matrix行列式determinant几何geometry点point线line面plane体solid线段segment射线radial平行parallel相交intersect角angle角度degree弧度radian锐角acute angle直角right angle钝角obtuse angle平角straight angle周角perigon底base边side高height三角形triangle锐角三角形acute triangle直角三角形right triangle斜边hypotenuse勾股定理Pythagorean theorem钝角三角形obtuse triangle不等边三角形scalene triangle等腰三角形isosceles triangle等边三角形equilateral triangle四边形quadrilateral平行四边形parallelogram矩形rectangle长length宽width菱形rhomb, rhombus, rhombi(pl.), diamond 正方形square梯形trapezoid直角梯形right trapezoid等腰梯形isosceles trapezoid五边形pentagon六边形hexagon七边形heptagon八边形octagon九边形enneagon十边形decagon十一边形hendecagon十二边形dodecagon多边形polygon正多边形equilateral polygon圆circle圆心centre(BrE), center(AmE)半径radius直径diameter圆周率pi弧arc半圆semicircle扇形sector环ring椭圆ellipse圆周circumference周长perimeter面积area轨迹locus, loca(pl.)相似similar全等congruent四面体tetrahedron五面体pentahedron六面体hexahedron平行六面体parallelepiped 立方体cube七面体heptahedron八面体octahedron九面体enneahedron十面体decahedron十一面体hendecahedron 十二面体dodecahedron二十面体icosahedron多面体polyhedron棱锥pyramid棱柱prism棱台frustum of a prism旋转rotation轴axis圆锥cone圆柱cylinder圆台frustum of a cone球sphere半球hemisphere底面undersurface表面积surface area体积volume空间space坐标系coordinates坐标轴x-axis, y-axis, z-axis 横坐标x-coordinate纵坐标y-coordinate原点origin双曲线hyperbola抛物线parabola三角trigonometry正弦sine余弦cosine正切tangent余切cotangent正割secant余割cosecant反正弦arc sine反余弦arc cosine反正切arc tangent反余切arc cotangent反正割arc secant反余割arc cosecant相位phase周期period振幅amplitude内心incentre(BrE), incenter(AmE)外心excentre(BrE), excenter(AmE)旁心escentre(BrE), escenter(AmE)垂心orthocentre(BrE), orthocenter(AmE)重心barycentre(BrE), barycenter(AmE)内切圆inscribed circle外切圆circumcircle统计statistics平均数average加权平均数weighted average方差variance标准差root-mean-square deviation, standard deviation 比例propotion百分比percent百分点percentage百分位数percentile排列permutation组合combination概率，或然率probability分布distribution正态分布normal distribution非正态分布abnormal distribution图表graph条形统计图bar graph柱形统计图histogram折线统计图broken line graph 曲线统计图curve diagram扇形统计图pie diagram。

广州市花都区秀全中学2022-2023学年高一上学期期末考试英语试题

秀全中学2022学年高一年级第一学期期末测试英语科试卷命题人：李洁审题人刘燕珍试题说明：本试卷分为选择题和非选择题两部分。

满分为150分，考试时间为120分钟。

注意事项：1、选择题：请直接在智学网—作业“练习中心”输入选项；2、非选择题：必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；拍照上传答案时一定要看清题号；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

第一部分单项选择(共15小题,每小题1分,满分15分)1.The________look of the people in the earthquake left a deep impression________the audience.A.frightening;toB.frightened;onC.frightened;withD.frightening;of2.The millionaire looked forward to________his old house in his hometown,but when he arrived,he found his hometown much________.A.find;changeB.finding;changingC.found;changedD.finding;changed3.I believe I can exchange my ideas________new friends and live a wonderful life________campus.A.for,inB.with,inC.with,onD.for,on4.________we don’t achieve success,we should compare failure________the mother of success.A.Even if;withB.Even if;toC.Even though;asD.As if;with5.________during our sports meeting________we had a good time with our classmates.A.That was;whenB.It was;whenC.That was;thatD.It was;that6.In the middle of the Zhixin Pond________several ducks.A.swimB.swimsC.is swimmingD.swimming7.The number of people who own a car________in the past10years.A.increaseB.increasedC.has increasedD.increases8.During the lockdown of the city,they________the community rather than________the city.A.pefered to serve;leavingB.preferred to serve;leaveC.prefered serving;leavingD.preferred serving;leave9.The school adviser recommended he________the lost time.A.made ofB.can make itC.making upD.make up for10.The whole class debated________for the class uniform.A.on what color they should chooseB.what color should they chooseC.about what color they to chooseD.what color should to choose11.He was late again,________made the teacher________.A.who;annoyingB.which;annoyedC.that;annoyingD.that;annoyed12.Frank,rather than his two sisters,________London next morning by train which________at8:30.A.is leaving to;will leaveB.are leaving to;leavesC.is leaving for,leavesD.will leave for,will leave13.After listening to the teacher’s instructions,I found the problem easy________.A.to be worked outB.working onC.to work outD.to work14.Tu Youyou has________traditional Chinese medical science.A.applied to studyB.been applied to studyC.been applied herself to studyD.been applying herself to studying15.My eldest son,________work takes him all over the world,is in New York at the moment.A.whoseB.hisC.whichD.who第二部分阅读(共两节，满分50分)第一节(共15小题，每小题2.5分，满分37.5分)阅读下列短文，从每题所给的A、B、C、D四个选项中选出最佳选项。

pdetoolbox-0802

Introduction to the Matlab Partial DifferentialEquation Toolbox——PDETOOLMatlab PDE Toolbox介绍(1) 可以求解(非)线性椭圆型PDE,以及线性抛物,双曲问题。

可以求解单个方程，也可以求解方程组：(2) 自适应网格加密, 区域分裂(如Lshape区域分为3部分进行计算, matlab有演示算例)(3) 有两种方式调用偏微分方程工具箱中的函数：⏹matlab script⏹GUI(by >>pdetool)如果采用GUI方式,一般的求解过程是：Starting the PDE Toolbox 开启工具箱Specifying the Domain 指定二维求解区域Specifying the Boundary Conditions 指定边界条件Specifying the PDE 指定PDE方程(椭圆、抛物、双曲)Specifying the Initial Mesh 指定初始网格Mesh Refinement 设置网格加密Solving boundary value problem and plotting solution 求解(初)边值问题并绘图 Working in the MA TLAB workspace (export data｛p,e,t,u｝) 对变量空间进行操作 Post-Processing the Solution 后处理数值解比如tri2grid(p,t,u,x,y)Visualization Commands 比如绘图命令pdemesh(p,e,t), pdesurf(p,t,u) (4) 非结构三角网格的网格数据结构下面是一个半圆形区域的非结构网格的剖分结果：(5) 一般的椭圆问题的系数矩阵c的输入法则：注意c可以写成Matlab PDE Toolbox 允许这样。

注意上面每个,,{1,1}ij c i j ∈都是一个22⨯的矩阵, 在GUI 中输入时写在一行按照(1,1),(2,1),(1,2),(2,2)的顺序输入(因为Matlab 的二维数组是按列优先存放的).(6) 非线性问题的2个例子, 非线性是指中的函数c,a,f 依赖于u ，ux 或者uy 。

清华-计算机图形学chap7-B-Spline-2

Computer GraphicsShi-Min HuShi Min HuTsinghua UniversityTsinghua UniversityToday s TopicsToday’s Topics•Why splines?•B-Spline Curves and properties •B-Spline surfacesB Spline surfaces•NURBS curves and SurfacesWhy to introduce B Spline(BWhy to introduce B-Spline (B样条)•Bezier curve/surface has many advantages, but they have two main shortcomings:e e cu ve/su ace ca ot be od ed oca y–Bezier curve/surface cannot be modified locally(局部修改).–It is very complex to satisfy geometric continuityIt i l t ti f t i ti itconditions for Bezier curves or surfaces joining.•History of B-splinesI1946S h b d li b d–In 1946, Schoenberg proposed a spline-basedmethod to approximate curves.–It’s motivated by runge-kutta problem ininterpolation: high degree polynomial may surge p g g p y y g upper and down–Why not use lower degree piecewise polynomial Wh t l d i i l i lwith continuous joining?–that’s Spline–But people thought it’s impossible to use Spline in shape design because complicatedin shape design, because complicated computation–In 1972, based on Schoenberg’s work, Gordon I1972b d S h b’k G d and Riesenfeld introduced “B-Spline” and lots of corresponding geometric algorithms.f di i l i h–B-Spline retains all advantages of Bezier curves, and overcomes the shortcomings of Bezier curves.•Tips for understanding B-Spline?–Spline function interpolation is well known, it can Spline function interpolation is well known it canbe calculated by solving a tridiagonalequations(三对角方程).i–For a given partition of an interval, we cancompute Spline curve interpolation similarly.–All splines over a given partition will form aAll splines over a given partition will form alinear space. The basis function of this linearspace is called B-Spline basis function.i ll d B S li b i f i–Similar to Bezier Curve using Bernstein basis functions, B-Spline curves uses B-Spline basis f nctions B Spline c r es ses B Spline basis functions.B-Spline curves and it’s p Properties•Formula of B-Spline Curve.n ]1,0[),()(,0∈=Σ=t t B P t P n i i n i are control points ∑==i k i i t N P t P 0,)()(–are control points. –(i=0,1,..,n) are the i-th B-Spline basis function ),,1,0(n i P i L =)(,t N k i of order k. B-Spline basis function is a order k (degree k -1) piecewise polynomial (分段多项式) determined by the knot vector, which is a non-decreasing set of numbers.g•Demo of B-splineThe story of order & degree•The story of order&degree–G Farin: degree, Computer Aided Geometric Design –Les Piegl: order, Computer Aided DesignL Pi l d C Aid d D iB Spline Basis Function B-Spline Basis Function•Definition of B-Spline Basis Function –de Boor-Cox recursion formula:⎧⎩⎨<<=+Otherwiset x t t N i i i 01)(11,−−,,11,111()()()i i k i k i k i k i k i i k i t t t t N t N t N t t t t t +−+−+−++=+−−–Knot Vector: a sequence of non-decreasing number L L L k n k n n n k k t t t t t t t t +−++−,,,,,,,,,,11110L L L•, i = 01k=•, i = 02k=⎧⎩⎨<<=+Otherwiset x t t N i i i 01)(11,,,11,111()()()i i k i k i k i k i k i i k i t t t t N t N t N t t t t t +−+−+−++−−=+−−B Spline Basis Function B-Spline Basis Function•Questions:–What is nonzero domain(非零区间) of B-Splinebasis function ?)(,t N k i –How many knots does it need?Wh t i th d fi iti d i ()f th –What is the definition domain(定义区间) of the curves?4,4()()i i P t PN t =∑0i =B Spline Basis Function B-Spline Basis Function•take k=4, n=4 as example 4,4()()i i P t PN t =∑876543210,,,,,,,,t t t t t t t t t 0i=B Spline Basis Function B-Spline Basis Function•Properties:N ti it d l l t–Non-negativity and local support •is non-negativeis a non ero pol nomial on ,()i k N t ]•is a non-zero polynomial on ⎧∈≥+t t t t N k i i ],[0[,i i k t t +,()i k N t –Partition of Unity⎩⎨=otherwisek i 0)(,•The sum of all non-zero order k basis functions onis 1 ∑n 11[,]k n t t −+=+−∈=i n k k i t t t t N011,],[1)(B Spline Basis Function B-Spline Basis Function•Properties:Diff ti l ti f th b i f ti–Differential equation of the basis function:,,11,11111()()()i k i k i k i k i i k i k k N t N t N t t t t t −+−+−++−−′=+−−–Please compare with the Bernstein base:)]B 10 )],()([)(1,1,1,n i t B t B n t n i n i n i ⋅⋅⋅=−=′−−−;,,,B SplineB-Spline•Category(分类) of B-Splineg g p–General Curves could be categorized to two groups by checking if the start point and the endpoint areoverlapped:•Open Curves•Close CurvesClose Curves–According to the distribution(分布) of the knots inknot vector, B-Spline could be classified to theknot vector B Spline could be classified to thefollowing four groups:Uniform B-Spline(均匀B样条)U if B S li–(1) Uniform B-Spline,,,,,,,,•The knots are uniformed distributed, like 0,1,2,3,4,5,6,7•This kind of knot vector defines uniform B-Spline basisfunctionuniform B-Spline of Degree 3if B S li f D3Quasi Uniform B Spline(Quasi-Uniform B-Spline(准均匀B样条)–(2) Quasi-Uniform B-Splinep•Different from uniform B-Spline, it has:–the start-knot and end-knot have repetitiveness(重复度) of k–Uniform B-Spline does not retain the “end point” property ofBezier Curve, which means the start point and end point ofuniform B-Spline are no-longer the same as the start point andend point of the control points. However, quasi-Uniform B-end point of the control points However quasi Uniform BSpline retains this “end point” propertyQuasi-uniform B-Spline curve of degree 3Piecewise Bezier Curve(Piecewise Bezier Curve(分段Bezier曲线)–(3) Piecewise Bezier Curvep()•the start-knot and end-knot have repetitiveness(重复度)of kp•all other knots have repetitiveness of k-1•Then each curve segment will be Bezier curvesPiecewise B-Spline Curve of degree 3Piecewise Bezier Curve(分段Bezier曲线) Piecewise Bezier Curve(•For piecewise Bezier curve, the different pieces of th l ti l i d d t M i ththe curve are relatively independent. Moving the control point will only influence the corresponding piece of curve, while other pieces of curves will be not change. Furthermore, the algorithms for Bezier not change.Furthermore,the algorithms for Bezier could also be used for piecewise Bezier Curve.•But this method need more data to define the curve (more control points, more knots).Non-uniform B-Spline (非均匀B p (样条)–(4) Non-uniform B-Spline•The knot vectors satisfy T t t t =L e o vec o s sa s y conditions that the sequence of knots is non-)01[,,,]n k +decreasing(非递减). –repetitiveness of two end knots, <= k –repetitiveness of other knots, <= k-1•This kind of knot vector defines the non-uniformB-Spline.Properties of B Spline Curves Properties of B-Spline Curves•Properties of B-Spline curvesL l(–Local(局部性)•The curve in interval is only affected ],[1+∈i i t t t by at most k control points , and is independent of other control points.),,1(i k i j P j L +−=•Changing the position of control point will only affect the curve on interval i P only affect the curve on interval),(k i i t t +n∑==i k i i t N P t P 0,)()(Properties of B Spline Properties of B-Spline–Continuity(连续性)P()i i d f i i•P(t) is continuous at a node of repetitiveness r.–Convex hull(凸包性)1k r C −−•A B-spline curve is contained in the convex hullof its control polygon More specifically if t is of its control polygon. More specifically, if t is in knot span , then P(t) is in the h ll f t l i t n i k t t i i ≤≤−+1),,(1convex hull of control points ik i P P ,,1L +−Properties of B Spline Properties of B-Spline–Piecewise polynomial (分段多项式)•In every knot span, P(t) is a polynomial of t whose y p ()p ydegree is less than k.–Derivative formula(Derivative formula(导数公式)′′nn)()()(0,0,'===⎟⎠⎞⎜⎝⎛=∑∑i k i i i k i i t N P t N P t P ],[)()1(111,111+−−=−+−∈⎟⎟⎠⎞⎜⎜⎝⎛−−−=∑n k k i ni i k i i i t t t t N t t P PkProperties of B SplineProperties of B-Spline–Variation Diminishing Property(变差缩减性)•this means no straight line intersects a B-splinethi t i ht li i t t B licurve more times than it intersects the curve'scontrol polygons.t l l–Geometry invariability(几何不变性)•The shape and position of curve are independentwith the choosing of coordinate system(坐标系).Properties of B Spline Properties of B-Spline–Affine invariability(仿射不变性)nI h h f f i i i i bl d h∑=+−∈=i n k k i i t t t t N P A t P A 011,],[,)(][)]([•It means that the form of equation is invariable under the affine transformation.–Line holding(直线保持性)•It means that if the control polygon degenerates to a line,the B-Spline curve also degenerates to a line.Properties of B Spline Properties of B-Spline–Flexibility(灵活性)U i B S li C il t t•Using B-Spline Curve we can easily construct special cases such as line segment(线段), cusp(尖)t t li ()点), tangent line(切线).•For example, for B-Spline of order 4 (degree 3), if li l dyou want to construct a line segment, you only need to specify collinear (共线). 321,,,+++i i i i P P P P •you only need to let12i i i P P P ++==Properties of B Spline Properties of B-Spline相•If you want the curve tangent(相切) to a specific line L,you only need to specify on line L, and21,,++i i i P P P repetitiveness of less than 2.3+i t iP 1+i P 2+i P P )(tPP 4+i (a)四顶点共线(b)二重顶点和三重顶点−i P 23()重节点和三重节点(c)二重节点和三重节点(d)三顶点共线图.1.26 三次B样条曲线的一些特例De Boor Algorithm De Boor Algorithm•To compute P(t) (a point on the curve), you could use B-Spline formula, but it is more efficient to use de pBoor algorithm.De Boor Algorithm:•De Boor Algorithm:)()()(,,==∑∑jki ink i i t NP t N P t P 10−+−+−==⎤⎡−+−=jk i i k j i i t N tt t N t t P )()(111,111,1−++−=+++−+⎤⎡−−⎥⎦⎢⎣−−∑jk i i k j i k i i k i k i i k i i t t t t t t t t ],[)(11,1111+−+−=−−+−+∈⎥⎦⎢⎣−+−=∑j j k i k j i i i k i i i k i t t t t N P t t P t tDe Boor Algorithm De Boor Algorithm•Let⎧⋅⋅⋅+−+−==k k i r P ,,2,1,0,⎪⎪⎨−−+−−=−−−+−t P t t t t t P t t t t jj j t P r i r k i r i i i r i ),()()(]1[1]1[][•Then⎪⎪⎩⋅⋅⋅++−++−=−⋅⋅⋅=−+−+j r k j r k j i k r ir k i i r k i ,,2,1;1,,2,1∑∑−==jk i ijki it N t Pt NP t P 1,]1[,)()()()(•This is De Boor Algorithm.+−=+−=k j i k j i 21De Boor Algorithm De Boor Algorithm•The recursion of De Boor Algorithm is as shown below:01P P 1[1]j k P −+M 22[1][2]333j k j k j k j k j k P PP P P −+−+−+−+−+→→→[1][2][1]k j jjjP PPP−→→M M M M nP MDe Boor Algorithm De Boor Algorithm•Geometric meaning (几何意义)of De Boor Algorithm–It has an intuitive geometric interpretation: corner g pcutting (割角).•It means that using line segment to cut][][r r It means that using line segment to cut corner . Begin frompolygon1i i P P +]1[−r i P ⋅⋅⋅polygon , after k-1 steps of cutting, fi ll i j k j k j P P P +−+−21P −P P j we finally get point on the curve P(t).)(]1[t r j +−k j P −P]1[P 4+−k j 1+−k j 2+k j jKnot Insertion Knot Insertion •Knot insertion–An important tool for practical interactive use of B-p pspline, which allows one to add a new knot to a B-spline without changing the shape or its degree.For spline without changing the shape or its degree. For instance, one may want to insert additional knots in order to be able to raise flexibility of shape control order to be able to raise flexibility of shape control.•Insert a new knot t to a knot span Th k t t b[]1,+i i t t •The knot vector becomes:[]k n i i t t t t t t T ++=,,,,,,,1101L L •denoted as:[]11121111101,,,,,,,1++++=k n i i i tt t t t t T L LKnot Insertion Knot Insertion•The new knot sequence defines a new group of B-Spline Basis F nctions The original c r e Spline Basis Functions. The original curve P(t)can be expressed by this new group of BasisFunctions and new control points , which are unknown.1jP +=111n t N P t P ∑=0,)()(j kjjKnot Insertion Knot Insertion•Boehm gives a formula for computing new control points:p ⎪⎧+−==1,,1,0 ,11k i j P P j j L ββ⎪⎩⎨++−==−+−=+−=−−1,,1 ,,,2 ,)1(111n r i j P P r i k i j P P P j jj j j j j L L ββj t t −=β•r is the repetitiveness of newly inserted knot in the knot jk j j t t −−+1s t e epet t ve ess o ew y se ted ot t t e ot sequence.Knot Insertion Knot Insertion1P 1P P 1P 03i points(totally k-1points)36points( totally k 1 points) are replaced by the right ones(totally k points)],[43t t t ∈See demo of knot insertionB Spline Surface(B B-Spline Surface(B样条曲面)•Given knot vectors in axes(参数轴) U and V:],,,[10p m u u u U +=L B S li f f d i d fi d],,,[10q n v v v V +=L •B-Spline surface of order p ×q is defined as:m n∑∑===i j q j p i ij v N u N P v u P 00,,)()(),(B Spline Surface B-Spline Surface•are the control points of B-Splineij P Surface, which are usually referred to as thecontrol net ).(控制网格、特征网格)•and are B-Spline basis)(,u N p i )(,v N q j functions of order p and q , one for each direction (and ),which could also be direction (U and V ), which could also be computed by de Boor-Cox formula.B Spline Surface B-Spline Surface03P 23P33P02P 22P 12P32P01P 11P 21P 31P P 10P 20P 0030PNURBS Curve and SurfaceNURBS Curve and Surface •Disadvantage of B-Spline curve and Bezier Curve:–can’t accurately represent conic(圆锥曲线) curveexcept parabola(抛物线),NURBS (Non Uniform Rational B Spline) •NURBS(Non-Uniform Rational B-Spline) (非均匀有理B样条)–In order to find a mathematical method that couldrepresent conic and conicoid(二次曲面) accurately. yNURBS•NURBS is too complex•Les Piegl s The NURBS Book,Les Piegl’s The NURBS Book–“NURBS from Projective Geometry to Practical Use”–Les Piegl，Graduated from Budapest University ofi l d d f d i i fHungary, many years in SDRC company for geometricmodeler designd l d iNURBSSome years ago a few researchers joked about NURBS,saying that the acronym really stands for NOBODYUnderstands Rational B-Splines, write the authors in their foreword; they formulate the aim of changing NURBS to EURBS, that is, Everybody.…There is no doubt that they have achieved this goal....I highly recommend the book to anyone who is interestedp y p in a detailed description of NURBS. It is extremely helpful for students, teachers and designers of geometric modeling ysystems. ——Helmut PottmannNURBS•Advantages of NURBS–It provide a general and accurate representation forrepresenting and designing free curves or surfaces(自由曲线曲面)–They offer one common mathematical form for bothstandard analytical shapes (e.g., conics) and free-formshapes (parametric form).–can be evaluated reasonably fast by numerically stableand accurate algorithms;NURBS•Advantages of NURBS–They are invariant under affine as well as perspectivetransformations.–the control points and weights can be modified, whichgives great flexibility for designing curves/surfaces.–non-rational B-Spline, non-rational and rational Beziercould be viewed as special cases of NURBS.NURBS•Some difficult problems in using NURBS –Require more storage than traditionalcurve/spline methods. (such as circle representation) p–If the weights are set inappropriately, the curvewill be abnormal(畸变).will be abnormal()–It is very complex to deal with situations likecurve overlap(曲线重叠).NURBS •Before discussing about NURBS, let’s first review the definition of B-Spline:n∑==i k i i t N P t P 0,)()()()()(1,111,1,t N t t t t t N t t t t t N k i i k i k i k i i k i i k i −++++−−+−−+−−=k n k n n n k k t t t t t t t t +−++−,,,,,,,,,,11110L LLNURBS•Definition of NURBS curve.–NURBS Curves are defined by piecewiserational B-Spline polynomial basis functionp p y(分段有理B样条多项式基函数):∑== =nnikiiitNP,)(ω∑∑==ikiinikiitRPtNtP,0,)( )()(ω=nki ik itNtR, ,)()(ω∑=jkjjt N,)(ωDefinition of NURBS Definition of NURBS•NURBS basis R i,k (t) retains all properties of B-Spline Basis.–Local support: Ri,k(t)=0，t ∉[ti, ti+k]–Partition of Unity:∑n Partition of Unity:–Differentiability(可微性): If is not a knot is infinitely differentiable()==i k i u R 0,1)(•If t is not a knot, P(t)is infinitely differentiable(无限次可微) in the knot interval. If t is a knot, P(t) is only C-(k-r) continuous.continuous. –If ωi =0, then R i,k (t)=0;If +th R (t)1–If ωi =+∞, then R i,k (t)=1;Definition of NURBSDefinition of NURBS•NURBS curve has similar geometric properties as the B Spline C r e:the B-Spline Curve:–Local support (局部支持性).–Variation Diminishing Property(变差缩减性)–Strong Convex hull(凸包性)–Affine invariability(仿射不变性)–Differentiability(y(可微性)–If the weight of a control point is 0, then correspondingcontrol point doesn t affect the curve.control point doesn’t affect the curve.Definition of NURBS Definition of NURBS–If , and , then N i l/i l B i d ∞→i ω],[k i i t t t +∈i P t P =)(–Non-rational/rational Bezier curves and non-rational B-Spline curves are special cases ofNURBS curve.。

单元素养评估(四)

单元素养评估(四)(120分钟150分)第一部分听力(共两节，满分30分)第一节(共5小题；每小题1.5分，满分7.5分)听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1．Who washed the vegetables?A．The man. B．The woman.C．The man's mother.2．How much cheaper is the blue one than the white one?A．$10. B．$20.C．$30.3．What does the man suggest the woman do?A．Go back home. B．Bring an umbrella.C．Check the weather report.4．What are the speakers talking about?A．A museum's paintings. B．A famous painter.C．A museum.5．What does the man want to eat today?A．Fish and cabbage. B．Chicken and fish.C．Chicken and a salad.第二节(共15小题；每小题1.5分，满分22.5分)听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

请听第6段材料，回答第6、7题。

6．Where is the man from?A．Canada. B．America.C．China.7．What's the relationship between the speakers?A．Neighbors. B．Colleagues.C．Classmates.听第7段材料，回答第8、9题。

希腊字母的读法

希腊字母的读法αΑalpha ['ælfa]βΒbeta ['bi:ta / 'beita]γΓgamma ['gæma]δΓdelta ['delta]εΔepsilon ['epsilan / ep'sailan]δΕzeta ['zi:ta]εΖeta ['i:ta / 'eita]ζΘtheta ['θita]ηΗiota [ai'outa]θΚkappa ['kæpa]ιΛlamda ['læmda]κΜmu [mju:]λΝnu [nju:]μΞxi [ksai / gzai / zai]νΟomicron [ou'maikran]πΠpi [pai]ξΡrho [rou]ζ΢sigma ['sigma]ηΣtau [tau]υΤupsilon ['ju:psilon / ju:p'sailan]o 是反c 。

θΦphi [fai]χΥchi [kai]ψΦpsi [psi:]ωΧomega ['oumiga / ou'mi:ga]各种符号的读法` 1.backquote 反引号；2.grave accent 重音符~ tilde! exclamation mark,不读@ at# number sign, 英语国家是hash，美语是pound sign,音乐里作sharp,如C# $ dollar% percent^ caret& ampersand* asterisk,star(美语),数学公式中作multiply( parenleft,opening parentheses) parenright,closing paretheses- minus; hyphen连字符,不读_ underscore+ plus= equal[ bracketleft,opening bracket] bracketright,closing bracket{ braceleft} braceright; semicolon: colon' quote" doublequote/ slash\ backslash 反斜杠| bar, comma< less> greater. period? questionspace 空格一些特殊符号的英文读法:＜ is less than＞ is more than≤ is not less than≥ is not more than≢ is less than or equal to 小于或等于号- hyphen 连字符≣ is more than or equal to 大于或等于号' apostrophe 省略号,英文中省略字符用的撇号;所有格符号％ percent－ dash 破折号‟ per mille∞ infinity 无限大号∝ varies as 与…成比例( ) parentheses 圆括号√ (square) root 平方根[ ] square brackets 方括号∵ since; because 因为《》 French quotes 法文引号;书名号∴ hence 所以… ellipsis 省略号∷ equals, as (proportion) 等于，成比例¨ tandem colon 双点号∟ angle 角∶ ditto 双点号≨ semicircle 半圆‖ parallel 双线号≦ circle 圆／ virgule 斜线号○ circumference 圆周～ swung dash 代字号△ triangle 三角形§ section; division 分节号≧ perpendicular to 垂直于→ arrow 箭号；参见号∪ union of 并，合集∩ intersection of 交，通集∫the integral of …的积分ª plus or minus 正负号∑ summation of 总和¬ is multiplied by 乘号© degree 度÷ is divided by 除号† minute 分‡ second 秒≠ is not equal to 不等于号≡ is equivalent to 全等于号℃ Celsius degree 摄氏度≌ is equal to or approximately equal to 等于或约等于号数学中的英语表示法一、小数表示法1、小数用基数词来表示，以小数点为界，小数点左首的数字为一个单位，表示整数，数字合起来读；小数点右首的数字为一个单位，表示小数，数字分开来读；小数点读作point，o读作zero或o［ou］，整数部分为零时，可以省略不读。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

arXiv:hep-th/0612255v1 23 Dec 2006φ4modelonacircleF.Loran∗DepartmentofPhysics,IsfahanUniversityofTechnology(IUT),Isfahan,Iran

ThefourdimensionalcriticalscalartheoryatequilibriumwithathermalbathattemperatureTisconsidered.Thethermalequilibriumstateislabeledbynthewindingnumberofthevacuaaroundthecompactimaginary-timedirectionwhichcompactiﬁcationradiusis1/T.Theeﬀectiveactionforzeromodesisathreedimensionalφ4scalartheoryinwhichthemassofthethescalarﬁeldisproportionalton/TresemblingtheKaluza-Kleindimensionalreduction.Similarresultsareobtainedforthetheoryatzerotemperaturebutinaone-dimensionalpotentialwell.Sinceparityisviolatedbythevacuawithoddvacuumnumbern,insuchcasesthereisalsoacubictermintheeﬀectivepotential.Theφ3-termcontributiontothevacuumshiftatone-loopisofthesameorderofthecontributionfromtheφ4-termintermsofthecouplingconstantofthefourdimensionaltheorybutbecomesnegligibleasntendstoinﬁnity.Finally,therelationbetweenthescalarclassicalvacuaandthecorrespondingSU(2)instantonsonS1×R3inthe’tHooftansatzisstudied.

PACSnumbers:11.10.Wx,11.25.Mj,11.10.Kk

I.INTRODUCTIONInfourdimensions,masslessφ4modelwithnon-positivepotentialisequivalenttoSU(2)Yang-Millstheoryinthe’tHooftansatz[1,2,3].Scalartheorieswithnonpositivepotentialsarealsofamiliaringravitytheories[4]whiletheymaybeproblematicinquantumﬁeldtheory.Inthispaperweobtainsolutionsofmasslessφ4modelwithnonpositivepotentialwhichareperiodicinonedirection.Weshowthatthisperiodicsolutioncanbeusedforthreepurposes.Theﬁrstoneistostudythecriticalφ4theoryatﬁnitetemperature.Thesecondoneistostudythetheoryinaone-dimensionalpotentialwellbyimposingtheDirichletboundaryconditiononφtobevanishingattheboundaries.ThethirdapplicationofthissolutionistoobtainSU(2)instantonsonS1×R3usingthe’tHooftansatz.Theorganizationofthepaperisasfollows.InsectionIIafterabriefreviewofscalarﬁeldtheoryatﬁnitetemperature,weconsiderthemasslessφ4-modelinonedimensionwherewestudytheperiodicsolutionoftheequationofmotiontobeusedinthefollowingsections.InsectionIIIweusetheresultofsectionIItostudythefourdimensionalmodelatﬁnitetemperature.Theresultingthreedimensionaleﬀectiveactionforzeromodesisshowntobeamassiveφ4theory.Themassofthescalarﬁeldisproportionaltothewindingnumberoftheclassicalvacua,consideredasthethermalequilibriumstate,aroundthecompactimaginary-timedirection.InsectionIVwestudythemasslessφ4theoryatzerotemperatureinapotentialwell.Inthiscasetheeﬀectivetheoryisrealizedintwodiﬀerentsectorscorrespondingtoevenandoddvacuumnumbers.Forevenvacuumnumbers,parityisconservedandtheinteractionisgivenbyaφ4term.Inthecaseofoddvacuumnumber,parityisviolatedandaφ3interactionisadded.Westudyandcomparethecontributionformbothinteractiontermstothevacuumshiftatone-loopandverifythatforlargevacuumnumbers,theφ3-termcontributionisnegligibleincomparisonwiththecontributionfromtheφ4term.InsectionVwebrieﬂydiscusstheSU(2)instantonscorrespondingtotheperiodicsolutionsinthe’tHooftansatz.ThereweshowthatindeedtheYang-MillsﬁeldequationcorrespondstothecriticaltheorywithpotentialV(φ)∼−e2φ4

whereeisthegaugeﬁeldcouplingconstant.SectionVIisdevotedtoconclusionandisclosedbydiscussingthedependenceoftheentropyofthethermalvacuaonthecorrespondingwindingnumber.

II.D=1φ4-MODELATTHERMALEQUILIBRIUMThestaticpropertiesofﬁnitetemperatureQFTcanbederivedfromthepartitionfunctionZ=tre−H/TwhereHistheHamiltonianofthequantumﬁeldtheoryandTisthetemperature.Forasimpletheorywithbosonﬁeldsφ2andEuclideanactionS(φ)thepartitionfunctionisgivenbythefunctionalintegralZ=󰀉[dφ]exp[−S(φ)],(1)whereS(φ)istheintegraloftheLagrangiandensityL(φ),S(φ)=󰀉1/T0dt󰀉ddxL(φ),(2)andtheﬁeldφsatisﬁesperiodicboundaryconditionsintheimaginary-timedirection,φ(t=0,x)=φ(t=1/T,x).(3)Theequationofmotionoftheφ4modelinonedimension,deﬁnedbytheEuclideanaction,

S=󰀉dt󰀌14φ4󰀎.(4)wherea′denotesonetimederivationwithrespecttot,isthefollowingnon-linearLaplaceequation,φ′′+gφ3=0,(5)Thisequationcanbeeasilyintegratedoncetoobtain,14φ4=c.(6)

Forc=0thesolutionφ∼t−1issingularatt=0.Forc>0,deﬁningc=L−4oneobtains,[11]φ=1g󰀎1/4sn󰀌g1/4t

󰀈2|m)denotesthecompleteellipticintegraloftheﬁrstkind.Consequentlythesolution(7)isperiodic,

φ(t)=φ󰀌t+n4LK(−1)

4K(−1)T−1