蚁群算法的基本原理及应用
蚁群算法
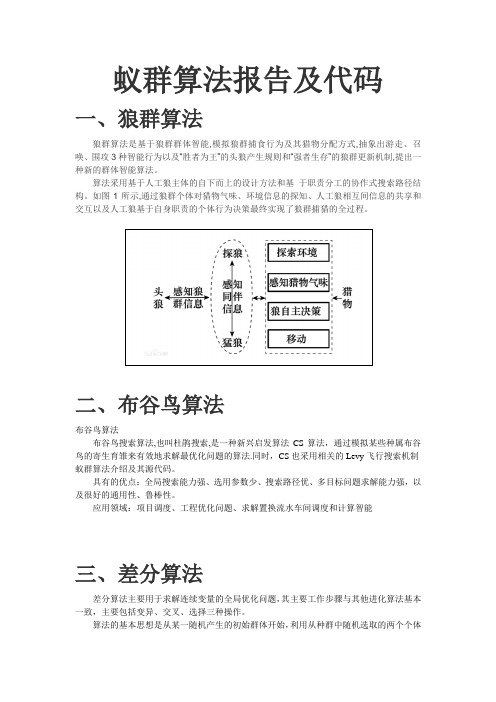
蚁群算法报告及代码一、狼群算法狼群算法是基于狼群群体智能,模拟狼群捕食行为及其猎物分配方式,抽象出游走、召唤、围攻3种智能行为以及“胜者为王”的头狼产生规则和“强者生存”的狼群更新机制,提出一种新的群体智能算法。
算法采用基于人工狼主体的自下而上的设计方法和基于职责分工的协作式搜索路径结构。
如图1所示,通过狼群个体对猎物气味、环境信息的探知、人工狼相互间信息的共享和交互以及人工狼基于自身职责的个体行为决策最终实现了狼群捕猎的全过程。
二、布谷鸟算法布谷鸟算法布谷鸟搜索算法,也叫杜鹃搜索,是一种新兴启发算法CS算法,通过模拟某些种属布谷鸟的寄生育雏来有效地求解最优化问题的算法.同时,CS也采用相关的Levy飞行搜索机制蚁群算法介绍及其源代码。
具有的优点:全局搜索能力强、选用参数少、搜索路径优、多目标问题求解能力强,以及很好的通用性、鲁棒性。
应用领域:项目调度、工程优化问题、求解置换流水车间调度和计算智能三、差分算法差分算法主要用于求解连续变量的全局优化问题,其主要工作步骤与其他进化算法基本一致,主要包括变异、交叉、选择三种操作。
算法的基本思想是从某一随机产生的初始群体开始,利用从种群中随机选取的两个个体的差向量作为第三个个体的随机变化源,将差向量加权后按照一定的规则与第三个个体求和而产生变异个体,该操作称为变异。
然后,变异个体与某个预先决定的目标个体进行参数混合,生成试验个体,这一过程称之为交叉。
如果试验个体的适应度值优于目标个体的适应度值,则在下一代中试验个体取代目标个体,否则目标个体仍保存下来,该操作称为选择。
在每一代的进化过程中,每一个体矢量作为目标个体一次,算法通过不断地迭代计算,保留优良个体,淘汰劣质个体,引导搜索过程向全局最优解逼近。
四、免疫算法免疫算法是一种具有生成+检测的迭代过程的搜索算法。
从理论上分析,迭代过程中,在保留上一代最佳个体的前提下,遗传算法是全局收敛的。
五、人工蜂群算法人工蜂群算法是模仿蜜蜂行为提出的一种优化方法,是集群智能思想的一个具体应用,它的主要特点是不需要了解问题的特殊信息,只需要对问题进行优劣的比较,通过各人工蜂个体的局部寻优行为,最终在群体中使全局最优值突现出来,有着较快的收敛速度。
蚁群算法及其应用新进展

在a t dn iy s s e 模型 中 : n — es t y tm
.
() 1 . 5
… 、 t・ J
。
1 蕾 蚁 时 懦÷ 阍 越 f 嚣剽 第 o 氓蚂 在 刺 l 缎 之
应用 技 术
I ■
Caiedc l i h e hoRe isnaTngew nccneoyv
蚁群 算法及其应 用新进展
刘 刚
哈 尔滨 100 ) 50 1 ( 黑龙 江省 龙视 网络有 限责任 公司 黑龙江 [ 要] 摘 蚁群算 法 (n o oy a gr t m 最早 是 由意 大利 学者 MD r g a t c l n lo ih ) .o io等于 2 世 纪 9 0 O年代 初提 出的 一种基 于种群 的 启发式 仿生进 化系 统 。蚁 群算 法 采用 分布式 正 反馈并 行计算 机制 , 易于 与其他 方法 结合 , 并具有 较强 的鲁 棒性特 点 。它最初 被用 于求 解著 名的旅 行 商 问题 (r v ln a e m n P o lm T a e i g s l s a r b e , 简称 T P 并获 得 了较好 的 效果 。 ) s 中图分类 号 :P 8 T I 文献 标识码 : A 文章编 号 :10 — 1X2 1) 50 1一 1 10 99 4 (00 1— 34 O
它们 的区别在 于: 后两 种模型 中, 利用 的是局部信 息, 而前者利用 的是整体 信 息, 求 解 T P问题 时, 能较 好, 在 S 性 因而通 常采 用它 为基 本模 型 。 2蚁群 算法 的特 点及 存在 的 问题 2 1蚁 群算 法的特 点 . 自治 性 (uo oo s : A tnm u )交互 性 (ne a tv) 适用性 (dp ie : Itr ci e : A atv )社会性 (o ibe : sca l) 移动性 (o ie : Mb l) 主动性 (ra tv )智能 性 (ne lg n)推 Po c ie : It liet ;
蚂蚁算法和蚁群算法

蚂蚁算法(Ant Colony Algorithm)和蚁群算法(Ant Colony Optimization)是启发式优化算法,灵感来源于蚂蚁在觅食和建立路径时的行为。
这两种算法都基于模拟蚂蚁的行为,通过模拟蚂蚁的集体智慧来解决组合优化问题。
蚂蚁算法和蚁群算法的基本原理类似,但应用领域和具体实现方式可能有所不同。
下面是对两者的简要介绍:蚂蚁算法:蚂蚁算法主要用于解决图论中的最短路径问题,例如旅行商问题(Traveling Salesman Problem,TSP)。
其基本思想是通过模拟蚂蚁在环境中寻找食物的行为,蚂蚁会通过信息素的释放和感知来寻找最优路径。
蚂蚁算法的核心概念是信息素和启发式规则。
信息素(Pheromone):蚂蚁在路径上释放的一种化学物质,用于传递信息和标记路径的好坏程度。
路径上的信息素浓度受到蚂蚁数量和路径距离的影响。
启发式规则(Heuristic Rule):蚂蚁根据局部信息和启发式规则进行决策。
启发式规则可能包括路径距离、路径上的信息素浓度等信息。
蚂蚁算法通过模拟多个蚂蚁的行为,在搜索过程中不断调整路径上的信息素浓度,从而找到较优的解决方案。
蚁群算法:蚁群算法是一种更通用的优化算法,广泛应用于组合优化问题。
除了解决最短路径问题外,蚁群算法还可应用于调度问题、资源分配、网络路由等领域。
蚁群算法的基本原理与蚂蚁算法类似,也是通过模拟蚂蚁的集体行为来求解问题。
在蚁群算法中,蚂蚁在解决问题的过程中通过信息素和启发式规则进行路径选择,但与蚂蚁算法不同的是,蚁群算法将信息素更新机制和启发式规则的权重设置进行了改进。
蚁群算法通常包含以下关键步骤:初始化:初始化蚂蚁的位置和路径。
路径选择:根据信息素和启发式规则进行路径选择。
信息素更新:蚂蚁在路径上释放信息素,信息素浓度受路径质量和全局最优解的影响。
全局更新:周期性地更新全局最优解的信息素浓度。
终止条件:达到预设的终止条件,结束算法并输出结果。
蚁群算法

基本蚁群算法程序流程图
开始 初始化
循环次数Nc← Nc+1
蚂蚁k=1 蚂蚁k=k+1
按式(1)选择下一元素 修改禁忌表 N Y K≥ m
按式(2)和式(3)进行信息量更新 满足结束条件 Y
Байду номын сангаас输出程序计算结果 结束 N
复杂度分析
对于TSP,所有可行的路径共有(n-1)!/2条,以 此路径比较为基本操作,则需要(n-1)!/2-1次基 本操作才能保证得到绝对最优解。 若1M FLOPS,当n=10, 需要0.19秒 n=20, 需要1929年 n=30, 需要1.4X10e17年
{ ij (t ) | ci , c j C}是t时刻集合C中元素
蚂蚁k(k=1,2,…,m)在运动过程中,根据各条路径上的信息 量决定其转移方向。这里用禁忌表tabuk来记录蚂蚁k当前 所走过的城市,集合随着tabuk进化过程做动态调整。在 搜索过程中,蚂蚁根据各条路径上的信息量及路径的启发 信息来计算状态转移概率。在t时刻蚂蚁k由元素(城市)i 转移到元素(城市)j的状态转移概率:
1) 标有距离的路径图 2) 在0时刻,路径上没有信息素累积,蚂蚁选择路径为任意 3) 在1时刻,路径上信息素堆积,短边信息素多与长边,所以蚂蚁更 倾向于选择ABCDE
特
点
(1)其原理是一种正反馈机制或称增强型学习系统;它通过 信息素的不断更新达到最终收敛于最优路径上; (2)它是一种通用型随机优化方法;但人工蚂蚁决不是对实 际蚂蚁的一种简单模拟,它融进了人类的智能; (3)它是一种分布式的优化方法;不仅适合目前的串行计算 机,而且适合未来的并行计算机; (4)它是一种全局优化的方法;不仅可用于求解单目标优化 问题,而且可用于求解多目标优化问题; 2 (5)它是一种启发式算法;计算复杂性为 O( NC m n ),其 中NC 是迭代次数,m 是蚂蚁数目,n 是目的节点数目。
蚁群算法的基本原理

蚁群算法的基本原理蚁群算法 (Ant Colony Optimization, ACO) 是一种基于群体智能的优化算法,模拟了蚂蚁在寻找食物时候的行为,被广泛应用于求解组合优化问题、路径规划等领域。
蚁群算法的基本思路蚁群算法的基本思路是通过模拟蚂蚁在寻找食物的过程中释放信息素来获取全局最优解。
具体过程如下:1.初始化信息素: 首先,需要在所有可行解的路径上放置一些信息素。
在开始时,信息素值可以选择为等量的值或一些默认值。
2.蚁群搜索: 一开始,所有的蚂蚁都分别随机选择一个节点作为起点,并开始在网络中搜索。
蚂蚁行动的过程中,会根据路径上信息素浓度的大小来选择下一步的方向。
同时,每只蚂蚁都会记录其所经过的路径和信息素值。
3.信息素更新: 每只蚂蚁到达终点之后,计算其所经过路径的费用,然后根据一定的规则更新路径上的信息素。
较优的路径上将会添加更多的信息素,使下一次蚂蚁选择该路径的概率更大。
4.重复搜索: 重复上面的步骤,直到满足一个停止条件为止。
一种常见的停止条件是达到预定的迭代次数。
蚁群算法的优势蚁群算法在解决组合优化问题时,具有以下的优势:1.全局优化能力极强: 因为每只蚂蚁都只关注自己所经过的路径上的信息素值,所以可以同时搜索并更新多个路径,从而有可能找到全局最优解。
2.能够避免陷入局部最优: 蚁群算法可以通过信息素的挥发、说长存、信息素值的启发式更新等手段来避免陷入局部最优解。
3.易于扩展和并行化: 蚁群算法通常是一种并行的算法,可以很轻松地应用于分布式计算环境中。
蚁群算法的应用蚁群算法在解决组合优化问题、路径规划、调度等方面有着广泛的应用,如下所示:1.旅行商问题: 蚁群算法可以用于解决旅行商问题。
2.线性规划问题: 蚁群算法可以用于求解线性规划问题。
3.路径规划问题: 蚁群算法可以用于车辆路径规划问题。
4.调度问题: 蚁群算法可以用于作业车间调度问题。
蚁群算法是一种基于群体智能的优化算法,模拟了蚂蚁在寻找食物时候的行为。
蒙特卡洛树蚁群算法

蒙特卡洛树蚁群算法一、引言蒙特卡洛树蚁群算法(Monte Carlo Tree Ant Colony Algorithm)是一种基于蚁群算法和蒙特卡洛树搜索的优化算法。
它结合了蚁群算法的全局搜索能力和蒙特卡洛树搜索的局部搜索能力,能够在解决复杂问题时提供较好的性能和效果。
二、蚁群算法简介蚁群算法是一种模拟蚂蚁觅食行为的启发式优化算法。
蚂蚁在觅食过程中,通过释放信息素来引导其他蚂蚁选择路径,从而实现全局最优解的搜索。
蚁群算法在解决旅行商问题、资源调度、路径规划等优化问题中具有优秀的性能。
三、蒙特卡洛树搜索简介蒙特卡洛树搜索(Monte Carlo Tree Search,简称MCTS)是一种用于决策问题的搜索算法。
它通过不断模拟随机决策,并根据模拟结果调整决策策略,最终找到最优解。
蒙特卡洛树搜索在围棋、五子棋等复杂博弈游戏中取得了重大突破。
四、蒙特卡洛树蚁群算法原理蒙特卡洛树蚁群算法是将蚁群算法和蒙特卡洛树搜索相结合的一种优化算法。
它通过蚁群算法的全局搜索能力找到问题的大致解空间,然后利用蒙特卡洛树搜索的局部搜索能力进一步优化解空间,从而得到最优解。
蒙特卡洛树蚁群算法的具体步骤如下:1. 初始化蚁群:在解空间中随机生成一组蚂蚁,并将它们放置在解空间的不同位置。
2. 全局搜索:每只蚂蚁根据信息素和启发式信息选择下一步的移动方向,并更新信息素。
3. 局部搜索:根据蒙特卡洛树搜索的原理,在当前解空间中随机选择一个节点进行模拟,并评估模拟结果。
4. 更新解空间:根据模拟结果调整解空间,并更新信息素。
5. 重复步骤2~4,直到达到停止条件。
6. 输出最优解:根据信息素的浓度和解空间的评估结果,输出最优解。
五、蒙特卡洛树蚁群算法的应用蒙特卡洛树蚁群算法在许多领域具有广泛的应用,如路径规划、资源调度、智能交通等。
以路径规划为例,蒙特卡洛树蚁群算法可以在复杂的道路网络中找到最短路径,并考虑交通流量、拥堵等因素,从而提供更加准确和可靠的路径规划结果。
蚁群算法简介

蚁群算法简介蚁群算法是一种优化技术,受到自然界中蚂蚁寻找食物的行为的启发。
这种算法模拟了蚂蚁的信息共享和移动模式,用于解决复杂的组合优化问题,如旅行商问题(TSP)、车辆路径问题(VRP)等。
一、蚁群算法的基本原理在自然界中,蚂蚁寻找食物的行为非常有趣。
它们会在路径上留下信息素,后续的蚂蚁会根据信息素的强度选择路径,倾向于选择信息素浓度高的路径。
这样,一段时间后,大多数蚂蚁都会选择最短或最佳的路径。
这就是蚁群算法的基本原理。
二、蚁群算法的主要步骤1.初始化:首先,为每条边分配一个初始的信息素浓度。
通常,所有边的初始信息素浓度都是相等的。
2.路径选择:在每一步,每个蚂蚁都会根据当前位置和周围信息素浓度选择下一步的移动方向。
选择概率与信息素浓度成正比,与距离成反比。
这意味着蚂蚁更倾向于选择信息素浓度高且距离短的路径。
3.释放信息素:当蚂蚁完成一次完整的路径后,它会在其经过的边上留下信息素。
信息素的浓度与解决问题的质量成正比,即如果蚂蚁找到了一条更好的路径,那么这条路径上的信息素浓度会增加。
4.更新:经过一段时间后,信息素会随时间的推移而挥发,这使得那些不再被认为是最优的路径上的信息素浓度逐渐减少。
同时,每条边上的信息素浓度也会随着时间的推移而均匀增加,这使得那些从未被探索过的路径也有被选择的可能性。
5.终止条件:算法会在找到满足条件的最优解或达到预设的最大迭代次数后终止。
三、蚁群算法的优势和局限性蚁群算法的优势在于其对于组合优化问题的良好性能和其自然启发式的搜索过程。
这种算法能够有效地找到全局最优解,并且在搜索过程中能够避免陷入局部最优解。
此外,蚁群算法具有较强的鲁棒性,对于问题的规模和复杂性具有较强的适应性。
然而,蚁群算法也存在一些局限性。
首先,算法的性能高度依赖于参数的设置,如信息素的挥发速度、蚂蚁的数量、迭代次数等。
其次,对于一些复杂的问题,可能需要很长的计算时间才能找到最优解。
此外,蚁群算法可能无法处理大规模的问题,因为这可能导致计算时间和空间的复杂性增加。
群智能算法(一)2024

群智能算法(一)引言概述:群智能算法是一种基于群体行为的智能算法,通过模拟群体中个体之间的相互作用和信息传递,来解决复杂问题。
本文将介绍群智能算法的基本原理、常见算法类型以及其应用领域。
正文内容:一、基本原理1.1 定义:群智能算法是一种通过模拟群体行为来解决问题的算法。
1.2 群体行为模拟:群体行为模拟是通过模拟生物或社会群体中个体之间的相互作用,来解决问题。
1.3 群体智能与个体智能:群体智能是由个体之间的相互作用和信息传递所产生的智能。
二、常见算法类型2.1 蚁群算法:模拟蚂蚁寻找食物的行为,通过信息素和启发式规则来进行搜索和优化。
2.2 粒子群算法:模拟鸟群寻找食物的行为,通过速度和位置的调整来进行搜索和优化。
2.3 鱼群算法:模拟鱼群觅食和迁徙的行为,通过个体的位置和速度来进行搜索和优化。
2.4 免疫算法:模拟免疫系统的优化过程,通过抗体的选择、克隆和突变来进行搜索和优化。
2.5 蜂群算法:模拟蜜蜂寻找蜜源和觅食的行为,通过信息素和距离计算来进行搜索和优化。
三、应用领域3.1 工程优化:群智能算法在工程优化中被广泛应用,例如在航空航天工程中的飞行控制系统优化、电力系统中的负荷分配优化等。
3.2 数据挖掘:群智能算法在数据挖掘中可以用于聚类分析、关联规则挖掘和分类预测等任务。
3.3 图像处理:群智能算法在图像处理中可以用于图像分割、目标检测和图像增强等任务。
3.4 交通规划:群智能算法在交通规划中可以用于路线规划、交通流优化和交通事故预测等任务。
3.5 金融市场:群智能算法在金融市场中可以用于股票预测、投资组合优化和风险管理等任务。
总结:群智能算法是一种通过模拟群体行为来解决复杂问题的智能算法。
它的基本原理是通过模拟生物或社会群体中个体之间的相互作用和信息传递,来获得群体智能。
常见的群智能算法有蚁群算法、粒子群算法、鱼群算法、免疫算法和蜂群算法。
这些算法在工程优化、数据挖掘、图像处理、交通规划和金融市场等领域都有广泛的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
蚁群算法的基本原理及应用
1. 简介
蚁群算法(Ant Colony Optimization,简称ACO)是一种模拟蚂蚁觅食行为的计算机算法。
蚁群算法最早由意大利学者Dorigo等人于1992年提出,它通过模拟蚂蚁在搜索食物时的行为规律,能够解决很多优化问题。
在近年来,蚁群算法在路线规划、任务分配、组合优化等方面得到了广泛的应用。
2. 基本原理
蚁群算法的基本原理是模拟蚂蚁在搜索食物过程中的行为规律。
蚂蚁在搜索食物的过程中,会释放一种称为信息素(pheromone)的化学物质,用以指引其他蚂蚁前往食物的路径。
当蚂蚁选择了一条路径后,它会在路径上释放信息素,并且信息素会随着时间的推移逐渐挥发。
蚂蚁在选择路径时具有一定的随机性,同时也受到信息素浓度的影响。
信息素浓度高的路径会更有可能被选择,从而使得路径上的信息素浓度进一步增加。
蚁群算法利用蚂蚁在搜索食物过程中的行为规律来解决优化问题。
算法首先随机生成一群蚂蚁,在每一次迭代中,蚂蚁根据信息素浓度和启发式信息(即问题本身的特征)来选择路径,并更新路径上的信息素浓度。
随着迭代次数的增加,信息素浓度会不断迭代更新,蚂蚁在路径选择时也会趋向于选择信息素浓度高的路径。
最终,蚁群算法通过大量蚂蚁的合作和信息素的反馈来寻找到最优解。
3. 应用领域
蚁群算法在很多优化问题中得到了广泛的应用。
以下是一些常见的应用领域:•路线规划:蚁群算法可以用于解决旅行商问题(TSP),在城市之间找到最优的路径,从而提高运输效率和降低成本。
•任务分配:蚁群算法可以用于解决多机器人的任务分配问题,将任务分配给不同的机器人来实现协作完成。
•组合优化:蚁群算法可以用于解决组合优化问题,例如在工程中安排最优的资源分配,或者在电信网络中找到最短的路径以优化网络流量。
4. 算法流程
蚁群算法的基本流程如下:
1.初始化信息素和启发式信息。
2.生成一群蚂蚁,放置在起始位置。
3.每只蚂蚁根据信息素浓度和启发式信息选择路径,并更新路径上的信
息素浓度。
4.计算每只蚂蚁的路径长度,并更新最优路径。
5.根据信息素的挥发程度和增加速度更新信息素浓度。
6.如果满足终止条件,则输出最优路径,否则返回第3步。
5. 算法优缺点
蚁群算法具有如下优点:
•全局搜索能力强:蚁群算法通过大量蚂蚁的合作和信息素的反馈来搜索解空间,具有较强的全局搜索能力。
•适用于复杂问题:蚁群算法适用于解决各种复杂问题,包括优化问题、路径规划问题等。
•并行性好:蚁群算法中的蚂蚁可以独立进行搜索,具有很好的并行性。
蚁群算法也存在一些缺点:
•对参数敏感:蚁群算法的性能很大程度上依赖于参数的选择,不同的问题需要调整不同的参数。
•收敛速度慢:蚁群算法需要通过多次迭代来搜索最优解,收敛速度比较慢。
6. 总结
蚁群算法是一种模拟蚂蚁觅食行为的计算机算法,通过模拟蚂蚁在搜索食物时
的行为规律,能够解决很多优化问题。
蚁群算法在路线规划、任务分配、组合优化等方面得到了广泛的应用。
蚁群算法的基本原理是模拟蚂蚁在搜索食物过程中的行为规律,蚂蚁通过释放信息素来引导其他蚂蚁选择路径,信息素的浓度受到蚂蚁选择路径的影响。
蚁群算法具有全局搜索能力强、适用于复杂问题、并行性好等优点,但也存在对参数敏感、收敛速度慢等缺点。
