高电压工程 行波的折、反射17
高电压技术_第四章线路及绕组中的波过程

高电压技术_第四章线路及绕组中的波过程第二篇电力系统过电压及其防护本篇的主要内容第四章线路及绕组中的波过程主要内容4.1 单导线波过程4.2 波的折射和反射4.3 行波通过串联电感和并联电容4.4 行波的多次折反射4.5 无损耗平行多导线系统中的波过程4.6 冲击电晕对线路波过程的影响4.7 变压器绕组中的波过程4.8 旋转电机绕组的波过程4.1 单导线波过程4.1 单导线波过程一均匀无损长线的波过程均匀无损长线等值电路4.1 单导线波过程磁场:磁通变化→导线自感压降,用参数L →L 0dx表征?电场:电场变化→导线对地电容电流,用参数C →C 0dx 表征导线电阻:iR 0线路绝缘子泄漏电流:uG 0.R<<="">4.1 单导线波过程设dt 时间内,行波前进了dx 距离,则长度为dx 的线路被充电,充电电容为C 0dx ,使其电位为U ,在这段时间内,导线获得的电荷为:充电电流:?同理,行波建立磁场的过程,行波前进了dx 距离,磁通的增加量:对地电压:dxC u dC u dq ××=×=0dtdxC u dt dCu dt dqi ??===0dx L i dL i d ××=×=0φdtdxL i dt dLi dt d u ??===0φ124.1 单导线波过程1、2两式相乘,得行波的传播速度1、2两式相除,得反映电压波和电流波关系的波阻抗01C L dt dx v ±==00C L i u Z ±==344.1 单导线波过程波阻抗:是表征分布参数电路特点的最重要的参数,它是储能元件,表示导线周围介质获得电磁能的大小,具有阻抗的量纲,其值决定于单位长度导线的电感和电容,与线路长度无关。
对单导线架空线,Z=500Ω左右,考虑电晕影响取400Ω左右,电缆的波阻抗约为十几至几十欧姆不等。
高电压技术_3波过程
•
一、波的折、反射规律 波的折、 若具有不同波阻抗的两条线路相连接,如图7-2-1 所 示,连接点为A。现将线路z1合闸于直流电源U 0 ,合闸后沿 线路 z1有一与电源电压相同的前行波电压 u1q自电源向结点A 传播,到达结点A遇到波阻抗 z 2 的线路,根据前节所述,在 结点A前后都必须保持单位长度导线的电场能与磁场能相等 的规律,由于线路z1与 z 2 的单位长度电感与对地电容都不相 同,因此当u1q 到达A点时要发生电压、电流的变化。也就是 说,在结点A处要发生行波的折射与反射,反射电压为 u1 f , 折射电压波为 u 2 q 。 2q
R 1 1
Z1
2u1 i2
R
u2
彼得逊规则的等值电路 这样一来,当行波投射到接有分布参数线路和集中 参数元件的节点上时,如果只需要求取节点上的投射波 和反射波,那么波过程的分析可以简化成集中参数电路 的暂态计算。
行波通过串联电感和并联电容(自学) §5-3 行波通过串联电感和并联电容(自学) 在电力系统中常常会遇到线路和电感与电容的各种方式 的连接。在线路上串联电感和并联电容是常见的方式,电感 、电容的存在将使线路上的行波的波形和幅值发生变化,下 面分析其影响。 一、无限长直角波通过串联电感
u1q
L
z1 z1
z2
L
u1 f
L
au1q
u2 q
z1
z2
z2
2u1q
(a )
i2 q
βu1q
(b)
图7 - 3 - 1 行波通过串联电感
(a )线路示意及等值电路; )折射波与反射波 (b
图7-3-1为一无限长直角波 u1q 投射到具有串联电感L的线 路上的情况,L前后两线路的波阻抗分别为z1 及 z 2 ,当z 2中的 反行波尚未到达两线连接点时,其等值电路如图7-3-1(a) 所示,由此可得
高电压技术——3电力系统波过程

波速度 波阻抗
v Z
' '
1 L0C0
L0 C0 "
u f1 ( x vt ), u f 2 ( x vt ) u " u i ,i Z Z
' '
行波方程解的意义
架空线路
C0
2 0 2h ln r
( F / m)
(16 5)
L0
因此,波速度为:
0
2
ln
2h r
( H / m)
(16 6)
1
LC
0
0
1
0
3 10 / s 300m / s
0
8
电缆线路,若:
波速度
r
4
150m / s
Propagation path
2.
单波的电场能量等于磁场能量
1 u L 1 Z ( ) ( ) ( ) C L i u 2 2 C i
0 2 0 0 0
2 2
对于架空线路有:
Z 60 ln
2 hc r
138 lg
2 hc r
( )
一般Z=500欧姆,分裂导线Z=300欧姆 对于电缆线路,因C0 大L0 小,故其波租要比架空线小得多, 且变化范围较大,约在10~50欧姆之间 线路上有两组电荷沿导线-地同步地以波速度分别向X正方 向或X负方向运动,它们在空间建立了电磁场,造就了导线上 的电压和电流。在此,导线——介质——大地起到了引导电磁 波的作用。因而这个过程被称为波过程。
高电压第七章 线路及绕组中的波过程

第二篇 电力系统过电压及其防护 电力系统中各种电气设备的绝缘在运行过程中除了长期受到工作电压的作用(要求它能够长期耐受、不损坏、也不会迅速老化)外,由于种种原因还会受到比工作电压高的多的电压作用,会直接危害到绝缘的正常工作,造成事故。我们称这种对绝缘有危险的电压升高和电位差升高为“过电压”。 一般来说,过电压都是由于系统中的电磁场能量发生了变化而引起的。究其原因,这种变化可能是由于系统外部突然加入一定的能量(例如雷击导线、设备或导线附近的大地)而引起的,或者是由于电力系统内部,当系统参数发生变化时,电磁场能量发生了重新分配而引起。因此可将过电压作如下分类。 电力系统过电压包括:雷电(大气)过电压、内部过电压 雷电过电压:直击雷电过电压、感应雷电过电压 内部过电压:操作过电压、暂时过电压【工频电压升高、谐振过电压】 不论哪种过电压,它们作用时间虽然很短(谐振过电压,有时较长),但其数值较高,可能使电力系统的正常运行受到破坏,使设备的绝缘受到威胁。因此为了保证系统安全、经济的运行,必须研究过电压产生的机理和物理过程、影响因素,从而提出限制过电压的措施,以保证电气设备能够正常运行和得到可靠地保护。
第七章 线路及绕组中的波过程
本章要求:过电压的定义和分类 无损单导线中的波过程:波动方程,波阻抗和波速,波的折射与反射,彼德逊等值电路,行波通过串联电感和并联电容 波的多次折反射。 冲击电晕对波过程的影响: 变压器绕组中的波过程:等值电路的建立,电压的初始分布与稳态分布,最大电位包络线,入口电容,三相变压器绕组中的波过程。 波的传递及电机绕组波过程简介 电力系统中各个元件都是通过导线连接成一个整体,而电力系统中的过电压绝大多数是发源于输电线路,在发生雷击或进行开关操作时,线路上都可能产生以流动波形式出现的过电压。 过电压在线路上的传播,就其本质而言是电磁场能量沿线路的传播过程,即在导线周
围空间逐步建立起电场E和磁场H的过程,也是在导线周围空间储存或传递电磁能的过程。这个过程的基本规律是储存在电场中的能量与储存在磁场中的能量彼此相等。空间中各个点的电场和磁场相互垂直,并处于同一个平面内,与波的传播方向也相互垂直,故为一维电磁波。若用电磁场方程来求解线路波过程就比较复杂,为了方便起见,一般采用输电线路上电压、电流波过程代替输电线路周围空间的电磁场波过程。 什么叫行波?为什么要研究波动过程? 答:沿着导线传输的电压、电流波叫行波,又叫流动波。波动过程,从本质上讲就是电磁能量沿导线的传播过程,就是分布参数电路的过渡过程。学习波动过程,主要是讨论电压波、电流波在输电线路、变压器、发电机绕组中的传播过程,为研究雷电波和操作波的传导过程打下理论基础。 什么叫分布参数电路?集中参数电路和分布参数电路有何区别?设备的等值电路采用分布参数和采用集中参数电路取决于什么? 答:对于长距离的输电线路或网络,不可能当始端的开关一合上,远处的用户立刻就能受电,总要经过一定的时间和一定的过渡过程,远方的设备才能受电。如图,当开关K一合上,将有电流流过电感线圈L1,附近的电容器C1同时被充电,这时后面的导线尚无电流。随着时间的加长,又有电流流过L2,然后C2又被充电,再往后是L3,C3被充电……如此下去,变化的电流形成变化的磁场,沿线产生了感应电动势,使得导线对地的电位也发生了变化,而由于沿线电场的变化,线路上存在位移电流,又使得电流也发生变化,随着导线上各点与电源的距离远近的不同,各点的电压、电流依次的建立,因此,像这种将沿线分布的电感、电容皆作为考虑因素的远距离的长线路的等值电路就是分布参数电路。 分布参数电路中以微分的观点分析电压、电流波对不同位置的点的影响,即认为各点的电压和电流的出现及其大小值,不仅与时间有关,还同该点和电源的距离有关。 集中参数电路吧元件理想化、质点化,忽略了元件的几何尺寸对波形的传播的影响,即认为元件两端电位是同时建立的,而仅仅考虑其所产生的压降 设备的等值电路采用分布参数还是集中参数电路,主要取决于电源的频率及电路的几何尺寸,一般直流线路中,因电源频率为零,故线路中的感抗为零,可视为短路;而容抗很大可视为开路。 但在雷电冲击波和操作过电压的冲击波作用下,因电源的频率很高,所以线路的感抗很大而不能看成是短路,容抗也相当的小而不能看做是开路。故分析远距离的长线路、变压器和发电机的绕组在冲击电压作用下的波传导过程应采用分布参数电路。
高电压技术——第十三讲 8.2 8.3

前行波电压、电流都由强制分量、自由分量组成。无穷长直角波 通过集中电感时,波头被拉长。当波到达电感瞬间,电感相当于 开路,使电压升高一倍,然后按指数规律变化。当 t →∞ 时,电 感相当于短路,折、反射系数 α,β 的与无电感时一样。
线 1 与导线 2 之间的波传播过程不再起任何作用。
线路中折射电压的最大陡度: 在 Z2 线路中折射电压的最大陡度:
du2f dt
t=0
m ax
2 u1f = Z 1C
t =0
最大空间陡度:
du2f dl
max
2u1f = Z1Cv
无穷长直角波旁过电容时,前行波电压、电流变为指数 波。最大空间陡度与 Z2 无关,仅与 Z1 有关。为了限制 波的陡度,采用并联电容或采用串联电感需要进行经济上 的核算。
例8-4 有一幅值 E = 100 kV 的直角波沿波阻抗 Z1 = 50Ω 的电缆线路侵入波阻抗为 Z2 = 800Ω 的发电机绕组,绕组 每匝长度为 3 m,匝间绝缘耐压为 600 V,绕组中波的传播 速度 v = 6×107 m/s。求用并联电容器或串联电感来保护匝 间绝缘时它们的数值。 最大空间陡度 解:电机允许承受的侵入波最大陡度为:
Z2 − Z1 u1f 2Z2 u1f −t / T + e i1b = − Z1 + Z2 Z1 Z1 + Z2 Z1
u2f ,i2f 均由零值按指数规律渐趋稳态值,直角波变为指数波, 波首变平,且稳态值只决定于波阻抗 Z1 与 Z2,与电容 C 无关。 这说明在直角波作用下,当 t →∞ 时, 电容相当于开路,对导
高电压技术 第07章 线路和绕组中的波过程

7.1 无损耗单导线线路中的波过程
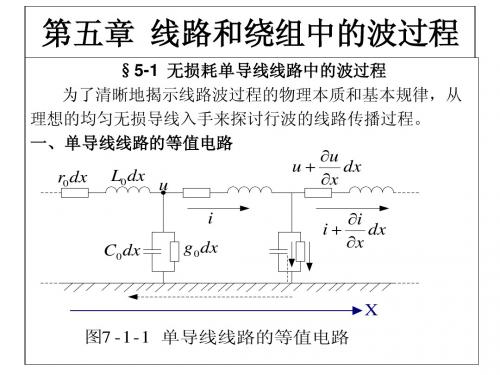
1、单导线线路等值电路:
r0 d x L 0 d x C 0dx g 0dx L0 d x
C 0dx
u x i x
L0 C0
i x u x
x x u uq t u f t v v i i t x i t x q f v v
2、行波:沿输电线路传输的电磁波。
前行波
x u uq t v
u
uq
x
0
2、行波:沿输电线路传输的电磁波。
前行波
x u uq t v
反行波
u
x u uf t v
uf
x
0
x x u uq t u f t v v i i t x i t x q f v v
i1 f
z1
A
z2
结论:折射(末端)电压波上升一倍,末端电流为零; 反射波到达之处,电压上升一倍,电流降为零; 即反射波到达之处,磁场能全部转化为电场能。
例7-2:线路z1末端短路,沿线路z1有一无限长的直角波 u1q向前传播。 u
1q
已知:z1、z2= 0、u1q、i1q 。 求:u2q、 i2q 、 u1f 、i1f 。 解:
i1 i 2 q
u1 f z1
u2q z2 u1q 2 z1 z 2 z1
t T t T
u1 f u 2 q u1q
z 2 z1 z 2 z1
u1q e
u u1q
高电压技术(7)
时间常数:
T
z1 z 2 c z1 z 2
电压折射系数:
z 2 z1 2 z2 u1 f u1q u1q e T z1 z 2 z1 z 2 t
du2 q
2 u1q e T dt z1c
t
电容中的电压不能突变, 初始瞬间相当于短路 直角波通过电容后改变为 指数波,降低了行波陡度
15
解: t
1s 时,U1到达B点,U2未到达B点
U B U 1 1000 (k V ) U B 1000 IB 2(k A) Z 500
t 1.5s 时,U1到达B点,U2也到达B点
U B U 1 U 2 1000 500 1500 (k V ) 1000 500 I B I1 I 2 1(k A) 500 500
18
以上电压波的折射反射系数也适用于线路末 端接有不同集中负载的情况。
19
2z2 u 2 q z z u1q u1q 1 2 z 2 z1 u1 f z z u1q u1q 1 2 2z2 电压折射系数, 0 2 z1 z 2 z 2 z1 电压反射系数, 1 1 z1 z 2 1
t 0
2u1q z 2 L
37
38
二、 无穷长直角波通过并联电容
Z1
U1q 2U1q i1 ic
Z1
C
Z2
C
Z2
i2q
U2q
(1)接线图
(2)等效电路
39
波通过并联电容
2u1q i1 z1 i2 q z 2
Z1
di2 q dt
行波总结
在电力系统正常工作下,输电线路、母线、电缆以及变压器和电机的绕组等元件,由于其尺寸远小于50Hz 交流电的波长(λ=6000km ),故可按集中参数元件处理。
在过电压作用下,由于电压的等效频率很高,其波长小于或与系统元件长度相当,此时就必须按分布参数元件处理。
行波的传播速度和波长电力线路在输送电能时是以电磁波的形式传播的,在忽略电阻和电导的情况下,其线性行波的传播速度为: 001C L t x v ==将线路的电感和电容代入上式,得s m 103180r 0r r r v μεμμεε⨯== 波的传播速度与导线几何尺寸、悬挂高度无关,仅由导线周围的介质所确定。
对架空线,,1,1==r r με所以 ()C v =⨯=s m 1038 (真空中的光速)对于电缆,,1,4=≈r r με所以 ()2m 105.18C v ≈⨯=,约为光速的一半。
行波波长是指行波相位差正好等于2π的两点之间的距离。
波阻抗00C L i uZ ==即波阻抗,通常用Z 表示,其单位为欧姆,其值取决于单位长度线路电感0L 和对地电容0C ,而与线路长度无关。
把0L 、0C 代人上式得 r h Z d r r2ln 2100εεμμπ=式中 0ε——真空介电常数;rε——相对介电常数;μ——真空导磁系数;rμ——相对导磁系数;dh——导线对地平均高度;r——导线半径。
对架空线,()Ω=rhZ d2ln60,一般单导线架空线路()Ω≈500Z。
同时看到,波阻抗不但与线路周围介质有关,且与导线的半径和悬挂高度有关。
电缆的波阻抗比架空线要小得多,大约为十几欧至几十欧不等。
波动方程电压波符号只决定导线对地电容上相应电荷的符号,和运动方向无关。
电流波的符号不但与相应的电荷符号有关,而且与运动方向有关,我们一般以x正方向作为电流的正方向。
这样,当前行波电压为正时,电流也为正,即电压波与电流波同号。
但当反行波电压为正时,由于反行波电流与规定的电流正方向相反,所以应为负。
高电压工程实验报告
沿面放电实验(一)实验目的:1.了解沿面放电的基本概念。
2.研究介质沿面放电的基本现象与影响沿面放电的一些因素。
(二)实验内容:固体介质处于不均匀电场中,且介质界面电场具有强垂直分量。
当所加电压还不高时,电极附近首先出现电晕放电,然后随着所加电压的不断升高,放电区域逐渐变成由许多平行的火花细线组成的光带,即出现辉光放电。
火花细线的长度随着电压的升高而增大,当电压超过某一临界值后,放电性质发生变化,出现滑闪放电。
当电压再升高一些,放电火花就将到达另一电极,发生沿面闪络。
仔细观察沿面放电的整个过程,了解各个阶段沿面放电现象的特点,并阐明发生沿面放电现象的原理。
(三)实验用仪器设备:1.800kV无局放工频试验变压器2.JJFB-1交流峰值电压表3.平板式电极〔小圆柱和平板为电极〕(四)实验用详细线路图或其它示意图:图1 沿面放电试验线路图图2 平板式电极〔小圆柱和平板为电极〕(五)实验有关原理与原始计算数据,所应用的公式:实验的有关原理请参考文献[4]和上述〔四〕中部分实验的原理图。
(六)实验数据记录:放电阶段施加电压放电特点电晕放电辉光放电滑闪放电表1空气间隙放电实验记录表的参考式样(七)实验结果的计算与曲线:本次实验沿面放电分为三个阶段:电晕放电、辉光放电和滑闪放电。
图3 电晕放电阶段图4辉光放电阶段图5滑闪放电阶段(八)对实验结果、实验中某些现象的分析讨论:思考并完成下述问题:1.进行高电压试验时为什么要特别注意安全?应采取那些安全措施?〔1〕因为在高电压下工作,由于疏忽,人体与带高电压设备部分的距离小于安全距离时极可能发生人身伤亡事故;因错接试验电路或错加更高的试验电压很可能使试验设备或被试设备发生损坏。
〔2〕为了保证实验安全的进行,可采取以下安全措施:○1充分做好实验前的准备工作,拟定好实验方案,严格按照相关规程和实验老师的的指导进行实验;○2多人协同工作,明确分工,同时相互提醒,也可专设一人负责安全监察;○3实验中,全体人员必须思想集中,全神贯注,不能闲聊、随意走动,更不可随意触碰;○4时刻注意与带电高压设备保持安全距离;等。
高电技术总结(7-10)
Z12 k= Z11
u1 − u2 = (1 − k )E < E
17
冲击电晕引起波 衰变和 冲击电晕引起波的衰变和变形 引起
只有衰减, 不会变形的条件 只有衰减, 不会变形的条件
R0 L0 R0 G0 = ,或 = =δ G0 C0 L0 C0
1 2 L0i R0i 2t 2 = 1 G0u 2t 2 C0u 2
3
行波的折 行波的折、反射规律 原因:参数突然改 原因:参数突然改变
1
u1q=E 2 A Z2
Z1
边界条件:在节点A只有一个电压和电流 一个电压和 边界条件: 节点A只有一个电压
u1q + u1 f = u2q i1q + i1 f = i2q
2Z2 u2q = E = αu E Z1 + Z2 Z2 − Z1 u1 f = E = βu E Z1 + Z2
7
集中参数等值电路(彼得逊法则) 集中参数等值电路(彼得逊法则) 等值电路 法则
Z1 u2(t) i2
u1q=E 1 Z1 A 2 Z2
2u1q(t) Z2
u1q (t ) + u1 f (t ) = u2 (t ) i1q (t ) + i1 f (t ) = i2 (t )
i1q (t ) = u1q (t ) / Z i1 f (t ) = −u1 f (t ) / Z
14
u (t )
α1 β1
波的多次折反射
u (t )
Z0 , τ
α2 β2
2Z0 α1 = Z1 + Z0
α 1u (t ) α 1u (t - τ) 1α 2u (t - τ) α α 1β 2u (t - τ) α 1β 2u (t - 2τ)
