概率论与数理统计课件3-2专
合集下载
概率论与数理统计(王明慈第二版)第3章随机变量的数字特征2-5节.ppt
则称E[X-E(X)]2称为X的方差, 记作D(X) 或 2( X )
即
D( X ) E[X E( X )]2 .
方差的算术平方根 D(X ) 称为 X 的标准差,
记作 (X ), 即
(X ) D(X ) 或 D(X ) 2(X ).
2021/3/18
5
方差
D( X ) E[X E( X )]2
E[ X 2 2XY Y 2 ] [E( X ) E(Y )]2
E(X 2 ) 2E(X )E(Y ) E(Y 2 ) [E(X )]2 [E(Y )]2 2E(X )E(Y )
{E( X 2 ) [E( X )]2}{E(Y 2 ) [E(Y )]2} D(X ) D(Y ).
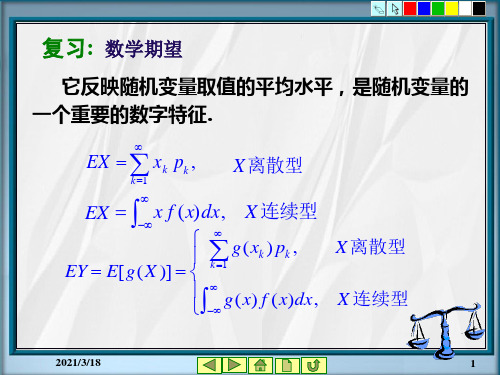
复习: 数学期望
它反映随机变量取值的平均水平,是随机变量的 一个重要的数字特征.
EX xk pk , k 1
X 离散型
EX x f (x)dx,
X 连续型
EY E[g( X )]
g(xk ) pk ,
k 1
Байду номын сангаас
g(x) f (x)dx,
X 离散型 X 连续型
2021/3/18
1
第二节 方差
(1)利用随机变量函数的数学期望公式
离散随机变量的方差
D( X ) [xi E( X )]2 pi
i
其中X的分布列为P( X xi ) pi , i 1,2,
连续随机变量的方差
D(X )
[x
E(X
)]2
f
(x)dx
其中X的概率密度为 f( x).
2021/3/18
7
(2)利用方差公式
基本内容: 一、方差的定义 二、方差的性质
概率论与数理统计课件(完整版)

21
蒲丰投针试验
例2 1777年,法国科学家蒲丰(Buffon)提出了投针 试验问题.平面上画有等距离为a(>0)的一些平行直 线,现向此平面任意投掷一根长为l ( <a )的针,试求 针与任一平行直线相交的概率.
a M
x
22
几何概型的概率的性质
(1) 对任一事件A ,有 0p(A )1;
( 2 )P ( ) 1 ,P ( ) 0 ; (3) 对于两两互个 斥事 的 A1,件 A 可 2, 列 , 多 P(A1A2 )P(A1)P(A2)
A -B A AB 显然: A-A=, A- =A, A-S=
s
A B
(4)AB
10
5.事件的互不相容(互斥):
若 A B,则A 与 称 B 是互不 ,或 相 互 ,即 容 斥
A 与 B 不能同 . 时发生
B
AB
A
11
6. 对立事件(逆事件): 若ABS且AB, 则A与 称B互 为 逆 事 件
P(B| A) P(AB) P(A)
为在事件A发生的条件下事件B发生的条件概率2.9
2. 性质: 条件概率符合概率定义中的三个条件, 即 10对于每 B有 一 ,1P 个 (|A B 事 )0.件
20 P(|A S)1.
30 设B1,B2,两 两 互 不,则 相 容
P( Bi |A) P(B i |A.)
i1
1i jn
P(A i A jAk )
1i jkn
(1)n1 P(A1 A 2 A n ).
27
例4. 设P(A)=p, P(B)=q, P(AB)=r, 用p, q, r表示下列 事件的概率: ( 1 ) P ( A B ) ( ; P ( 2 A B ) ( ) ; P ( 3 A B ) ) ( ; ( 4 A B )
蒲丰投针试验
例2 1777年,法国科学家蒲丰(Buffon)提出了投针 试验问题.平面上画有等距离为a(>0)的一些平行直 线,现向此平面任意投掷一根长为l ( <a )的针,试求 针与任一平行直线相交的概率.
a M
x
22
几何概型的概率的性质
(1) 对任一事件A ,有 0p(A )1;
( 2 )P ( ) 1 ,P ( ) 0 ; (3) 对于两两互个 斥事 的 A1,件 A 可 2, 列 , 多 P(A1A2 )P(A1)P(A2)
A -B A AB 显然: A-A=, A- =A, A-S=
s
A B
(4)AB
10
5.事件的互不相容(互斥):
若 A B,则A 与 称 B 是互不 ,或 相 互 ,即 容 斥
A 与 B 不能同 . 时发生
B
AB
A
11
6. 对立事件(逆事件): 若ABS且AB, 则A与 称B互 为 逆 事 件
P(B| A) P(AB) P(A)
为在事件A发生的条件下事件B发生的条件概率2.9
2. 性质: 条件概率符合概率定义中的三个条件, 即 10对于每 B有 一 ,1P 个 (|A B 事 )0.件
20 P(|A S)1.
30 设B1,B2,两 两 互 不,则 相 容
P( Bi |A) P(B i |A.)
i1
1i jn
P(A i A jAk )
1i jkn
(1)n1 P(A1 A 2 A n ).
27
例4. 设P(A)=p, P(B)=q, P(AB)=r, 用p, q, r表示下列 事件的概率: ( 1 ) P ( A B ) ( ; P ( 2 A B ) ( ) ; P ( 3 A B ) ) ( ; ( 4 A B )
概率论与数理统计课件(PPT)

随机现象:不确定性与统计规律性
概率论——研究和揭示随机现象 的统计规律性的科学
目录
• • • • • • 第一章 随机事件及其概率 第二章 随机变量 第三章 随机变量的数字特征 第四章 样本及抽样分布 第五章 参数估计 第六章 假设检验
第一章 随机事件及其概率
• 随机事件及其运算 • 概率的定义及其运算 • 条件概率 • 事件的独立性
注意到不论是对概率的直观理 解,还是频率定义方式,作为事件 的概率,都应具有前述三条基本性 质,在数学上,我们就可以从这些 性质出发,给出概率的公理化定义
1.定义(p8) 若对随机试验E所对应的样本空间中 的每一事件A,均赋予一实数P(A),集合函数
P(A)满足条件:
(1) P(A) ≥0;
(2) P()=1;
历史上曾有人做过试验,试图证明抛掷匀质硬币时 ,出现正反面的机会均等。
实验者
De Morgan Buffon K. Pearson K. Pearson
n
2048 4040 12000 24000
nH
1061 2048 6019 12012
fn(H)
0.5181 0.5069 0.5016 0.5005
N ( A) P( A) N ()
P(A)具有如下性质(P7)
(1) 0 P(A) 1;
(2) P()=1; P( )=0 (3) AB=,则 P( A B )= P(A) +P(B)
例:有三个子女的家庭,设每个孩子是男是女的概率 相等,则至少有一个男孩的概率是多少?
解:设A--至少有一个男孩,以H表示某个孩子是男孩 ={HHH,HHT,HTH,THH,HTT,TTH,THT,TTT}
1.1随机事件及其概率
概率论——研究和揭示随机现象 的统计规律性的科学
目录
• • • • • • 第一章 随机事件及其概率 第二章 随机变量 第三章 随机变量的数字特征 第四章 样本及抽样分布 第五章 参数估计 第六章 假设检验
第一章 随机事件及其概率
• 随机事件及其运算 • 概率的定义及其运算 • 条件概率 • 事件的独立性
注意到不论是对概率的直观理 解,还是频率定义方式,作为事件 的概率,都应具有前述三条基本性 质,在数学上,我们就可以从这些 性质出发,给出概率的公理化定义
1.定义(p8) 若对随机试验E所对应的样本空间中 的每一事件A,均赋予一实数P(A),集合函数
P(A)满足条件:
(1) P(A) ≥0;
(2) P()=1;
历史上曾有人做过试验,试图证明抛掷匀质硬币时 ,出现正反面的机会均等。
实验者
De Morgan Buffon K. Pearson K. Pearson
n
2048 4040 12000 24000
nH
1061 2048 6019 12012
fn(H)
0.5181 0.5069 0.5016 0.5005
N ( A) P( A) N ()
P(A)具有如下性质(P7)
(1) 0 P(A) 1;
(2) P()=1; P( )=0 (3) AB=,则 P( A B )= P(A) +P(B)
例:有三个子女的家庭,设每个孩子是男是女的概率 相等,则至少有一个男孩的概率是多少?
解:设A--至少有一个男孩,以H表示某个孩子是男孩 ={HHH,HHT,HTH,THH,HTT,TTH,THT,TTT}
1.1随机事件及其概率
概率论与数理统计示范课公开课一等奖课件省赛课获奖课件

PAB PA PB a 1 3 a a 13 a
22
4
而,PA B PA PB PAB
PA B a 1 3 a a 13 a 7
22
4
9
a 5 或a 7
3
3
关于X的边缘分布函数为
FX
x
F
x,
1 0,
x
,
x0 其他
关于Y的边缘分布函数为
FY
y
F
,
y
1 0,
y
,
y0 其他
Fx, y FX x FY y
3.2.2 二维离散型随机变量的独立性
二维离散型随机变量的独立性概念 P74
P65例3-6:(1)有放回摸球状况核心字:互相独立(例3-15)
Y X
0 1 P ●j
0
1
33 55 3 2 55
3 5
23 55 22 55
2 5
Pi ●
3 5 2 5
Y X
y1
y2
…
yj
…
x1
p11
p12
…
p1j
…
x2
p21
p22
…
p2j
…
︰
︰
︰
︰
xi
pi1
pi2
…
pij
…
︰
︰
︰
︰︰
P .j
∑pij
i
pij Pi•P• j Pij Pij
j
i
Pi .
∑pij
▪ 定义3-9(X与Y互相独立)P73
定义3-9(X与Y互相独立)的数学体现
联合分
P73 X分量的边沿
布函数
概率论与数理统计 第三章
x y e 2u |0 e v |0 , x 0, y 0, 其它, 0,
(1 e 2 x )(1 e y ), x 0, y 0, 其它, 0,
例2-续3
(3)求概率P{Y≤X}. 只需在概率密度f的非零 区域与事件区域 G={(x,y)|y≤x} 的交集D上积分. 由公式
0 F ( x, y) 1; ;
F ( x, y )关于x、y均单调不减右连续.
分布函数与离散型二维随机变量分布律、连 续型二维随机变量概率密度的关系[见后].
三、离散型二维随机变量
1、二维均匀分布
两种常见的二维连续型分布
设G为一个平面有界区域,其
二维均匀分布
面积为A.如果二维连续型随机变量(X,Y)的概率密
度为
1 , ( x, y ) G , f ( x, y ) A 0, 其它,
则称(X,Y)服从区域G上的均匀分布,记为(X,Y)~U(G).
2、二维正态分布
域”的概率.
分布函数具有下列基本性质:
对任意点 ( x1 , y1 ), ( x2 , y2 ), x1 x2 , y1 y2 均有:
随机向量落在矩 形区域的概率
P{x1 X x2 , y1 Y y2 }
F ( x1 , y1 ) F ( x2 , y2 ) F ( x1 , y2 ) F ( x2 , y1 ) 0;
D
x
例2-续4
2 e
0
2 x
(1 e )dx [e
x
2 x
2 3 x 2 1 e ] |0 1 . □ 3 3 3
本例是一个典型题.大家应熟练掌握分析与计算 的方法。特别是会根据不同形状的概率密度非零区域 与所求概率的事件区域G来处理这类问题。 就P.73:例3来共同考虑如何分段?应分几段?怎 样计算各段值?(板书)
(1 e 2 x )(1 e y ), x 0, y 0, 其它, 0,
例2-续3
(3)求概率P{Y≤X}. 只需在概率密度f的非零 区域与事件区域 G={(x,y)|y≤x} 的交集D上积分. 由公式
0 F ( x, y) 1; ;
F ( x, y )关于x、y均单调不减右连续.
分布函数与离散型二维随机变量分布律、连 续型二维随机变量概率密度的关系[见后].
三、离散型二维随机变量
1、二维均匀分布
两种常见的二维连续型分布
设G为一个平面有界区域,其
二维均匀分布
面积为A.如果二维连续型随机变量(X,Y)的概率密
度为
1 , ( x, y ) G , f ( x, y ) A 0, 其它,
则称(X,Y)服从区域G上的均匀分布,记为(X,Y)~U(G).
2、二维正态分布
域”的概率.
分布函数具有下列基本性质:
对任意点 ( x1 , y1 ), ( x2 , y2 ), x1 x2 , y1 y2 均有:
随机向量落在矩 形区域的概率
P{x1 X x2 , y1 Y y2 }
F ( x1 , y1 ) F ( x2 , y2 ) F ( x1 , y2 ) F ( x2 , y1 ) 0;
D
x
例2-续4
2 e
0
2 x
(1 e )dx [e
x
2 x
2 3 x 2 1 e ] |0 1 . □ 3 3 3
本例是一个典型题.大家应熟练掌握分析与计算 的方法。特别是会根据不同形状的概率密度非零区域 与所求概率的事件区域G来处理这类问题。 就P.73:例3来共同考虑如何分段?应分几段?怎 样计算各段值?(板书)
概率论与数理统计课件完整版.ppt

k 1
3.积事件: 事件A B={x|x A 且 x B}称A与B的
积,即事件A与BA同时发生. A B 可简记为AB.
类似地,
事件
SAK
为可列B 个事件A1,
A2,
...的积事件.
k 1
(2)A B
A B
(3)A B
S
9
4.差事件:
事件A-B={x|xA且xB} 称为A与B的差. 当且仅当 A发生, B不发生时事件A-B发生. 即:
A - B A AB
显然: A-A=, A- =A, A-S=
s
A B
(4)A B
10
5.事件的互不相容(互斥): 若A B ,则称A与B是互不相容的,或互斥的,即
A与B不能同时发生.
B
A B
A
11
6. 对立事件(逆事件):
若A B S且A B ,则称A与B互为逆事件,也称
P(A1 A2 …)=P(A1)+P(A2)+… (可列可加性)
25
2.概率的性质:
性质1. P() 0.
性质2. 若 A1, A2, , An是两两互不相容的事件, 则 P(A1 A2 An)
P(A1) P(A2) P(An). (有限可加性)
性质3. 若A B,则有 P(B A) P(B) P(A);
2. 频率的基本性质:
(1) 0 f(n A) 1;(非负性)
(2) fn(S) 1;
(规范性)
(3)若A1,A2, , Ak两两互不相容,则
fn ( A1 A2 Ak ) fn ( A1 ) fn ( A2 ) fn ( Ak ).(有限可加性)
3. 频率的特性: 波动性和稳定性.
东华大学《概率论与数理统计》课件-第3章概率论基础
重复排列:从n个不同元素中取r个(可重复),考 虑先后顺序共有nr=n n …. n种不同结果。
3.5 等可能样本空间
例7 琼斯先生有10本书要放在书架上,其中有 4本数学书,3本化学书,2本历史书,还有1本 语言书。琼斯想把同一种类的书放在一起,共 有几种不同的可能结果?如果是随意放置,恰 好同一种类的书放在一起的概率多大?
分步乘法计数原理:完成一件事,需要分成几 个步骤,每一步的完成有多种不同的方法,则 完成这件事的不同方法总数是各步骤不同方法 数的乘积。
例:网上预订行程,从郑州到上海共有12种不 同选择,从上海到香港共有4种不同的选择,那 么从郑州经上海到香港共有4×12=48种不同的 选择。
3.5 等可能样本空间
解法一:宿舍是无编号的,
解法二:宿舍是有编号的,
3.5 等可能样本空间
例11 如果一个房间里有n个人,没有两个人的 生日是同一天的概率是多大?如果希望概率小 于0.5,需要多少人?
习题
P53 ex18, ex20
引例: (1)假设某人投掷一对骰子,两个骰子点数之
和为8概率多大?
(2)如果已知第一个骰子最终朝上的数字为3, 那么两个骰子点数之和为8的概率为多少?
3.3文图和事件的代数表示
3.3文图和事件的代数表示
德·摩根律
例2
掷骰子一次,A=“掷出奇数点”,B=“点数不超 过3”,C=“点数大于2”,D=“掷出5点”。求
A B, B C, AB, BD, Ac , AcC
3.4 概率论公理
集函数P(E)称为事件E的概率,如果它满足下 列三条公理
3.5 等可能样本空间
例8 概率论课程上有6个男生,4个女生。对学 生进行考试,按照成绩排名。假定没有两个学 生的成绩是一样的,
3.5 等可能样本空间
例7 琼斯先生有10本书要放在书架上,其中有 4本数学书,3本化学书,2本历史书,还有1本 语言书。琼斯想把同一种类的书放在一起,共 有几种不同的可能结果?如果是随意放置,恰 好同一种类的书放在一起的概率多大?
分步乘法计数原理:完成一件事,需要分成几 个步骤,每一步的完成有多种不同的方法,则 完成这件事的不同方法总数是各步骤不同方法 数的乘积。
例:网上预订行程,从郑州到上海共有12种不 同选择,从上海到香港共有4种不同的选择,那 么从郑州经上海到香港共有4×12=48种不同的 选择。
3.5 等可能样本空间
解法一:宿舍是无编号的,
解法二:宿舍是有编号的,
3.5 等可能样本空间
例11 如果一个房间里有n个人,没有两个人的 生日是同一天的概率是多大?如果希望概率小 于0.5,需要多少人?
习题
P53 ex18, ex20
引例: (1)假设某人投掷一对骰子,两个骰子点数之
和为8概率多大?
(2)如果已知第一个骰子最终朝上的数字为3, 那么两个骰子点数之和为8的概率为多少?
3.3文图和事件的代数表示
3.3文图和事件的代数表示
德·摩根律
例2
掷骰子一次,A=“掷出奇数点”,B=“点数不超 过3”,C=“点数大于2”,D=“掷出5点”。求
A B, B C, AB, BD, Ac , AcC
3.4 概率论公理
集函数P(E)称为事件E的概率,如果它满足下 列三条公理
3.5 等可能样本空间
例8 概率论课程上有6个男生,4个女生。对学 生进行考试,按照成绩排名。假定没有两个学 生的成绩是一样的,
概率论与数理统计完整版课件全套ppt教学教程-最全电子讲义(最新)
点”或“6 点”3 个基本事件,即 A {2 ,4 ,6} 。
四、事件的关系与运算
在一个样本空间中显然可以定义不止一个事件。概率论的重要研究课 题之一是希望从简单事件的概率推算出复杂事件的概率。为此,需要研究 事件间的关系与运算。
事件是一个集合,因此事件间的关系和运算自然按照集合之间的关系 和运算来处理。
1 事件的包含与相等
若 A B ,则称事件 B 包含事件 A ,这里指的是事件 A 发生必然导致事件 B 发生, 即属于 A 的样本点都属于 B ,如图1-2所示。显然,对任何事件A,必有 A 。
若 A B 且 B A ,则称事件 A 与 B 相等,记为 A B。
图1-2 A B
事件 A B {x | x A或x B},称为事件A与事件B的和事件,即当且仅当事件 A 或 事件 B 至少有一个发生时,和事件 A B 发生。它由属于 A 或 B 的所有公共样本点构 成,如图 1-4 所示。
图 1-4 A B
4 事件的差
事件 A B {x | x A且x B}称为事件 A 与事件 B 的差事件,即当且仅当事件 A 发 生但事件 B 不发生时,积事件A B发生。它是由属于 A 但不属于 B 的样本点构成的集 合,如图1-5所示。差事件 A B 也可写作 AB 。
定义1 在相同的条件下重复进行了 n 次试验,如果事件 A 在这 n 次试验中出现
了 nA
次,则称比值
nA n
为事件 A
发生的频率,记为fn ( 源自) ,即fn( A)
nA n
显然,频率 fn ( A) 的大小表示了在 n 次试验中事件 A 发生的频繁程度。频率 大,事件 A 发生就频繁,在一次试验中 A 发生的可能性就大,也就是事件 A 发
四、事件的关系与运算
在一个样本空间中显然可以定义不止一个事件。概率论的重要研究课 题之一是希望从简单事件的概率推算出复杂事件的概率。为此,需要研究 事件间的关系与运算。
事件是一个集合,因此事件间的关系和运算自然按照集合之间的关系 和运算来处理。
1 事件的包含与相等
若 A B ,则称事件 B 包含事件 A ,这里指的是事件 A 发生必然导致事件 B 发生, 即属于 A 的样本点都属于 B ,如图1-2所示。显然,对任何事件A,必有 A 。
若 A B 且 B A ,则称事件 A 与 B 相等,记为 A B。
图1-2 A B
事件 A B {x | x A或x B},称为事件A与事件B的和事件,即当且仅当事件 A 或 事件 B 至少有一个发生时,和事件 A B 发生。它由属于 A 或 B 的所有公共样本点构 成,如图 1-4 所示。
图 1-4 A B
4 事件的差
事件 A B {x | x A且x B}称为事件 A 与事件 B 的差事件,即当且仅当事件 A 发 生但事件 B 不发生时,积事件A B发生。它是由属于 A 但不属于 B 的样本点构成的集 合,如图1-5所示。差事件 A B 也可写作 AB 。
定义1 在相同的条件下重复进行了 n 次试验,如果事件 A 在这 n 次试验中出现
了 nA
次,则称比值
nA n
为事件 A
发生的频率,记为fn ( 源自) ,即fn( A)
nA n
显然,频率 fn ( A) 的大小表示了在 n 次试验中事件 A 发生的频繁程度。频率 大,事件 A 发生就频繁,在一次试验中 A 发生的可能性就大,也就是事件 A 发
概率论与数理统计(最新完整版)ppt课件
(1) 试验可以在相同的条件下重复地进行;
.
(2) 试验的所有可能结果:
正面,反面; (3) 进行一次试验之前不能
确定哪一个结果会出现.
故为随机试验.
同理可知下列试验都为随机试验
1.“抛掷一枚骰子,观察出现的点数”.
2.“从一批产品中,依次任选三件, 记 录出现正品与次品的件数”.
.
3. 记录某公共汽车站 某日上午某时刻的等 车人 数.
(3)分 配 律
A(BC)(A B)(AC)AB AC ,
A (BC)AB AC
( A B ) C ( A C ) ( B C ) ( A C ) B C ( )
(对 4律 ):偶 A B A B ,A B A B .
n
n
Ai Ai,
i1
i1
.
n
n
Ai Ai
i1
i1
三 完备事件组
4. 考察某地区 10 月 份的平均气温.
5. 从一批灯泡中任取 一只,测试其寿命.
.
四、概率的统计定义
1、随机事件:在试验的结果中,可能发生、也可能不发 生的事件。比如,抛硬币试验中,”徽花向上”是随机事 件;掷一枚骰子中,”出现奇数点”是一个随机事件等。
2、频率:设A为实验E中的一个随机事件,将E重复n次, A发生m次,称f(A)=m/n为事件A的频率. 随着实验次数n的增加,频率将处于稳定状态.比如投 硬币实验,频率将稳定在1/2附近.
B A
.
6. 事件的互逆(对立)
若事件 A 、B 满足 A B 且 A B .
则称 A 与B 为互逆(或对立)事件. A 的逆记作 A .
实例 “骰子出现1点”对立 “骰子不出现1点”
.
(2) 试验的所有可能结果:
正面,反面; (3) 进行一次试验之前不能
确定哪一个结果会出现.
故为随机试验.
同理可知下列试验都为随机试验
1.“抛掷一枚骰子,观察出现的点数”.
2.“从一批产品中,依次任选三件, 记 录出现正品与次品的件数”.
.
3. 记录某公共汽车站 某日上午某时刻的等 车人 数.
(3)分 配 律
A(BC)(A B)(AC)AB AC ,
A (BC)AB AC
( A B ) C ( A C ) ( B C ) ( A C ) B C ( )
(对 4律 ):偶 A B A B ,A B A B .
n
n
Ai Ai,
i1
i1
.
n
n
Ai Ai
i1
i1
三 完备事件组
4. 考察某地区 10 月 份的平均气温.
5. 从一批灯泡中任取 一只,测试其寿命.
.
四、概率的统计定义
1、随机事件:在试验的结果中,可能发生、也可能不发 生的事件。比如,抛硬币试验中,”徽花向上”是随机事 件;掷一枚骰子中,”出现奇数点”是一个随机事件等。
2、频率:设A为实验E中的一个随机事件,将E重复n次, A发生m次,称f(A)=m/n为事件A的频率. 随着实验次数n的增加,频率将处于稳定状态.比如投 硬币实验,频率将稳定在1/2附近.
B A
.
6. 事件的互逆(对立)
若事件 A 、B 满足 A B 且 A B .
则称 A 与B 为互逆(或对立)事件. A 的逆记作 A .
实例 “骰子出现1点”对立 “骰子不出现1点”
概率论与数理统计 课件
05
多元统计分析
多元正态分布
01
多元正态分布的定义
多元正态分布是多个连续随机变量的 联合分布,其概率密度函数是多元高 斯函数。
02
多元正态分布的性质
多元正态分布具有旋转对称性、椭球 等高性、最大似然估计等性质。
03
多元正态分布的应用
在多元统计分析中,多元正态分布被 广泛用于描述多维数据的分布特征, 例如在回归分析、主成分分析、因子 分析等中都有应用。
正态分布与指数分布
正态分布
一种常见的连续概率分布,其概率密 度函数呈钟形曲线,对称轴为均值, 形状由标准差决定。
指数分布
描述随机事件在单位时间内发生的次 数,其概率密度函数为指数函数。
均匀分布与对数正态分布
均匀分布
在一定区间内随机变量取值的可能性相等,其概率密度函数 为常数。
对数正态分布
描述随机变量取值的对数服从正态分布的情况,其概率密度 函数在对数尺度上呈正态分布。
因子分析
因子分析的定义
因子分析是一种探索性 统计分析方法,通过寻 找隐藏在数据中的公共 因子来解释变量之间的 相关性。
因子分析的步骤
包括确定因子个数、因 子旋转、因子得分计算 等步骤。
因子分析的应用
在多元统计分析中,因 子分析被广泛应用于市 场细分、顾客满意度分 析、社会问题研究等方 面。
06
随机过程与时间序列分析
描述随机变量取离散值的概率规 律。
02
离散概率分布的特 点
随机变量取值有限或可数,概率 质量函数定义了每个可能取值的 概率。
03
离散概率分布的表 示方法
列表法、图示法、概率质量函数 。
二项分布与泊松分布
1 2
