正弦函数余弦函数的图象
正弦,余弦,正切函数的图像 与性质

性
典例一:1.函数y=sin(π+x),x∈的单调增区间是____________. 2. 求下列函数的单调增区间.
(1)y=1-sin ; (2)y=log(cos 2x).
典例二:1.函数y=的定义域是____________. 2.函数y=的定义域是________________. 3. 求函数f(x)=lg sin x+的定义域. 典例三:1.函数y=3tan的对称中心的坐标是 ________________________________ 2.函数y=sin的最小正周期是,则ω=______. 典例四:1.怎样由函数y=sin x的图象变换得到y=sin的图象,试叙述这 一过程.
课后作业 1.某同学给出了以下论断: ①将y=cos x的图象向右平移个单位,得到y=sin x的图象; ②将y=sin x的图象向右平移2个单位,可得到y=sin(x+2)的图象; ③将y=sin(-x)的图象向左平移2个单位,得到y=sin(-x-2)的图象; ④函数y=sin的图象是由y=sin 2x的图象向左平移个单位而得到的. 其中正确的结论是______(将所有正确结论的序号都填上).
4.下列函数中,不是周期函数的是( ) A.y=|cos x| B.y=cos|x| C.y=|sin x| D.y=sin|x|
5.定义在R上的函数f(x)既是奇函数又是周期函数,若f(x)的最小正周期 为π,且当x∈时,f(x)=sin x,则f的值为( ) A.- B. C.- D.
6.为了得到函数y=sin的图象,只需把函数y=sin的图象( ) A.向左平移个长度单位 B.向右平移个长度单位 C.向左平移个长度单位 D.向右平移个长度单位
2.函数y=tan(sin x)的值域为( ). A. B. C.[-tan 1,tan 1] D.以上均不对
正弦余弦正切函数图象

1-
643 34 6
y 3 1 3 3 1 3 0
3
3
o
1 -
2
-
3
2
x
2
(2) 描点
2-
(3) 连线
正切函数图像: ytanx,
y
xxR,且 xk2,kZ
思考:
2
正切函数 ytanx
1
图像是否有渐近线?
3 2
2
o
1 2
3 2
x
渐近线方程:
2
xk,(kZ)
2
二、三角函数图象的性质
上平移一个
单位得到的
.●
2
x
y=sinx
(2)按五个关键点列表
x
0
2
3 2
2
cosx 1 0 -1 0 1
-cosx
.y
1
o
-1 ●
-1 0 1 0 -y1= -cosx和
y=cosx 关
. y= cosx x [0,2 ] 于X轴对称 ●
.●
2
.
.3●
2
2
●
x
y= - cosx x [0, 2]
y=cosx
左移
2
y=cosx y=sinx
余弦曲线
返回目录
二、正弦函数的“五点画图法”
(0,0)、( , 1)、( ,0)、( 3 ,-1)、 (2 ,0)
2
2
y
1
●
●
0Hale Waihona Puke 2-1●3
2
●
●
2
x
y
●
1
●
0
2
-1
4.8正弦、余弦函数的图象

2 ,1)
(
( 2 ,1)
(
2
,1)
( 2 ,1)
( 2 ,1)
( (
2
2
,1) ,1)
,0) 3
(
2
( ,0) 2
(
((((((,,0,00),)0,),(003)2))(32,(-312,(1)32,)1((3,)3(21(23(323)2,2,1-,1,-),-1-)11)))
2 ,0) x
-
o
6
3
2
2 3
5 6
7 6
4 3
3 2
5 3
11 6
2
x
-
-
-1 -
l
24-3-99
正弦、余弦函数的图象
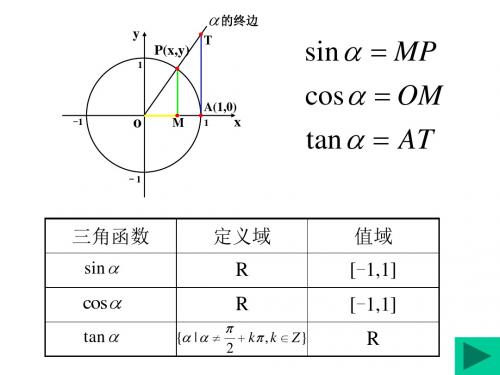
三角函数
三角函数线
正弦函数 sin=MP 正弦线 MP
余弦函数 cos=OM 余弦线 OM
正切函数 tan=AT 正切线 AT
y PT
注意:三角
-1
O
M A(1,0) x
函数线是有
向线段!
正弦、余弦函数的图象
-
-
-
-
o1
M-1 1A
o
6
3
2
2 3
5 6
7 6
4 3
3 2
5 3
11 6
2
x
-1 -
y
Q1
1-
Q2
-
o1 M2 M1-1
-
o
6
3
2
2 3
5 6
7 6
4 3
3 2
5 3
11 6
2
x
-
-
-1 -
正余弦函数图像

1.4.1
正弦函数.余弦函数的图象 y = sin x, x∈R y 1 x o -1
2 3 4
-2
-
注:1、正弦函数余弦函数的图像是一致的,只是位 置不同,故可以通过平移得到。 2、在x轴上方,图像都是上凸,在x轴下方,图像都 是下凸。
1.4.1
正弦函数.余弦函数的图象
四、当堂检测
y y=2+sin 3 2 1 2. π π . . . . 0 x
2
3 2
x x∈[0,2π]
-1
y=sin x -1 x∈[0,2π]
y=sin 3x x∈[0,2π]
1.4.1
正弦函数.余弦函数的图象
三、小结 1、五点作图法
π 2
1
x
0
π
0
3π 2
-1
2π
0
sinx
x
0
0 1
π 2
0
π
y
1
4 3
2
3 2
2
2
3
4
7 2
5 2
0
-1
2
3 2
5 2
7 2
x
y=sin x, x∈R
思考与交流:图中,起着关键作用的点
是那些?找到它们有什么作用呢? 3 0,0 ,1 ,0 , 1 2
2
2 ,0
五点:最高点、最低点、与 x 轴的交点
找到这五个关键点,就可以画出正弦曲线了!
如下表 x y=sin x 0 0 y
2
1
0
3 2
2
0
高一数学正弦函数余弦函数的图象
-
,1)
y
y cos x
-
x [0, 2 ]
1--1ຫໍສະໝຸດ o-1 - 6
3
2
2 3
5 6
7 6
4 3
3 2
5 3
11 6
2
x
在函数 y cos x, x [0, 2 ] 的图象上,起关键作用的点有: 最高点: (0,1) (2 ,1) 最低点:
( , 1)
-1
x
y cos x sin( x) 2
余弦函数的图像可以通过正弦曲线向左平移 各单位长度而得到. 2
正弦曲线:y sin x
xR
y
1
-1
x
y cos x 余弦曲线:
xR
y
1
-1
x
y
1-
y sin x
x [0, 2 ]
3 6
11 6
y
1
● ●
y sin x ( x [0, 2 ])
●
● ● ●
7 6 4 3 5 3
7 4 3 5 11 6 6 3 2 3
2
●
2
0
6
3
2
2 3
5 6
●
●
正弦函数与余弦函数的图像

52 3 2 2 2
o
-1
2
3 2 5 3 2 2
4
x
主页
§1. 4. 1 正弦函数余弦函数的图象
五点法作图(正弦函数)
(1) 列表
x
sinx
(2) 描点
0 0
(3) 连线
2
0
3 2
2
1
-1
0
y
1
o
-1
2
3 2
2
x
主页
§1. 4. 1 正弦函数余弦函数的图象
思考:
(1)通过今天得到的函数图像,你能 说出正弦 函数,余弦函数具备哪些性质? (2)你能画出函数 y 2sin(2 x ) 3
课堂作业:
课本:P.34 练习2
预习:课本:P.34-38
主页
3 4
y
6
2
1
● ●
● ● ● ●
4 3
O
3
2
6
2 3
5 6
●
7 4 6 3
● ●
3 2
5 11 2 3 6
●
●
● ●
x
7 4
-1
y=sinx (x∈[0, 2π] )
主页
§1. 4. 1 正弦函数余弦函数的图象
探索二:如何画函数y =sinx(x∈R)的图象?
0
2
1
0
-1
3 2
2
0
1
o
-1
3 2
2
x
主页
§1. 4. 1 正弦函数余弦函数的图象
正弦(余弦)函数一般解析式的图像及性质
正弦函数一般解析式:f(x)= Asin(ωx+φ)+h, |A|≠0, |ω|≠0 定义域:实数集R值域公式:[-|A|+h ,|A|+h]周期公式:2π/|ω|奇偶性:奇函数对称轴公式:直线x=(π/2−φ+kπ)/ω,k∈Z对称中心公式:((-φ+ kπ)/ω,h),k∈Z单调性公式:当A>0,ω>0时,或者A<0,ω<0时[(-π/2−φ+2kπ)/ω,(π/2−φ+2kπ)/ω],k∈Z 上单调递增[(π/2−φ+2kπ)/ω,(3π/2−φ+2kπ)/ω],k∈Z 上单调递减当A>0,ω<0时,或者A<0,ω>0时[(-π/2−φ+2kπ)/ω,(π/2−φ+2kπ)/ω],k∈Z 上单调递增[(π/2−φ+2kπ)/ω,(3π/2−φ+2kπ)/ω],k∈Z 上单调递减最值公式:当A>0,ω>0时,或者A<0,ω<0时最大值:当x=(π/2−φ+2kπ)/ω,k∈Z时,f(x)= A+h最小值:当x=(3π/2−φ+2kπ)/ω,k∈Z时,f(x)= -A+h 当A>0,ω<0时,或者A<0,ω>0时最小值:当x=(π/2−φ+2kπ)/ω,k∈Z时,f(x)= A+h最大值:当x=(3π/2−φ+2kπ)/ω,k∈Z时,f(x)= -A+h从原A图像f(x)= A1sin(ω1x+φ1)+h1如何移动变成B图像f(x)= A2sin(ω2x+φ2)+h2注意:求三角函数图像移动问题,三角函数一定要化简成正弦(余弦)一般解析式,一定要转化成A>0,ω>0当A>0,ω>0时,或者A<0,ω<0时①分别找到A图像与B图像的对称中心A图像的对称中心:A((-φ1+ kπ)/|ω1|,h1)B图像的对称中心:B((-φ2+ kπ)/|ω2|,h2)②计算移动的值:B图像的对称中心- A图像的对称中心(x B-x A,y B-y A)=((-φ2+ kπ)/|ω2|-(-φ1+ kπ)/|ω1|,h2-h1)当A>0,ω<0时,或者A<0,ω>0时A图像的对称中心:A((-φ1+π)/ω1,h1)B图像的对称中心:B((-φ2+π)/ω2,h2)①计算移动的值:B图像的对称中心- A图像的对称中心(x B-x A,y B-y A)=((-φ2+ π)/|ω2|-(-φ1+π)/ω1,h2-h1)表述原则:左正右负,正上负下若x B-x A>0,则A图像向左移动了(x B-x A)单位若x B-x A<0,则A图像向右移动了(x B-x A)单位若y B-y A>0,则A图像向上移动了(y B-y A)单位若y B-y A<0, 则A图像向下移动了(y B-y A)单位特别注意:三角函数转化,需要把()中的正负符号整体提取,不能单独提取x 前的符号f(x)= sin(-2x+ππ/44)≠ssss ss(2222+ππ/44+ππ)f(x)= sin(-2x-ππ/44)=−ssss ss(2222+ππ/44)=ssss ss(2222+ππ/44+ππ)余弦函数一般解析式:f(x)= Acos(ωx+φ)+h,|A|≠0, |ω|≠0 定义域:实数集R值域公式:[-|A|+h , |A|+h]周期公式:2π/|ω|奇偶性:偶函数对称轴公式:直线x=(−φ+kπ)/|ω|,k∈Z对称中心公式:((π/2-φ+ kπ)/|ω|,h),k∈Z单调性公式:当A>0时,与ω的正负性无关[(π−φ+2kπ)/ω,(2π−φ+2kπ)/ω],k∈Z 上单调递增[(−φ+2kπ)/ω,(π−φ+2kπ)/ω],k∈Z上单调递减当A<0时,与ω的正负性无关[(π−φ+2kπ)/ω,(2π−φ+2kπ)/ω],k∈Z上单调递减[(−φ+2kπ)/ω,(π−φ+2kπ)/ω],k∈Z 上单调递增最值公式:当A>0时最大值:当x=(−φ+2kπ)/ω,k∈Z时,f(x)= A+h最小值:当x=(π−φ+2kπ)/ω,k∈Z时,f(x)= -A+h当A<0时最小值:当x=(−φ+2kπ)/ω,k∈Z时,f(x)= A+h最大值:当x=(π−φ+2kπ)/ω,k∈Z时,f(x)= -A+h从原A图像f(x)= A1cos(ω1x+φ1)+h1如何移动变成B图像f(x)= A2cos(ω2x+φ2)+h2注意:求三角函数图像移动问题,三角函数一定要化简成正弦(余弦)一般解析式。
正弦、余弦函数图像
正弦函数、余弦函数的图像(一)给定任意一个角,其正弦值、余弦值均存在,且满足唯一性,即角与正弦、余弦值之间可以建立一一对应关系,符合函数的要求。
形如(ω≠0)的函数称为正弦函数;形如的函数称为余弦函数;其中、是正弦函数与余弦函的基本形式:所有的正弦函数、余弦函数,通过“换元”思想,都可以转化为与y=cosx 的形式,故二者是研究正弦函数与余弦函数的基石。
(二)在诱导公式的帮助下,我们可以将任意一个角的三角函数值转化为求某一个锐角的三角函数,再以有序实数对(角,三角函数)的形式在坐标系内描点,从而得到三角函数的图象;除了基础的描点法,我们也可以利用三角函数线,得到函数的图象。
做法:①等分单位圆:以单位圆与x轴交点A为起点,将圆等分为12份;②作正弦线:过单位圆的各分点作x 轴的垂线,得等角的正弦线;③平移画图:在x轴上等分0到为12份,将正弦线平移到相应的角上,连接正弦线的终点,从而得到0到的正弦函数图象。
(三)到,是任意角的冰山一角;0到一段上的函数图象,也仅仅是三角函数图象的一部分.另一方面,当角的终边旋转一周后继续旋转,角的大小在逐渐变化的同时,角的正弦线“玩接力”样依次重复出现,可以预见,到,到,到,…,是到一段上函数图象的“复制”与“粘贴”,每一段的首尾相接,便是函数图象的“真身”。
(四)正弦函数、余弦函数的图象告诉我们:①从自变量x的角度看,函数图象可沿着x 轴正、负方向无限延伸,即x轴上任何一个数值都对应函数图象上一个点,故正弦函数、余弦函数的定义域为全体实数R;②从因变量y的角度看,正弦函数、余弦函数的图象是在由与两条互相平行的直线围成的条形带中,故正弦函数、余弦函数的值域为,好比正弦函数、余弦函数为一个“加工厂”,投入的角多大多小,产成品----“函数值”只能在;③正弦函数、余弦函数的图象可以看作某一部分(如图中的阴影部分)的重复拼接,故画函数图象时,可以以此为单元。
(五)基于正弦函数、余弦函数图象的特征,有了重复单元,就有了整个正弦函数、余弦函数的图象;在画函数图象时,重复单元的绘制显得尤为重要。
正弦函数和余弦函数的图像
思考:如何画函数y =sinx(x∈R)的图象?
y=sinx x∈[0,2π] sin(x+2kπ)=sinx, k∈Z y
1 −π −1
y=sinx x∈ R
−4π
−3π
−2π
o
π
2π
3π
4π
x
正弦函数y=sinx, x∈R的图象叫正弦曲线.
主页
§1. 4. 1 正弦函数余弦函数的图象
2.用描点法作图(在精确度要求不太高时)?
例3.作函数 y=1-cosx, x∈[0, 2π]的简图. x 1-cosx y
0
π
2
π
3π 2
2π
0
1
2
1
0
o
主页
x
§1. 4. 1 正弦函数余弦函数的图象
例4.作函数y=|sinx|,x∈R的简图 y o x
主页
§1. 4. 1 正弦函数余弦函数的图象
1.方程 sin x = lg x的解有几个 ?
正弦函数、余弦函数的图象
一、正弦函数 y =sinx(x∈R)的图象
§1. 4. 1 正弦函数余弦函数的图象
1.几何法作图:
问题:如何作出正弦函数的图象? 途径:利用单位圆中正弦线来解决. y
1
. . .o . .A.
1
o
π /2
. π
3π/2
2π
x
-1
函数y=sinx,x∈[0,2π]的图象
主页
1
O -1
π 2
1 y = 2
π
3π 2
2π
x
5p p [0 , ] U[ , 2p ] 3 3
主页
§1. 4. 1 正弦函数余弦函数的图象
第四讲 正弦、余弦、正切函数的图象与性质(解析版)
第四讲 正弦、余弦和正切函数的图像与性质知识提要1. 用五点法作正弦函数和余弦函数的简图正弦函数y =sin x ,x ∈[0,2π]的图象中,五个关键点是:(0,0),(π2,1),(π,0),(3π2,-1),(2π,0).余弦函数y =cos x ,x ∈[0,2π]的图象中,五个关键点是:(0,1),(π2,0),(π,-1),(3π2,0),(2π,1).2. 正弦函数、余弦函数、正切函数的图象和性质函数 y =sin x y =cos x y =tan x图象定义域 R R {x |x ∈R 且x ≠π2+k π,k ∈Z }值域[-1,1][-1,1]R单调性[-π2+2k π,π2+2k π](k ∈Z )上递增; [π2+2k π,3π2+2k π](k ∈Z )上递减 [-π+2k π,2k π](k ∈Z )上递增;[2k π,π+2k π](k ∈Z )上递减(-π2+k π,π2+k π) (k ∈Z )上递增最值x =π2+2k π(k ∈Z )时,y max =1;x =-π2+2k π(k ∈Z )时,y min =-1x =2k π(k ∈Z )时,y max =1;x =π+2k π(k ∈Z )时,y min =-1奇偶性 奇函数 偶函数 奇函数 对称中心 (k π,0)(k ∈Z ) (π2+k π,0) (k ∈Z ) (k π2,0)(k ∈Z ) 对称轴方程x =π2+k π(k ∈Z ) x =k π(k ∈Z )周期2π2ππ※ 学习评价1、判断下面结论是否正确(请在括号中打“√”或“×”)(1)常数函数f (x )=a 是周期函数,它没有最小正周期. ( √ ) (2)y =cos x 在第一、二象限上是减函数. ( × ) (3)y =tan x 在整个定义域上是增函数.( × )(4)y =k sin x +1(x ∈R ),则y max =k +1. ( × )2、函数f (x )=sin ⎝⎛⎭⎫x -π4的图象的一条对称轴是( )A .x =π4B .x =π2C .x =-π4D .x =-π2解析:方法一 ∵正弦函数图象的对称轴过图象的最高点或最低点,故令x -π4=k π+π2,k ∈Z ,∴x =k π+3π4,k ∈Z . 取k =-1,则x =-π4.方法二 用验证法.x =π4时,y =sin ⎝⎛⎭⎫π4-π4=0,不合题意,排除A ; x =π2时,y =sin ⎝⎛⎭⎫π2-π4=22,不合题意,排除B ; x =-π4时,y =sin ⎝⎛⎭⎫-π4-π4=-1,符合题意,C 项正确; x =-π2时,y =sin ⎝⎛⎭⎫-π2-π4=-22,不合题意,故D 项也不正确. 3、若函数f (x )=sin ωx (ω>0)在区间⎣⎡⎦⎤0,π3上单调递增,在区间⎣⎡⎦⎤π3,π2上单调递减,则ω等于( )A .23B .32C .2D .3解析:∵f (x )=sin ωx (ω>0)过原点,∴当0≤ωx ≤π2,即0≤x ≤π2ω时,y =sin ωx 是增函数;当π2≤ωx ≤3π2,即π2ω≤x ≤3π2ω时,y =sin ωx 是减函数. 由f (x )=sin ωx (ω>0)在⎣⎡⎦⎤0,π3上单调递增, 在⎣⎡⎦⎤π3,π2上单调递减知,π2ω=π3,∴ω=32.例1 求函数y =1+sin ⎝⎛⎭⎫-12x +π4,x ∈[-4π,4π]的单调减区间. 解析:y =1+sin ⎝⎛⎭⎫-12x +π4=-sin ⎝⎛⎭⎫12x -π4+1. 由2k π-π2≤12x -π4≤2k π+π2(k ∈Z ).解得4k π-π2≤x ≤4k π+32π(k ∈Z).令k =0时,-π2 ≤x ≤32π; 令k =1时,72π≤x ≤4π+32π. 令k =-1时,-4π-π2≤x ≤-52π;∵-4π≤x ≤4π,∴函数y =1+sin ⎝⎛⎭⎫-12x +π4的单调减区间为 [-4π,-52π],[-π2,32π],[72π,4π].变式:(1)已知ω>0,函数f (x )=sin(ωx +π4)在(π2,π)上单调递减,则ω的取值范围是( )A .[12,54]B .[12,34]C .(0,12]D .(0,2](2)已知函数f (x )=2cos(ωx +φ)+b 对任意实数x 有f (x +π4)=f (-x )成立,且f (π8)=1,则实数b 的值为( )A .-1B .3C .-1或3D .-3解析:(1)由π2<x <π得π2ω+π4<ωx +π4<πω+π4,由题意知(π2ω+π4,πω+π4)⊆[π2,3π2],∴⎩⎨⎧π2ω+π4≥π2,πω+π4≤3π2,∴12≤ω≤54,故选A.解析:由f (x +π4)=f (-x )可知函数f (x )=2cos(ωx +φ)+b 关于直线x =π8对称,又函数f (x )在对称轴处取得最值,故±2+b =1,∴b =-1或b =3. 故选C. 例2 求函数f (x )=lg sin x +16-x 2的定义域.解析:由题意,x 满足不等式组⎩⎪⎨⎪⎧ sin x >016-x 2≥0,即⎩⎪⎨⎪⎧-4≤x ≤4sin x >0,作出y =sin x 的图象,如图所示.结合图象可得:x ∈[-4,-π)∪(0,π). 例3 求下列函数的周期.(1)y =sin ⎝⎛⎭⎫2x +π3 (x ∈R); (2)y =cos(1-πx )(x ∈R); (3)y =|sin x | (x ∈R). 解析:(1)方法一 令z =2x +π3,∵x ∈R ,∴z ∈R ,函数f (z )=sin z 的最小正周期是2π,就是说变量z 只要且至少要增加到z +2π,函数f (z )=sin z (z ∈R)的值才能重复取得, 而z +2π=2x +π3+2π=2(x +π)+π3,所以自变量x 只要且至少要增加到x +π,函数值才能重复取得,从而函数y =sin ⎝⎛⎭⎫2x +π3 (x ∈R)的周期是π..方法二 y =sin ⎝⎛⎭⎫2x +π3(x ∈R)的周期为2π2=π. (2)设f (x )=cos(1-πx ),则f (x )=cos(πx -1).∵cos[(πx -1)+2π]=cos[(πx +2π)-1]=cos[π(x +2)-1]=co s(πx -1). ∴f (x +2)=f (x ),从而函数y =cos(1-πx )(x ∈R)的周期是2. (3)作出y =|sin x |(x ∈R)的图象.由图象可知,y =|sin x |(x ∈R)的周期为π.例4 (1) 求函数y =cos ⎝⎛⎭⎫x +π6,x ∈⎣⎡⎦⎤0,π2的值域. (2) 求函数y =sin 2x -sin x +1,x ∈R 的值域.解 (1)∵0≤x ≤π2,∴π6≤x +π6≤23π. ∴cos 23π≤cos ⎝⎛⎭⎫x +π6≤cos π6,∴-12≤y ≤32(2)设t =sin x ,t ∈[-1,1],f (t )=t 2-t +1. ∵f (t )=t 2-t +1=⎝⎛⎭⎫t -122+34. ∵-1≤t ≤1, ∴当t =-1,即sin x =-1时,y max =f (t )max =3; 当t =12,即sin x =12时,y min =f (t )min =34.∴函数y =sin 2x -sin x +1,x ∈R 的值域为⎣⎡⎦⎤34,3.巩固提高※夯实基础1.下列函数中,周期为π,且在⎣⎡⎦⎤π4,π2上为减函数的是( A )A .y =sin(2x +π2)B .y =cos(2x +π2)C .y =sin(x +π2)D .y =cos(x +π2)2、函数y =2sin(2x +π3)(-π6≤x ≤π6)的值域是________.[0,2]3、求函数y =tan ⎝⎛⎭⎫π3x +π4的定义域、周期、单调区间和对称中心. 解析:①由π3x +π4≠k π+π2,k ∈Z ,得x ≠3k +34,k ∈Z .∴ 函数的定义域为{x |x ∈R ,且x ≠3k +34,k ∈Z }.②T =ππ3=3,∴函数的周期为3.③由k π-π2<π3x +π4<k π+π2,k ∈Z . 解得3k -94<x <3k +34,k ∈Z .∴函数的单调增区间为⎝⎛⎭⎫3k -94,3k +34,k ∈Z . ④由π3x +π4=k π2,k ∈Z . 解得x =3k 2-34,k ∈Z .∴函数的对称中心是⎝⎛⎭⎫3k 2-34,0,k ∈Z . 4. 设|x |≤π4,求函数f (x )=cos 2x +sin x 的最小值.解析:f (x )=cos 2x +sin x =1-sin 2x +sin x =-⎝⎛⎭⎫sin x -122+54. ∵|x |≤π4,∴-22≤sin x ≤22. ∴当sin x =-22时,f (x )min =1-22.5. 已知a >0,函数f (x )=-2a sin ⎝⎛⎭⎫2x +π6+2a +b ,当x ∈⎣⎡⎦⎤0,π2时,-5≤f (x )≤1. (1)求常数a ,b 的值;(2)设g (x )=f ⎝⎛⎭⎫x +π2且lg g (x )>0,求g (x )的单调区间. 解 (1)∵x ∈⎣⎡⎦⎤0,π2,∴2x +π6∈⎣⎡⎦⎤π6,7π6. ∴sin ⎝⎛⎭⎫2x +π6∈⎣⎡⎦⎤-12,1, ∴-2a sin ⎝⎛⎭⎫2x +π6∈[-2a ,a ]. ∴f (x )∈[b,3a +b ], 又∵-5≤f (x )≤1, ∴b =-5,3a +b =1,因此a =2,b =-5. (2)由(1)得,f (x )=-4sin ⎝⎛⎭⎫2x +π6-1, g (x )=f ⎝⎛⎭⎫x +π2=-4sin ⎝⎛⎭⎫2x +7π6-1 =4sin ⎝⎛⎭⎫2x +π6-1, 又由lg g (x )>0,得g (x )>1,∴4sin ⎝⎛⎭⎫2x +π6-1>1,∴sin ⎝⎛⎭⎫2x +π6>12, ∴2k π+π6<2x +π6<2k π+5π6,k ∈Z , 其中当2k π+π6<2x +π6≤2k π+π2,k ∈Z 时,g (x )单调递增,即k π<x ≤k π+π6,k ∈Z ,∴g (x )的单调增区间为⎝⎛⎦⎤k π,k π+π6,k ∈Z . 又∵当2k π+π2<2x +π6<2k π+5π6,k ∈Z 时,g (x )单调递减,即k π+π6<x <k π+π3,k ∈Z . ∴g (x )的单调减区间为⎝⎛⎭⎫k π+π6,k π+π3,k ∈Z .※能力提高6、将函数f (x )=sin ωx (其中ω>0)的图象向右平移π4个单位长度,所得图象经过点⎝⎛⎭⎫3π4,0,则ω的最小值是 ( )A.13B .1C.53D .2解析:根据题意平移后函数的解析式为y =sin ω⎝⎛⎭⎫x -π4, 将⎝⎛⎭⎫3π4,0代入得sin ωπ2=0,则ω=2k ,k ∈Z ,且ω>0,故ω的最小值为2. 7、函数y =|sin x +cos x |-1的定义域是( )A .[k π,k π+π2](k ∈Z )B .[2k π,2k π+π2](k ∈Z )C .[-π2+k π,k π](k ∈Z )D .[-π2+2k π,2k π](k ∈Z )解析:|sin x +cos x |-1≥0⇒(sin x +cos x )2≥1 ⇒sin 2x ≥0,∴2k π≤2x ≤2k π+π,k ∈Z ,故原函数的定义域是[k π,k π+π2](k ∈Z ).8、已知函数)2sin()(ϕ+=x x f ,其中ϕ为实数,若|)6(|)(πf x f ≤对R x ∈恒成立,且)()2(ππf f >,则)(x f 的单调递增区间是 ( ) (A) )(6,3Z k k k ∈⎥⎦⎤⎢⎣⎡+-ππππ (B) )(2,Z k k k ∈⎥⎦⎤⎢⎣⎡+πππ(C) )(32,6Z k k k ∈⎥⎦⎤⎢⎣⎡++ππππ (D) )(,2Z k k k ∈⎥⎦⎤⎢⎣⎡-πππ 解析:∵|)6(|)(πf x f ≤, ∴)6(πf 为)(x f 的最小值或最大值,∴ 1)62sin()6(±=+⨯=ϕππf , ∴ Z k k ∈+=+,23ππϕπ,∴ Z k k ∈+=,6ππϕ.当6πϕ=时,2167sin )622sin()2(-==+⨯=ππππf ,216sin )62sin()(==+=ππππf . 这与)()2(ππf f >矛盾,舍去。
